Gradient-Based Recursive Identification Methods for Input Nonlinear Equation Error Closed-Loop Systems

Abstract

The identification problem of closed-loop or feedback nonlinear systems is a hot topic. Based on the hierarchical identification principle, this paper presents a hierarchical stochastic gradient algorithm and a hierarchical multi-innovation stochastic gradient algorithm for feedback nonlinear systems. The simulation results show that the hierarchical multi-innovation stochastic gradient can more effectively estimate the parameters of the feedback nonlinear systems than the hierarchical stochastic gradient algorithm.

1 Introduction

The mathematical models are basic for controller design [40, 41]. System identification is the theory and methods of establishing the mathematical models of systems. In general, the identification algorithm is derived by defining and minimizing a cost function [27–29, 38, 39]. Linear system identification has been mature [5, 7], and nonlinear systems have received extensive attention [6, 20, 24]. Nonlinear phenomena and nonlinear systems are ubiquitous. Almost all systems in real world are nonlinear to a certain degree. Recently, a series of estimation algorithms have been reported for nonlinear systems [22, 23, 34]. There are various forms of nonlinear systems. Bai [1] studied Hammerstein–Wiener systems and proposed an optimal two-stage identification algorithm. Li et al. [14] proposed an observer-based adaptive sliding mode control method for nonlinear Markovian jump systems. Bai and Cai [2] designed the identification scheme for nonlinear parametric Wiener system under Gaussian inputs. Wang and Ding [25] presented the recursive parameter and state estimation algorithm for an input nonlinear state space system using the hierarchical identification principle. Wang and Ding [26] discussed the recursive parameter estimation algorithms and convergence for a class of nonlinear systems with colored noise. Wang and Tang [32] tackled the iterative identification problems for a class of nonlinear systems with colored noises. Recently, a new fault detection design scheme was proposed for interval type-2 Takagi–Sugeno fuzzy systems [13]. Ding et al. [8] proposed recursive least squares parameter estimation for a class of output nonlinear systems based on the model decomposition.

Closed-loop control has received much attention [31]. The closed-loop subspace identification algorithms have been applied to various fields [21]. Wei et al. [36] presented a method for sensor fault diagnosis (detection and isolation) applied to large-scale wind turbine systems. The wind turbine model was built for the wind dynamics based on the closed-loop identification technique. On-line order estimation and parameter identification algorithms were presented for linear stochastic feedback control systems [19].

The multi-innovation identification method is effective for identifying systems [35, 42, 43]. In comparison with the previous algorithms, Mao and Ding [17] introduced a multi-innovation stochastic gradient identification algorithm for Hammerstein controlled autoregressive autoregressive systems based on the filtering technique. The multi-innovation identification method can combine with other identification methods to solve complex problems, such as the least squares algorithm [12], the forgetting gradient algorithm [37].

On the basis of the work in [10], this paper presents a hierarchical stochastic gradient algorithm and a hierarchical multi-innovation stochastic gradient algorithm for closed-loop nonlinear systems. The basic idea is, by means of the hierarchical identification principle, to decompose a feedback nonlinear system into two subsystems and to derive a hierarchical stochastic gradient algorithm. This work differs from the hierarchical least squares algorithms in [22] and the multistage least squares-based iterative estimation for feedback nonlinear systems with moving average noises [10].

This paper is organized as follows. Section 2 derives the identification problem for feedback nonlinear systems. Section 3 describes a hierarchical stochastic gradient algorithm. Section 4 presents a hierarchical multi-innovation stochastic gradient algorithm. Two examples are given in Sect. 5 to illustrate the effectiveness of the proposed algorithms. Finally, concluding remarks are offered in Sect. 6.

2 Problem Description

Let us define some notation. “$X:=A$” or “$A=:X$” means “A is defined as X”; $\mathbf I$ represents an identity matrix of appropriate sizes; the superscript T denotes the matrix transpose.

Fig. 1

The feedback nonlinear closed-loop system

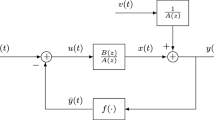
Consider the following feedback nonlinear stable system in Fig. 1,

$$\begin{aligned} y(t)= & {} -\sum _{i=1}^{n_a}a_iy(t-i)+\sum _{i=1}^{n_b}b_i\bar{u}(t-i)+v(t), \end{aligned}$$

(1)

$$\begin{aligned} u(t)= & {} r(t)-y(t),\end{aligned}$$

(2)

$$\begin{aligned} \bar{u}(t)= & {} g(u(t)), \end{aligned}$$

(3)

where $r(t)\in {\mathbb {R}}$ is the reference input of the system, $u(t)\in {\mathbb {R}}$ is the control input of the system, $\bar{u}(t)\in {\mathbb {R}}$ is the output of the nonlinear block, $y(t)\in {\mathbb {R}}$ is the system output, $v(t)\in {\mathbb {R}}$ is a stochastic white noise with zero mean and variance $\sigma ^2$ and A(z) and B(z) are the polynomials in the shift operator $z^{-1}$:

$$\begin{aligned} A(z):= & {} 1+a_1z^{-1}+a_2z^{-2}+\cdots +a_{n_a}z^{-n_a},\\ B(z):= & {} b_1z^{-1}+b_2z^{-2}+\cdots +b_{n_b}z^{-n_b}. \end{aligned}$$

Suppose that the nonlinear output $\bar{u}(t)$ is a linear combination of a known basis ${\varvec{g}}:=(g_1,g_2,\ldots , g_{n_\gamma })$ with unknown coefficients $(\gamma _1, \gamma _2, \ldots , \gamma _{n_\gamma })$ and can be expressed as

$$\begin{aligned} \bar{u}(t)=g(u(t))= & {} \gamma _1g_1(u(t))+\gamma _2g_2(u(t))+\cdots +\gamma _{n_\gamma }g_{n_\gamma }(u(t))\nonumber \\= & {} \gamma _1g_1(r(t)-y(t))+\gamma _2g_2(r(t)-y(t))+\cdots +\gamma _{n_\gamma }g_{n_\gamma }(r(t)-y(t))\nonumber \\= & {} {\varvec{g}}(r(t)-y(t)){\varvec{{\gamma }}}. \end{aligned}$$

(4)

Define the parameter vectors ${\varvec{a}}$ and ${\varvec{b}}$ of the linear subsystems and ${\varvec{{\gamma }}}$ of the nonlinear part:

$$\begin{aligned} {\varvec{a}}:= & {} [a_1, a_2, \ldots , a_{n_a}]^{\tiny \text{ T }}\in {\mathbb {R}}^{n_a},\\ {\varvec{b}}:= & {} [b_1, b_2, \ldots , b_{n_b}]^{\tiny \text{ T }}\in {\mathbb {R}}^{n_b},\\ {\varvec{{\gamma }}}:= & {} [\gamma _1, \gamma _2, \ldots , \gamma _{n_\gamma }]^{\tiny \text{ T }}\in {\mathbb {R}}^{n_\gamma },\\ {\varvec{{\vartheta }}}:= & {} \left[ \begin{array}{c} {\varvec{a}} \\ {\varvec{b}} \\ \varvec{\gamma } \end{array}\right] \in {\mathbb {R}}^{n_a+n_b+n_\gamma }, \end{aligned}$$

and the information vector and matrix

$$\begin{aligned} {\varvec{{\varphi }}}_y(t):= & {} [-y(t-1), -y(t-2), \ldots , -y(t-n_a)]^{\tiny \text{ T }}\in {\mathbb {R}}^{n_a},\\ {\varvec{G}}(t):= & {} [{\varvec{g}}(r(t-1)-y(t-1)), {\varvec{g}}(r(t-2)-y(t-2)),\ldots , {\varvec{g}}(r(t-n_b)-y(t-n_b))]^{\tiny \text{ T }}\\= & {} \left[ \begin{array}{cccc} g_1(r(t-1)-y(t-1)) &{} g_2(r(t-1)-y(t-1)) &{} \cdots &{} g_{n_\gamma }(r(t-1)-y(t-1))\\ g_1(r(t-2)-y(t-2)) &{} g_2(r(t-2)-y(t-2)) &{} \cdots &{} g_{n_\gamma }(r(t-2)-y(t-2))\\ \vdots &{} \vdots &{} &{} \vdots \\ g_1(r(t-n_b)-y(t-n_b)) &{} g_2(r(t-n_b)-y(t-n_b)) &{} \cdots &{} g_{n_\gamma }(r(t-n_b)-y(t-n_b)) \end{array}\right] \in {\mathbb {R}}^{n_b\times n_\gamma }. \end{aligned}$$

From (1)–(4), we have

$$\begin{aligned} y(t)= & {} -\sum _{i=1}^{n_a}a_iy(t-i)+\sum _{i=1}^{n_b}b_i\bar{u}(t-i)+v(t)\nonumber \\= & {} -a_1y(t-1)-a_2y(t-2)-\cdots -a_{n_a}(y-n_a)\nonumber \\&+\sum _{i=1}^{n_b}b_i[\gamma _1g_1(u(t-i))+\gamma _2g_2(u(t-i))+\cdots \nonumber \\&+\,\gamma _{n_\gamma }g_{n_\gamma }(u(t-i))]+v(t)\nonumber \\= & {} {\varvec{{\varphi }}}_y^{\tiny \text{ T }}(t){\varvec{a}}+{\varvec{b}}^{\tiny \text{ T }}{\varvec{G}}(t){\varvec{{\gamma }}}+v(t). \end{aligned}$$

(5)

The right-hand side of (5) contains the product of ${\varvec{b}}$ and ${\varvec{{\gamma }}}$. In order to get the unique parameter estimates, we use the standard constraint on ${\varvec{{\gamma }}}$. In general, assume that the system is stable and $\Vert {\varvec{{\gamma }}}\Vert =1$ and the first entry of ${\varvec{{\gamma }}}$ is positive, i.e., $\gamma _1>0$ where the norm of a matrix ${\varvec{X}}$ is defined as $\Vert {\varvec{X}}\Vert ^2:=\mathrm{tr}[{\varvec{X}}{\varvec{X}}^{\tiny \text{ T }}]$. The method proposed in the paper can be extended to identify the parameters of the system with known controller.

3 The Hierarchical Stochastic Gradient Algorithm

According to the hierarchical identification principle, Eq. (5) can be decomposed into two subsystems, and they contain the parameter vectors ${\varvec{{\gamma }}}$ and ${\varvec{{\theta }}}:=\left[ \begin{array}{c} {\varvec{a}} \\ {\varvec{b}} \end{array} \right]$, respectively.

Define the generalized information vectors ${\varvec{{\phi }}}({\varvec{{\gamma }}},t)$ and ${\varvec{{\psi }}}({\varvec{b}},t)$ and the fictitious output $y_1(t)$ as

$$\begin{aligned} {\varvec{{\phi }}}({\varvec{{\gamma }}},t):= & {} \left[ \begin{array}{c} {\varvec{{\varphi }}}_y(t) \\ {\varvec{G}}(t){\varvec{{\gamma }}} \end{array} \right] \in {\mathbb {R}}^{n_a+n_b},\nonumber \\ {\varvec{{\psi }}}({\varvec{b}},t):= & {} {\varvec{G}}^{\tiny \text{ T }}(t){\varvec{b}}\in {\mathbb {R}}^{n_\gamma },\nonumber \\ y_1(t):= & {} y(t)-{\varvec{{\varphi }}}^{\tiny \text{ T }}_y(t){\varvec{a}}. \end{aligned}$$

(6)

From (5) and (6), we can obtain two subsystems:

$$\begin{aligned} \mathrm{S}_1:&y_1(t) ={\varvec{{\psi }}}^{\tiny \text{ T }}({\varvec{b}},t){\varvec{{\gamma }}}+v(t),\end{aligned}$$

(7)

$$\begin{aligned} \mathrm{S}_2:&y(t)={\varvec{{\phi }}}^{\tiny \text{ T }}({\varvec{{\gamma }}},t){\varvec{{\theta }}}+v(t). \end{aligned}$$

(8)

Subsystem (7) contains $n_\gamma$ parameters, and Subsystem (8) contains $n_a+n_b$ parameters. The vectors ${\varvec{{\gamma }}}$ in ${\varvec{{\phi }}}({\varvec{{\gamma }}},t)$ and ${\varvec{b}}$ in ${\varvec{{\psi }}}({\varvec{b}},t)$ are the associate terms between two subsystems.

Define two criterion functions:

$$\begin{aligned} J_1({\varvec{{\gamma }}}):= & {} \frac{1}{2}\left[ y_1(t)-{\varvec{{\psi }}}^{\tiny \text{ T }}({\varvec{b}},t)\gamma \right] ^2,\\ J_2({\varvec{{\theta }}}):= & {} \frac{1}{2}\left[ y(t)-{\varvec{{\phi }}}^{\tiny \text{ T }}({\varvec{{\gamma }}},t){\varvec{{\theta }}}\right] ^2. \end{aligned}$$

Let $\hat{{\varvec{{\gamma }}}}(t)$ be the estimate of ${\varvec{{\gamma }}}$ at time t, and $\hat{{\varvec{{\theta }}}}(t):=\left[ \begin{array}{c} \hat{{\varvec{a}}}(t) \\ \hat{{\varvec{b}}}(t) \end{array} \right]$ be the estimate of ${\varvec{{\theta }}}=\left[ \begin{array}{c} {\varvec{a}} \\ {\varvec{b}} \end{array} \right]$ at time t. Replacing ${\varvec{{\gamma }}}$ with preceding estimate $\hat{{\varvec{{\gamma }}}}(t-1)$. The gradients of $J_1({\varvec{{\gamma }}})$ and $J_2({\varvec{{\theta }}})$ are given by

$$\begin{aligned} \mathrm{grad}[J_1(\hat{{\varvec{{\gamma }}}}(t-1))]= & {} \left. \frac{\partial J_1({\varvec{{\gamma }}})}{\partial {\varvec{{\gamma }}}}\right| _{{{\varvec{{\gamma }}}}=\hat{{\varvec{{\gamma }}}}(t-1)} =-{\varvec{{\psi }}}({\varvec{b}},t)[y_1(t)-{\varvec{{\psi }}}^{\tiny \text{ T }}({\varvec{b}},t)\hat{\gamma }(t-1)],\\ \mathrm{grad}[J_2(\hat{{\varvec{{\theta }}}}(t-1))]= & {} \left. \frac{\partial J_2({\varvec{{\theta }}})}{\partial {\varvec{{\theta }}}}\right| _{{{\varvec{{\theta }}}}=\hat{{\varvec{{\theta }}}}(t-1)} =-{\varvec{{\phi }}}({\varvec{{\gamma }}},t)[y(t)-{\varvec{{\phi }}}^{\tiny \text{ T }}({\varvec{{\gamma }}},t)\hat{{\varvec{{\theta }}}}(t-1)]. \end{aligned}$$

Using the gradient search and optimizing the criterion functions $J_1({\varvec{{\gamma }}})$ and $J_2({\varvec{{\theta }}})$, we can get the following recursive relations:

$$\begin{aligned} \hat{{\varvec{{\gamma }}}}(t)= & {} \hat{{\varvec{{\gamma }}}}(t-1)-\frac{1}{r_1(t)}\mathrm{grad}[J_1(\hat{{\varvec{{\gamma }}}}(t-1))]\\= & {} \hat{{\varvec{{\gamma }}}}(t-1)+\frac{{\varvec{{\psi }}}({\varvec{b}},t)}{r_1(t)}[y(t)-{\varvec{{\varphi }}}^{\tiny \text{ T }}_y(t){\varvec{a}}-{\varvec{{\psi }}}^{\tiny \text{ T }}({\varvec{b}},t)\hat{{\varvec{{\gamma }}}}(t-1)],\\ \hat{{\varvec{{\theta }}}}(t)= & {} \hat{{\varvec{{\theta }}}}(t-1)-\frac{1}{r_2(t)}\mathrm{grad}[J_2(\hat{{\varvec{{\theta }}}}(t-1))]\\= & {} \hat{{\varvec{{\theta }}}}(t-1)+\frac{{\varvec{{\phi }}}(\hat{{\varvec{{\gamma }}}}(t),t)}{r_2(t)}[y(t)-{\varvec{{\phi }}}^{\tiny \text{ T }}({\varvec{{\gamma }}},t)\hat{{\varvec{{\theta }}}}(t-1)]. \end{aligned}$$

Furthermore, taking

$$\begin{aligned} r_1(t)= & {} r_1(t-1)+\mathrm{tr}[{\varvec{{\psi }}}({\varvec{b}},t){\varvec{{\psi }}}^{\tiny \text{ T }}({\varvec{b}},t)]=r_1(t-1)+\Vert {\varvec{{\psi }}}({\varvec{b}},t)\Vert ^2,\\ r_2(t)= & {} r_2(t-1)+\mathrm{tr}[{\varvec{{\phi }}}({\varvec{{\gamma }}},t){\varvec{{\phi }}}^{\tiny \text{ T }}({\varvec{{\gamma }}},t)]=r_2(t-1)+\Vert {\varvec{{\phi }}}({\varvec{{\gamma }}},t)\Vert ^2, \end{aligned}$$

we can acquire the following stochastic gradient algorithm:

$$\begin{aligned} \hat{{\varvec{{\gamma }}}}(t)= & {} \hat{{\varvec{{\gamma }}}}(t-1)+\frac{{\varvec{{\psi }}}({\varvec{b}},t)}{r_1(t)}[y(t)-{\varvec{{\varphi }}}^{\tiny \text{ T }}_y(t){\varvec{a}}-{\varvec{{\psi }}}^{\tiny \text{ T }}({\varvec{b}},t)\hat{{\varvec{{\gamma }}}}(t-1)], \end{aligned}$$

(9)

$$\begin{aligned} r_1(t)= & {} r_1(t-1)+\Vert {\varvec{{\psi }}}({\varvec{b}},t)\Vert ^2, \quad r_1(0)=1, \end{aligned}$$

(10)

$$\begin{aligned} e_1(t)= & {} y(t)-{\varvec{{\varphi }}}^{\tiny \text{ T }}_y(t){\varvec{a}}-{\varvec{{\psi }}}^{\tiny \text{ T }}({\varvec{b}},t)\hat{{\varvec{{\gamma }}}}(t-1), \end{aligned}$$

(11)

$$\begin{aligned} \hat{{\varvec{{\theta }}}}(t)= & {} \hat{{\varvec{{\theta }}}}(t-1)+\frac{{\varvec{{\phi }}}({\varvec{{\gamma }}},t)}{r_2(t)}\left[ y(t)-{\varvec{{\phi }}}^{\tiny \text{ T }}({\varvec{{\gamma }}},t)\hat{{\varvec{{\theta }}}}(t-1)\right] , \end{aligned}$$

(12)

$$\begin{aligned} r_2(t)= & {} r_2(t-1)+\Vert {\varvec{{\phi }}}({\varvec{{\gamma }}},t)\Vert ^2, \quad r_2(0)=1, \end{aligned}$$

(13)

$$\begin{aligned} e_2(t)= & {} y(t)-{\varvec{{\phi }}}^{\tiny \text{ T }}({\varvec{{\gamma }}},t)\hat{{\varvec{{\theta }}}}(t-1). \end{aligned}$$

(14)

$\mathrm{sgn}[X]$ is a sign function that extracts the sign of a real number, and we use $\mathrm{sgn}[\hat{\gamma }_1(t)]$ to stand for the sign of the first element of $\hat{{\varvec{{\gamma }}}}(t)$ and normalize $\hat{{\varvec{{\gamma }}}}(t)$ with the first positive element

$$\begin{aligned} \hat{{\varvec{{\gamma }}}}(t):=\mathrm{sgn}[\hat{\gamma }_1(t)]\frac{\hat{{\varvec{{\gamma }}}}(t)}{\Vert \hat{{\varvec{{\gamma }}}}(t)\Vert }. \end{aligned}$$

where the first entry of ${\varvec{{\gamma }}}$ is positive, the initial values $\Vert \hat{\gamma }(0)\Vert =1$.

Replacing the unknown vectors ${\varvec{a}}$ and ${\varvec{b}}$ in (9) and ${\varvec{{\gamma }}}$ in (12) with their preceding estimates $\hat{{\varvec{a}}}(t-1)$ and $\hat{{\varvec{b}}}(t-1)$ and the current estimate $\hat{{\varvec{{\gamma }}}}(t)$, we can obtain the following hierarchical stochastic gradient algorithm for the feedback nonlinear system (the FN-HSG algorithm for short):

$$\begin{aligned} \hat{{\varvec{{\gamma }}}}(t)= & {} \hat{{\varvec{{\gamma }}}}(t-1)+\frac{{\varvec{{\psi }}}(\hat{{\varvec{b}}}(t-1),t)}{r_1(t)}e_1(t), \end{aligned}$$

(15)

$$\begin{aligned} e_1(t)= & {} y(t)-{\varvec{{\varphi }}}^{\tiny \text{ T }}_y(t)\hat{{\varvec{a}}}(t-1)-{\varvec{{\psi }}}^{\tiny \text{ T }}(\hat{{\varvec{b}}}(t-1),t)\hat{{\varvec{{\gamma }}}}(t-1), \end{aligned}$$

(16)

$$\begin{aligned} r_1(t)= & {} r_1(t-1)+\Vert {\varvec{{\psi }}}(\hat{{\varvec{b}}}(t-1),t)\Vert ^2, \quad r_1(0)=1, \end{aligned}$$

(17)

$$\begin{aligned} {\varvec{{\varphi }}}_y(t)= & {} [-y(t-1), -y(t-2), \ldots , -y(t-n_a)]^{\tiny \text{ T }}, \end{aligned}$$

(18)

$$\begin{aligned} {\varvec{{\psi }}}(\hat{{\varvec{b}}}(t-1),t)= & {} {\varvec{G}}^{\tiny \text{ T }}(t)\hat{{\varvec{b}}}(t-1), \end{aligned}$$

(19)

$$\begin{aligned} {\varvec{G}}(t)= & {} \left[ \begin{array}{cccc} g_1(r(t-1)-y(t-1)) &{} g_2(r(t-1)-y(t-1)) &{} \cdots &{} g_{n_\gamma }(r(t-1)-y(t-1))\\ g_1(r(t-2)-y(t-2)) &{} g_2(r(t-2)-y(t-2)) &{} \cdots &{} g_{n_\gamma }(r(t-2)-y(t-2))\\ \vdots &{} \vdots &{} &{} \vdots \\ g_1(r(t-n_b)-y(t-n_b) &{} g_2(r(t-n_b)-y(t-n_b)) &{} \cdots &{} g_{n_\gamma }(r(t-n_b)-y(t-n_b)) \end{array}\right] ,\nonumber \\ \end{aligned}$$

(20)

$$\begin{aligned} \hat{{\varvec{{\theta }}}}(t)= & {} \hat{{\varvec{{\theta }}}}(t-1)+\frac{{\varvec{{\phi }}}(\hat{{\varvec{{\gamma }}}}(t),t)}{r_2(t)}e_2(t), \end{aligned}$$

(21)

$$\begin{aligned} e_2(t)= & {} y(t)-{\varvec{{\phi }}}^{\tiny \text{ T }}(\hat{{\varvec{{\gamma }}}}(t),t)\hat{{\varvec{{\theta }}}}(t-1), \end{aligned}$$

(22)

$$\begin{aligned} r_2(t)= & {} r_2(t-1)+\Vert {\varvec{{\phi }}}(\hat{{\varvec{{\gamma }}}}(t),t)\Vert ^2, \quad r_2(0)=1, \end{aligned}$$

(23)

$$\begin{aligned} {\varvec{{\phi }}}(\hat{{\varvec{{\gamma }}}}(t),t)= & {} \left[ {\varvec{{\varphi }}}_y^{\tiny \text{ T }}(t), {\varvec{G}}^{\tiny \text{ T }}(t)\hat{{\varvec{{\gamma }}}}^{\tiny \text{ T }}(t)\right] ^{\tiny \text{ T }}, \end{aligned}$$

(24)

$$\begin{aligned} \hat{{\varvec{{\gamma }}}}(t)= & {} \mathrm{sgn}[\hat{\gamma }_1(t)]\frac{\hat{{\varvec{{\gamma }}}}(t)}{\Vert \hat{{\varvec{{\gamma }}}}(t)\Vert }, \end{aligned}$$

(25)

$$\begin{aligned} \hat{{\varvec{{\theta }}}}(t)= & {} \left[ \hat{{\varvec{a}}}^{\tiny \text{ T }}(t), \hat{{\varvec{b}}}^{\tiny \text{ T }}(t)\right] ^{\tiny \text{ T }}. \end{aligned}$$

(26)

The procedures of computing the parameter estimation vectors $\hat{{\varvec{{\gamma }}}}(t)$ and $\hat{{\varvec{{\theta }}}}(t)$ in (15)–(26) are listed in the following.

• 1. Let $t=1$, give the data length $L_e$, and set the initial values $\Vert \hat{{\varvec{{\gamma }}}}(0)\Vert =1$ with $\hat{\gamma }_1(0)>0$, $\hat{{\varvec{{\theta }}}}(0)=\left[ \begin{array}{c} \hat{{\varvec{a}}}(0) \\ \hat{{\varvec{b}}}(0) \end{array} \right] =\mathbf{1}_{n_a+n_b}/p_0$, $r_1(0)=1$, $r_2(0)=1$.

• 2. Collect the input–output data r(t) and y(t), and compute $r_1(t)$ using (17).

• 3. Form ${\varvec{{\varphi }}}_y(t)$ using (18), ${\varvec{G}}(t)$ using (20), and compute ${\varvec{{\psi }}}(\hat{{\varvec{b}}}(t-1),t)$ using (19).

• 4. Update the estimate $\hat{{\varvec{{\gamma }}}}(t)$ using (15), and normalize $\hat{{\varvec{{\gamma }}}}(t)$ using (25).

• 5. Compute $r_2(t)$ using (22), and form ${\varvec{{\phi }}}(\hat{{\varvec{{\gamma }}}}(t),t)$ using (24).

• 6. Update the estimate $\hat{{\varvec{{\theta }}}}(t)$ using (21).

• 7. If $t<L_e$, increase t by 1 and go to Step 2. Otherwise, terminate the procedure and obtain the parameter estimates.

The flowchart of computing the parameter estimates $\hat{{\varvec{{\gamma }}}}(t)$ and $\hat{{\varvec{{\theta }}}}(t)$ is shown in Fig. 2.

Fig. 2

The flowchart for computing the parameter estimates

4 The Hierarchical Multi-Innovation Stochastic Gradient Algorithm

In order to improve the convergence rate and parameter estimation accuracy of the FN-HSG algorithm, based on the algorithm in (15)–(26), according to the multi-innovation identification theory, we expand the scalar innovations $e_1(t)=y(t)-{\varvec{{\varphi }}}^{\tiny \text{ T }}_y(t)\hat{{\varvec{a}}}(t-1)-{\varvec{{\psi }}}^{\tiny \text{ T }}(\hat{{\varvec{b}}}(t-1), t)\hat{{\varvec{{\gamma }}}}(t-1)$ in (16) and $e_2(t)=y(t)-{\varvec{{\phi }}}^{\tiny \text{ T }}(\hat{{\varvec{{\gamma }}}}(t),t)\hat{{\varvec{{\theta }}}}(t-1)$ in (22) to the innovation vectors:

$$\begin{aligned} {\varvec{E}}_1(p,t):= & {} \left[ \begin{array}{c} y(t)-{\varvec{{\varphi }}}^{\tiny \text{ T }}_y(t)\hat{{\varvec{a}}}(t-1)-{\varvec{{\psi }}}^{\tiny \text{ T }}(\hat{{\varvec{b}}}(t-1),t)\hat{{\varvec{{\gamma }}}}(t-1) \\ y(t-1)-{\varvec{{\varphi }}}^{\tiny \text{ T }}_y(t-1)\hat{{\varvec{a}}}(t-1)-{\varvec{{\psi }}}^{\tiny \text{ T }}(\hat{{\varvec{b}}}(t-1),t-1)\hat{{\varvec{{\gamma }}}}(t-1) \\ \vdots \\ y(t-p+1)-{\varvec{{\varphi }}}^{\tiny \text{ T }}_y(t-p+1)\hat{{\varvec{a}}}(t-1)-{\varvec{{\psi }}}^{\tiny \text{ T }}(\hat{{\varvec{b}}}(t-1),t-p+1)\hat{{\varvec{{\gamma }}}}(t-1) \end{array}\right] \in {\mathbb {R}}^p,\nonumber \\ \end{aligned}$$

(27)

$$\begin{aligned} {\varvec{E}}_2(p,t):= & {} \left[ \begin{array}{c} y(t)-{\varvec{{\phi }}}^{\tiny \text{ T }}(\hat{{\varvec{{\gamma }}}}(t),t)\hat{{\varvec{{\theta }}}}(t-1) \\ y(t-1)-{\varvec{{\phi }}}^{\tiny \text{ T }}(\hat{{\varvec{{\gamma }}}}(t),t-1)\hat{{\varvec{{\theta }}}}(t-1) \\ \vdots \\ y(t-p+1)-{\varvec{{\phi }}}^{\tiny \text{ T }}(\hat{{\varvec{{\gamma }}}}(t),t-p+1)\hat{{\varvec{{\theta }}}}(t-1) \end{array}\right] \in {\mathbb {R}}^p. \end{aligned}$$

(28)

where p denotes the innovation length.

Define the stacked output vector ${\varvec{Y}}(p,t)$ and the information matrices, $\hat{{\varvec{\varPsi }}}(p,t)$ and $\hat{{\varvec{\varPhi }}}(p,t)$ as

$$\begin{aligned} {\varvec{Y}}(p,t):= & {} [y(t), y(t-1),\ldots , y(t-p+1)]^{\tiny \text{ T }}\in {\mathbb {R}}^p,\\ {\varvec{\varPhi }}_y(p,t):= & {} [{\varvec{{\varphi }}}_y(t), {\varvec{{\varphi }}}_y(t-1),\ldots , {\varvec{{\varphi }}}_y(t-p+1)]\in {\mathbb {R}}^{n_a \times p},\\ \hat{{\varvec{\varPsi }}}(p,t):= & {} [{\varvec{{\psi }}}(\hat{{\varvec{b}}}(t-1),t), {\varvec{{\psi }}}(\hat{{\varvec{b}}}(t-1),t-1),\ldots , {\varvec{{\psi }}}(\hat{{\varvec{b}}}(t-1),t-p+1)]\\&\in {\mathbb {R}}^{(n_a+n_b) \times p},\\ \hat{{\varvec{\varPhi }}}(p,t):= & {} [{\varvec{{\phi }}}(\hat{{\varvec{{\gamma }}}}(t),t), {\varvec{{\phi }}}(\hat{{\varvec{{\gamma }}}}(t),t-1),\ldots , {\varvec{{\phi }}}(\hat{{\varvec{{\gamma }}}}(t),t-p+1)]\in {\mathbb {R}}^{n_\gamma \times p}. \end{aligned}$$

Then, Eqs. (27) and (28) can be expressed as

$$\begin{aligned} {\varvec{E}}_1(p,t)= & {} {\varvec{Y}}(p,t)-{\varvec{\varPhi }}_y^{\tiny \text{ T }}(p,t)\hat{{\varvec{a}}}(t-1)-\hat{{\varvec{\varPsi }}}^{\tiny \text{ T }}(p,t)\hat{{\varvec{{\gamma }}}}(t-1),\\ {\varvec{E}}_2(p,t)= & {} {\varvec{Y}}(p,t)-\hat{{\varvec{\varPhi }}}^{\tiny \text{ T }}(p,t)\hat{{\varvec{{\theta }}}}(t-1). \end{aligned}$$

Equations (15) and (21) can be rewritten as

$$\begin{aligned} \hat{{\varvec{{\gamma }}}}(t)= & {} \hat{{\varvec{{\gamma }}}}(t-1)+\frac{\hat{{\varvec{\varPsi }}}(p,t)}{r_1(t)}{\varvec{E}}_1(p,t),\\ \hat{{\varvec{{\theta }}}}(t)= & {} \hat{{\varvec{{\theta }}}}(t-1)+\frac{\hat{{\varvec{\varPhi }}}(p,t)}{r_2(t)}{\varvec{E}}_2(p,t). \end{aligned}$$

Table 1 The FN-HMISG parameter estimates and errors with $\sigma ^2=0.30^2$

We can drive the hierarchical multi-innovation stochastic gradient algorithm for feedback nonlinear systems (the FN-HMISG for short) as follows:

$$\begin{aligned} \hat{{\varvec{{\gamma }}}}(t)= & {} \hat{{\varvec{{\gamma }}}}(t-1)+\frac{\hat{{\varvec{\varPsi }}}(p,t)}{r_1(t)}{\varvec{E}}_1(p,t), \end{aligned}$$

(29)

$$\begin{aligned} r_1(t)= & {} r_1(t-1)+\Vert {\varvec{{\psi }}}(\hat{{\varvec{b}}}(t-1),t)\Vert ^2, \quad r_1(0)=1, \end{aligned}$$

(30)

$$\begin{aligned} {\varvec{E}}_1(p,t)= & {} {\varvec{Y}}(p,t)-{\varvec{\varPhi }}_y^{\tiny \text{ T }}(p,t)\hat{{\varvec{a}}}(t-1)-\hat{{\varvec{\varPsi }}}^{\tiny \text{ T }}(p,t)\hat{{\varvec{{\gamma }}}}(t-1), \end{aligned}$$

(31)

$$\begin{aligned} \hat{{\varvec{{\theta }}}}(t)= & {} \hat{{\varvec{{\theta }}}}(t-1)+\frac{\hat{{\varvec{\varPhi }}}(p,t)}{r_2(t)}{\varvec{E}}_2(p,t), \end{aligned}$$

(32)

$$\begin{aligned} r_2(t)= & {} r_2(t-1)+\Vert {\varvec{{\phi }}}(\hat{{\varvec{{\gamma }}}}(t),t)\Vert ^2, \quad r_2(0)=1, \end{aligned}$$

(33)

$$\begin{aligned} {\varvec{E}}_2(p,t)= & {} {\varvec{Y}}(p,t)-\hat{{\varvec{\varPhi }}}^{\tiny \text{ T }}(p,t)\hat{{\varvec{{\theta }}}}(t-1), \end{aligned}$$

(34)

$$\begin{aligned} {\varvec{{\psi }}}(\hat{{\varvec{b}}}(t-1),t)= & {} {\varvec{G}}^{\tiny \text{ T }}(t)\hat{{\varvec{b}}}(t-1), \end{aligned}$$

(35)

$$\begin{aligned} {\varvec{Y}}(p,t)= & {} [y(t), y(t-1),\ldots , y(t-p+1)]^{\tiny \text{ T }}, \end{aligned}$$

(36)

$$\begin{aligned} {\varvec{\varPhi }}_y(p,t)= & {} [{\varvec{{\varphi }}}_y(t), {\varvec{{\varphi }}}_y(t-1),\ldots , {\varvec{{\varphi }}}_y(t-p+1)], \end{aligned}$$

(37)

$$\begin{aligned} {\varvec{{\varphi }}}_y(t)= & {} [-y(t-1), -y(t-2), \ldots , -y(t-n_a)]^{\tiny \text{ T }}, \end{aligned}$$

(38)

$$\begin{aligned} \hat{{\varvec{\varPsi }}}(p,t)= & {} [{\varvec{{\psi }}}(\hat{{\varvec{b}}}(t-1),t), {\varvec{{\psi }}}(\hat{{\varvec{b}}}(t-1),t-1),\ldots , {\varvec{{\psi }}}(\hat{{\varvec{b}}}(t-1),t-p+1)],\nonumber \\ \end{aligned}$$

(39)

$$\begin{aligned} {\varvec{G}}(t)= & {} \left[ \begin{array}{cccc} g_1(r(t-1)-y(t-1)) &{} g_2(r(t-1)-y(t-1)) &{} \cdots &{} g_{n_\gamma }(r(t-1)-y(t-1))\\ g_1(r(t-2)-y(t-2)) &{} g_2(r(t-2)-y(t-2)) &{} \cdots &{} g_{n_\gamma }(r(t-2)-y(t-2))\\ \vdots &{} \vdots &{} &{} \vdots \\ g_1(r(t-n_b)-y(t-n_b) &{} g_2(r(t-n_b)-y(t-n_b)) &{} \cdots &{} g_{n_\gamma }(r(t-n_b)-y(t-n_b)) \end{array}\right] ,\nonumber \\ \end{aligned}$$

(40)

$$\begin{aligned} \hat{{\varvec{\varPhi }}}(p,t):= & {} [{\varvec{{\phi }}}(\hat{{\varvec{{\gamma }}}}(t),t), {\varvec{{\phi }}}(\hat{{\varvec{{\gamma }}}}(t),t-1),\ldots , {\varvec{{\phi }}}(\hat{{\varvec{{\gamma }}}}(t),t-p+1)], \end{aligned}$$

(41)

$$\begin{aligned} {\varvec{{\phi }}}(\hat{{\varvec{{\gamma }}}}(t),t)= & {} [{\varvec{{\varphi }}}_y^{\tiny \text{ T }}(t), {\varvec{G}}^{\tiny \text{ T }}(t)\hat{{\varvec{{\gamma }}}}^{\tiny \text{ T }}(t)]^{\tiny \text{ T }},\end{aligned}$$

(42)

$$\begin{aligned} \hat{{\varvec{{\theta }}}}(t)= & {} [\hat{{\varvec{a}}}^{\tiny \text{ T }}(t), \hat{{\varvec{b}}}^{\tiny \text{ T }}(t)]^{\tiny \text{ T }}. \end{aligned}$$

(43)

The procedures of computing the parameter estimation vectors $\hat{{\varvec{{\gamma }}}}(t)$ and $\hat{{\varvec{{\theta }}}}(t)$ in (29)–(43) are listed in the following.

• 1. Let $t=1$, give the data length $L_e$, and set the initial values $\Vert \hat{{\varvec{{\gamma }}}}(0)\Vert =1$ with $\hat{\gamma }_1(0)>0$, $\hat{{\varvec{{\theta }}}}(0)=\left[ \begin{array}{c} \hat{{\varvec{a}}}(0) \\ \hat{{\varvec{b}}}(0) \end{array} \right] =\mathbf{1}_{n_a+n_b}/p_0$, $r_1(0)=1$, $r_2(0)=1$.

• 2. Collect the input–output data r(t) and y(t), and form ${\varvec{Y}}(p,t)$, ${\varvec{{\varphi }}}_y(t)$ and ${\varvec{G}}(t)$ using (36), (38) and (40).

• 3. Form ${\varvec{{\psi }}}(\hat{{\varvec{b}}}(t-1),t)$, ${\varvec{\varPhi }}_y(p,t)$ and $\hat{{\varvec{\varPsi }}}(p,t)$ using (35), (37) and (39).

• 4. Compute $r_1(t)$ and ${\varvec{E}}_1(p,t)$ using (30) and (31).

• 5. Update the estimate $\hat{{\varvec{{\gamma }}}}(t)$ using (29).

• 6. Form $\hat{{\varvec{\varPhi }}}(p,t)$ and ${\varvec{{\phi }}}(\hat{{\varvec{{\gamma }}}}(t),t)$ using (41) and (42), and compute $r_2(t)$ and ${\varvec{E}}_2(p,t)$ using (33) and (34).

• 7. Update the estimate $\hat{{\varvec{{\theta }}}}(t)$ using (32).

• 8. If $t<L_e$, increase t by 1 and go to Step 2. Otherwise, terminate the procedure and obtain the parameter estimates.

Equations (29)–(43) form the FN-HMISG algorithm for the feedback nonlinear system. Obviously, when $p=1$, the FN-HMISG algorithm reduces into the FN-HSG algorithm.

Fig. 3

The FN-HMISG parameter estimation errors $\sigma$ versus t ($\sigma ^2=0.30^2$)

Table 2 The parameter estimates based on the 20 Monte Carlo runs ($\sigma ^2=0.30^2)$

5 Examples

In this section, two examples are given to test the FN-HMISG algorithm.

Example 1

Consider the following nonlinear system:

$$\begin{aligned} y(t)= & {} (1-A(z))y(t)+B(z)g(r(t)-y(t))+v(t),\\ A(z)= & {} 1+a_1z^{-1}+a_2z^{-2}=1+0.50z^{-1}+0.25z^{-2},\\ B(z)= & {} b_1z^{-1}+b_2z^{-2}=0.80z^{-1}+1.40z^{-2},\\ g(r(t)-y(t))= & {} 0.60\sin (r(t)-y(t))+0.80\sin ((r(t)-y(t))^2),\\ {\varvec{{\theta }}}= & {} [a_1, a_2, b_1, b_2]^{\tiny \text{ T }}=[0.50, 0.25, 0.80, 1.40]^{\tiny \text{ T }},\\ {\varvec{{\gamma }}}= & {} [\gamma _1, \gamma _2]^{\tiny \text{ T }}=[0.60, 0.80]^{\tiny \text{ T }}. \end{aligned}$$

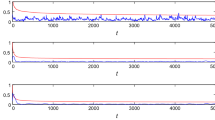
In simulation, the input r(t) is taken as uncorrelated stochastic sequence with zero mean and v(t) as a white noise sequence zero and variance $\sigma ^2=0.30^2$. Take the data length $L_e=4000$ and $\Vert {\varvec{{\gamma }}}\Vert ^2=\gamma _1^2+\gamma _2^2=1$. Applying the FN-HMISG algorithm to estimate the parameters of this nonlinear system, the parameter estimates and their errors are shown in Table 1 with $p=1$, $p=2$, $p=5$ and $p=7$. The estimation errors $\delta :=\Vert \hat{{\varvec{{\vartheta }}}}(t)-{\varvec{{\vartheta }}}\Vert /\Vert {\varvec{{\vartheta }}}\Vert$ versus t are shown in Fig. 3.

Furthermore, using the Monte Carlo simulations with 20 sets of noise realizations, the parameter estimates and the variances of the FN-HMISG algorithm are shown in Table 2 with $\sigma ^2=0.30^2$, $p=7$ and $L_e=4000$. From Table  2, we can see that the average values of the parameter estimates are very close to the true parameters.

Fig. 4

The FN-HMISG parameter estimation errors $\sigma$ versus t ($\sigma ^2=0.30^2$)

Example 2

Consider the following nonlinear system:

$$\begin{aligned} y(t)= & {} (1-A(z))y(t)+B(z)g(r(t)-y(t))+v(t),\\ A(z)= & {} 1+a_1z^{-1}+a_2z^{-2}+a_3z^{-3}=1+0.30z^{-1}+0.48z^{-2}+0.45z^{-3},\\ B(z)= & {} b_1z^{-1}+b_2z^{-2}+b_3z^{-3}=0.79z^{-1}+0.84z^{-3},\\ g(r(t)-y(t))= & {} 0.48\sin (r(t)-y(t))+0.87\sin ((r(t)-y(t))^2)\\&+0.096\cos (r(t)-y(t)),\\ {\varvec{{\theta }}}= & {} [a_1, a_2, a_3, b_1, b_2, b_3]^{\tiny \text{ T }}=[0.30, 0.48, 0.45, 0.79, 0.00, 0.84]^{\tiny \text{ T }},\\ {\varvec{{\gamma }}}= & {} [\gamma _1, \gamma _2, \gamma _3]^{\tiny \text{ T }}=[0.48, 0.87, 0.096]^{\tiny \text{ T }}, \ \Vert {\varvec{{\gamma }}}\Vert ^2=\gamma _1^2+\gamma _2^2+\gamma _3^2=1. \end{aligned}$$

The simulation conditions are similar to those in Example 1. We apply the FN-HMISG algorithm to estimate the parameters of this nonlinear system, the parameter estimates and their errors are shown in Table 3 with $p=1$, $p=2$, $p=4$ and $p=8$, and the estimation errors $\delta$ versus t are shown in Fig. 4.

Table 3 The FN-HMISG parameter estimates and errors with $\sigma ^2=0.30^2$

From Tables 1 and 3 and Figs. 3 and 4, we can draw the following conclusions.

• 1. The parameter estimation errors given by the FN-HMISG algorithm are becoming smaller with the innovation length p increasing.

• 2. The proposed FN-HMISG algorithm becomes more accurate as the data length t increases.

• 3. The parameter estimates of the FN-HMISG algorithm with $p > 1$ converge faster to their true values than the parameter estimates of the FN-HSG algorithm.

• 4. These results confirm that the FN-HMISG algorithm with $p > 1$ can estimate the parameters more accurately than the FN-HSG algorithm.

6 Conclusions

This paper proposes a hierarchical stochastic gradient algorithm and a hierarchical multi-innovation stochastic gradient algorithm for feedback nonlinear systems. The simulation results indicate that the multi-innovation stochastic gradient algorithm can improve the parameter estimation accuracy compared with the stochastic gradient algorithm. The method used in this paper can be extended to study the identification problems of nonlinear control systems with colored noise [15, 16] and applied to hybrid switching-impulsive dynamical networks [11] or applied to other fields [3, 4, 9, 18, 30, 33].