1 Introduction

System identification is the theory and method of establishing mathematical models of linear stochastic systems and nonlinear stochastic systems [2, 69, 79]. As most natural systems have nonlinear behaviors, the identification and modeling of nonlinear systems are meaningful [29,30,31,32,33]. Common nonlinear systems include Hammerstein systems, Wiener systems and Wiener-Hammerstein systems. Over the past several decades, a dozen studies have been conducted on identification methods for nonlinear systems. In [1], the estimating function approach was introduced, which can construct estimators that are asymptotically optimal with respect to a specific class of estimators for the identification of nonlinear stochastic dynamical models. Li et al. proposed a linear variable weight particle swarm method for Hammerstein-Wiener nonlinear systems with unknown time delay by utilizing the parallel search ability of the particle swarm optimization and the iterative identification technique [46].

Nonlinear systems can be constructed from dynamical linear subsystems and static nonlinear elements in many different ways, including series, parallel and feedback connections [23, 35, 58]. Here, we focus on a class of nonlinear feedback systems whose forward channels are dynamical linear subsystems and feedback channels are static nonlinearities. Recently, many publications have been devoted to studying the estimation and application of feedback nonlinear systems [20, 21]. For example, Wei et al. derived an overall recursive least squares algorithm and an overall stochastic gradient algorithm to estimate nonlinear feedback systems disturbed by white noise [93]. Based on filtering technology, a linear filter was constructed to convert the colored noise into white noise and a filtering-based multi-innovation stochastic gradient algorithm was obtained deduced for Hammerstein equation-error autoregressive systems [70] by employing the multi-innovation theory [47,48,49,50,51].

In the area of parameter estimation, the iterative technique is an effective tool that has been widely applied to optimize the parameters of the estimated models [41,42,43]. In contrast to recursive algorithms, iterative algorithms use batch data at each iteration and make full use of measurement data, which can improve parameter estimation accuracy [38,39,40]. By combining different search principles, various iterative algorithms can be formed, such as the least squares-based iterative algorithm, the gradient-based iterative algorithm and the Newton iteration algorithm. Several gradient-based iterative algorithms have been studied in previous works [80, 110]. For instance, Fan et al. presented a two-stage auxiliary model gradient-based iterative algorithm for an input nonlinear controlled autoregressive system with variable-gain nonlinearity [18]. Iterative identification is a class of offline identification methods. To track time-varying parameters in real time, Jiang et al. presented a moving data window gradient-based iterative algorithm for a generalized time-varying system with a measurable disturbance vector [36].

To improve the parameter estimation results, hierarchical identification methods were proposed based on the decomposition-coordination principle of large-scale systems [37, 68]. The basic idea is to reduce the scales of the estimated models through decomposition and to perform joint estimation for the models. In [96,97,98,99,100, 102], a separable multi-innovation Newton iterative signal modeling method was derived and implemented to estimate sine multi-frequency signals and periodic signals, in which the measurements are sampled and used dynamically. Wang et al. proposed a two-stage gradient-based iterative algorithm by minimizing two criterion functions for a fractional-order nonlinear system with autoregressive noise [83]. Hu et al. presented a two-stage recursive least squares algorithm for nonlinear feedback systems based on the auxiliary model identification idea and the hierarchical identification principle [27].

The parameter estimation of system models is important for controller design and filter design [112,113,114,115,116]. Some signal processing filters are designed based on parameter estimation algorithms and some self-tuning control and model-based predicted control methods rely on parameter estimation methods [117,118,119,120,121]. The previous works in [104] discussed the multi-innovation gradient-based iterative identification method and the decomposition multi-innovation gradient-based iterative identification methods for nonlinear feedback systems by using the decomposition technique. This paper studies the gradient-based iterative estimation algorithm and the hierarchical gradient-based iterative estimation algorithm to solve the parameter estimation problems of feedback nonlinear systems. The main contributions of this paper are as follows.

  • To make full use of measurement data to estimate the parameters of the nonlinear feedback systems, we utilize the gradient search principle as the optimization strategy and present a gradient-based iterative (GI) algorithm.

  • The system to be identified can be decomposed into two subsystems based on the hierarchical identification principle. Then, a hierarchical gradient-based iterative (H-GI) algorithm is derived to improve the parameter estimation accuracy.

  • The performance of the proposed algorithms is tested by a numerical example, including the computational costs and the parameter estimation accuracy.

In summary, the rest of this paper is organized as follows. Section 2 describes the identification problem for nonlinear feedback systems. A gradient-based iterative algorithm is derived in Sect. 3. Section 4 presents a hierarchical gradient-based iterative algorithm and analyzes the computational costs of the algorithms. Section 5 provides a numerical example for testing the effectiveness of the proposed algorithms. Finally, some concluding remarks are given in Sect. 6.

This paper studies two iterative estimation algorithms to solve parameter estimation problems for nonlinear feedback systems. The proposed iterative identification algorithms for the nonlinear feedback systems can be combined with other techniques and strategies to address parameter estimation problems for different systems and can be applied to other fields, such as information processing and communication.

2 System Description

Let us introduce some symbols used in this paper. The symbol \({\textbf{I}}_n\) stands for an identity matrix of order n; \(\textbf{1}_n\) stands for an n-dimensional column vector whose elements are 1; the superscript \({\textrm{T}}\) stands for vector/matrix transpose; and the norm of a matrix (or a column vector) \({{\varvec{X}}}\) is defined by \(\Vert {\varvec{X}}\Vert ^2:=\textrm{tr}[{\varvec{X}}{\varvec{X}}^{\textrm{T}}]\).

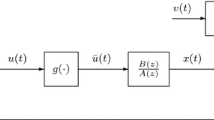
Consider the nonlinear feedback system shown in Fig. 1, where the forward channel is described by a controlled autoregressive (CAR) model:

$$\begin{aligned} y(t)+ & {} a_1y(t-1)+a_2y(t-2)+\cdots +a_{n_a}y(t-n_a)\nonumber \\= & {} b_1u(t-1)+b_2u(t-2)+\cdots +b_{n_b}u(t-n_b)+v(t), \end{aligned}$$
(1)

y(t) is the output of the system, u(t) is the input of the linear part, v(t) is a white noise sequence with zero mean and variance \(\sigma ^2\), and \(y(t)=0\) and \(u(t)=0\) for \(t\leqslant 0\). The feedback channel of the system is a memoryless nonlinear block whose output \(\bar{y}(t)\) can be regarded as a nonlinear function of a known nonlinear basis \({\varvec{h}}:=(h_1,h_2,\cdots ,h_m)\):

$$\begin{aligned} \bar{y}(t)= & {} h(y(t))\nonumber \\= & {} q_1h_1(y(t))+q_2h_2(y(t))+\cdots +q_mh_m(y(t))\nonumber \\= & {} {\varvec{h}}(y(t)){\varvec{q}}, \end{aligned}$$
(2)

where \(q_i\) \((i=1,2,\ldots ,m)\) are the unknown nonlinear coefficients and m is the nonlinear order. The input u(t) of the linear part, the output \(\bar{y}(t)\) of the nonlinear feedback part and the input r(t) of the system have the following relation

$$\begin{aligned} u(t):=r(t)-\bar{y}(t). \end{aligned}$$
(3)
Fig. 1
figure 1

The nonlinear feedback CAR system

Full size image

Define the parameter vectors \({\varvec{a}}\) and \({\varvec{b}}\) of the linear part, and \({\varvec{q}}\) of the nonlinear part as

$$\begin{aligned} {\varvec{a}}:=\left[ \begin{array}{c} a_1 \\ a_2 \\ \vdots \\ a_{n_a} \end{array}\right] \in {\mathbb {R}}^{n_a},\quad {\varvec{b}}:=\left[ \begin{array}{c} b_1 \\ b_2 \\ \vdots \\ b_{n_b} \end{array}\right] \in {\mathbb {R}}^{n_b},\quad {\varvec{q}}:=\left[ \begin{array}{c} q_1 \\ q_2 \\ \vdots \\ q_{m} \end{array}\right] \in {\mathbb {R}}^{m}, \end{aligned}$$

and define the output information vector \({\varvec{\varphi }}_a(t)\), the input information vector \({\varvec{\varphi }}_b(t)\), and the feedback information matrix \({\varvec{H}}(t)\) as

$$\begin{aligned} {\varvec{\varphi }}_a(t):= & {} \left[ \begin{array}{c} -y(t-1) \\ -y(t-2) \\ \vdots \\ -y(t-n_a) \end{array}\right] \in {\mathbb {R}}^{n_a},\quad {\varvec{\varphi }}_b(t):=\left[ \begin{array}{c} r(t-1) \\ r(t-2) \\ \vdots \\ r(t-n_b) \end{array}\right] \in {\mathbb {R}}^{n_b},\nonumber \\ {\varvec{H}}(t):= & {} \left[ \begin{array}{cccc} -h_1(y(t-1)) &{} -h_2(y(t-1)) &{} \cdots &{} -h_{m}(y(t-1))\\ -h_1(y(t-2)) &{} -h_2(y(t-2)) &{} \cdots &{} -h_{m}(y(t-2))\\ \vdots &{} \vdots &{} &{} \vdots \\ -h_1(y(t-{n_b})) &{} -h_2(y(t-{n_b})) &{} \cdots &{} -h_{m}(y(t-{n_b}))\end{array}\right] \in {\mathbb {R}}^{n_b\times m}. \end{aligned}$$

From Eqs. (1)–(3), we have

$$\begin{aligned} y(t)= & {} -a_1y(t-1)-a_2y(t-2)-\cdots -a_{n_a}y(t-n_a)+b_1r(t-1)+b_2r(t-2)+\cdots +b_{n_b}r(t-n_b)\nonumber \\{} & {} -b_1q_1h_1(y(t-1))-b_2q_2h_2(y(t-2))-\cdots -b_{n_b}q_mh_m(y(t-n_b))+v(t)\nonumber \\= & {} -\sum _{j=1}^{n_a}a_jy(t-j)+\sum _{j=1}^{n_b}b_jr(t-j) -\sum _{j=1}^{n_b}b_j\sum _{i=1}^{m}q_ih_i(y(t-j))+v(t)\nonumber \\= & {} {\varvec{\varphi }}_a^{\textrm{T}}(t){\varvec{a}}+{\varvec{\varphi }}_b^{\textrm{T}}(t){\varvec{b}}+{\varvec{b}}^{\textrm{T}}{\varvec{H}}(t){\varvec{q}}+v(t). \end{aligned}$$
(4)

The parameter identification algorithms proposed in this paper are based on identification model in (4). Many identification methods are derived according to the identification models of the systems [24,25,26, 28, 54, 94, 95, 109], and these methods can be used to estimate the parameters of other linear systems and nonlinear systems [60,61,62,63,64,65,66,67] and can be applied to engineering areas [44, 45, 92, 101, 103,104,105,106] such as information processing and process control systems.

Remark 1

In Equation (4), there is a cross product between parameter vectors \({\varvec{b}}\) in the linear block and \({\varvec{q}}\) in the nonlinear block, which can be called the bilinear-in-parameter identification model. To identify the parameters of the linear part and the nonlinear part, we can decompose the nonlinear feedback system based on the hierarchical identification principle.

Remark 2

This article considers the feedback nonlinear systems disturbed by white noise. In future research, we will consider identification problems with colored noise, i.e., autoregressive noise, moving average noise, autoregressive moving average noise [19, 34, 111] and so on.

3 The Gradient-Based Iterative Algorithm

Based on negative gradient search, this section derives the GI algorithm for estimating the parameters of a nonlinear feedback system from the measurement data.

Define the information vectors \({\varvec{\varphi }}(t)\) and \({\varvec{\varphi }}_m(t)\) and the parameter vector \({\varvec{\vartheta }}\) as

$$\begin{aligned} {\varvec{\varphi }}(t):= & {} [{\varvec{\varphi }}^{\textrm{T}}_a(t),{\varvec{\varphi }}^{\textrm{T}}_b(t),{\varvec{\varphi }}^{\textrm{T}}_m(t)]^{\textrm{T}}\in {\mathbb {R}}^n,\nonumber \\ {\varvec{\varphi }}_m(t):= & {} {\varvec{H}}^{\textrm{T}}(t){\varvec{b}}\in {\mathbb {R}}^m,\nonumber \\ {\varvec{\vartheta }}:= & {} [{\varvec{a}}^{\textrm{T}},{\varvec{b}}^{\textrm{T}},{\varvec{q}}^{\textrm{T}}]^{\textrm{T}}\in {\mathbb {R}}^n,\nonumber \\ n:= & {} n_a+n_b+m. \end{aligned}$$

The identification model for the nonlinear feedback system in (4) is given by

$$\begin{aligned} y(t)= & {} {\varvec{\varphi }}_a^{\textrm{T}}(t){\varvec{a}}+{\varvec{\varphi }}_b^{\textrm{T}}(t){\varvec{b}}+{\varvec{b}}^{\textrm{T}}{\varvec{H}}(t){\varvec{q}}+v(t)\nonumber \\= & {} [{\varvec{\varphi }}^{\textrm{T}}_a(t),{\varvec{\varphi }}^{\textrm{T}}_b(t),{\varvec{\varphi }}^{\textrm{T}}_m(t)] \left[ \begin{array}{c} {\varvec{a}} \\ {\varvec{b}} \\ {\varvec{q}} \end{array}\right] +v(t)\nonumber \\= & {} {\varvec{\varphi }}^{\textrm{T}}(t){\varvec{\vartheta }}+v(t). \end{aligned}$$
(5)

Let L be the data length \((L\gg n)\) and define the stacked output vector \({\varvec{Y}}(L)\), the stacked information matrices \({\varvec{\varPsi }}(L)\), \({\varvec{\varPhi }}_a(L)\), \({\varvec{\varPhi }}_b(L)\) and \({\varvec{\varPhi }}_m(L)\) as

$$\begin{aligned} {\varvec{Y}}(L):= & {} [y(1),y(2),\cdots ,y(L)]^{\textrm{T}}\in {\mathbb {R}}^L,\nonumber \\ {\varvec{\varPsi }}(L):= & {} [{\varvec{\varPhi }}^{\textrm{T}}_a(L),{\varvec{\varPhi }}^{\textrm{T}}_b(L),{\varvec{\varPhi }}^{\textrm{T}}_m(L)]^{\textrm{T}}\in {\mathbb {R}}^{L\times n},\nonumber \\ {\varvec{\varPhi }}_a(L):= & {} [{\varvec{\varphi }}_a(1),{\varvec{\varphi }}_a(2),\cdots ,{\varvec{\varphi }}_a(L)]^{\textrm{T}}\in {\mathbb {R}}^{L\times n_a},\nonumber \\ {\varvec{\varPhi }}_b(L):= & {} [{\varvec{\varphi }}_b(1),{\varvec{\varphi }}_b(2),\cdots ,{\varvec{\varphi }}_b(L)]^{\textrm{T}}\in {\mathbb {R}}^{L\times n_b},\nonumber \\ {\varvec{\varPhi }}_m(L):= & {} [{\varvec{\varphi }}_m(1),{\varvec{\varphi }}_m(2),\cdots ,{\varvec{\varphi }}_m(L)]^{\textrm{T}}\in {\mathbb {R}}^{L\times m}. \end{aligned}$$

Define the criterion function as

$$\begin{aligned} J_1({\varvec{\vartheta }}):= & {} \frac{1}{2}\Vert {\varvec{Y}}(L)-{\varvec{\varPsi }}(L){\varvec{\vartheta }}\Vert ^2. \end{aligned}$$
(6)

We make the following definitions.

  1. (i)

    \(k=1,2,3,\cdots \) is the iteration variable.

  2. (ii)

    \(\hat{{\varvec{\vartheta }}}_k\) is the estimate of the parameter vector \({\varvec{\vartheta }}\) at iteration k.

  3. (iii)

    \(\mu _{1,k}\) is the iteration step-size.

By means of the negative gradient search, and minimizing the criterion function \(J_1({\varvec{\vartheta }})\) with respect to \({\varvec{\vartheta }}\), we can obtain the iterative relation:

$$\begin{aligned} \hat{{\varvec{\vartheta }}}_k= & {} \hat{{\varvec{\vartheta }}}_{k-1}-\mu _{1,k}\textrm{grad}[J_1(\hat{{\varvec{\vartheta }}}_{k-1})]\nonumber \\= & {} \hat{{\varvec{\vartheta }}}_{k-1}+\mu _{1,k}{\varvec{\varPsi }}^{\textrm{T}}(L) [{\varvec{Y}}(L)-{\varvec{\varPsi }}(L)\hat{{\varvec{\vartheta }}}_{k-1}], \end{aligned}$$
(7)

where the information matrices \({\varvec{\varPhi }}_m(L)\) in \({\varvec{\varPsi }}(L)\) are unknown. Because the information vector \({\varvec{\varphi }}_m(t)\) in \({\varvec{\varPhi }}_m(L)\) contains the unknown parameter vector \({\varvec{b}}\), Eq. (7) cannot yield the estimate \(\hat{{\varvec{\vartheta }}}_k\) directly. Our approach is to replace the unknown variable \({\varvec{b}}\) in \({\varvec{\varphi }}_m(t)\) with its estimate \(\hat{{\varvec{b}}}_{k-1}\) at the (\(k-1\))\(\mathrm th\) iteration. The estimate \(\hat{{\varvec{\varphi }}}_{m,k}(t)\) of the information vector \({\varvec{\varphi }}_m(t)\) at iteration k is given by

$$\begin{aligned} \hat{{\varvec{\varphi }}}_{m,k}(t):= & {} {\varvec{H}}^{\textrm{T}}(t)\hat{{\varvec{b}}}_{k-1}\in {\mathbb {R}}^m. \end{aligned}$$

Replacing \({\varvec{\varPhi }}_m(L)\) and \({\varvec{\varPsi }}_k(L)\) with their estimates \(\hat{{\varvec{\varPhi }}}_{m,k}(L)\) and \(\hat{{\varvec{\varPsi }}}_k(L)\) at k, we have

$$\begin{aligned} \hat{{\varvec{\varPhi }}}_{m,k}(L):= & {} [\hat{{\varvec{\varphi }}}_{m,k}(1),\hat{{\varvec{\varphi }}}_{m,k}(2),\cdots , \hat{{\varvec{\varphi }}}_{m,k}(L)]^{\textrm{T}}\in {\mathbb {R}}^{L\times m},\nonumber \\ \hat{{\varvec{\varPsi }}}_k(L):= & {} [{\varvec{\varPhi }}^{\textrm{T}}_a(L),{\varvec{\varPhi }}^{\textrm{T}}_b(L), \hat{{\varvec{\varPhi }}}^{\textrm{T}}_{m,k}(L)]^{\textrm{T}}\in {\mathbb {R}}^{L\times n}. \end{aligned}$$

Utilizing the estimate \(\hat{{\varvec{\varPsi }}}_k(L)\) to replace the information matrix \({\varvec{\varPsi }}(L)\) in (7), we obtain

$$\begin{aligned} \hat{{\varvec{\vartheta }}}_k= & {} \hat{{\varvec{\vartheta }}}_{k-1}+\mu _{1,k}\hat{{\varvec{\varPsi }}}^{\textrm{T}}_k(L) [{\varvec{Y}}(L)-\hat{{\varvec{\varPsi }}}_k(L)\hat{{\varvec{\vartheta }}}_{k-1}]\nonumber \\= & {} [{\varvec{I}}_n-\mu _{1,k}\hat{{\varvec{\varPsi }}}^{\textrm{T}}_k(L)\hat{{\varvec{\varPsi }}}_k(L)] \hat{{\varvec{\vartheta }}}_{k-1}+\mu _{1,k}\hat{{\varvec{\varPsi }}}^{\textrm{T}}_k(L){\varvec{Y}}(L). \end{aligned}$$
(8)

Equation (8) can be seen as a discrete-time system. To ensure the convergence of \(\hat{{\varvec{\vartheta }}}_k\), all the eigenvalues of matrix \([{\varvec{I}}_n-\mu _{1,k}\hat{{\varvec{\varPsi }}}^{\textrm{T}}_k(L)\hat{{\varvec{\varPsi }}}_k(L)]\) must be in the unit circle. Thus, the step-size \(\mu _{1,k}\) can be conservatively chosen as

$$\begin{aligned} 0<\mu _{1,k}\leqslant \frac{2}{\lambda _{\max }[\hat{{\varvec{\varPsi }}}^{\textrm{T}}_k(L)\hat{{\varvec{\varPsi }}}_k(L)]} =2\lambda ^{-1}_{\max }[\hat{{\varvec{\varPsi }}}^{\textrm{T}}_k(L)\hat{{\varvec{\varPsi }}}_k(L)]. \end{aligned}$$

From the above derivations, we can summarize the GI algorithm for the nonlinear feedback system as

$$\begin{aligned} \hat{{\varvec{\vartheta }}}_k= & {} \hat{{\varvec{\vartheta }}}_{k-1}+\mu _{1,k}\hat{{\varvec{\varPsi }}}^{\textrm{T}}_k(L) [{\varvec{Y}}(L)-\hat{{\varvec{\varPsi }}}_k(L)\hat{{\varvec{\vartheta }}}_{k-1}], \end{aligned}$$
(9)
$$\begin{aligned} \mu _{1,k}\leqslant & {} 2\lambda ^{-1}_{\max }[\hat{{\varvec{\varPsi }}}^{\textrm{T}}_k(L)\hat{{\varvec{\varPsi }}}_k(L)], \end{aligned}$$
(10)
$$\begin{aligned} {\varvec{Y}}(L)= & {} [y(1),y(2),\ldots ,y(L)]^{\textrm{T}}, \end{aligned}$$
(11)
$$\begin{aligned} \hat{{\varvec{\varPsi }}}_k(L)= & {} [{\varvec{\varPhi }}^{\textrm{T}}_a(L),{\varvec{\varPhi }}^{\textrm{T}}_b(L), {\varvec{\varPhi }}^{\textrm{T}}_{m,k}(L)]^{\textrm{T}}, \end{aligned}$$
(12)
$$\begin{aligned} {\varvec{\varPhi }}_a(L)= & {} [{\varvec{\varphi }}_a(1),{\varvec{\varphi }}_a(1), \ldots ,{\varvec{\varphi }}_a(L)]^{\textrm{T}}, \end{aligned}$$
(13)
$$\begin{aligned} {\varvec{\varPhi }}_b(L)= & {} [{\varvec{\varphi }}_b(1),{\varvec{\varphi }}_b(2), \ldots ,{\varvec{\varphi }}_b(L)]^{\textrm{T}}, \end{aligned}$$
(14)
$$\begin{aligned} \hat{{\varvec{\varPhi }}}_{m,k}(L)= & {} [\hat{{\varvec{\varphi }}}_{m,k}(1),\hat{{\varvec{\varphi }}}_{m,k}(2), \ldots ,\hat{{\varvec{\varphi }}}_{m,k}(L)]^{\textrm{T}}, \end{aligned}$$
(15)
$$\begin{aligned} {\varvec{\varphi }}_a(t)= & {} [-y(t-1),-y(t-2),\ldots ,-y(t-n_a)]^{\textrm{T}}, \end{aligned}$$
(16)
$$\begin{aligned} {\varvec{\varphi }}_b(t)= & {} [r(t-1),r(t-2),\ldots ,r(t-n_b)]^{\textrm{T}}, \end{aligned}$$
(17)
$$\begin{aligned} \hat{{\varvec{\varphi }}}_{m,k}(t)= & {} {\varvec{H}}^{\textrm{T}}(t)\hat{{\varvec{b}}}_{k-1}, \end{aligned}$$
(18)
$$\begin{aligned} \hat{{\varvec{\varphi }}}_k(t)= & {} [{\varvec{\varphi }}_a(t),{\varvec{\varphi }}_b(t),\hat{{\varvec{\varphi }}}_{m,k}(t)]^{\textrm{T}}, \end{aligned}$$
(19)
$$\begin{aligned} {\varvec{H}}(t):= & {} [-{\varvec{h}}^{\textrm{T}}(y(t-1)),-{\varvec{h}}^{\textrm{T}}(y(t-2)),\ldots , -{\varvec{h}}^{\textrm{T}}(y(t-n_b))]^{\textrm{T}}, \end{aligned}$$
(20)
$$\begin{aligned} \hat{{\varvec{\vartheta }}}_k= & {} [\hat{{\varvec{a}}}^{\textrm{T}}_k,\hat{{\varvec{b}}}^{\textrm{T}}_k,\hat{{\varvec{q}}}^{\textrm{T}}_k]^{\textrm{T}}, \end{aligned}$$
(21)
$$\begin{aligned} \hat{{\varvec{a}}}_k= & {} [\hat{a}_{1,k},\hat{a}_{2,k},\ldots ,\hat{a}_{n_a,k}]^{\textrm{T}}, \end{aligned}$$
(22)
$$\begin{aligned} \hat{{\varvec{b}}}_k= & {} [\hat{b}_{1,k},\hat{b}_{2,k},\ldots ,\hat{b}_{n_b,k}]^{\textrm{T}}, \end{aligned}$$
(23)
$$\begin{aligned} \hat{{\varvec{q}}}_k= & {} [\hat{q}_{1,k},\hat{q}_{2,k},\ldots ,\hat{q}_{m,k}]^{\textrm{T}}. \end{aligned}$$
(24)

The steps of computing the parameter estimation vector \(\hat{{\varvec{\vartheta }}}_k\) by the GI algorithm in (9)–(24) are listed as follows.

  1. 1.

    To initialize: let \(k=1\), \(\hat{{\varvec{\vartheta }}}_0=[\hat{a}_{1,0},\ldots ,\hat{a}_{n_a,0}, \hat{b}_{1,0},\ldots ,\hat{b}_{n_b,0}, \hat{q}_{1,0},\ldots ,\hat{q}_{m,0}]^{\textrm{T}}\) be any real vector, \(r(t-j)=1/p_0\) and \(y(t-j)=1/p_0\), \(j=1,2,\ldots ,\max [n_a,n_b]\), \(t=1,2,\ldots ,L\), \(p_0=10^6\). Set the data length L (\(L\gg n\)), the parameter estimation precision \(\varepsilon >0\) and the basis function \(h(\cdot )\).

  2. 2.

    Collect the input and output data r(t) and y(t), \(t=1,2,\ldots ,L\), and form \({\varvec{Y}}(L)\) by (11).

  3. 3.

    Form \({\varvec{H}}(t)\) by (20), form \({\varvec{\varphi }}_a(t)\) and \({\varvec{\varphi }}_b(t)\) by (16) and (17), \(t=1,2,\ldots ,L\).

  4. 4.

    Form \({\varvec{\varPhi }}_a(L)\) and \({\varvec{\varPhi }}_b(L)\) by (13) and (14).

  5. 5.

    Compute \(\hat{{\varvec{\varphi }}}_{m,k}(t)\) by (18), form \(\hat{{\varvec{\varphi }}}_k(t)\) by (19), \(t=1,2,\ldots ,l+L\).

  6. 6.

    Form \(\hat{{\varvec{\varPhi }}}_{m,k}(L)\) by (15), form \(\hat{{\varvec{\varPsi }}}_k(L)\) by (12).

  7. 7.

    Select a large step-size \(\mu _{1,k}\) according to (10), and update the parameter estimation vector \(\hat{{\varvec{\vartheta }}}_k\) by (9).

  8. 8.

    Read out the parameter estimation vectors \(\hat{{\varvec{a}}}_k\), \(\hat{{\varvec{b}}}_k\) and \(\hat{{\varvec{q}}}_k\) from \(\hat{{\varvec{\vartheta }}}_k\) in Eq. (21).

  9. 9.

    Compare \(\hat{{\varvec{\vartheta }}}_k\) with \(\hat{{\varvec{\vartheta }}}_{k-1}\): if \(\Vert \hat{{\varvec{\vartheta }}}_k-\hat{{\varvec{\vartheta }}}_{k-1}\Vert >\varepsilon \), increase k by 1 and go to Step 5; otherwise, output the parameter estimate \(\hat{{\varvec{\vartheta }}}_k\), and terminate this iterative calculation process.

Remark 3

The parameter estimation methods proposed in this paper can be combined with other estimation approaches to study parameter estimation problems for linear stochastic systems and nonlinear stochastic systems, and they can be applied to engineering application systems, such as atomic force microscope cantilever modeling, heat exchange processes, and the identification by microwave crystal detectors.

4 The Hierarchical Gradient-Based Iterative Algorithm

Inspired by the hierarchical identification principle, we employ the H-GI algorithm for nonlinear feedback systems to improve parameter estimation accuracy. The feedback nonlinear system in (4) is decomposed into two subsystems, which contain the parameter vectors \({\varvec{{\theta }}}_{1}:=[{\varvec{a}}^{\textrm{T}},{\varvec{b}}^{\textrm{T}}]^{\textrm{T}}\in {\mathbb {R}}^{n_a+n_b}\) and \({\varvec{{\theta }}}_m:={\varvec{q}}\in {\mathbb {R}}^m\).

Define the system information vectors \({\varvec{\varphi }}_{1}(t)\) and \({\varvec{\varphi }}_m(t)\), and the intermediate variable \(y_m\) as

$$\begin{aligned} {\varvec{\varphi }}_{1}(t):= & {} [{\varvec{\varphi }}^{\textrm{T}}_a(t),{\varvec{\varphi }}^{\textrm{T}}_b(t)+{\varvec{q}}^{\textrm{T}}{\varvec{H}}^{\textrm{T}}(t)]^{\textrm{T}} \in {\mathbb {R}}^{n_a+n_b},\nonumber \\ {\varvec{\varphi }}_m(t):= & {} {\varvec{H}}^{\textrm{T}}(t){\varvec{b}}\in {\mathbb {R}}^m,\nonumber \\ y_m:= & {} y(t)-{\varvec{\varphi }}_a^{\textrm{T}}(t){\varvec{a}}-{\varvec{\varphi }}_b^{\textrm{T}}(t){\varvec{b}}\nonumber \\= & {} {\varvec{\varphi }}_m^{\textrm{T}}(t){\varvec{{\theta }}}_m+v(t). \end{aligned}$$
(25)

Eq. (4) can be equivalently written as

$$\begin{aligned} y(t)={\varvec{\varphi }}_{1}^{\textrm{T}}(t){\varvec{{\theta }}}_{1}+v(t). \end{aligned}$$
(26)

Let L be the data length \((L \gg n)\) and define the stacked output vectors \({\varvec{Y}}(L)\) and \({\varvec{Y}}_m(L)\), the stacked information matrices \({\varvec{\varPhi }}_{1}(L)\), \({\varvec{\varPhi }}_m(L)\), \({\varvec{\varPhi }}_a(L)\) and \({\varvec{\varPhi }}_b(L)\) as

$$\begin{aligned} {\varvec{Y}}(L):= & {} [y(1),y(2),\ldots ,y(L)]^{\textrm{T}}\in {\mathbb {R}}^L,\nonumber \\ {\varvec{Y}}_m(L):= & {} [y_m(1),y_m(2),\ldots ,y_m(L)]^{\textrm{T}}\in {\mathbb {R}}^L,\nonumber \\ {\varvec{\varPhi }}_{1}(L):= & {} [{\varvec{\varphi }}_{1}(1),{\varvec{\varphi }}_{1}(2),\ldots ,{\varvec{\varphi }}_{1}(L))]^{\textrm{T}}\in {\mathbb {R}}^{L\times (n_a+n_b)},\nonumber \\ {\varvec{\varPhi }}_m(L):= & {} [{\varvec{\varphi }}_m(1),{\varvec{\varphi }}_m(2),\ldots ,{\varvec{\varphi }}_m(L)]^{\textrm{T}} \in {\mathbb {R}}^{L\times m},\nonumber \\ {\varvec{\varPhi }}_a(L):= & {} [{\varvec{\varphi }}_a(1),{\varvec{\varphi }}_a(2),\ldots ,{\varvec{\varphi }}_a(L)]^{\textrm{T}} \in {\mathbb {R}}^{L\times n_a},\nonumber \\ {\varvec{\varPhi }}_b(L):= & {} [{\varvec{\varphi }}_b(1),{\varvec{\varphi }}_b(2),\ldots ,{\varvec{\varphi }}_b(L)]^{\textrm{T}} \in {\mathbb {R}}^{L\times n_b}. \end{aligned}$$

Define two criterion functions,

$$\begin{aligned} J_2({\varvec{{\theta }}}_{1}):= & {} \frac{1}{2}\Vert {\varvec{Y}}(L)-{\varvec{\varPhi }}_{1}(L){\varvec{{\theta }}}_{1}\Vert ^2,\nonumber \\ J_3({\varvec{{\theta }}}_m):= & {} \frac{1}{2}\Vert {\varvec{Y}}_m(L)-{\varvec{\varPhi }}_m(L){\varvec{{\theta }}}_m\Vert ^2. \end{aligned}$$

Using negative gradient search and the definitions of \({\varvec{Y}}(L)\) and \({\varvec{Y}}_m(L)\), and minimizing the criterion functions \(J_2({\varvec{{\theta }}}_{1})\) and \(J_3({\varvec{{\theta }}}_m)\) with respect to \({\varvec{{\theta }}}_{1}\) and \({\varvec{{\theta }}}_m\), we can obtain the iterative relations:

$$\begin{aligned} \hat{{\varvec{{\theta }}}}_{1,k}= & {} \hat{{\varvec{{\theta }}}}_{1,k-1}-\mu _{2,k}\textrm{grad}[J_2(\hat{{\varvec{{\theta }}}}_{1,k-1})]\nonumber \\= & {} \hat{{\varvec{{\theta }}}}_{1,k-1}+\mu _{2,k}{\varvec{\varPhi }}^{\textrm{T}}_{1}(L) [{\varvec{Y}}(L)-{\varvec{\varPhi }}_{1}(L)\hat{{\varvec{{\theta }}}}_{1,k-1}]\nonumber \\= & {} [{\varvec{I}}_{n_a+n_b}-\mu _{2,k}{\varvec{\varPhi }}^{\textrm{T}}_{1}(L) {\varvec{\varPhi }}_{1}(L)]\hat{{\varvec{{\theta }}}}_{1,k-1} +\mu _{2,k}{\varvec{\varPhi }}^{\textrm{T}}_{1}(L){\varvec{Y}}(L), \end{aligned}$$
(27)
$$\begin{aligned} \hat{{\varvec{{\theta }}}}_{m,k}= & {} \hat{{\varvec{{\theta }}}}_{m,k-1}-\mu _{3,k}\textrm{grad}[J_3(\hat{{\varvec{{\theta }}}}_{m,k-1})]\nonumber \\= & {} \hat{{\varvec{{\theta }}}}_{m,k-1}+\mu _{3,k}{\varvec{\varPhi }}^{\textrm{T}}_m(L) [{\varvec{Y}}(L)-{\varvec{\varPhi }}_a(L){\varvec{a}}-{\varvec{\varPhi }}_b(L){\varvec{b}}-{\varvec{\varPhi }}_m(L)\hat{{\varvec{{\theta }}}}_{m,k-1}]\nonumber \\= & {} [{\varvec{I}}_m-\mu _{3,k}{\varvec{\varPhi }}^{\textrm{T}}_m(L) {\varvec{\varPhi }}_m(L)]\hat{{\varvec{{\theta }}}}_{m,k-1} +\mu _{3,k}{\varvec{\varPhi }}^{\textrm{T}}_m(L)[{\varvec{Y}}(L)-{\varvec{\varPhi }}_a(L){\varvec{a}}-{\varvec{\varPhi }}_b(L){\varvec{b}}], \end{aligned}$$
(28)

where \(\mu _{2,k}>0\) and \(\mu _{3,k}>0\) are iterative step-sizes and Eqs. (27)–(28) can be seen as two discrete-time systems. To ensure the convergences of \(\hat{{\varvec{{\theta }}}}_{1,k}\) and \(\hat{{\varvec{{\theta }}}}_{m,k}\), all the eigenvalues of matrices \([{\varvec{I}}_{n_a+n_b}-\mu _{2,k}{\varvec{\varPhi }}^{\textrm{T}}_{1}(L) {\varvec{\varPhi }}_{1}(L)]\) and \([{\varvec{I}}_{m}-\mu _{3,k}{\varvec{\varPhi }}^{\textrm{T}}_m(L){\varvec{\varPhi }}_m(L)]\) must be in the unit circle, that is to say \(\mu _{2,k}\) and \(\mu _{3,k}\) should satisfy \(-{\varvec{I}}_{n_a+n_b}\leqslant {\varvec{I}}_{n_a+n_b}-\mu _{2,k}{\varvec{\varPhi }}^{\textrm{T}}_{1}(L) {\varvec{\varPhi }}_{1}(L)\leqslant {\varvec{I}}_{n_a+n_b}\) and \(-{\varvec{I}}_{m}\leqslant {\varvec{I}}_{m}-\mu _{3,k}{\varvec{\varPhi }}^{\textrm{T}}_m(L){\varvec{\varPhi }}_m(L)\leqslant {\varvec{I}}_{m}\), and the conservative choices of \(\mu _{2,k}\) and \(\mu _{3,k}\) are

$$\begin{aligned} 0<\mu _{2,k}\leqslant & {} \frac{2}{\lambda _{\max }[{\varvec{\varPhi }}^{\textrm{T}}_{1}(L){\varvec{\varPhi }}_{1}(L)]} =2\lambda ^{-1}_{\max }[{\varvec{\varPhi }}^{\textrm{T}}_{1}(L){\varvec{\varPhi }}_{1}(L)],\nonumber \\ 0<\mu _{3,k}\leqslant & {} \frac{2}{\lambda _{\max }[{\varvec{\varPhi }}^{\textrm{T}}_m(L){\varvec{\varPhi }}_m(L)]} =2\lambda ^{-1}_{\max }[{\varvec{\varPhi }}^{\textrm{T}}_m(L){\varvec{\varPhi }}_m(L)], \end{aligned}$$

where \(\lambda _{\max }[{\varvec{X}}]\) denotes the maximum eigenvalue of the square matrix \({\varvec{X}}\). The right-hand sides of (27)–(28) contain the unknown parameter vectors \({\varvec{{\theta }}}_{1}\), \({\varvec{{\theta }}}_m\) and the unknown information matrices \({\varvec{\varPhi }}_{1}(L)\) and \({\varvec{\varPhi }}_m(L)\), so we cannot directly compute the estimates \(\hat{{\varvec{{\theta }}}}_{1,k}\) and \(\hat{{\varvec{{\theta }}}}_{m,k}\). The solution is to replace \({\varvec{\varPhi }}_{1}(L)\) in (27) with their estimates \(\hat{{\varvec{\varPhi }}}_{1,k}(L)\), and to replace \({\varvec{\varPhi }}_m(L)\), \({\varvec{a}}\) and \({\varvec{b}}\) in (28) with their estimates \(\hat{{\varvec{\varPhi }}}_{m,k}(L)\), \(\hat{{\varvec{a}}}_k\) and \(\hat{{\varvec{b}}}_k\). We can summarize the H-GI algorithm for the nonlinear feedback system as

$$\begin{aligned} \hat{{\varvec{{\theta }}}}_{1,k}= & {} \hat{{\varvec{{\theta }}}}_{1,k-1}+\mu _{2,k}\hat{{\varvec{\varPhi }}}^{\textrm{T}}_{1,k}(L) [{\varvec{Y}}(L)-\hat{{\varvec{\varPhi }}}_{1,k}(L)\hat{{\varvec{{\theta }}}}_{1,k-1}], \end{aligned}$$
(29)
$$\begin{aligned} \mu _{2,k}\leqslant & {} 2\lambda ^{-1}_{\max }[{\varvec{\varPhi }}^{\textrm{T}}_{1,k}(L){\varvec{\varPhi }}_{1,k}(L)], \end{aligned}$$
(30)
$$\begin{aligned} \hat{{\varvec{{\theta }}}}_{m,k}= & {} \hat{{\varvec{{\theta }}}}_{m,k-1}+\mu _{3,k}\hat{{\varvec{\varPhi }}}^{\textrm{T}}_{m,k}(L) [{\varvec{Y}}(L)-{\varvec{\varPhi }}_a(L)\hat{{\varvec{a}}}_k-{\varvec{\varPhi }}_b(L)\hat{{\varvec{b}}}_k -\hat{{\varvec{\varPhi }}}_{m,k}(L)\hat{{\varvec{{\theta }}}}_{m,k-1}], \end{aligned}$$
(31)
$$\begin{aligned} \mu _{3,k}\leqslant & {} 2\lambda ^{-1}_{\max }[{\varvec{\varPhi }}^{\textrm{T}}_{m,k}(L){\varvec{\varPhi }}_{m,k}(L)], \end{aligned}$$
(32)
$$\begin{aligned} {\varvec{Y}}(L)= & {} [y(1),y(2),\ldots ,y(L)]^{\textrm{T}}, \end{aligned}$$
(33)
$$\begin{aligned} \hat{{\varvec{\varPhi }}}_{1,k}(L)= & {} [\hat{{\varvec{\varphi }}}_{1,k}(1),\hat{{\varvec{\varphi }}}_{1,k}(2), \ldots ,\hat{{\varvec{\varphi }}}_{1,k}(L)]^{\textrm{T}}, \end{aligned}$$
(34)
$$\begin{aligned} \hat{{\varvec{\varPhi }}}_{m,k}(L)= & {} [\hat{{\varvec{\varphi }}}_{m,k}(1),\hat{{\varvec{\varphi }}}_{m,k}(2), \ldots ,\hat{{\varvec{\varphi }}}_{m,k}(L)]^{\textrm{T}}, \end{aligned}$$
(35)
$$\begin{aligned} {\varvec{\varPhi }}_a(L)= & {} [{\varvec{\varphi }}_a(1),{\varvec{\varphi }}_a(2),\ldots ,{\varvec{\varphi }}_a(L)]^{\textrm{T}}, \end{aligned}$$
(36)
$$\begin{aligned} {\varvec{\varPhi }}_b(L)= & {} [{\varvec{\varphi }}_b(1),{\varvec{\varphi }}_b(2),\ldots ,{\varvec{\varphi }}_b(L)]^{\textrm{T}}, \end{aligned}$$
(37)
$$\begin{aligned} \hat{{\varvec{\varphi }}}_{1,k}(t)= & {} [{\varvec{\varphi }}^{\textrm{T}}_a(t), {\varvec{\varphi }}^{\textrm{T}}_b(t)+\hat{{\varvec{q}}}^{\textrm{T}}_{k-1}{\varvec{H}}^{\textrm{T}}(t)]^{\textrm{T}} \end{aligned}$$
(38)
$$\begin{aligned} \hat{{\varvec{\varphi }}}_{m,k}(t)= & {} {\varvec{H}}^{\textrm{T}}(t)\hat{{\varvec{b}}}_{k-1}, \end{aligned}$$
(39)
$$\begin{aligned} {\varvec{\varphi }}_a(t)= & {} [-y(t-1),-y(t-2),\ldots ,-y(t-n_a)]^{\textrm{T}}, \end{aligned}$$
(40)
$$\begin{aligned} {\varvec{\varphi }}_b(t)= & {} [u(t-1),u(t-2),\ldots ,u(t-n_b)]^{\textrm{T}}, \end{aligned}$$
(41)
$$\begin{aligned} {\varvec{H}}(t):= & {} [-{\varvec{h}}^{\textrm{T}}(y(t-1)),-{\varvec{h}}^{\textrm{T}}(y(t-2)),\ldots , -{\varvec{h}}^{\textrm{T}}(y(t-n_b))]^{\textrm{T}}, \end{aligned}$$
(42)
$$\begin{aligned} \hat{{\varvec{{\theta }}}}_{1,k}= & {} [\hat{{\varvec{a}}}^{\textrm{T}}_k,\hat{{\varvec{b}}}^{\textrm{T}}_k]^{\textrm{T}}, \end{aligned}$$
(43)
$$\begin{aligned} \hat{{\varvec{{\theta }}}}_{m,k}= & {} \hat{{\varvec{q}}}_k, \end{aligned}$$
(44)
$$\begin{aligned} \hat{{\varvec{a}}}_k= & {} [\hat{a}_{1,k},\hat{a}_{2,k},\ldots ,\hat{a}_{n_a,k}]^{\textrm{T}}, \end{aligned}$$
(45)
$$\begin{aligned} \hat{{\varvec{b}}}_k= & {} [\hat{b}_{1,k},\hat{b}_{2,k},\ldots ,\hat{b}_{n_b,k}]^{\textrm{T}}, \end{aligned}$$
(46)
$$\begin{aligned} \hat{{\varvec{q}}}_k= & {} [\hat{q}_{1,k},\hat{q}_{2,k},\ldots ,\hat{q}_{m,k}]^{\textrm{T}}. \end{aligned}$$
(47)

The methods proposed in this paper can combine some statistical tools and strategies [84,85,86,87] and identification algorithms [59, 81, 82, 89,90,91] to study the parameter estimation algorithms of other linear and nonlinear stochastic systems and can be applied to other fields [13,14,15,16,17, 52,53,54,55,56,57] such as paper-making and chemical engineering systems. The steps of computing the parameter estimation vectors \(\hat{{\varvec{{\theta }}}}_{1,k}\) and \(\hat{{\varvec{{\theta }}}}_{m,k}\) by the H-GI algorithm in (29)–(47) are listed as follows.

  1. 1.

    To initialize: let \(k=1\), \(\hat{{\varvec{{\theta }}}}_{1,0} =[\hat{a}_{1,0},\ldots ,\hat{a}_{n_a,0}, \hat{b}_{1,0},\ldots ,\hat{b}_{n_b,0}]^{\textrm{T}}\), \(\hat{{\varvec{{\theta }}}}_{m,0} =[\hat{q}_{1,0},\ldots ,\hat{q}_{m,0}]^{\textrm{T}}\) be any real vector, \(r(t-j)=1/p_0\) and \(y(t-j)=1/p_0\), \(j=1,2,\ldots ,\max [n_a,n_b]\), \(t=1,2,\ldots ,L\), \(p_0=10^6\). Set the data length L (\(L\gg n\)), the parameter estimation precision \(\varepsilon >0\) and the basis function \(h(\cdot )\).

  2. 2.

    Collect the input and output data r(t) and y(t), \(t=1,2,\ldots ,L\), and form \({\varvec{Y}}(L)\) by (33).

  3. 3.

    Form \({\varvec{H}}(t)\) by (42), and form \({\varvec{\varphi }}_a(t)\) and \({\varvec{\varphi }}_b(t)\) by (40) and (41), \(t=1,2,\ldots ,L\).

  4. 4.

    Compute \(\hat{{\varvec{\varphi }}}_{1,k}(t)\) and \(\hat{{\varvec{\varphi }}}_{m,k}(t)\) by (38) and (39), \(t=1,2,\ldots ,L\).

  5. 5.

    Form \(\hat{{\varvec{\varPhi }}}_{1,k}(L)\) and \(\hat{{\varvec{\varPhi }}}_{m,k}(L)\) by (34) and (35).

  6. 6.

    Select the large step-sizes \(\mu _{2,k}\) and \(\mu _{3,k}\)according to (30) and (32), and update the parameter estimation vectors \(\hat{{\varvec{{\theta }}}}_{1,k}\) and \(\hat{{\varvec{{\theta }}}}_{m,k}\) by (29) and (31).

  7. 7.

    Read out the parameter estimation vectors \(\hat{{\varvec{a}}}_k\) and \(\hat{{\varvec{b}}}_k\) from \(\hat{{\varvec{{\theta }}}}_{1,k}\) in (43), and \(\hat{{\varvec{q}}}_k\) from \(\hat{{\varvec{{\theta }}}}_{m,k}\) in (44).

  8. 8.

    If \(\Vert \hat{{\varvec{{\theta }}}}_{1,k}-\hat{{\varvec{{\theta }}}}_{1,k-1}\Vert +\Vert \hat{{\varvec{{\theta }}}}_{m,k}-\hat{{\varvec{{\theta }}}}_{m,k-1}\Vert >\varepsilon \), increase k by 1 and go to step 4; otherwise, output the parameter estimates \(\hat{{\varvec{{\theta }}}}_{1,k}\) and \(\hat{{\varvec{{\theta }}}}_{m,k}\), terminate this iterative calculation process.

Remark 4

Previous works presented an overall recursive least squares algorithm and an overall stochastic gradient algorithm to estimate the nonlinear feedback systems disturbed by white noise [93] and proposed a two-stage recursive least squares algorithm for nonlinear feedback systems based on auxiliary model identification [27]. In contrast to the recursive algorithms proposed in [93] and [27], this paper proposes an iterative estimation method for nonlinear feedback systems and introduces the hierarchical principle to reduce the calculation costs and to improve the identification accuracy.

The computational cost for an identification algorithm can be evaluated by the number of floating point operation (flops for short). An addition or multiplication counts as a flop. The computational costs for each iteration of the GI and H-GI algorithms are listed in Tables 1, 2. The total numbers of flops of these two algorithms are \(N_1:=2n^2L+4nL+2L+2mn_b-n^2-m\) and \(N_2:=4L(n_a+n_b+m)+4L+2(n_a+n_b)L+2m^2L+2(n_a+n_b)^2L+2mn_b-m^2-(n_a+n_b)^2-m\), respectively. The difference between the computation loads of these two algorithms at each iteration is \(N_1-N_2=2L((n_a+n_b)(2m-1)-1)+(n_a+n_b)^2+m^2>0\), thus, the H-GI algorithm has less computation load than the GI algorithm.

Table 1 The computational loads of the GI algorithm at each iteration
Full size table
Table 2 The computational loads of the H-GI algorithm at each iteration
Full size table
Table 3 The GI parameter estimates and errors
Full size table
Table 4 The H-GI parameter estimates and errors
Full size table

5 The Simulation Example

Consider the following nonlinear feedback system:

$$\begin{aligned} A(z)y(t)= & {} B(z)[r(t)-\bar{y}(t)]+v(t), \nonumber \\ A(z)= & {} 1+a_1z^{-1}+a_2z^{-2}=1+0.35z^{-1}+0.65z^{-2},\nonumber \\ B(z)= & {} b_1z^{-1}+b_2z^{-2}=1.68z^{-1}-0.32z^{-2},\nonumber \\ \bar{y}(t)= & {} 0.80\sin (y^2(t))+0.60\sin (y^3(t)). \end{aligned}$$

The parameters to be identified are

$$\begin{aligned} {\varvec{\vartheta }}=[a_1, a_2, b_1, b_2, q_1, q_2]^{\textrm{T}} =[0.35, 0.65, 1.68, -0.32, 0.80, 0.60]^{\textrm{T}}. \end{aligned}$$

The simulation of the algorithms in this paper is performed in MATLAB. In the simulation, we set the input and output data and noise as follows.

Fig. 2
figure 2

The GI parameter estimation errors \(\delta \) versus k with different \(\sigma ^2\)

Full size image
Fig. 3
figure 3

The H-GI parameter estimation errors \(\delta \) versus k with different \(\sigma ^2\)

Full size image
Fig. 4
figure 4

The GI estimation errors \(\delta _i\) under different \(\sigma ^2\)

Full size image
Fig. 5
figure 5

The H-GI estimation errors \(\delta _i\) under different \(\sigma ^2\)

Full size image

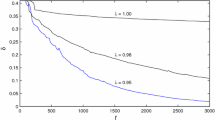
Take the noise variances \(\sigma ^2=1.00^2\), \(\sigma ^2=2.00^2\) and \(\sigma ^2=3.00^2\), respectively, and apply the GI and H-GI algorithms to estimate the parameters of this example system. The parameter estimates and the corresponding errors are given in Tables 3, 4, and the parameter estimation errors \(\delta :=\parallel \hat{{\varvec{\vartheta }}}_k-{\varvec{\vartheta }}\parallel /\parallel {\varvec{\vartheta }}\parallel \) versus k are shown in Figs. 2, 3. In addition, to show the estimation results of each parameter under each algorithm more clearly, define \(\delta _i:=| \hat{\vartheta }_{i,k}-\vartheta _i|/|\vartheta _i|\). Hence, under different noise variances \(\sigma ^2\), the estimation errors \(\delta _i\) of each parameter at \(k=200\) as shown in Figs. 4, 5.

Table 5 The H-GI parameter estimates and errors (\(\sigma ^2=1.00^2\))
Full size table

Apply the H-GI algorithm with the noise variance \(\sigma ^2=1.00^2\) and the data lengths \(L=1000\), \(L=2000\) and \(L=3000\) to identify this example system, respectively. The parameter estimates and the corresponding errors are shown in Table 5, and the parameter estimation errors \(\delta \) versus k are shown in Fig. 6.

Taking the noise variance \(\sigma ^2=1.00^2\), the parameter estimation errors \(\delta \) versus k with different algorithms are plotted in Fig. 7. The GI and H-GI estimates of the parameters \(a_1\), \(a_2\), \(b_1\), \(b_2\), \(q_1\) and \(q_2\) versus k are shown in Figs. 8, 9.

Fig. 6
figure 6

The H-GI parameter estimation errors \(\delta \) versus k with different data length L (\(\sigma ^2=1.00^2\))

Full size image
Fig. 7
figure 7

The GI and H-GI estimation errors \(\delta \) versus k (\(\sigma ^2=1.00^2\))

Full size image
Fig. 8
figure 8

The GI parameter estimates versus k (\(\sigma ^2=1.00^2\)). Asterisk: the parameter estimates, Circle: the true values

Full size image
Fig. 9
figure 9

The H-GI parameter estimates versus k (\(\sigma ^2=1.00^2\)). Asterisk: the parameter estimates, Circle: the true values

Full size image

For model validation, we use the remaining \(L_r=200\) observations from \(t=L_e+1\) to \(t=L_e+L_r\) and the models predicted by the GI and H-GI algorithms with \(\sigma ^2=1.00^2\). The predicted outputs \(\hat{y}_i(t)\) (\(i=1,2\)), the actual outputs y(t) and their errors are plotted in Figs. 10, 11.

The predicted outputs are

$$\begin{aligned} \hat{y}_i(t)= & {} [1-\hat{A}(z)]y(t)+\hat{B}(z)[r(t)-\hat{\bar{y}}(t)]. \end{aligned}$$
(48)

Use the GI estimates in Table 3 with the noise variance \(\sigma ^2=1.00^2\) and \(k=200\) to construct the GI estimated model:

$$\begin{aligned} \hat{y}_1(t)= & {} [1-\hat{A}(z)]y(t)+\hat{B}(z)[r(t)-\hat{\bar{y}}(t)],\nonumber \\ \hat{A}(z)= & {} 1+0.35872z^{-1}+0.65213z^{-2},\nonumber \\ \hat{B}(z)= & {} 1.68640z^{-1}-0.30294z^{-2},\nonumber \\ \hat{\bar{y}}(t)= & {} 0.79598\sin (y^2(t))+0.56727\sin (y^3(t)),\nonumber \\ \hat{{\varvec{\vartheta }}}= & {} [\hat{a}_1, \hat{a}_2, \hat{b}_1, \hat{b}_2, \hat{q}_1, \hat{q}_2]^{\textrm{T}}\nonumber \\= & {} [0.35872, 0.65213, 1.68640, -0.30294, 0.79598, 0.56727]^{\textrm{T}}. \end{aligned}$$

Use the H-GI estimates in Table 4 with the noise variance \(\sigma ^2=1.00^2\) and \(k=200\) to construct the H-GI estimated model:

$$\begin{aligned} \hat{y}_2(t)= & {} [1-\hat{A}(z)]y(t)+\hat{B}(z)[r(t)-\hat{\bar{y}}(t)],\nonumber \\ \hat{A}(z)= & {} 1+0.35576z^{-1}+0.65136z^{-2},\nonumber \\ \hat{B}(z)= & {} 1.68515z^{-1}-0.31432z^{-2},\nonumber \\ \hat{\bar{y}}(t)= & {} 0.79648\sin (y^2(t))+0.56761\sin (y^3(t)),\nonumber \\ \hat{{\varvec{\vartheta }}}= & {} [\hat{a}_1, \hat{a}_2, \hat{b}_1, \hat{b}_2, \hat{q}_1, \hat{q}_2]^{\textrm{T}}\nonumber \\= & {} [0.35576, 0.65136, 1.68515, -0.31432, 0.79648, 0.56761]^{\textrm{T}}. \end{aligned}$$

To evaluate the prediction performance, we define and compute the root-mean-square errors (RMSEs):

$$\begin{aligned} Error(\hat{y}_1(t)):= & {} \left[ \frac{1}{L_r}\sum _{t=L_e+1}^{L_e+L_r} [\hat{y}_1(t)-y(t)]^2\right] ^{\frac{1}{2}}=1.00249,\nonumber \\ Error(\hat{y}_2(t)):= & {} \left[ \frac{1}{L_r}\sum _{t=L_e+1}^{L_e+L_r} [\hat{y}_2(t)-y(t)]^2\right] ^{\frac{1}{2}}=1.00206. \end{aligned}$$
Fig. 10
figure 10

The predicted outputs \(\hat{y}_1(t)\), the actual outputs y(t) and their errors versus t based on the GI estimates

Full size image
Fig. 11
figure 11

The predicted outputs \(\hat{y}_2(t)\), the actual outputs y(t) and their errors versus t based on the H-GI estimates

Full size image

From Tables 3, 4, 5 and Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, we can draw the following conclusions.

  • Throughout the entire simulation process, shown in Tables 3, 4 and Figs. 2, 3, 4, 5, we find that the parameter estimation errors of the GI and H-GI algorithms decrease as the iteration number k increases, and the estimation accuracy improves as the noise level reduces. However, the H-GI algorithm yields more exact estimates than the GI algorithm under the same iteration and noise variance—see Fig. 7.

  • For the same noise variance, the parameter estimation errors of the H-GI algorithm become smaller as the data length L and iteration k increase—see Table 5 and Fig. 6.

  • For sufficiently large data length, the parameter estimates of the GI and H-GI algorithms gradually approach the true values with the increase of the iteration k, which verifies the effectiveness of the GI and H-GI algorithms—see Figs. 8, 9.

  • The predicted outputs of the GI and H-GI algorithms verge on the true values and the differences between them are small—see Figs. 10,11. This shows that the estimated models based on the GI and H-GI algorithms have good prediction performance and can acquire the dynamics of the feedback nonlinear systems well.

6 Conclusions

This paper studies the parameter identification problem for nonlinear feedback system. By negative gradient search, a GI algorithm is derived for estimating the unknown parameters. Inspired by the hierarchical identification principle, the nonlinear feedback system is decomposed into two subsystems and an H-GI algorithm is proposed for the nonlinear feedback system. Compared with the GI algorithm, the H-GI algorithm has a higher computational efficiency and a comparable parameter estimation accuracy. The simulation results demonstrate the performance of the proposed algorithms. The approaches presented in this paper can be extended to investigate the modeling and optimization of some production and process systems [22, 88, 107, 108] and can be applied to other control and schedule areas [3,4,5,6,7,8,9,10,11,12] such as information processing systems and transportation communication systems [71,72,73,74,75,76,77,78] and so on.