1 Introduction

The dynamics of wave packets in the ocean is driven by dispersion and weak nonlinearity in deep and intermediate water depth. Therefore, both key features have been well-studied and understood in such water depth conditions. Assuming uni-directionality of wave propagation, it is also well-known that narrow-band wave trains can become unstable and undergo a focusing process, also referred to as modulation instability (Dudley et al. 2019). That said, waves in shallow coastal areas are stable to long wave perturbations; however, the latter undergo breaking, which is driving sediment transport (Elfrink and Baldock 2002), marine erosion (Zhang et al. 2004) and other complex coastal processes. With the increase of ocean wave heights over the last decades (Young and Ribal 2019), it is becoming evident to expect more damaging waves reaching shorelines according to the trend described in (Martins et al. 2017). As such, extreme wave transformation process modeling in the surf and near-shore zones will become increasingly relevant, for instance in the assessment of large swell-impact on the shoreline (Baldock and Holmes 1999; Baldock and Huntley 2002; Kimmoun and Branger 2007; Didenkulova et al. 2007; Viotti et al. 2014). Several experimental studies have investigated the fundamental characteristics of nonlinear wave propagation over a variable bathymetry, using deterministic frameworks (Shemer et al. 1998), and extreme wave statistics (Zeng and Trulsen 2012; Trulsen et al. 2012; Gramstad et al. 2013; Kashima and Mori 2019; Zhang et al. 2019; Trulsen et al. 2020; Li et al. 2021b). Recently, the role of second-order effects in the formation of extreme events for narrow-band linear wave packets (Li et al. 2021c; Li et al. 2021a) and the transformation of narrow-band nonlinear wave groups (Ducrozet et al. 2021), both experiencing sudden depth transitions, have been highlighted. Simplified weakly nonlinear model have been suggested since the late 1970s to predict water wave dynamics over variable bathymetry in finite water depth (Djordjević and Redekopp 1978; Grimshaw and Annenkov 2011; Slunyaev 2005). These take into account the variation of dispersion and nonlinearity with the change of water depth as well as bottom friction effects. A rigorous multiple scales approach can be applied to the Euler equations (Hasimoto and Ono 1972; Mei et al. 2005) to derive such wave evolution equations. In the case of energy-conserved narrow-band wave fields in deep-water, the latter models reduce to the famous nonlinear Schrödinger equation (Zakharov 1968). The depth-adapted nonlinear Schrödinger equation (DNLS) as proposed in (Djordjević and Redekopp 1978) can be considered as the simplest deterministic nonlinear wave model, which takes into account third-order effects and can be utilized to analyze steep wave packets undergoing a run-up process. We emphasize that directional effects are crucial for an accurate description of coastal wave dynamics and extreme wave events (Holthuijsen 2010), particularly, during interactions with the bathymetry in shallow zones: refraction, diffraction and sediment transport are also essential and non-negligible processes. Nevertheless, understanding the key properties’ variations of uni-directional wave packets is an essential starting point towards a deterministic and statistical prediction of coastal extreme wave shoaling physics. Such weakly nonlinear models can be also implemented to address more complex and realistic configurations (Mei et al. 2005; Klein et al. 2020).

Our experimental study aims to track and predict the behavior of unstable and steep wave groups, also known as breathers, while propagating over linearly varying beds. We particularly focus on wave packets which undergo modulation instability in deep-water and then evolve into a relatively shallow water zone. In this context, shallow water regime is characterized by dimensionless depth values kh (k and h being the wavenumber and water depth, respectively) below 1.363. In such conditions, it is known that modulation instability cannot be triggered or unfold (Mei et al. 2005) as a result of disappearance of third-order nonlinear interactions (Yuen and Lake 1982). It is shown that when the floor has a gentle inclination the breather wave packets tend to quickly decay. On a steep slope, however, breathers last longer and even propagate far into the shallow water kh < 1.363 region, as has recently been conjectured (Kashima and Mori 2019). Since these unstable wave groups can be considered as extreme waves, we assume that the lifetime of some large-amplitude waves formed in deep water can be extended when making their way into shallow regions over a steep slope. All breather transformation measurements show a very good agreement with the DNLS model. We have extended our experimental investigation to uni-directional JONSWAP-type wave fields, which undergo the same shoaling process as the deterministic breathers. The evaluation of skeweness and kurtosis show that the DNLS is only accurate when the wave field is narrow-band.

2 Steep wave packets modeling in variable water depth

Starting point of our deterministic model validation for wave groups evolving over a variable water depth is the so-called DNLS (Djordjević and Redekopp 1978).

$$ \begin{array}{@{}rcl@{}} \text{i}\left( \frac{\partial {{\varPsi}}}{\partial x}+ \frac 1{c_{g}}\frac{\partial {{\varPsi}}}{\partial t}\right)&=& \alpha \frac{\partial^{2} {{\varPsi}}}{\partial t^{2}}+\beta|{{\varPsi}}|^{2}{{\varPsi}}\\ &&-\text{i}\mu\frac{\text{d}(kh)}{\text{d}x}{{\varPsi}} - \text{i} \mathfrak{D} {{\varPsi}}, \end{array} $$
(1)

where

$$ \begin{array}{@{}rcl@{}} \sigma&=& \tanh(kh),\\ \omega&=&\sqrt{gk\sigma},\\ c_{p}&=&\frac{\omega}{k},\\ c_{g}&=&\frac{\partial\omega}{\partial k},\\ \alpha&=&\frac 1{2 \omega c_{g}}\left [1-\frac{gh}{c_{g}^{2}}(1-kh\sigma)\left( 1-\sigma^{2}\right) \right],\\ \beta&=&\frac{k^{4}}{4\omega \sigma^{2}c_{g}} \left [9-10 \sigma^{2}+9 \sigma^{4}-\frac{2 \sigma^{2} c_{g}^{2}}{gh-c_{g}^{2}}\right.\\ &&\left.\left( 4\frac{c_{p}^{2}}{c_{g}^{2}}+ \frac{4c_{p}}{c_{g}}(1-\sigma^2)+ \frac{gh}{c_{g}^{2}}\left( 1-\sigma \right)^{2} \right)\right], \\ \mu&=&\frac{(1-\sigma^{2})(1-kh\sigma)}{{\sigma+kh(1-\sigma^{2})}}, \end{array} $$

and \(\mathfrak {D}\) being a supplementary linear dissipation rate parameter. g is the gavitational acceleration and ω the wave frequency while cp and cg denote the phase and group velocity, respectively.

When considering the case of energy conservation and deep-water condition, Eq. 1 reduces to the famed NLS (Zakharov 1968; Osborne 2010). When kh > 1.363 the NLS is known to model Stokes waves, which undergo modulation instability. This latter process can also emerge in the ocean (Zakharov and Ostrovsky 2009; Annenkov and Shrira 2009; Babanin 2011; Waseda 2020). There are different ways to trigger or generate such unstable steep wave groups in a laboratory environment, i.e. in water wave tanks (Dudley et al. 2019). One possibility to initiate the modulation instability (Benjamin and Feir 1967) is to seed side-bands within the instability frequency range (Tulin and Waseda 1999; Houtani et al. 2018) or simply by using deterministic Akhmediev breathers (ABs), which are known to describe the nonlinear stage of modulation instability (Akhmediev et al. 1985; Chabchoub et al. 2017). Details on the respective parametrization in hydrodynamics can be found in Kimmoun et al. (2016). Note that when adopting the latter breather parametrization for a given modulated carrier wave with amplitude a, wavenumber k and wave frequency ω, the breather parameter \(\mathfrak {a}\) is related to the modulation frequency Ω by \(\mathfrak {a}=\frac {1}{2}-\frac {{{\varOmega }}}{2\sqrt {2}ak\omega }\). The evolution of the respective wave trains over a pre-defined bottom topography profile following Eq. 1 is determined numerically by integrating the envelope along the co-ordinate x of wave direction using the split-step method.

3 Experimental and numerical set-up

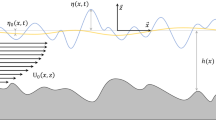
The laboratory experiments have been conducted in two large-scale water wave flumes, which we will refer to as the midsize and the large tank. Both facilities are installed at the Tainan Hydraulics Laboratory of the National Cheng-Kung University in Taiwan. The waves are generated using a hydraulic piston wave maker while the evolution of the free surface is measured using 48 capacitance wave gauges, which were installed along both facilities in the direction of wave propagation. The artificial and linearly varying floors as installed in these facilities are made of concrete with a smooth surface. Schematics of both facilities together with the locations of the wave gauges and the inclined floors are shown in Fig. 1

Fig. 1
figure 1

Water wave facilities, in which the experiments have been conducted, including the location of the wave gauges and the artificial floor slopes. Top: midsize tank. Bottom: large tank

Full size image

The exact dimensions of both facilities are described in Table 1.

Table 1 Dimensions of the two water wave tanks in which the experiments have been conducted
Full size table

Different bottom topographies have been installed. The characteristics of these artificial bathymetries are given in Table 2.

Table 2 Bed bathymetry properties in the corresponding water wave flume
Full size table

The slope values of the two floor sections in each tank is 1/40 followed by 1/200 in the midsize tank and 1/188 followed by 1/100 for the large tank.

The initial temporal wave profiles, as imposed to the wave maker, have been programmed to initiate either periodically modulated and unstable wave trains or irregular wave fields which satisfy referenced JONSWAP sea states (Hasselmann et al. 1973). In order to start the instability from very small amplitude modulation the initial unstable side-band amplitudes as modeled by the breather have been determined to achieve the maximal focusing at the dimensionless depth condition kh = 1.363, where the switch to shallow-water conditions occurs. Both facilities provide sufficient propagation distance for the instability to develop and decline. It is obvious that the variations of the local water depth parameter kh and the wave steepness ak are crucial in this type of experiment. This will be shown and discussed in the next section.

Finally, the numerical scheme, used for the integration of the DNLS, was adapted according to the parameters of the studied model. It is based on the robust split-step method, which has been proven to be very stable and accurate in the integration of weakly nonlinear evolution equations. We refer to Hardin and Tappert (1973) for more details.

4 Wave group shoaling

4.1 Deterministic evolution of unstable wave groups

We start reporting on breather experiments, which have been conducted in the midsize facility with a major gentle slope section as described in the previous Section. The initial modulationally unstable wave train has a frequency of f = 0.92 Hz and a wave amplitude a = 0.02 m while the modulation frequency, as imposed by the breather dynamics, corresponds to the case of maximal growth rate Ω = 0.45 s− 1. The maximal envelope compression is expected to occur 76.2 m from the wave maker, which corresponds to the location in which the dimensionless threshold depth condition kh = 1.363 is satisfied. The evolution of the unstable modulated wave train while the comparison with DNLS simulations are shown in Fig. 2.

Fig. 2
figure 2

Left: Evolution of narrow-band wave field, subject to modulation instability, as expected from DNLS. Right: evolution of the measured wave field in the midsize wave tank. Top: evolution of the wave envelope. Bottom: evolution of the wave train at different gauge locations. The wave amplitude and wave steepness are a = 0.020 m and ak = 0.07, respectively, while the modulation frequency is Ω = 0.45 s− 1

Full size image

Note that the wave envelope can be easily extracted from the surface measurements using the Hilbert-transform (Osborne 2010). Indeed, we can clearly observe an excellent focusing and defocusing trend between the deterministic and expected wave transformation as described by the DNLS and the wave measurements in the tank. This is also confirmed in the next experiment, which have been performed in the same wave facility and visualized in Fig. 3.

Fig. 3
figure 3

Same as Fig. 2. The wave amplitude and wave steepness are a = 0.026 m and ak = 0.09, respectively, while the modulation frequency is Ω = 0.51 s− 1

Full size image

Here, the frequency, amplitude and modulation frequency are f = 0.92 Hz, a = 0.026 m and Ω = 0.51 s− 1, respectively. That is, the corresponding steepness is now ak = 0.09. This is very encouraging when considering the location of wave focusing reached, the significant propagation distance as well as the complex wave-bottom interaction effects at play. Obviously, wave reflection is inevitable and the reflection coefficient has been quantified to be of 11% for both experiments conducted in the midsize facility.

Before discussing the envelope compression and de-compression process, we will present the results of the experiments conducted in the larger facility with having a steeper large slope section. The first case corresponds to carrier parameters a = 0.075 m and f = 0.6 Hz, which define a carrier steepness of ak = 0.11. Also here, the boundary conditions have been determined to fulfill a maximal wave focusing at kh = 1.363. The modulation frequency has been chosen to be Ω = 0.27 s− 1. The respective measurements and comparison with the DNLS estimations are represented in Fig. 4. The reflection coefficient is 4.6% in this case.

Fig. 4
figure 4

Same as Figs. 2 and 3. The wave amplitude and wave steepness are a = 0.075 m and ak = 0.11, respectively, while the modulation frequency is Ω = 0.27 s− 1

Full size image

Another experiment has been performed by the increasing the value of amplitude to a = 0.088 m and Ω = 0.30 s− 1 while keeping the same wave frequency. Thus, we have increased the value of wave steepness to ak = 0.13. The experimental and numerical evolution is shown in Fig. 5. The reflection coefficient here is 7%.

Fig. 5
figure 5

Same as Figs. 2, 3 and 4. The wave amplitude and wave steepness are a = 0.088 m and ak = 0.13, respectively, while the modulation frequency is Ω = 0.30 s− 1

Full size image

Once again, the measured wave field evolution is in good agreement with the simplified weakly nonlinear theory as described by Eq. 1.

It is also interesting to compare the lifetime trend of the wave focusing in the presence of gentle-inclination steep floor in the midsize tank with the steeper but still moderate inclination in the large facility. It is particularly insightful to understand the wave packet dynamics in the wave flume around the dimensionless depth of kh = 1.363, a region where the deep-water four-wave interactions are expected to weaken while second-order effects remain active. At this dimensionless depth value the nonlinear coefficient in the Schrödinger equation vanishes and wave packets are stable below this value (Johnson 1977).

The evolution profiles provide a qualitative understanding of the focusing behavior of unstable wave groups approaching shallow regions. When the floor has a mild inclination, the steep wave packets decay even before reaching kh = 1.363. In contrast, when the slope is rather steep, the (rogue) wave envelopes keep their extreme form over a large distances in relatively shallow regime. The reported wave behavior is in agreement with the recent numerical study (Lyu et al. 2021). We now focus on tracking the maxima and minima of the unstable wave group data around the threshold of kh = 1.363, see Fig. 6.

Fig. 6
figure 6

Evolution of normalized maxima and minima of the upper wave envelope. Top left: case as in Fig. 2. Bottom left: case as in Fig. 3. Top right: case as in Fig. 4. Bottom right: case as in Fig. 5

Full size image

Note that the dissipation and friction resulting from the interaction of the waves with the floor play a key role in the evolution as suggested by the modeling. This attests that deep-water wave groups, which are subject to modulation instability, may in fact maintain their large amplitudes and pervade far into shallow waters when the continental slope is steep, as previously reported in Kashima and Mori (2019) and Lyu et al. (2021) while the DNLS is well-suited to describe such steep wave group (breather) hydrodynamics. Since we have carried out the experiments with different wave steepness values, we conjecture that third-order nonlinear interactions are substantial when unstable wave packets propagate over steep linear slopes before and after kh = 1.363 as a result of a slow relaxation of the four-wave resonance in the shallow zone (Trulsen et al. 2020). On similar but mild inclinations on the other hand, third-order interactions considerably weaken and the role of second-order effects appear to be more dominant in such configurations (Li et al. 2021a). Moreover, observed breather wave groups experience a generic broadening as has been reported by Didenkulova et al. (2013).

4.2 Irregular wave evolution

In this subsection, we turn our attention to the DNLS model validation for irregular and therefore more broadband wave processes as modeled according to the JONSWAP-spectrum parametrization (Hasselmann et al. 1973)

$$ \begin{array}{@{}rcl@{}} S(f)=\frac{\alpha}{f^{5}}\exp\left[-\frac{5}{4}\left( \frac{f_{p}}{f}\right)^{4}\right]\gamma^{\exp\left[-\frac{\left( f-f_{p}\right)^{2}}{2\sigma^{2}{f_{p}^{2}}}\right]}. \end{array} $$
(3)

We chose a representative peakedness parameter γ of 3.3 and 7 to investigate the role and influence of the bandwidth on the DNLS model accuracy. These experiments have been conducted in the large tank, and thus, only in the facility with the initial very mild, followed by the steeper bottom slope configuration. Characteristic relevant indicators for the wave statistics are the skewness and kurtosis (Mori and Janssen 2006; Zhang et al. 2019), which are key parameters to assess the role of second- and third-order nonlinear effects, respectively. Moreover, we investigate the role of nonlinearity in the shoaling process by including depth-adapted linear Schrödinger equation (DLS) simulations. We will not introduce the Benjamin-Feir index (BFI) in this study, since it is well-known that the kurtosis depends on the square of BFI (Mori and Janssen 2006). All experiments have been conducted with a peak frequency of fp = 0.4 Hz, therefore the condition kh = 1.363 is satisfied at 52 m from the wave maker. The results for γ = 3.3 while Hs = 0.10 m and Hs = 0.12 m are shown in Fig. 7.

Fig. 7
figure 7

Evolution of skewness and kurtosis for fp = 0.4 Hz and a JONSWAP peakedness parameter of γ = 3.3. Left: Hs = 0.10 m. Right: Hs = 0.12 m. Red lines: DNLS simulations; Black lines DLS simulations; Blue lines: experimental values

Full size image

The results suggest that both DLS and DNLS simulations match reasonably well the experimental skewness values, including its peak; however, the kurtosis prediction is far to be accurate and the mismatch can be observed for both significant wave height values chosen. We conclude that such weakly nonlinear models are not sufficiently accurate for the description of such broadband processes and that second-order effects from wave steepness are highly likely to govern such evolution hydrodynamics (Lyu et al. 2021; Li et al. 2021b). In the very shallow region, the wave process appears to be dominated by purely linear effects and the wave field does not relax back to a pure Gaußian process. We surmise that the latter might be due to wave reflection, which is very challenging to quantify for the broadband JONSWAP wave field adopted. The next experiment comprise an increased JONSWAP peakedness parameter value of 7. The comparison of skewness and kurtosis variation with the DLS and DNLS simulations for this case are reported in Fig. 8.

Fig. 8
figure 8

Evolution of skewness and kurtosis for fp = 0.4 Hz and a JONSWAP peakedness parameter of γ = 7. Left: Hs = 0.10 m. Right: Hs = 0.12 m. Red lines: DNLS simulations; black lines DLS simulations; blue lines: experimental values

Full size image

We can confirm that the agreement with the experimental skewness and kurtosis values have been significantly improved in this case. The relaxation and convergence of the kurtosis parameter back to three in the shallow region after the experienced shoaling peak is well-captured by the DNLS, suggesting the significance of third-order nonlinearities for this narrow-band and nonlinear wave trains propagating on linear bottom topographies while the skewness is significantly influenced by second-order effects in the shoaling process. These results are indeed in agreement with the extensive nonlinear Schrödinger-based numerical simulations recently published (Lyu et al. 2021). Overall, our results confirm the usefulness of the DNLS in the accurate modelling of narrow-band and uni-directional waves undergoing a run-up.

5 Conclusion

We have reported an experimental study for the purpose of weakly nonlinear model validation for uni-directional water waves evolving over uneven bottom topographies. Both, time-periodic steep wave groups (breathers) and irregular JONSWAP wave fields with two distinct significant wave height values and two peakedness parameters have been considered in this study. The DNLS model, which captures dispersion, weak nonlinearity, water depth variation and simplified bottom friction effects, has been used to track intrinsic wave field characteristics as measured in large-scale water wave facilities with different linear slopes. When investigating breathers, it is found that when these unstable wave packets propagate over a gentle slope, the wave amplitudes attenuate quickly and the focusing is not significant. This highlights the dominant role of second-order terms from wave steepness while four-wave interactions gradually weaken during the propagation. Then again, when the breather propagate over a steeper slope the third-order effects appear to be crucial even for kh < 1.363 and consequently, the focused wave amplitudes persist and remain large in the shallow zone. All surface elevations measured along the water wave facilities are in very good agreement with the DNLS model. For the case of JONSWAP wave fields, we conjecture that independently of the significant wave height chosen, the DNLS is very accurate when considering narrow-band wave processes (γ = 7) and substantially loses its high accuracy in forecasting the kurtosis peak and its decay when broadening the spectrum (γ = 3.3). All JONSWAP cases show a relaxation of the wave filed to a (nearly-)Gaußian process in very shallow regions.

We cannot draw a final conclusion on the role of the nonlinear four-wave interactions in the wave shoaling process due to the limited cases considered here. Nevertheless, our conclusions are in line with the recent findings (Trulsen et al. 2020; Zhang and Benoit 2021; Lyu et al. 2021; Li et al. 2021b). We intend to explore supplementary types of linear and nonlinear wave packet transformations as next. In addition, future studies will be focusing on considering additional bottom topography designs and extending the range of spectral bandwidth. Moreover, we will adopt more sophisticated nonlinear wave models to improve the understanding of extreme wave hydrodynamics and statistics in coastal areas.