Chaotic Time Series Prediction Using Random Fourier Feature Kernel Least Mean Square Algorithm with Adaptive Kernel Size

Abstract

The random Fourier feature kernel least mean square (RFF-KLMS) algorithm provides a finite dimensional approximation to the kernel least mean square algorithm with radially symmetric Gaussian kernel. RFF-KLMS was introduced to curb the continuously growing radial basis function (RBF) network which prohibits online application of KLMS. RFF-KLMS assumes a fixed kernel size and the application of the method in nonlinear online regression can be quite tedious because it is not always obvious which kernel size to choose for a particular problem. In this paper, we incorporate a stochastic gradient approach in RFF-KLMS to update the kernel size. The efficacy of the new approach is demonstrated in the online prediction of time series generated from two different chaotic systems. In both examples, the RFF-KLMS algorithm with adaptive kernel size demonstrates very good tracking ability.

The authors would like to acknowledge the financial support from Universiti Sains Malaysia through Research University Grant (RUI) (acc. No. 1001/PMATHS/8011040).

1 Introduction

Modeling of processes in complex systems can be divided into two basic approaches; i) the study of mathematical models which tries to capture the most important qualitative features of the complex systems behavior, ii) the reconstruction of the underlying structure of a nonlinear dynamical system from measured data with use of methods of mathematical statistics, statistical learning, data mining and so on. The second approach is more popularly known as time-delay embedding (also known as the Taken’s delay embedding theorem [1]). The theorem states that the dynamics of a system (i.e. the attractor) can be reconstructed from vectors of time-shifted (shift T) states of single variable with nested dimension N

$$\mathbf{x} (t) = (x(t),x(t + T),...,x(t + \left[ N - 1\right] T))^T,$$

where $N > 2d_A+1$ and $d_A$ is the dimension of the attractor. Takens embedding theorem lays the foundation for nonlinear time series analysis that allows for the reconstruction of complete system dynamics using a single time series [1]. Although the initial motivation of the theorem was to look for chaotic behaviour in experimental systems, the potential use of the method in a broader range of signal processing activities was soon recognized [2, 3].

Recent developments in chaotic time series prediction witness an increasing number of effort in online time series prediction [4,5,6,7,8,9,10,11]. Online prediction is a sequential or adaptive learning process where the underlying pattern representations from time series data are extracted in a sequential manner. When new data arrive at any time, they are observed and learned by the system. In addition, as soon as the learning procedure is completed, the observations are discarded, without having the necessity to store too much historical information. The online learning setting is significantly in contrast with offline learning, where the learning process has access to the entire data, and is able to go through the data multiple times to train a model, leading to higher accuracy than their online counterparts. Nonlinear online learning [12,13,14] has drawn a considerable amount of attention as it captures nonlinearity in the data which cannot be effectively modeled in a linear online learning method, and usually achieves better accuracy. One group of nonlinear online learning is based on kernels, that is, kernel-based online learning.

Kernel adaptive learning is a class of kernel-based online learning which are derived in Reproducing Kernel Hilbert Space (RKHS) [15]. In contrast to nonlinear approximators such as the polynomial state-space models [16] and neural networks [10], kernel based learning inherits the convex optimization of its linear counterparts. Typical algorithms from the kernel adaptive filtering (KAF) family include Kernel Least Mean Square (KLMS) [17], Kernel Recursive Least Square [18], Kernel Affine Projection Algorithms [19], Extended Kernel Recursive Least Squares [20]. KLMS is by far the simplest to implement and has been proven to be computationally efficient. In KLMS (and KAFs in general), the solution is given in terms of a linear expansion of kernel functions (centered at the current input data). This linear expansion grows with each incoming data rendering its application prohibitive both in terms of memory as well as computational resources. The centers that make up the linear expansion of solution constitutes the so-called dictionary. Sparsification methods [21, 22] are commonly used to keep the dictionary sufficiently small, however they too require significant computational resources.

A more recent trend in curbing the ever growing structure of the KAFs algorithm is by using approximation methods such as the Nystrom method [23] and the random Fourier features (RFF) [24,25,26,27]. While the Nystrom based method is data-dependent, the RFF based methods are drawn from a distribution that is randomly independent from the training data hence providing a good solution in non-stationary circumstances. The RFF-KLMS algorithm [24, 25] can be seen as a finite-dimensional approximation of the conventional KLMS algorithm, in which the kernel function is approximated by a finite-dimensional inner products. The RFF-KLMS algorithm has been proven to provide good approximation of the Gaussian kernel due to its symmetry and the shift-invariant property [25, 26]. The normalized Gaussian kernel is

$$\begin{aligned} \kappa (\mathbf{x} (i),\mathbf{x} (j)) = e^{-\Vert \mathbf{x} (i) - \mathbf{x} (j) \Vert ^2/2\sigma ^2}, \end{aligned}$$

(1)

where $\sigma > 0$ is the kernel size. In both KLMS and RFF-KLMS, the kernel size is treated as a free parameter which is often manually set. The choice of kernel size can be very different from one data set to another, therefore to choose an appropriate kernel size, one may have to resort to empirical approach. Although there are various methods to choose kernel size in batch learning such as using cross validation [28,29,30], penalizing functions [31] and plug-in methods [31, 32], these methods are computationally intensive and unsuitable for online kernel learning.

In this paper, we introduce a variant of the RFF-KLMS algorithm which allows the kernel size to be adapted using a stochastic gradient method. This technique for adapting kernel size is similar to the technique used in [33, 34]. The effectiveness of our method is demonstrated through the online prediction of chaotic time series generated by two dynamical systems, 1) the Lorenz system, and, 2) the chaotic system proposed by Zhang et al. [36]. The rest of this paper is structured as follows: In Sect. 2 we give a description of nonlinear regression in RKHS, and extend the discussion to online regression via KLMS and RFF-KLMS algorithms in Sect. 3. In Sect. 4, we provide an outline of the RFF-KLMS algorithm with adaptive kernel size, followed by example applications in Sect. 5. Finally, we present the conclusion in Sect. 6.

2 Nonlinear Regression in RKHS

Assume we have a discrete system generating a time series at a single time step forward of the form $\{x(1), x(2), x(3), \dots , x(n), \dots \}$, a general nonlinear prediction model of the time series is of the form [1, 2, 37, 38]

$$x(n+1) \approx y(n) = F(\mathbf{x} (n)) \in V,$$

where $\mathbf{x} (n) = [x(n), x(n-1), \dots , x(n-N+1)]^T$, V is a vector space which we hope to contain the attractor that explains the long-term dynamics of the time series, and $N > 2d_A + 1$ where N is the dimension of V and $d_A$ is the dimension of the attractor. If the basis functions of V is known, ${\phi _1(.), \phi _2(.), \dots , \phi _N(.)}$ say, then we may write F as a linearly separable function in terms of the basis functions so that

$$y(n) = \varPhi (\mathbf{x} (n))^T\mathbf{w} = w_1\phi _1(\mathbf{x} (n)) + w_2\phi _2(\mathbf{x} (n)) + \dots + w_N\phi _N(\mathbf{x} (n)).$$

The least squares approach to determining the parameters $\mathbf{w} = [w_1,w_2, \dots , w_N]^T$ requires the minimization of a loss function of the form

$$\begin{aligned} f(\mathbf{w} ) = \sum _{i=1}^{n} \left| x(i+1) - \mathbf{w} ^T\varPhi (\mathbf{x} (i))\right| ^2. \end{aligned}$$

(2)

This problem is just a standard nonlinear regression and this is the approach used in [16, 39, 40] where the basis functions are assumed to be from a class of universal approximators. The difficulty in this approach is that the state space V is most likely infinite dimensional which means N has to be very large to achieve sufficiently accurate prediction.

Alternatively one can avoid working with $\varPhi$ directly by transforming vectors in the state space construction into the so-called Reproducing Kernel Hilbert space (RKHS). Let $\mathbf{x} (1), \mathbf{x} (2), \dots , \mathbf{x} (n) \in \mathbb {R}^N$ and let the RKHS be $\mathcal {H}$. The similarity between the elements in $\mathcal {H}$ is measured using its associated inner product $(.,.)_{\mathcal {H}}$ and it is computed via a kernel function $\kappa : \mathbb {R}^N \times \mathbb {R}^N \rightarrow \mathbb {R}$ such that $(\mathbf{x} _i, \mathbf{x} _j) \rightarrow \kappa (\mathbf{x} _i, \mathbf{x} _j)$. For positive definite kernel functions, we can ensure that for all $\mathbf{x} , \mathbf{x} ' \in \mathbb {R}^N$,

$$\begin{aligned} (\varPhi (\mathbf{x} ), \varPhi (\mathbf{x} '))_{\mathcal {H}} = \kappa (\mathbf{x} , \mathbf{x} '). \end{aligned}$$

(3)

The property in (3) is called the ‘kernel trick’ [41]. In RKHS, the optimum prediction model, if determined using the least squares approach, is a minimization problem of the form

$$\begin{aligned} \min _\mathbf{w \in \mathbb {R}^N} \sum _{i=1}^{n} \left| x(i+1) - (\mathbf{w} ,\varPhi (\mathbf{x} (i))\right| ^2. \end{aligned}$$

(4)

The loss function in (4) can be written as

$$\begin{aligned} f(\mathbf{w} ) = \Vert \hat{\mathbf{x }} - \mathbf{K} {} \mathbf{w} \Vert ^2 = \hat{\mathbf{x }}^T\hat{\mathbf{x }} - 2\hat{\mathbf{x }}^T\mathbf{K} {} \mathbf{w} + \mathbf{w} ^T\mathbf{K} ^T\mathbf{K} {} \mathbf{w} , \end{aligned}$$

(5)

where

$$\hat{\mathbf{x }} = [x(2),x(3),\dots ,x(n+1)]^T, \mathbf{K} = [\varPhi (\mathbf{x} (1), \varPhi (\mathbf{x} (2)), \dots , \varPhi (\mathbf{x} (n))]^T.$$

Matrix $\mathbf{G} = \mathbf{K} ^T\mathbf{K}$ has entries $\mathbf{G} _{ij} = (\varPhi (\mathbf{x} (i)),\varPhi (\mathbf{x} (i))_\mathcal {H} = \kappa (\mathbf{x} (i),\mathbf{x} (j))$ which is positive definite if the kernel function $\kappa (.,.)$ is positive definite. As a consequence, the loss function in (5) is a convex function and the problem in (4) is a convex minimization. To guarantee a convex minimization problem, in the rest of the paper, we adopt the Gaussian kernel in (1).

3 Online Regression in the RKHS via Kernel Least Mean Square Algorithm

In the online scenario, data is collected one at a time in a sequential manner and only a limited set of the most current data is stored while older data are discarded. In this situation, due to the incomplete knowledge of the data set, the loss function (5) needs to be estimated in order to determine the regression parameters. One way to perform online regression is to use the instantaneous approximation of (5), where at any particular time n the current prediction of the time series is of the form $(\varPhi (\mathbf{x} (n)),\mathbf{w} )_\mathcal {H}$ and the estimated loss function is given by

$$\begin{aligned} f_{inst}(\mathbf{w} ) = (e(n))^2 = (x(n+1) - (\varPhi (\mathbf{x} (n)),\mathbf{w} )_\mathcal {H})^2. \end{aligned}$$

(6)

A gradient based minimization of (6) searches for the optimum parameter vector $\mathbf{w}$ along the negative instantaneous gradient direction which is given by

$$\begin{aligned} -\nabla _\mathbf{w }f(\mathbf{w} ) = 2e(n)\varPhi (\mathbf{x} (n)). \end{aligned}$$

(7)

The update equation for $\mathbf{w}$ is then

$$\begin{aligned} \mathbf{w} (n+1) = \mathbf{w} (n) + \mu e(n)\varPhi (\mathbf{x} (n)). \end{aligned}$$

(8)

Assuming $\mathbf{w} (0) = 0$, it can be shown that [15]

$$\begin{aligned} \mathbf{w} (n) = \mu \sum _{i=0}^{n-1}e(i)\varPhi (\mathbf{x} (i)). \end{aligned}$$

(9)

As a result, the current prediction can be update as follows:

$$\begin{aligned} y(n) = (\varPhi (\mathbf{x} (n)),\mathbf{w} (n))_H= & {} \mu \sum _{i=0}^{n}e(i)(\varPhi (\mathbf{x} (n)),\varPhi (\mathbf{x} (i))_\mathcal {H} \nonumber \\= & {} \mu \sum _{i=0}^{n}e(i)\kappa (\mathbf{x} (n),\mathbf{x} (i)). \end{aligned}$$

(10)

It is clear from (10) that the current prediction can be computed using only knowledge of the kernel function.

Next, we describe two online gradient based algorithms which attempt to minimize the instantaneous estimated loss function (6).

3.1 The KLMS Algorithm

A straightforward implementation of (7)–(10) leads to the Kernel Least Mean Square (KLMS) algorithm. The basic sequential rule for KLMS is as follows:

Input: Training samples $\{(x(n),d(n))\}$, step-size $\mu$, kernel function $\kappa (.,.)$, set $y(0) = 0$

For $n = 1, 2, \dots$

$\hat{y}(n) = \sum _{i=0}^{n-1}e(i)\kappa (\mathbf{x} (n),\mathbf{x} (i))$

$e(n) = d(n) - y(n-1)$

$y(n) = \hat{y}(n) + \mu e(n)\kappa (\mathbf{x} (n),.)$

where $\hat{y}(n)$ is the apriori prediction. The apriori prediction is an ever-growing sum; the size of the sum grows with each update and it relies on the entire dictionary $\{\mathbf {x}(1), \mathbf {x}(2), \dots , \mathbf {x}(n-1)\}$. The ever-growing dictionary size results in an increase in computational resources and memory, thus making the application of KLMS rather prohibitive.

3.2 Random Fourier Feature KLMS (RFF-KLMS)

The prediction in the KLMS algorithm is achieved by first mapping the state vector $\mathbf{x} (n)$ to an infinite dimensional RKHS $\mathcal {H}$, using an implicit map $\phi (\mathbf{x} (n))$, and with the help of the kernel trick, computes the prediction after n data updates as a linear expansion (10) which grows indefinitely as n increases. To overcome the growing sum problem, Rahimi and Recht [24] proposed mapping the state-space vector $\mathbf{x} (n)$ onto a finite dimensional Euclidean space using a randomized map $\varTheta : \mathbb {R}^N \rightarrow \mathbb {R}^D$. The Bochner’s theorem [42] guarantees that the Fourier transform of a positive definite, appropriately scaled, shift-invariant kernel is a probability density, $p(\theta )$ say, such that

$$\begin{aligned} k(\mathbf{x} (i) - \mathbf{x} (j))= & {} k(\mathbf{x} (i),\mathbf{x} (j)) \nonumber \\= & {} \int _{R^N} p(\theta )e^{j\theta ^T(\mathbf{x} (i) - \mathbf{x} (j)}d\theta = E[\varTheta (\mathbf{x} (i))^H\varTheta (\mathbf{x} (j))], \end{aligned}$$

(11)

where, the last equality in (11) is obtained by defining $\varTheta (\mathbf{x} ) = e^{j\theta ^T\mathbf{x} }$ (H is the conjugate transpose). According to [43], given (11), the D-dimensional random Fourier feature (RFF) of the state-space vector $\mathbf{x} (n)$ that can approximate $\kappa (.,.)$ with $L_2$ error less than $O(1/\sqrt{D})$ is given by

$$\begin{aligned} \varTheta (\mathbf{x} ) = \left[ \psi _1(\mathbf{x} ), \psi _2(\mathbf{x} ), \dots , \psi _D(\mathbf{x} )\right] ^T, \end{aligned}$$

(12)

where $\psi _i(\mathbf{x} )= \sqrt{2}\cos (\theta _{i}^{T}{} \mathbf{x} + b_i)$, $i = 1,2,\dots ,D$, with $\theta _i \in R^N$. In other words, $\varTheta (\mathbf{x} (i))^H\varTheta (\mathbf{x} (j))$ is an unbiased estimate of $\kappa (\mathbf{x} (i),\mathbf{x} (j))$ when $\theta$ is drawn from p. Here we exploit the symmetric property of $\kappa (.,.)$ in which case $\varTheta (\mathbf{x} (n))$ can be expressed using real-valued cosine bases. For approximating a Gaussian kernel of size $\sigma$ given in (1), $\theta _i$ is drawn from the Gaussian distribution with zero-mean and covariance matrix $\frac{1}{\sigma ^2}{} \mathbf{I} _N$ with $\mathbf{I} _N$ being an $N \times N$ identity matrix, and, $b_i$ is uniformly sampled from $[0,2\pi ]$ [26, 44].

With the finite dimensional map $\varTheta (.)$ defined by (12), the prediction at time n is just $\varTheta (\mathbf{x} (n))^T\mathbf{w}$, and the instantaneous loss function is then

$$\begin{aligned} F_{inst}(\mathbf{w} ) = (e(n))^2 = (x(n+1) - \varTheta (\mathbf{x} (n))^T\mathbf{w} )^2. \end{aligned}$$

(13)

It follows that, the negative instantaneous gradient direction with respect to $\mathbf{w}$ is $-\nabla _\mathbf{w} F(\mathbf{w} ) = 2e(n)\varTheta (\mathbf{x} (n))$ which results in an update equation for $\mathbf{w}$ in the form

$$\begin{aligned} \mathbf{w} (n+1) = \mathbf{w} (n) + \mu e(n)\varTheta (\mathbf{x} (n)). \end{aligned}$$

(14)

The update equation in (14) results in the RFF-KLMS algorithm and it requires a computational complexity of a fixed linear order which is O(D). Mean square convergence of RFF-KLMS is presented in [45].

4 RFF-KLMS with Adaptive Kernel Size

In the KLMS and the RFF-KLMS algorithm described in this paper, the kernel function is defined in the form given in (1). This definition requires knowledge of a pre-determined parameter which is the kernel size $\sigma$. In the large sample size regime, the asymptotic properties of the mean square approximation are independent of $\sigma$, i.e., the choice of $\sigma$ does not affect the convergence of KLMS and RFF-KLMS. However, $\sigma$ does affect the dynamics of the algorithm. In particular, in the transient stage when the sample size is small, an optimal kernel size is important to speed up the convergence to the neighbourhood of the optimal solution.

A method for adjusting $\sigma$ in a sequential optimization framework is proposed in [33] for the KLMS algorithm. An update equation for $\sigma$ is derived from the minimization of the instantaneous loss function (6) and optimizing it along the negative gradient direction (with respect to $\sigma$), i.e.,

$$\sigma _{n+1}=\sigma _n -\rho \frac{\partial f_{inst}}{\partial \sigma _{n}},$$

where $\sigma _n$ is the kernel size at time n and $\rho$ is a step-size parameter. The resulting update equation is given by

$$\begin{aligned} \sigma _{n+1} = \sigma _n + \rho e(n-1)e(n)\Vert \mathbf{x} (n-1) - \mathbf{x} (n)\Vert _{2}^{2}\frac{\kappa _{\sigma _n}(\mathbf{x} (n-1), \mathbf{x} (n))}{\sigma _{n}^{3}}. \end{aligned}$$

(15)

Since RFF-KLMS is an approximation of KLMS in a D dimensional space, the update equation in (15) can also be used to adapt the kernel size in the RFF-KLMS algorithm. In RFF-KLMS, the kernel size determines the probability density function $p(\theta )$ from which $\theta _i$ ($i=1,2,\dots ,N$) is drawn. Thus, adjusting $\sigma$ also means adjusting $\theta$. To incorporate this adjustment in the algorithm, we initialize $\theta _i$ with an N-dimensional vector drawn from the Gaussian distribution with zero-mean and covariance matrix $I_N$. At each update at time n, a new vector $\theta _{i}^{(n)}$ is used in place of $\theta _i$, where $\theta _{i}^{(n)}$ is drawn from the Gaussian distribution with zero-mean and covariance matrix $\frac{1}{\sigma _{n}^{2}}I_N$. The complete algorithm is summarized in Table 1.

Table 1 The RFF-KLMS algorithm with adaptive kernel size

5 Simulation Examples

In this section, we present several examples to illustrates the performance and application of RFF-KLMS algorithm with adaptive kernel size in short-term prediction of chaotic time series. Two chaotic systems are used: i) the Lorenz system [35], and, ii) the chaotic system proposed by Zhang et al. [36].

5.1 Example 1: Lorenz Chaotic System

Consider the Lorenz oscillator whose state equations are

$$\begin{aligned} \frac{dx}{dt}= & {} -\beta x + yz \nonumber \\ \frac{dy}{dt}= & {} \delta (z - y) \\ \frac{dz}{dt}= & {} -xy + \lambda y - z \nonumber \end{aligned}$$

(16)

where parameters are set as $\beta = 8/3$, $\delta = 10$ and $\lambda = 28$. Sample time series of x, y and z are given in Fig. 1. The goal is to predict x(t), y(t) and z(t) using the previous eight consecutive samples. The well-known Lorenz attractor is observable in 3-dimensional space (i.e. $d_A = 3$), therefore it is reasonable to choose $N = 8 > 2d_A +1$.

Mean Squared Error (MSE) Performance. First, we compare the performance of RFF-KLMS with fixed kernel sizes ($\sigma = 1, 2, 5$) and RFF-KLMS with adaptive kernel size. The parameter values used in this experiment are as follows: $\mu = 0.5$, $\rho =0.005$ and $D = 500$.

Fig. 1

Time series of the three states in the Lorenz system

Fig. 2

(Left) Comparison of MSE performance of RFF-KLMS between fixed kernel sizes ($\sigma = 1, 2, 5$) and adaptive kernel size. (Right) Evolution of adaptive kernel size in the course of iteration

For each kernel size, 20 independent (Monte Carlo) simulations are run with different segments of the time series. In each segment, 1000 samples are used for training and a further 100 samples are used for testing. To evaluate the convergence behaviour of the algorithm, the mean squared error (MSE) is used which is defined as MSE = $(\sum _{i}^{n_{test}} \hat{e}(i)^2)/n_{test}$, where $n_{test}$ is the length of test data. The ith test error $\hat{e}(i)$ is computed based on the test data using the learned weight vector $\mathbf{w} (n)$ and $\sigma _n$ at that iteration, i.e., $\hat{e}(i) = x_{test}(i+1) - \varTheta _{\sigma _n}(\mathbf{x} _{test}(i))^T\mathbf{w} (n)$. All simulation results are averaged over 20 Monte Carlo runs.

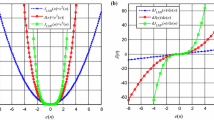
Convergence of MSE for each kernel size is shown in Fig. 2(left). It can be seen that RFF-KLMS achieves the best performance in terms of convergence as well as achieving the minimum steady-state MSE. The evolution of the value of kernel size during the learning process is shown in Fig. 2(right) where it is observed that the steady-state (optimum) kernel size is about 3.2. The steady-state MSE for the training and testing are listed in Table 2. The relative sizes of training and testing MSE are comparable between all kernel sizes which shows that tendency to overlearn is comparable between all kernel sizes.

Prediction. Here we present the time series and the associated Lorenz attractor. The predicted Lorenz attractor is constructed based on the values of the predictions at steady-state.

The Constructed Time Series. Due to space limitation, only the learned prediction of state variable x is presented and this is shown in Fig. 3. The prediction is compared for different values of the kernel size. As expected, the predicted model trained using RFF-KLMS with adaptive kernel size is able to capture the dynamics of the time series optimally at steady-state.

Table 2 Steady-state MSE

Fig. 3

Predicted time series for state variable x during training

Construction of the Lorenz Attractor. Next we reconstruct the Lorenz attractor using the steady-state prediction of state variables x, y and z. For ease of comparison, we choose to present the views of the predicted Lorenz attractor in the 2D planes (x, y) and (x, z) respectively. In Fig. 4, the plots on the left depicts the phase reconstruction using our trained model while the plots on the right depicts the actual Lorentz attractor. It is clearly observed that RFF-KLMS has successfully captured the overall structure of the attractor.

Predicting Sudden Change in Dynamics. In online prediction it is important to analyze the ability of an algorithm to track a time series which is subjected to sudden changes. In order to do so, we have created two time series, $(x^{(1)},y^{(1)},z^{(1)})$ and $(x^{(2)},y^{(2)},z^{(2)})$, each of which is generated from Lorenz systems with two different values of the parameter $\lambda$ (the other two parameters are fixed, i.e., $\beta = 10/3$ and $\delta = 10$). The time series $(x^{(1)},y^{(1)},z^{(1)})$ is generated with $\lambda = 28$ while the time series $(x^{(2)},y^{(2)},z^{(2)})$ is generated with $\lambda = 15$. These two values results in two completely different dynamics; $\lambda = 28$ results in time series that lie in an invariant manifold associated with the Lorenz chaotic attractor while $\lambda = 15$ results in an invariant manifold associated with a stable focus.

Tracking of Time Series. Only the tracking of the time series of state variable x is shown for the purpose of illustration and this is found in Fig. 5 (Top). The sudden change in the time series occurs at sample $n = 5861$. The corresponding evolution of kernel size $\sigma _n$ during the tracking process in shown in Fig. 5 (Bottom). It is clearly seen in Fig. 5 that, as the RFF-KLMS algorithm tracks the optimum kernel size the predicted time series becomes more similar to the actual time series. Moreover, once the optimum kernel size is found, minimal adaptation is needed to detect the change in dynamics.

Fig. 4

Lorenz attractor in (x, y) plane (top) and in the (x, z) plane (bottom): Predicted (left), original (right)

Fig. 5

Tracking sudden changes in the time series: Sudden change occurs at sample $n = 5861$

Tracking of Invariant Manifolds. The invariant manifolds are reconstructed from the predicted time series x, y and z. The views of the predicted invariant manifolds in the 2D planes (x, y) and (x, z) are presented in Figs. 6 and 7 respectively. In both Figs. 6 and 7, the top figure depicts the predicted manifolds while the bottom figure depicts the actual observed manifolds. It is evident from these figures that, regardless of the sudden change in $\lambda$ at $n = 5861$, the overall structure of the manifolds before and after the change have clearly been captured well. This results confirm the extremely good tracking ability of the RFF-KLMS algorithm with adaptive kernel size.

Fig. 6

Lorenz system: Invariant manifold in (x, y) plane. Predicted (top), original (bottom)

Fig. 7

Lorenz system: Invariant manifold in (x, z) plane. Predicted (top), original (bottom)

5.2 Example 2: Chaotic System by Zhang et al. [36]

The chaotic system proposed in [36] is a system of differential equations in term of state variables x, y and z given by

$$\begin{aligned} \frac{dx}{dt}= & {} -ax + by - yz \nonumber \\ \frac{dy}{dt}= & {} x + xz\\ \frac{dz}{dt}= & {} cz + y^2 \nonumber \end{aligned}$$

(17)

where parameters are set as $a = 10$, $b = 28$ and $c = 6$. In this section, all experiments are conducted using noisy time series where the time series of x, y and z are corrupted by zero-mean Gaussian noise with variance 0.01, 0.1 and 1, with equivalent signal-to-noise ratio (SNR) of 40.8 dB, 30.8 dB and 20.8 dB respectively.

Prediction. Prediction of the chaotic attractor of (17) is done for the three SNR values: 40.8 dB, 30.8 dB and 20.8 dB. The predicted chaotic attractor is constructed based on the values of the time series predictions at steady-state.

The Constructed Time Series. For the purpose of illustration, only the prediction of state variable x is presented and this is shown in Fig. 8. The prediction is compared for different SNR values. Here it is observed that the decrease in SNR value (i.e. increase in noise strength) does have some effect on the accuracy of predictions. Table 3 provides a list of the steady-state training MSE for the three different values of SNR from which one can see the increase in steady-state MSE as SNR decreases. This gives a quantitative measure of the decrease in performance as noise strength increases.

Fig. 8

Predicted time series for state variable x during training

Table 3 Steady-state MSE for different SNR values

Construction of the Chaotic Attractor. The choice of the parameters $a = 10$, $b = 28$ and $c = 6$ is associated with a chaotic attractor [36]. Using the steady-state prediction of state variables x, y and z, the projections of the attractor in the 2D planes (x, y) and (x, z) are reconstructed and for all the SNR values used in the experiments, it is observed that RFF-KLMS is able to capture the overall structure of the attractor. However the accuracy of the trajectories tend to reduce as SNR value decreases. As an illustration, the reconstruction of the chaotic attractor in the (x, y) plane is shown in Fig. 9 for the three SNR values.

Fig. 9

Reconstruction of the chaotic attractor in the (x, y) plane for different levels of noise strength

Predicting Sudden Change in Dynamics. To investigate the capibility of the RFF-KLMS algorithm with adaptive kernel size in predicting change in dynamics, we have created two time series, $(x^{(1)},y^{(1)},z^{(1)})$ and $(x^{(2)},y^{(2)}, z^{(2)})$, each of which is generated from (17) with two different values of the parameter c (the other two parameters are fixed, i.e., $a = 10$ and $b = 28$). The time series $(x^{(1)},y^{(1)},z^{(1)})$ is generated with $c = 6$ while the time series $(x^{(2)},y^{(2)}, z^{(2)})$ is generated with $c = 158$. These two values results in two completely different dynamics; $c = 6$ results in time series that lie in an invariant manifold associated with the chaotic attractor while $c = 158$ results in an invariant manifold associated with a stable limit cycle [36]. To study the capability of RFF-KLMS in predicting the change in dynamics in the presence of noise, zero-mean Gaussian noise with variances 0.01 (SNR = 40.8 dB), 0.1 (SNR = 30.8 dB) and 1 (SNR = 20.8 dB) is added to both time series.

Tracking of Time Series. Only the tracking of the time series of state variable x is shown for the purpose of illustration. The sudden change in the time series occurs at sample $n = 6197$. The steady-state time series obtained with clean input signal x is compared with the steady-state time series obtained for input signals having SNR 40.8 dB, 30.8 dB and 20.8 dB respectively and the result is shown in Fig. 10. It is clearly seen in Fig. 10 that the sudden change in dynamics is successfully detected by RFF-KLMS algorithm with adaptive kernel size and its ability does not appear to be affected much by the presence of noise. Although some accuracy is loss in the predicted time series when SNR = 20.8 dB, but the overall behaviour of the time series is quite apparent.

Fig. 10

Comparison of the predicted time series for the state variable x with and without noise: Sudden change in the time series occurs at $n = 6197$.

Tracking of Invariant Manifolds. The invariant manifolds are reconstructed from the predicted time series x, y and z obtained for input signals having SNR 40.8 dB, 30.8 dB and 20.8 dB respectively and the results are compared with the invariant manifold obtained from clean input signal. The views of the predicted invariant manifolds in the 2D planes (x, y) and (x, z) are shown in Figs. 11 and 12 respectively for the most severe case (i.e. SNR = 20.8 dB). In both Figs. 11 and 12, the top figure depicts the predicted manifolds for $c = 6$ while the bottom figure depicts the predicted manifolds for $c = 158$. It is evident from these figures that, regardless of the sudden change in c at $n = 6197$, the overall structure of the manifolds before and after the change have clearly been captured well. The presence of noise somewhat affects the accuracy of trajectories within the manifold, but the presence of the invariant structures are still evident. This results further confirm the robustness of the RFF-KLMS algorithm with adaptive kernel size.

Fig. 11

Invariant manifold in (x, y) plane: c = 6 (top), c = 158 (bottom), clean input signal (left), noisy input signal (right)

Fig. 12

Invariant manifold in (x, z) plane: c = 6 (top), c = 158 (bottom), clean input signal (left), noisy input signal (right)

6 Conclusion

The kernel size in RFF-KLMS determines the probability density function from which the random features are drawn. In other words, it determines the finite dimensional subspace defines by the feature maps in RFF-KLMS. Quality of approximation by RFF-KLMS is directly determined by this subspace. Therefore, for optimal finite-dimensional mapping, optimal kernel size is needed.

In this paper, we described a procedure for optimizing the kernel size sequentially using a stochastic gradient descent approach. Empirical studies on online prediction of chaotic time series highlights the tracking capability of RFF-KLMS with adaptive kernel size. It not only tracks the time series and the ensuing dynamics of the system well, but the algorithm is also capable of predicting sudden change in dynamics. MSE performance of RFF-KLMS algorithm with adaptive kernel size is also more superior than the MSE of RFF-KLMS with fixed kernel size. The experimental results also highlight the robustness of the algorithm with respect to noise in the input signal. Although some loss in accuracy is observed in the presence of noise, the algorithm can still capture the overall steady-state dynamics of a system.

An immediate future direction of this study is to explore other aspects of the algorithm, for example, combining kernel size adaptation with stepsize adaptation. It is also interesting to investigate the application of RFF-KLMS with adaptive kernel size to look into the possibility of predicting other aspects of system dynamics such as the Lyapunov exponent.