1 Introduction

1.1 Previous work

The least mean square (LMS) algorithm is the most widely used algorithm for adaptive filters because of its low-cost. However, it suffers from slow convergence rate and its performance may degrade when the measurement noise is non-Gaussian noise. To address these problems, several LMS-type algorithms were proposed, including sign algorithms [22, 39], adjustable step size algorithms [16, 21, 62], and algorithms that employ the convex combination method [19, 32, 36]. Apart from these algorithms, some approaches have been developed for combating non-Gaussian interference, such as entropy criterion [24, 25, 38] and M-estimate [66, 67].

An important issue in adaptive prediction is the effect of measurement noise on the results. The measurement noise is often assumed to be a random process with finite second-order statistics (SOS), making the mean square error (MSE) performs well for prediction. However, in real-world situations, the noise may not possess finite SOS and can be described more accurately using non-Gaussian noise models [24, 57]. When adaptive algorithms are used in time series prediction with non-Gaussian noise, it is reasonable to take the higher order information of measurement noise and error signal into account.

The loss functions based on the high-order error power (HOEP) criterion are a good solution to learn with non-Gaussian data in general [45]. The HOPE-based algorithms, which are derived by minimizing the p-norm, can achieve improved performance in the presence of non-Gaussian noise. For \(p=2\), it reduces to the LMS algorithm. When the signal is contaminated by impulsive noise, the sign algorithm with \(p=1\) is preferred [22, 39]. If we select \(p=3\), the HOEP becomes the least mean absolute third (LMAT) algorithm [23, 45, 65], and for the choice of \(p=4\), the least mean-fourth (LMF) algorithm is obtained [18, 48]. It is worth to note that both LMAT and LMF algorithms outperform the conventional LMS algorithm for the case where the measurement noise is a non-Gaussian noise. Furthermore, many variants based on the mixed-norm and p-power (\(1<p<2\)) were proposed for suppressing specific noises, such as those proposed in [5, 8, 9, 31, 33, 43] and references therein.

Kernel method has become rather popular and has been successfully applied to machine learning [47, 51], kernel principal component analysis [46, 63], and information/signal processing [2,3,4, 7, 20, 29, 64]. Due to its universal nonlinear-modeling capability, the kernel adaptive filters (KAFs) have attracted considerable attention. The main idea of the KAF is that recast the input data into a high-dimensional feature space via a reproducing kernel Hilbert space (RKHS). Then, the linear adaptive filter is applied in the feature space [29]. Based on these considerations, several kernel adaptive algorithms were proposed, e.g., kernel LMS (KLMS) algorithms [13, 27, 38, 55, 58, 60], kernel recursive least squares (KRLS) algorithms [14, 17, 26], and kernel affine projection (KAPAs) [10, 28, 54]. By applying the minimum error entropy (MEE) criterion to KAF, Chen et al. proposed the kernel minimum error entropy (KMEE) algorithm and its quantized version [11]. As we noticed, the KMEE algorithm has moderate computational complexity and achieves improved performance in low impulsive noise environment. To further improve the performance of KAF in the presence of \(\alpha \)-stable noise, Chen et al. proposed some KAFs based on maximum correntropy criterion (MCC) [52, 59], which can diminish the significance of the outliers on the nonlinear system. Alternatively, to improve the performance of the KAF, an interesting and effective way is to use p-norm and mixed-norm criterions. Several classes of KAFs for nonlinear estimation have been proposed, including [30, 35, 37, 41, 49]. Particularly, Ma et al. [37] developed the kernel least mean p-power (KLMP) and the kernel recursive least mean p-power (KRLP) algorithms, which overcome the performance degradation of the algorithm when training data are corrupted by impulsive noises. However, the adaptation of KLMP and KRLP is largely dependent on p, and it is necessary for the prior knowledge or estimation of p in the presence of \(\alpha \)-stable noise. Very recently, the KAFs based on diffusion LMS and suitable for nonlinear distributed network were proposed [15, 42]. These algorithms follow the Adapt-Then-Combine (ATC) mode of cooperation and can be extended to the distributed parameter estimation applications like cooperative spectrum sensing and massive multiple input multiple output (MIMO) receiver design [42]. Although the above-mentioned algorithms have some advantages, they carry one main drawback in common: the algorithms are not suitable for different noise environments.

Table 1 Aforementioned contributions
Full size table

1.2 Motivation

In the last decades, the fields of adaptive signal processing have witnessed remarkable advances in cost function based on the HOEP criterion. Closer to the LMAT loss is the LMF function (LMF algorithm) [48], which minimizes the fourth power of the error signal, but its stability about the Wiener solution depends upon the adaptive filter input power and noise power [48]. Moreover, the LMF algorithm with Gaussian noise is not mean square stability even for a small step size. The LMAT loss function, in contrast, has a stable performance in Gaussian scenarios and its convergence performance only depends on the power of the input signal [65]. The advantages of using the LMAT loss function are listed as below. (1) The LMAT loss is a convex function, so it has no local minima. (2) When the measurement noise is non-Gaussian processes, the LMAT may have better optimum solution than the Wiener solution. Another closer to the LMAT loss is the work of Chambers et al. [9] which combines the error norms and can deal with non-stationary signal statistics through an appropriate combination. In [41], Miao and Li proposed the kernel least mean mixed-norm (KLMMN) algorithm for nonlinear system identification. However, the selection of the mixing parameter of the KLMMN algorithm may prohibit its practical applications. Table 1 summarizes the aforementioned contributions. According to this table, the KAF based on LMAT loss has not been developed. From the above analysis, we can see that the use of LMAT loss in kernel method is reasonable.

1.3 Contributions of this paper

The contribution of this paper is threefold. (1) To improve the robustness of KAF against interferences with various probability densities, we proposed a kernel LMAT (KLMAT) algorithm. Moreover, the stability and convergence property analysis of the KLMAT algorithm are performed. (2) To address the conflicting requirement of fast convergence rate and low steady-state prediction error for the fixed learning rate, a novel variable learning rate (VLR) adjustment process based on the Lorentzian function is incorporated into the KLMAT algorithm. (3) The recursive version of the KLMAT algorithm is developed for time series prediction. The motivation in developing this kernel extension is based on the KRLS algorithm. The weights in the kernel at each iteration are solved recursively by an exponentially weighted mechanism, which emphasizes on recent data and de-emphasizes data from the remote past.

This paper is structured as follows. In Sect. 2, we briefly review the kernel method. In Sect. 3, a KLMAT and a VLR–KLMAT algorithms are proposed based on the kernel method. In Sect. 4, we analyze the convergence property of the KLMAT algorithm. In Sect. 5, an extension of KLMAT is developed. In Sect. 6, we show the advantages of our proposal through some simulation results. Finally, in Sect. 7, we give the conclusion.

Fig. 1
figure 1

a Comparison of the cost functions. b The gradients of the cost functions

Full size image

2 Kernel method

Kernel method is a powerful nonparametric modeling tool. The key to kernel method is transforming input data (input space \({\mathbb {U}})\) into a high-dimensional feature space \({\mathbb {F}}\) by using a certain nonlinear mapping

$$\begin{aligned} {\varvec{\varphi }} :{\mathbb {U}}\rightarrow {\mathbb {F}} \end{aligned}$$
(1)

where \({\varvec{\varphi }}\) is the feature vector in kernel method. To apply the kernel method in linear adaptive filter, the kernel function \(\kappa \) is developed. As a result, the inner product operations in the linear adaptive filters are translated into the calculation of a kernel function \(\kappa \) in the feature space without knowing the nonlinear mapping.

By using the Mercer theorem [29], the inner products in RKHS can be calculated as

$$\begin{aligned} \kappa ({{\varvec{u,{u}}}}')={{\varvec{\varphi }}} {{\varvec{(u)}}}{\varvec{\varphi }} ^{T}({{\varvec{u}}}') \end{aligned}$$
(2)

where u is the input data. It is well known that Mercer kernel is a continuous, symmetric, and positive-definite kernel. Thus, the output of KAF can be expressed by the inner product with test data \({\varvec{\varphi }} {{\varvec{(u)}}}\) and training data \({\varvec{\varphi }} ({{\varvec{u}}}_j )\)

$$\begin{aligned} f{{\varvec{(u)}}}=\sum _{j=1}^n {a_j \langle {\varvec{\varphi }} {{\varvec{(u)}}},} {\varvec{\varphi }} ({{\varvec{u}}}_j )\rangle \end{aligned}$$
(3)

where \(a_j\) is the coefficient n and \(\langle \cdot \rangle \) is the inner product operation, respectively.

3 Proposed algorithms

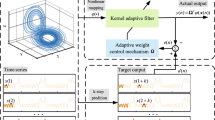
3.1 KLMAT algorithm

To improve the performance of the KLMS algorithm, the LMAT algorithm is first applied in RKHS. This strategy yields a novel KAF (KLMAT) for adaptive prediction. The \(M\times 1\) input data \({{\varvec{u}}}(n)=\left[ {u(n),u(n-1),\ldots ,u(n-1+M)} \right] \) at time n are transformed into RKHS as \({\varvec{\varphi }} ({{\varvec{u}}}(n))\). For convenience of notation, \({\varvec{\varphi }} ({{\varvec{u}}}(n))\) is replaced by \({\varvec{\varphi }} (n)\) throughout this paper. The weight vector \({{\varvec{w}}}(n)\) in feature space is defined as \({\varvec{\Omega }}(n)\). Define \({\varvec{\Omega }}(1)=\mathbf{0}\) and the error signal \(e(n)=d(n)-{\varvec{\Omega }}^{T}(n){\varvec{\varphi }} (n)\), where d(n) denotes the desired signal. The cost function of KLMAT algorithm is defined as

$$\begin{aligned} J(n)\buildrel \Delta \over = \left| {e(n)} \right| ^{3}. \end{aligned}$$
(4)

As shown in Fig. 1a, J(n) is less steep than \(J_{LMF}(n)\) and both are steeper than a quadratic function. Because the cost function J(n) is much steeper than the square of the error, the value of the gradient is significantly larger than that of the gradient of the squared error with respect to the coefficients (Fig. 1b). Therefore, the kernel algorithm with LMAT loss function converges faster than the KLMS algorithm for a given constant learning rate.

Minimizing the instantaneous third power of absolute error value, the adaptation of KLMAT algorithm in RKHS can be expressed as

$$\begin{aligned} {\varvec{\Omega }}(n+1)={\varvec{\Omega }}(n)-\frac{\mu }{3}\nabla _{{\varvec{\Omega }}(n)} J(n) \end{aligned}$$
(5)

where \(\nabla _{{\varvec{\Omega }}(n)} J(n)=-3e^{2}(n)sign\{e(n)\}{\varvec{\varphi }} (n)\) is the gradient vector, \(\mu \) is the learning rate (step size), and \(sign\{x\}\) denotes the sign function of the variable x, i.e., if \(x\ge 0\), then \(sign\{x\}=1\), otherwise \(sign\{x\}=-1\). Thus, we can use (5) to obtain a recursion on the new example sequence \(\{{\varvec{\varphi }} (n),d(n)\}\)

$$\begin{aligned} {\varvec{\Omega }}(n+1)={\varvec{\Omega }}(n)+\mu e^{2}(n)sign\{e(n)\}{\varvec{\varphi }} (n). \end{aligned}$$
(6)

Repeating the application of (6), we obtain

$$\begin{aligned} {\varvec{\Omega }}(n+1)= & {} {\varvec{\Omega }}(n-1)+\mu e^{2}(n-1)\nonumber \\&\times \,sign\{e(n-1)\}{\varvec{\varphi }} (n-1)\nonumber \\&+\,\mu e^{2}(n)sign\{e(n)\}{\varvec{\varphi }} (n). \end{aligned}$$
(7)

Rearranging (7), we have

$$\begin{aligned} {\varvec{\Omega }}(n+1)=\mu \sum _{j=1}^n {\left[ {e^{2}(j)sign\{e(j)\}} \right] } {\varvec{\varphi }} (j). \end{aligned}$$
(8)

Here, \({\varvec{\varphi }} (n)\) is only implicitly known and its dimensionality is infinite for the Gaussian kernel. For this reason, the derivation method of the KLMS algorithm [27] is adopted to the KLMAT algorithm. That is, compute the filter output \(y(n+1)\) directly rather than expressing the weight vector. By using the Mercer kernel, the filter output can be calculated through kernel evaluations

$$\begin{aligned} y(n+1)= & {} {\varvec{\Omega }}^{T}(n){\varvec{\varphi }} (n+1)\nonumber \\= & {} \mu \sum _{j=1}^n {\left[ {e^{2}(j)sign\{e(j)\}} \right] } \kappa (j,n+1) \end{aligned}$$
(9)

where \(\kappa ({{\varvec{u,{u}}}}')=\exp \left( {-h\left\| {{{\varvec{u-{u}}}}'} \right\| ^{2}} \right) \) stands for the Gaussian kernel and h denotes the kernel size. The KLMAT algorithm adds a new space \(e(n)sign\{e(n)\}\) for \({{\varvec{u}}}(n+1)\) at each iteration, slightly increasing the computational complexity as compared with the KLMS algorithm. We define \(f_n\) as a nonlinear mapping at the nth iteration, and the learning process of the KLMAT algorithm can be summarized as follows:

$$\begin{aligned} f_n= & {} \mu \mathop {\varvec{\sum }}\limits _{j=1}^n {\left[ {e^{2}(j)sign\{e(j)\}} \right] } \kappa ({{\varvec{u}}}(j),\cdot ),\nonumber \\ f_n ({{\varvec{u}}}(n))= & {} \mu \mathop {\varvec{\sum }}\limits _{j=1}^n {\left[ {e^{2}(j)sign\{e(j)\}} \right] } \kappa ({{\varvec{u}}}(j),{{\varvec{u}}}(n+1)),\nonumber \\ e(n+1)= & {} d(n+1)-f_n ({{\varvec{u}}}(n+1)),\nonumber \\ f_{n+1}= & {} f_n +\mu e^{2}(n+1)sign\{e(n+1)\}\nonumber \\&\,\times \, \kappa ({{\varvec{u}}}(n+1),\cdot ). \end{aligned}$$
(10)

From (10), it can be observed that if the kernel function is replaced by a radial kernel, the KLMAT algorithm reduces to the radial basis function (RBF) network by allocating a new kernel unit for every new example with input. For simplicity, the coefficient \(a_j (n+1)\) is defined as:

$$\begin{aligned} a_j (n\!+\!1)\!=\!\mu \left[ {e^{2}(j)sign\{e(j)} \right] , \quad j\!=\!1,\ldots ,n+1\nonumber \\ \end{aligned}$$
(11)

and

$$\begin{aligned} {{\varvec{C}}}(n+1)=\left[ {{{\varvec{C}}}(n),{{\varvec{u}}}(n+1)} \right] \end{aligned}$$
(12)

where \({{\varvec{C}}}(n)=\{{{\varvec{c}}}_j \}_{j=1}^n \) is the center set or dictionary which stores the new center at each iteration. For n=1, \({{\varvec{C}}}(1)=[{{\varvec{u}}}(1)]\).

3.2 VLR–KLMAT algorithm

An important limitation of the KLMAT algorithm is the convergence rate vs. misadjustment trade-off imposed by the selection of a certain value for the learning rate. Motivated by the VLR scheme and the Lorentzian function in [6], in this section, we proposed a novel VLR scheme for the KLMAT algorithm. Replacing \(\mu \) with \(\mu \)(n) for each iteration, \(\mu (n)\) is adapted by using the following expression

$$\begin{aligned} \mu (n)=\beta \log \left( {1+\frac{1}{2}\frac{e^{2}(n)}{l^{2}}} \right) \end{aligned}$$
(13)

where \(\beta \) is a scalar factor which controls the value range of the function and l is the positive parameter. The large value of \(\beta \) leads to fast convergence rate at the initial stage and high misadjustment. By using some nonlinear function, the VLR scheme has been developed in several previous studies, including Sigmoid function [53] and Versiera function [56]. It can be observed from Fig. 2 that the Lorentzian function is much steeper than the other functions for the same small error signal. Therefore, such function can achieve fast convergence rate and improved tracking capability.

Fig. 2
figure 2

Comparison of Lorentzian function, Versiera function, and Sigmoid function

Full size image

To further improve the performance of the VLR scheme, an estimation of \(e^{2}(n)\) is introduced to (13)

$$\begin{aligned} \delta _e (n+1)=\theta \delta _e (n)+(1-\theta )e^{2}(n) \end{aligned}$$
(14)

where \(\theta \) is the forgetting factor that governs the averaging time constant and \(\delta _e (n+1)\) is a low-pass filtered estimation of \(e^{2}(n)\). In stationary environments, the previous samples include information that is relevant to determining a measure of update, i.e., the proximity of the adaptive filter coefficients to the optimal ones. Hence, \(\theta \) is close to 1. We set to \(\theta =0.9\) for the VLR–KLMAT algorithm. Moreover, for the stability of the VLR strategy, \(\mu (n)\) is further limited by

$$\begin{aligned} \mu (n+1)=\left\{ {\begin{array}{ll} \mu _{\max } , &{} \mu (n)>\mu _{\max } \\ \mu _{\min } ,&{}\mu (n)<\mu _{\min } \\ \mu (n),&{} otherwise \\ \end{array}} \right. \end{aligned}$$
(15)

where \(\mu _{\max }=2\) and \(\mu _{\min } = 0.01 (0<\mu _{\min } < \mu _{\max })\).

Remark 1

\(\mu _{\max } = 2\) is normally selected near the point of instability of the algorithm to provide the maximum possible convergence rate and \(\mu _{\min } = 0.01\) is chosen as a trade-off between the steady-state prediction error and the tracking capabilities of the algorithm [1, 12].

4 Performance analysis

The convergence analysis of the algorithm is performed in this section. For tractable analysis, the following assumptions are made:

(A1):

The measurement noise v(n) is zero mean, independent, identically distributed (i.i.d.) and is independent of input \({\varvec{\varphi }} (n)\) . The variance of measurement noise is \(\sigma _v^2 .\)

(A2):

The a priori error \(e_a (n)\) is zero mean and independent of the noise v(n).

The above assumptions have been successfully used in analyzing KAFs [12, 44, 50]. It can solve the problem of calculating expected values of some expressions involving contaminated Gaussian noise which is often used to model interference environments in the literature.

Consider the desired response arising from the model

$$\begin{aligned} d(n)={\varvec{\Omega }}_o^T {\varvec{\varphi }} (n)+v(n) \end{aligned}$$
(16)

where \({\varvec{\Omega }}_o \) denotes the optimal weight vector.

The error weight vector \({{\varvec{V}}}(n)\) is defined as

$$\begin{aligned} {{\varvec{V}}}(n)={\varvec{\Omega }}_o -{\varvec{\Omega }}(n). \end{aligned}$$
(17)

Thus, the error signal of the algorithm can be expressed as

$$\begin{aligned} e(n)= & {} d(n)-{\varvec{\Omega }}^{T}(n){\varvec{\varphi }} (n)\nonumber \\= & {} {{\varvec{V}}}^{T}(n){\varvec{\varphi }} (n)+v(n). \end{aligned}$$
(18)

Define the a prior error and a posteriori error of the KLMAT algorithm, respectively, as

$$\begin{aligned} e_a (n)={{\varvec{V}}}^{T}(n){\varvec{\varphi }} (n) \end{aligned}$$
(19)

and

$$\begin{aligned} e_a (n)={{\varvec{V}}}^{T}(n+1){\varvec{\varphi }} (n). \end{aligned}$$
(20)

Combining (19) and (20), we have

$$\begin{aligned}&{{\varvec{V}}}(n+1)-{{\varvec{V}}}(n)={\left[ {e_p (n)-e_a (n)} \right] }/{{\varvec{\varphi }} (n)}\nonumber \\&\quad ={\left[ {e_p (n)-e_a (n)} \right] {\varvec{\varphi }} (n)}/{\kappa ({{\varvec{u}}}(n),{{\varvec{u}}}(n)).} \end{aligned}$$
(21)

Squaring both sides of (21), we have the energy conservation relation (ECR) for KLMAT:

$$\begin{aligned}&\left\| {{{\varvec{V}}}(n+1)} \right\| _{\mathbb {F}}^2 +\frac{e_a^2 (n)}{\kappa ({{\varvec{u}}}(n),{{\varvec{u}}}(n))}=\left\| {{{\varvec{V}}}(n)} \right\| _{\mathbb {F}}^2\nonumber \\&\quad +\frac{e_p^2 (n)}{\kappa ({{\varvec{u}}}(n),{{\varvec{u}}}(n))} \end{aligned}$$
(22)

where \(||{{\varvec{V}}}(n)||_{\mathbb {F}}^2 \buildrel \Delta \over = {{\varvec{V}}}^{T}(n){{\varvec{V}}}(n)\) denotes the weight error power in \({\mathbb {F}}\). Taking expectations of both sides of (22), we have

$$\begin{aligned}&\hbox {E}\left[ {\left\| {{{\varvec{V}}}(n+1)} \right\| _{\mathbb {F}}^2 } \right] +\hbox {E}\left[ {\frac{e_a^2 (n)}{\kappa ({{\varvec{u}}}(n),{{\varvec{u}}}(n))}} \right] \nonumber \\&\quad =\hbox {E}\left[ {\left\| {{{\varvec{V}}}(n)} \right\| _{\mathbb {F}}^2 } \right] +\hbox {E}\left[ {\frac{e_p^2 (n)}{\kappa ({{\varvec{u}}}(n),{{\varvec{u}}}(n))}} \right] \end{aligned}$$
(23)

where \(\hbox {E}\left[ \mathbf{\cdot } \right] \) stands for taking expectation.

Substituting (19) and (20) into (23), the ECR can be given as

$$\begin{aligned} \hbox {E}\left[ {||{{\varvec{V}}}(n+1)||_{\mathbb {F}}^2 } \right]= & {} \hbox {E}\left[ {||{{\varvec{V}}}(n)||_{\mathbb {F}}^2 } \right] \nonumber \\&-\,2\mu \hbox {E}\left[ {e_a (n)f(e(n))} \right] \nonumber \\&+\,\mu ^{2}\hbox {E}\left[ {\kappa ({{\varvec{u}}}(n),{{\varvec{u}}}(n))f^{2}(e(n))} \right] \nonumber \\ \end{aligned}$$
(24)

where \(f(e(n))=e^{2}(n)sign\{e(n)\}\) is the error function. For Gaussian kernel \(\kappa ({{\varvec{u}}}(n),{{\varvec{u}}}(n))\equiv 1\), we obtain

$$\begin{aligned}&\hbox {E}\left[ {||{{\varvec{V}}}(n+1)||_{\mathbb {F}}^2 } \right] =\hbox {E}\left[ {||{{\varvec{V}}}(n)||_{\mathbb {F}}^2 } \right] \nonumber \\&\quad -\,2\mu \hbox {E}\left[ {e_a (n)f(e(n))} \right] +\mu ^{2}\hbox {E}\left[ {f^{2}(e(n))} \right] . \end{aligned}$$
(25)

Hence, the weight vector in the KLMAT algorithm can converge if and only if

$$\begin{aligned}&\hbox {E}\left[ {||{{\varvec{V}}}(n+1)||_{\mathbb {F}}^2 } \right] \le \hbox {E}\left[ {||{{\varvec{V}}}(n)||_{\mathbb {F}}^2 } \right] \nonumber \\&\quad \Leftrightarrow -2\mu \hbox {E}\left[ {e_a (n)f(e(n))} \right] +\mu ^{2}\hbox {E}\left[ {f^{2}(e(n))} \right] \le 0 \nonumber \\&\quad \Leftrightarrow \mu \le \frac{2\hbox {E}\left[ {e_a (n)f(e(n))} \right] }{\hbox {E}\left[ {f^{2}(e(n))} \right] }. \end{aligned}$$
(26)

Combing \(f(e(n))=e^{2}(n)sign\{e(n)\}\) results in

$$\begin{aligned} \mu \le \frac{2\hbox {E}\left[ {e_a (n)e^{2}(n)sign\{e(n)\}} \right] }{\hbox {E}\left[ {\hbox {E}^{4}(n)} \right] }. \end{aligned}$$
(27)

Consider \(e(n)=e_a (n)+v(n)\) and A2, we have

$$\begin{aligned} \mu \le \frac{2\left\{ {\hbox {E}\left[ {(e_a^3 (n)sign\{e(n)\}} \right] +\hbox {E}\left[ {e_a (n)v^{2}(n)sign\{e(n)\}} \right] } \right\} }{\hbox {E}\left[ {e_a^4 (n)} \right] +2\hbox {E}\left[ {e_a^2 (n)v^{2}(n)} \right] +\hbox {E}\left[ {v^{4}(n)} \right] }.\nonumber \\ \end{aligned}$$
(28)

According to the Price theorem [36, 40], we obtain

$$\begin{aligned} \mu \le \frac{2\sqrt{\frac{2}{\pi }}\frac{1}{\sigma _e }\hbox {E}\left[ {e_a^3 (n)e(n)} \right] +2\sqrt{\frac{2}{\pi }}\frac{1}{\sigma _e }\hbox {E}\left[ {e_a (n)v^{2}(n)e(n)} \right] }{\hbox {E}\left[ {e_a^4 (n)} \right] +2\hbox {E}\left[ {e_a^2 (n)} \right] \sigma _v^2 +\hbox {E}\left[ {v^{4}(n)} \right] }\nonumber \\ \end{aligned}$$
(29)

where \(\sigma _e\) is the standard deviation of e(n). Thus, a sufficient condition for the mean square convergence of KLMAT is formulated as

$$\begin{aligned} \mu\le & {} \frac{2\sqrt{\frac{2}{\pi }}\frac{1}{\sigma _e }\left\{ {\hbox {E}\left[ {e_a^4 (n)} \right] +\hbox {E}\left[ {e_a^3 (n)v(n)} \right] } \right\} +2\sqrt{\frac{2}{\pi }}\frac{1}{\sigma _e }\left\{ {\hbox {E}\left[ {\hbox {E}_a^2 (n)v^{2}(n)} \right] +\hbox {E}\left[ {e_a (n)v^{3}(n)} \right] } \right\} }{\hbox {E}\left[ {e_a^4 (n)} \right] +2\hbox {E}\left[ {e_a^2 (n)} \right] \sigma _v^2 +\sigma _v^4 } \nonumber \\= & {} \frac{2\sqrt{\frac{2}{\pi }}\frac{1}{\sigma _e }\left\{ {\hbox {E}\left[ {e_a^4 (n)} \right] +\hbox {E}\left[ {e_a^2 (n)} \right] \sigma _v^2 } \right\} }{\hbox {E}\left[ {e_a^4 (n)} \right] +2\hbox {E}\left[ {e_a^2 (n)} \right] \sigma _v^2 +\sigma _v^4 },\;\;\;if\;\;\forall n \end{aligned}$$
(30)

Note that the energy of weight error \(\hbox {E}\left[ {\left\| {{{\varvec{V}}}(n)} \right\| _{\mathbb {F}}^2 } \right] \) should decrease monotonically if the learning rate satisfies the above inequality.

Remark 2

The above sufficient condition for the mean square convergence of the KLMAT algorithm is only of theoretical importance. In practical test, it is difficult to check exactly. In conventional LMS algorithm, the mean square convergence behavior can be rigorously analyzed. However, since the central limit theorem is not applicable in the nonlinear model (nonlinear prediction), \(\hbox {E}\left[ {e_a^2 (n)} \right] \) cannot be assumed to be Gaussian.

5 Extension of KLMAT

To further improve the performance of the KLMAT and VLR–KLMAT algorithms, the recursive strategy is applied in the LMAT loss function, namely the kernel recursive least mean absolute third (KRLAT) algorithm. To derive the KRLAT algorithm in RKHS, the novel LMAT function using an exponentially weighted [29] is firstly defined by

$$\begin{aligned} J_r (n)= & {} \mathop {\min }\limits _{{\varvec{\Omega }}(n)} \left\{ \sum _{j=1}^n \lambda ^{n-j}\left| {d(j)-{\varvec{\Omega }}^{T}(n){\varvec{\varphi }} (j)} \right| ^{3}\right. \nonumber \\&\left. +\frac{1}{2}\lambda ^{n}\chi \left\| {{\varvec{\Omega }}(n)} \right\| ^{2} \right\} \end{aligned}$$
(31)

where \(0\ll \lambda <1\) is the forgetting factor and \(\chi \) is the small regularization factor which de-emphasizes regularization as time progresses. The algorithm achieves slow convergence rate and small misadjustment when \(\lambda \) is close to one. When \(\lambda \) is small, the algorithm converges fast while has high steady-state error. Note that, \(\frac{1}{2}\lambda ^{n}\chi \left\| {{\varvec{\Omega }}(n)} \right\| ^{2}\) is a norm penalizing term, which can guarantee the existence of the inverse of the autocorrelation matrix, especially during the initial update stages [29]. Then, taking the gradient of \(J_r (n)\) with respect to \({\varvec{\Omega }}(n)\), we get

$$\begin{aligned}&\frac{\partial J_r (n)}{\partial {\varvec{\Omega }}(n)}=-\sum _{j=1}^n {\lambda ^{n-j}} \frac{\left( {d(j)-{\varvec{\Omega }}^{T}(n){\varvec{\varphi }} (j)} \right) ^{2}}{\left| {d(j)-{\varvec{\Omega }}^{T}(n){\varvec{\varphi }} (j)} \right| } \nonumber \\&\qquad \times \left( {d(j)-{\varvec{\varphi }} ^{T}(j){\varvec{\Omega }}(n)} \right) {\varvec{\varphi }} (j) +\lambda ^{n}\chi {\varvec{\Omega }}(n)\nonumber \\&\quad =-\sum _{j=1}^n {\lambda ^{n-j}} \frac{\left( {d(j)-{\varvec{\Omega }}^{T}(n){\varvec{\varphi }} (j)} \right) ^{2}}{\left| {d(j)-{\varvec{\Omega }}^{T}(n){\varvec{\varphi }} (j)} \right| }d(j){\varvec{\varphi }} ^{T}(j)\nonumber \\&\quad \quad +\sum _{j=1}^n {\lambda ^{n-j}} \frac{\left( {d(j)-{\varvec{\Omega }}^{T}(n){\varvec{\varphi }} (j)} \right) ^{2}}{\left| {d(j)-{\varvec{\Omega }}^{T}(n){\varvec{\varphi }} (j)} \right| }{\varvec{\varphi }} ^{T}(j){\varvec{\varphi }} (j){\varvec{\Omega }}(n)\nonumber \\&\quad \quad +\,\lambda ^{n}\chi {\varvec{\Omega }}(n)\nonumber \\&\quad =-\sum _{j=1}^n {\lambda ^{n-j}} \frac{\left( {d(j)-{\varvec{\Omega }}^{T}(n){\varvec{\varphi }} (j)} \right) ^{2}}{\left| {d(j)-{\varvec{\Omega }}^{T}(n){\varvec{\varphi }} (j)} \right| }d(j){\varvec{\varphi }} ^{T}(j)\nonumber \\&\qquad +\left( \sum _{j=1}^n {\lambda ^{n-j}} \frac{\left( {d(j)-{\varvec{\Omega }}^{T}(n){\varvec{\varphi }} (j)} \right) ^{2}}{\left| {d(j)-{\varvec{\Omega }}^{T}(n){\varvec{\varphi }} (j)} \right| }\right. \nonumber \\&\qquad \times \left. {\varvec{\varphi }} ^{T}(j){\varvec{\varphi }} (j)+\,\lambda ^{n}\chi \right) {\varvec{\Omega }}(n). \end{aligned}$$
(32)

Setting (32) to zero gives

$$\begin{aligned} {\varvec{\Omega }}(n)={\varvec{\Xi \Psi }} \end{aligned}$$
(33)

where

$$\begin{aligned} {\varvec{\Xi }}=\left( \mathop {\sum \limits _{j=1}^n {\lambda ^{n-j}} \frac{\left( {d(j)-{\varvec{\Omega }}^{T}(n){\varvec{\varphi }} (j)} \right) ^{2}}{\left| {d(j)-{\varvec{\Omega }}^{T}(n){\varvec{\varphi }} (j)} \right| }{\varvec{\varphi }} ^{T}(j){\varvec{\varphi }} (j)+\lambda ^{n}\chi } \right) ^{-1} \end{aligned}$$

and \({\varvec{\Psi }}=\mathop {\sum }_{j=1}^n {\lambda ^{n-j}} \frac{\left( {d(j)-{\varvec{\Omega }}^{T}(n){\varvec{\varphi }} (j)} \right) ^{2}}{\left| {d(j)-{\varvec{\Omega }}^{T}(n){\varvec{\varphi }} (j)} \right| }d(j){\varvec{\varphi }} ^{T}(j)\).

Define the desired signal vector and global input vector at time n, respectively, as

$$\begin{aligned} {{\varvec{d}}}(n)= & {} \left[ {d(1),d(2),\ldots ,d(n)} \right] \end{aligned}$$
(34)
$$\begin{aligned} {{\varvec{\Phi }} }(n)= & {} \left[ {{\varvec{\varphi }} (1),{\varvec{\varphi }} (2),\ldots ,{\varvec{\varphi }} (n)} \right] ,\nonumber \\ { {\varvec{\Phi }} }(n)= & {} \left\{ {{{\varvec{\Phi }} }(n-1),{\varvec{\varphi }} (n)} \right\} \end{aligned}$$
(35)

and let

$$\begin{aligned}&{\varvec{\Lambda }}(n)= diag\left[ \lambda ^{n-1}\frac{\left( {d(1)-{\varvec{\Omega }}^{T}(1){\varvec{\varphi }} (1)} \right) ^{2}}{\left| {d(1)-{\varvec{\Omega }}^{T}(1){\varvec{\varphi }} (1)} \right| },\right. \nonumber \\&\quad \lambda ^{n-2}\frac{\left( {d(2)-{\varvec{\Omega }}^{T}(2){\varvec{\varphi }} (2)} \right) ^{2}}{\left| {d(2)-{\varvec{\Omega }}^{T}(2){\varvec{\varphi }} (2)} \right| },\left. \ldots ,\frac{\left( {d(n)-{\varvec{\Omega }}^{T}(n){\varvec{\varphi }} (n)} \right) ^{2}}{\left| {d(n)-{\varvec{\Omega }}^{T}(n){\varvec{\varphi }} (n)} \right| } \right] .\nonumber \\ \end{aligned}$$
(36)

Then, (33) can be rewritten as below

$$\begin{aligned} {\varvec{\Omega }}(n)= & {} \left( {{ {\varvec{\Phi }} }(n){{\varvec{\Lambda }}}(n){ {\varvec{\Phi }} }^{T}(n)+\lambda ^{n}{{\chi }} \mathbf{I}} \right) ^{-1}\nonumber \\&\times {{\varvec{\Phi }} }(n){{\varvec{\Lambda }}}(n){{\varvec{d}}}(n). \end{aligned}$$
(37)

Applying the matrix inversion lemma [29]

$$\begin{aligned}&(A+BCD)^{-1}=A^{-1}-A^{-1}B(C^{-1}\nonumber \\&\quad +DA^{-1}B)^{-1}DA^{-1} \end{aligned}$$
(38)

to (37), with the identifications

$$\begin{aligned} A=\chi \lambda ^{n},\;\;B={ {\varvec{\Phi }} }(n),\;\;C={\varvec{\Lambda }}(n),\;\;D={ {\varvec{\Phi }} }^{T}(n)\nonumber \\ \end{aligned}$$
(39)

we obtain

$$\begin{aligned}&\left( {{ {\varvec{\Phi }} }(n){\varvec{\Lambda }}(n){ {\varvec{\Phi }} }^{T}(n)+\lambda ^{n}\chi \mathbf{I}} \right) ^{-1}{ {\varvec{\Phi }} }(n){\varvec{\Lambda }}(n)\nonumber \\&\quad ={ {\varvec{\Phi }} }(n)\left( {{ {\varvec{\Phi }} }(n){ {\varvec{\Phi }} }^{T}(n) +\lambda ^{n}\chi {\varvec{\Lambda }}(n)^{-1}} \right) ^{-1}. \end{aligned}$$
(40)

Substituting the above result into (37), we obtain

$$\begin{aligned} {\varvec{\Omega }}(n)={ {\varvec{\Phi }} }(n)\left( {{ {\varvec{\Phi }} }(n){{\varvec{\Phi }} }^{T}(n)+\lambda ^{n}\chi {\varvec{\Lambda }}(n)^{-1}} \right) ^{-1}{{\varvec{d}}}(n).\nonumber \\ \end{aligned}$$
(41)

The weight vector can be expressed explicitly as a linear combination of the transformed data, that is

$$\begin{aligned} {\varvec{\Omega }}(n)={ {\varvec{\Phi }} }(n){\varvec{\Upsilon }} (n) \end{aligned}$$
(42)

where \({\varvec{\Upsilon }} (n)=\left( {{ {\varvec{\Phi }} }(n){ {\varvec{\Phi }} }^{T}(n)+\lambda ^{n}\chi {\varvec{\Lambda }}(n)^{-1}} \right) {{\varvec{d}}}(n)\) is the coefficients vector of the weight, which can be computed by kernel method. For simplicity, we define

$$\begin{aligned} {\varvec{\Theta }}(n)=\left( {{ {\varvec{\Phi }} }(n){ {\varvec{\Phi }} }^{T}(n)+\lambda ^{n}\chi {\varvec{\Lambda }}(n)^{-1}} \right) ^{-1}. \end{aligned}$$
(43)

Then, we have

$$\begin{aligned} \begin{array}{l} {\varvec{\Theta }}(n)=\left[ {\begin{array}{l} { {\varvec{\Phi }} }(n){ {\varvec{\Phi }} }^{T}(n-1)+\lambda ^{n}\chi {\varvec{\Lambda }}(n)^{-1}\,\,\,\,\,\,{ {\varvec{\Phi }} }^{T}(n-1){\varvec{\varphi }} (n) \\ \;\;\;\;\;\;\;{\varvec{\varphi }} ^{T}(n){ {\varvec{\varphi }} }(n-1)\;\;\;\;{\varvec{\varphi }} ^{T}(n){\varvec{\varphi }} (n)+\lambda ^{n}\chi \left[ {\frac{\left( {d(n)-{\varvec{\Omega }}^{T}(n){\varvec{\varphi }} (n)} \right) ^{2}}{\left| {d(n)-{\varvec{\Omega }}^{T}(n){\varvec{\varphi }} (n)} \right| }} \right] ^{-1} \\ \end{array}} \right] ^{-1} \\ \;\;\;\;\;\;\;\hbox {=}\left[ {\begin{array}{l} { {\varvec{\Phi }} }(n){ {\varvec{\Phi }} }^{T}(n-1)+\lambda ^{n}\chi {\varvec{\Lambda }}(n)^{-1}\;\;\;\;{ {\varvec{\Phi }} }^{T}(n-1){\varvec{\varphi }} (n) \\ \;\;\;\;\;\;\;{\varvec{\varphi }} ^{T}(n){ {\varvec{\Phi }} }(n-1)\;\;\;\;\;\;\;\;{\varvec{\varphi }} ^{T}(n){\varvec{\varphi }} (n)+\lambda ^{n}\chi \vartheta (n) \\ \end{array}} \right] ^{-1} \\ \end{array} \end{aligned}$$
(44)

where \(\vartheta (n)=\left[ {\frac{\left( {d(n)-{\varvec{\Omega }}^{T}(n){\varvec{\varphi }} (n)} \right) ^{2}}{\left| {d(n)-{\varvec{\Omega }}^{T}(n){\varvec{\varphi }} (n)} \right| }} \right] ^{-1}\). We can observe that

$$\begin{aligned} {\varvec{\Theta }}(n)^{-1}=\left[ {\begin{array}{l} \;\;\;\;\;\;\;{\varvec{\Theta }}(n-1)^{-1}\,\,\,\,\,\,\,\,\,\,\,{\varvec{\theta }} (n) \\ {\varvec{\theta }} ^{T}(n){\varvec{\varphi }} (n){ {\varvec{\Phi }} }(n-1)\;\;\;\lambda ^{n}\chi \vartheta (n)+\;{\varvec{\varphi }} ^{T}(n){\varvec{\varphi }} (n) \\ \end{array}} \right] ^{-1}\nonumber \\ \end{aligned}$$
(45)

where \({\varvec{\theta }} (n)={ {\varvec{\Phi }} }^{T}(n-1){\varvec{\varphi }} (n)\). Then applying the following block matrix inversion identity

$$\begin{aligned} \left[ {\begin{array}{l} A\;\;B \\ C\;\;D \\ \end{array}} \right] =\left[ {\begin{array}{l} \;\;\;\;\;\;(A-BD^{-1}C)^{-1}\;\;\;\;\;-A^{-1}B(D-CA^{-1}B)^{-1} \\ \;-D^{-1}C(A-BD^{-1}C)^{-1}\;\;\;\;\;\;(D-CA^{-1}B)^{-1} \\ \end{array}} \right] .\nonumber \\ \end{aligned}$$
(46)

Using (46), (42) becomes

$$\begin{aligned}&{\varvec{\Theta }}(n)^{-1}=\rho ^{-1}(n)\nonumber \\&\quad \times \left[ {\begin{array}{l} {\varvec{\Theta }}(n-1)\rho (n)+{{\varvec{q}}}(n){{\varvec{q}}}^{T}(n)\;\;\;-{{\varvec{q}}}(n) \\ -{{\varvec{q}}}^{T}(n) \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,1 \\ \end{array}} \right] \end{aligned}$$
(47)

where \({{\varvec{q}}}(n)={\varvec{\Theta }}(n-1){\varvec{\theta }} (n)\) and \(\rho (n)=\lambda ^{n}\chi \vartheta (n)+{\varvec{\varphi }} ^{T}(n){\varvec{\varphi }} (n)-{{\varvec{q}}}^{T}(n){\varvec{\theta }} (n)\).

Combining (37) and (47), we arrive the following relation

$$\begin{aligned} {\varvec{\Psi }}(n)= & {} {\varvec{\Theta }}(n){{\varvec{d}}}(n)\nonumber \\= & {} \left[ {\begin{array}{l} {\varvec{\Theta }}(n-1)+{{\varvec{q}}}(n){{\varvec{q}}}^{T}(n)\rho ^{-1}(n)\,\,\,\,-{{\varvec{q}}}(n)\rho ^{-1}(n) \\ {{\varvec{-q}}}(n)\rho ^{-1}(n)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\rho ^{-1}(n) \\ \end{array}} \right] \nonumber \\&\left[ {\begin{array}{l} {{\varvec{d}}}(n-1) \\ \;\;d(n) \\ \end{array}} \right] \nonumber \\= & {} \left[ {\begin{array}{l} {\varvec{\Psi }}(n-1)-{{\varvec{q}}}(n)\rho ^{-1}(n)e(n)\; \\ \,\,\,\,\,\,\,\rho ^{-1}(n)e(n)\; \\ \end{array}} \right] . \end{aligned}$$
(48)

6 Simulation results

We conduct a series of simulations to evaluate the performance of the proposed algorithms, including simulations on a Mackey–Glass (MG) chaotic time series prediction and simulations on a sunspot number time series analysis. We compare the estimation results of the proposed algorithms with those of the KLMS algorithm and the KRLS algorithm. In the simulation study, the effectiveness is assessed in terms of MSE in the testing stage, which is defined as \(\hbox {MSE}=10\log _{10} \left\{ {e^{2}(n)} \right\} \) [37]. The parameters in algorithms (learning rate, kernel size, etc.) are selected to guarantee the fast and stable convergence of the algorithms. All the simulation results below are averaged over 100 independent Monte Carlo runs.

6.1 Example 1: MG chaotic time series prediction

In this example, the simulation studies are carried out for the MG chaotic time series prediction. The MG series is generated by a delay ordinary differential equation [27, 29]:

$$\begin{aligned} \frac{\mathrm{d}x(t)}{\mathrm{d}t}=-qx(t)+\frac{mx(t-\tau )}{1+x(t-\tau )^{10}} \end{aligned}$$
(49)

where \(q=0.1, m=0.2\), and \(\tau =30\). The sampling period is 6 s, and time embedding (filter order) is 10. The white Gaussian noise (WGN) with zero mean and standard deviation \(\sigma _G =0.02\) is used as a measurement noise. A segment of 2000 samples is used as the training data and another 2000 as the test data. If the number of testing iteration 2000 is achieved, then stop the algorithm.

Fig. 3
figure 3

Testing MSE curves for kernel sizes (\(\mu =1\))

Full size image

Firstly, we let h of the KLMAT algorithm vary within \(0.1 \sim 2\) to test the performances of algorithms under different kernel sizes. When the kernel size is too small for the data samples, the performance of the algorithm may degrade since the lack of information needed in inner product calculation. When the kernel size is relatively small but in a reasonable range for the data samples, the algorithm converges quickly with relatively high steady-state error. When the kernel size is getting larger, the crest around the global optimum becomes wider, so under the fixed learning rate, the smaller misadjustment and lower convergence rate are obtained. From Fig. 3, we observed that, for \(h\in (0.5,2)\), the results are quite similar. In following simulations, we set \(h=1.5\), for small steady-state error. Then, we test the prediction performance of the proposed algorithms in Figs. 4 and 5. Figure 4 shows the testing MSE under WGN environment. Observe that the KLMAT and VLR–KLMAT algorithms achieve improved performance as compared with the KLMS algorithm. Besides, the VLR–KLMAT algorithm outperforms the KLMAT algorithm, since it reaches the similar steady-state error level within fewer iterations. Owing to using the recursive method, the KRLS and KRLAT algorithms converge faster than other algorithms. Additionally, the KRLAT algorithm provides improvement with WGN noise.

Fig. 4
figure 4

Testing MSE curves of the algorithms

Full size image
Fig. 5
figure 5

Testing MSE curves of the NC-based algorithms

Full size image

Note that the network size of the KAF linearly increases with the number of training data, which means that there is a total of 2000 expansion coefficients at the end of our simulations. This may prohibit the practical implementation of these algorithms for a large training set. Therefore, the novelty criterion (NC) strategy [29] is considered to be a possible solution to the limitation of the proposed algorithms. The NC computes the distance of \({{\varvec{u}}}(n+1)\) to the present dictionary \(c_j \). If the distance is smaller than some preset threshold \(\zeta _1 (\zeta _1 >0)\), new input data \({{\varvec{u}}}(n+1)\) will not be added to the dictionary. Only if the magnitude of the prediction error is larger than another preset threshold \(\zeta _2 (\zeta _2 >0)\), new input data will be accepted as a new center. Guided by this method, the NC–KLMAT and NC–KRLAT algorithms can be easily derived by introducing NC in the KLMAT and KRLAT algorithms. To curb the network size, we have used a NC–KLMAT filter with \(\zeta _1 =0.1\) and \(\zeta _2 =0.001\). For the NC–KRLAT algorithm, we use 20 values of \(\zeta _1 \) and \(\zeta _2 \) uniformly in the interval of [0.04, 0.2] for the enhanced NC [29]. As can be seen from Fig. 5, the NC method provides overwhelmingly smaller network size as comparison to other algorithms with sacrifice of the prediction accuracy.

Table 2 Average computation time per run of the algorithms
Full size table

Finally, to quantify the computational burden, we measured the average run execution time of the algorithm on a 2.1-GHz AMD processor with 2 GB of RAM, running MATLAB R2013a on Windows 7 environment. As one see from Table 2, the KLMS algorithm is the fastest method owing to utilizing gradient descent. The KRLAT algorithm increases the computation time, but the faster convergence rate and stable performance are achieved as compared to other algorithms.

Table 3 Steady-state testing MSEs
Full size table
Fig. 6
figure 6

Predicted values of the KRLAT algorithm and target values

Full size image
Fig. 7
figure 7

Sunspot number time series

Full size image
Table 4 Steady-state testing MSEs
Full size table

6.2 Example 2: Effect of the measurement noise

In the second example, we focus on the performance of the proposed algorithms in MG time series prediction for various probability densities. The experimental conditions are considered to be same as in the example 1, but the measurement noise is considered as non-Gaussian noise. Since in many physical environments, the noise is characterized by non-Gaussian distribution. We generate the uniform noise from the uniform distribution of probability density function \({{u}}\sim \frac{1}{b-a}\), where \(b=0.1\) and \(a=-0.1\). We set \({{\varvec{u}}}(n)=\sqrt{-2\sigma _R^2 \log (1-{{\varvec{y}}}(n))}\) for Rayleigh noise, where \({{\varvec{y}}}(n)\) is a uniform random variable in (0,1) and \(\sigma _R^2 =0.05\) is the variance. The square function is employed to generate the rectangular noise in MATLAB. The Sinusoidal noise is generated by \(u(n)=sin(200\pi n)+sin(1000\pi n)+sin(1800\pi n)\). To compare the steady-state performance of the algorithms fairly, we change the parameters so that they has the similar initial convergence rate. Table 3 shows a comparison of the KLMS, KLMAT, VLR–KLMAT, KRLS and KRLAT algorithms. The predicted values of the KRLAT and Target values are shown in Fig. 6. We can clearly see that the KLMAT and VLR–KLMAT algorithms outperform the KLMS and LMAT algorithms for all of the probability densities. The KRLS and KRLAT algorithms perform better than the KLMS-based algorithms, and the KRLAT algorithm achieves good prediction results in all these cases. The predicted value of the KRLAT algorithm agrees with the target well. Specifically, the performance of the proposed algorithms is much better than that of the existing algorithms with uniform noise and rectangular noise.

6.3 Example 3: Application of the sunspot number time series analysis

To test the performance of algorithms in realistic applications, the proposed algorithms are applied to adaptive prediction of the annually recorded sunspot time series for the years 1700–1997 [61]. A segment of the processed sunspot number series is shown in Fig. 7. The testing MSE is calculated based on 100 test data. The time embedding is 2. We choose to termination the algorithm when the testing iteration 100 is achieved. For the sake of a fair comparison, we let the algorithms use the different learning rates to accomplish similar convergence rate. In Table 4, the prediction results for WGN with \(\sigma _G =0.1\) are illustrated. It is concluded that the proposed algorithms are superior to the existing algorithms in terms of the steady-state prediction error.

7 Conclusion

We proposed a KAF based on LMAT loss function named KLMAT, which was derived by utilizing the kernel method and gradient descent method. Besides, its VLR version was proposed by using Lorentzian function to accelerate the initial convergence rate. In the analysis, it has been shown the upper bound of the KLAMT algorithm for mean square convergence. To further enhance the performance of the proposed algorithms, we developed a kernel extension of the KLMAT algorithm in a recursive strategy. The new KRLAT algorithm incorporates an exponentially weighted into the LMAT loss function to adapt the tap-weight vector in feature space which can maintain robustness against different noise environments and can increase the convergence rate for time series prediction. We carried out simulations that confirmed the superiority of the proposed algorithms. Our future works will concern with using real data in adaptive prediction. Some initial works have been done.