Keywords

1 Introduction

In civil and mechanical engineering, determining the capability of structures to support different types of loadings plays a central role. The recent trend for increasing application of composite material and the gradual replacement of conventional metallic materials in structural components, set forth new challenges for this classic problem. In the context of heterogeneous materials, it is known that the strength depends on their microstructural features [17, 40]. Thus to fully exploit the potential of such materials, it requires to understand decisive factors influencing composite’s strength, especially the contribution of material’s microstructure.

Particulate Reinforced Metal Matrix Composites (PRMMC) consist of the ductile binder and brittle inclusion particles. This combination constitutes a large class of existing composite structures. Compared to fiber reinforced composites PRMMCs generally show higher isotropy and demand less effort for manufacturing [20]. However, the randomness in the distribution of reinforcement grains entails considerable spatial variation of material behavior. This leads to two consequences: first, material’s response to external loading is quite localized; second, representative volume elements (RVE) do not exist in a strict sense—it means not a singular model of finite size is capable to completely reflect the overall material behavior [39]. The randomness of microstructure also introduces difficulties in the numerical representation of the material. Two prominent problems are the modeling technique of the microstructural geometry and the size effect of RVE investigated in many studies [5, 14, 21, 32, 36, 46].

For PRMMC with high binder content, the matrix failure is a major cause of overall material failure [38] and the strength of the composite is highly depends on matrix phase’s capability to resist plastic failure. Similar to single phase material, strength of a globally elasto-plastic composite can be characterized by three strengths: yield strength, ultimate strength and endurance limit. They correspond to elastic limit, plastic limit and shakedown limit of the material, respectively.

The link between endurance limit and shakedown on micro scale has already been noted by Drucker [13]. The idea has further been studied by Dang Van who developed his well known criterion [12], which calculates the condition of elastic shakedown on grain level and allows determining the endurance of material under complex multi-axial loading situations. Nevertheless, since often serious stress and strain localization will be observed within the heterogeneous material, this criterion is not fully satisfying for composites. To take into account the contribution of the composite structure, one has to consider numerical approaches [7, 16].

Applying direct methods (DM) in the Melan-Koiter path-independent spirit [23, 30] to study the problem has some advantages. On the one hand, it allows to consider the composite structure and on the other hand it avoids performing cumbersome step-by-step calculation. This method has become increasingly popular in recent decades: as example, Weichert et el. [42], Schwabe [35], Maier [28], Magoariec et al. [27], Zhang et al. [45], You et al. [44], Chen et al. [10, 11] solve the problem by a static approach. In contrast, Carvelli [6], Chen and Ponter [9], Li [26], and Barrera [3] deal the problem by the kinematic approach.

The implementation of DM according to Melan’s theorem involves solving a constrained extremal problem, and conventional mathematical programming methods cause serious difficulties when model size grows. This is the main reason that existing studies, to the authors’ knowledge, are restricted to idealized microstructures. To study more complex microstuctures, one has to rely on highly efficient optimization algorithms. The interior point method introduced by Karmarkar [22] has demonstrated high efficiency in solving linear programming (LP) problems and it attracted interests from different disciplines [15, 41]. More recently, the algorithm has been introduced to solve nonlinear programming (NP) problems. An additional advantage of the interior point method is its capability in dealing with large scale problems. The number of iterations it requires to converge is much smaller than the polynomial upper bound and is almost independent upon the problem size [43]. Therefore, many researchers have incorporate this algorithm with DM. This includes problem-tailored codes [25, 33, 37, 47], and reformulating problems in such a way that they can be efficiently solved by general-purpose solvers [4, 18, 31].

In the present study, WC-70 Wt.% Co is used as a typical PRMMCs to study both monotonic and cyclic limit loads. The technique developed in a previous study [8] is applied in order to overcome the aforementioned main obstacles. Using a series of scanning electron microscope (SEM) images obtained from the material finite element (FE) models are built. Then first, static limit and shakedown problems are constructed on each RVE and solved by an interior-point method based solver. In the second step, the load domains obtained in the previous step are converted to macroscopic strength through the homogenization technique. To estimate the dependence of the strength on structure, the obtained results are evaluated statistically. In order to identify factors that influence the quality of numerical results, several characteristics of FE models, e.g. the impact of RVE’s size, mesh density, as well as the difference between 2D and 3D model, are investigated and discussed in detail.

2 Limit and Shakedown Analysis of Random PRMMC Material

2.1 Micromechanical Homogenization of Elasto-Plastic Materials

Homogenization theory links physical fields in two well-separated scales, i.e. the microscale \( \varvec{y}\) in which structural details of RVE are distinguishable and the macro scale \(\varvec{x}\) in which a RVE is recognized as a macroscopic point. For a heterogeneous composite, once exposed to external loading, its microscopic stress field \(\varvec{\Sigma }\) in \(\varvec{y}\) and the macroscopic counterpart in \(\varvec{x}\) satisfy the relationship:

$$\begin{aligned} \varvec{\Sigma } =\frac{1}{\Omega }\int \limits _{\varOmega }{\varvec{\sigma }(y)dv}. \end{aligned}$$
(1)

Here \(\Omega \) indicates the RVE domain. Analogously, macroscopic strain \(\varvec{E}\) can be defined as

$$\begin{aligned} \varvec{E} =\frac{1}{\Omega }\int \limits _{\varOmega }{\varvec{\varepsilon }(y)dv}. \end{aligned}$$
(2)

When all constituents of the composite are elastic, \(\varvec{\Sigma }\) and \(\varvec{E}\) are correlated by the effective elastic tensor \(\overline{\varvec{C}}\):

$$\begin{aligned} \varvec{\Sigma } =\overline{\varvec{C}}:\varvec{E}. \end{aligned}$$
(3)

For a globally isotropic composite, \(\varvec{C}\) depends only on the effective Young’s modulus \(\overline{E}\) and effective Poisson’s ratio \(\overline{\upsilon }\).

A characteristic of PRMMCs is that stress and strain are strongly non-uniform due to heterogenity, thus the onset of local plasticity can take place even when \(\varvec{\Sigma }\) is fairly low. To assess the plastic strain in the macro scale, Suquet [38] proposed a measure: the effective plastic strain \(\varvec{E^p}\) which is a work conjugate to \(\varvec{\Sigma }\) defined as:

$$\begin{aligned} \varvec{E^p} =\varvec{E}-\overline{\varvec{C}}^{-1}:\varvec{\Sigma }. \end{aligned}$$
(4)

This way, the global yield strength of a composite \( \varvec{\Sigma }^Y \) can be set as the stress leading to 0.1 % global strain:

$$\begin{aligned} \varvec{\Sigma }^Y=\arg (E^p_{eq}(\Sigma _{eq})=0.1\,\%). \end{aligned}$$
(5)

Here, \(E^p_{eq}\) and \(\Sigma _{eq}\) represent equivalent macroscopic plastic strain and stress, respectively. In the present study, all phases are assumded to obey the von Mises yield criterion. Thus \(E^p_{eq}\) and \(\Sigma _{eq}\) can be formulated as:

$$\begin{aligned} E^p_{eq}&=\sqrt{ \frac{2}{ 3 } (\varvec{E^p})':(\varvec{E^p})'} , \end{aligned}$$
(6a)
$$\begin{aligned} \Sigma _{eq}&=\sqrt{ \frac{3}{ 2 } \varvec{\Sigma }':\varvec{\Sigma }'} . \end{aligned}$$
(6b)

The apostrophe in (6a, 6b) indicates the deviatoric part of a tensor. It is important to note that an individual RVE is not isotropic, despite macroscopic isotropy of WC-Co in the elastic as well as the plastic range. For this reason, we take the average of strength in two orthogonal directions \( \Sigma ^Y_{11} \) and \(\Sigma ^Y_{22} \) as the measure of composite’s global strength.

2.2 Static Theorem and Its Numerical Reformulation

The static shakedown criterion for a elastic-perfectly plastic material can be formulated as follows: shakedown occurs if there exist a safety factor \( \alpha >1 \) and a time-independent residual stresses field \(\overline{\varvec{\rho }}\), whose superposition with the purely elastic stresses \(\varvec{\sigma }^E\) does not exceed the yield condition \(F\) at any time \(t>0\):

$$\begin{aligned} F\left( \alpha {\varvec{\sigma }^{E}(\varvec{y},t)}+\varvec{\bar{\rho }},\text { }\!\!~\!\!\text { }{{\sigma }_{Y}} \right)&\le 0, \end{aligned}$$
(7a)
$$\begin{aligned} \varvec{\nabla } \cdot \bar{\varvec{\rho } }&=\varvec{0}\text { in }\Omega , \end{aligned}$$
(7b)
$$\begin{aligned} \varvec{\sigma }^E(y,t) \cdot \varvec{n}&=\varvec{t}\text { on } \partial \Omega _t, \end{aligned}$$
(7c)
$$\begin{aligned} \bar{\varvec{\rho }} \cdot \varvec{n}&=\varvec{0}\text { on } \partial \Omega _t. \end{aligned}$$
(7d)

Here \( \Omega _t \) denotes the part of the boundary where tractions \( \varvec{t} \) are prescribed. In case of von Mises yield criterion, the function \(F\) becomes:

$$\begin{aligned} F(\varvec{\sigma },\sigma ^Y) =\sqrt{ \frac{3}{ 2 } \varvec{\sigma }':\varvec{\sigma }'}-\sigma ^Y . \end{aligned}$$
(8)

By employing (7a–7d) to each RVE, its respective admissible load domains will be identified. Since plastic limit can be regarded as a special case of shakedown where \( \varvec{\sigma }^E \) evolves monotonically through \( t \), this condition holds as well for the limit analysis.

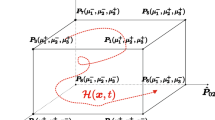
When \( \varvec{\sigma }^E \) is entailed by a set of \( \text {NL} \) independent loads \( \varvec{P}_i \), due to linearity following relationship holds:

$$\begin{aligned} {{\varvec{\sigma }}^{E}}\left( \sum \limits _{i=1}^{NL}{{\varvec{P}_{i}}(y)} \right) =\sum \limits _{i=1}^{NL}{{{\varvec{\sigma }}^{E}}\left( {\varvec{P}_{i}}(y)\right) }. \end{aligned}$$
(9)

Here, an individual load \( \varvec{P}_i \) can be separated into two parts including a varying magnitude scalar \( \mu _i \) and a time invariant base vector \( \hat{\varvec{P}}_i \):

$$\begin{aligned} \varvec{P}_i(y,t)=\mu _i(t)\varvec{\hat{P}}_i(y). \end{aligned}$$
(10)

Since each particular load \( \mu _i \) varies within the interval \( [\mu ^-_i,\mu ^+_i] \), a loading profile can be considered as a trajectory in space \( \fancyscript{L} \) spanned by \( \{\hat{\varvec{P}}_i \}\). As shown by König [24], it is sufficient to only consider the convex hull of the loading history, which is defined by the \( \text {NC}=2^{\text {NL}} \) corners of the polyhedral loading domain. This way, (7a) can be simplified to a time independent form:

$$\begin{aligned} F\left( \alpha {\varvec{\sigma }^{E}(\varvec{\hat{P}}_i)}+\varvec{\bar{\rho }},\text { }\!\!~\!\!\text { }{{\sigma }_{Y}} \right) \le 0, \quad i\in [1\ldots \text {NC}] \end{aligned}$$
(11)

By FE discretization and replacing (7a) by (11), the shakedown condition (7a–7d) becomes:

(12a)
(12b)
(12c)

Here, \(\text {NGS}\) is the number of total Gaussain points in a model, and matrix \( \varvec{C}\) the self-equilibrium matrix defined as:

$$\begin{aligned}{}[\varvec{C}]=\sum \limits _{m=1}^{\text {NGS}}{{{{w}_{m}}\left| {{J}_{m}} \right| }}{{[\varvec{B}_{m}]}^{T}}. \end{aligned}$$
(13)

Matrix \(\varvec{B}\) consists of spatial derivatives of shape functions and maps displacements into strains; \( w \) is the weight factor of integration points; \( J \) is the determinant of the Jacobian matrix. For FE models having \( \text {NK}\) nodes and \( \text {NDoF} \) degrees of freedom for each node, one obtains \(\varvec{C}\in \mathbb {R}^{\text {NDoF}\cdot \text {NK}\times 6\text {NGS}}\) where \( \text {NDoF} \) equals 3 for 3D case, and 2 for 2D case.

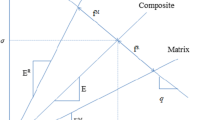
In the current study, ultimate strength \( \varvec{\Sigma }^U \) and endurance limit \( \varvec{\Sigma }^{\infty } \) are considered for the non-reverse axial loading which correspond to \( 1 \) load vertex and \( 2 \) load vertices in \( \fancyscript{L} \), respectively. To exclude anisotropy, strengths will be evaluated on various directions and their average value will be taken. The simplest way to achieve this is following the approach illustrated in Fig. 1: arbitrary orthogonal stresses \( \varvec{\Sigma }^E_{11}\) and \( \varvec{\Sigma }^E_{22}\) are prescribed alternately on a purely elastic reference RVE, and entailed microscopic stress fields \( \varvec{\sigma }^E_{11}(\varvec{y})\) and \( \varvec{\sigma }^E_{22}(\varvec{y})\) are calculated, respectively. By introducing an angle \( \theta \), a combined loading \(\hat{\varvec{P}}_1 \) can be formed as a joint effect of \( \varvec{\Sigma }^E_{11}\) and \( \varvec{\Sigma }^E_{22}\). Therefore, to calculate \( \varvec{\Sigma }^{U} \), the shakedown condition is required to be satisfied at vertex \(\hat{\varvec{P}}_1 \). Analogously, to calculate \( \varvec{\Sigma }^{\infty } \), the same condition should hold simultaneously at vertices \(\hat{\varvec{P}}_1 \) and \(\hat{\varvec{P}}_2\).

Fig. 1
figure 1

Superposition of elastic stress

Full size image

Some efficiency issues associated with the implementation of shakedown theorem (12a–12c) has been noticed concerning inequality constraints (12c). For pragmatic reasons, this condition should be reformulated to improve the efficiency of optimization algorithm. Akoa et al. [2] have suggested to convert convex quadratic constraints into Euclidean ball constraints. Several key steps of this approach are briefly introduced here.

For the original shakedown problem \( {\fancyscript{P}}_{\text {ORI}} \) in (12a–12c), primal variables are components of residual stress at every Gaussian point. More specifically:

  1. 1.

    \(\varvec{\bar{\rho }}=\{\bar{\rho }_{11},\bar{\rho }_{22},\bar{\rho }_{33},\bar{\rho }_{12},\bar{\rho }_{13},\bar{\rho }_{23}\}^T\)    for 3D case,

  2. 2.

    \(\varvec{\bar{\rho }}=\{\bar{\rho }_{11},\bar{\rho }_{22},\bar{\rho }_{12}\}^T\)    for 2D plane stress case,

  3. 3.

    \(\varvec{\bar{\rho }}=\{\bar{\rho }_{11},\bar{\rho }_{22},\bar{\rho }_{33},\bar{\rho }_{12}\}^T\)    for 2D plane strain case.

The reformulation introduced in [2] changes the primal variables to a linear transformation of total stress \( \varvec{\sigma } \) where \( \varvec{\sigma }=\alpha \varvec{\sigma }^E+ \varvec{\bar{\rho }}\). The relationship between the new primary variable \( \{ \varvec{u},v \}\) and \( \varvec{\sigma } \) in the 3D case follows:

$$\begin{aligned} \left\{ \begin{matrix} {{u}_{1}} \\ {{u}_{2}} \\ {{u}_{3}} \\ {{u}_{4}} \\ {{u}_{5}} \\ {v} \end{matrix} \right\} =\frac{1}{{{\sigma }^{Y}}}\left[ \begin{matrix} 1 &{} -1/2 &{} -1/2 &{} 0 &{} 0 &{} 0 \\ 0 &{} \sqrt{3}/2 &{} -\sqrt{3}/2 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} \sqrt{3} &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} \sqrt{3} &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \sqrt{3} \\ 1 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 \\ \end{matrix} \right] \left\{ \begin{matrix} {{\sigma }_{11}} \\ {{\sigma }_{22}} \\ {{\sigma }_{33}} \\ {{\sigma }_{12}} \\ {{\sigma }_{23}} \\ {{\sigma }_{13}} \\ \end{matrix} \right\} , \end{aligned}$$
(14)

and in 2D plane strain case:

$$\begin{aligned} \left\{ \begin{matrix} {{u}_{1}} \\ {{u}_{2}} \\ {{u}_{3}} \\ {v} \end{matrix} \right\} =\frac{1}{{{\sigma }^{Y}}}\left[ \begin{matrix} 1 &{} -1/2 &{} -1/2 &{} 0 \\ 0 &{} \sqrt{3}/2 &{} -\sqrt{3}/2 &{} 0 \\ 0 &{} 0 &{} 0 &{} \sqrt{3} \\ 1 &{} 0 &{} 1 &{} 0 \\ \end{matrix} \right] \left\{ \begin{matrix} {{\sigma }_{11}} \\ {{\sigma }_{22}} \\ {{\sigma }_{33}} \\ {{\sigma }_{12}} \\ \end{matrix} \right\} , \end{aligned}$$
(15)

and in 2D plane stress case:

$$\begin{aligned} \left\{ \begin{matrix} {{u}_{1}} \\ {{u}_{2}} \\ {{u}_{3}} \\ \end{matrix} \right\} =\frac{1}{{{\sigma }^{Y}}}\left[ \begin{matrix} 1 &{} -1/2 &{} 0 \\ 0 &{} \sqrt{3}/2 &{} 0 \\ 0 &{} 0 &{} \sqrt{3} \\ \end{matrix} \right] \left\{ \begin{matrix} {{\sigma }_{11}} \\ {{\sigma }_{22}} \\ {{\sigma }_{12}} \\ \end{matrix} \right\} . \end{aligned}$$
(16)

This transformation matrix denoted by \(\varvec{U}\) is applied to each \( \varvec{\sigma } \), and \( v \) retained from all Gaussian points are put collectively into a global vector \( \varvec{v}=\{v_1,v_2,\ldots ,v_m\}^T\) where \( m=\text {NGS} \) and \( \varvec{v}\in \mathbb {R}^{\text {NGS}}\). Applying the new primal variable, shakedown problem \( {\fancyscript{P}}_{\text {ORI}} \) in (12a–12c) can be reformulated into an equivalent form:

$$\begin{aligned} ({{\fancyscript{P}}_{\text {Reform}}})\mathop {\max .} \alpha , \end{aligned}$$
(17a)
$$\begin{aligned} s.t.:\underset{r=1}{\overset{\text {NGS}}{\sum }}\, \left[ \varvec{A}_{r} \right] \left\{ \varvec{u}_{r}^{1}\right\} + \left[ \varvec{B} \right] \left\{ \varvec{v}^{1}\right\} -\alpha {\left\{ \varvec{w}^{1}\right\} }&=0, \end{aligned}$$
(17b)
$$\begin{aligned} \text {Where:}\left\{ \varvec{w}^1 \right\}&=[\varvec{C}]\{\varvec{\sigma }^E(\hat{\varvec{P}}_1)\} \end{aligned}$$
(17c)
$$\begin{aligned} \left\{ \varvec{u}_{r}^{2}\right\} -\left\{ \varvec{u}_{r}^{1}\right\}&=\alpha \left[ \varvec{U} \right] \left\{ \varvec{\sigma } _{r}^{2,E}-\varvec{\sigma } _{r}^{1,E} \right\} \end{aligned}$$
(17d)
$$\begin{aligned} \left\| \varvec{u}_{r}^{1,2}\right\|&\le 1. \end{aligned}$$
(17e)

In (17a–17e), number within superscript indicates load vertex. For all 2D and 3D models, \( [\varvec{A}_r ] \) is defined as:

$$\begin{aligned}{}[\varvec{A}_r ] = \sqrt{2}\sigma ^Y[\varvec{D}_r ][\varvec{L}^{-T}] \end{aligned}$$
(18)

The other variables of (18) in 3D case are defined by:

$$\begin{aligned} \varvec{L}^\text {3D}&=\left[ \begin{matrix} \sqrt{2} &{} 0 &{} 0 &{} 0 &{} 0 \\ \sqrt{2}/2 &{} \sqrt{3}/\sqrt{2} &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 1 \\ \end{matrix} \right] \end{aligned}$$
(19a)
$$\begin{aligned} \varvec{D}_r^\text {3D}&=\left[ \begin{matrix} (\varvec{C}_r\varvec{T})^1&(\varvec{C}_r\varvec{T})^2&(\varvec{C}_r\varvec{T})^4&(\varvec{C}_r\varvec{T})^5&(\varvec{C}_r\varvec{T})^6 \end{matrix}\right] \end{aligned}$$
(19b)
$$\begin{aligned} \varvec{B}^\text {3D}&=\left[ \begin{matrix} (\varvec{C}_1\varvec{T})^3&(\varvec{C}_2\varvec{T})^3&\cdots&(\varvec{C}_\text {NGS}\varvec{T})^3 \end{matrix}\right] \end{aligned}$$
(19c)
$$\begin{aligned} \varvec{T}^\text {3D}&=\left[ \begin{matrix} 1/2 &{} 1/2 &{} 1/2 &{} 0 &{} 0 &{} 0\\ -1/2 &{} 1/2 &{} 1/2 &{} 0 &{} 0 &{} 0\\ -1/2 &{} -1/2 &{} 1/2 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1/\sqrt{6} &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 1/\sqrt{6} &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1/\sqrt{6} \\ \end{matrix} \right] \end{aligned}$$
(19d)

while in 2D plane strain case:

$$\begin{aligned} \varvec{L}^\text {P. Strain}&=\left[ \begin{matrix} \sqrt{2} &{} 0 &{} 0 \\ \sqrt{2}/2 &{} \sqrt{3}/\sqrt{2} &{} 0 \\ 0 &{} 0 &{} 1 \\ \end{matrix} \right] \end{aligned}$$
(20a)
$$\begin{aligned} \varvec{D}_r^\text {P. Strain}&=\left[ \begin{matrix} (\varvec{C}_r\varvec{T})^1&(\varvec{C}_r\varvec{T})^2&(\varvec{C}_r\varvec{T})^4 \end{matrix}\right] \end{aligned}$$
(20b)
$$\begin{aligned} \varvec{B}^\text {P. Strain}&=\left[ \begin{matrix} (\varvec{C}_1\varvec{T})^3&(\varvec{C}_2\varvec{T})^3&\cdots&(\varvec{C}_\text {NGS}\varvec{T})^3 \end{matrix}\right] \end{aligned}$$
(20c)
$$\begin{aligned} \varvec{T}^\text {P. Strain}&=\left[ \begin{matrix} 1/2 &{} 1/2 &{} 1/2 &{} 0\\ -1/2 &{} 1/2 &{} 1/2 &{} 0\\ -1/2 &{} -1/2 &{} 1/2 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1/\sqrt{6} \\ \end{matrix} \right] \end{aligned}$$
(20d)

and in 2D plane stress case:

$$\begin{aligned} \varvec{L}^\text {P. Stress}&=\left[ \begin{matrix} 1 &{} -1/2 &{} 0 \\ 0 &{} \sqrt{3}/2 &{} 0 \\ 0 &{} 0 &{} \sqrt{3} \\ \end{matrix} \right] \end{aligned}$$
(21a)
$$\begin{aligned} \varvec{D}_r^\text {P. Stress}&=\varvec{C}_r \end{aligned}$$
(21b)

Here \((\varvec{X})^i \) represents the \(i\)th column of matrix \( \varvec{X}\). We note that, according to (16), the converted variable does not contain \( v \) for the plane stress case. Thus the term \( [\varvec{B}] \{\varvec{v}^{1}\} \) does not exist in this case as well.

When the numerical scheme (17a–17e) is used for limit analysis, due to the absence of \(\hat{\varvec{P}}_2 \), equality constraints (17d) is removed.

2.3 Solving the Quadratically Constrained Programming (QCP) by Primal-Dual Interior Point Method

In order to obtain the shakedown factor \( \alpha \), the optimization problem (17a–17e) has to be solved. This is a typical QCP problem because inequality constraints (17e) are quadratic functions. By introducing the slack variable \( \varvec{s} \) to convert inequality to equality constraints, this problem can be written in a general form:

$$\begin{aligned} ({{\fancyscript{P}}_{\text {Standard}}})\mathop {\min .} -\varvec{\alpha }&=f(\varvec{x}), \end{aligned}$$
(22a)
$$\begin{aligned} s.t.: \varvec{c}_E(\varvec{x})&=\varvec{0}, \end{aligned}$$
(22b)
$$\begin{aligned} \varvec{c}_I(\varvec{x})-\varvec{s}&=\varvec{0}, \end{aligned}$$
(22c)
$$\begin{aligned} \varvec{s}&\ge \varvec{0}. \end{aligned}$$
(22d)

The vector \( \varvec{x} \) consists of \( \varvec{u}_r \) and \( \varvec{v} \) for all elements at all \( \varvec{\hat{P}}_i \) as well as the loading factor \( \alpha \). By denoting the dimension of the converted variable in each Gaussian point as \( DCV \), then depending on if model is in 3D, plane strain or plane stress, \( DCV \) equals 6, 4, or 3, respectively. Within the given QCP problem, primal variables are \( \varvec{x}\) and \( \varvec{s} \). In 3D or plane strain case \( \varvec{x}\in \mathbb {R}^{[\text {NC}\cdot (\text {DCV}-1)+1]\cdot \text {NGS}+1} \), while in plane stress case \( \varvec{x}\in \mathbb {R}^{\text {NC}\cdot \text {DCV}\cdot \text {NGS}+1} \) due to the absence of \( \varvec{v}^1 \). Meanwhile, for all three cases, \(\varvec{s}\) is constantly a vector in \(\mathbb {R}^{\text {NC}\cdot \text {NGS}} \). The objective function (23a) is linear with negative loading factor as the function value. Equality constraints (23b) are obtained from self-equilibrium condition (17b) and time-independence condition (17d). The quadratic inequality constraints (23c) represent the von Mises yield criterion.

To avoid the complication of direct dealing with (22d) a barrier problem is constructed:

$$\begin{aligned} \min _{\varvec{x},\varvec{s}} f(\varvec{x})-\mu \sum _{i=1}^{m}{\log {s_i}}, \end{aligned}$$
(23a)
$$\begin{aligned} s.t.: \varvec{c}_E(\varvec{x})&=\varvec{0}, \end{aligned}$$
(23b)
$$\begin{aligned} \varvec{c}_I(\varvec{x})-\varvec{s}&=\varvec{0}. \end{aligned}$$
(23c)

Here \( \mu \) is a positive barrier parameter.

The first-order Karush-Kuhn-Tucker (KKT) conditions of (23a–23c) write:

$$\begin{aligned} \varvec{\nabla }f(\varvec{x})-\fancyscript{A}_E^T(\varvec{x})\varvec{y}-\fancyscript{A}_I^T(\varvec{x})\varvec{z}&= \varvec{0}, \end{aligned}$$
(24a)
$$\begin{aligned} -\mu \varvec{S}^{-1}\varvec{e}+\varvec{z}&=\varvec{0}, \end{aligned}$$
(24b)
$$\begin{aligned} \varvec{c}_E(\varvec{x})&=\varvec{0}, \end{aligned}$$
(24c)
$$\begin{aligned} \varvec{c}_I(\varvec{x})-\varvec{s}&=\varvec{0}. \end{aligned}$$
(24d)

In (24a–24d), dual variables \( \varvec{y} \) and \( \varvec{z} \) are lagrangian multipliers to equality constraints and inequality constraints, respectively. \( \fancyscript{A}_E \) consists of gradients of equality constraints where \( \fancyscript{A}_E=[{\nabla }c_{E,1},{\nabla }c_{E,2},\ldots ,{\nabla }c_{E,n} ]\). Because the equality constraints are linear, their gradients become constant values. In 3D and plane strain models \(\fancyscript{A}_E\) has \((\text {NK}\cdot \text {NDoF})+(\text {NC}-1)\cdot (\text {DCV}-1)\cdot \text {NGS} \) rows and \( [\text {NC}\cdot (\text {DCV}-1)+1]\cdot \text {NGS} \) columns, while in plane stress models, \(\fancyscript{A}_E\) has \((\text {NK}\cdot \text {NDoF})+(\text {NC}-1)\cdot \text {DCV}\cdot \text {NGS} \) rows and \( \text {NC}\cdot \text {DCV}\cdot \text {NGS} \) columns. Similar to \( \fancyscript{A}_E\), \( \fancyscript{A}_I\) is defined as \([{\nabla }c_{I,1},{\nabla }c_{I,2},\ldots ,{\nabla }c_{I,m} ]\). Because \( c_I \) are quadratic, their gradients \( \varvec{\nabla }c_I \) are linear functions. The number of rows in \( \fancyscript{A}_I\) is same as \( \fancyscript{A}_E\), but the number of its columns is \( \text {NC}\cdot \text {NGS} \), which is independent on the model type. Matrix \( \varvec{S} \) in (24b) is defined by \( \varvec{S}=\text {diag}(\varvec{s}) \), and \( \varvec{e} \) is a unit vector. The term \(\mu \varvec{S}^{-1}\varvec{e}\) in (24b) is yielded from \( {\varvec{\nabla }}_{\varvec{s}}(\mu \sum _{i=1}^{m}{\log {s_i}})\).

The nonlinear system (24a–24d) can be solved with Newton’s method by given numerical scheme:

(25)

In (25), \( \fancyscript{L} \) represents the lagrangian for the barrier problem (23a–23c):

$$\begin{aligned} \fancyscript{L}(\varvec{x},\varvec{s},\varvec{y},\varvec{z})=f(\varvec{x})-\varvec{y}^T\fancyscript{A}_E(\varvec{x})-\varvec{z}^T(\fancyscript{A}_I(\varvec{x})-\varvec{s}). \end{aligned}$$
(26)

whereas \( \varvec{Z} \), analogous to \( \varvec{S} \), is defined as \( \varvec{Z}=\text {diag}(\varvec{z}) \); \( \varvec{I} \) is the unit matrix.

To implement the primal-dual interior point method, one starts with a predefined barrier parameter \( \mu \) and a feasible initial solution \( \{\varvec{x}_0,\varvec{s}_0,\varvec{y}_0,\varvec{z}_0\}^T \). By solving the system (25) a Newton’s step can be calculated. This step will be corrected with respect to the fraction to boundary rule, and the corrected step will be taken to update both primal and dual variables. This procedure will be repeated, and once the error function \( \fancyscript{E} \) defined as:

$$\begin{aligned} \fancyscript{E} = \max \{ ||\varvec{\nabla }_{x}f(\varvec{x})-\fancyscript{A}_E^T(\varvec{x})\varvec{y}-\fancyscript{A}_I^T(\varvec{x})\varvec{z}||, ||\varvec{Sz}-\mu \varvec{e}||,||\varvec{c}_E(\varvec{x}) ||,||\varvec{c}_I(\varvec{x})-\varvec{s} ||\} \end{aligned}$$
(27)

drops below a predefined threshold, \( \mu \) will be updated and solution to the evolved barrier problem will be calculated by the same iterative scheme. One can prove that with \( \mu \downarrow 0 \), solution to the barrier problem is exactly the same as the one to original problem.

3 Numerical Results

3.1 Finite Element Models for Statistical Analysis

20 RVE models with different microstructure have been prepared. We distinguish two groups: Group 1 consists of 10, each 30 \({\upmu }\)m-by-30 \({\upmu }\)m, RVEs numbered consecutively from 1 to 10. The models in Group 2, however, have a size 40 \({\upmu }\)m-by-40 \({\upmu }\)m with numbers from 11 to 20. All models are based on real WC-Co microstructures obtained from a scanning electron microscope (SEM) observation using a backscattering detector (Fig. 2). In these images the dark grey area is the Co phase, while the bright areas are the WC grains with their characteristic prismatic shape. The average grain size is \( d_{WC}=2.35\) \({\upmu }\)m . To convert these SEM images to the corresponding FE models an automatic technique developed in [8] is employed. This technique is capable of generating a triangular element based adaptive finite element mesh. It adopts a denser mesh in vicinity to phase interfaces and a coarser mesh elsewhere (Fig. 2).

Fig. 2
figure 2

a SEM image b RVE model converted from SEM image

Full size image
Table 1 Material properties of both phases
Full size table

Both plane stress and plane strain models are investigated. It should be noted that in previous studies plane strain models are observed to give more accurate prediction on the elasto-plastic behavior of given composite in small strain regime [8, 34]. To check the error caused by finite element type, the current study considers also a special typed 3D model which consists of a thin layered wedge elements obtained by extracting the 2D model in the 3rd direction for 1 \({\upmu }\)m. Intuitively, we refer these 3D models to 2.5D models, and they are regarded as compromise between plane stress and plane strain, which correspond to two extremes about the stiffness in the 3rd direction.

For simplicity, the materials for both constituents are considered as elastic-perfect plastic materials with parameters illustrated in Table 1. It is worthy to note that current study is restricted to small deformation and assumes plastic failure as the only failure mechanism.

The procedure of numerical limit and shakedown analysis can be summarized as follows: first, RVE models are built in commercial finite element software ABAQUS 6.12 [1]. By using a self-developed Python script, these models are prescribed with global loading as explained in Sect. 2.2 and reference elastic stress fields are calculated. In the second step, the geometrical setup of models and their associated stress results are output to MATLAB [29] to build the optimization problem (17a–17e). In the subsequent step, the constructed QCP problem is submitted to an interior point method solver, Gurobi [19], to calculate loading factor \( \alpha \). By taking a series of \( \theta \in {[0,\pi ]} \) strengths in many different directions are calculated and they together form an entire feasible load domain. By projecting this domain to \( \pi \)-plane and fit the projection to a perfect semi-circle, a direction-independent strength value is obtained which best characterizes the overall strength of a RVE. In the final step, strength of each RVE retrieved from the best fit are collected and interpreted by a statistical analysis. In such analysis three measures of a random variable \( x \) are evaluated. These measures include mean value \( \bar{x} \), standard deviation \( x_{SD} \), and coefficient of variance defined as:

$$\begin{aligned} C_{x}=\frac{x_{SD}}{\bar{x}}. \end{aligned}$$
(28)

3.2 Comparative Study Between Plane Stress, Plane Strain and 2.5D Models

In [8] it has been shown that the discrepancy between plane stress and plane strain models becomes more obvious when global plasticity accumulates. Also, once global plasticity has reached a critical level, the mechanical behavior reflected by these two model variances are fundamentally different. In the present study, we further studied how these two element types influence the strength prediction.

It should be noticed, even for a FE model with fixed mesh pattern, the scale of its associated optimization problem still greatly depends on the element type: a 2D RVE model is arbitrarily picked to illustrate this difference. The model is taken from Group 2 and consists of 17,739 elements and 17,915 nodes. The scale of the optimization problem related to this model is given in Table 2. The table shows that the problem scale increases significantly when a 2D model is extended to 2.5D. A comparison of plane stress and 2.5D model pointed out that the number of primal variables has increased for around 6 times, while dual variables for around 2.5 times.

Table 2 Scale of optimization problem for a FE mesh with different element types
Full size table
Fig. 3
figure 3

RVE model with different mesh density

Full size image
Fig. 4
figure 4

Limit and shakedown domains for RVE Nr. 2 meshed with different element types

Full size image

As has been stressed, plane stress and plane strain correspond to two extreme cases about strength in the 3rd direction and the original intention to introduce 2.5D model is to overcome such obstacle. However, beside such advantage 2.5D model also, unexpectedly, exhibits advantage in mesh insensitivity. For a 30 \(\upmu \)m-by-30 \(\upmu \)m RVE, two element densities are adopted. As can be observed from Fig. 3, the model with coarse mesh contains only 5,784 elements, whereas the number of elements in fine mesh model is almost doubled which renders 9,940. Limit and shakedown domains for both models are shown in Fig. 4. The domains obtained in limit analysis enlarge along with the increase of out-of-plane strength. Meanwhile, it is also evident that plane strain models have extremely high strength around \( \theta =\pi /4. \) This can be explained as follows: for plane strain, \( \theta =\pi /4 \) corresponds to the loading condition of globally hydrostatic stress. Since hydrostatic stress does not contribute to the von-Mises yield condition, material under this load can sustain exceptionally high global stress.

Unlike limit domains that are insensitive to discretization, shakedown domains appear to have more dependence on the mesh density, which means the local behavior has more influence on the overall performance of material. Comparing shakedown domains of different model types, it is manifest that 2.5D model is least sensitive to mesh density. For this reason, 2.5D models are used in the remaining part of our study.

3.3 Statistical Analysis and Study on the Size Effect

To prepare finite element models for statistical analysis, a uniform mesh setting is adopted to all involved models. For each individual microstructure, elements covering the non-critical regions were assigned with a global size of 0.8 \({\upmu }\)m; and near the phase boundaries a finer mesh is used with an edge size of 0.2\(\,{\upmu }\)m. Under this configuration, the number of elements for 30 \({\upmu }\)m-by-30 \({\upmu }\)m RVEs varies roughly between 6,000–9,000, and 13,000–18,000 for 40 \({\upmu }\)m-by-40 \({\upmu }\)m RVEs. The size of the optimization problem can be estimated by referring to Table 2.

Table 3 Statistics of selected global material properties
Full size table

As Table 3 indicates results are dispersively distributed. Because RVEs inside the same group are fixed in size and constituents, this reflects the contribution of the microstructure. Results shown in Table 3 can be interpreted as follows: The micro-structure has a considerable impact on different global material properties which is in general strong for the nonlinear than the linear ones. For example, the normalized variance of Poisson’s ratio for Group 1, \( C_{\bar{\upsilon }}^{\text {Group2}} \) is less than 0.013. But the same indicator of endurance limit, \( C_{\Sigma ^U}^{\text {Group2}} \), becomes 0.193. A transverse comparison has been made between the distribution of \( \Sigma ^{U} \) and \( \Sigma ^{\infty } \) (Fig. 5). According to Fig. 5, the scatter of \( \Sigma ^{U} \) is more pronounced than \( \Sigma ^{\infty } \), for the reason outlined above. This indicates the structure to have more influence on the former parameter.

Fig. 5
figure 5

Distribution of \( \Sigma ^{U} \) and \( \Sigma ^{\infty } \) associated to models in Group 1

Full size image
Fig. 6
figure 6

Deoendence of \( \Sigma ^{U} \)’s distribution on size

Full size image

Normally larger RVEs will retain smaller \( C_x \) compared to smaller RVEs, but exceptions can occasionally be observed: e.g. \( C_{\Sigma ^U}^{\text {Group1}} \) is 0.176, but \( C_{\Sigma ^U}^{\text {Group2}}\) increases to 0.193 (Fig. 6). More interestingly, the size effect also depends on properties being considered. For example, it happens simultaneously that \( C^{\text {Group2}}<C^{\text {Group1}} \) for \( \Sigma ^U \) , and in contract \(C^{\text {Group2}}>C^{\text {Group1}} \) for the other properties including \( \bar{E},\bar{\upsilon },\Sigma ^Y\). A possible reason can be the effect of localization: when a global feature depends severely on some localized material behavior, the increase of RVE size can not fully expel the occurrence of such local effect and thus will not enhance the quality of a model.

Localization is the cause of another noteworthy phenomenon: for both model groups \( \Sigma ^{\infty } \) are smaller than \( \Sigma ^{Y} \). In the first glance, this result may seems disturbing, nevertheless it can be well understood from the difference between \( \Sigma ^{Y} \) and load leading to the onset of local plasticity. To a certain extent, the development of local plasticity does not contribute much to \( \Sigma ^{Y} \) because of its limited share of volume. However, for \( \Sigma ^{\infty } \), since it doesn’t allow alternating plasticity to take place at any material point, its value is sensitive to stress concentration. In summary, \( \Sigma ^{\infty } <\Sigma ^{Y} \) reflects serious stress concentration, and it also implies that alternating plasticity is the major cause of the plastic failure of current composite.

4 Conclusions

In this paper, it is presented how lower-bound DM, homogenization technique and statistical analysis can be used to study the strength of non-periodic PRMMC materials. The material investigated, WC-30 Wt.% Co, is a typical random PRMMC with complex microstructure. Main findings:

  • By adopting an efficient algorithm, DM can be used to study composites with complex real microstructure.

  • Although 2.5D models lead to optimization problems of greater size, this model type is more advantageous: first, the out-of-plane strengths in 2.5D models are more reasonable. Second, in shakedown analysis these models are more mesh insensitive.

  • \( \Sigma ^U \) is relatively mesh insensitive, increasing with the increase of the out-of-plane stiffness.

  • Size effect of RVEs is not absolute; its increase does not necessarily leads to decrease of disparity among models. If a macroscopic material behavior to be studied depends strongly on localized behavior, then enlarging RVE size will not continuously make the model more objective.

  • Highly localized alternating plasticity is the major cause of the failure and it leads to \(\Sigma ^Y>\Sigma ^\infty \).

Finally, it should be emphasized that the material model and failure scenario assumed in this paper is over-restrictive. Future work should take into account kinematic hardening and material damage. Also, for reliable results, the statistical investigations have to be performed on an much larger number of numerical tests.