Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The prediction of structure failure behavior under variable loads with unknown time history is very difficult. Direct methods, namely limit and shakedown analysis, can help to overcome this difficulty. Application of shakedown analysis to composites, especially long fiber-reinforced metal matrix composites, upsurge these years. For heterogeneous materials, there are generally two scales concerned. On the microscopic level, local stress and strain analysis are performed and the influence of each phase (fiber or matrix) is investigated. On the macroscopic scale, the global response of the composite is analyzed with the help of homogenization theory. This methodology was first proposed for the case of limit analysis of heterogeneous media in [37, 39]. In a similar way, some authors carried out shakedown analysis of periodic composites with static approach [46, 47], as well as the kinematic approach [9, 31, 32]. Furthermore, some scholars also considered geometrical effects and damage in micro-level [14, 19, 20, 45].

Besides the issue of optimization, the implementation of lower bound direct methods includes also the finite element method. Finite elements are used to obtain local stress or local strain, as well as the equilibrium matrix. Previously, two-dimensional finite elements have usually been used to deal with plane strain or plane stress cases [5, 8, 33]. The disadvantage of the plane element is in the restriction of the applied load. Recently, work concerned with metal matrix composites has been extended to solid elements, which makes loads perpendicular to the transverse direction of composites possible [49]. However, the 20-node solid elements usually lead to large numbers of variables, because the scale of the optimization problem depends mainly on the type of finite element.

Moreover, combined with homogenization theory, the material performances as a whole are discussed, such as the influence of fiber distribution and volume fraction [15, 33, 50]. From the knowledge of the local (or microscopic) material properties, the global (or macroscopic) mechanical response of fiber-reinforced composites is predicted. The evaluation of elastic properties involves classical constitutive laws and homogenization theory [10, 35]. The prediction of nonlinear macroscopic behavior has been mostly performed by using 3-D models based on limit analysis for periodic heterogeneous material [40, 41].

In this work, a non-conforming three-dimensional finite element coupled with direct methods and homogenization technique is presented for the limit and shakedown analysis of periodic metal-matrix composites.

2 Analytical Model on Micro-level

2.1 Multi-scale Approach

Periodic composites, especially fiber-reinforced metal matrix composites (MMCs), are investigated in our work. There is at least one ductile phase. For the interface, perfect bonding is assumed. For the ductile phase, we use the theory of elasto-plasticity.

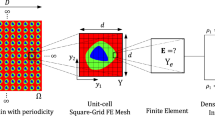
Figure 1 shows the procedure of homogenization theory, which is composed mainly into two steps:

  • Localization: Any macroscopic point in a heterogeneous structure is investigated in a representative volume element (RVE). This process is termed localization or representation.

  • Globalization: The inverse procedure, by which microscopic properties origi-nating in the RVE are idealized at the marco level is called globalization or homo-genization.

Fig. 1
figure 1

Homogenization theory

Full size image

Each periodic micro structural block is usually called a Representative Volume Element (RVE) or Unit Cell, denoted by V. We introduce a small parameter δ [2], e.g. the “slow” variables x, y (or global coordinates), and the “fast” variables ξ, η (or local coordinates). The relationship between the two coordinates are as follows:

$$ \xi=\frac{x}{\delta},\qquad\eta=\frac{y}{\delta} $$
(1)

δ determines the size of the RVE, which plays an important role in studying the heterogeneous material, especially for non-uniform structure. There has been much research about how to determine a representative volume element. The various classes and definitions of RVE and the main practical approaches can be referred to in [29]. Briefly, the RVE of a heterogeneous material with random spatial distribution is investigated through the “Window” technique [34]. For a heterogeneous material with periodic distribution, the smallest unit is normally defined as the RVE.

The macroscopic strain E and stress Σ are linked to the microscopic strain ε and stress σ by the following relationships [37]:

(2)
(3)

Here, 〈⋅〉 stands for the averaging operator.

In the static shakedown theory for composite materials with periodic microstructure, the macroscopic stress is decomposed into a purely elastic part σ E and a time-independent residual one \(\bar{\boldsymbol{\rho}}\):

$$ \boldsymbol{\varSigma}(x,y,z)=\frac{1}{V} \int_V \bigl(\alpha\boldsymbol{\sigma}^{E}+\bar{\boldsymbol{\rho}}\bigr ) dV= \frac{1}{V} \int_V \alpha\boldsymbol{ \sigma}^E dV+ \frac{1}{V} \int_V \bar{ \boldsymbol{\rho}} dV $$
(4)

On the basis of homogenization theory, the first step is to obtain the local stress and strain in the RVE. According to the type of the prescribed loading condition, either a strain approach or a stress approach can be used.

2.2 Stress and Strain Approaches

For heterogeneous materials, especially random ones, it is impossible to determine the material characteristics precisely. This results from an incomplete knowledge of the material structure, such as the spatial distribution of different phases or the strength of interface coherence. Therefore, effective (or homogenized) material properties are studied to replace the actual ones. Combined with homogenization theory, the stress approach and the strain approach are mainly used [25, 26, 37].

2.2.1 Strain Approach

As the name implies, the macroscopic strain E is imposed at the boundary of a representative volume element. In practice, the macroscopic strain is amounted to displacement loading. Let the displacement u be decomposed as [6, 24]:

$$ \boldsymbol{u}=\boldsymbol{E}\cdot x + \boldsymbol{u}^{per} $$
(5)

where u per is the periodic displacement field. Then, the local strain ε can be derived as:

$$ \boldsymbol{\varepsilon }=\boldsymbol{E} + \boldsymbol{\varepsilon }^{per} $$
(6)

where ε per is the fluctuating part in every representative volume element. Note that the periodicity of u per implies that the average of ε per on the RVE vanishes and therefore the average of ε is E.

To find σ E and ε per, the elastic localization problem can be written as:

$$ P_{strain}= \begin{cases} \operatorname{div} \boldsymbol{\sigma^{E}}=0 &\text{in}\ V \\ \boldsymbol{\sigma^{E}}=\boldsymbol{d}:(\boldsymbol{E}+\boldsymbol {\varepsilon ^{per}}) &\text{in}\ V \\ \boldsymbol{\sigma^{E}} \cdot\boldsymbol{n} &\text{anti-periodic on}\ \partial V \\ \boldsymbol{u}^{per} & \text{periodic on}\ \partial V \end{cases} $$
(7)

Here, V is the domain of the representative volume element in R 3. Furthermore, σ E is the purely elastic stress and n is the out-normal vector on the surface of the RVE under consideration. The anti-periodicity of σ E⋅n on ∂V implies that σ E⋅n has opposite values on opposite sides of ∂V. The periodicity of u per means that u per is the same at two opposite points of the boundary.

In our work, we consider the particular case that a uniform displacement is imposed on the boundary. After deformation, the edges of each element are still straight (Fig. 2). Considering symmetry, the investigated model can be simplified to one quarter of the representative volume element.

Fig. 2
figure 2

Strain method

Full size image

Thus, the problem can be formulated as [37]:

$$ P^{*}_{strain}= \begin{cases} \operatorname{div} \boldsymbol{\sigma^{E}}=0 &\text{in}\ V \\ \boldsymbol{\sigma^{E}}=\boldsymbol{d}:\boldsymbol{E} &\text{in}\ V \\ \boldsymbol{u}^{s} & \text{symetric condition on}\ \partial V \\ \boldsymbol{u}^{per}=0 & \text{on}\ \partial V \end{cases} $$
(8)

For the shakedown analysis of composites, we still need to consider the residual stress field \(\bar{\boldsymbol{\rho}}\), which should satisfy the self-equilibrated condition and periodicity conditions.

$$ P^{res}_{strain}= \begin{cases} \operatorname{div} \bar{\boldsymbol{\rho}}=0 &\text{in}\ V \\ \bar{\boldsymbol{\rho}} \cdot\boldsymbol{n} &\text{anti-periodic on}\ \partial V \end{cases} $$
(9)

2.2.2 Stress Approach

In this approach, the macroscopic stress Σ is imposed at the boundary. After deformation, the boundary displacement is not uniform anymore (Fig. 3).

Fig. 3
figure 3

Stress method

Full size image

The elastic localization problem can then be written as [37]:

$$ P_{stress}= \begin{cases} \operatorname{div} \boldsymbol{\sigma^{E}}=0 &\text{in}\ V \\ \boldsymbol{\sigma^{E}}=\boldsymbol{d}:\boldsymbol{\varepsilon } &\text{in}\ V \\ \boldsymbol{\sigma^{E}} \cdot\boldsymbol{n}=\boldsymbol{\varSigma }\cdot\boldsymbol{n} &\text{on}\ \partial V \end{cases} $$
(10)

The residual stress field \(\bar{\boldsymbol{\rho}}\) is also self-equilibrated and satisfies the periodicity condition. However, in the stress method, we need an additional condition, that the average value of \(\bar{\boldsymbol{\rho}}\) should equal zero.

$$ P^{res}_{stress}= \begin{cases} \operatorname{div} \bar{\boldsymbol{\rho}}=0 &\text{in}\ V \\ \bar{\boldsymbol{\rho}} \cdot\boldsymbol{n}=0 &\text{on}\ \partial V \end{cases} $$
(11)

For the finite element solution, this requirement could be satisfied by adding a fictive node in each element of the meshed RVE [12, 25, 40].

2.3 Transformation Between Two Scales

After analysis on the level of a representative volume element, we may transfer the local displacement domain to a global stress domain in the principal direction with the help of the particular case of the homogenization theory presented in Sect. 2.2.1 [33]. Take the case of two-dimensional plane stress as an example (Fig. 4). The material is homogeneous, with Young’s modulus E and Poisson’s ratio ν. In terms of Hooke’s law:

$$ \begin{cases} \varepsilon _{x}=\frac{1}{E} (\sigma_{x}-\nu\sigma_{y}) \\ \varepsilon _{y}=\frac{1}{E} (\sigma_{y}-\nu\sigma_{x}) \\ \gamma_{xy}=\frac{2(1+\nu)}{E} \tau_{xy} \end{cases} \Longrightarrow \quad \begin{cases} \sigma_{x}=\frac{E}{1-\nu^2} (\varepsilon _{x}+\nu \varepsilon _{y}) \\ \sigma_{y}=\frac{E}{1-\nu^2} (\varepsilon _{y}+\nu \varepsilon _{x}) \\ \tau_{xy}=0 \end{cases} $$
(12)
Fig. 4
figure 4

2D homogeneous material under plane stress

Full size image

The case of homogeneous plane stress is characterized by the fact that there is no residual stress field and all the local stresses have the same value.

With this, we obtain:

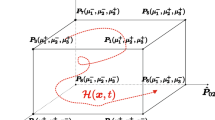
$$ \begin{cases} \varSigma^{e}_{1}=\sigma_{x}\\ \varSigma^{e}_{2}=\sigma_{y} \end{cases} $$
(13)

Consider four points in the shakedown displacement load domain (Fig. 5).

Fig. 5
figure 5

Transformation relationship

Full size image

For P2:

$$ \begin{cases} U_{1}=\alpha_{SD} U^{0}_{1} \\ U_{2}=0 \end{cases} \Longrightarrow\quad \begin{cases} \varepsilon _{x}= U^{0}_{1}/L\\ \varepsilon _{y}=0 \end{cases} \Longrightarrow\quad \begin{cases} \sigma_{x}=\frac{E \varepsilon _x}{1- \nu^2} \\ \sigma_{y}=\frac{\nu E \varepsilon _x}{1- \nu^2}=\nu\sigma_{x} \end{cases} $$
(14)

Therefore, the point P2 in the shakedown macroscopic stress domain has the value:

$$ \begin{cases} \varSigma_{1}=\alpha_{SD} \varSigma^{e}_{1}\\ \varSigma_{2}=\alpha_{SD} \nu\varSigma^{e}_{1} \end{cases} $$
(15)

After transformation, P2 in the local displacement domain rotated through an angle φ 1 in the macroscopic stress domain:

$$ \varphi_1=\arctan\frac{\varSigma_2}{\varSigma_1}= \arctan(\nu) $$
(16)

Similarly, for P4:

$$ \begin{cases} \varSigma_{1}=\alpha_{SD} \nu\varSigma^{e}_{2}\\ \varSigma_{2}=\alpha_{SD} \varSigma^{e}_{2} \end{cases} $$
(17)

The rotated angle φ 2 is:

$$ \varphi_2=\operatorname{arctan} \frac{\varSigma_1}{\varSigma_2}= \operatorname {arctan}(\nu) $$
(18)

According to the constitutive law (12), we may obtain the macroscopic elastic stress for P3 as:

$$ \begin{cases} \varSigma^{e*}_{1}=\frac{E}{1- \nu^2} (\varepsilon _x-\nu \varepsilon _y)\\ \noalign{\vspace{3pt}} \varSigma^{e*}_{2}=\frac{E}{1- \nu^2} (\nu \varepsilon _x-\varepsilon _y) \end{cases} $$
(19)

Also the angle φ ∗ between the X-axis and a line from the origin to P3 is:

$$ \varphi^*=\operatorname{arctan} \frac{\varSigma^*_2}{\varSigma^*_1} $$
(20)

The positions of load vertexes in different domains are listed in Table 1.

Table 1 The positions of points in different domains
Full size table

For composite materials, we need to keep in mind that the macroscopic stress is obtained basing on the particular case of homogenization theory by using strain approach. Since the average of the residual stresses equals to zero, the macroscopic stress at different states can be defined as:

  • Elastic state: Σ EL =α EL Σ e

  • Shakedown state: Σ SD =α SD Σ e

  • Limit state: Σ LM =α LM Σ e

  • Alternating plasticity state: Σ AP =α AP Σ e

A numerical example will be illustrated in Sect. 4.2.

3 Numerical Solution

The implementation of lower bound direct methods mainly involves two numerical tools: finite element method and large scale nonlinear optimization method.

Any discretized version of lower bound direct methods preserves the relevant bounding properties only if the following conditions are satisfied simultaneously: (i) the solution of the purely elastic response is exact; (ii) the residual stress field satisfies pointwise the homogeneous equilibrium equations; (iii) the yield condition is satisfied in each point of the considered material.

The existence of these bounding properties was the reason why many authors used the finite element stress method with a discretization of the stress field. Moreover, since the lower bound direct methods is formulated in static quantities, it is meaningful to discretize the stress field rather than the displacement field. However, most of the available finite element codes are based on displacement formulations. On the other hand, it is very difficult to preserve in this case the bounding properties. Especially the first condition can hardly be satisfied, if other than particular structures are studied. Thus, to use the proposed method with commercial codes, we prefer here the displacement method. In this case all the well-known displacement element formulations can be used. For that purpose it is necessary to transform the statical equations from their local form into the equivalent weak form.

3.1 Non-conforming Finite Element Discretization

The accuracy of a finite element analysis can be improved by using higher order elements. For instance, an 8 node element can be replaced with a 20 node element, which costs more computer time and storage. Wilson et al. [48] introduced non-conforming elements by including additional incompatible displacement modes, which increase the basic accuracy still using a simple (first order) element and avoid the “shear locking” numerical problem [36, 38].

The scale of the optimization problem is mainly determined by the number of elements and the used element type. Therefore non-conforming element is adopted here. Comparative study using different element types is presented in Sect. 4.1.

In terms of the principle of virtual work, the external virtual work is equal to the internal virtual work, when equilibrated forces and stresses undergo unrelated but consistent displacements and strains:

$$ \int_{V} \bigl\{\varepsilon ^* \bigr \}^T \bigl\{\alpha\boldsymbol{\sigma}^E+\bar{\boldsymbol{ \rho}} \bigr\} \,\mathrm{d}V =\int_{\partial V} \bigl\{ \boldsymbol{ \delta}^* \bigr\}^T \bigl\{ \boldsymbol{p}^* \bigr\} \,\mathrm{d} S+\int _{ V} \bigl\{ \boldsymbol{\delta}^* \bigr\}^T \bigl\{ \boldsymbol{f}^* \bigr\} \,\mathrm{d} V $$
(21)

Here, ε ∗ is the virtual strain, and δ ∗ is the virtual displacement. These discretizations have to be carried out for both the purely elastic stress field σ E and the residual stress field \(\bar{\boldsymbol{\rho}}\).

Let u, v and w be displacements in the x, y and z-directions, respectively, then:

(22)

Here, N i is the shape function, \(N_{i} = \frac{1}{8} (1 + rr_{i}) (1 + ss_{i}) (1 + tt_{i})\); r, s, t are natural coordinates, and r i , s i , t i are the values of the natural coordinates of node i. P 1=1−r 2, P 2=1−s 2 and P 3=1−t 2. One important feature is that P 1, P 2 and P 3 are zero at eight nodes, which maintains the displacement compatibility at nodes. {a} is the vector of additional degrees of freedom.

$$\{a \} = \{ a_1 \ a_2 \ a_3 \ a_4 \ a_5 \ a_6 \ a_7 \ a_8 \ a_9 \}^{T} $$

The element stiffness matrix is defined as follows:

(23)

Here, B is the strain matrix, computed from the derivatives of shape functions; D is the fourth-order tensor of elastic modulus; |J| is the determinant of the Jacobian matrix, which is evaluated at the centre of the element [22], i.e. r=s=t=0; w are weighting factors; ngl1, ngl2, ngl3 are the number of Gauss points along r, s, t directions, respectively. Using Gauss quadrature, the 2×2×2 scheme has found to be adequate. The dimension of element stiffness matrix is 33×33, instead of 24×24 for standard 8 node finite element. For 20-node solid element, the stiffness matrix can be evaluated using 3×3×3 Gauss points. However, a reduced 14 points integration rule is also used, since this rule gives the same accuracy with less computational effort [22].

In a similar way, the residual stress can be discretized as follows (see e.g. [28]):

(24)

The weighting factors w r =w s =w t =1, when using 2 Gauss points at each axis direction. Therefore, we obtain:

$$ [\boldsymbol{C} ]^e =\int_{-1}^{1} \int_{-1}^{1} \int_{-1}^{1} \boldsymbol{B}^{T} =\sum_{m=1}^{\mathit{NGE}} |J| \begin{bmatrix} {\boldsymbol{B}_{O}}^{T} \\ {\boldsymbol{B}_{A}}^{T} \end{bmatrix} = \sum_{n=1}^{\mathit{NGE}} \bigl[ \boldsymbol{C}^e_m \bigr] $$
(25)

NGE is the total number of Gauss points in each element: NGE=ngl1×ngl2×ngl3=8. For the whole system,

$$ [\boldsymbol{C} ] = \sum_{n=1}^{\mathit{NE}} \sum _{m=1}^{\mathit{NGE}} |J| \boldsymbol{B}^{T} = \sum_{n=1}^{\mathit{NE}} [\boldsymbol{C} ]^{e} = \sum_{n=1}^{\mathit{NE}} \left[ \begin{array}{c} {\boldsymbol{C}_{O}}^{e} \\ {\boldsymbol{C}_{A}}^{e} \end{array} \right] = \left[ \begin{array}{c} \boldsymbol{C}_{O} \\ \boldsymbol{C}_{A} \end{array} \right] $$
(26)

NE is the total number of elements. The equilibrium matrix [C] is composed of two parts: [C O ], with the dimension 3NK×6NGS and the additional matrix [C A ], with the dimension 9NE×6NGS, corresponding to the extra shape function of non-conforming finite element.

Finally, the shakedown problem can be formulated as the following mathematical problem:

(27)

Here, \(\bar{\boldsymbol{\rho}}\) is the time-independent periodic residual stress field; F is the von-Mises yield condition; NGS is the number of Gauss points of the considered representative element; n is the number of independent loads; [C] is the constant equilibrium matrix, uniquely defined by the discretized representative volume element with respect to boundary conditions; σ Yi is the yield stress; P k is the load vertex.

3.2 Interior Point Method

The static shakedown problem is finally reduced to a large-scale nonlinear optimization problem after discretization by using finite elements. Nowadays, different methods are developed to solve large-scale nonlinear optimization problems [16, 17], such as sequential quadratic programming (SQP), augmented Lagrangian method and interior point method. Correspondingly, different software packages are available. Here, we focus on the interior-point-method-based software packages IPDCA and IPOPT.

IPDCA (Interior Point with DC regularization Algorithm), is a C-programming package, using quasi-definite matrix techniques [1], which is specially designed for shakedown and limit analysis, and characterized by high speed and large scale number of variables [27, 28].

IPOPT (Interior Point Optimizer) is an open source software package for large-scale nonlinear optimization [44]. It implements an interior-point line-search filter method. However, the algorithm is only trying to find the local minimizer of the problem [43]. For non-convex problems, many stationary points may exist. As a matter of fact, the static shakedown problem is convex, and thus any local minimizer is also global minimizer as well. IPOPT is designed to solve the general mathematical optimization forms:

(28)

Note that the equality constraints can be formulated by setting c L =c U . To simplify the notation, the following problem formulation is considered:

(29)

where f:R n→R, and c:R n→R m are twice continuously differentiable functions. As an interior point (or barrier) method, the proposed algorithm computes solutions for a sequence of barrier problems, with the barrier parameter μ>0.

$$ \begin{aligned}[c] &\min&&\varphi_\mu( x ) := f ( x ) -\mu \sum_{i=1}^{n} \log( x_i ) \\ &\text{s.t.} && c ( x ) =0 \end{aligned} $$
(30)

The KKT conditions for (30) are:

$$ \begin{aligned}[c] \nabla\varphi_\mu( x )+ \lambda\nabla c ( x ) &=0 \\ c ( x ) &=0 \end{aligned} $$
(31)

Solving this system directly by a Newton-type method leads to a so-called primal method, which treats only the primal variables x and the multipliers λ. However, the term ∇φ μ (x) includes components μ/x i . It indicates, that system (31) is not defined at the optimal solution x ∗ of system (29) with bound \(x^{*}_{ ( i )}=0\), i.e. an optimal solution will be in the interior of the region defined by x≥0.

The amount of influence of barrier term relies on the size of μ. Under certain conditions, the optimal solution x ∗(μ) of system (31) converges to x ∗ of the original system (29): As x i →0, log(x i )→∞; As μ→0, x ∗(μ)→x ∗.

Instead of using this primal approach, dual variables z are introduced: z i =μ/x i . Therefore, the KKT conditions (31) are equivalent to the perturbed KKT conditions or primal-dual equations [42]:

(32)

where \(X=\operatorname{Diag}(x)\), \(Z=\operatorname{Diag}(z)\) and e=(1,…,1)T. Note, that Eqs. (32) for μ=0 together with (x≥0, z≥0) are KKT conditions for original system (36). The optimality error for the above barrier problem is defined as:

$$ E_{\mu} ( x, \lambda, z )= \text{max} \biggl\{ \frac{\|\nabla f ( x ) + \lambda\nabla c ( x ) \|_{\infty }}{s_d},\bigl\|c ( x ) \bigr\|_{\infty} , \frac{\|XZe-\mu e \|_{\infty}}{s_c} \biggr\} $$
(33)

s d and s c are scaling factors, under the definition:

$$ s_d=\max \biggl\{s_{\text{max}}, \frac{\|\lambda\|_1 + \|z \|_1}{m+n} \biggr \} \Big/s_{\max} ,\qquad s_c=\max\biggl\{ s_{\text{max}}, \frac{\|z \|_1}{n} \biggr\} \Big/s_{\text{max}} $$
(34)

s max is a fixed number, in IPOPT s max=100. Let E 0=(x, λ, ,z) denote the optimality error for the original problem. The overall algorithm terminates if an approximate solution satisfies:

$$ E_{\mu} \bigl( \tilde{x}^*, \tilde{\lambda}^*, \tilde{z}^* \bigr ) \leq \theta_{tol} $$
(35)

θ tol is the user provided convergence tolerance. In order to solve the barrier problem for a given fixed value μ j , a Newton method is applied to nonlinear systems of equation (32):

(36)

Here A k :=∇c(x k ); \(W_{k}:= \nabla_{x} ( \nabla f (x_{k} ) +A_{k} ) = \nabla^{2}_{xx} L ( x_{k}, \lambda_{k}, z_{k} )\); L(x,λ,z):=f(x)+c(x)T λ−z; \(d^{x}_{k}:=x_{k+1}-x_{k} \); \(d^{\lambda}_{k}:=\lambda_{k+1}-\lambda_{k}\); \(d^{z}_{k}:=z_{k+1}-z_{k}\).

Reformulating Eqs. (36) into a symmetric system:

(37)

Here \(\nabla\varphi_{\mu j} ( x_{k} )=\nabla f (x_{k} )-\mu_{j} X^{-1}_{k} e\); \(\varSigma_{k}=X^{-1}_{k} Z_{k}\).

In order to avoid a singularity or ill-conditioned problem, the iteration matrix is modified by adding a diagonal correction, i.e. regularization:

(38)

δ w and δ c are two scalars, called “numeric damping coefficient”. These choices for each iteration can be determined by Algorithm IC (Inertia Correction) [44]. The next iteration is then determined by:

(39)

α k is primal step length; \(\alpha^{z}_{k}\) is dual step length.

From the above description, one may observe, that either the Newton method or the damped Newton method uses the first and second derivatives (gradient and Hessian) to find the stationary point. Meanwhile, IPOPT also offers an option to approximate the Hessian of the Lagrangian by a limited-memory quasi-Newton method (L-BFGS) [7]. L-BFGS stands for “limited memory BFGS”, which uses the Broyden-Fletcher-Goldfarb-Shanno update to approximate the Hessian matrix. That is, by using quasi-Newton method, the Hessian matrix of second derivatives of function does not need to be computed, which can be updated by analyzing successive gradient vectors instead.

4 Results and Discussion

To show the validity of the proposed methods, several numerical results are presented. The input data for the optimization procedure are obtained from customized ANSYS and Matlab, and the optimization is carried out with IPOPT.

4.1 Comparison of Different Elements

To show the advantage of non-conforming element, we tested the limit analysis of MMCs by step-by-step method using the following element types: (a) 8-node brick element with bilinear shape function (LSF); (b) 8-node brick element with extra shape function (ESF), i.e. non-conforming element; (c) 20-node brick element with quadratic shape function. Square pattern of periodicity (Fig. 8, Left) under plane strain condition is considered and subjected to the uniaxial stress Σ 11. Material properties is shown in Table 2, with the assumption that each phase is isotropic and elastic-perfectly plastic.

Table 2 Material properties Al/Al2O3
Full size table

Using an 8-node solid element with a bilinear shape function, we can observe that in the limit uniaxial stress Σ 11 is extremely large (Fig. 6). However, an 8-node solid element with extra shape function produces reasonable results, similar to the 20-node solid element. Because 8-node element with bilinear shape functions can not represent flexural response.Therefore, the key point of the non-conforming element is to add quadratic terms on the basis of linear shape function.

Fig. 6
figure 6

Limit state of macroscopic stress with fiber volume fraction

Full size image

4.2 Illustration of Transformation

The transformation given in Sect. 2.1 is illustrated by considering a thin plate with square pattern (Fig. 8, Left). The side of RVE is 100 mm, the width is 2 mm and the fiber radius is 15 mm. Material model is the same as in Sect. 4.1. It is subjected to two independent displacement loadings: \(U_{1}^{0}=U_{0}\); \(U_{2}^{0}=U_{0}\). The elastic and shakedown domains are normally scaled (Fig. 7). Benchmark U 0 is 0.02 mm and σ Y is the yield stress of the matrix.

Fig. 7
figure 7

Transformation between two scales

Full size image

According to Eq. (16) in Sect. 2.3, the characteristic angle here is φ=−16.65∘ and the elastic and shakedown safety factors are: α EL =2.06 and α SD =2.71.

For the same pattern and material properties, but under plane strain conditions, the change of characteristic angles φ in terms of the fiber volume fraction is shown in Table 3.

Table 3 Characteristic angle for uniaxial macroscopic stress under plane strain conditions
Full size table

4.3 Fiber Distribution and Volume Fraction

The influence of fiber distribution and fiber volume fraction is investigated under plane strain condition (Fig. 8). The dimensions of RVEs are given in Table 4. They are subjected to two independent displacement loadings, \(U_{1}^{0}=U_{2}^{0}=U_{0}=0.02\ \mathrm{mm}\).

Fig. 8
figure 8

Fiber distribution: (Left) Square pattern (SQ); (Middle) Rotated square pattern (TS); (Right) Hexagonal pattern (HEX)

Full size image
Table 4 Dimensions of RVEs
Full size table

Figure 9 presents the admissible displacement domain (left side) and the corresponding transformed macroscopic stress domain (right side) for periodic composites under plane strain case. The fiber ratio is 40 %. From top to bottom are square, rotated square and hexagonal pattern, respectively. Note that, the quadratic and rotated composites are anisotropic. We use the transformation described in Sect. 2.3 to obtain stresses along the principal direction. After transformation, the macroscopic stress domain of hexagonal pattern also becomes symmetric in the principal directions. It satisfies the reality that the unidirectional continuous fiber with hexagonal periodicity is approximately isotropic in transverse direction.

Fig. 9
figure 9

Admissible displacement domain (Left) and related maximal macroscopic stress domain (Right) for periodic composites with different fiber pattern

Full size image

Figure 10 shows the variation of the macroscopic limit stress in one axial direction with fiber volume fraction. For square pattern, the axial limit stress increases remarkably from around 35 %. For hexagonal pattern, the axial limit stress increases stably from 10 % to 50 %. While for the rotated pattern, the axial limit stress varies quite slightly, i.e. the fiber volume fraction has almost no influence on the macroscopic performance.

Fig. 10
figure 10

Axial macroscopic limit stress

Full size image

Figure 11 shows that the square pattern has the biggest macroscopic stress domain when the fiber volume fraction is 50 %. In macroscopic view, choose which kind of fiber pattern depends on the external loading.

Fig. 11
figure 11

Macroscopic limit stress domain for different patterns

Full size image

In principle, the square pattern and rotated square pattern are the same. However, the loading domains, either in local level or global level, are different. It illustrates that periodic composites with square pattern is essentially not transversely isotropic, although in the traditional micromechanics of laminate they are treated as such [13].

4.4 Homogenized Elastic Material Properties

The homogenized elastic properties are determined for fiber reinforced composite given in Sect. 4.3. For square pattern and rotated square pattern, the characteristic angles φ 1 and φ 2 should equal to each other because of the geometric symmetry. It is also verified in our numerical calculation. The unit cell of hexagonal distributed periodic composites is not symmetric. The characteristic angles at two directions are different. However, in macroscopic view, the homogenized material properties for all three patterns should be the same, in restrict words, that same in X and Y directions. According to the former methods, the homogenized transverse Young’s modulus (Fig. 12) and Poisson ratios (Fig. 13) of different patterns with variation of fiber volume fraction can be obtained.

Fig. 12
figure 12

Homogenized Young’s modulus

Full size image
Fig. 13
figure 13

Homogenized Poisson ratio

Full size image

Figure 12 presents the homogenized transverse Young’s modulus for the three patterns. Generally, with the increment of fiber ratio, the transverse modulus increases, and among three patterns, the square one increased a little stronger than other two.

Their Poisson ratios are assumed the same value 0.3. Figure 13 presents the difference among three patterns. For the hexagonal pattern, with the variation of fiber volume fraction, Poisson’s ratio is almost constant, while for the square pattern, it decreases, and for the rotated square pattern, it increases slightly.

From Fig. 12 and Fig. 13 we may conclude, that the fiber distributed pattern affects the transversely effective material properties. And after the transformation, the hexagonal pattern shows the transversely isotropic characteristics on the macroscopic level.

4.5 Homogenized Plastic Material Properties

Based on the homogenization theory and mechanical constitute law, we may give a prediction of the effective elastic material properties of the composites. The biggest difficulty consists in how to define the plastic material properties, such as yield strength. During numerical simulation, we observed that the yielding process can be regarded as three states: firstly, it begins to yield, then the debonding of the inter-face, finally, the ductile phase exhibits overall plastic flow. By combination of lower bound direct methods and homogenization technique, the yield strength of periodic composites can be defined in three states [11, 18]:

  1. 1.

    Onset of plasticity: Σ YEL =α EL Σ V

  2. 2.

    Shakedown state: Σ YSD =α SD Σ V

  3. 3.

    Limit state: Σ YLM =α LM Σ V

Here, Σ YEL , Σ YSD and Σ YLM are the yield strengths corresponding to purely elastic, shakedown and limit states, respectively; Σ V is the macroscopic equivalent stress. Admissible macroscopic stress domains from beginning of plasticity to the limit state are obtained with the help of homogenization theory. Since three states are defined, for a uniaxial macroscopic stress Σ 1 (Σ 2=Σ 3=0), we therefore get even for the elastic-perfectly matrix a “structural hardening” effect, due to the microscopic inhomogeneous stress distribution in the composite.

The stress components Σ ij depend on the orientation of the coordinate system. Nevertheless, there are certain invariants associated with every tensor which are independent of the coordinate system. By solving the characteristic equation, we may obtain three principal stresses. For plane stress case, Σ 3 is zero. Therefore, yield curve fitting is carried out only in plane. This is one of the reasons, that why the yield criterion for sheets are developed a lot. For plane strain case, or general stress state, the principal stresses are distributed in the space.

Numerous anisotropic yield criteria have been developed and tested for anisotropic plastic deformation [3, 4, 30]. The simplest, however, is the quadratic Hill yield criterion [21], which is a straightforward extension of the von Mises yield criterion. It has the form:

(40)

Here F, G, H, L, M, N are constants that have to be determined by experiments. The expressions of these parameters are defined as:

$$ \begin{aligned}[c] & F=\frac{1}{2} \biggl(\frac{1}{Y^2}+ \frac{1}{Z^2}+\frac{1}{X^2}\biggr),\qquad G=\frac{1}{2} \biggl( \frac{1}{Z^2}+\frac{1}{X^2}+\frac{1}{Y^2}\biggr),\\ & H= \frac{1}{2} \biggl(\frac{1}{X^2}+\frac{1}{Y^2}+\frac{1}{Z^2} \biggr) \\ & L=\frac{1}{2P^2},\qquad M=\frac{1}{2S^2},\qquad N=\frac{1}{2T^2} \end{aligned} $$
(41)

Here X, Y, Z are the normal yield stress with respect to the axes of anisotropy in 1, 2 and 3 directions; P, S, T are the shear yield stresses in 23, 13 and 12 directions, respectively. By choosing the reference system in principle stress directions, we get:

$$ F(\sigma_2-\sigma_3)^2+G( \sigma_3-\sigma_1)^2+H(\sigma_1- \sigma_2)^2-1=0 $$
(42)

Under the assumption, that the investigated material is isotropic in transverse direction, i.e. F=G. As defined above, X and Z are the tensile equivalent stress in and along the normal to the sheet plane, respectively. This implies:

(43)
(44)

From (43) and (44):

$$ \biggl( \frac{Z}{X} \biggr)^2=\frac{F+H}{2F} \quad\Rightarrow\quad\frac{H}{F}=2 \biggl(\frac{Z}{X} \biggr)^2-1 $$
(45)

Substitute (44) and (45) into (42), we may obtain the criterion in terms of the equivalent stresses:

$$ (\sigma_2-\sigma_3)^2+( \sigma_3-\sigma_1)^2+(\sigma_1- \sigma_2)^2 \biggl[ 2 \biggl(\frac{Z}{X} \biggr)^2-1 \biggr]=2Z^2 $$
(46)

According to the associated flow rule, we have:

$$ \varepsilon ^p_i=\lambda\frac{\partial f}{\partial\sigma_i} \quad\Rightarrow\quad\frac{\mathrm{d}\varepsilon ^p_i}{\mathrm {d}\lambda }=\frac{\partial f}{\partial\sigma_i} $$
(47)

For plane stress σ 3=0, which gives:

$$ \begin{aligned}[c] & \frac{\mathrm{d}\varepsilon ^p_1}{\mathrm {d}\lambda}=\frac {\partial f}{\partial\sigma_1}= 2 \sigma_1 +2(\sigma_1 - \sigma_2) \biggl[ 2 \biggl(\frac{Z}{X} \biggr)^2-1 \biggr] \\ & \frac{\mathrm{d}\varepsilon ^p_2}{\mathrm{d}\lambda}=\frac{\partial f}{\partial\sigma_2}= 2\sigma_2 -2( \sigma_{1} - \sigma_2) \biggl[ 2 \biggl( \frac{Z}{X}^2 \biggr)-1 \biggr] \\ & \frac{\mathrm{d}\varepsilon ^p_3}{\mathrm{d}\lambda}=\frac{\partial f}{\partial\sigma_3}=-2(\sigma_1 + \sigma_2) \end{aligned} $$
(48)

Import the R-value [23] which is a measure of the plastic anisotropy of a rolled metal sheet. Let R 0 and R 90 are the ratio of the in-plane and out-of plane plastic strains under uniaxial stress σ 1 and σ 2, respectively:

$$ \begin{aligned}[c] & R_0=\frac{\mathrm{d}\varepsilon ^p_2}{\mathrm{d}\varepsilon ^p_3}=2 \biggl( \frac{Z}{X} \biggr)^2-1 \\ & R_{90}=\frac{\mathrm{d}\varepsilon ^p_1}{\mathrm{d}\varepsilon ^p_3}=2 \biggl (\frac{Z}{X} \biggr)^2-1 \end{aligned} $$
(49)

Thus,

$$ R=R_0=R_{90}=2 \biggl(\frac{Z}{X} \biggr)^2-1 $$
(50)

Substitute Eq. (50) into (46), we have:

$$ \sigma_1^2+\sigma_2^2- \biggl(\frac{R+1}{2} \biggr) \sigma_1 \sigma_2=X^2 $$
(51)

From mathematical point of view, Eq. (51) represents an ellipse by a 45 degrees rotation of a canonical ellipse with the centre (0, 0). Assume that the semimajor and semiminor are a and b, respectively. Take composites with square pattern fiber volume fraction 7.07 % as an illustrative example, and with the dimension as reported in Sect. 4.1. Material parameters of two phases, as well as homogenized parameters are shown in Table 5. The macroscopic admissible domain of the composites, transformed in principal stress directions, is shown in Fig. 14, where the bounds of the elastic (EL), limit (LM) and shakedown (SD) domains are represented. Based on least-square method, Hill_1 and Hill_2 are fitted yield surface according to the limit and shakedown domain, respectively.

Fig. 14
figure 14

Admissible macroscopic stress domain and yield surface fitting

Full size image
Table 5 Parameters by yield surface fitting
Full size table

Hill_1: with R-value 1.0194, which means, it can be treated as von Mises yield criterion approximately. Hill_2: with R-value 1.3204. The other related parameters are shown in Table 5.

If we fit the yield surface with von Mises yield criterion (R=1) according to macroscopic stress under limit state, the homogenized elastic and plastic properties of periodic composite material are shown in Table 6.

Table 6 Homogenized material parameters
Full size table

We note that the yield surface fitting according to shakedown domain is only suitable for a specific loading domain.

5 Conclusion

This paper shows how the lower bound shakedown analysis combined with homogenization theory can be used to determine safe loading domains for composites and how to calculate global homogenized material parameters. We conclude that a three-dimensional non-conforming element will fit for the direct methods with the same accuracy as second order element but with much less computational cost. The yield surface fitting according to shakedown domain is only suitable for arbitrarily chosen but specific loading domains.