Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

To predict safe service conditions of structures or structural elements made of heterogeneous materials under variable loads beyond elasticity is a challenging task in civil and mechanical engineering. There are two major difficulties: to consider variable loads with unknown evolution in time and to determine the effective material properties. The former difficulty can be overcome by direct methods (DM), namely limit and shakedown analysis. Limit analysis only requires the load range, and shakedown analysis needs the envelope of the independent loads [13]. Therefore, the application of DM to composites arose many interests these years. To solve the latter difficulty, multi-scale modeling method and homogenization theory are involved [27]. Either using the lower-bound [14, 23, 33, 34] or upper-bound [3, 21, 22] approach, periodic composites are investigated at the representative volume element (RVE) level with the elastic perfectly plastic material properties of each phase.

DM has been formulated for structures assuming elastic perfectly plastic material behavior. However, work-hardening occurs most notably for ductile materials, like metals. Thus DM for plasticity models with hardening has also been investigated for long time [15, 16, 18, 20, 32], where the studied objects are homogeneous global structures [2, 19, 25]. In this work, we applied the lower-bound approach of DM to periodic composites with the consideration of work-hardening.

As the global effective material properties are concerned, in [7], homogenized elastic parameters are obtained basing on the homogenization theory and the constitutive laws of elastic materials. The plastic properties are only studied for the composites under plane stress case by using yield loci fitting. Here, the predictions for unidirectional periodic composites are discussed.

The numerical tools required for the lower-bound approach are the finite-element method and non-linear optimization. To reduce the scale of optimization problem, non-conforming three-dimensional finite elements are used to discretize the RVE, and the interior-point-algorithm based optimization tool (IPOPT) [29, 31] together with the pre-programming language AMPL [11] are used.

2 Direct Methods Applied to Composites

2.1 Elements of Homogenization Theory

For periodic heterogeneous media, two different scales are adopted: the macroscopic (or global) scale and the mesoscopic (or local) scale. The homogenization method describes the relation between these two scales mainly by two stages: localization and globalization [27].

With x and ξ as the global and local coordinates (Fig. 1), respectively, the following relationship holds:

$$ \boldsymbol{\xi}=\frac{\boldsymbol{x}}{\delta}, $$
(1)

δ is a small scale parameter, which determines the size of the representative volume element (RVE). It plays an important role in studying the heterogeneous material, especially for non-uniform structures. For a heterogeneous material with periodic distribution, the smallest possible unit is normally defined as the RVE. The macroscopic strain E and stress Σ are linked to mesoscopic strain ϵ and stress σ by:

$$\begin{aligned} \boldsymbol{E}(\boldsymbol{x}) =& \frac{1}{V} \int_V {\boldsymbol {\epsilon}(\boldsymbol{\xi})} \, \text{d} V = \bigl\langle \boldsymbol {\epsilon}(\boldsymbol{\xi}) \bigr\rangle, \end{aligned}$$
(2)
$$\begin{aligned} \boldsymbol{\varSigma}(\boldsymbol{x}) =& \frac{1}{V} \int _V {\boldsymbol {\sigma}(\boldsymbol{\xi})} \, \text{d} V = \bigl\langle\boldsymbol {\sigma} (\boldsymbol{\xi}) \bigr\rangle. \end{aligned}$$
(3)

Here, 〈⋅〉 stands for the averaging operator. In DM for periodic heterogeneous materials, the macroscopic stress is decomposed as [34]:

$$ \boldsymbol{\varSigma}= \frac{1}{V} \int_V \bigl( \alpha\boldsymbol{\sigma }^E+\bar{\boldsymbol{\rho} } \bigr) \, \text{d} V= \frac{1}{V} \int_V \alpha\boldsymbol{ \sigma}^E \, \text{d}V + \frac {1}{V} \int_V \bar{\boldsymbol{\rho} } \, \text{d} V \quad\text{with} \ \frac{1}{V} \int_V \bar{\boldsymbol{\rho} } \, \text{d} V =0 $$
(4)

where α is the safety factor, σ E is the purely elastic stress field and \(\bar{\boldsymbol{\rho}}\) is the time-independent residual stress field.

Fig. 1
figure 1

Homogenization theory

Full size image

2.2 Boundary Conditions

One of the difficulties in the localization problem lies in introducing appropriate boundary conditions. Usually, three types of boundary conditions are considered on the local scale [1, 27].

Strain approach :

Uniform strain is imposed on ∂V,

$$ \boldsymbol{u}=\boldsymbol{E}\cdot\boldsymbol{\xi} \quad \text{on} \ \partial V. $$
(5)
Stress approach :

Uniform stress is imposed on ∂V,

$$ \boldsymbol{\sigma} \cdot\boldsymbol{n} = \boldsymbol{\varSigma} \cdot \boldsymbol{n} \quad \text{on} \ \partial V. $$
(6)
Periodicity :

Constraints are required for both fields.

  • The stress vectors on the opposite sides have the same value but opposite direction,

    $$ \boldsymbol{\sigma} \cdot\boldsymbol{n} \quad\text{anti-periodic}. $$
    (7)

  • The local strain can be split into an overall strain E and a fluctuating field ϵ per, where the average of ϵ per over RVE vanishes,

    $$ \boldsymbol{\epsilon}(\boldsymbol{u})=\boldsymbol{E}+\boldsymbol {\epsilon} \bigl(\boldsymbol{u}^{\text{per}}\bigr) = \boldsymbol{E} + \boldsymbol { \epsilon}^{\text{per}}, $$
    (8)
    $$ \bigl\langle\boldsymbol{\epsilon}^{\text{per}} \bigr\rangle= 0. $$
    (9)

In the numerical implementation, to carry out the strain approach, uniform displacement is imposed on the boundary, see Fig. 2(L). For Stress approach, besides the uniform stress imposed on the boundary, one degree of freedom of the boundary is coupled in order to maintain the periodic deformation, as shown in Fig. 2(M). These two approaches are normally suitable for the periodic RVE, while the third one is more realistic, especially for non-periodic unit cell. Figure 2(R) describes the constraints for periodicity method:

$$ u_{i}'-u_i+u_{i}^{d}=0 $$
(10)

here, \(u_{i}'\) and u i are the displacements of the relative opposite periodic node pairs and \(u_{i}^{d}\) is the macroscopic displacement. Figure 3 illustrates the deformations of a non-periodic RVE under pure thermal loading by using strain approach and periodicity approach, respectively.

Fig. 2
figure 2

Boundary conditions

Full size image
Fig. 3
figure 3

Deformations of the non-periodic RVE under different boundary conditions

Full size image

The common ground in these three approaches is the consistent deformation of boundaries. The strain energies, by using different boundary conditions, are ordered in the following way [27]:

$$ \boldsymbol{E}:\hat{\boldsymbol{d}}{}^{\text{hom}}:\boldsymbol{E} \leq \boldsymbol{E}:\boldsymbol{d}{}^{\text{hom}}_{\text{per}}:\boldsymbol{E} \leq \boldsymbol{E}:\tilde{\boldsymbol{d}}{}^{\text{hom}}:\boldsymbol{E}. $$
(11)

\(\hat{\boldsymbol{d}}{}^{\text{hom}}\), \(\boldsymbol{d}^{\text{hom}}_{\text {per}}\) and \(\tilde{\boldsymbol{d}}{}^{\text{hom}}\) are the 4th order tensors of elastic stiffness, under uniform stress, periodicity and uniform strain, respectively, which depend on the micro variable ξ.

The objective studied in this work is the periodic composites under mechanical loading, and the strain approach was adopted as the boundary condition. The localization of the elastic mechanical problem can be written as [14]:

$$ \textit{P}_{\text{strain}}= \begin{cases} \text{div} \boldsymbol{\sigma}^E=0 & \text{in $V$}, \\ \boldsymbol{\sigma}^E=\boldsymbol{d}:(\boldsymbol{E}+\boldsymbol {\epsilon}^{\text{per}}) & \text{in $V$}, \\ \boldsymbol{\sigma}^E \cdot\boldsymbol{n} & \text{anti-periodic on $\partial V$}, \\ \boldsymbol{u}^{\text{per}} & \text{periodic on $\partial V$}, \\ \langle\boldsymbol{\epsilon} \rangle= \boldsymbol{E}. \end{cases} $$
(12)

The residual stress field \(\bar{\boldsymbol{\rho}}\) should satisfy the self-equilibrium condition and periodicity conditions:

$$ \textit{P}^{\text{res}}_{\text{strain}}= \begin{cases} \text{div} \bar{\boldsymbol{\rho}}=0 & \text{in $V$}, \\ \bar{\boldsymbol{\rho}} \cdot\boldsymbol{n} & \text{anti-periodic on $\partial V$}. \end{cases} $$
(13)

Anti-periodicity means that either σ E⋅n or \(\bar{\boldsymbol{\rho}} \cdot\boldsymbol{n}\) has opposite values on opposite sides of ∂V. Periodicity of u per indicates that the displacements at two opposite points of the boundary are the same. For strain approach, we assume that u per=0 and ϵ per=0.

2.3 Finite Element Discretization

In order to satisfy the equilibrium conditions for the elastic stress σ E and time-independent residual stress \(\bar {\boldsymbol{\rho}}\) in weak form, the principle of virtual work, demanding that the external virtual work equals to the internal virtual work for unrelated but consistent displacements and strains, is used:

$$ \int_{V} \{\delta\boldsymbol{\epsilon} \}^T \bigl\{\alpha \boldsymbol{\sigma}^E+\bar{\boldsymbol{ \rho}} \bigr\} \text{d}V =\int_{\partial V} \{\delta\boldsymbol{u} \}^T \{ \textbf{p} \} \text{d} S+\int_{ V} \{ \delta\boldsymbol{u} \}^T \{ \textbf{f} \} \text{d} V. $$
(14)

Here, δ ϵ is the virtual strain, and δu is the virtual displacement. p and f are surface force and body force, respectively. For periodic heterogeneous materials, the external loads can be either macroscopic stresses Σ or macroscopic strains E. The left side of Eq. (14) implies that the discretization here has to be carried out for the purely elastic stress field σ E and the residual stress field \(\bar{\boldsymbol{\rho}}\). Since the scale of the optimization problem is mainly determined by the type and the number of finite elements, the choice of a proper element type is very important. In this work, a non-conforming solid element was applied in the limit and shakedown analysis of composites because of its accuracy and efficiency [5].

The lower-bound problem of DM for periodic composites with elastic perfectly plastic material model can be formulated finally as the following mathematical programming:

$$ \text{max} \ \alpha\quad \left \{ \begin{array}{l} [\boldsymbol{C} ] \{\bar{\boldsymbol{\rho}} \} = 0,\\ F (\alpha \boldsymbol{\sigma_{i}^{E}} (P_{k}) + \bar{\boldsymbol {\rho}}_i,\sigma_{Yi} ) \leq 0, \quad i \in [1 , \mathit{NGS} ].\\ \end{array} \right . $$
(15)

α is the load factor, P k is the vertices of load envelope and NGS is the number of Gaussian points and σ Y is the yield strength. F is the von Mises yield criterion.

2.4 Large Scale Optimization

The lower-bound approach of DM applied to a real structure or structural element will lead usually to a large scale optimization problem. To solve such kind of problem, there are many optimization algorithms and corresponding software packages, like LANCELOT [9], which is based on an augmented Lagrangian method, and IPDCA (Interior Point with DC regularization Algorithm), which is based on interior-point method and especially designed for shakedown problems. The efficiency of IPDCA was proved in [17]. However, the present version is suitable for elastic perfectly plastic material model. Another user-developed software package is IPSA [24, 25], which is also based on interior-point method. The additional selective algorithm makes the application of DM on large structures possible. In this work, AMPL+IPOPT are adopted as the numerical solver [4]. AMPL (A Modeling Language for Mathematical Programming) is a comprehensive and powerful algebraic modeling language for linear and nonlinear optimization problems with discrete or continuous variables [11]. IPOPT, short for “Interior Point OPTimizer” is an open software library for large scale nonlinear optimization of continuous systems [30].

3 Hardening Material Models

DM with hardening has been investigated for long time, however, the studied objects are only homogeneous global structures [2, 19, 24].

Here, the lower-bound approach of DM for periodic composites with the consideration of hardening matrix is applied on the RVE. The material model for the fiber is assumed as elastic perfectly plastic. Some abbreviations used in this work are introduced in Table 1.

Table 1 Abbreviations of some terms
Full size table

3.1 Isotropic Hardening

The isotropic hardening material model assumes that the yield surface increases in size, but keeps its shape. The subsequent yield surface and initial yield surface have the same center, as shown in Fig. 4.

Fig. 4
figure 4

Isotropic hardening

Full size image

The lower-bound approach of DM with isotropic hardening matrix can be formulated as:

$$ \text{max} \ \alpha \quad \left \{ \begin{array}{l} [\boldsymbol{C} ] \{\bar{\boldsymbol{\rho}} \} = 0,\\ F (\alpha \boldsymbol{\sigma}_{i}^{E} (P_{k}) + \bar{\boldsymbol{\rho}}_i,\sigma_{Yi}^{\text{f}} ) \leq 0, \quad i \in [1 , \mathit{NGSF} ],\\ F (\alpha \boldsymbol{\sigma}_{j}^{E} (P_{k}) + \bar{\boldsymbol{\rho}}_j,\sigma_{Uj}^{\text{m}} ) \leq 0, \quad j \in [1 , \mathit{NGSM} ]\\ \end{array} \right . $$
(16)

where \(\sigma_{Uj}^{\text{m}}\) is the ultimate strength for the matrix. Superscript ‘m’ and ‘f’ indicate matrix and fiber respectively.

3.2 Unlimited Kinematic Hardening

The kinematic hardening model allows the yield surface to translate, without changing its shape, as shown in Fig. 5. π is the time-independent back stress. The discretized formulation of the lower-bound problem for the linear unlimited kinematic hardening condition is:

$$ \text{max} \ \alpha\quad \left \{ \begin{array}{l} [\boldsymbol{C} ] \{\bar{\boldsymbol{\rho}} \} = 0,\\ F (\alpha \boldsymbol{\sigma}_{i}^{E} (P_{k}) + \bar{\boldsymbol{\rho}}_i,\sigma_{Yi}^{\text{f}} ) \leq 0,\quad i \in [1 , \mathit{NGSF} ]\\ F (\alpha \boldsymbol{\sigma}_{j}^{E} (P_{k}) + \bar{\boldsymbol{\rho}}_j - \bar{\boldsymbol{\pi}}_j,\sigma_{Yj}^{\text{m}} ) \leq 0, \quad j \in [1 , \mathit{NGSM} ]\\ \end{array} \right . $$
(17)

where \(\bar{\boldsymbol{\pi}}\) is the back stress field. It is important to note that, for matrix with unlimited kinematic hardening, there is no optimal solution for limit analysis, since the ultimate strength of the material is infinite.

Fig. 5
figure 5

Unlimited kinematic hardening

Full size image

3.3 Limited Kinematic Hardening

To overcome the shortcoming of the unlimited linear kinematic hardening material model, two-surface model of limited kinematic hardening has been introduced [32], as shown in Fig. 6. With the consideration of the linear limited kinematic hardening, the lower bound problem has an analogous discretized form like unlimited kinematic hardening. Moreover, due to the back stress limitation, there is an additional inequality constraint, as shown in (18a) or (18b).

$$ \text{max} \; \alpha \quad \left \{ \begin{array}{l} [\boldsymbol{C} ] \{\bar{\boldsymbol{\rho}} \} = 0,\\ F (\alpha \boldsymbol{\sigma}_{i}^{E} (P_{k}) + \bar{\boldsymbol{\rho}}_i,\sigma_{Yi}^{\text{f}} ) \leq 0, \quad i \in [1 , \mathit{NGSF} ],\\ F (\alpha \boldsymbol{\sigma}_{j}^{E} (P_{k}) + \bar{\boldsymbol{\rho}}_j - \bar{\boldsymbol{\pi}}_j,\sigma_{Yj}^{\text{m}} ) \leq 0, \quad j \in [1 , \mathit{NGSM} ], \\ F (\alpha \boldsymbol{\sigma}_{j}^{E} (P_{k}) + \bar{\boldsymbol{\rho}}_j,\sigma_{Uj}^{\text{m}} ) \leq 0, \quad (\text{a})\\ \text{or} \quad F (\bar{\boldsymbol{\pi}}_j, \boldsymbol{\sigma }^{\text{m}}_{Uj}-\boldsymbol{\sigma}^{\text{m}}_{Yj} ) \leq 0. \quad (\text{b}) \end{array} \right . $$
(18)
Fig. 6
figure 6

Limited kinematic hardening

Full size image

As shown in Fig. 7, Eq. (18a) indicates that the subsequent yield surfaces stays always inside the bounded loading surface [32]. Equation (18b) means that motion of the origin center of the subsequent yield surface is bounded by the back stress surface [26]. The mathematical equality of both conditions is proved in [19]. Nevertheless, the obtained optimized value of back stresses under the two conditions are slightly different [6].

Fig. 7
figure 7

Conditions a and b in limited kinematic hardening

Full size image

With the assumption that the material model of fiber is elastic, the material model of matrix is elastic-perfectly, isotropic hardening, unlimited kinematic hardening and limited kinematic hardening, respectively, the sizes of static shakedown problem are shown in Table 2.

Table 2 Sizes of optimization problem with different material models
Full size table

4 Failure Criterion for Composites

Every material has certain strength, expressed in terms of stress or strain, beyond which the structure fractures or fails to carry the load. For heterogeneous materials, consisting of two or more phases, the determination of failure criteria is in fact one of the most important issues in the design process. Some phenomenological failure criteria that use experimental data to determine material constants have been proposed, like maximum stress theory, maximum strain theory, distortional energy (Tsai-Hill) criterion, Tsai-Wu criterion, Hashin’s criterion and so on [28].

In this section, a general method to identify material parameters for a given failure criterion for composites is proposed and discussed.

4.1 Definition of Homogenized Stress

The effective elastic material properties related to different fiber distributions and volume fractions, are predicted with the aid of homogenization theory and mechanical constitutive law [4], which can be generally described as:

$$ \boldsymbol{\varSigma} = \boldsymbol{d}^{\text{hom}}:\boldsymbol{E}, $$
(19)

d hom are the homogenized elasticity tensor.

Homogenized plastic material properties can be determined experimentally or numerically. Although the results from experiments are generally more accurate, the cost is normally very high and only the strength in one or more principle directions may be obtained. Through the numerical method, we provide a rough but complete prediction of plastic properties after neglecting some defects caused in the manufacturing process.

In our former work, the yield criterion of periodic composites under plane stress case are discussed [7]. Firstly, three states during the failure are defined [8, 12]:

  • Onset of plasticity (Homogenized elastic stress): Σ EL =α EL 〈σ E〉.

  • Shakedown state (Homogenized shakedown stress): Σ SD =α SD 〈σ E〉.

  • Limit state (Homogenized limit stress): Σ LM =α LM 〈σ E〉.

〈σ E〉 is the homogenized macroscopic stress of purely elastic stress field. Based on limit homogenized macroscopic stress domain, there are two possibilities to derive the yield criteria:

  • To find the best fitted mathematical formulation;

  • To identify the related parameters by using existing yield criteria.

The former approach seems quite difficult because of the uncertainty of the number of parameters. Therefore, the latter is adopted to seek a feasible solution. Since the studied object in the numerical example is the unidirectional fiber reinforced periodic composites, whose global material behavior can be treated as an orthotropic one, Hill’s yield criterion is hypothesized to fit the limit domain.

However, the stress components, either in micro-/mesoscropic level σ ij or in macroscopic level Σ ij depend on the orientation of the coordinate system. Nevertheless, there are certain invariants associated with every tensor. The three principle stresses are calculated through the characteristic equation:

$$ \boldsymbol{\sigma}^3-I_1 \boldsymbol{\sigma}^2+ I_2 \boldsymbol{\sigma } + I_3 =0, $$
(20)

I 1, I 2 and I 3 are the first, second, and third stress invariants, respectively.

4.2 Projection into π-Plane

In principle stresses, Hill’s yield criterion is written as:

$$ F(\sigma_2-\sigma_3)^2+G( \sigma_3-\sigma_1)^2+H(\sigma_1- \sigma_2)^2=1 $$
(21)

with:

$$\begin{aligned} \displaystyle F =&\frac{1}{2} \biggl(\frac{1}{Y^2} + \frac{1}{Z^2} - \frac {1}{X^2} \biggr), \\ \displaystyle G =&\frac{1}{2} \biggl(\frac{1}{Z^2} + \frac{1}{X^2} - \frac {1}{Y^2} \biggr), \\ \displaystyle H =&\frac{1}{2} \biggl(\frac{1}{X^2} + \frac{1}{Y^2} - \frac {1}{Z^2} \biggr). \end{aligned}$$
(22)

Here X,Y and Z are axial strengths of the orthotropic material. σ 1=σ 2=σ 3 is defined as the hydrostatic axis, σ 1+σ 2+σ 3=0 is named as π-plane or deviatoric plane. Hill’s yield surfaces in principal stress coordinate circumscribes an ellipse column around the hydrostatic axis.

Let (x 1–y 1–z 1) and (x 2–y 2–z 2) denote the original principle stress and transformed coordinate systems, respectively. As shown in Fig. 8, z 2 is coincident with the hydrostatic axis.

Fig. 8
figure 8

Illustration of two coordinate systems

Full size image

(x 2–y 2–z 2) can be achieved using a specific sequence of intrinsic rotations (mobile frame rotations), whose values are called the Euler Angles of the target frame. Here we use “y-convention”, i.e. (Z,Y′,Z″):

  • Rotate the x 1 y 1 z 1 -system about the z 1-axis (Z) by angle φ;

  • Rotate the current system about the new y-axis (Y′) by angle θ;

  • Rotate the current system about the new z-axis (Z″) by angle ϕ.

$$ \left \{ \begin{array}{c} x_1 \\ y_1 \\ z_1 \\ \end{array} \right \} = T \left \{ \begin{array}{c} x_2 \\ y_2 \\ z_2 \\ \end{array} \right \}. $$
(23)

T is the rotation matrix,

$$ T_{x_1 y_1 z_1}= \begin{pmatrix} \text{cos} \varphi & -\text{sin} \varphi & 0 \\ \text {sin} \varphi & \text{cos} \varphi & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} \text{cos} \theta& -\text{sin} \theta & 0 \\ \text {sin} \theta & \text{cos} \theta & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} \text{cos} \phi& -\text{sin} \phi & 0 \\ \text{sin} \phi & \text{cos} \phi & 0 \\ 0 & 0 & 1 \end{pmatrix}. $$
(24)

Here, \(\varphi=\frac{\pi}{4}\), \(\theta=\text{tan}^{-1}(\sqrt{2})\) and \(\phi=-\frac{\pi}{4}\).

Let:

$$\left \{ \begin{array}{c} \sigma_1 \\ \sigma_2 \\ \sigma_3\\ \end{array} \right \} = T \left \{ \begin{array}{c} \gamma_1 \\ \gamma_2 \\ \gamma_3 \\ \end{array} \right \}, $$

the projection of Hill criterion into π-plane is:

$$ (F+1.866H+0.134G)\gamma^2_1 + (F+0.134H+1.866G)\gamma^2_2 + (G-2F+H) \gamma_1 \gamma_2 =1. $$
(25)

Equation (25) implies that the projection of Hill criterion onto π-plane is an ellipse.

4.2.1 Homogeneous Material

For homogeneous material, X=Y=Z, i.e. F=G=H, which leads to the von Mises yield criterion, as shown in Eq. (26). It is a special case of Hill’s yield criterion and there is only one parameter to determine:

$$ ( \sigma_1 -\sigma_2 )^2 + ( \sigma_2 -\sigma_3 )^2+ ( \sigma_3 -\sigma_1 )^2 - 2 \sigma^2_Y \leq0. $$
(26)

If the von Mises criterion is projected to π plane, Eq. (25) can be written as:

$$ \gamma^2_1+\gamma^2_2 =C \quad\text{with} \ C=\frac{1}{3F}=\frac {2}{3} \sigma^2_Y. $$
(27)

The projection of the von Mises yield criterion on (σ 1,σ 2)-plane and π-plane is shown in Fig. 9, and the ellipse from Hill’s criterion becomes a circle.

Fig. 9
figure 9

Projection of the von Mises yield criterion

Full size image

4.2.2 Transversely Homogeneous Material

For transversely homogeneous material, with the assumption Y=Z, i.e. G=H, Eq. (25) can be written as:

$$ (F+2H)\gamma^2_1+(F+2H) \gamma^2_2+(2H-2F)\gamma_1 \gamma_1=1. $$
(28)

There is two parameters to determine. From Eq. (22), we may obtain:

$$ F=\frac{1}{2} \biggl(\frac{2}{Y^2} - \frac{1}{X^2} \biggr) ; \qquad G= H=\frac{1}{2} \biggl( \frac{1}{X^2} \biggr). $$
(29)

Rewrite Eq. (29):

$$ X=\frac{1}{\sqrt{2H}} ; \qquad Y=\frac{1}{\sqrt{F+H}}. $$
(30)

An ellipse in general position can be expressed parametrically as the path of a point (x(t),y(t)), where:

$$ \begin{aligned} x(t) =x_c+a\cos(t) \cos(\psi)-b \sin(t) \sin (\psi),\\ y(t) =y_c+a\cos(t) \cos(\psi)+b \sin(t) \sin (\psi). \end{aligned} $$
(31)

Here, (x c ,y c ) is the center of the ellipse, ψ is the angle between the X-axis and the major axis of the ellipse, parameter t varies from 0 to 2π, a and b are major and minor radii, respectively.

In the case of transversely homogeneous material, x c =y c =0 and \(\psi =\frac{\pi}{4}\). Substitute the known value into Eq. (31), we get:

$$\begin{aligned} & \biggl( \frac{x+y}{\sqrt{2}a} \biggr)^2 + \biggl( \frac {x-y}{\sqrt{2}b} \biggr)^2 =1\quad \Longrightarrow \\ &\biggl(\frac{1}{2a^2}+\frac{1}{2b^2} \biggr) x^2+ \biggl(\frac{1}{2a^2}+\frac{1}{2b^2} \biggr) y^2 + \biggl(\frac {1}{a^2}-\frac{1}{b^2} \biggr) xy =1. \end{aligned}$$
(32)

Comparing Eqs. (28) and (32), we get:

$$ \left \{ \begin{array}{l} F+2H = \displaystyle\frac{1}{2a^2}+\frac{1}{2b^2}, \\ H-F = \displaystyle\frac{1}{2a^2}-\frac{1}{2b^2} \\ \end{array} \right . \quad\Longrightarrow\quad \left \{ \begin{array}{l} H = \displaystyle\frac{1}{3a^2}, \\ F = \displaystyle\frac{1}{2b^2}-\frac{1}{6a^2}. \\ \end{array} \right . $$
(33)

4.2.3 General Orthotropic Material

For the general orthotropic material, there are three parameters to determine. Equation (31) can be written as a general implicit ellipse equation:

$$ c_1 x^2+c_2 xy+c_3 y^2+c_4 x+c_5 y+c_6 =0. $$
(34)

In our case, c 4=c 5=0 and c 6=−1. Comparing Eqs. (25) and (34), we get the following three equations:

$$ \left \{ \begin{array}{l} F+1.866H+0.134G = c_1, \\ F+0.134H+1.866G = c_2, \\ G-2F+H = c_3. \\ \end{array} \right . $$
(35)

In conclusion, the methodology to determine the yield criterion of unidirectional fiber reinforced periodic metal matrix composites is:

  1. 1.

    Calculation of limit macroscopic stresses based on homogenization theory;

  2. 2.

    Calculation of stress invariants;

  3. 3.

    Projection of principle stresses into π plane;

  4. 4.

    Ellipse fit using least squares criterion;

  5. 5.

    Parameters determination of yield criterion.

5 Numerical Examples

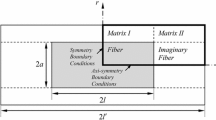
Take the square patterned unidirectional fiber reinforced periodic metal matrix composites as an example, the RVE is shown in Fig. 10, with perfect interface. The fiber ratio is 40 %. Because of symmetry, the quarter of the RVE is used for the finite element analysis (see Fig. 11), with the dimension l x =l y =50 mm. The RVE is subjected to two independent uniform displacement loadings, U1∗=U2∗=U0=0.02 mm.

Fig. 10
figure 10

Square patterned periodic composites

Full size image
Fig. 11
figure 11

Finite element model

Full size image

The material properties of each phase are shown in Table 3, with the assumption that each phase is isotropic.

Table 3 Material properties Al/Al2O3
Full size table

8-node non-conforming elements are applied for the calculation of purely elastic stress field σ E and the self-equilibrated constant matrix [C]. Since the unidirectional fiber reinforced composites can be treated as plane strain case, all degrees of freedoms in the fiber direction are fixed, i.e. there is no displacement deformation in the fiber direction. AMPL+IPOPT are used as the optimization tool.

Besides the limit load factor α LM and the shakedown load factor α SD , the elastic load factor α EL and the alternating plastic load factor α AP are also calculated for the comparison in this work. The elastic load factor α EL under two independent loads L 1 and L 2 is defined as:

$$ \text{max}\;\alpha_{EL} \quad F \bigl(\alpha \boldsymbol{\sigma}_E^i (P_k), \sigma_{Yi} \bigr) \leq 0, \quad i \in [1 , \mathit{NGS} ], \ k=1 $$
(36)

where the load vertex P 1 indicates the combination of L 1 and L 2.

The alternating plasticity load factor α AP under two independent loads L 1 and L 2 can be simplified as follows:

$$ \text{max} \;\alpha_{AP}\quad \left \{ \begin{array}{l} F ( \frac{1}{2} \alpha [ \boldsymbol{\sigma}^E_i (L_1)+\boldsymbol{\sigma}^E_i (L_2) ] ,\sigma_{Yi} ) \leq 0, \\ F ( \frac{1}{2} \alpha [ \boldsymbol{\sigma}^E_i (L_1)-\boldsymbol{\sigma}^E_i (L_2) ] ,\sigma_{Yi} ) \leq 0, \quad i \in [1 , \mathit{NGS} ].\\ \end{array} \right . $$
(37)

Figure 12 shows the different load domains of the considered example, assuming that both phases have elastic perfectly plastic material behavior.

Fig. 12
figure 12

Load domains of periodic composites with the fiber volume fraction 40 % under plane strain case, with EL: elastic load factor; SD: shakedown load factor; LM: limit load factor and AP: alternating plasticity load factor. (L) Displacement domain; (R) Macroscopic stress domain

Full size image

Considering the hardening, the shakedown domains for different matrix material models are shown in Fig. 13. We observe that the shakedown domain with isotropic hardening is only enlarged compared to the elastic perfectly plastic model. The shakedown domain with unlimited kinematic hardening is bounded by the alternating plasticity load domain.

Fig. 13
figure 13

Shakedown domains of all material models, with SD-ElasPer: elastic perfectly plastic; SD-IsoHard: isotropic hardening; SD-LKHard: Limited kinematic hardening; SDH-ULKHard: Unlimited kinematic hardening

Full size image

If the RVE is under loading U1=U2, the shakedown load factors of elastic perfectly plastic, limited kinematic hardening and unlimited kinematic hardening have the same value, as shown Fig. 13. However, the mechanisms are obviously different. For example, under loading U1=U2=−α SD U0, the equivalent stress fields obtained under different material models are shown in Fig. 14.

Fig. 14
figure 14

Different stress fields under different material models: (L) Elastic perfectly plastic material model; (M) Limited kinematic hardening material model; (R) Unlimited kinematic hardening material model

Full size image

Although based on the same elastic stress field σ E, the residual stress fields \(\bar{\boldsymbol{\rho}}\) and back stress fields \(\bar{\boldsymbol{\pi}}\), obtained from the optimization programming, are quite different. For the elastic perfectly plastic material model, obviously there is no back stress field. Nevertheless, the total equivalent stress fields of these three different material models are similar.

Figure 15 shows us merely the limit domains with elastic perfectly plastic and limited kinematic hardening material models, since there is no bound for limit load of matrix with unlimited kinematic hardening.

Fig. 15
figure 15

Limit domains, with LM-ElasPer:elastic perfectly plastic; LM-LKHard: Limited kinematic hardening

Full size image

According to the limit displacement domain of the elastic perfectly plastic material model, with the aid of homogenization approach and stress invariant theory, the macroscopic principle stresses domain is obtained, as shown in Fig. 16(L), which is projected into π-plane afterwards, see Fig. 16(R). Based on the least square fitting method, the obtained parameters of Hill’s criterion are as follow:

$$ \text{Major axis of ellipse:}\quad a=241.8306; \qquad\text{Minor axis of ellipse:} \quad b=67.7779. $$
Fig. 16
figure 16

Yield criterion fitting: (L) Homogenized stresses (Σ 1-Σ 2) domain; (R) Hill’s yield criterion fitting based on the projection into π plane

Full size image

From Eqs. (33) and (30), we get the axial strength of the unidirectional periodic composites:

$$ X=296.1808~\text{MPa}=3.70\sigma^m_Y; \qquad Y=Z=94.6217~\text{MPa}= 1.18 \sigma^m_Y. $$

According to the micromechanics of unidirectional composites [10], the effective yield tensile strength in fiber direction is defined as:

$$ \varSigma^X_Y=\eta_{\text{m}} E_{\text{m}} \epsilon_c +\eta_{\text{f}} E_{\text{f}}\epsilon_c. $$
(38)

Indices ‘f’ and ‘m’ represent fiber and matrix, respectively. ϵ c is the critical strain defined by:

$$ \epsilon_c = \text{min} \biggl\{ \frac{\sigma^{\text{m}}_Y}{E_{\text {m}}}, \frac{\sigma^{\text{f}}_Y}{E_{\text{f}}} \biggr\}. $$
(39)

Therefore, the effective yield strength based on micromechanics is:

$$ \varSigma^X_Y=217.14~\text{MPa} = 2.17 \sigma^m_Y. $$

The maximum tensile stress criterion is:

$$ \varSigma^{\text{t}}_Y = \frac{1-\nu_{\text{m}}}{k_{\sigma}(1+\nu_{\text {m}})(1-2\nu_{\text{m}})} ( \sigma_{\text{mt}} -\epsilon_{\text {rm}}E_{\text{m}}) $$
(40)

where, index ‘t’ means the transverse direction. ϵ rm is the radial maximum residual strain, which is approximated to zero in our case. k σ is the stress concentration factor, with the definition:

$$ k_{\sigma}=\frac{\sigma_{\text{max}}}{\sigma_p}, $$
(41)

σ p is the outer force that is applied on the RVE or mesoscopic components. According to the numerical result, k σ is around 1.15. Therefore, the effective transverse yield strength based on micromechanics is:

$$ \varSigma^Y_Y=\varSigma^Z_Y=93.65~\text{MPa} = 1.17 \sigma^m_Y. $$

When compared with the analytical results from microscopic mechanics, we observe that the predicted strength in transverse direction matches well. However, the numerical value of the strength in fiber direction is bigger than the analytical one. The possible reason lies in the too restrict constraints in the numerical analysis: the degrees of freedom in fiber direction are completely fixed which leads to a greater homogenized elastic stress in fiber direction. Nevertheless, the advantages of numerical methods are obvious, which consist in the possibility to consider the fiber distributions, imperfect bounded interfaces, or other types of composites, instead of the unidirectional one.

6 Conclusions

In this paper, the lower-bound approach of DM is applied on periodic composites, including hardening material models for the matrix. As expected, for isotropic hardening, the shakedown domain is enlarged with the same shape as elastic perfectly plastic one. For unlimited kinematic hardening, there is no bound for the limit load and shakedown domain is bounded by alternating plasticity. Two yield surfaces of limited kinematic hardening model provide more realistic solutions. Furthermore, in combination with homogenization theory, plastic material parameters are predicted by using yield surface fitting on the macroscopic limit homogenized stress domain. However, the present work is based on the assumption that fiber and matrix have perfect interfaces. The debonding failure will be studied in the further work.