A review on micromechanical methods for evaluation of mechanical behavior of particulate reinforced metal matrix composites

Abstract

Particulate reinforced metal matrix composites (PRMMC) are the most promising alternative for applications where the combination of high strength, elastic modulus, specific stiffness, strength-to-weight ratio and ductility is essential. Experimental investigation does not provide insightful information about microstructural aspects affecting the mechanical behavior of PRMMC, while the micromechanical methods can describe effectively. This paper presents the review on various analytical and computational micromechanical methods to evaluate the mechanical properties of particulate reinforced metal matrix composites. The effects of particle size, shape and orientation and interface strength on the mechanical behavior are presented. Stress–strain relationships, damage evolution, elastic and plastic deformations are also described. Computational micromechanical methods were found to provide better estimate of properties than analytical micromechanical methods. The order of preference among computational micromechanical methods is serial sectioning method, statistical synthetic method, multi-cell method, 2D real microstructure method and unit-cell method. However, serial sectioning method is highly expensive and demands lot of experimental and computational resources while the statistical synthetic method is economical and doesn’t require many resources. Therefore, statistical synthetic method can be a better choice for computational micromechanics of particulate reinforced metal matrix composites to evaluate the mechanical behavior without experimentation.

Introduction

Metal matrix composites (MMCs) are applied widely in aero craft [1], automotive [2], aviation [3], infrastructure industries [4], electronic packing [5], thermal management equipments [6] and many more due to their high strength-to-weight ratio, elastic modulus, specific stiffness, thermal conductivity, electrical conductivity, etc. With ample applications, it is important to study the properties of metal matrix composites. Most of the mechanical properties of metal matrix composites are influenced significantly by the properties and attributes of reinforcements. The most commonly used reinforcements for metal matrix composites are particulates. With the knowledge of the relationship between the microstructure constituents and the macroscale response, it is possible to optimize the mechanical properties of metal matrix composites as per the requirement. In general, the macroscale properties of MMCs are evaluated through experimentation. Some of the experimental investigations presented in literature are described [7,8,9,10,11,12,13,14,15,16]. Balasubramanian et al. [7] investigated the mechanical behavior of 5, 10 and 15 wt% AA6063/SiC aluminum matrix composite manufactured by stir casting technique. Rao et al. [8] investigated the mechanical properties of 5, 10 and 15 wt% Al7075/SiC composites fabricated through stir casting method. Umasankar et al. [9] evaluated the mechanical properties of 5, 10 and 15 wt% AA6061/SiC aluminum matrix composite fabricated by powder processing. Amouri et al. [10] investigated the mechanical properties of 5 wt% A356/SiC aluminum matrix composite produced by stir casting technique. Shirvanimoghaddam et al. [11] performed mechanical investigation on 15 vol% A356/B₄C metal matrix composites fabricated using stir casting method. Sajjadi et al. [12] reported the mechanical properties of 1, 3, 5 and 7.5 wt% A356/Al₂O₃ aluminum matrix composites fabricated by stir casting and compo-casting. Muralidharan et al. [13] investigated the mechanical behavior of 2.5, 5, 7.5 and 10 wt% AA2024/ZrB₂ aluminum matrix composite. Pazhouhanfar et al. [14] experimentally investigated the mechanical properties of 3%, 6% and 9 wt% Al6061/TiB₂ composites fabricated by stir casting method. Ravi Kumar et al. [15] studied the mechanical behavior of 2, 4, 6, 8 and 10 wt% A6063/TiC aluminum matrix composite fabricated by stir casting method. Wang et al. [16] evaluated the mechanical properties of 5%, 10% and 15% vol% MgZnCa/SiC metal matrix composites fabricated by stir casting method. However, experimental investigation of mechanical properties did not provide insightful information on the influence of microstructural aspects such as particle size, particle orientation, particle shape, particle–matrix interfacial strength, porosity and thermal mismatch between particle and matrix on the mechanical properties. Therefore, the effect of microstructural aspects on the mechanical properties of MMC can only be described by micromechanics. Hence, various analytical and numerical methods were developed to understand the micromechanics of MMC. By these methods, the influence of the reinforcement size, shape, distribution and interphase bonding on the macroscale response of composites can be studied and optimized. The micro scale stress–strain regions and dynamic failure evolution during loading can be studied. Also, multi-axial loading can be applied to the composite materials, which are difficult practically using equipments. Hence, keeping in view of advantages at these analytical or computational methods, many researchers are adopting these methods to analyze the mechanical behavior of any new composite before actual experimentation to reduce the time and cost. Micromechanical methods are not only limited to MMCs but also deployed in alloys [17,18,19,20], polycrystals [21, 22], fiber reinforced polymer matrix composites [23,24,25], etc. Srinivasu et al. [17] developed a 2D RVE based on vol% of α and β phases of titanium alloy (Ti–10V–4.5Fe–3Al) to predict the stress–strain curve numerically. Ramazani et al. [18] developed 2D RVE from real microstructure and 3D RVE using multi-cell method to evaluate the flow curve of DP steels numerically. Amirmaleki et al. [19] developed 3D micromechanical model of DP500 and DP600 steels by multi-cell method to obtain stress–strain relationships. Ouyang et al. [20] developed a 3D RVE based on multi-cell method to evaluate the strength and ductility of bimodal nanostructured metals. Groeber et al. [21] generated statistically equivalent synthetic microstructures of polycrystals using serial sectioning data of the microstructures for structure property correlation. Salahouelhadj et al. [22] developed 2D and 3D RVEs to simulate tensile test of isotropic copper polycrystals. Pan et al. [23] developed a 3D RVE of randomly oriented chopped E-glass reinforced urethane matrix composite to obtain the overall elastic properties. Liu et al. [24] developed a 3D RVE for estimating the elastic constants of randomly oriented short fiber reinforced composites. Fliegener et al. [25] developed RVEs of 10, 20 and 30 wt% long glass fiber reinforced polypropylene matrix composite and predicted the elastic properties numerically.

In this review, various analytical and computational micromechanical methods developed to predict the mechanical properties of PRMMCs are discussed comprehensively. The major evaluations from micromechanical methods are stress–strain relationships, damage evolution, elastic and plastic deformation in composite. Also, the micromechanical methods estimate the relationship between microstructural characteristics and macroscale properties of the composites with variable degree of error. Hence, this review provides the advantages, limitations and accuracy levels of various analytical and computational micromechanical methods for selection of suitable micromechanical method based on the researcher requirements.

Analytical methods

Analytical methods are incorporated to develop the commercial simulation software programs in any field. Similarly, it was extended to microstructure modeling as well. Hence, knowledge on analytical methods helps in understanding the background of simulation software programs. Some of the software packages for microstructure modeling will be discussed in the later stage of this paper. Analytical methods are broadly classified as rule-of-mixtures method and micromechanical method. Table 1 shows the sub-classification of analytical methods.

Table 1 Sub-classification of analytical methods

Rule-of-mixtures method

Rule of mixtures

Rule-of-mixtures method was derived based on Voigt and Reuss estimations. The Voigt approximation assumes equal strain in both the phases when the load is applied. The composite stress is the sum of constituent stresses. Therefore, the Young’s modulus of metal matrix composite is the average of the moduli of the each phase weighted by the volume fraction given as:

$$ E = E^{\mathrm{M}} f^{\mathrm{M}} + E^{\mathrm{R}} f^{\mathrm{R}} $$

(1.1)

The Reuss approximation assumes equal stress in both the phases when the load is applied. The strain in the composite is the sum of the strains carried by each phase, and the Young’s modulus of composite is given by

$$ E = \left( {\frac{{f^{\mathrm{M}} }}{{E^{\mathrm{M}} }} + \frac{{f^{\mathrm{R}} }}{{E^{\mathrm{R}} }}} \right)^{ - 1} $$

(1.2)

Hill [26] has shown Voigt approximation and Reuss approximation are the upper bound and lower bound of the elastic moduli of a composite, respectively. However, the values estimated by rule of mixtures are not accurate for particulate reinforced metal matrix composites.

Modified rule of mixtures

To predict the elastic modulus more accurately, the modified rule of mixtures was proposed by Tomoda [27], Williamson [28] and Giannakopulos [29]. The uniaxial stresses and strains in terms of the average uniaxial stress, strain and the volume fraction are given as:

$$ \sigma = f^{\mathrm{M}} \sigma^{\mathrm{M}} + f^{\mathrm{R}} \sigma^{\mathrm{R}} $$

(1.3)

$$ \varepsilon = f^{\mathrm{M}} \varepsilon^{\mathrm{M}} + f^{\mathrm{R}} \varepsilon^{\mathrm{R}} $$

(1.4)

The stress-to-strain transfer ratio, $q$, is given by

$$ q = - \frac{{\sigma^{\mathrm{M}} - \sigma^{\mathrm{R}} }}{{\varepsilon^{\mathrm{M}} - \varepsilon^{\mathrm{R}} }} $$

(1.5)

The parameter, q, considers numerous factors such as microstructural arrangements, compositions, internal constraints and others. Figure 1 represents the significance of q.

Figure 1

Representation of parameter, q

The overall Young’s modulus of composite is expressed as:

$$ E = \frac{{f^{\mathrm{M}} \left( {q + E^{\mathrm{R}} } \right)E^{\mathrm{M}} }}{{f^{\mathrm{M}} \left( {q + E^{\mathrm{R}} } \right) + f^{\mathrm{R}} \left( {q + E^{\mathrm{M}} } \right)}} + \frac{{f^{\mathrm{R}} \left( {q + E^{\mathrm{M}} } \right)E^{\mathrm{R}} }}{{f^{\mathrm{M}} \left( {q + E^{\mathrm{R}} } \right) + f^{\mathrm{R}} \left( {q + E^{\mathrm{M}} } \right)}} $$

(1.6)

Rule-of-mixtures method failed to evaluate the mechanical properties accurately and can be observed from “Comparisons of micromechanical results and experimental results” section. Hence, micromechanics methods were evolved. The evaluation of average elastic properties of composites is one of the classical problems in micromechanics. Many authors have proposed several micromechanical models and contributed for evaluating the mechanical response of a composite material.

Micromechanical methods

Eshelby method

Eshelby [30] considered an ellipsoid inclusion in an infinite isotropic matrix for solving the three-dimensional elasticity problem. Ellipsoid inclusion is treated as discontinuous reinforcement and has elastic constants different from rest of the material. This model has been employed rigorously in various modified forms by several authors in the analyses of discontinuously reinforced composite materials. Eshelby equations [38] for the bulk modulus, K, and shear modulus, G, are

$$ K = {{K^{\mathrm{M}} } \mathord{\left/ {\vphantom {{K^{\mathrm{M}} } {\left[ {1 + \mathop \sum \limits_{R = 1}^{n} f^{\mathrm{R}} \left( {K^{\mathrm{M}} - K^{\mathrm{R}} } \right)/\left( {K^{\mathrm{M}} + s_{1} \left( {K^{\mathrm{R}} - K^{\mathrm{M}} } \right)} \right)} \right]}}} \right. \kern-0pt} {\left[ {1 + \mathop \sum \limits_{R = 1}^{n} f^{\mathrm{R}} \left( {K^{\mathrm{M}} - K^{\mathrm{R}} } \right)/\left( {K^{\mathrm{M}} + s_{1} \left( {K^{\mathrm{R}} - K^{\mathrm{M}} } \right)} \right)} \right]}} $$

(1.7)

$$ G = {{G^{\mathrm{M}} } \mathord{\left/ {\vphantom {{G^{\mathrm{M}} } {\left[ {1 + \mathop \sum \limits_{R = 1}^{n} f^{\mathrm{R}} {{\left( {G^{\mathrm{M}} - G^{\mathrm{R}} } \right)} \mathord{\left/ {\vphantom {{\left( {G^{\mathrm{M}} - G^{\mathrm{R}} } \right)} {\left( {G^{\mathrm{M}} + s_{2} \left( {G^{\mathrm{R}} - G^{\mathrm{M}} } \right)} \right)}}} \right. \kern-0pt} {\left( {G^{\mathrm{M}} + s_{2} \left( {G^{\mathrm{R}} - G^{\mathrm{M}} } \right)} \right)}}} \right]}}} \right. \kern-0pt} {\left[ {1 + \mathop \sum \limits_{R = 1}^{n} f^{\mathrm{R}} {{\left( {G^{\mathrm{M}} - G^{\mathrm{R}} } \right)} \mathord{\left/ {\vphantom {{\left( {G^{\mathrm{M}} - G^{\mathrm{R}} } \right)} {\left( {G^{\mathrm{M}} + s_{2} \left( {G^{\mathrm{R}} - G^{\mathrm{M}} } \right)} \right)}}} \right. \kern-0pt} {\left( {G^{\mathrm{M}} + s_{2} \left( {G^{\mathrm{R}} - G^{\mathrm{M}} } \right)} \right)}}} \right]}} $$

(1.8)

The terms $s_{1}$ and $s_{2}$ in Eqs. 1.7, 1.8 are represented in terms of Poison’s ratio of matrix and are given by Eqs. 1.9, 1.10, respectively. The overall Young’s modulus and Poison’s ratio of composite can be obtained from Eqs. 1.11, 1.12, respectively:

$$ s_{1} = \frac{{1 + v^{\mathrm{M}} }}{{3\left( {1 - v^{\mathrm{M}} } \right)}} $$

(1.9)

$$ s_{2} = \frac{{2\left( {4 - 5v^{\mathrm{M}} } \right)}}{{15\left( {1 - v^{\mathrm{M}} } \right)}} $$

(1.10)

$$ E = \frac{9K}{1 + 3K/G} $$

(1.11)

$$ v = \frac{3K - 2G}{{2\left( {G + 3K} \right)}} $$

(1.12)

Hashin and Shtrikman (H–S) method

Hashin and Shtrikman [31] treated the composite as an isotropic aggregate and proposed upper bound and lower bound of elastic constants based on the variational principles of linear elasticity. Walpole derived the H–S bounds using classical energy principles [32] and also extended to anisotropic materials [33]. Halpin–Tsai (H–T) [34] proposed a semiempirical method to evaluate the effective elastic moduli of composite. The upper and lower bounds of the overall bulk modulus K and shear modulus G were described in Eqs. 1.13–1.16. The overall Young’s modulus and Poison’s ratio of composite can be obtained from Eqs. 1.11, 1.12, respectively:

$$ K^{\mathrm{UPPER}} = K^{\mathrm{R}} + \left( {1 - f^{\mathrm{R}} } \right)\left[ {\frac{1}{{K^{\mathrm{M}} - K^{\mathrm{R}} }} + \frac{3f}{{3K^{\mathrm{R}} + 4G^{\mathrm{R}} }}} \right]^{ - 1} $$

(1.13)

$$ K^{\mathrm{LOWER}} = K^{\mathrm{M}} + f^{\mathrm{R}} \left[ {\frac{1}{{K^{\mathrm{R}} - K^{\mathrm{M}} }} + \frac{{3\left( {1 - f^{\mathrm{R}} } \right)}}{{3K^{\mathrm{M}} + 4G^{\mathrm{M}} }}} \right]^{ - 1} $$

(1.14)

$$ G^{\mathrm{UPPER}} = G^{\mathrm{R}} + \left( {1 - f^{\mathrm{R}} } \right)\left[ {\frac{1}{{G^{\mathrm{M}} - G^{\mathrm{R}} }} + \frac{{6f^{\mathrm{R}} \left( {K^{\mathrm{R}} + 2G^{\mathrm{R}} } \right)}}{{3K^{\mathrm{R}} + 4G^{\mathrm{R}} }}} \right]^{ - 1} $$

(1.15)

$$ G^{\mathrm{LOWER}} = G^{\mathrm{M}} + f^{\mathrm{R}} \left[ {\frac{1}{{G^{\mathrm{R}} - G^{\mathrm{M}} }} + \frac{{6\left( {1 - f^{\mathrm{R}} } \right)\left( {K^{\mathrm{M}} + 2G^{\mathrm{M}} } \right)}}{{5G^{\mathrm{M}} \left( {3K^{\mathrm{M}} + 4G^{\mathrm{M}} } \right)}}} \right]^{ - 1} $$

(1.16)

Mori–Tanaka method

Mori–Tanaka method was designed based on Eigen strains for calculating the average stresses in the composite material. This method does not provide the explicit relations for the effective stiffness tensor of composite. Benveniste [35] explained the Mori–Tanaka method in more simplified way and proposed a closed-form expressions for evaluating the effective elastic constants. Isotropic ellipsoid reinforcement was considered in a matrix to relate the average strain in inclusion to average strain in matrix material by a fourth-order tensor. The stress and strain tensors from Mori–Tanaka method are represented in Eqs. 1.17–1.21, respectively:

$$ {{\left( {K - K^{\mathrm{M}} } \right)} \mathord{\left/ {\vphantom {{\left( {K - K^{\mathrm{M}} } \right)} {\left( {K^{\mathrm{R}} - K^{\mathrm{M}} } \right)}}} \right. \kern-0pt} {\left( {K^{\mathrm{R}} - K^{\mathrm{M}} } \right)}} = {{v^{\mathrm{R}} \alpha^{\prime}} \mathord{\left/ {\vphantom {{v^{\mathrm{R}} \alpha^{\prime}} {\left( {v^{\mathrm{M}} + v^{\mathrm{R}} \alpha^{\prime}} \right)}}} \right. \kern-0pt} {\left( {v^{\mathrm{M}} + v^{\mathrm{R}} \alpha^{\prime}} \right)}} $$

(1.17)

$$ {{\left( {G - G^{\mathrm{M}} } \right)} \mathord{\left/ {\vphantom {{\left( {G - G^{\mathrm{M}} } \right)} {\left( {G^{\mathrm{R}} - G^{\mathrm{M}} } \right)}}} \right. \kern-0pt} {\left( {G^{\mathrm{R}} - G^{\mathrm{M}} } \right)}} = {{v^{\mathrm{R}} \beta^{\prime}} \mathord{\left/ {\vphantom {{v^{\mathrm{R}} \beta^{\prime}} {\left( {v^{\mathrm{M}} + v^{\mathrm{R}} \beta^{\prime}} \right)}}} \right. \kern-0pt} {\left( {v^{\mathrm{M}} + v^{\mathrm{R}} \beta^{\prime}} \right)}} $$

(1.18)

$$ \alpha^{\prime} = {{\left( {K^{\mathrm{M}} + 4G^{\mathrm{M}} /3} \right)} \mathord{\left/ {\vphantom {{\left( {K^{\mathrm{M}} + 4G^{\mathrm{M}} /3} \right)} {\left( {K^{\mathrm{R}} + 4G^{\mathrm{M}} /3} \right)}}} \right. \kern-0pt} {\left( {K^{\mathrm{R}} + 4G^{\mathrm{M}} /3} \right)}} $$

(1.19)

$$ \beta^{\prime} = {{\left( { G^{\mathrm{M}} + F^{0} } \right)} \mathord{\left/ {\vphantom {{\left( { G^{\mathrm{M}} + F^{0} } \right)} {\left( { G^{\mathrm{R}} + F^{0} } \right)}}} \right. \kern-0pt} {\left( { G^{\mathrm{R}} + F^{0} } \right)}} $$

(1.20)

$$ F^{0} = (G^{\mathrm{M}} /6)\left[ {( {9K^{\mathrm{M}} + 8G^{\mathrm{M}} } ) / ( {K^{\mathrm{M}} + 2G^{\mathrm{M}} } )} \right] $$

(1.21)

where $\alpha^{\prime },\;\beta^{\prime},\;F^{0}$ are correlation coefficients of modulus of matrix and reinforcement.

Weng [39] proposed a model based on Mori–Tanaka approach and Eshelby solutions. The stress and strain of constituent phases, elastic energy, stress concentrations at the interface and overall moduli of the composite were derived by considering an ellipsoidal inclusion. Torquato [36, 37] provided the approximate relations to evaluate effective overall shear and bulk moduli of 2D and 3D isotropic dispersions by truncating after third order of Mori–Tanaka equations. Mura [38] provided the estimates for finite concentrations of reinforcements using Mori–Tanaka equations. But, Mura model is valid only for small volume fractions of reinforcement i.e. < 0.25. The Mura expressions for the overall bulk modulus and shear modulus by considering the reinforcement geometry as spherical were given in Eqs. 1.22, 1.23. The effective Young’s modulus and Poison’s ratio of composite can be obtained from Eqs. 1.11, 1.12, respectively:

$$ G = G^{\mathrm{M}} \left[ {{{1 + f^{\mathrm{R}} (G^{\mathrm{M}} - G^{\mathrm{R}} )} \mathord{\left/ {\vphantom {{1 + f^{\mathrm{R}} (G^{\mathrm{M}} - G^{\mathrm{R}} )} {\left\{ {G^{\mathrm{M}} + 2(G^{\mathrm{R}} - G^{\mathrm{M}} )\left( {\frac{{4 - 5v^{\mathrm{M}} }}{{15(1 - v^{\mathrm{M}} )}}} \right)} \right\}}}} \right. \kern-0pt} {\left\{ {G^{\mathrm{M}} + 2(G^{\mathrm{R}} - G^{\mathrm{M}} )\left( {\frac{{4 - 5v^{\mathrm{M}} }}{{15(1 - v^{\mathrm{M}} )}}} \right)} \right\}}}} \right]^{ - 1} $$

(1.22)

$$ K = K^{\mathrm{M}} \left[ {{{1 + f^{\mathrm{R}} (K^{\mathrm{M}} - K^{\mathrm{R}} )} \mathord{\left/ {\vphantom {{1 + f^{\mathrm{R}} (K^{\mathrm{M}} - K^{\mathrm{R}} )} {\left\{ {K^{\mathrm{M}} + \frac{1}{3}(K^{\mathrm{R}} - K^{\mathrm{M}} )\left( {\frac{{1 + v^{\mathrm{M}} }}{{1 - v^{\mathrm{M}} }}} \right)} \right\}}}} \right. \kern-0pt} {\left\{ {K^{\mathrm{M}} + \frac{1}{3}(K^{\mathrm{R}} - K^{\mathrm{M}} )\left( {\frac{{1 + v^{\mathrm{M}} }}{{1 - v^{\mathrm{M}} }}} \right)} \right\}}}} \right]^{ - 1} $$

(1.23)

Self-consistent method

For spherical reinforcements with large volume fractions i.e. > 0.5, the effective Young’s modulus of composites can be found by self-consistent method. Kroner [40] and Budiansky [41] proposed the self-consistent method by considering the Eshelby’s model. It was assumed that the overall moduli of the composite were equal to the moduli of the infinite medium. Budiansky’s [41] relations for spherical inclusions are given by Eqs. 1.24, 1.25. The overall Young’s modulus and Poison’s ratio of composite can be obtained from Eqs. 1.11, 1.12, respectively:

$$ G = G^{\mathrm{M}} + \frac{{f^{\mathrm{R}} G\left( {G^{\mathrm{R}} - G^{\mathrm{M}} } \right)}}{{G + 2\left( {G^{\mathrm{R}} - G} \right)\left( {4 - 5v} \right)\left\{ {15\left( {1 - v} \right)} \right\}^{ - 1} }} $$

(1.24)

$$ K = K^{\mathrm{M}} + \frac{{f^{\mathrm{R}} K\left( {K^{\mathrm{R}} - K^{\mathrm{M}} } \right)}}{{K + \frac{1}{3}\left( {K^{\mathrm{R}} - K} \right)\left( {1 + v} \right)\left\{ {1 - v} \right\}^{ - 1} }} $$

(1.25)

Not only the elastic constants, but also the elasto-plastic response of PRMMC was explained analytically by some of the researchers. It is very important to understand the nonlinear behavior of PRMMC as the matrix exhibits ductile nature and reinforcement exhibits brittle nature. For instance, Liu et al. [42] and Hu [43] explained the elasto-plastic response based on secant modulus approach. Another study by Castaneda et al. [44] proposes the use of variational approach based on the theory of nonlinear infinitesimal elasticity to describe the elasto-plastic response. Also, the study by Liu et al. [42] proposes the use of micropolar theory for describing the nonlinear behavior of PRMMC.

The micromechanical methods discussed so far are two-phase models, i.e., matrix and reinforcement, considering infinite interface strength between them. But, the interface strength between matrix and reinforcement is finite. Therefore, analytical methods with third phase as interface might depict the actual behavior of PRMMC. For instance, Christensen et al. [45] evaluated the shear properties by considering spherical and cylindrical reinforcements with a interphase around them. To determine the effective shear modulus, Eshelby equations were used. The expression for shear modulus of composite by considering the interphase shear modulus developed by Christensen et al. [45] was presented in Eqs. 1.26. Similarly, Nie et al. [46] and Xu et al. [47] evaluated the elastic properties such as Young’s modulus and Poisson’s ratio of a composite by considering the imperfect interface bond between matrix and reinforcement. Also, the interface strength might vary within the interface thickness depending on thickness and wettability of matrix and reinforcement. Therefore, the variation in interface strength with respect to thickness was incorporated by Yao et al. [48] using power law and linear one. For a constant tensile load and interphase strength, it was reported that the reinforcement in the linear variation case was subjected to a lower tensile stress than that in the power law case.

$$ \frac{G}{{G^{\mathrm{M}} }} = 1 - \left[ {\frac{{15(1 - V^{\mathrm{M}} )[1 - (G^{\mathrm{I}} /G^{\mathrm{M}} )]f^{\mathrm{R}} }}{{(7 - 5V^{\mathrm{M}} ) + 2(4 - 5V^{\mathrm{M}} )(G^{\mathrm{I}} /G^{\mathrm{M}} )}}} \right] $$

(1.26)

The interface debonding, particle fracture and matrix damage were illustrated analytically to understand the microstructural damage mechanisms in PRMMC. For instance, Zhao et al. [49] presented the interface debonding and damage mechanisms of Al/SiC composite by considering partially debonded reinforcement. The partially debonded reinforcement was replaced by a perfectly bonded fictitious reinforcement of unknown transverse isotropic elastic property. The anisotropy of the fictitious reinforcement was evaluated by eliminating tensile and shear stresses in the debonded direction. It was assumed that the stress is transmitted in bonded direction, and therefore, elastic properties were considered in bonded direction only. This adjustment allows the use of Eshelby’s method and self-consistent method to evaluate the mechanical response of PRMMC. In another study, Nan et al. [50] and Jiang et al. [51] simulated the stress–strain curve of Al/SiC composite by considering the particle fracture during deformation. At every iteration, the stress for each particle was evaluated. The particle was considered as a fractured particle if the stress exceeds fracture stress at any stage. The fracture stress was evaluated based on Griffith criterion. If the particle was found to be fractured, it was considered as a void in subsequent iterations. This way, stress–strain curve was constructed by incorporating the progressive debonding to analyze the flow behavior of PRMMC. It was observed that the particle cracking is high for large-sized particles, which lead to degradation of flow stress. In another study, Ban et al. [52] and Ban et al. [53] used the approach of low order strain gradient plasticity theory to understand the microstructure damage evolution and hardening effect. The microstructural damage was incorporated in the secant modulus method for generating the stress–strain curve to study the nonlinear mechanical behavior of PRMMC. It was reported that interface debonding contributes significantly to the damage effects under tensile load. Cai et al. [54, 55] studied the effect of matrix failures on the damage mechanics of PRMMC by using generalized method of cells (GMC). Also, Ye et al. [56, 57] developed a multi-scale modeling method based on the high-fidelity generalized method of cells (HFGMC) for evaluating the damage analysis of a composite. HFGMC at microscale was employed to obtain the microstress distributions in the RVE. At macroscale, a viscoplastic constitutive model was engaged to define the nonlinear behaviors and the damage evolution of composites. Composite structures always undergo temperature variations in service. Therefore, studies on coupled thermomechanical responses of PRMMC were essential to depict the real-time behavior. Ye et al. [58, 59] used the approach of generalized method of cells (GMC) to estimate the thermomechanical responses. GMC method found to predict thermal conductivity coefficients and nonlinear stress–strain responses effectively.

The other micromechanical method in evaluating the mechanical response of PRMMC was finite-volume direct averaging micromechanics (FVDAM). This method deploys homogenization theory in the individual sub-volumes of the discretized unit cell by local displacement fields. The local/global stiffness matrix based on displacement interfacial continuity conditions and satisfaction of traction was used in the solution of the unit-cell microstructure problem [60]. This supersedes the HFGMC, which was based on two-level unit-cell discretization and the associated agreement of different moments of equilibrium equations [60, 61]. For instance, Ye et al. [62] used FVDAM theory for estimating the elastic moduli of PRMMC. Xi et al. [63] used FVDAM approach to study the effect of cracks on the mechanical response of composite.

Analytical methods approximate inclusion shapes to simple shapes such as ellipsoid and spherical. This simplifies the heterogeneous microstructure of the composite. This indicates that analytical methods do not account for the microstructural factors. Hence, it was revealed that analytical methods don’t depict the complete mechanical behavior and local damage characteristics of the composite that are dependent on the microstructure inherently. Thus, analytical methods failed to predict the effective mechanical properties more accurately. However, these methods are incorporated in the currently available microstructure modeling and simulation software programs such as ABAQUS, ANSYS, Digimat and Dream.3D to evaluate the properties more accurately by using finite element analysis. In addition, these software programs also incorporate microstructural complexities such as the irregular morphology of the particles, inhomogeneous spatial distribution of particles and anisotropy in particle orientation. With these features, numerical methods can able to predict the mechanical properties, macroscopic deformation behavior in elastic and plastic zone and localized damage of a composite more accurately, which analytical methods couldn’t explain. Hence, it is advisable to adopt numerical methods for structure–property correlation of particulate reinforced metal matrix composite materials.

Computational micromechanical methods

Computational techniques such as finite element analysis (FEA) have become more popular as they provide innumerous advantages over analytical methods. The complex geometry and thermomechanical history of the constituents can be incorporated to obtain realistic microstructures. Hence, it is important to understand the micromechanical modeling and analysis to define and solve the problem of micromechanics of metal matrix composites computationally.

Micromechanical modeling procedure

Microstructural constituents have a substantial influence on the mechanical behavior of composites. But, microstructural characteristics were not reflected in finite element modeling (FEM) of macro mechanics. In macro mechanics, elastic and plastic factors such as Young’s modulus, yield strength, ultimate tensile strength, shear modulus, bulk modulus, Poisson’s ratio, hardening exponent and hardening modulus were considered. Unlike macro mechanical models, micromechanical models consider composition, volume fraction, distribution, morphology and size of the constituents along with elastic and plastic factors. Hence, micromechanical modeling can be regarded as the most reliable modeling technique for structure–property correlation in particulate reinforced metal matrix composites. Various steps involved in micromechanical modeling are presented in Fig. 2.

Figure 2

Various steps involved in micromechanical modeling using RVE

The representative volume element (RVE)

Computational micromechanics start with modeling of representative volume element (RVE). RVE represents a small volume of microstructure which has the characteristic features of the entire composite such as volume fraction, shape, size, randomness of the matrix and reinforcement. The modeled RVE will be a replica of real microstructure, describing the features of the whole microstructure. RVE is a well-known micromechanical modeling technique for particulate reinforced metal matrix composites to predict the microstructure–properties relationships. This technique helps to evaluate the impact of microstructure features on the mechanical properties and hence is used for optimization of constituent parameters. An RVE should be adequately large enough to incorporate all the necessary microstructural features. Simultaneously, the RVE should be as small as possible such that the state of stress and strain can be considered uniform in entire RVE. Also, the smaller the RVE, the lesser will be the usage of computational resources such as RAM, ROM and run time to simulate the response. Mostly, RVEs were generated in 2D or 3D to describe the mechanical behavior of composite. While generating RVE, the reinforcement was considered as inclusions and was uniformly distributed in a matrix. The most commonly used software programs for generation of RVEs are ABAQUS, ANSYS, Digimat and Dream.3D. These software programs use Mori–Tanaka’s approach or random sequential adsorption algorithm approach or modified random sequential adsorption algorithm approach or real microstructure approach for generating RVEs of a composite material. The greatest advantage of micromechanical modeling by RVE lies in providing a detailed depiction of the stress and strain distributions in entire matrix and reinforcement during finite element analysis.

Defining constituent characteristics

The mechanical properties such as Young’s, bulk and shear moduli, yield stress, ultimate tensile stress, Poisson’s ratio, hardening exponent and hardening modulus have to be defined for each phase. Additionally, particle size, shape and volume fraction of reinforcement are defined for generating RVE. The RVE generated has particles distributed uniformly inside the RVE. The nearest distance between any two particles inside the RVE will be same everywhere. The size of RVE depends on particle volume fraction, shape, size. The other way of generating RVE is from real microstructures of composite, which will be discussed in detail in the later stage of paper.

Applying boundary conditions

The mechanical behavior of an RVE can be investigated by applying suitable boundary conditions such as loading and constraints. This can be solved using finite element method (FEM) by considering as a problem in continuum solid mechanics. Kouznetsova et al. [64] proposed the theory of boundary conditions for micromechanical modeling of multi-phase materials. A brief description of the theory is described below.

The initial position vector of RVE deformation field is represented as $\vec{X}$ in the reference domain $V_{0}$, and the actual position of vector is represented as $\vec{x}$ in the current domain V termed by the deformation gradient tensor

$$ F_{\mathrm{m}} = \left( {\nabla_{0\mathrm{m}} \vec{x}} \right)^{c} $$

(3.1)

where $\nabla_{0\mathrm{m}}$ is the gradient operator of RVE with respect to the reference deformation field. As the RVE is in equilibrium state, it can be mathematically represented by an equilibrium equation using Cauchy stress tensor $\sigma_{\mathrm{m}}$. This can be represented in terms of the first Piola–Kirchhoff stress tensor of $P_{\mathrm{m}}$ as

$$ \nabla_{\mathrm{m}} \cdot \sigma_{\mathrm{m}} = \vec{0} \;{\text{or}}\; \nabla_{0\mathrm{m}} \cdot P_{\mathrm{m}}^{c} = \vec{0} $$

(3.2)

$$ P_{\mathrm{m}} = \det \left( {F_{\mathrm{m}} } \right)\sigma_{\mathrm{m}} \cdot \left( {F_{\mathrm{m}}^{c} } \right)^{ - 1} $$

(3.3)

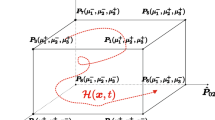
where $\nabla_{\mathrm{m}}$ is the gradient operator of RVE with reference to the current deformation. The macro- to microconversion can be attained by incorporating the macroscopic deformation gradient tensor $F_{\mathrm{m}}$ on the RVE. The simplest way of imposing is using Taylor or Voigt approximation which assumed that the constituents of microstructure are subjected to a constant deformation. Another assumption is that of Sachs or Russ which assumed that constant stress is being applied to all the constituents. These simplified assumptions can’t provide the actual deformation of the RVE. Therefore, more accurate averaging strategies are required for macro- to microtransition of RVE with the help of boundary conditions. Figure 3 shows the schematic of 2D RVE. Typically, RVE boundary conditions are of three types. They are (1) prescribed displacements, (2) prescribed forces and (3) prescribed periodicity.

Figure 3

2D schematic of typical RVE [64]

The position vector in the deformed state for displacement boundary conditions is represented as:

$$ \vec{x} = F_{\mathrm{M}} \cdot\vec{X}\;{\text{with}}\;\vec{X}\;{\text{on}}\;\Gamma_{0} $$

(3.4)

where $\Gamma_{0}$ represents the undeformed boundary and $F_{\mathrm{M}}$ represents the macroscopic deformation gradient tensor of the RVE. The traction boundary conditions are defined as:

$$ \tilde{t} = \tilde{n} \cdot \sigma_{\mathrm{m}} \;{\text{on}}\; \Gamma \;{\text{or}}\; \tilde{P} = \tilde{N} \cdot P_{\mathrm{M}}^{c} \;{\text{on}}\; \Gamma_{0 } $$

(3.5)

where $\tilde{N}$ is normal to the initial $(\Gamma_{0} )$ RVE boundary and $\tilde{n}$ is normal to the current ($\Gamma$) RVE boundary. Macroscale and microscale quantities are represented by “M” and “m,” respectively. The RVEs are arranged periodically to represent bulk composite material. Hence, the periodic boundary conditions are the ideal RVE boundary conditions. Periodic arrangement emphasizes that every RVE in the composite material has the same deformation and there is no separation, gap and overlap, etc. between the neighborhood RVEs after deformation. The periodic deformation of the RVE is represented as

$$ \vec{x}^{ + } - \vec{x}^{ - } = F_{\mathrm{M}} \cdot \left( {\vec{X}^{ + } - \vec{X}^{ - } } \right) $$

(3.6)

The parts of RVE boundary $\Gamma_{0}^{ - }$ and $\Gamma_{0}^{ + }$ are defined such that $\vec{N}^{ - } = - \vec{N}^{ + }$ at corresponding points on $\Gamma_{0}^{ - }$ and $\Gamma_{0}^{ + }$. The periodic boundary conditions were represented as:

$$ \vec{x}_{\mathrm{T}} = \vec{x}_{\mathrm{B}} + \vec{x}_{4} - \vec{x}_{1} $$

(3.7)

$$ \vec{x}_{\mathrm{R}} = \vec{x}_{\mathrm{L}} + \vec{x}_{2} - \vec{x}_{1} $$

(3.8)

$$ \vec{x}_{3} = \vec{x}_{2} + \vec{x}_{4} - \vec{x}_{1} $$

(3.9)

where $\vec{x}_{\mathrm{R}} ,\;\vec{x}_{\mathrm{L}} ,\; \vec{x}_{\mathrm{T}} ,\;{\text{and}}\; \vec{x}_{\mathrm{B}}$ are the position vectors at the right, left, top and bottom boundaries of the RVE, respectively. $\vec{x}_{i}$ (i = 1–4) are the position vectors in the deformed state of the corner points 1, 2, 3 and 4, respectively. The position vectors of RVE are described as:

$$ \vec{x}_{i} = F_{\mathrm{M}} \cdot\vec{X}_{i} \;{\text{and}}\; i = 1,2,3,4. $$

(3.10)

First-order homogenization

The physical and mechanical properties of the constituents are considered always in a small scale. One of the best tools for composite discretization and the computer simulation is the homogenization method. The microscale behavior of a composite is related to its macroscopic behavior by homogenization method. Computational homogenization method has proved to be ideal tool for establishing the nonlinear structure–property relations. This method assumes that the composite is homogeneous at macroscale and heterogeneous at the microscale due to the presence of inclusions and interfaces. There are two types of homogenization methods available in the literature, and they are (1) first-order homogenization and (2) second-order homogenization. As first-order homogenization is the mostly used technique, a brief description is given below.

Kouznetsova et al. [64] have presented the theory of micromechanical homogenization for simulating multi-phase materials. The inhomogeneity in the RVE is represented as global and local periodicity. They are illustrated in Fig. 4. The global periodicity assumes that the inhomogeneity is uniform throughout the microstructure. The local periodicity assumes that inhomogeneities with different morphologies can be repeated at every individual macroscopic point. It also considers the effect of non-uniform distribution of the constituents at the macroscopic level which is quite realistic Hence, local periodicity is chosen for computational homogenization of RVE as it considers the most of the effects.

Figure 4

Schematic of a local and b global periodic microstructure [64]

A stepwise description of first-order homogenization method by Kouznetsova et al. [64] for RVE is as follows:

Step 1 The deformation tensor, $F_{\mathrm{M}}$, is evaluated at all the macroscopic points of mesh in an RVE

Step 2$F_{\mathrm{M}}$ at a particular macroscopic point was used to frame the boundary conditions of the RVE located at that point. By this, the field variable, i.e., deformation of the RVE is evaluated.

Step 3 The stress tensor, $P_{\mathrm{M}}$, of the initial macroscopic point is estimated by averaging the stress field of the RVE over the entire volume. Hill [26] developed the integral averaging expressions.

The stress tensor and the deformation tensor obtained are used to establish the numerical stress–deformation and stress–strain relationships at the macroscopic point. First-order homogenization method is also represented schematically in Fig. 5. However, the experimental stress–deformation and stress–strain relationships are evaluated traditionally by universal testing machine (UTM).

Figure 5

Schematic representation of first-order homogenization [65] (with permission)

Post-processing

The outcomes after simulation are processed to evaluate the mechanical behavior of heterogeneous microstructure. The major outcomes are deformation and stress. A brief description of equations used for obtaining deformation and stress is presented below.

(1) Deformation

The macroscale and microscale deformations and stresses are coupled by the applying integral averaging theorems. It is assumed that the volume average of the microscale deformation gradient tensor $F_{\mathrm{m}}$ results in the macroscopic deformation gradient tensor $F_{\mathrm{M}}$

$$ F_{\mathrm{M}} = \frac{1}{{V_{0} }}\mathop \int \limits_{{V_{0} }} F_{\mathrm{m}} {\text{d}}V_{0} $$

(3.11)

$$ F_{\mathrm{M}} = \frac{1}{{V_{0} }}\mathop \int \limits_{{\Gamma_{0} }} \vec{x}\vec{N}{\text{d}}\Gamma_{0} $$

(3.12)

where $V_{0}$ is the initial undeformed RVE volume. The volume integral of the RVE is transformed to a surface integral with the help of divergence theorem. As periodic boundary conditions are the most commonly used boundary conditions for the RVE, the validation of macroscopic deformation gradient tensor $F_{\mathrm{M}}$ for the above-mentioned periodic boundary conditions Eqs. (3.7)–(3.9) is shown below.

$$ F_{\mathrm{M}} = \frac{1}{{V_{0} }}\left\{ {\mathop \int \limits_{{\Gamma_{0}^{ + } }} \vec{x}^{ + } \vec{N}^{ + } {\text{d}}\Gamma_{0} + \mathop \int \limits_{{\Gamma_{0}^{ - } }} \vec{x}_{0} \vec{N}^{ - } {\text{d}}\Gamma_{0} } \right\} $$

(3.13)

$$ F_{\mathrm{M}} = \frac{1}{{V_{0} }}\mathop \int \limits_{{\Gamma_{0}^{ + } }} \left( {\vec{x}^{ + } - \vec{x}^{ - } } \right)\vec{N}^{ + } {\text{d}}\Gamma_{0} $$

(3.14)

$$ F_{\mathrm{M}} = \frac{1}{{V_{0} }}F_{\mathrm{M}} \cdot\mathop \int \limits_{{\Gamma_{0}^{ + } }} \left( {\vec{X}^{ + } - \vec{X}^{ - } } \right)\vec{N}^{ + } {\text{d}}\Gamma_{0} $$

(3.15)

$$ F_{\mathrm{M}} = \frac{1}{{V_{0} }}F_{\mathrm{M}} \cdot\mathop \int \limits_{{\Gamma_{0} }} \vec{X}\vec{N}{\text{d}}\Gamma_{0} = F_{\mathrm{M}} $$

(3.16)

where $\vec{X}$ and $\vec{x}$ are the position vectors in the undeformed state and deformed state, respectively. $\vec{N}$ and $\vec{n}$ are the normal to initial and the current RVE boundaries, respectively.

(2) Stress

The averaging relation for the first Piola–Kirchhoff stress tensor is:

$$ P_{\mathrm{M}} = \frac{1}{{V_{0} }}\mathop \int \limits_{{V_{0} }} P_{\mathrm{m}} {\text{d}}V_{0} $$

(3.17)

The macroscopic Piola–Kirchhoff stress tensor $P_{\mathrm{M}}$ in the microscopic quantities represented on the RVE surface is given as:

$$ \nabla_{0\mathrm{m}} \cdot P_{\mathrm{m}}^{c} = \vec{0}\;{\text{for microscopic equilibrium}} $$

(3.18)

$$ \nabla_{0\mathrm{m}} \vec{X} = I\;{\text{for microstructure equality}} $$

(3.19)

$$ P_{\mathrm{m}} = \left( {\nabla_{0\mathrm{m}} \cdot P_{\mathrm{m}}^{c} } \right)\vec{X} + P_{\mathrm{m}} \cdot \left( {\nabla_{0\mathrm{m}} \vec{X}} \right) $$

(3.20)

$$ P_{\mathrm{m}} = \nabla_{0\mathrm{m}} \cdot \left( {P_{\mathrm{m}}^{c} \vec{X}} \right) $$

(3.21)

By substituting Eqs. (3.18–3.21) into Eq. (3.17) and applying the first Piola–Kirchhoff stress vector according to Eq. (3.1), the divergence theorem, $P_{\mathrm{M}}$, of RVE is obtained over the surface:

$$ \vec{p} = \vec{N} \cdot P_{\mathrm{m}}^{c} $$

(3.22)

$$ P_{\mathrm{M}} = \frac{1}{{V_{0} }}\mathop \int \limits_{{V_{0} }} \nabla_{0\mathrm{m}} \cdot \left( {P_{\mathrm{m}}^{c} \vec{X}} \right){\text{d}}V_{0} $$

(3.23)

$$ P_{\mathrm{M}} = \frac{1}{{V_{0} }}\mathop \int \limits_{{\Gamma_{0} }} \vec{N} \cdot P_{\mathrm{m}}^{c} \vec{X}{\text{d}}\Gamma_{0} $$

(3.24)

$$ P_{\mathrm{M}} = \frac{1}{{V_{0} }}\mathop \int \limits_{{\Gamma_{0} }} \vec{p}\vec{X}{\text{d}}\Gamma_{0} $$

(3.25)

By considering the RVE periodicity conditions Eqs. (3.7)–(3.10) as shown in Fig. 3, it can be proved that the external loading was the only applied boundary condition contributing to the boundary integral Eq. (3.25) as defined at the three prescribed corner nodes by the following expression:

$$ P_{\mathrm{M}} = \frac{1}{{V_{0} }}\mathop \sum \limits_{i = 1,2,3,4} \overrightarrow {{f_{i} }} \overrightarrow {{X_{i} }} $$

(3.26)

where $\overrightarrow {{X_{i} }}$ are the position vectors in the undeformed state and $\overrightarrow {{f_{i} }}$ are the resulting external forces at the boundary nodes.

2D models

In general, 2D RVEs are generated from the SEM/Optical microscope image of microstructure sample. Different stages of 2D RVE evolution from real microstructure and numerical simulation of generated RVE are depicted in Fig. 6. Real microstructure image from SEM/optical is segmented into dark and white areas, where white area represents matrix and dark area represents reinforcement. The microstructures are converted from raster format to vector format. The vector format will not alter or modify the original microstructure. Now, the vector format file was converted into CAD file format (IGES) and then imported to the finite element analysis (FEA) software for numerical analysis. ANSYS and ABAQUS are the commonly used software programs for 2D micromechanical analysis.

Figure 6

Schematic of 2D RVE generation from real microstructure and numerical simulation [66] (with permission)

Estimation of mechanical behavior

The literature reports that the 2D RVEs generated from real microstructure or from statistics were used to study the influence of particle size, particle shape, particle orientation, RVE size, voids, particle clustering, loading conditions, etc. on the elastic, plastic behavior, stress–strain relations, mechanical properties and failure behavior of PRMMC. For instance, the effect of particle clustering on 20 vol% Al2080/SiC [67], 15 vol% Al/SiC [68, 69] composites was studied. It was found that the mechanical behavior in the matrix and the particles was sensitive to particle clustering. From the results, it was observed that the interface decohesion and particle percentage cracking was largest in particle clustering than in random arrangement. Clustering behavior of 15 vol% Al/SiC composites was studied by considering one-cluster, two-cluster and random arrangement. Stress–strain curves with different arrangements are shown in Fig. 7. Random arrangement yielded better results than clustering. This emphasizes the need for achieving homogeneous distribution of particles in matrix phase during casting of PRMMC, and the similar conclusions were derived by Scudino et al. [70] and Liu et al. [71] by experimental investigation.

Figure 7

Stress–strain curves with different distributions [69]

Similarly, Chawla et al. [67] modeled a 2D RVE from real microstructure to evaluate the mechanical behavior of 20 vol% Al2080/SiC particulate reinforced composites. It was observed that the particle exerted higher stress than the matrix, and rectangular-shaped reinforcement particles are under higher stress. The mechanical behavior at different volume fractions of B₄C was studied by Sharma et al. [72] by developing a object-oriented 2D finite element method for 4, 8 and 12 vol% Al/B₄C PRMMC. The numerical results are in good correlation with experimental results for all volume fractions of B₄C. Local stress and equivalent plastic strain of 2D RVE are presented in Fig. 8. It was reported that the elastic modulus is greatly influenced by B₄C content and porosity.

Figure 8

Local stress and equivalent plastic strain distribution of 12 vol% Al/B4C composites [72] (with permission)

The simulation results are sensitive to particle size, shape, clustering effect, RVE size and boundary conditions as well. The particle size has a significant role in altering the mechanical performance of PRMMC. The lower the particle size, the higher will be the strength of composite. However, numerical methods can’t predict the effect of particle size using classical elastic–plastic theory directly. It is because that no length scale-dependent parameters or constraints were involved in the classical theory. However, with the use strain gradient plasticity theory, the effect of particle size on the mechanical properties can be evaluated. For example, Yueguang [73] and Chen et al. [74] successfully estimated the effect of particle size using strain gradient plasticity theory by considering ellipsoidal and cylindrical particle shapes. The numerical and experimental results were in good agreement for Al/SiC composites at particle size of 160 μm. Also, damage evolution in PRMMC was explained effectively using strain gradient plasticity theory by Legarth [75] and Azizi et al. [76]. Monotonic effect and non-monotonic effect of scale-dependent cohesive parameter on the failure strain were evaluated effectively with the use of consistent cohesive law within higher-order strain gradient plasticity theory. Just like particle size, particle shape will certainly effect the mechanical strength of composites. For instance, Qing [77] studied the effect of particle shape on the strength and damage behavior of Al/SiC composites by developing a 2D RVE consisting of square-, hexagon-, octagon- and circle-shaped SiC particulates using RSA algorithm. It was observed that the failure particles increase as the particle shapes change from circular to octagon, octagon to hexagon and hexagon to square. Therefore, the maximum strength was experienced by circular-shaped particles. But in reality, the reinforcements can never be circular rather irregular. The clustering effect of particles was studied by Mishnaevsky [78] by generating 2D RVE with different gradients. With the increase in the degree of gradient, it was observed that the failure strain increases, and as a result, flow stress and stiffness of composites decrease. Also, it was observed that the damage begins in the particles located in the transition zone between high particle density zone and the particle-free zone. The effect of RVE size and boundary conditions was studied by Chen et al. [79] and Chen et al. [80] in which a 2D RVE was developed based on real microstructure of 30 vol% WC–Co hard metal. It was reported that a smaller RVE size would be enough to predict effective material parameters. It was also reported that the results were no longer size dependent after certain RVE size because homogenization of properties will be a problem at large RVE sizes. Plasticity study requires larger RVE size than pure elastic study. The model behavior was not influenced severely with the change of boundary conditions from KUBC to KPBC, but altered fundamentally by shifting element type from plane strain to plane stress.

Most of the simulations were performed considering the infinite strength between matrix and reinforcement. But, in reality, the interface strength will be finite and there can be chances of failure of PRMMC at interface. Therefore, it is really important to understand the behavior of PRMMC for finite interface strength. Few authors, Qing et al. [81], Qing et al. [82] and Kan et al. [83] investigated the effect of interface strength on the mechanical properties of the 2D RVE of Al/SiC particulate reinforced composites, while Zhang et al. [84] investigated on 20 and 40 vol% ZTA/Fe45 composites. It was found that interphase strength and particle arrangements play a significant role in tensile strength of composite. The debonding behavior of interface and microscale damage evolution of composites were observed. Also, the brittle failure in SiC particles and ductile failure in matrix along with interfacial debonding were observed. It was found that the average stresses of particles for the cohesive interfaces are lower than those with perfect interfaces. The damage evolution rate in the particles was found to be higher for low particle content than high particle content. It was also found that the number of interface debondings increased with the increase in vol% of particles. The interfacial debonding for a particular vol% of particles was reduced by increasing interfacial cohesive strength and cohesive energy. The stress–strain curve for different interface strengths of 20 vol% AA2009/SiC PRMMC is presented in Fig. 9. It can be found that the model with interface strengths 300 MPa is the softest and interface strength 500 MPa is the strongest, which fitted well with the experiment results. Therefore, interface strength of 20 vol% AA2009/SiC can be considered as 500 MPa. The results specify that damage initiates at the interface and propagates along the weaker direction until the composite failure. Similar study was performed by Qing [81] to identify the influence of interface strength on the mechanical behavior and damage evolutions for different loading conditions such as tensile, shear and combined tensile/shear loads. It was observed that interphase strength played a significant role in tensile strength, while the significance is little for shear strength. Also, the sensitiveness under shear loading was higher for lower interphase strength, while it was quite opposite under tensile loading. It can be noted that the failure initiation and propagation also depend on the type of loading along with the constituent properties and geometrical parameters. For instance, the failure mechanism of Al/SiC PRMMC was studied for static and dynamic loading conditions by Linul et al. [85] and fatigue and creep loading conditions by Rutecka et al. [86], respectively. Two predominant failure mechanisms observed under static and dynamic loading conditions were: face failure and core shear failure. An increase in vol% of the SiC content improved the fatigue and creep resistance.

Figure 9

Tensile stress–strain curves with different contact stresses [83] (with permission)

3D models

Representation of microstructures in 2D provides some information on the microstructure morphology, but it is not fully representative of the composite material. Although 2D modeling is used to obtain tensile deformation and fracture, the analysis is carried out in either plane stress (σz = 0) or plane strain (εz = 0). This simplifies the three-dimensional stress states of the actual composite. Also, 2D microstructure inherently models the particles as disks. Thus, 3D analysis is essential to evaluate the composite microstructure, microscopic and macroscopic mechanical deformation. Different 3D micromechanical models are unit-cell method, multi-cell method, serial sectioning method and statistical synthetic method. All these 3D micromechanical methods are discussed in detail in the following sections.

3D unit-cell method

One of the 3D methods to predict the mechanical behavior of the particulate reinforced metal matrix composites is unit-cell method. In this method, the reinforcements were approximated to a single regular shape such as unit cylinder, double cone, truncated cylinder, sphere and ellipsoid and placed at the center of matrix and are simulated by applying appropriate boundary conditions. It is important to note that the particles are distributed uniformly in the actual composites. Also, the particles embedded in matrix usually contain sharp corners; thus, spherical and ellipsoid particles are not a realistic choice for modeling and simulation. ANSYS and ABAQUS are the commonly used software programs for 3D unit-cell method.

Chawla et al. [87] presented various unit-cell methods and provided a comparative analysis of mechanical properties predicted by various unit-cell methods, analytical methods and experimental results of 20 vol% Al/SiC metal matrix composites. The stress strain curves predicted by unit-cell methods are shown in Fig. 10. The stress values in Fig. 10 are normalized by the yield strength of matrix for easy comparison. It is evident that particle shape has a significant impact on the effective mechanical behavior of the composite. It can be observed that the unit cylinder strengthens the composite than the other three shapes for a particular vol% of reinforcement. However, this does not indicate that particles with sharp corners necessarily have pronounced strengthening effect because double cone particles, which possess the sharpest corners, exhibited low strengthening effect. It can also be seen that double cone and unit cylinder particles resulted in the lowest and highest degrees of disturbance for the plastic flow in the matrix, respectively. In general, when the particle fraction is small, the unit-cell method provides relatively accurate results in the elastic region. But, the behavior of composite will be dominated by the boundary conditions at higher volume fractions. So, a careful investigation is required in interpreting the simulation result. Alavi et al. [88] investigated the role of spherical particles on the macroscopic and microscopic behavior of Al/SiC metal matrix composites in the absence of damage using a unit-cell approach. It was found that spherical particles do not estimate the mechanical properties accurately. Similarly, the influence of the reinforcing particle shape in Al/Al₂O₃ was studied by Romanova et al. [89] by varying the particle shape from spherical to strongly irregular for studying the fracture behavior of PRMMC. It was observed that the particle fracture occurred by two mechanisms: one by interface debonding and the other by particle cracking. In spherical particles, interface debonding dominated the particle cracking, while for strongly irregular-shaped particles, particle cracks dominated.

Figure 10

Tensile curves of 20 vol% Al/SiC composite predicted by unit-cell methods [87] (with permission)

Multi-cell model

Although unit-cell method is able to model the microstructure in 3D, it failed to predict the mechanical properties accurately. This is majorly because of uneven particle distribution in matrix. Also, the particle shape was simplified to rectangular, cylindrical, cubical, spherical, etc., which is not realistic. The simplification aids in computations but fails to capture particle size, shape and distribution. Also, the simulation methodology used in unit-cell approach can’t show the realistic deformation. This resulted in poor prediction of the overall mechanical behavior of metal matrix composites. Consequently, this demands for use of realistic microstructure-based models to analyze the elasto-plastic response. Therefore, an approach called multi-cell method was developed to generate the multiple reinforcement particles in the matrix with different shapes, sizes and volume fractions. The most used algorithms to generate multiple reinforcement particles are random sequential adsorption algorithm (RSA) and modified random sequential adsorption algorithm (MRSA). Also, a software called Digimat is developed for multi-cell modeling of particulate reinforced metal matrix composites [90, 91]. It uses the statistical information obtained from real microstructure. Not only particles, but also short fiber reinforced, long fiber reinforced and woven composites can be modeled in Digimat software. It uses a random sequential adsorption (RSA) algorithm for distribution of particles [92, 93]. Digimat, ANSYS and ABAQUS are the commonly used software programs for 3D multi-cell method.

An example of 3D RVE generated with randomly distributed icosahedron alumina particles in aluminum matrix using Digimat software and 3D RVE generated with spherical SiC inclusions in aluminum matrix using MSRA is shown in Figs. 11 and 12, respectively. An example of loading conditions applied for simulation is presented in Fig. 13. One end of the RVE is constrained in all directions, and other end is provided with certain displacement in Y-direction (Table 2).

Figure 11

3D RVE of 5 vol% Al₂O₃/Al composite with icosahedron particles using Digimat [95] (with permission)

Figure 12

3D RVE of 60 vol% SiC/Al composite with spherical particles generated with MSRA a RVE, b only SiC inclusions and c meshed RVE [94] (with permission)

Figure 13

Applied boundary conditions for the 3D RVE generated [96] (with permission)

Table 2 Few of the 3D RVE details generated using multi-cell method

Estimation of mechanical behavior

The shape of the reinforcement is one of the significant factors for determining the mechanical behavior accurately. The effect of reinforcement shape was studied by Chawla et al. [67] and Moumen et al. [100] with spherical and ellipsoid particles of 20 vol% Al2080/SiC and of 0.13 and 0.23 vol% Al/SiC, respectively, and also Galli et al. [99] with tetrahedral particles and Kari et al. [94] with spherical particles of 17 vol% Al2124/SiC. Ellipsoid inclusions found to provide better estimate of properties than spherical inclusions. Tetrahedral shape of particles resembles the ceramic powders often used as reinforcement. The model with tetrahedral particles predicted the Young’s modulus with 3% error. Therefore, particle shape approximation plays a major role in predicting the mechanical properties of PRMMC. The mechanical properties obtained by multi-cell method were compared with various analytical methods, and they are found to be in good agreement. The comparisons with various other numerical models are shown in “Comparisons of micromechanical results and experimental results” section.

Not only particle shape but also particle arrangement, particle aspect ratio and RVE size influence the mechanical behavior of PRMMC. For instance, Mishnaevsky et al. [101] studied the effect of particle arrangement and Zhang et al. [102] studied the effect of particle aspect ratio for Al/SiC composites. It was found that the flow stress and the strain hardening increased with change in particle arrangement such as gradient, clustered, random and regular arrangements [101]. The order was as follows: regular > clustered > random > gradient microstructure. Similar study by Mishnaevsky et al. [103] on clustering effect was performed by generating the automatic voxel-based 3D RVE with random and graded microstructures. It was reported that yield stresses of a graded composite decrease with the increase in clustering effect and the same is true for critical strain and damage growth. The study by Zhang et al. [102] reported that increasing the aspect ratio decreased the stress in matrix and increased in particles, when the load is applied in longitudinal direction. Also, it was reported that the stress concentration factor of the matrix increased and decreased during the elastic and plastic deformation stage, respectively [102]. SiC particles with aspect ratio of 2.5 yielded better results. A comparison between experimental and simulated stress–strain curves with aspect ratio of 2.5 is presented in Fig. 14. Another study by Ma et al. [104] on A356/Al₃Ti metal matrix composites reported that decreasing the Al₃Ti particles size improved the yield strength. Additionally, the damage evolution in A356 matrix with smaller Al₃Ti particles was more uniform and slower when compared to the larger Al₃Ti particles. The prediction of mechanical properties by RVE method depends on RVE size as well. Hence, it is crucial to consider RVE size during RVE design. For instance, Zhang et al. [105] developed 3D RVEs of different sizes to investigate the isotropic hardening function, Young’s modulus and Poisson’s ratio of 17 vol% Al/SiC particulate reinforced composites. It was found that the minimum RVE size depends on the plastic deformation and temperature. RVE with aspect ratio 20 was employed as the minimum RVE in the temperature region of 0–500 °C and the effective plastic strain region of [0, 40] × 10⁴. RVE based models found to predict the results more precisely than the unit-cell models and analytical models.

Figure 14

Simulated and experimental tensile stress–strain curves of 17 vol% Al2014/SiC composite [102] (with permission)

Particulate reinforced metal matrix composites fabricated by powder processing techniques develop inherent residual stress due to mismatch of matrix and reinforcement properties. The matrix will be under net tension, and the particles are under net compression due to the residual stresses. Therefore, RVEs must be simulated for thermal residual stresses generated during cooling from sintering to room temperature before studying mechanical deformation. For instance, the mechanical behavior of 5 and 10 vol% Al/Al₂O₃ and 4, 8 and 12 vol% Al/B₄C particulate reinforced composites fabricated by powder metallurgy technique was simulated by Sharma et al. [95, 98]. RVEs were generated initially for the internal residual stresses by applying temperature field followed by mechanical load to evaluate the mechanical behavior of composite. The stresses obtained at elastic and plastic regions are presented in Fig. 15. Due to thermal mismatch, high concentration of residual stresses was observed at the interface sites of B₄C and Al for Al/B₄C composites and similarly at the interface sites of Al₂O₃ and Al for Al/Al₂O₃ composites. This resulted in void growth and nucleation at the interface of matrix and reinforcement. The effects of voids were analyzed by modeling the void nucleation and growth by using Gurson Tvergaard Needleman model [90, 91]. The results state that the interphase strength of PRMMC will be reduced due to thermal mismatch of matrix and reinforcement. Therefore, it can be concluded that processing conditions also play a major role in the mechanical deformation along with volume fractions and properties of the reinforcement in determining the properties of PRMMC.

Figure 15

Stress distribution at 125 °C for a elastic zone and b plastic zone for 5 vol% Al/Al₂O₃ composite [95] (with permission)

The strength at the interface of the matrix and the reinforcement is finite. The composite may fail due to particle fracture, matrix failure or interfacial debonding. Therefore, it is necessary to consider interfacial strength as well to understand the fracture behavior of PRMMC. Segurado et al. [106] developed a 3D FE model with random and clustered spherical SiC particles to study the influence of interface decohesion on the mechanical behavior of 15 vol% Al/SiC composites. It was found that the fracture at interface was localized earlier between clustered particles and oriented along the loading axis. Also, the interfacial strength and damage mechanisms for 7 vol% Al7004/SiC composites were reported by Su et al. [107] and Zhang et al. [97] using interfacial behaviors such as cohesion, adhesion and friction interfaces. It was found that tensile fracture was initiated by particle fracture followed by interfacial debonding due to stress concentration and lower particle strength. An example of crack propagation and plastic strain distribution is presented in Fig. 16. It was observed that weaker interfaces accelerate the interface debonding and thereby decreases the composite strength and stiffness. The tensile stress–strain curves with different interfacial behaviors are shown in Fig. 17. The tensile stress–strain relations of Al/SiC composite with cohesive interface are in good relation with the experimental results than adhesive and frictional interface. Tables 3 and 4 show the comparison of mechanical properties predicted by cohesive interface of multi-cell method and experimental results. The simulation results are in good accordance with experiment results for cohesive interface. Therefore, cohesive interface can provide a better estimate of mechanical properties for PRMMC.

Figure 16

Crack propagation and plastic strain distribution of Al/SiC composite [97] (with permission)

Figure 17

Stress–strain curves Al7004/SiC composites with various interfacial behaviors a 14 vol% and b 7 vol% [107] (with permission)

Table 3 Mechanical properties of 7 vol% Al/SiC composite [97] (with permission)

Table 4 Mechanical properties of Al7004/SiC composites [107] (with permission)

The optimum interfacial strength of PRMMC can be analyzed RVE method, while the experimental characterization of mechanical behavior fails to explain the interface strength. For instance, Zhang et al. [96] developed an RVE based on 3D multi-cell method with interface phase to study the failure, damage and deformation behaviors of 17 vol% Al2009/SiC metal matrix composites. The interface phase of 3D RVE was designed with an average thickness of 50 nm with different interfacial strengths of 700, 600, 500 and 300 MPa for analyzing the optimum interfacial strength. The individual matrix phase, reinforcement phase and interphase phase of the RVE are shown in Fig. 18. The results indicated that the composite strength and the total elongation decreased at weaker interfaces because of early interface damage. The simulation results had a good agreement with experiment results at 600 MPa interface strength. Hence, the interface strength of 600 MPa was considered as optimum interface strength. The stress–strain curves with different interfacial strengths are presented in Fig. 19. Hence, the mechanical properties were predicted for 600 MPa interfacial strength and are presented in Table 5 along with experimental results. It is obvious that the interfacial strength has a significant effect on the mechanical properties of particulate reinforced composites. As discussed earlier, cohesive interface was found to provide better estimate of mechanical properties for PRMMC. Therefore, few authors used cohesive zone model to evaluate the interfacial strength at different conditions. Su et al. [107] evaluated the interfacial strength of extruded 7 vol% 7A04/SiC composites as 326 MPa, while the interfacial strength of solution heat treated was estimated as 400 MPa [108]. Guo et al. [109] estimated the shear interfacial strength of Al/4H–SiC pillars was about 133 MPa, which yields an interfacial strength of about 230 MPa. However, the fracture surface and the cohesive element boundary coincide in the cohesive zone model, which limits its application and accuracy.

Figure 18

Realistic microstructure-based RVE model of 17 vol% Al/SiC composite [96] (with permission)

Figure 19

Stress–strain curves with different interfacial strengths of 17 vol% Al2009/SiC composite [96] (with permission)

Table 5 Experimental and numerical results of 17 vol% Al2009/SiC composite [96] (with permission)

Serial sectioning method

In reality, the composite microstructure is highly complex. Apart from the volume fraction, reinforcement morphology, shape, size, distribution and spatial orientation are also the vital aspects of microstructure geometry, which affect the mechanical properties significantly. Although multi-cell method could able to incorporate most of the inhomogeneties, it failed to model realistic microstructure because it considers the regular shape and uniform size of particles although the matrix. But, in actual case, not all the particles have same shape, size and aspect ratio. Hence, multi-cell method failed to deploy the actual orientation, shape and actual size of particles in matrix. Hence, serial sectioning method was developed to generate 3D RVE from the set of 2D images of microstructure. Serial sectioning is a method that quantifies the 3D microstructures by using computational metallography techniques such as computational serial sectioning integrated with reconstruction. Modeling based on real microstructures is highly essential to co-relate the microstructure with the mechanical behavior of the composite. The serial sectioning technique starts with the acquisition of several 2D microstructures through the thickness of the composite followed by reconstruction of the microstructure in 3D using the 2D information. With the evolution of technology, the computational capabilities have greatly improved, resulted in more simplified, accurate and efficient serial sectioning technique. A schematic of serial sectioning procedure of particulate reinforced composites is represented in Fig. 20. The first step in serial sectioning is to identify the representative region of the microstructure. Fiducial marks with Vickers indentation were made to measure the loss in thickness of material during polishing. The amount of material thickness removed can be evaluated as the geometry of the indenter is known. Material removal thickness is evaluated at four different regions to maintain the uniformity by making four indentations. Cyclic polishing and imaging were performed to generate a series of 2D microstructure sections. The polishing plays a major role in controlling the material removal and for obtaining better surface finish for microstructural characterization. The microstructure is captured with an optical microscope after each polishing cycle. The images of microstructures are sent to image analysis software like ImageJ for segmenting into black and white regions. The segmented images are stacked one upon the other, and the particle morphology is reconstructed by using vectoral format software such as SURFDriver. The morphology of particles is slightly simplified during reconstruction to help in simulation. The simplifications do not change the actual morphology of the particles significantly. The real microstructure obtained through serial sectioning process was exported to CAD software followed by ABAQUS for meshing and analysis. ImageJ, SURFDriver, ANSYS and ABAQUS are the software programs being used for 3D serial sectioning methods.

Figure 20

Serial sectioning procedure [67] (with permission)

With the advancement of technology, new serial sectioning methods were developed for serial sectioning, imaging, modeling and 3D microstructure reconstruction. Slicing of specimen is automated, and microstructure image was captured using SEM instead of optical microscope. The process was fully automated in the new methods. Most popular recent developments for 3D microstructure quantification are: (1) serial block-face scanning electron microscopy (SBEM), (2) atomic force microscopy (AFM) and (3) focused ion beam (FIB). A brief description of newly developed serial sectioning techniques and their comparisons are provided below.

3D serial block-face scanning electron microscope (SBEM)

Denk et al. [110] developed the 3D Serial block-face scanning electron microscopy (SBEM). This method involves the generation of the microstructures of soft materials over hundreds of microns with an image resolution equivalent to SEM. This method is now applied in materials science for the characterization of composites if the material is ductile enough for a diamond knife to slice. Zankel et al. [111] and Trueman et al. [112] reconstructed a 3D microstructure of composites using this method. This method demands for an electron microscope that provides images of electrically non-conductive samples without any coating. The sample should be soft enough for slicing and simultaneously hard enough to avoid smearing. The sample size used is about 0.6 × 0.6 × 0.6 mm³. The evolution of 3D microstructure involves thin slicing of a specimen by a diamond knife and then imaging the block face of the sample. The imaging of the microstructure at required magnification is done by using backscattered electrons (BSE). The slice thickness depends on the preparation, material and the signal used for imaging. Cyclic cutting and imaging are fed with a motor up to 600 μm. The cut slices accumulate at the back of the knife as debris. The serial sectioned images are well aligned and hence eliminate sources of error. Therefore, SBEM is the most reliable serial sectioning method for soft materials.

3D atomic force microscopy

In 3D atomic force microscope, a diamond knife cuts the sample like in SBEM, but a scanning probe microscope is used for imaging the block face. The slice thickness can be varied between 10 and 2000 nm and can slice 10 sections per hour. Here, serial sectioned image alignment is an issue relative to SBEM. However, the misalignment of the serial sectioned images after each step is resolved by Efimov et al. [113] by using a post-processing software called ImagePro Plus. 3D AFM is now used for imaging composite materials from last few years.

3D focused ion beam

SEBM and AFM are usually applicable for ductile materials, which can be sliced by a diamond knife. For hard materials, 3D focused ion beam microscope can be the best choice. The combination of 3D-FIB and electron backscatter diffraction (3D-EBSD) was first commercially developed by Mulders et al. [114]. Currently, 3D-FIB methods are well-established techniques and helping research community in conveying new understanding about the texture, morphology, grain orientation and grain shape for a wide variety of materials such as ceramics, metals, alloys and composites [115, 116]. The region of interest is segregated before serial sectioning with an FIB. Generally, a layer of carbon/platinum with a thickness of 1–2 μm is deposited on the top of the region of interest. Schaffer et al. [117] reported that the platinum layer is very crucial for surface protection and for the prevention of the rounding of cross sections while milling. The imaging is done by placing the specimen at the eucentric point, the point where the ion beam and the electron beam converge in a conventional FIB system. Holzer et al. [118] reported the convergence of the ion beam and the electron beam at an angle of 52°. The ion beam removes the material slice by slice by milling periodically, and after each cut, the electron beam images the exposed surface with electrons.

Comparison of SBEM, 3DAFM and 3D FIB methods

Zankel et al. [119] in his review provided the comparison of SBEM, 3DAFM and 3D FIB. The summary of comparisons is presented in Table 6. The methods differ, in particular, in the sample volume of interest and the lateral resolution. The serial sectioning process for SBEM and 3D AFM is almost similar, i.e., cutting with a diamond knife. The possible slice thickness is determined by the serial sectioning performance. The recorded image alignment was much better in SBEM than AFM and FIB. The resolution of images recorded is dependent on the resolution of the microscope while the resolution in the perpendicular direction to the block face is dependent on minimum slice thickness.

Table 6 Comparison of SBEM, 3D-AFM and 3D-FIB [119] (with permission)

Estimation of mechanical behavior

The mechanical properties of PRMMC are better estimated by serial sectioning method as it considers the real particle size, shape, orientation in 3D. For instance, Chawla et al. [120] and Kenesei et al. [121] developed a 3D RVE from real microstructure through serial sectioning process of 20 vol% Al2080/SiC and Al6061/Al₂O₃ particulate reinforced composites, respectively, to evaluate the stress strain behavior and Young’s modulus. The results were converged for an RVE size of 243 μm³. The method predicted the experimental results with an error of about 4%. Also, a comparative analysis of the stress strain behavior and Young’s modulus for different numerical methods with experimental results is carried out and presented in “Comparisons of micromechanical results and experimental results” section. Similarly, Mignone et al. [122] and Jung et al. [123] reconstructed 3D RVE from serial sectioning data acquired from 3D FIB of bi-continuous tungsten–copper (W-Cu) composites and 10 and 20 vol% pure Al/SiC composites to evaluate the elastic properties such as Poisson’s ratio, yield strength and Young’s modulus of the composite. The 3D RVEs reconstructed using serial sectioning for 20 vol% pure Al/SiC composites are presented in Fig. 21. The elastic properties predicted by serial sectioning method were within 3.6% of the experimental results. The serial sectioning method was found to predict the results much more accurately than unit-cell methods such as unit cube or unit sphere and multi-cell method. The simulated results of equivalent von Mises stress and strain are presented in Fig. 22. Simulated stress–strain behavior and elastic modulus obtained from serial sectioning method were in good agreement with experimental results.

Figure 21

3D RVE of 10 vol% Al/SiC composite, a initially reconstructed, b simplified surface and c further simplified [123]

Figure 22

Simulated response of a equivalent strain and b equivalent von Mises stress [123]

The actual clustering and porosity can be easily considered in 3D RVE by serial sectioning process during vectorization of serial section layers. Hence, the realistic effect of clustering and porosity can be incorporated and studied by serial sectioning method. For example, Sreeranganathan et al. [124] developed a 3D RVE to study the influence of particle clustering and porosity on the mechanical properties of Al6061/SiC particulate reinforced composites. It was considered porosity as a separate phase, which resulted in three-phase segmentation. RVE of size 400 × 200 × 100 μm³ was used for uniaxial loading simulations. The longest dimension of RVE is along extrusion direction. It was reported that the particle clustering reduced the strain hardening of the composite and the porosity lowered the 0.2% offset yield strength significantly. Also, the interface behavior can be evaluated more accurately by this method. For instance, Williams et al. [125] modeled a 3D RVE with perfect interface and interfacial debonding with user-defined cohesive elements to study the tensile deformation, interfacial debonding and localized strains and stresses in matrix and reinforcement of 10, 20 and 30 vol% Al2080/SiC particulate reinforced composites. It was observed that the model response was the same with a perfect interface and cohesive zone elements prior to debonding. A shift in plastic zone was observed from the matrix to the interface after debonding. Also, a comparative study on multi-cell method and serial sectioning method with different interfacial behaviors was studied and is presented in Fig. 23. The influence of debonding is much more prominent in serial sectioning method than in multi-cell method. It was concluded that the serial sectioning method was more sensitive to interfacial debonding and exhibited higher degree of load transfer.

Figure 23

Comparison of stress–strain curves for multi-cell method and serial sectioning method of 20 vol% 2080Al/SiC composites [125] (with permission)

Similar to serial sectioning method, scanning electron microscopy images were utilized to generate the finite element model of PRMMC by image-based modeling. Large number of samples will be generated based on mesoscale scanning electron microscopy images using a stochastic reconstruction algorithm. By using image processing techniques, images will be transformed to finite element models. Finite element analysis is utilized to evaluate the effective mechanical properties and to establish the correlation between microstructure features to the macroscopic property [126]. For instance, the mechanical properties based on image modeling of composites were evaluated by Jung et al. [127] and Wang et al. [128]. However, the output responses obtained can be further utilized to predict the mechanical properties for unknown cases by deep neural networks. For example, Li et al. [126] adopted deep neural networks to predict the mechanical property by using the fundamental responses obtained from image-based modeling.

Statistical synthetic method

Statistical synthetic method is an advanced method of multi-cell method. Modeling and simulation using statistical synthetic method have a huge advantage over multi-cell and serial sectioning methods because it offers simple, efficient and quick means in synthesizing a 3D RVE either from a set of auto-generated statistics or from statistics of one’s own experimental results [129]. DREAM.3D software package is used currently to model the 3D RVE from the statistical data. The statistical information such as volume fraction, average particle size, shape and orientation is utilized for 3D RVE generation and simulation conditions such as strain rate, strain hardening exponent and heating rate for evaluating the mechanical behavior. The particle size is varied with the help of mean and standard deviation value of lognormal distribution function. The shape of particle can be approximated by choosing shape such as cube, cylinder, ellipsoid and super ellipsoid in the software DREAM.3D and the particle aspect ratio. A brief procedure for generating 3D RVE using statistical synthetic method is described below.

The first step for 3D RVE generation was statistical characterization, which builds a list of statistically measurable descriptors. Statistical parameters include average particle shape, size distribution, particle volume, number of neighbor particles and the size of contiguous neighbor particles. Particle shape was defined using sub-parameters such as particle aspect ratio and orientations of principal axes. Now, based on the statistical information, particle generator generates particles with specified size, shape and size distributions. Ellipsoid and super ellipsoid are commonly used particle shapes to describe the irregular shapes of reinforcement. Log-normal distribution is the commonly used distribution function for size distribution of particles in matrix phase. Now, the particle packer models the spatial particle arrangement and distribution using the assigned number and size of contiguous neighboring particles. Lastly, particle orientations are defined using distribution function such as orientation function, mis-orientation function and microtexture function. After defining all the statistics, the synthetic volume generation is initialized.

Resolution and dimensions in all directions were controlled while synthesizing statistical model. Dimension and resolution are the technical terminologies defined in DREAM.3D software. Resolution is the size of each element in every direction while dimension is the ratio of number of elements and the total volume in each direction. The 3D RVE size can be calculated by multiplying resolution and dimension in every direction, respectively. The volume fractions of the generated RVE can differ from targeted due to statistical variations. Hence, the volume factions of each phase should be re-calculated after generating the statistical synthetic model. The procedure is repeated till the required volume fractions achieved, and finally, synthesized 3D structures are exported to commercially available finite element software programs such as ABAQUS and ANSYS for meshing and micromechanical analysis. Statistical synthetic method can be considered as the most effective and efficient modeling method for a wide range of PRMMCs based on the cost, accuracy and flexibility [130]. Statistical synthetic method uses DREAM.3D for modeling 3D RVE and FEA software programs such as ABAQUS and ANSYS for simulation and analysis. It is important to note that DREAM.3D is open-source software.

Estimation of mechanical behavior

Park et al. [131] developed a 3D RVE based on statistical synthetics of 10 and 20 vol% SiC/Al particulate reinforced metal matrix composites using DREAM.3D software to evaluate the stress–strain relationship and mechanical properties. The particle size distribution in the RVE was based on the average SiC size. The average SiC particle sizes measured during serial sectioning were 97.5 μm and 98.3 μm for 10 and 20 vol% SiC, respectively. The size distributions were established using lognormal distribution for matrix and particles. Super ellipsoid shapes were considered for both Al matrix and SiC particles. The dimension was varied in between 20 and 80 by fixing the resolution to 8 for finding out the appropriate 3D RVE size and volume fractions of each phase. The targeted volume fractions were 10 and 20 vol% SiC and obtained were 10 and 19.94 vol%. SiC with standard deviations of 0.24% and 0.34%, respectively, and are shown in Fig. 24. 3D RVEs generated were imported to FEA software, ABAQUS for meshing, simulation and analysis. The RVE was meshed with 3D 8-node linear isoparametric element (C3D8), and displacement boundary conditions were applied to obtain stress–strain relationships. The stress–strain curves of 20 vol% Al/SiC composite were obtained for different dimensions and are shown in Fig. 25. It can be observed that the stress–strain curves were in good agreement for dimensions larger than 20 and highly deviating for dimensions 10 and 15. The stress–strain curves with dimensions 60 and 80 were almost similar. Thus, the optimal model dimension is set to 60 to reduce the computational time. It should be noted that all the simulations were performed by considering perfect interface, no fracture criteria on SiC particles and Al/SiC interphase during deformations. The equivalent stress and equivalent plastic strain distributions for 10 vol% Al/SiC matrix composite generated by serial sectioning method are shown in Fig. 26. High deformation and high stress can be observed at low SiC regions. This shows the importance of the homogenous distribution of SiC particles in the matrix during fabrication. Similarly, Cai et al. [132] developed a 3D RVE based on the statistical results of advanced micro-CT scanner. As a result, the practical orientation of particles, voids created during sample fabrication were captured by the μ-CT images and the same was incorporated in the simulation model. This is the greatest advantage of statistical synthetic model. The model was simplified by considering spherical shapes of reinforcements. The elastic modulus evaluated by statistical synthetic method was in great agreement with experimental results.

Figure 24

Statistical synthetic structure of a 10 vol% and b 20 vol% SiC/Al composite [131] (with permission)

Figure 25

Stress–strain curves for dimensions 10–80 [131] (with permission)

Figure 26

Local response of a plastic strain and b stress for 10 vol% Al/SiC composite [131] (with permission)

Comparisons of micromechanical results and experimental results

Comparison of analytical and experimental results

Analytical methods predict the properties of composite for simple shapes of the phases. Comparison of analytical results with experimental results for different volume fractions of Al2024/SiC metal matrix composite is shown in Fig. 27. Although analytical (H–S) and empirical (H–T) methods estimate the results, it fails to predict the experimentally observed, microstructure-dependent anisotropy in modulus. Elastic modulus predicted by various analytical methods of Al2024/SiC composite is shown in Table 7. From the results, the increasing order of accuracy of properties predicted by different methods is found as follows: Rule-of-mixtures method < Eshelby method < Hashin and Shtrikman method < Halpin–Tsai method < Mori–Tanaka method < self-consistent method. The rule-of-mixtures method does not consider the effect of particle shape and size, while the Eshelby method holds good only for ellipsoidal particle [133]. Hence, rule-of-mixtures method and Eshelby method have the lowest prediction accuracy.

Figure 27

Assessment of analytical and experimental results for different vol% of Al2024/SiC composites [67] (with permission)

Table 7 Elastic modulus of Al2024/SiC composites predicted by various analytical methods

The effective Young’s modulus of Al3.5Cu/SiC composite predicted by unit-cell method is represented in Fig. 28 and compared with analytical predictions. It can be found that the unit cylinder has superior stiffening effect than unit sphere. Both numerical curves were in between H–S bounds described by Eqs. 1.13–1.16. Also, Mura’s model described by Eqs. 1.22 and 1.23 has a good agreement with the numerical prediction of unit sphere at low volume fraction of reinforcement, but deviated significantly at larger volume fractions. It can also be found that the Budiansky self-consistent prediction method (Eqs. 1.24, 1.25) has a good agreement with the numerical prediction of unit sphere at low volume fraction less than about 0.35. Above this, Budiansky method predicted a stiffer response with the unit sphere than FEM. Although unit cylinders contain sharp corners, the predictions by unit cylinder method are higher than the experimental values. This can be due to particle clustering and development of particle fracture and residual stresses during thermomechanical processing of PRMMC. Figure 30 clearly specifies that a simple rule-of-mixtures method will not be valid in evaluating the overall modulus of particle reinforced metal matrix composites. The rule-of-mixtures method was based on the isostrain condition between reinforcement and matrix and hence can be validated only for continuous long fiber reinforcement with high aspect ratios.

Figure 28

Comparison of effective Young’s modulus among the unit-cell methods and analytical results of Al3.5Cu/SiC composite [87] (with permission)

Comparison of 3D micromechanical and experimental results

3D micromechanical methods predict the microstructure-dependent anisotropy in modulus accurately. A comparative analysis of the stress–strain curves for different 3D micromechanical methods with experimental results is shown in Fig. 29 [120]. The highest and lowest moduli were found for unit rectangular prism and unit sphere, respectively. This can be due to the highest degree of load transfer for unit rectangular prism than the unit sphere. The serial sectioning method showed the highest degree of strengthening because the inherent aspect ratio and actual alignment of the SiC particles were incorporated [120]. Therefore, the serial sectioning method predicts the experimental behavior more accurately. As seen, the rest of the models shown in Fig. 30 are all clustered together and predict the results lower than the experiment. It is more important to note that the localized plasticity that results from angular and sharp corners of SiC particles can only be revealed in the serial sectioning method. It is worthy to note that multi-cell methods consisting of spheres or ellipsoids do not provide accurate results like serial sectioning method. Young's modulus predicted by various 3D micromechanical methods and experiment results is shown in Table 8. It can be observed that the serial sectioning result was closest to the experiment, with Young's modulus of 108 GPa. While simplified geometries such as sphere or ellipsoid do not represent the shape of particles accurately, they failed to predict the strength of PRMMC accurately.

Figure 29

Comparisons of stress strain predictions from various 3D micromechanical methods of 20 vol% Al2080/SiC composite [67] (with permission)

Figure 30

True stress–strain curves by various 3D micromechanical methods and experiment results of a 10 vol% and b 20 vol% Pure Al/SiC [131] (with permission)

Table 8 Young's modulus predicted by various 3D micromechanical methods and experiment of 20 vol% Al2080/SiC composite [67] (with permission)

Figure 30 displays the stress–strain behavior predicted by various 3D micromechanical methods of 10 and 20 vol% Al/SiC composites. It can be found that the statistical synthetic method provides good agreement with experiments than the unit-cell models in the elastic region. Therefore, it can be stated that the statistical synthetic method estimates the mechanical behavior of PRMMCs accurately and efficiently than serial sectional method. The Young’s modulus estimated from each method is shown in Table 9. It can be observed that the unit-cell method overestimated the Young’s modulus while the statistical synthetic method predicted well for both 10 and 20 vol% SiC. Although the material properties and volume fraction in all of the methods were identical, the results were not same because each model deviate fundamentally in the particle shape and distribution. The results emphasized that statistical synthetic method and serial sectioning method can predict the mechanical response accurately than the other methods.

Table 9 Young’s modulus by various 3D micromechanical methods and experimentation [131] (with permission)

Conclusion

According to a study of National Research Council (2008), the Integrated Computational Materials Engineering (ICME) aims at linking the computational tools with material performance analysis for reducing the cost and time of new materials characterization. One of the key objectives of ICME is the simulation of structure–property relationships using computational intelligence. Keeping in view of demand for computational tools in materials characterization, an attempt was made to summarize various computational methods being used in composite characterization. Computational micromechanical methods present many advantages than analytical micromechanical methods in analyzing the mechanical behavior of metal matrix composites. The influences of the reinforcement shape, size, spatial orientation and interphase strength on the macroscale response of metal matrix composites can be studied with computational micromechanical methods while the analytical micromechanical methods simplify the inhomogeneities. Also, the microscale stress–strain regions and failure evolution during loading can be studied in detail with computational micromechanical methods.

Experimental investigation of mechanical properties of PRMMC does not provide insightful information about the effect of microstructural aspects such as particle size, particle orientation, particle shape, particle–matrix interfacial strength, porosity, thermal mismatch between particle and matrix, etc., on the mechanical properties. Therefore, the effect of microstructural aspects on the mechanical properties of MMC can only be studied by micromechanics. Among micromechanical methods, computational micromechanical methods are found to provide better estimate of mechanical properties than analytical micromechanical methods.

Among computational methods, 2D RVE method and unit-cell method underestimate the properties, whereas 3D RVE methods predict the results more accurately. However, 3D RVEs demand for advanced computational facilities and also increase the time of calculations significantly. Multi-cell model, serial sectioning model and statistical synthetic model capture most of the inhomogeneities well. Hence, these models provide better estimation of mechanical behavior. Among these models, the serial sectioning model predicts the experimental behavior quite well but highly expensive. Statistical synthetic model is the modified form of multi-cell model. The user will have more control in modeling the 3D RVE from the statistical information of constituents in statistical synthetic method than in multi-cell method. Therefore, more realistic microstructures can be generated using statistical synthetic method. Hence, statistical synthetic method predicts the results more accurately than multi-cell method. The decreasing order for best predicted results is serial sectioning model, statistical synthetic model, multi-cell model, unit-cell model and analytical methods. It was found that there was no much deviation in results between serial sectioning method and statistical synthetic method, but the earlier one is very expensive. Hence, it is concluded that statistical synthetic model can be a reliable, accurate and economical micromechanical method for predicting the mechanical behavior of particulate reinforced metal matrix composites.

Scope for future work

Most of the computational micromechanics reported in literature are based on SiC reinforced aluminum matrix composites. Very little work was being carried out on other particles and other matrixes. Also, statistical synthetic model is not reported much in the literature as it is developed very recently. Dream.3D is the software being developed for statistical synthetic modeling. So, a detailed study on statistical synthetic modeling of particulate reinforced metal matrix composites other than Al/SiC composites is essential.