Frequency Analysis of Microbeam with Axial Pretension Using MSGT

Abstract

This paper presents the variation in natural frequencies of Euler-Bernoulli microbeams when subjected to axial pretension. The influence of size effects has been analysed using modified strain gradient theory (MSGT). The governing equation of motion has been derived using extended Hamilton’s principle and variational calculus. The sixth order non-local governing differential equation is solved by analytical procedure and numerical differential quadrature method (DQM). The three end conditions of beams are considered: cantilever, simply supported, and clamped-clamped beams. It is found that MSGT accurately models the size effects compared to other theories. As the axial pretension increases from 0.0001 to 1 N, the natural frequency values for the beam with different boundary conditions increase. Subsequently, surface elasticity effects have been analysed for a silicon and aluminium-based nanobeams with the pretension of 0.0001 N for all boundary conditions. From the results of surface elasticity modeling, it has been concluded that the natural frequencies of the nanobeam get influenced either positive or negative based on the value of surface elastic modulus. The difference in natural frequency values with and without surface elasticity effects are approximately 5 and $2\%$ for Si and Al nanobeams respectively. The methodology presented in this work can further be validated for nanoscale devices in which the higher-order strain gradient and surface elasticity effects subjected to pretension dominate.

1 Introduction

Microstructures like beams, bars and membranes are used in micro-electro-mechanical systems (MEMS). Generally, MEMS-based sensors or actuators consist of a microbeam as the sensing element [1]. Due to rapid advancements in nanotechnology and fabrication methods, MEMS devices have various applications in the engineering, medical, and navigation sectors [2]. As many researchers have reported in their work [3,4,5,6], microbeams are designed for some basic requirements like natural frequencies of the beams and deflection. In the past, researchers [7,8,9] have studied the mechanical behaviour of microbeams within the context of classical continuum-based theories. These classical continuum-based theories are just an approximation due to the absence of material length scale parameters to capture the size effect phenomenon, which will influence the performance of the microbeam at the microlevel. Initially, [10,11,12,13,14,15] have conducted experiments to understand the influence of size effects on the mechanical behaviour of the structures at a microlevel .

Hence, size-dependent higher-order continuum-based theories have been developed to deal with the failure of the classical elasticity theory at small scales. These higher-order continuum-based theories can capture the effects of strain gradient (size effects) through material length scale parameters absent in classical continuum mechanics. Recently, Lam et al. [14] have proposed a modified strain gradient theory (MSGT), in which higher-order stresses and moments of couples are considered along with equilibrium equations. MSGT can be used effectively to predict the static and dynamic responses of microbeams. According to MSGT, the total strain energy density function contains the symmetric strain, dilatation, deviatoric stretch, and rotation gradient tensors. As a result, MSGT has three material length scale parameters to capture dilatation , deviatoric and rotation gradients of isotropic linear elastic materials, respectively and two classical elastic constants(Lame’s constants).

Due to its superior characteristics of handling systems at the microlevel, MSGT has received more attention in recent times. Based on MSGT, researchers have done many developments in MEMS. Lu et al. [16] have used nonlocal elasticity theory [17] to investigate the dynamic behaviour of axially prestressed microbeams. Kong et al. [18] have formulated an analytical solution for static and dynamic response of epoxy-based Euler-Bernoulli cantilever beam using MSGT. Results have shown that MSGT predicts the higher natural frequency of microbeam when compared to other theories like classical theory and modified couple stress theory (MCST). Wang et al. [19] have found an analytical solution for static bending and free vibrations of the Timoshenko beam model for simply supported end conditions using MSGT. Akgöz and Civalek [20] have performed buckling analysis of axially loaded epoxy-based, simply-supported and cantilever Euler-Bernoulli microbeams with the help of MSGT. Vatankhah and Kahrobaiyan [21] have investigated vibrational characteristics of the clamped-clamped resonator with attached mass, subjected to axial load, based on MSGT, and results are compared with MCST and classical elasticity theory(CT). Sajal et al. [1] have performed free vibration analysis of epoxy microbeams based on MSGT using the differential quadrature method. Zhao et al. [22] have used MSGT to develop a new Euler-Bernoulli beam model.

In addition to strain gradients, surface elasticity has other effects that affect the dynamic response of the micro/nanostructure. Surface elasticity arises due to forming a surface layer with different mechanical properties than a bulk medium [23]. There are mainly two reasons for the formation surface layer one is surface relaxation [24], and the other is surface reconstruction [25]. Both surface residual stresses and surface elasticity effects are considered to model the surface-related effects in the nano/microstructures [26, 27]. Earlier, Lagowski et al. [28] have performed frequency analysis on the microcantilever beam and found that the surface stress is the primary cause for the shift in the natural frequency of the structure. Later Gurtin et al. [29] stated that the surface elasticity is the only phenomenon that causes the shift in the natural frequencies of the structure and is independent of surface stresses. Zhang et al. [30] have measured the shift in resonant frequencies of micro/nanostructure to study surface related effects. Gangele and Pandey [31] have performed frequency analysis using a multi-scale finite element approach on silicon nanocomposites with surface effects. Recently, Fu et al. [32] have used SGT and surface elasticity theory to perform dynamic analysis on the Euler-Bernoullis nanobeam with size and surface-related effects.

Hence, from the above literature, it is found that there is a need to understand the dynamic response of microbeams with axial pretension by considering size and surface elasticity effects. This work presents a dynamic analysis of microbeams with pretension based on MSGT for different end conditions. The sixth order non-local governing differential equation is solved through the analytical procedure and then numerically using the differential quadrature method (DQM). Numerical examples are presented for the three(cantilevered, simply supported, and calmped-clamped) boundary conditions. We show that these two solution methods converge well. The method we developed here can model micro and nanostructures’ size and surface elasticity effects.

This paper first presents the general formulation of MSGT and surface-related effects, using Hamilton’s principle for the Euler-Bernoulli beam with cantilever, clamped-clamped and simply-supported boundary conditions at varying pretension. Subsequently, we described the analytical and DQM based numerical method and discussed their performance at different pretension.

2 Mathematical Formulation

This section described the modified strain gradient theory (MSGT) and applied it to obtain the governing differential equation.

2.1 Modified Strain Gradient Theory

According to the modified strain gradient theory (MSGT), in addition to the classical strain tensor ($\epsilon _{ij}$),deviatoric stretch gradient tensor ($\tilde{\eta }_{ijk}$), dilatation tensor ($\gamma _i$), and symmetric rotation gradient tensor ($\chi ^S_{ij}$) are introduced. Therefore MSGT uses three-length scale parameters to consider the size effects.

For a linear isotropic elastic material with V as volume element and occupying region $\varOmega$, the total strain energy is defined as [14]

$$\begin{aligned} U_t = \int \limits _{\varOmega }\left( \sigma _{ij}\epsilon _{ij} + p_i\gamma _i + \tilde{\tau }_{ijk}\tilde{\eta }_{ijk}+m_{ij}^S\chi ^S_{ij}\right) dV, \end{aligned}$$

(1)

where, $\epsilon _{ij}$, $\gamma _i$, $\chi ^S_{ij}$ and $\tilde{\eta }_{ijk}$ are defined as

$$\begin{aligned} \epsilon _{ij} = \frac{1}{2}\left( \partial _iu_j+\partial _ju_i\right) , \end{aligned}$$

(2)

$$\begin{aligned} \gamma _i = \partial _i\epsilon _{nn}, \end{aligned}$$

(3)

$$\begin{aligned} \chi _{ij}^S = \frac{1}{2}\left( e_{ipq}\partial _p\epsilon _{qj} + e_{jpq}\partial _p\epsilon _{qi} \right) , \end{aligned}$$

(4)

$$\begin{aligned} \tilde{\eta }_{ijk}=\frac{1}{3}\left( \partial _i\epsilon _{jk}+\partial _j\epsilon _{ki}+\partial _k\epsilon _{ij}\right) -\frac{1}{15}\delta _{ij}\left( \partial _k\epsilon _{mm}+2\partial _m\epsilon _{mk}\right) \nonumber \\ - \frac{1}{15}\left[ \delta _{jk}\left( \partial _i\epsilon _{mm}+2\partial _m\epsilon _{mi}\right) + \delta _{ki}\left( \partial _j\epsilon _{mm}+2\partial _m\epsilon _{mj}\right) \right] , \end{aligned}$$

(5)

where $\partial _i$ is the differential operator, $u_j$, $\epsilon _{nn}$, $\delta _{ij}$ and $e_{ijk}$ are the displacement vector, dilation strain tensor, Kronecket delta, and permutation tensor respectively. Here, subscripts (i, j, k) are summed over 1–3.

The work-conjugates of the strain gradients $\gamma _i$,$\chi _{ij}^S$ , and $\tilde{\eta }_{ijk}$ are defined by the higher-order stresses $p_i$, $m_{ij}^S$, and $\tilde{\tau }_{ijk}$ respectively. Therefore the stress measures are related to the strains given by the following relationships

$$\begin{aligned} \sigma _{ij} = k\delta _{ij}\epsilon _{nn} + 2\mu \epsilon _{ij}', \end{aligned}$$

(6)

$$\begin{aligned} p_i = 2\mu l_0^2\gamma _i, \end{aligned}$$

(7)

$$\begin{aligned} \tilde{\tau }_{ijk} = 2\mu l_1^2\tilde{\eta }_{ijk}, \end{aligned}$$

(8)

$$\begin{aligned} m_{ij}^S = 2\mu l_2^2\chi _{ij}^S, \end{aligned}$$

(9)

where, k represents the bulk modulus and $\mu$ is shear modulus of the material. $\epsilon _{ij}'$ is given by $\epsilon _{ij} - \frac{1}{3}\epsilon _{nn}\delta _{ij}$ and known as deviatoric strain, $\epsilon _{ij}$ is the strain tensor. $l_0$, $l_1$ and $l_2$ are the three material length scale parameters related to the material’s dilation, deviatoric and symmetric gradients, respectively.

2.2 Surface Elasticity

When the characteristic dimensions of the beam are in the order of micro or nanometer range, surface related effects often play an essential role in the design of MEMS/NEMS structures; this is due to an increase in the ratio between the surface area to volume of the structure. Due to surface effects, the layer on the structure’s bulk will have different mechanical properties than the bulk medium. Classical theory is just an approximation where the surface effects are not considered to perform frequency analysis. Hence classical theory would require proper corrections which can capture the small scale and surface-related effects. The drawback of the classical elasticity theory can be overcome by adequately incorporating the surface elasticity effects to determine its impact on the mechanical properties of micro/nanostructures.

From the basic assumption involved in the design of micro/nanostructure is that “Structure = Bulk + Surface” [23], the effective elastic modulus of micro/nanobeam as [31, 33]

$$\begin{aligned} E^*=E\left[ 1+6 \frac{h_0}{h}+2\frac{h_0}{b}\right] , \end{aligned}$$

(10)

here, $h_0=\frac{C_s}{E}$ is a material length parameter to capture the surface related effects at micro/nano level and $C_s$ is the surface elastic modulus (${\text {Nm}}^{-1}$). Equation (10) will be used in governing equation of motion to perform frequency analysis of micro/nanobeam by considering the surface elasticity effects.

2.3 Governing Equation of Motion

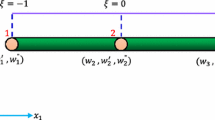
Let us consider a prismatic beam as shown in Fig. 1 of length L, having cross sectional area A, and the axial load $N_0$. The area of cross-section is specified by the x (longitudinal) and y (lateral) axes. The load q is applied in the transverse direction, i.e., the z axis.

Let the displacements in the x, y, and z directions are represented by u, v, w respectively. The displacement field for the beam from the Euler-Bernoulli beam model is defined as

$$\begin{aligned} u = -z\frac{\partial w(x)}{\partial x}, v = 0, w = w(x). \end{aligned}$$

(11)

The non-local governing differential equation of motion and the corresponding boundary conditions are derived using extended Hamilton’s and variational principle.

$$\begin{aligned} \delta \left[ \int \limits _{t_1}^{t_2}\left( T-U_t+W_{ext}\right) dt\right] =0, \end{aligned}$$

(12)

here, $\delta$ indicates the first variation, T, $U_t$ and $W_{ext}$ are kinetic energy, strain energy and work done by the external forces respectively.

The governing differential equation the motion (GDE) of the microbeam by MSGT is found as

$$\begin{aligned} P\frac{\partial ^4 w}{\partial x^4} - Q\frac{\partial ^6 w}{\partial x^6} - N_0\frac{\partial ^2 w}{\partial x^2} + \rho A \frac{\partial ^2 w}{\partial t^2} + q(x) = 0, \end{aligned}$$

(13)

and the corresponding boundary conditions are

$$\begin{aligned} \left[ \left( V - Pw^{(3)} + Qw^{(5)} - N_0 w' \right) \delta w\right] _0^L = 0, \end{aligned}$$

(14)

$$\begin{aligned} \left[ \left( M + Pw^{(2)} - Qw^{(4)} \right) \delta w'\right] _0^L = 0, \end{aligned}$$

(15)

$$\begin{aligned} \left[ \left( M^h + Qw^{(3)}\right) \delta w''\right] _0^L = 0. \end{aligned}$$

(16)

Fig. 1.

Beam configuration when subjected to flexural and axial loads

Here, P and Q are,

$$\begin{aligned} P = EI+2\mu Al_0^2+\frac{8}{15}\mu Al_1^2 + \mu Al_2^2, Q = I\left( 2\mu l_0^2+\frac{4}{5}\mu l_1^2\right) . \end{aligned}$$

(17)

When the two material length scale parameters, $l_0 = l_1 = 0$, the sixth order non-local GDE (Eq. 13) is reduces to MCST. Hence, the equation of motion based on MCST is obtained as

$$\begin{aligned} \left( EI + \mu A l_2^2\right) \frac{\partial ^4 w}{\partial x^4} - N_0\frac{\partial ^2 w}{\partial x^2} + \rho A \frac{\partial ^2 w}{\partial t^2} + q = 0, \end{aligned}$$

(18)

and the boundary conditions are

$$\begin{aligned} \left[ \left( V - \left( EI + \mu A l_2^2\right) w^{(3)} - N_0 w' \right) \delta w\right] _0^L = 0, \end{aligned}$$

(19)

$$\begin{aligned} \left[ \left( M + \left( EI + \mu A l_2^2\right) w^{(2)}\right) \delta w'\right] _0^L = 0. \end{aligned}$$

(20)

If all the three material length scale parameters are assumed to zero, then the GDE (Eq. 13) is reduced to classical elasticity theory.

3 Solution Procedure

This section will discuss the analytical procedure and implementation of the DQM numerical method to solve the governing differential equation.

3.1 Analytical Solution

Now, we discuss the solution of the GDE (Eq. 13). The transverse load ($q(x)=0$) is assumed to zero. Hence, the governing differential equation becomes

$$\begin{aligned} P\frac{\partial ^4 w}{\partial x^4} - Q\frac{\partial ^6 w}{\partial x^6} - N_0\frac{\partial ^2 w}{\partial x^2} + m\frac{\partial ^2 w}{\partial t^2} = 0, \end{aligned}$$

(21)

where, $m = \rho A$.

Let us consider the solution to the above equation as

$$\begin{aligned} w(x,t) = \tilde{w}(x)e^{i\omega t}. \end{aligned}$$

(22)

Substituting Eq. (22) into the Eq. (21), we get

$$\begin{aligned} P\tilde{w}^{(4)}(x)-Q\tilde{w}^{(6)}(x) - N_0\tilde{w}^{(2)}(x) - m\omega ^2\tilde{w} = 0. \end{aligned}$$

(23)

Equation (23) has the solution of the form

$$\begin{aligned} \tilde{w}(x) = \sum _{i=1}^{6}C_ie^{\lambda _ix}. \end{aligned}$$

(24)

The exponents, $\lambda _i (i = 1,2,\ldots ,6)$ are complex in nature and $C_i$ are the constants of integration and found by using the boundary conditions.

$$\begin{aligned} P\lambda ^4 - Q\lambda ^6 - N_0\lambda ^2 - m\omega ^2 = 0, \end{aligned}$$

(25)

The auxiliary equation (25) has six roots ($\lambda _{i}$) which are complex in nature and can be found as,

let $\alpha ' = -36N_0PQ -108m\omega ^2Q^2 + 8P^3$ and

$$ \alpha _1 = \left( \alpha ' +12\sqrt{3} \sqrt{4N_0^3Q - N_0^2P^2 + 18N_0PQm\omega ^2 + 27m^2\omega ^4Q^2-4m\omega ^2P^3}K \right) ^\frac{1}{3} ,$$

$$\begin{aligned} \lambda _1 = \frac{-1}{\sqrt{6Q\alpha _1}}\left( \alpha _1^2 - 12N_0Q + 4P^2 + 2P\alpha _1\right) ^\frac{1}{2} , \end{aligned}$$

$$\begin{aligned} \lambda _2 = \frac{1}{\sqrt{6Q\alpha _1}}\left( \alpha _1^2 - 12N_0Q + 4P^2 +2P\alpha _1\right) ^\frac{1}{2} , \end{aligned}$$

$$\begin{aligned} \lambda _3 = \frac{-1}{2\sqrt{3Q\alpha _1}}\left( -\alpha _1^2 + 12N_0Q - 4P^2 + 4P\alpha _1 - I\sqrt{3}\alpha _1^2 - 12I\sqrt{3}N_0Q + 4I\sqrt{3}P^2\right) ^\frac{1}{2} , \end{aligned}$$

$$\begin{aligned} \lambda _4 = \frac{1}{2\sqrt{3Q\alpha _1}}\left( -\alpha _1^2 + 12N_0Q - 4P^2 + 4P\alpha _1 - I\sqrt{3}\alpha _1^2 - 12I\sqrt{3}N_0Q + 4I\sqrt{3}P^2\right) ^\frac{1}{2} , \end{aligned}$$

$$\begin{aligned} \lambda _5 = \frac{-1}{2\sqrt{3Q\alpha _1}}\left( -\alpha _1^2 + 12N_0Q - 4P^2 + 4P\alpha _1 + I\sqrt{3}\alpha _1^2 + 12I\sqrt{3}N_0Q - 4I\sqrt{3}P^2\right) ^\frac{1}{2} , \end{aligned}$$

$$\begin{aligned} \lambda _6 = \frac{1}{2\sqrt{3Q\alpha _1}}\left( -\alpha _1^2 + 12N_0Q - 4P^2 + 4P\alpha _1 + I\sqrt{3}\alpha _1^2 + 12I\sqrt{3}N_0Q - 4I\sqrt{3}P^2\right) ^\frac{1}{2} . \end{aligned}$$

Here, I represents the complex nature of the roots.

Now, we discuss the application of the above described analytical procedure to find the natural frequencies of the microbeam for different boundary conditions.

Simply Supported Beam Let us consider the case of simply supported beam with length L, the classical boundary conditions in terms of displacement and moments are

$$\begin{aligned} \tilde{w}(0) = \tilde{w}(L) = 0, \end{aligned}$$

(26)

$$\begin{aligned} M(0) = M(L) = 0, \end{aligned}$$

(27)

and the non-classical boundary conditions are

$$\begin{aligned} \tilde{w}^{(4)}(0) = \tilde{w}^{(4)}(L) = 0. \end{aligned}$$

(28)

By substituting the Eq. (24) into the above equations, we get the matrix form of the equation as

$$\begin{aligned}{}[B(\omega )]\{C\}=\{0\}. \end{aligned}$$

(29)

In the Eq. (29), $\{C\} = \{C_i\}^T,i=1,2,\ldots ,6$ and the matrix $[B(\omega )]$ is found as

$$\begin{aligned} B_{1i} = 1, B_{2i} = e^{\lambda _iL}, B_{3i} = \lambda _i^2, B_{4i} = \lambda _i^2e^{\lambda _iL} \nonumber \\ B_{5i} = \lambda _i^4,B_{6i} = \lambda _i^4e^{\lambda _iL}, \end{aligned}$$

(30)

where $\lambda _i = \lambda _i(\omega )$ are the six roots of the Eq. (31) and $i=1,2,\ldots ,6$.

In order to get the non-zero trivial solution of the Eq. (29), the following condition has to be satisfied,

$$\begin{aligned} {\textbf {det}}[B(\omega )]=0. \end{aligned}$$

(31)

The above Eq. (31) is called the "frequency equation". The analytical solution of the above system gives all the microbeam natural frequencies that can be found using a complex arithmetic procedure [1].

Clamped-Clamped Beam Let us consider a clamped-clamped beam with length L, having fixed at both the ends, the classical boundary conditions in terms of displacement and slope are

$$\begin{aligned} \tilde{w}(0) = \tilde{w}(L) = 0, \end{aligned}$$

(32)

$$\begin{aligned} \tilde{w}'(0) = \tilde{w}'(L) = 0, \end{aligned}$$

(33)

and the non-classic boundary conditions are

$$\begin{aligned} \tilde{w}^{(4)}(0) = \tilde{w}^{(4)}(L) = 0. \end{aligned}$$

(34)

By substituting the Eq. (24) into the above equations, we get the matrix form of the equation as

$$\begin{aligned}{}[B(\omega )]\{C\}=\{0\} . \end{aligned}$$

(35)

In the Eq. (35), $\{C\} = \{C_i\}^T,i=1,2,\ldots ,6$ and the matrix $[B(\omega )]$ is found as

$$\begin{aligned} B_{1i} = 1, B_{2i} = e^{\lambda _iL}, B_{3i} = \lambda _i, B_{4i} = \lambda _ie^{\lambda _iL} \nonumber \\ B_{5i} = \lambda _i^4,B_{6i} = \lambda _i^4e^{\lambda _iL}. \end{aligned}$$

(36)

By following the procedure mentioned above, we can find the natural frequencies of the clamped-clamped beam with axial pretension.

Cantilever Beam Consider a cantilever microbeam with length L, one end is clamped and other end is free to move, the classical boundary conditions are

$$\begin{aligned} \tilde{w}(0) = \tilde{w}'(0) = 0, \end{aligned}$$

(37)

$$\begin{aligned} Q\tilde{w}^{(5)}(L)-P\tilde{w}^{(3)}(L) + N_0\tilde{w}'(L) = 0, P\tilde{w}''(L) - Q \tilde{w}^{(4)}(L) = 0, \end{aligned}$$

(38)

and the non-classical boundary conditions are

$$\begin{aligned} \tilde{w}''(0) = \tilde{w}^{(3)}(0) = 0. \end{aligned}$$

(39)

By substituting the Eq. (24) into the above equations, we get the matrix form of the equation as

$$\begin{aligned}{}[B(\omega )]\{C\}=\{0\}. \end{aligned}$$

(40)

In the Eq. (40), $\{C\} = \{C_i\}^T,i=1,2,\ldots ,6$ and the matrix $[B(\omega )]$ is found as

$$\begin{aligned} B_{1i} = 1, B_{2i} = {\lambda _i}, B_{3i} = \lambda _i^2, B_{4i} = \lambda _i^3e^{\lambda _iL} \nonumber \\ B_{5i} = \left( \lambda _i^5Q-\lambda _i^3P + N_0\lambda _i\right) e^{\lambda _iL}, B_{6i} = \left( \lambda _i^2P-\lambda _i^4Q\right) e^{\lambda _iL}. \end{aligned}$$

(41)

Following the procedure mentioned earlier, we can find the natural frequencies of the cantilevered microbeam subjected to axial pretension.

Now, we discuss the theoretical framework and implementation of the differential quadrature method (DQM) to solve the sixth order governing differential equation of motion.

3.2 Differential Quadrature Method (DQM)

The differential quadrature method(DQM) was proposed by Bellman et al. [34]. The DQM is a numerical method that approximates a function’s derivative at a point by taking the sum of weighted functional values at other grid points in the discretized domain. The first derivative of the function f(x) is expressed as [35]

$$\begin{aligned} f_x(x_i)=\frac{df}{dx}|_{x_i} = \sum _{j=1}^{N}a_{ij}\cdot f(x_j), \end{aligned}$$

(42)

where $f(x_j)$ is the functional value at the jth sampling point, $a_{ij}$ are the weighting coefficients and $N_s$ is the number of grid points in the domain. It reduces the differential equations into a set of algebraic equations.

The Chebyshev-Gauss-Lobatto distribution will discretise the domain into $N_s$ sampling points.

$$\begin{aligned} X_i = \frac{1}{2}\left[ 1-cos\left( \frac{i-1}{N_s-1}\pi \right) \right] , \end{aligned}$$

(43)

The weighting coefficients are defined as

$$\begin{aligned} a_{ii}^{(1)} = - \sum _{j=1,j\ne i}^{N_s}a_{ij}^{(1)}, i=j, \end{aligned}$$

(44)

$$\begin{aligned} a_{ij}^{(1)} = \frac{L^{(1)}(x_i)}{(x_i - x_j)L^{(1)}(x_j)}, i\ne j, \end{aligned}$$

(45)

here, $L^{(1)}(x_i)$ is the Lagrange interpolating polynomials’ first derivative, and it is written as

$$\begin{aligned} L^{(1)}(x_i) = \prod _{k=1, k \ne i}^{N_s}\left( x_i - x_k\right) , \end{aligned}$$

(46)

The higher order weighted coefficient matrices can be obtained using

$$\begin{aligned} a_{ii}^{(n)} = - \sum _{j=1,j\ne i}^{N_s}a_{ij}^{(n)}, i=j, n = 2,3,\ldots ,N_s-1. \end{aligned}$$

(47)

$$\begin{aligned} a_{ij}^{(n)}=n\left( a_{ij}^{(n-1)}a_{ij}^{(1)}-\frac{a_{ij}^{(n-1)}}{x_i - x_j}\right) , i\ne j, n = 2,3,\ldots ,N_s-1, \end{aligned}$$

(48)

here, note that the subscripts i, j are repeated indices from 1 to $N_s$.

Hence, from the DQM, the differential equation of motion Eq. (13), can be written as [41]

$$\begin{aligned} P \sum _{n=1}^{N_s}a_{mn}^{(4)}\tilde{w}_n-Q\sum _{n=1}^{N_s}a_{mn}^{(6)}\tilde{w}_n - N_0\sum _{n=1}^{N_s}a_{mn}^{(2)}\tilde{w}_n -\rho A\omega ^2\tilde{w}_n =0,m=1,2,\ldots ,N_s. \end{aligned}$$

(49)

Various approaches are proposed to apply the boundary conditions for solving the Eq. (49). In DQM method, the vibrational problems are solved with the SBCGE (Substitution of Boundary Conditions into Governing Equations) technique [36] and $\delta$-technique [37], used for clamped-clamped end simply-supported and conditions. The complete details of DQM, implementation of boundary conditions, and solution method are available in the literature [1].

4 Results and Discussion

This section discusses the implementation of MSGT for the different sets of beams and compares both analytical and numerical DQM results. For the frequency analysis, we considered epoxy-based microbeam with strain gradient effects.

4.1 Strain Gradient Effects

Now we discuss the influence of the strain gradient effects on the microbeams at varying axial pretension. To study the effect of pretension, the following properties are considered for the numerical purpose, the beam properties are taken as that of epoxy [14], and the material properties are, Young’s Modulus $(E) = 1.44$ GPa, Poisson’s ratio $(\nu ) = 0.38$ and density $(\rho )= 1000 {\text {kg}}/{\text {m}}^3$ [18] and corresponding geometrical information has provided in Table 1. From MSGT material length scales for epoxy micro beam are considered as $l_0 = l_1 = l_2 = l = 17.6\times 10^{-6}\, \upmu$m.

Table 1. Set of Epoxy microbeams with different geometries

Table 2 shows the three fundamental modal frequencies of the simply-supported (SS) microbeam with a thickness of $20\, \upmu$m using the analytical method, differential quadrature method (DQM). The obtained results are compared with Zhao et al. [38] and matched with each other. Hence, MSGT can be effectively used to model and design micro/nanobeams with axial pretension.

Table 2. Comparison of the first three natural frequencies of simply supported beam ($h = 20 \,\upmu$m) with axial pretension

Simply-Supported Microbeam Figures 2, 3 and 4 show the first three natural frequencies for the simply supported (SS) microbeam, subjected to different axial loads ($N_0=1, 0.01, 0.0001\,{\text {N}}$). The analytical method and the numerical technique (DQM) give closer results in the case of the simply supported beam, with the error being less than $0.2\%$. One important observation found is that when the thickness of the microbeam is reduced from $200 \mu m$ to $10\mu m$, there was an appreciable difference in different theories, and strain gradients effects have prevailed. The natural frequencies found in the different theories are separated by reducing the axial force. With the reduction in the axial force, the natural frequencies decrease, and the size effects are turned up. The MSGT gives a higher value of natural frequencies than the MCST and classical theory because the formulation of MSGT considers the extra equilibrium equations, thereby accounting for the additional length scale effects. The present results show the same trend, with MSGT giving higher values of natural frequencies than MCST and classical theory. The effect of material length scale parameters reduces as the beam’s size increases, and all the theories’ results converge.

Clamped-Clamped Microbeam In Figs. 5, 6 and 7, the first three fundamental natural frequency values of the clamped-clamped beams with three different axial loads ($N_0=1, 0.01, 0.0001\,{\text {N}}$) are compared. The MSGT gives high values of natural frequencies, and the classical theory gives lower frequency values. In this case, both analytical and differential quadrature methods give closer values with an error less than $2\%$. The same trend is observed here; with the reduction in the axial force, the microbeam becomes softened. Hence, the natural frequencies decrease, and the size effects are turned up. The effect of material length scale parameters reduces as the beam’s size increases, and the results from all the theories converge. The clamped-clamped beam is slightly stiffer for the same geometrical configuration as the SS beam. Hence, the first three natural frequencies of the clamped-clamped beam are higher than the SS beam for the same axial pretension. Hence, the results show that thin beams need to be modeled accurately by considering strain gradients at low pretension values.

Cantilever Microbeam Figures 8, 9 and 10 show the first three natural frequencies of the cantilever beam obtained from MSGT, MCST and classical theories. The natural frequencies obtained from MSGT are higher than those obtained from MCST and classical theory. The analytical and DQ methods give closer results, with the error being less than $9.71\%$. In the case of the cantilever beam, the error is slightly higher than the SS beam and FF beams due to the application of boundary conditions in the differential quadrature method. As we are applying the boundary conditions at a distance of $\delta$ away from the boundaries, this gives a slight variation in natural frequencies [1]. The difference in natural frequency from different theories increases by reducing the axial pretension value. For lower values of pretension, MSGT is capable enough to capture size effects quite accurately compared to other theories. As the thickness of the beam increases, all the theories converge well, and size effects are reduced. A cantilever microbeam has lower natural frequencies than a simply supported and clamped-clamped beam for the same geometrical configuration.

Fig. 2.

Comparison of the first three natural frequencies ((a), (b) and (c)) of SSB with axial load $N_0 = 1\,{\text {N}}$

Fig. 3.

Comparison of the first three natural frequencies ((a), (b) and (c)) of SSB with axial load $N_0 = 0.01\,{\text {N}}$

Fig. 4.

Comparison of the first three natural frequencies ((a), (b) and (c)) of SSB with axial load $N_0 = 0.0001\,{\text {N}}$

Fig. 5.

Comparison of the first three natural frequencies ((a), (b) and (c)) of clamped-clamped beam with axial load $N_0 = 1\,{\text {N}}$

Fig. 6.

Comparison of the first three natural frequencies ((a), (b) and (c)) of clamped-clamped beam with axial load $N_0 = 0.01\,{\text {N}}$

Fig. 7.

Comparison of the first three natural frequencies ((a), (b) and (c)) of clamped-clamped beam with axial load $N_0 = 0.0001\,{\text {N}}$

Fig. 8.

Comparison of the first three natural frequencies ((a), (b) and (c)) of Cantilever beam with axial load $N_0 = 1\,{\text {N}}$

4.2 Strain Gradient with Surface Elasticity

This section discusses the effect of strain gradients and surface elasticity effects in Silicon and Aluminium-based nanobeams using MSGT theory. The first three natural frequencies of the nanobeam with a pretension of $0.0001\,{\text {N}}$ have been computed for different boundary conditions using the analytical method.

Silicon Nanobeam For frequency analysis on silicon-based nanobeam with different configurations, Table 3 and the corresponding mechanical properties are presented in Table 4. The analytical method computed the first three natural frequencies for different end conditions using MSGT with and without considering the surface elasticity effects with axial pretension of $0.0001\,{\text {N}}$. Figures 11, 12 and 13 show the first fundamental three natural frequencies for SSB, clamped-clamped and cantilever beam respectively. In Silicon nanobeams, surface-related effects negatively influence natural frequencies because of Silicon’s negative surface elastic modulus $(C_S)$, making the structure soften. Considering surface elasticity effects, the maximum difference in natural frequencies is approximately $5\%$. Hence, the effect of surface elasticity will have an appreciable influence on the frequency response of the nanobeams.

Table 3. Set of nanobeams with different geometries (From Fu et al. [32])

Table 4. Mechanical properties of Si and Al-based nanobeams

Fig. 9.

Comparison of the first three natural frequencies ((a), (b) and (c)) of Cantilever beam with axial load $N_0 = 0.01\,{\text {N}}$

Fig. 10.

Comparison of the first three natural frequencies ((a), (b) and (c)) of Cantilever beam with axial load $N_0 = 0.0001\,{\text {N}}$

Fig. 11.

Comparison of the first three natural frequencies ((a), (b) and (c)) of Silicon SSB including surface elasticity effects and subjected to axial load of $N_0 = 0.0001$

Fig. 12.

Comparison of the first three natural frequencies ((a), (b) and (c)) of Silicon clamped-clamped beam including surface elasticity effects and subjected to axial load of $N_0 = 0.0001$

Fig. 13.

Comparison of the first three natural frequencies ((a), (b) and (c)) of Silicon cantilever beam including surface elasticity effects and subjected to axial load of $N_0 = 0.0001$

Aluminum Nanobeam Subsequently, we also performed frequency analysis on Aluminum based nanobeam with considering the surface elasticity effects and the corresponding geometrical configurations and mechanical properties are shown in Tables 3 and 4, respectively. The first three natural frequencies have been computed for different end conditions using analytical method of MSGT with and without considering surface elasticity effects when they are subjected to axial loading of $0.0001\,{\text {N}}$. Figures 14, 15, and 16 show the first three fundamental natural frequencies of Aluminium-based SSB, clamped-clamped and cantilever beam respectively. From Figs. 14, 15 and 16, the natural frequencies corresponding to surface elasticity effects are higher than those without surface elasticity effects. In the case of Aluminum nanobeam, surface-related effects positively influence natural frequencies because of positive surface elastic modulus $(C_S)$, making the structure stiffer. The natural frequency values with surface elasticity are approximately $2\%$ higher than those without surface effects. When the dimensions increase further, the difference in frequencies is reduced. This difference is small because the choice of geometrical configuration (length, width and thickness) greatly influences the structure’s frequency response. The surface elasticity effects in Silicon and Aluminum nanobeams become significant at lower thickness and length of the beam. These effects are accurately captured by introducing an effective elastic modulus [31]. Hence, the effect of surface elasticity on the structure’s natural frequency can’t be neglected to have the optimum design of nanobeams.

Fig. 14.

Comparison of the first three natural frequencies ((a), (b) and (c)) of Al SSB including surface elasticity effects and subjected to axial load of $N_0 = 0.0001\,{\text {N}}$

Fig. 15.

Comparison of the first three natural frequencies ((a), (b) and (c)) of Al clamped-clamped beam including surface elasticity effects and subjected to axial load of $N_0 = 0.0001\,{\text {N}}$

Fig. 16.

Comparison of the first three natural frequencies ((a), (b) and (c)) of Al cantilever beam including surface elasticity effects and subjected to axial load of $N_0 = 0.0001\,{\text {N}}$

Further, from the above discussion, we can state that the surface elasticity effects will affect the system’s frequency response at the nanolevel either positively or negatively, depending upon the surface elastic modulus of the beam [30]. Therefore it is critical to consider surface elasticity effects in addition to strain gradients while modeling the systems at the micro/nano level.

5 Conclusions

This work presented the frequency analysis of epoxy-based microbeams with axial pretension using modified strain gradient theory. Theoretical formulation and corresponding governing equation of motion has been derived by using extended Hamilton’s principle. Three end conditions are considered (SSB, Clamped-Clamped, and Cantilever). The governing sixth order differential equation has been solved using the standard analytical method and numerical differential quadrature technique. The first three natural frequencies are found for different beam configurations by varying the axial pretension. The obtained results are validated with existing literature and showed good agreement. The results show that MSGT can capture size effects accurately compared to other theories like MCST and classical theory. As we increase the axial pretension from 0.0001N to 1N, the microbeam’s stiffness increases, increasing natural frequency for all end conditions. The results have shown that the frequency response of the micro/nanostructure is affected by size effects when the characteristic dimensions are in the orders of material length scales. Subsequently, surface elasticity effects have been analysed for Silicon and Aluminium-based nanobeams with the pretension of 0.0001 N for different boundary conditions. Results of surface elasticity modeling have shown that the frequency response of the nanobeam is either positive or negative depending on the value of the material length scale, $h_{0}$. The maximum difference in natural frequencies is $5\%$ and $2\%$ for Silicon and Aluminum based nanobeams, respectively. Hence, the present methodology can effectively model the strain gradients and surface elasticity effects in micro/nanostructures.

Appendix

In this section, we derived the governing equation of motion and the corresponding boundary conditions using extended Hamilton’s principle.

Consider a prismatic beam of length L, having cross sectional area A, is subjected to the distributed load q(x) and the axial load $N_0$ as shown in Fig. 1. The cross-section is specified by the x (longitudinal) and y (lateral) axes. The load q is applied in the transverse direction, i.e., the z axis.

Let u, v, w are the displacements in the x, y, and z directions, respectively. From the Euler-Bernoulli theory, the displacements can be written as :

$$\begin{aligned} u = -z\frac{\partial w(x)}{\partial x}, v = 0, w = w(x). \end{aligned}$$

(50)

On substitution of the above expression in the Eqs. (2) and (3),

$$\begin{aligned} \epsilon _{xx} = -z\frac{\partial ^2 w}{\partial x^2}, \gamma _x = -z\frac{\partial ^3 w}{\partial x^3}, \gamma _y = 0, \gamma _z = -\frac{\partial ^2 w}{\partial x^2}, \end{aligned}$$

(51)

and from the Eqs. (4) and (5) we get

$$\begin{aligned} \chi _{xy}^S = \chi _{yx}^S = -\frac{1}{2}\frac{\partial ^2 w}{\partial x^2} \end{aligned}$$

(52)

$$\begin{aligned} \nonumber \tilde{\eta }_{111} = -\frac{2}{5}\left( z\frac{\partial ^3 w}{\partial x^3}\right) , \tilde{\eta }_{113} = -\frac{4}{15}\left( \frac{\partial ^2 w}{\partial x^2}\right) , \tilde{\eta }_{122} = \frac{1}{5}\left( z\frac{\partial ^3 w}{\partial x^3}\right) \\ \nonumber \tilde{\eta }_{133} = \frac{1}{5}\left( z\frac{\partial ^3 w}{\partial x^3}\right) , \tilde{\eta }_{212} = \frac{1}{5}\left( z\frac{\partial ^3 w}{\partial x^3}\right) , \tilde{\eta }_{221} = \frac{1}{5}\left( z\frac{\partial ^3 w}{\partial x^3}\right) \\ \tilde{\eta }_{223} = \frac{1}{15}\left( \frac{\partial ^2 w}{\partial x^2}\right) , \tilde{\eta }_{232} = \frac{1}{15}\left( \frac{\partial ^2 w}{\partial x^2}\right) , \tilde{\eta }_{311} = -\frac{4}{15}\left( \frac{\partial ^2 w}{\partial x^2}\right) \\ \nonumber \tilde{\eta }_{313} = \frac{1}{5}\left( z\frac{\partial ^3 w}{\partial x^3}\right) , \tilde{\eta }_{322} = \frac{1}{15}\left( \frac{\partial ^2 w}{\partial x^2}\right) , \tilde{\eta }_{331} = \frac{1}{5}\left( z\frac{\partial ^3 w}{\partial x^3}\right) \\ \nonumber \tilde{\eta }_{333} = \frac{1}{5}\left( z\frac{\partial ^3 w}{\partial x^3}\right) , \tilde{\eta }_{131} = -\frac{4}{15}\left( \frac{\partial ^2 w}{\partial x^2}\right) \end{aligned}$$

(53)

On substitution of Eqs. (51)–(53) in Eq. (1) and after simplification, we get the following equation for the total strain energy $U_t$ of linear isotropic elastic material is found as,

$$\begin{aligned} U_t = \frac{1}{2}\int \limits _{0}^{L}\left[ P\cdot \left( w''\right) ^2 + Q\cdot \left( w^{(3)}\right) ^2\right] dx, \end{aligned}$$

(54)

where, w is the transverse deflection, $w'' = \frac{\partial ^2 w}{\partial x^2}$, $w^{(3)} = \frac{\partial ^3 w}{\partial x^3}$ and P, Q are defined as,

$$\begin{aligned} P = EI+2\mu Al_0^2+\frac{8}{15}\mu Al_1^2 + \mu Al_2^2, Q = I\left( 2\mu l_0^2+\frac{4}{5}\mu l_1^2\right) . \end{aligned}$$

(55)

and A is the area of cross section and I is the moment of inertia of the beam. $\mu$ is the shear modulus of the material(Lame’s constant) and is given by $\mu = \frac{E}{2\left( 1+\nu \right) }$. The first variation of integral of the kind $H = \int _{0}^{L}F\left( w'',w^{(3)}\right) dx$ can be defined as,

$$\begin{aligned} \nonumber \delta H = \int \limits _{0}^{L}\left[ \frac{d^2}{dx^2}\left( \frac{\partial F}{\partial w''}\right) -\frac{d^3}{dx^3}\left( \frac{\partial F}{\partial w^{(3)}}\right) \right] \delta wdx \\ + \left[ \left[ -\frac{d}{dx}\left( \frac{\partial F}{\partial w''}\right) + \frac{d^2}{dx^2}\left( \frac{\partial F}{\partial w^{(3)}}\right) \right] \delta w\right] _0^L \\ \nonumber + \left[ \left[ \left( \frac{\partial F}{\partial w''}\right) - \frac{d}{dx}\left( \frac{\partial F}{\partial w^{(3)}}\right) \right] \delta w'\right] _0^L + \left[ \frac{\partial F}{\partial w^{(3)}}\delta w''\right] _0^L. \end{aligned}$$

(56)

In the present method ,consider $H = U_t$ of Eq. (54) and the Lagrangian function F is defined by,

$$\begin{aligned} F = \frac{1}{2}\left[ P\cdot \left( w''\right) ^2 + Q\cdot \left( w^{(3)}\right) ^2\right] . \end{aligned}$$

(57)

With the use of above relations one can write the first variation (Eqn.(56)) of the total strain energy as,

$$\begin{aligned} \nonumber \delta U_t = \int \limits _{0}^{L}\left[ Pw^{(4)}-Qw^{(6)}\right] \delta wdx + \left[ -Pw^{(3)}+Qw^{(5)}\right] \delta w|_0^L \\ + \left[ Pw'' - Qw^{(4)}\right] \delta w'|_0^L + Qw^{(3)}\delta w''|_0^L, \end{aligned}$$

(58)

where, $w' = \frac{\partial w}{\partial x}, w^{(3)} = \frac{\partial ^3 w}{\partial x^3}, w^{(4)} = \frac{\partial ^4 w}{\partial x^4}, w^{(5)} = \frac{\partial ^5 w}{\partial x^5}$, & $w^{(6)} = \frac{\partial ^6 w}{\partial x^6}.$

The variational kinetic energy and the work due to external forces can be written as :

$$\begin{aligned} \delta T = \left[ \int \limits _{0}^{L}\rho A \frac{\partial ^2 w}{\partial t^2} \right] \delta w dx, \end{aligned}$$

(59)

$$\begin{aligned} \delta W_{ext} = \int \limits _{0}^{L}\left( q + N_0\frac{\partial ^2 w}{\partial x^2}\right) \delta w dx + \left[ V \delta w\right] _0^L + \left[ M \delta w'\right] _0^L + \left[ M^h \delta w''\right] _0^L. \end{aligned}$$

(60)

Substituting the Eqs. (58)–(60), into the extended Hamilton’s principle Eq. (12), we get the following governing differential equation (GDE) the motion of the beam by modified strain gradient theory (MSGT) as,

$$\begin{aligned} P\frac{\partial ^4 w}{\partial x^4} - Q\frac{\partial ^6 w}{\partial x^6} - N_0\frac{\partial ^2 w}{\partial x^2} + \rho A \frac{\partial ^2 w}{\partial t^2} + q(x) = 0, \end{aligned}$$

(61)

and the corresponding boundary conditions which satisfy the equations are,

$$\begin{aligned} \left[ \left( V - Pw^{(3)} + Qw^{(5)} - N_0 w' \right) \delta w\right] _0^L = 0, \end{aligned}$$

(62)

$$\begin{aligned} \left[ \left( M + Pw^{(2)} - Qw^{(4)} \right) \delta w'\right] _0^L = 0, \end{aligned}$$

(63)

$$\begin{aligned} \left[ \left( M^h + Qw^{(3)}\right) \delta w''\right] _0^L = 0. \end{aligned}$$

(64)

When the two material length scale parameters, i.e., related with dilatation gradient and deviatoric stretch gradient becomes zero ($l_0 = l_1 = 0$) then the governing differential equation reduces to that of modified couple stress theory (MCST). Hence, the governing differential equation of motion based on MCST is,

$$\begin{aligned} \left( EI + \mu A l_2^2\right) \frac{\partial ^4 w}{\partial x^4} - N_0\frac{\partial ^2 w}{\partial x^2} + \rho A \frac{\partial ^2 w}{\partial t^2} + q = 0 \end{aligned}$$

(65)

and the boundary conditions become

$$\begin{aligned} \left[ \left( V - \left( EI + \mu A l_2^2\right) w^{(3)} - N_0 w' \right) \delta w\right] _0^L = 0, \end{aligned}$$

(66)

$$\begin{aligned} \left[ \left( M + \left( EI + \mu A l_2^2\right) w^{(2)}\right) \delta w'\right] _0^L = 0. \end{aligned}$$

(67)

When all the three material length scale parameters re assumed to zero ($l_0 = l_1 = l_2 = 0$), then the governing differential equation of motion is reduces to that of classical elasticity theory.