Keywords

Introduction

The miniaturized (small-sized) structures have a wide range of applications in nano- and micro-electromechanical systems (NEMS andMEMS) due to the rapid improvements in technology (Younis et al. 2003; Li and Fang 2010; Wu et al. 2010). Microbeamis one of the essential structures frequently used in MEMS/NEMS such as micro-resonators (Zook et al. 1992), atomic force microscopes (Torii et al. 1994), micro-actuators (Hung and Senturia 1999), and microswitches (Xie et al. 2003). Because of the characteristics dimensions of the microbeams (thickness, width, and length) are on the order of microns and submicrons, size effects should be taken into consideration on the determination of the mechanical characteristics of such structures. However, it has been experimentally observed for several materials that microstructural effects appear and have considerable effect on mechanical properties and deformation behavior for smaller sizes (Poole et al. 1996; Lam et al. 2003; McFarland and Colton 2005). Unfortunately, the well-known classical continuum theories, which are independent of scale of the structure’s size, fail to estimate and explain of size dependency in micro- and nanoscale structures. Subsequently, various nonclassical continuum theories, which include at least one additional material length-scale parameter, have been developed like couple stress theory (Mindlin and Tiersten 1962; Koiter 1964; Toupin 1964), micropolar theory (Eringen 1967), nonlocal elasticity theory (Eringen 1972, 1983), and strain gradient theory (Fleck and Hutchinson 1993; Vardoulakis and Sulem 1995; Altan et al. 1996).

One of the higher-order continuum theories, named as strain gradient theory, developed by Fleck and Hutchinson (1993, 2001), can be viewed as extended form of the Mindlin’s simplified theory (Mindlin 1965). This theory requires five additional material length-scale parameters related to second-order deformation gradients. Subsequently, Lam et al. (2003) proposed a more useful form of the strain gradient theory which is named as modified strain gradient theory (MSGT) and includes three additional material length-scale parameters for linear elastic isotropic materials.

This theory has been employed by many researchers to analyze size-dependent microbeams. For instance, Bernoulli-Euler and Timoshenko models were introduced for static bending, free vibration, and buckling behaviors of microbeams by Kong et al. (2009), Wang et al. (2010), and Akgöz and Civalek (2012, 2013a). Furthermore, Kahrobaiyan et al. (2012) and Ansari et al. (2011) introduced Bernoulli-Euler and Timoshenko beam models for functionally graded microbeams, respectively. Artan and Batra (2012) employed the method of initial values for the free vibration of Bernoulli-Euler strain gradient beams with four different boundary conditions as simply supported-simply supported, clamped-free, clamped-clamped, and clamped-simply supported. Approximate solutions for static and dynamic analyses of microbeams were also carried out by finite element method based on Bernoulli-Euler and Timoshenko beam theories, respectively (Kahrobaiyan et al. 2013; Zhang et al. 2014a).

Presently, various beam theories have been proposed and used to investigate the mechanical behaviors of beams. Influences of shear deformation can be neglected for slender beams with a large aspect ratio. However, effects of shear deformation and rotary inertia become more prominent and cannot be ignored for moderately thick beams and vibration responses on higher modes. In this manner, several shear deformation beam theories have been developed to account for the effects of transverse shear. One of the earlier shear deformation beam theories is the first-order shear deformation beam theory (commonly named as Timoshenko beam theory (TBT)) (Timoshenko 1921). This theory assumes that shear stress and strain are constant along the height of the beam. In fact, the distributions of these are not uniform, and also there are no transverse shear stress and strain at the top and bottom surfaces of the beam. For this reason, a shear correction factor is needed, as a disadvantage of the theory. After that, some higher-order shear deformation beam theories, which satisfy the condition of no shear stress and strain without any shear correction factors, have been presented such as parabolic (third-order) beam theory (Levinson 1981; Reddy 1984), trigonometric (sinusoidal) beam theory (Touratier 1991), hyperbolic beam theory (Soldatos 1992), exponential beam theory (Karama et al. 2003), and general exponential beam theory (Aydogdu 2009a). These theories have been used less than Euler-Bernoulli beam theory (EBT) and TBT on prediction of the mechanical responses of microstructures on the basis of the nonclassical continuum theories (Aydogdu 2009b; Salamat-talab et al. 2012; Şimşek and Reddy 2013a, b; Thai and Vo 2012, 2013; Akgöz and Civalek 2013b, 2014a, b, c, 2015; Zhang et al. 2014b).

In the present study, a new size-dependent trigonometric (sinusoidal) shear deformation beam model in conjunction with modified strain gradient theory is developed. This model captures both the microstructural and shear deformation effects without the need for any shear correction factors. The governing differential equations and related boundary conditions are derived by using Hamilton’s principle. The free vibration response of simply supported microbeams is investigated. Analytical solutions for the first three natural frequencies are presented. In order to indicate the accuracy and validity of the present model, the results are comparatively presented with the results of other beam theories. A detailed parametric study is carried out to indicate the influences of material length-scale parameter, slenderness ratio, and shear correction factors on the natural frequencies of microbeams.

Modified Strain Gradient Theory

The modified strain gradient elasticity theory was proposed by Lam et al. (2003) in which contains not only classical strain tensor but also second-order deformation gradients (first-order strain gradients) such as dilatation gradient vector and deviatoric stretch gradient and symmetric rotation gradient tensors. The strain energy U on the basis of the modified strain gradient elasticity theory can be written by (Lam et al. 2003; Kong et al. 2009):

$$ U=\frac{1}{2}{\int}_0^L{\int}_A\left({\sigma}_{{ij}}{\varepsilon}_{{ij}}+{p}_i{\gamma}_i+{\tau}_{{ij}{k}}^{(1)}{\eta}_{{ij}{k}}^{(1)}+{m}_{{ij}}^s{\chi}_{{ij}}^s\right){dA}\ {dx} $$
(1)
$$ {\varepsilon}_{{ij}}=\frac{1}{2}\left({u}_{i,j}+{u}_{j,i}\right) $$
(2)
$$ {\gamma}_i={\varepsilon}_{{mm},i} $$
(3)
$$ \begin{array}{c}{\eta}_{{ij}{k}}^{(1)}=\frac{1}{3}\left({\varepsilon}_{{jk},i}+{\varepsilon}_{{ki},j}+{\varepsilon}_{{ij},k}\right)-\frac{1}{15}\left[{\delta}_{{ij}}\left({\varepsilon}_{{mm},k}+2{\varepsilon}_{{mk},m}\right)\right.\\ \left. \quad + \,{\delta}_{{jk}}\left({\varepsilon}_{{mm},i}+2{\varepsilon}_{{mi},m}\right)+{\delta}_{ki}\left({\varepsilon}_{mm,j}+2{\varepsilon}_{{mj},m}\right)\right]\end{array} $$
(4)
$$ {\chi}_{{ij}}^s=\frac{1}{2}\left({\theta}_{i,j}+{\theta}_{j,i}\right) $$
(5)
$$ {\theta}_i=\frac{1}{2}{e}_{{ijk}}{u}_{k,j} $$
(6)

where ui, θi, εij, γi, \( {\eta}_{{ijk}}^{(1)} \) and \( {\chi}_{{ij}}^s \) denote the components of the displacement vector u, the rotation vector θ, the strain tensor ε, the dilatation gradient vector γ, the deviatoric stretch gradient tensor η(1), and the symmetric rotation gradient tensor χs, respectively. Also, δ is the symbol of Kronecker delta and eijk is the permutation symbol.

Furthermore, the components of the classical stress tensor σ and the higher-order stress tensors p, τ(1), and ms defined as (Lam et al. 2003).

$$ {\sigma}_{{ij}}={\lambda \varepsilon}_{{mm}}{\delta}_{{ij}}+2{\mu \varepsilon}_{{ij}} $$
(7)
$$ {p}_i=2\mu {l}_0^2{\gamma}_i $$
(8)
$$ {\tau}_{{ijk}}^{(1)}=2\mu {l}_1^2{\eta}_{{ijk}}^{(1)} $$
(9)
$$ {m}_{{ij}}^s=2\mu {l}_2^2{\chi}_{{ij}}^s $$
(10)

where l0,l1,l2 are additional material length-scale parameters related to dilatation gradients, deviatoric stretch gradients, and rotation gradients, respectively. Furthermore, λ and μ are the Lamé constants defined as

$$ \lambda =\frac{{Ev}}{\left(1+v\right)\left(1-2v\right)},\, \mu =\frac{E}{2\left(1+v\right)} $$
(11)

where E is Young’s modulus and v is Poisson’s ratio.

Trigonometric Shear Deformation Microbeam Model

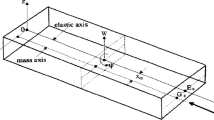
The displacement components of an initially straight beam on the basis of trigonometric sh ear deformation beam theory (see Fig. 1) can be written as (Touratier 1991).

$$ \begin{aligned}&{u}_1(x,z,t)=u(x,t)-z\frac{\partial w(x,t)}{\partial x}+R(z)\phi (x,t) \\ & {u}_2(x,z,t)=0 \\ & {u}_3(x,z,t)=w(x,t) \end{aligned} $$
(12)
Fig. 1
figure 1

Geometry, coordinate system, and cross section of a simply supported microbeam

Full size image

in which

$$ \phi \left(x,t\right)=\frac{\partial w\left(x,t\right)}{\partial x}-\varphi \left(x,t\right) $$
(13)

where u1, u2 and u3 are the x−, y− and z− components of the displacement vector, and also u and w are the axial and transverse displacements, φ is the angle of rotation of the cross section about y− axis of any point on the midplane of the beam, respectively. R(z) is a function which depends on z and plays a role in determination of the transverse shear strain and stress distribution throughout the height of the beam. In order to satisfy no shear stress and strain condition at the upper (z = −h/2) and lower (z = h/2) surfaces of the beam, R(z) is selected as following without need for any shear correction factors:

$$ R(z)=\frac{h}{\pi}\operatorname{sin}\left(\frac{\pi z}{h}\right) $$
(14)

It can be noted that the displacement components for EBT and TBT will be obtained by setting R(z) in Eq. 12 equal to (0) and (z), respectively. With the use of Eqs. 12, 13, and 14 into Eq. 2, the nonzero strain components are obtained as

$$ \begin{array}{cc}\hfill \displaystyle{\varepsilon}_{11}=\displaystyle\frac{\partial u}{\partial x}-z\frac{\partial^2w}{\partial {x}^2}+R\displaystyle\frac{\partial \phi }{\partial x},\hfill & \displaystyle\hfill {\varepsilon}_{13}=\frac{1}{2} S\phi \hfill \end{array} $$
(15)

where

$$ S(z)=\operatorname{cos}\left(\frac{\pi z}{h}\right) $$
(16)

and from Eq. 15 and Eq. 3, the components of dilatation gradient vector γ are expressed as

$$ \begin{array}{c}\hfill {\gamma}_1=\frac{\partial^2u}{\partial {x}^2}-z\frac{\partial^3w}{\partial {x}^3}+R\frac{\partial^2\phi }{\partial {x}^2}\hfill \\[3pt] {}\hfill {\gamma}_2=0,\hfill \\[3pt] {}\hfill {\gamma}_3=-\frac{\partial^2w}{\partial {x}^2}+S\frac{\partial \phi }{\partial x}\hfill \end{array} $$
(17)

By inserting Eq. 15 in Eq. 4, the nonzero components of deviatoric stretch gradient tensor η(1) can be obtained as

$$ \begin{array}{l}{\eta}_{111}^{(1)}=\frac{1}{5}\left[2\left(\frac{\partial^2u}{\partial {x}^2}-z\frac{\partial^3w}{\partial {x}^3}+R\frac{\partial^2\phi }{\partial {x}^2}\right)+\frac{\pi^2}{h^2} R\phi \right],\hfill \\[5pt] {}{\eta}_{113}^{(1)}={\eta}_{131}^{(1)}={\eta}_{311}^{(1)}=-\frac{4}{15}\left(\frac{\partial^2w}{\partial {x}^2}-2S\frac{\partial \phi }{\partial x}\right),\hfill \\[5pt] {}{\eta}_{122}^{(1)}={\eta}_{212}^{(1)}={\eta}_{221}^{(1)}=-\frac{1}{5}\left(\frac{\partial^2u}{\partial {x}^2}-z\frac{\partial^3w}{\partial {x}^3}+R\frac{\partial^2\phi }{\partial {x}^2}-\frac{\pi^2}{3{h}^2} R\phi \right),\hfill \\[5pt] {}{\eta}_{133}^{(1)}={\eta}_{313}^{(1)}={\eta}_{331}^{(1)}=-\frac{1}{5}\left(\frac{\partial^2u}{\partial {x}^2}-z\frac{\partial^3w}{\partial {x}^3}+R\frac{\partial^2\phi }{\partial {x}^2}+\frac{4}{3}\frac{\pi^2}{h^2} R\phi \right),\hfill \\[5pt] {}{\eta}_{223}^{(1)}={\eta}_{232}^{(1)}={\eta}_{322}^{(1)}=\frac{1}{15}\left(\frac{\partial^2w}{\partial {x}^2}-2S\frac{\partial \phi }{\partial x}\right),{\eta}_{333}^{(1)}=\frac{1}{5}\left(\frac{\partial^2w}{\partial {x}^2}-2S\frac{\partial \phi }{\partial x}\right)\hfill \end{array} $$
(18)

Also, the use of Eq. 12 in Eq. 6 gives

$$ {\theta}_1=0,{\theta}_2=-\frac{\partial w}{\partial x}+\frac{1}{2} S\phi, {\theta}_3=0 $$
(19)

and the nonzero components of the symmetric part of the rotation gradient tensor χs can be achieved by using of Eq. 19 into Eq. 5 as

$$ {\chi}_{12}^s={\chi}_{21}^s=-\frac{1}{2}\left(\frac{\partial^2w}{\partial {x}^2}-\frac{1}{2}S\frac{\partial \phi }{\partial x}\right),{\chi}_{23}^s={\chi}_{32}^s=-\frac{\pi^2}{4{h}^2} R\phi $$
(20)

With the use of Eq. 15 in Eq. 7, the nonzero components of classical stress tensor σ can be written as

$$ \begin{array}{l}\begin{array}{cc}\hfill {\sigma}_{11}= E\eta \left(\frac{\partial u}{\partial x}-z\frac{\partial^2w}{\partial {x}^2}+R\frac{\partial \phi }{\partial x}\right),\hfill & \hfill {\sigma}_{13}=\mu S\phi \hfill \end{array}\hfill \\[5pt] {}{\sigma}_{22}={\sigma}_{33}=\frac{{Ev}}{\left(1+v\right)\left(1-2v\right)}\left(\frac{\partial u}{\partial x}-z\frac{\partial^2w}{\partial {x}^2}+R\frac{\partial \phi }{\partial x}\right)\hfill \end{array} $$
(21)

where

$$ \eta =\frac{\left(1-v\right)}{\left(1+v\right)\left(1-2v\right)} $$
(22)

It is notable that Poisson’s effect is neglected by choosing η = 1 in Eq. 22 (Reddy 2011). From Eq. 8 and Eq. 15, the nonzero components of higher-order stress tensor p are obtained as

$$ \begin{array}{cc}\hfill {p}_1=2\mu {l}_0^2\left(\frac{\partial^2u}{\partial {x}^2}-z\frac{\partial^3w}{\partial {x}^3}+R\frac{\partial^2\phi }{\partial {x}^2}\right),\hfill & \hfill {p}_3=-2\mu {l}_0^2\left(\frac{\partial^2w}{\partial {x}^2}-S\frac{\partial \phi }{\partial x}\right)\hfill \end{array} $$
(23)

By inserting Eq. 18 in Eq. 9, the nonzero components of higher-order stress tensor τ(1) are written as

$$ \begin{array}{l}{\tau}_{111}^{(1)}=\frac{2}{5}\mu {l}_1^2\left[2\left(\frac{\partial^2u}{\partial {x}^2}-z\frac{\partial^3w}{\partial {x}^3}+R\frac{\partial^2\phi }{\partial {x}^2}\right)+\frac{\pi^2}{h^2} R\phi \right],\hfill \\[5pt] {}{\tau}_{113}^{(1)}={\tau}_{131}^{(1)}={\tau}_{311}^{(1)}=-\frac{8}{15}\mu {l}_1^2\left(\frac{\partial^2w}{\partial {x}^2}-2S\frac{\partial \phi }{\partial x}\right),\hfill \\[5pt] {}{\tau}_{122}^{(1)}={\tau}_{212}^{(1)}={\tau}_{221}^{(1)}=-\frac{2}{5}\mu {l}_1^2\left(\frac{\partial^2u}{\partial {x}^2}-z\frac{\partial^3w}{\partial {x}^3}+R\frac{\partial^2\phi }{\partial {x}^2}-\frac{\pi^2}{3{h}^2} R\phi \right),\hfill \\[5pt] {}{\tau}_{133}^{(1)}={\tau}_{313}^{(1)}={\tau}_{331}^{(1)}=-\frac{2}{5}\mu {l}_1^2\left(\frac{\partial^2u}{\partial {x}^2}-z\frac{\partial^3w}{\partial {x}^3}+R\frac{\partial^2\phi }{\partial {x}^2}+\frac{4}{3}\frac{\pi^2}{h^2} R\phi \right),\hfill \\[5pt] {}\begin{array}{cc}\hfill {\tau}_{223}^{(1)}={\tau}_{232}^{(1)}={\tau}_{322}^{(1)}=\frac{2}{15}\mu {l}_1^2\left(\frac{\partial^2w}{\partial {x}^2}-2S\frac{\partial \phi }{\partial x}\right),\hfill & \hfill {\tau}_{333}^{(1)}=\frac{2}{5}\mu {l}_1^2\left(\frac{\partial^2w}{\partial {x}^2}-2S\frac{\partial \phi }{\partial x}\right)\hfill \end{array}\hfill \end{array} $$
(24)

Similarly, the nonzero components of higher-order stress tensor ms are determined by using of Eq. 20 into Eq. 10:

$$ \begin{array}{cc}\hfill {m}_{12}^s={m}_{21}^s=-\mu {l}_2^2\left(\frac{\partial^2w}{\partial {x}^2}-\frac{1}{2}S\frac{\partial \phi }{\partial x}\right),\hfill & \hfill {m}_{23}^s={m}_{32}^s=-\frac{\mu {l}_2^2}{2}\frac{\pi^2}{h^2} R\phi \hfill \end{array} $$
(25)

With the substitution of Eqs. 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, and 25 into Eq. 1, the first variation of strain energy of microbeam is expressed as

$${\fontsize{8.9}{10}\selectfont{\begin{array}{l} \delta U={\int}_0^L{\int}_A\left({\sigma}_{{ij}}{\delta \varepsilon}_{{ij}}+{p}_i{\delta \gamma}_i+{\tau}_{{ij}{k}}^{(1)}{\delta \eta}_{{ij}{k}}^{(1)}+{m}_{{ij}}^s{\delta \chi}_{{ij}}^s\right){dA}\ {dx}\\[5pt] \;\;\quad={\int}_0^L{\int}_A\left({\sigma}_{11}{\delta \varepsilon}_{11}+2{\sigma}_{13}{\delta \varepsilon}_{13}+{p}_1{\delta \gamma}_1+{p}_3{\delta \gamma}_{3+}{\tau}_{111}^{(1)}{\delta \eta}_{111}^{(1)}+3{\tau}_{113}^{(1)}{\delta \eta}_{113}^{(1)}\right.+3{\tau}_{122}^{(1)}{\delta \eta}_{122}^{(1)}\\[5pt] \;\;\qquad+3{\tau}_{133}^{(1)}{\delta \eta}_{133}^{(1)}+3{\tau}_{223}^{(1)}{\delta \eta}_{223}^{(1)}+{\tau}_{333}^{(1)}{\delta \eta}_{333}^{(1)}+2{m}_{12}^s\left.{\delta \chi}_{12}^s+2{m}_{23}^s{\delta \chi}_{23}^s\ \right){dA}\ {dx}\\[5pt] \;\;\quad={\int}_0^L\left[A\left(-E\frac{\partial^2u}{\partial {x}^2}{+}2\mu {k}_1\frac{\partial^4u}{\partial {x}^4}\right)\delta u\right.{+}\left({k}_2\phi {-}{k}_3\frac{\partial^2\phi }{\partial {x}^2}{+}{k}_4\frac{\partial^3w}{\partial {x}^3}{+}\frac{12}{\pi^2}\mu {{Ik}}_1\!\left(\!\frac{\partial^4\phi }{\partial {x}^4}\,{-}\,\frac{4}{\pi}\frac{\partial^5w}{\partial {x}^5}\right)\!\right)\delta \phi \\[5pt] \;\qquad\left.+\left({k}_5\frac{\partial^4w}{\partial {x}^4}-{k}_4\frac{\partial^3\phi }{\partial {x}^3}-2\mu {{Ik}}_1\left(\frac{\partial^6w}{\partial {x}^6}-\frac{24}{\pi^3}\frac{\partial^5\phi }{\partial {x}^5}\right)\right)\delta w\ \right]{dx}+\left[A\left(E\frac{\partial u}{\partial x}-2\mu {k}_1\frac{\partial^3u}{\partial {x}^3}\right)\delta u\ \right.\\[5pt] \;\qquad+2\mu {{Ak}}_1\frac{\partial^2u}{\partial {x}^2}\delta \left(\frac{\partial u}{\partial x}\right)+\left(\left({k}_3+{k}_6\right)\frac{\partial \phi }{\partial x}-\left({k}_4+{k}_7\right)\frac{\partial^2w}{\partial {x}^2}-\frac{12}{\pi^2}\mu {{Ik}}_1\left(\frac{\partial^3\phi }{\partial {x}^3}-\frac{4}{\pi}\frac{\partial^4w}{\partial {x}^4}\right)\right)\delta \phi \\[5pt] \;\qquad+\left({k}_6\phi {+}\frac{12}{\pi^2}\mu {{Ik}}_1\left(\frac{\partial^2\phi }{\partial {x}^2}{-}\frac{4}{\pi}\frac{\partial^3w}{\partial {x}^3}\right)\!\right)\delta \left(\frac{\partial \phi }{\partial x}\right){+}\left({k}_4\frac{\partial^2\phi }{\partial {x}^2}{-}{k}_5\frac{\partial^3w}{\partial {x}^3}{+}2\mu {{Ik}}_1\left(\frac{\partial^5w}{\partial {x}^5}{-}\frac{24}{\pi^3}\frac{\partial^4\phi }{\partial {x}^4}\right)\!\right)\delta w\\[5pt] \;\qquad+\left({k}_5\frac{\partial^2w}{\partial {x}^2}-{k}_4\frac{\partial \phi }{\partial x}-2\mu {{Ik}}_1\left(\frac{\partial^4w}{\partial {x}^4}-\frac{24}{\pi^3}\frac{\partial^3\phi }{\partial {x}^3}\right)\right)\delta \left(\frac{\partial w}{\partial x}\right)\\[5pt] \;\qquad{\left.+\left(-{k}_7\phi +2\mu {{Ik}}_1\left(\frac{\partial^3w}{\partial {x}^3}-\frac{24}{\pi^3}\frac{\partial^2\phi }{\partial {x}^2}\right)\right)\delta \left(\frac{\partial^2w}{\partial {x}^2}\right)\right]}_0^L\end{array}}} $$
(26)

where L is length of the microbeam, A is the area of cross section, I is the second moment of area:

$$ \begin{array}{l} {k}_1={l}_0^2+\frac{2}{5}{l}_1^2,{k}_2=\mu A\left(\frac{1}{2}+\frac{\pi^2}{h^2}\left(\frac{4}{15}{l}_1^2+\frac{1}{8}{l}_2^2\right)\right),\\[5pt] {}{k}_3=\frac{6}{\pi^2}{EI}+\mu A\left({l}_0^2+\frac{2}{3}{l}_1^2+\frac{1}{8}{l}_2^2\right),\hfill \\[5pt] {}{k}_4=\frac{1}{\pi}\left(\frac{24}{\pi^2}{EI}+\mu A\left(4{l}_0^2+\frac{4}{3}{l}_1^2+{l}_2^2\right)\right),\\[5pt] {}{k}_5={EI}+\mu A\left(2{l}_0^2+\frac{8}{15}{l}_1^2+{l}_2^2\right),\hfill \\[5pt] {}{k}_6=\frac{1}{5}\mu {{Al}}_1^2,{k}_7=\frac{4}{5\pi}\mu {{Al}}_1^2\hfill \end{array} $$
(27)

The kinetic energy of the microbeam is given by

$$ T=\int^{L}_{0}\int_{A}\frac{1}{2}\rho \left[{\left(\frac{\partial {u}_1}{\partial t}\right)}^2+{\left(\frac{\partial {u}_2}{\partial t}\right)}^2+{\left(\frac{\partial {u}_3}{\partial t}\right)}^2\right]{dA}\ {dx} $$
(28)

where ρ is the mass density. From Eqs. 12 and 28, the first variation of the kinetic energy can be expressed as

$$ \begin{array}{ll}\delta T\hfill & =\int^L_0 \left\{{m}_0\left[\dfrac{\partial u}{\partial t}\dfrac{\partial \delta u}{\partial t}+\dfrac{\partial w}{\partial t}\dfrac{\partial \delta w}{\partial t}\right]\right.\hfill \\ {}\hfill &\quad +\left.{m}_2\left[\dfrac{\partial^2w}{\partial x\partial t}\ \dfrac{\partial^2\delta w}{\partial x\partial t}-\dfrac{24}{\pi^3}\left(\dfrac{\partial \phi }{\partial t}\dfrac{\partial^2\delta w}{\partial x\partial t}+\dfrac{\partial^2w}{\partial x\partial t}\dfrac{\partial \delta \phi}{\partial t}\right)+\dfrac{6}{\pi^2}\dfrac{\partial \phi }{\partial t}\dfrac{\partial \delta \phi}{\partial t}\right]\right\}{dx}\hfill \end{array} $$
(29)

where (m0, m2) are the mass inertias as.

$$ \left({m}_0,{m}_2\right)=\rho {\int}_A\left(1,{z}^2\right){dA} $$
(30)

The first variation of the work done by external forces can be written as

$$ \begin{array}{l}\delta W=\int^L_0 \left(f\delta u+ q\delta w\right){dx}+\left[{\widehat{Q}}_1\delta u+{\widehat{Q}}_2\delta \left(\frac{\partial u}{\partial x}\right)+{\widehat{Q}}_3\delta w\right.\hfill \\ {}{\left.\quad\qquad+{\widehat{Q}}_4\delta \left(\frac{\partial w}{\partial x}\right)+{\widehat{Q}}_5\delta \left(\frac{\partial^2w}{\partial {x}^2}\right)+{\widehat{Q}}_6\delta \phi +{\widehat{Q}}_7\delta \left(\frac{\partial \phi }{\partial x}\right)\right]}_0^L\hfill \end{array} $$
(31)

where f(x, t) and q(x, t) are the axial and transverse distributed loads, respectively. In addition, \( {\widehat{Q}}_i\left(i= 1, 2,\dots, 7\right) \) are the specified forces or moment of forces at the end of the microbeam. After that, with the aid of Hamilton’s principle as

$$ 0={\int}_0^T\left(\delta T-\delta U+\delta W\right){dt} $$
(32)

and by substituting Eqs. 26, 29, and 31 into Eq. 32, integrating by parts, and setting the coefficients δu, δw, and δϕ equal to zero, the governing equations of motion of the microbeam based on SBT can be obtained as (Akgöz and Civalek 2013b).

$$ \delta u:-{m}_0\frac{\partial^2u}{\partial {t}^2}+A\left(E\frac{\partial^2u}{\partial {x}^2}-2\mu {k}_1\frac{\partial^4u}{\partial {x}^4}\right)+f=0 $$
(33)
$$ \begin{aligned} \delta w:&-{m}_0\frac{\partial^2w}{\partial {t}^2}+{m}_2\left(\frac{\partial^4w}{\partial {x}^2\partial {t}^2}-\frac{24}{\pi^3}\frac{\partial^3\phi }{\partial x\partial {t}^2}\right)-{k}_5\frac{\partial^4w}{\partial {x}^4}\\[5pt] &\quad+{k}_4\frac{\partial^3\phi }{\partial {x}^3}+2\mu {{Ik}}_1\left(\frac{\partial^6w}{\partial {x}^6}-\frac{24}{\pi^3}\frac{\partial^5\phi }{\partial {x}^5}\right)+q=0\end{aligned} $$
(34)
$$ \begin{aligned}&\delta \phi :\frac{24}{\pi^3}{m}_2\frac{\partial^3w}{\partial x\partial {t}^2}-\frac{6}{\pi^2}{m}_2\frac{\partial^2\phi }{\partial {t}^2}-{k}_2\phi +{k}_3\frac{\partial^2\phi }{\partial {x}^2}\\[5pt] & \quad-{k}_4\frac{\partial^3w}{\partial {x}^3}-\frac{12}{\pi^2}\mu {{Ik}}_1\left(\frac{\partial^4\phi }{\partial {x}^4}-\frac{4}{\pi}\frac{\partial^5\mathrm{w}}{\partial {x}^5}\right)=0\end{aligned} $$
(35)

and boundary conditions at x = 0 and x = L

$$ \mathrm{either}\;A\left(E\frac{\partial u}{\partial x}-2\mu {k}_1\frac{\partial^3u}{\partial {x}^3}\right)={\widehat{Q}}_1\;\mathrm{or}\;u=0 $$
(36)
$$ \mathrm{either}\;2\mu {{Ak}}_1\frac{\partial^2u}{\partial {x}^2}={\widehat{Q}}_2\;\mathrm{or}\;\frac{\partial u}{\partial x}=0 $$
(37)
$$ \begin{aligned}&\mathrm{either}-{k}_5\frac{\partial^3w}{\partial {x}^3}+{k}_4\frac{\partial^2\phi }{\partial {x}^2}+2\mu {{Ik}}_1\left(\frac{\partial^5w}{\partial {x}^5}-\frac{24}{\pi^3}\frac{\partial^4\phi }{\partial {x}^4}\right)\\ & -{m}_2\left(\frac{24}{\pi^3}\frac{\ {\partial}^2\phi }{\partial {t}^2}-\frac{\partial^3w}{\partial x\partial {t}^2}\right)={\widehat{Q}}_3 \mathrm{or}\;w=0 \end{aligned} $$
(38)
$$ \mathrm{either}\;{k}_5\frac{\partial^2w}{\partial {x}^2}-{k}_4\frac{\partial \phi }{\partial x}-2\mu {{Ik}}_1\left(\frac{\partial^4w}{\partial {x}^4}-\frac{24}{\pi^3}\frac{\partial^3\phi }{\partial {x}^3}\right)={\widehat{Q}}_4\;\mathrm{or}\;\frac{\partial w}{\partial x}=0 $$
(39)
$$ \mathrm{either}-{k}_7\phi +2\mu {{Ik}}_1\left(\frac{\partial^3w}{\partial {x}^3}-\frac{24}{\pi^3}\frac{\partial^2\phi }{\partial {x}^2}\right)={\widehat{Q}}_5\;\mathrm{or}\;\frac{\partial^2w}{\partial {x}^2}=0 $$
(40)
$$ \mathrm{either}\;\left({k}_3+{k}_6\right)\frac{\partial \phi }{\partial x}{-}\left({k}_4+{k}_7\right)\frac{\partial^2w}{\partial {x}^2}{-}\frac{12}{\pi^2}\mu {{Ik}}_1\left(\frac{\partial^3\phi }{\partial {x}^3}{-}\frac{4}{\pi}\frac{\partial^4w}{\partial {x}^4}\right)={\widehat{Q}}_6\;\mathrm{or}\;\phi =0 $$
(41)
$$ \mathrm{either}\;{k}_6\phi +\frac{12}{\pi^2}\mu {{Ik}}_1\left(\frac{\partial^2\phi }{\partial {x}^2}-\frac{4}{\pi}\frac{\partial^3w}{\partial {x}^3}\right)={\widehat{Q}}_7\;\mathrm{or}\;\frac{\partial \phi }{\partial x}=0 $$
(42)

Analytical Solutions for Free Vibration Problem of Simply Supported Microbeams

Here, in order to solve free vibration problem of simply supported microbeams, the Navier solution procedure is used. The well-known geometric boundary conditions for a simply supported end can be defined as zero deflection and nonzero slope and/or rotation of the cross section as

$$ w=0,\ \ \frac{\partial w}{\partial x}\ne 0, \ \phi \ne 0 $$
(43)

In view of Eq. 43, the left sides of Eqs. 39 and 41 must vanish. Hence, the following relations can be written by Eqs. 36, 37, 38, 39, 40, 41, 42, and 43 as

$$ \dfrac{\partial u}{\partial x}=0,\quad \frac{\partial^2w}{\partial {x}^2}=0, \quad \dfrac{\partial \phi }{\partial x}=0, \quad {\widehat{Q}}_1=0, \quad {\widehat{Q}}_4=0, \quad {\widehat{Q}}_6=0 $$
(44)

The following expansions of generalized displacements which include undetermined Fourier coefficients and certain trigonometric functions can be successfully employed as

$$ w\left(x,t\right)=\sum_{n=1}^{\infty }{W}_n\operatorname{sin}\alpha x\;{e}^{i{\omega}_nt} $$
(45)
$$ \phi \left(x,\mathrm{t}\right)=\sum_{n=1}^{\infty }{H}_n\operatorname{cos}\alpha x\;{e}^{i{\omega}_nt} $$
(46)

where Wn and Hn are the undetermined Fourier coefficients, ωn is natural frequency, and \( \alpha =\frac{n\pi}{L} \). This means that Eqs. 45 and 46 must satisfy the corresponding boundary conditions. Substituting Eqs. 45 and 46 into Eqs. 35 and 36 as the governing equations for free vibration, the following equation is obtained as

$$ \left(\left[\begin{array}{cc}\hfill {K}_{11}\hfill & \hfill {K}_{12}\hfill \\ {}\hfill {K}_{21}\hfill & \hfill {K}_{22}\hfill \end{array}\right]-{\omega}^2\left[\begin{array}{cc}\hfill {M}_{11}\hfill & \hfill {M}_{12}\hfill \\ {}\hfill {M}_{21}\hfill & \hfill {M}_{22}\hfill \end{array}\right]\right)\left\{\begin{array}{c}\hfill {H}_n\hfill \\ {}\hfill {W}_n\hfill \end{array}\right\}=\left\{\begin{array}{c}\hfill 0\hfill \\ {}\hfill 0\hfill \end{array}\right\} $$
(47)

where.

$$ \begin{aligned} {K}_{11} & ={k}_2+{\alpha}^2{k}_3+{\alpha}^4\frac{12}{\pi^2}\mu {{Ik}}_1,\ \ {K}_{12}={K}_{21}=-{\alpha}^3\left({k}_4+{\alpha}^2\frac{48}{\pi^3}\mu {{Ik}}_1\right),\\ {K}_{22} &={\alpha}^4\left({k}_5+{\alpha}^22\mu {{Ik}}_1\right) \\ {M}_{11}&=\frac{6}{\pi^2}{m}_2, {M}_{12}={M}_{21}=-\alpha \frac{24}{\pi^3}{m}_2, {M}_{22}=\left({m}_0+{\alpha}^2{m}_2\right)\\[-35pt] \end{aligned} $$
(48)

For a nontrivial solution, the determinant of coefficient matrix must be vanished and the characteristic equation can be reached by providing this condition. The eigenvalues are obtained by solving the characteristic equation. It can be noted that the smallest root of the characteristic equation gives the first natural (fundamental) frequency.

Numerical Results and Discussion

In this section, free vibration problem of a simply supported microbeam is analytically solved with the Navier-type solution based on trigonometric shear deformation beam theory in conjunction with modified strain gradient theory. For illustration purpose, the microbeam is taken to be made of epoxy with the following material properties: Young’s modulus E = 1.44 GPa, Poisson’s ratio v = 0.38, the mass density ρ = 1,220 kg/m3 and the material length-scale parameter l = 11.01 μm (Kahrobaiyan et al. 2013). The microbeam has a rectangular cross section, and the width-to-thickness ratio is taken to be constant as b/h = 2, while the length-to-thickness ratio is taken several values as L/h = 5∼80. All material length-scale parameters are considered to be equal to each other as l0 = l1 = l2 = l.

As stated before, Timoshenko beam theory (TBT) needs a shear correction factor to take into consideration the nonuniformity of transverse shear strain and stress throughout the beam thickness. For rectangular cross-section beams, the most commonly used shear correction factors can be defined as ks = 5/6 (used here) and ks = (5 + 5v)/(6 + 5v). The classical results evaluated by TBT and other shear deformation beam theories such as third-order (parabolic), trigonometric (sinusoidal), hyperbolic, and exponential shear deformation beam theories are in good agreement. However, this agreement may decrease for the results of higher-order continuum theories, and this situation can be seen from the previous works (Akgöz and Civalek 2013b; Şimşek and Reddy 2013a, b). Consequently, a new modified shear correction factor\( \left({k}_s^{\ast}\right) \) is used for Timoshenko microbeam model (TBT*)-based MSGT as follows (Akgöz and Civalek 2014a):

$$ {k}_s^{\ast }={k}_s{k}_{{ac}}^{{MSGT}} $$
(49)

where

$$ {k}_{{ac}}^{{MSGT}}=\raisebox{1ex}{$15{\left(\frac{l_0+{l}_1+{l}_2}{3}\right)}^a\!\!\!\!$}\!\left/\raisebox{1ex}{${h}^a$}\right.\;a={3}^{{\left(\raisebox{1ex}{$h$}\!\left/ \!\raisebox{-1ex}{$\left(\frac{l_0+{l}_1+{l}_2}{3}\right)$}\right.\right)}^{0.08}}-0.45 $$
(50)

It can be noted that \( {k}_s^{\ast } \) will be equal to ks by setting material length-scale parameters equal to zero in Eq. 50. In order to demonstrate the accuracy and validity of the present analysis, some illustrative examples are comparatively given with other beam theories.

Dimensionless first three natural frequencies for various values of l/h and slenderness ratios corresponding to different beam theories are tabulated in Tables 1, 2, and 3, respectively. It can be clearly observed from the tables that the dimensionless natural frequencies predicted by both CT and TBT are lower than the other ones, while those obtained by both MSGT and EBT are larger than the other ones. Also, an increase in l/h leads to an increment in the difference between dimensionless natural frequencies corresponding to classical and nonclassical models, and also this difference becomes more prominent for higher modes. On the other hand, difference between the results corresponding to EBT and shear deformation beam theories (TBT, TBT*, and SBT) is more significant for short beams. This situation can be interpreted as the effect of shear deformation is minor for slender beams with a large slenderness ratio. In addition, it can be clearly seen from the tables that the natural frequencies predicted by SBT and TBT* are in good agreement, while the divergence between the natural frequencies of SBT and TBT is considerable especially for bigger values of l/h.

Table 1 Dimensionless fundamental frequencies \( \left({\overline{\omega}}_1={\omega}_1{L}^2\sqrt{m_0/{EI}}\right) \)
Full size table
Table 2 Dimensionless second natural frequencies \( \left({\overline{\omega}}_2={\omega}_2{L}^2\sqrt{m_0/{EI}}\right) \)
Full size table
Table 3 Dimensionless third natural frequencies \( \left({\overline{\omega}}_3={\omega}_3{L}^2\sqrt{m_0/{EI}}\right) \)
Full size table

Variations of the dimensionless first three natural frequencies of the simply supported microbeam with respect to the slenderness ratio corresponding to different beam models are depicted in Figs. 2, 3, and 4, respectively. It is observed that an increase in slenderness ratio leads to a decrement on effects of shear deformation, and differences between the dimensionless natural frequencies based on EBT, TBT, TBT*, and SBT are diminishing for L/h ≥ 50. Moreover, it can be concluded that the dimensionless natural frequencies evaluated by TBT, TBT*, and SBT are nearly equal to each other for CT, but the difference between TBT and SBT is more considerable in the higher-order models for lower slenderness ratios and higher modes.

Fig. 2
figure 2

Variations of the dimensionless natural frequency versus slenderness ratio (first mode). (a) CT (b) MSGT

Full size image
Fig. 3
figure 3

Variations of the dimensionless natural frequency versus slenderness ratio (second mode). (a) CT (b) MSGT

Full size image
Fig. 4
figure 4

Variations of the dimensionless natural frequency versus slenderness ratio (third mode). (a) CT (b) MSGT

Full size image

Influences of h/l ratio on the first three dimensionless natural frequencies for L = 7h are illustrated in Figs. 5, 6, and 7, respectively. These figures reveal that natural frequencies based on MSGT are always bigger than CT. Also, it is found that the effects of shear deformation and small size are more considerable for smaller values of h/l and higher modes.

Fig. 5
figure 5

Effects of thickness-to-material length-scale parameter ratio on the first dimensionless natural frequency (L = 7 h)

Full size image
Fig. 6
figure 6

Effects of thickness-to-material length-scale parameter ratio on the second dimensionless natural frequency (L = 7 h)

Full size image
Fig. 7
figure 7

Effects of thickness-to-material length-scale parameter ratio on the third dimensionless natural frequency (L = 7 h)

Full size image

Conclusion

In this study, a size-dependent sinusoidal shear deformation beam model in conjunction with modified strain gradient elasticity theory (MSGT) is developed. The model captures both the microstructural and shear deformation effects without any shear correction factors. The governing differential equations and corresponding boundary conditions are derived by using Hamilton’s principle. The free vibration behavior of simply supported microbeams is investigated. Analytical solutions for the first three natural frequencies are presented by the Navier solution technique. The results are compared with other beam theories for the validation of the present model. A detailed parametric study is carried out to show the influences of thickness-to-material length-scale parameter ratio, slenderness ratio, and shear deformation on the free vibration response of simply supported microbeams. The obtained results can be summarized as:

  • Microbeams based on MSGT are stiffer than based on the classical theory.

  • The natural frequencies obtained by both MSGT and EBT are always greater than those predicted by the other considered beam models and theories.

  • The difference between the natural frequencies decreases as the thickness-to-material length-scale parameter ratio increases.

  • Effect of shear deformation becomes more considerable for both smaller slenderness ratios and higher modes.

  • Use of modified shear correction factors is more suitable for Timoshenko microbeam models based on higher-order continuum theories.