1 Introduction

Microscale beams are widely used in microstructure devices and systems, such as sensors [1,2,3,4,5] and actuators [6, 7], in which thickness of beams is typically on the order of microns and submicrons. The experimental evidences indicate that a strong size effect exists in metals [8, 9], polymers [10, 11] as well as engineering structures [12]. The classical elasticity theory failed to describe the size-dependent behavior of micro- and nanoscale structures due to the lack of internal length scale parameters [13]. This motivated the development of beam models using higher-order continuum theories that contain additional material length scale parameters.

The use of gradient elasticity to simulate the size effect is not a novel idea [14,15,16]. Cosserat and Cosserat [14] equipped the kinematics equations with the displacement components as well as the micro-rotations and included the couple stresses, which are conjugated to the micro-rotations, in the equation of equilibrium. The classical couple stress elasticity theory, originated by Mindlin and Tiersten [17], Mindlin [15, 18] and Toupin [19], contained two classical and two additional material constants for isotropic elastic materials. By using Cosserat theory and Mindlin’s theory, Kang and Xi [20] and Zhou and Li [21] studied the free vibration of micro-Bernoulli–Euler beam, respectively. Fleck and Hutchinson [22, 23] extended and reformulated the classical couple stress theory and renamed it the strain gradient theory. The concepts of Mindlin’s [18] theory as well as Casal’s [24] theory are combined by Vardoulakis and Sulem [25], and then a simple theory of gradient elasticity with surface energy is proposed. On the basis of Vardoulakis and Sulem’s [25] theory, Papargyri-Beskou [26] developed a Bernoulli–Euler beam model and the problems of bending and stability of Bernoulli–Euler beams are solved analytically.

In addition, many microbeam models based on gradient theories have been proposed in recent years. Park and Gao [27] and Kong et al. [28] proposed a linear homogenous Bernoulli–Euler beam model, and the static problem and the dynamic problem are studied, respectively. Ma et al. [29] developed a linear homogenous Timoshenko beam model; the static bending, free vibration and Poisson effect problems are discussed. A variety of beam models are also proposed by Asghari et al. e.g., nonlinear homogenous Timoshenko beam model [30], linear functionally graded Bernoulli–Euler model [31] and Timoshenko beam model [32]. In these beam models, the equilibrium of the moment of couples is introduced as an additional equation for the couple stresses, and the couple stress tensor must be symmetric.

Besides that, under the framework of another gradient elasticity theory, Kong et al. [33] studied the static and dynamic problems for Bernoulli–Euler beams. Wang et al. [34] developed a microscale Timoshenko beam model, by which the static and dynamic analysis and Poisson’s effect are discussed. A Bernoulli–Euler beam model is also developed by Akgöz and Civalek, and the bulking problem [35] and various boundary conditions [36] are discussed. Moreover, it is extended to their functionally graded Bernoulli–Euler beam model. In these beam models, the dilatation gradients, deviatoric stretch gradients and rotation gradients are included in the governing equation. However, the constitutive formulation is extremely complicated and difficult for the analysis of structural behaviors.

As the development of higher-order continuum theories, the modified gradient elastic theory (MGE) has been proposed by Zhao et al. and Song et al. [37, 38], in which the micro-curvature as well as the gradients of normal strain is included. The internal length scales of MGE are defined anew by the partial derivative of the strain on the strain gradient. In such a way, the complexity decomposition of the strain gradient tensor is avoided, and the physical meaning of internal length scales gets clearer.

The purpose of this paper is to develop a microscale Bernoulli–Euler beam model based on the modified gradient elasticity. The rest parts are organized as follows. After the basic equations of MGE are reviewed, the governing equation as well as the boundary conditions of Bernoulli–Euler beam theory is derived by the variational principle based on MGE in Sect. 2. In Sect. 3, the static problems of cantilever beam subjected to bending moment or concentrated force are solved. In Sect. 4, the new beam model and some higher-order beam models are compared, and the influence of internal length scales on size effect is discussed. Finally, some major conclusions are given in Sect. 5.

2 Theory and beam model

2.1 A review of modified gradient elasticity

In references [37,38,39], the modified gradient elasticity (MGE) assumed that the strain energy density, \(W^{\mathrm {m}}\), depends on both the classical strain tensor \(\varepsilon _{ij}\) and the strain gradient tensor \(\eta _{ijk}\):

$$\begin{aligned} W^{\mathrm {m}}= & {} W^{\mathrm {m}}(\varepsilon _{ij} ,\eta _{ijk}), \end{aligned}$$
(1)
$$\begin{aligned} {\dot{W}}^{\mathrm {m}}= & {} \left( \frac{\partial W^{m}}{\partial \varepsilon _{ij} }\right) {\dot{\varepsilon }}_{ij} +\left( \frac{\partial W^{m}}{\partial \eta _{ijk}}\right) {\dot{\eta }}_{ijk} . \end{aligned}$$
(2)

The strain \(\varepsilon _{ij}\) and the strain gradient \(\eta _{ijk}\) are related to the displacement \(u_{i}\) by

$$\begin{aligned} \varepsilon _{ij} =\frac{1}{2}\left( u_{i,j} +u_{j,i}\right) \end{aligned}$$
(3)

and

$$\begin{aligned} \eta _{ijk} =\frac{\partial \varepsilon _{ij} }{\partial x_k }. \end{aligned}$$
(4)

For an isothermal and infinitesimal deformation process, \({\dot{W}}^{\mathrm {m}}\) can be written as:

$$\begin{aligned} {\dot{W}}^{\mathrm {m}}=\sigma _{ij} \dot{\varepsilon }_{ij} +\tau _{ijk} {\dot{\eta }}_{ijk} , \end{aligned}$$
(5)

where \(\sigma _{ij}\) is the Cauchy stress and \(\tau _{ijk}\) is the higher-order stress.

The substitution of Eq. (5) into (2) yields:

$$\begin{aligned} \left( {\left( \frac{\partial W^{\mathrm {m}}}{\partial \varepsilon _{ij} }\right) -\sigma _{ij} )} \right) {\dot{\varepsilon }}_{ij} +\left( {\left( \frac{\partial W^{\mathrm {m}}}{\partial \eta _{ijk} }\right) -\tau _{ijk} } \right) {\dot{\eta }}_{ijk} = 0 . \end{aligned}$$
(6)

Equation (6) holds for the arbitrary values of \({\dot{\varepsilon }}_{ij} \) and \({\dot{\eta }}_{ijk} \), which requires \(\sigma _{ij }\) and \(\tau _{ijk}\) to be conjugated with \(\varepsilon _{ij}\) and \(\eta _{ijk}\):

$$\begin{aligned} \frac{\partial W^{\mathrm {m}}}{\partial \varepsilon _{ij} }=\sigma _{ij} , \quad \frac{\partial W^{\mathrm {m}}}{\partial \eta _{ijk} }=\tau _{ijk} . \end{aligned}$$
(7)

Let

$$\begin{aligned} l_k = \frac{\partial \varepsilon _{ij} }{\partial \eta _{ijk}} (k=x, y, z), \end{aligned}$$
(8)

where \(l_{k}\) is a new extra material constant vector, called the internal length scale vector. It has the dimension of length, and it is the scale of microstructure interactions (physical meaning).

The initial state of a material is \(\varepsilon _{ij}=0\), \(\sigma _{ij}=0\), \(\eta _{ijk} =0\). Taylor’s series of the strain energy density with respect to \(\varepsilon _{ij}\) and \(\eta _{ijk}\) is expanded to the second power of \(\varepsilon _{ij}\) and \(\eta _{ijk}\):

$$\begin{aligned} W^{\mathrm {m}}= & {} W_0^{\mathrm{m}} +\left( {\frac{\partial W^{\mathrm {m}}}{\partial \varepsilon _{ij} }} \right) _0 \varepsilon _{ij} +\left( {\frac{\partial W^{\mathrm {m}}}{\partial \eta _{ijk} }} \right) _0 \eta _{ijk} +\frac{1}{2}\left( {\frac{\partial ^{2}W^{\mathrm {m}}}{\partial \varepsilon _{ij} \partial \varepsilon _{kl} }} \right) _0 \varepsilon _{ij} \varepsilon _{kl}\nonumber \\&+\frac{1}{2}\left( {\frac{\partial ^{2}W^{\mathrm {m}}}{\partial \eta _{ijk} \partial \eta _{mnq} }} \right) _0 \eta _{ijk} \eta _{mnq} +\left( {\frac{\partial ^{2}W^{\mathrm {m}}}{\partial \varepsilon _{ij} \partial \eta _{mnq} }} \right) _0 \varepsilon _{ij} \eta _{mnq} +\cdots \end{aligned}$$
(9)

Let

$$\begin{aligned} A_{ij} =\left( {\frac{\partial W^{\mathrm {m}}}{\partial \varepsilon _{ij} }} \right) _0 , \quad D_{ijkl} =\left( {\frac{\partial ^{2}W^{\mathrm {m}}}{\partial \varepsilon _{ij} \partial \varepsilon _{kl} }} \right) _0 , \end{aligned}$$
(10)

then

$$\begin{aligned} \left( {\frac{\partial W^{\mathrm {m}}}{\partial \eta _{ijk} }} \right) _0= & {} \left( {\frac{\partial W^{\mathrm {m}}}{\partial \varepsilon _{ij} }\frac{\partial \varepsilon _{ij} }{\partial \eta _{ijk} }} \right) _0 =\left( {\frac{\partial W^{\mathrm {m}}}{\partial \varepsilon _{ij} }} \right) _0 l_k = A_{ij} l_k, \end{aligned}$$
(11)
$$\begin{aligned} \left( {\frac{\partial ^{2}W^{\mathrm {m}}}{\partial \varepsilon _{ij} \partial \eta _{mnq} }} \right) _0= & {} D_{ijmn} l_q, \end{aligned}$$
(12)
$$\begin{aligned} \left( {\frac{\partial ^{2}W^{\mathrm {m}}}{\partial \eta _{ijk} \partial \eta _{mnq} }} \right) _0= & {} D_{ijmn} l_{q} l_{k}. \end{aligned}$$
(13)

The substitution of Eqs. (11)–(13) into (9) yields:

$$\begin{aligned} W^{\mathrm {m}}= & {} W_{0}^{\mathrm{m}} +A_{ij} \varepsilon _{ij} +A_{ij} l_{k} {\eta }_{ijk} +0.5D_{ijkl} \varepsilon _{ij} \varepsilon _{kl} \nonumber \\&+\,0.5D_{ijmn} l_{k} l_{q} \eta _{ijk} \eta _{mnq} +D_{ijmn} l_q {\varepsilon }_{ij} \eta _{mnq} . \end{aligned}$$
(14)

The substitution of Eq. (14) into (7) yields:

$$\begin{aligned} \sigma _{ij}= & {} \frac{\partial W^{\mathrm {m}}}{\partial \varepsilon _{ij} }= A_{ij} +D_{ijmn} \varepsilon _{mn} +D_{ijmn} l_{q}\eta _{mnq} , \end{aligned}$$
(15)
$$\begin{aligned} \tau _{ijk}= & {} \frac{\partial W^{\mathrm {m}}}{\partial \eta _{ijk} }= A_{ij} +D_{ijmn} \varepsilon _{mn} l_k +D_{ijmn} l_q l_{k} \eta _{mnq} . \end{aligned}$$
(16)

When material is unloaded completely to the initial state, \(\sigma _{ij}=0\), \(\varepsilon _{kl}=0\), \(\eta _{mnq}=0\), from Eqs. (15) and (16), it is found that \(A_{ij}=0\), \(W_{0}=0\); then, Eqs. (14)–(16) can be written as:

$$\begin{aligned} W^{\mathrm {m}}= & {} 0.5\cdot D_{ijkl} \varepsilon _{ij} \varepsilon _{kl} +\,0.5\cdot D_{ijmn} l_{k}l_{q} \eta _{ijk} \eta _{mnq}\nonumber \\&+D_{ijmn} l_{q} \varepsilon _{ij} \eta _{mnq} , \end{aligned}$$
(17)
$$\begin{aligned} \sigma _{ij}= & {} D_{ijmn} \left( {\varepsilon _{mn} +l_q \eta _{mnq} } \right) , \end{aligned}$$
(18)
$$\begin{aligned} \tau _{ijk}= & {} D_{ijmn} \left( {\varepsilon _{mn} +l_q \eta _{mnq} } \right) l_k, \end{aligned}$$
(19)

where \(D_{ijmn}\) is the elastic tensor.

Then, the modified gradient elasticity (MGE) was derived directly from the strain energy density expansion method. When the influence of strain gradients is neglected \((\eta _{ijk}=0)\), the internal length scales \(l_{k}\,(k=x,y,z)\) vanish, and the modified gradient elasticity can be simplified to the classical elastic constitutive equations. Note that both micro-curvature and gradients of normal strain are included in this theory.

2.2 Bernoulli–Euler beam model based on MGE

The classical Bernoulli–Euler beam theory assumes that the beam thickness is much less than the radius of curvature for a slender beam. The shear deformation is neglected, and the radius of curvature is induced only by bending moment. The coordinate system is chosen as Fig. 1, in which, the x-axis is along the beam length and coincides with the neutral axis, y-axis is along the beam wide, and z-axis is along the thickness. The cross-sectional area of the beam is constant Aalong the length of the beam. The component of the displacements along the wide direction is secondary and neglected in the beam theory.

Fig. 1
figure 1

Geometry and loading of the Bernoulli–Euler beam

Full size image

When the axial deformation is taken into account, the displacement is only the functions of x and z coordinates. Then, the displacement fields in a Bernoulli–Euler beam can be represented by [27, 40]

$$\begin{aligned} u=-z\phi (x), \quad v=0, \quad w=w(x), \end{aligned}$$
(20)

where u, v and w are, respectively, the x, y and z components of the displacement vector u, and \(\phi \) is the rotation angle of the neutral axis and is given by

$$\begin{aligned} \phi (x)=\frac{\hbox {d}w(x)}{\hbox {d}x}. \end{aligned}$$
(21)

From Eqs. (3), (20) and (21), it follows that

$$\begin{aligned} \varepsilon _{xx} =-z\frac{\hbox {d}^{2}w}{\hbox {d}x^{2}}, \quad \varepsilon _{yy} =\varepsilon _{zz} =\varepsilon _{xy} =\varepsilon _{yz} =\varepsilon _{zx} =0. \end{aligned}$$
(22)

The approach to establish a Bernoulli–Euler beam model based on MGE is proposed as follows.

Firstly, by substituting Eq. (22) into (4), the nonzero strain gradients \(\eta _{ijk}\) are

$$\begin{aligned} \eta _{xxx} =-z\frac{\hbox {d}^{3}w}{\hbox {d}x^{3}}, \eta _{xxz} =-\frac{\hbox {d}^{2}w}{\hbox {d}x^{2}}. \end{aligned}$$
(23)

For a slender Bernoulli–Euler beam with a large aspect ratio, the Poisson’s effect is secondary and may be neglected. By substituting Eqs. (22)–(23) into Eqs. (18)–(19), the nonzero stress components are obtained as

$$\begin{aligned} \sigma _{xx}= & {} -E\left( {z\frac{\hbox {d}^{2}w}{\hbox {d}x^{2}}+z\frac{\hbox {d}^{3}w}{\hbox {d}x^{3}}l_x +\frac{\hbox {d}^{2}w}{\hbox {d}x^{2}}l_z } \right) , \end{aligned}$$
(24)
$$\begin{aligned} \tau _{xxx}= & {} -E\left( {z\frac{\hbox {d}^{2}w}{\hbox {d}x^{2}}+z\frac{\hbox {d}^{3}w}{\hbox {d}x^{3}}l_x +\frac{\hbox {d}^{2}w}{\hbox {d}x^{2}}l_z } \right) l_x , \end{aligned}$$
(25)
$$\begin{aligned} \tau _{xxz}= & {} -E\left( {z\frac{\hbox {d}^{2}w}{\hbox {d}x^{2}}+z\frac{\hbox {d}^{3}w}{\hbox {d}x^{3}}l_x +\frac{\hbox {d}^{2}w}{\hbox {d}x^{2}}l_z } \right) l_z , \end{aligned}$$
(26)

where E is the Young’s modulus.

Secondly, the total strain energy U in a deformed isotropic linear elastic material occupying region \(\varOmega \) can be written as

$$\begin{aligned} U=\frac{1}{2}\int _\varOmega {(\sigma _{ij} \cdot \varepsilon _{ij} +\tau _{ijk} \cdot \eta _{ijk} )\hbox {d}\varOmega } . \end{aligned}$$
(27)

By substituting Eqs. (22)–(26) into (27), the total strain energy in the beam can be determined as

$$\begin{aligned} U=-\frac{1}{2}\int _0^L {M_{xx} \cdot \frac{\hbox {d}^{2}w}{\hbox {d}x^{2}}\hbox {d}x} -\frac{1}{2}\int _0^L {Y_{xxx} \cdot \frac{\hbox {d}^{3}w}{\hbox {d}x^{3}}\hbox {d}x} -\frac{1}{2}\int _0^L {Y_{xxz} \cdot \frac{\hbox {d}^{2}w}{\hbox {d}x^{2}}\hbox {d}x} , \end{aligned}$$
(28)

where L is the length of beam. \(M_{xx}\) and \(Y_{xxx}\) are classical bending moment and higher-order bending moment, respectively. \(Y_{xxz}\) is a new quantity which has the dimension of bending moment. \(M_{xx}\), \(Y_{xxx}\) and \(Y_{xxz}\) are defined as

$$\begin{aligned} M_{xx} =\int _A {\sigma _{xx} z\hbox {d}A} , \quad Y_{xxx} =\int _A {\tau _{xxx} z} \hbox {d}A, \quad Y_{xxz} =\int _A {\tau _{xxz} \hbox {d}A} . \end{aligned}$$
(29)

Substituting Eqs. (24)–(26) into (29), it follows that

$$\begin{aligned} M_{xx}= & {} -EI_y \frac{\hbox {d}^{2}w}{\hbox {d}x^{2}}-EI_y l_x \frac{\hbox {d}^{\mathrm {3}}w}{\hbox {d}x^{3}}, \end{aligned}$$
(30)
$$\begin{aligned} Y_{xxx}= & {} -EI_y l_x \frac{\hbox {d}^{2}w}{\hbox {d}x^{2}}-EI_y l_x^2 \frac{\hbox {d}^{3}w}{\hbox {d}x^{3}}, \end{aligned}$$
(31)
$$\begin{aligned} Y_{xxz}= & {} -EAl_z^2 \frac{\hbox {d}^{2}w}{\hbox {d}x^{2}}, \end{aligned}$$
(32)

where \(I_y =\int _A {z^{2}} \hbox {d}A\) is the second-order moment of the cross-sectional area with respect to the neutral axis.

By neglecting the body force, the work done by the external force is given by

$$\begin{aligned} W=\int _0^L {q(x)\cdot w\hbox {d}x} +\left. {[V\cdot w]} \right| _0^L +\left. {\left[ M\cdot \frac{\hbox {d}w}{\hbox {d}x}\right] } \right| _0^L +\left. {\left[ M^{\mathrm {h}}\cdot \frac{\hbox {d}^{2}w}{\hbox {d}x^{\mathrm {2}}}\right] } \right| _0^L , \end{aligned}$$
(33)

where q(x) is the lateral loading distributed along the longitudinal axis x of the beam, V is the boundary shear force, M is the boundary bending moment, and \(M^{h}\) is the boundary higher-order moment.

From Eqs. (28) and (33), the total potential energy \(\Pi \) in the loaded beam can be written as

$$\begin{aligned} \prod= & {} U-W \nonumber \\= & {} -\frac{1}{2}\int _0^L {\left( {M_{xx} \cdot \frac{\hbox {d}^{2}w}{\hbox {d}x^{2}}+Y_{xxx} \cdot \frac{\hbox {d}^{3}w}{\hbox {d}x^{3}}+Y_{xxz} \cdot \frac{\hbox {d}^{2}w}{\hbox {d}x^{2}}} \right) \hbox {d}x}\nonumber \\&-\int _0^L {q(x)\cdot w\hbox {d}x} -\left. {[V\cdot w]} \right| _0^L -\left. {\left[ M\cdot \frac{\hbox {d}w}{\hbox {d}x}\right] } \right| _0^L -\left. {\left[ M^{\mathrm {h}}\cdot \frac{\hbox {d}^{2}w}{\hbox {d}x^{\mathrm {2}}}\right] } \right| _0^L . \end{aligned}$$
(34)

The first variation of \(\prod \) is

$$\begin{aligned} {\updelta }\prod= & {} \int _0^L {\left[ {\delta }w\cdot \left( \frac{\hbox {d}^{\mathrm {3}}Y_{xxx} }{\hbox {d}x^{3}}-\frac{\hbox {d}^{\mathrm {2}}M_{xx} }{\hbox {d}x^{2}}-\frac{\hbox {d}^{\mathrm {2}}Y_{xxz} }{\hbox {d}x^{2}}-q\right) \right] d}x +\left. {\left[ \delta w\cdot \left( \frac{\hbox {d}M_{xx} }{\hbox {d}x}+\frac{\hbox {d}Y_{xxz} }{\hbox {d}x}-\frac{\hbox {d}^{2}Y_{xxx} }{\hbox {d}x^{2}}-V\right) \right] } \right| _0^L\nonumber \\&+\left. {\left[ \left( \frac{\hbox {d}Y_{xxx} }{\hbox {d}x}-M_{xx} -Y_{xxz} -M\right) \cdot \frac{\hbox {d}\delta w}{\hbox {d}x}\right] } \right| _0^L +\left. {\left[ \left( -Y_{xxx} -M^{\mathrm {h}}\right) \cdot \frac{\hbox {d}^{2}{\delta }w}{\hbox {d}x^{2}}\right] } \right| _0^L . \end{aligned}$$
(35)

Lastly, considering the minimum total potential energy principle, i.e., \(\delta \prod =0\) for the equilibrium state, and using the fundamental lemma of the calculus of variation and the arbitrary value of \(\delta w\), it can be given from Eq. (35) that

$$\begin{aligned} -\frac{\hbox {d}^{\mathrm {2}}M_{xx}}{\hbox {d}x^{2}}+\frac{\hbox {d}^{\mathrm {3}}Y_{xxx}}{\hbox {d}x^{3}}-\frac{\hbox {d}^{\mathrm {2}}Y_{xxz}}{\hbox {d}x^{2}}=q(x)\quad \quad \forall x\epsilon (0,L), \end{aligned}$$
(36)

as the governing equation, and

$$\begin{aligned} {\overline{V}}= & {} \frac{\hbox {d}M_{xx} }{\hbox {d}x}-\frac{\hbox {d}^{\mathrm {2}}Y_{xxx} }{\hbox {d}x^{2}}+\frac{\hbox {d}Y_{xxz} }{\hbox {d}x}\quad \hbox { or }\quad {\delta }w=0\qquad \hbox { at }x=0\hbox { and }x=L, \end{aligned}$$
(37)
$$\begin{aligned} {\overline{M}}= & {} -M_{xx} -Y_{xxz} +\frac{\hbox {d}Y_{xxx} }{\hbox {d}x}\quad \quad \,\hbox { or }\quad \frac{\hbox {d}\delta w}{\hbox {d}x}=0\quad \,\,\hbox { at }x=0\hbox { and }x=L, \end{aligned}$$
(38)
$$\begin{aligned} \overline{M^{\mathrm {h}}}= & {} -Y_{xxx}\qquad \qquad \qquad \qquad \qquad \quad \hbox { or }\quad \frac{\hbox {d}^{\mathrm {2}}{\delta }w}{\hbox {d}x^{2}}=0 \quad \hbox { at }x=0\hbox { and }x=L, \end{aligned}$$
(39)

as the boundary conditions, where the overbar represents the prescribed value at a boundary.

Substituting Eqs. (30)–(32) into Eqs. (36)–(39), the governing equation becomes

$$\begin{aligned} EI_y \frac{\hbox {d}^{4}w}{\hbox {d}x^{4}}-EI_y l_x^2 \frac{\hbox {d}^{6}w}{\hbox {d}x^{6}}+EAl_z^2 \frac{\hbox {d}^{4}w}{\hbox {d}x^{4}}=q(x), \end{aligned}$$
(40)

and the boundary conditions become

$$\begin{aligned} {\overline{V}}= & {} -EI_y \frac{\hbox {d}^{3}w}{\hbox {d}x^{3}}-EAl_z^2 \frac{\hbox {d}^{3}w}{\hbox {d}x^{3}}+EI_y l_x^2 \frac{\hbox {d}^{5}w}{\hbox {d}x^{5}}\quad \hbox { or }\quad {\delta }w=0\qquad \,\hbox { at }x=0 \hbox { and }x=L, \end{aligned}$$
(41)
$$\begin{aligned} {\overline{M}}= & {} EI_y \frac{\hbox {d}^{2}w}{\hbox {d}x^{2}}+EAl_z^2 \frac{\hbox {d}^{2}w}{\hbox {d}x^{2}}-EI_y l_x^2 \frac{\hbox {d}^{4}w}{\hbox {d}x^{4}}\quad \quad \hbox { or }\quad \frac{\hbox {d}\delta }{w}{\hbox {d}x}=0\quad \hbox { at }x=0\hbox { and }x=L, \end{aligned}$$
(42)
$$\begin{aligned} \overline{M^{\mathrm {h}}}= & {} EI_y l_x \frac{\hbox {d}^{2}w}{\hbox {d}x^{2}}+EI_y l_x^2 \frac{\hbox {d}^{3}w}{\hbox {d}x^{3}}\qquad \qquad \qquad \qquad \hbox { or }\quad \frac{\hbox {d}^{\mathrm {2}}\delta w}{\hbox {d}x^{2}}=0\quad \hbox { at } x=0\hbox { and }x=L. \end{aligned}$$
(43)

It can be seen from Eqs. (40)–(43) that the MGE Bernoulli–Euler beam model contains two additional material constants, i.e., \(l_{x}\) and \(l_{z}\). It can also be seen from Eqs. (41)–(43) that in the higher-order beam model, not only the classical boundary conditions but also the non-classical boundary conditions should be satisfied. When the influence of strain gradients is neglected (i.e., \(l_{x}\) and \(l_{z}\) vanish), the present beam model can be simplified to the classical Bernoulli–Euler beam theory.

3 Examples: cantilever beam problem

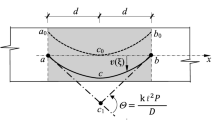
A rectangular cantilever beam is studied by MGE Bernoulli–Euler beam model in this section. The geometry and cross-sectional shape are shown in Fig. 2. Two typical loadings, a bending moment M (case 1) and a concentrated force Q (case 2), are applied at the free end, respectively. The classical beam properties are taken to be same with [11, 33, 41]: \(b/h=2\), \(L=20h\) and \( E=1.44\hbox {GPa}\). The additional length parameters, i.e., \(l_{x}\) and \(l_{z}\), are taken to be comparable to the thickness of beam, like the references [11, 33, 41], so the internal length scales are taken the values in the interval of 0.5h–1.5h.

Fig. 2
figure 2

A cantilever beam subjected to a moment (case 1) or a concentrated force (case 2) at the free end

Full size image

3.1 Boundary conditions statement

There are two possible boundary conditions (BC1 and BC2) illustrated in references [33]. The difference between these two boundary conditions is that the non-classical boundary conditions at the fixed end are different.

The classical boundary conditions for the cases shown in Fig. 2 are specified, for case 1:

$$\begin{aligned} \left. w \right| _{x=0} =0, \quad \left. {\frac{\hbox {d}w}{\hbox {d}x}} \right| _{x=0} =0, \quad \left. {{\overline{V}} } \right| _{x=L} =0, \quad \left. {{\overline{M}} } \right| _{x=L} =M, \end{aligned}$$
(44)

and for case 2:

$$\begin{aligned} \left. w \right| _{x=0} =0, \quad \left. {\frac{\hbox {d}w}{\hbox {d}x}} \right| _{x=0} =0, \quad \left. {{\overline{V}} } \right| _{x=L} =Q, \quad \left. {{\overline{M}} } \right| _{x=L} =0. \end{aligned}$$
(45)

The two possible non-classical boundary conditions for both case 1 and case 2 are

BC1:

$$\begin{aligned} \left. {\overline{M^{\mathrm {h}}} } \right| _{x=0} =0, \quad \left. {\overline{M^{\mathrm {h}}} } \right| _{x=L} =0. \end{aligned}$$
(46)

BC2:

$$\begin{aligned} \left. {\frac{\hbox {d}^{\mathrm {2}}w}{\hbox {d}x^{2}}} \right| _{x=0} =0, \quad \left. {\overline{M^{\mathrm {h}}} } \right| _{x=L} =0. \end{aligned}$$
(47)

As discussed in references [33], there is no much difference between the two boundary conditions. In this paper, the non-classical boundary conditions are chosen as BC1.

3.2 Case 1: bending moment loading

Firstly, the cantilever beam is only subjected to a bending moment, M, at the free end \((Q=0, q(x)=0)\). The governing equation Eq. (40) becomes

$$\begin{aligned} EI_y \frac{\hbox {d}^{4}w}{\hbox {d}x^{4}}-EI_y l_x^2 \frac{\hbox {d}^{6}w}{\hbox {d}x^{6}}+EAl_z^2 \frac{\hbox {d}^{4}w}{\hbox {d}x^{4}}=0. \end{aligned}$$
(48)

According to the general solution of differential equation, the solution of Eq. (48) can be written as

$$\begin{aligned} w(x)=C_1 +C_2 x+C_3 x^{2}+C_4 x^{3}+C_5 \mathrm{{e}}^{\lambda x}+C_6 \mathrm{{e}}^{-\lambda x}, \end{aligned}$$
(49)

where \(\lambda =\sqrt{EI_y +EAl_z^2 }/\sqrt{EI_y l_x^2 }\).

The boundary conditions can be derived from Eqs. (44) and (46) as

$$\begin{aligned} \left. w \right| _{x=0}= & {} 0, \end{aligned}$$
(50a)
$$\begin{aligned} \left. {\frac{\hbox {d}w}{\hbox {d}x}} \right| _{x=0}= & {} 0, \end{aligned}$$
(50b)
$$\begin{aligned} \left. {{\overline{V}} } \right| _{x=L}= & {} \left. {\left( {-EI_y \frac{\hbox {d}^{3}w}{\hbox {d}x^{3}}-EAl_z^2 \frac{\hbox {d}^{3}w}{\hbox {d}x^{3}}+EI_y l_x^2 \frac{\hbox {d}^{5}w}{\hbox {d}x^{5}}} \right) } \right| _{x=L} =0, \end{aligned}$$
(50c)
$$\begin{aligned} \left. {{\overline{M}} } \right| _{x=L}= & {} \left. {\left( {EI_y \frac{\hbox {d}^{2}w}{\hbox {d}x^{2}}+EAl_z^2 \frac{\hbox {d}^{2}w}{\hbox {d}x^{2}}-EI_y l_x^2 \frac{\hbox {d}^{4}w}{\hbox {d}x^{4}}} \right) } \right| _{x=L} =M, \end{aligned}$$
(50d)
$$\begin{aligned} \left. {\overline{M^{\mathrm {h}}} } \right| _{x=0}= & {} \left. {\left( {EI_y l_x \frac{\hbox {d}^{2}w}{\hbox {d}x^{2}}+EI_y l_x^2 \frac{\hbox {d}^{3}w}{\hbox {d}x^{3}}} \right) } \right| _{x=0} =0, \end{aligned}$$
(50e)
$$\begin{aligned} \left. {\overline{M^{\mathrm {h}}} } \right| _{x=L}= & {} \left. {\left( {EI_y l_x \frac{\hbox {d}^{2}w}{\hbox {d}x^{2}}+EI_y l_x^2 \frac{\hbox {d}^{3}w}{\hbox {d}x^{3}}} \right) } \right| _{x=L} =0. \end{aligned}$$
(50f)

Substituting Eq. (50a–50f) into (49), the boundary conditions can be written as

$$\begin{aligned}&C_1 +C_5 +C_6 =0 \end{aligned}$$
(51a)
$$\begin{aligned}&C_2 +C_5 \lambda -C_6 \lambda =0 \end{aligned}$$
(51b)
$$\begin{aligned}&-\Big (EI_y +EAl_z^2 \Big )\Big (6C_4 +C_5 \lambda ^{3}\hbox {e}^{\lambda L}-C_6 \lambda ^{3}\hbox {e}^{-\lambda L}\Big )+EI_y l_x^2 \Big (C_5 \lambda ^{5}\hbox {e}^{\lambda L}-C_6 \lambda ^{5}\hbox {e}^{-\lambda L}\Big )=0 \end{aligned}$$
(51c)
$$\begin{aligned}&\Big (EI_y +EAl_z^2 \Big )\Big (2C_3 +6C_4 L+C_5 \lambda ^{2}\hbox {e}^{\lambda L}+C_6 \lambda ^{2}\hbox {e}^{-\lambda L}\Big )-EI_y l_x^2 \Big (C_5 \lambda ^{4}\hbox {e}^{\lambda L}+C_6 \lambda ^{4}\hbox {e}^{-\lambda L}\Big )=M\qquad \quad \end{aligned}$$
(51d)
$$\begin{aligned}&EI_y l_x \Big (2C_3 +C_5 \lambda ^{2}+C_6 \lambda ^{2}\Big )+EI_y l_x^2 \Big (6C_4 +C_5 \lambda ^{3}-C_6 \lambda ^{3}\Big )=0 \end{aligned}$$
(51e)
$$\begin{aligned}&EI_y l_x \Big (2C_3 +6C_4 L+C_5 \lambda ^{2}\hbox {e}^{\lambda L}+C_6 \lambda ^{2}\hbox {e}^{-\lambda L}\Big )+EI_y l_x^2 \Big (6C_4 +C_5 \lambda ^{3}\hbox {e}^{\lambda L}-C_6 \lambda ^{3}\hbox {e}^{-\lambda L}\Big )=0. \end{aligned}$$
(51f)

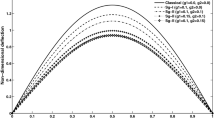
Equation (51a–51f) is solvable, so that the coefficients \(C_{1}-C_{6}\) can be calculated. However, the forms of \(C_{1}-C_{6}\) are too long and prohibit their presentation here. Nevertheless, when \(h=20\,\upmu \hbox {m}\), \(M=0.03\,\upmu \hbox {N}\,\hbox {m}\) and \(l_{x}=l_{z}\), an application is worked out to indicate the influence of the internal length scales included in the beam governing equation and boundary conditions. The deflection curves of the cantilever beam are shown in Fig. 3. It can be seen that, when \(l_{x}=l_{z}=10\,\upmu \hbox {m}\,(0.5h)\), the ratio between the deflections of MGE Bernoulli–Euler beam theory and the classic beam theory is about 25.61%. The deflections of MGE Bernoulli–Euler beam theory decrease with the increment of internal length scales.

Fig. 3
figure 3

Deflections of cantilever beam subjected to bending moment

Full size image

3.3 Case 2: concentrated force loading

Secondly, another typical loading Q is applied to the cantilever beam at the free end \((M=0, q(x)=0)\); the governing equation can be written as

$$\begin{aligned} EI_y \frac{\hbox {d}^{4}w}{\hbox {d}x^{4}}-EI_y l_x^2 \frac{\hbox {d}^{6}w}{\hbox {d}x^{6}}+EAl_z^2 \frac{\hbox {d}^{4}w}{\hbox {d}x^{4}}=0. \end{aligned}$$
(52)

The solution of Eq. (52) also can be written as

$$\begin{aligned} w(x)=C_1 +C_2 x+C_3 x^{2}+C_4 x^{3}+C_5 e^{\lambda x}+C_6 \mathrm{{e}}^{-\lambda x}. \end{aligned}$$
(53)

The boundary conditions can be derived from Eqs. (45) and (46) as:

$$\begin{aligned} \left. w \right| _{x=0}= & {} 0, \end{aligned}$$
(54a)
$$\begin{aligned} \left. {\frac{\hbox {d}w}{\hbox {d}x}} \right| _{x=0}= & {} 0, \end{aligned}$$
(54b)
$$\begin{aligned} \left. {{\overline{V}} } \right| _{x=L}= & {} \left. {\left( {-EI_y \frac{\hbox {d}^{3}w}{\hbox {d}x^{3}}-EAl_z^2 \frac{\hbox {d}^{3}w}{\hbox {d}x^{3}}+EI_y l_x^2 \frac{\hbox {d}^{5}w}{\hbox {d}x^{5}}} \right) } \right| _{x=L} =Q, \end{aligned}$$
(54c)
$$\begin{aligned} \left. {{\overline{M}} } \right| _{x=L}= & {} \left. {\left( {EI_y \frac{\hbox {d}^{2}w}{\hbox {d}x^{2}}+EAl_z^2 \frac{\hbox {d}^{2}w}{\hbox {d}x^{2}}-EI_y l_x^2 \frac{\hbox {d}^{4}w}{\hbox {d}x^{4}}} \right) } \right| _{x=L} =0, \end{aligned}$$
(54d)
$$\begin{aligned} \left. {\overline{M^{\mathrm {h}}} } \right| _{x=0}= & {} \left. {\left( {EI_y l_x \frac{\hbox {d}^{2}w}{\hbox {d}x^{2}}+EI_y l_x^2 \frac{\hbox {d}^{3}w}{\hbox {d}x^{3}}} \right) } \right| _{x=0} =0, \end{aligned}$$
(54e)
$$\begin{aligned} \left. {\overline{M^{\mathrm {h}}} } \right| _{x=L}= & {} \left. {\left( {EI_y l_x \frac{\hbox {d}^{2}w}{\hbox {d}x^{2}}+EI_y l_x^2 \frac{\hbox {d}^{3}w}{\hbox {d}x^{3}}} \right) } \right| _{x=L} =0. \end{aligned}$$
(54f)

By substituting Eq. (54a–54f) into (53), a solvable equation set can be obtained. In spite of the solvability of Eq. (54a–54f), the forms of \(C_{1}\)–\(C_{6}\) are long and difficult to be reported here. However, when \(h=20\,\upmu \hbox {m}\), \(Q=100\,\upmu \hbox {N}\) and \(l_{x}=l_{z}\), an application has been worked out to demonstrate the influence of the internal length scales on deflections. The deflection curves of the cantilever beam are shown in Fig. 4. It can be seen that, when \(l_{x}=l_{z}=10\,\upmu \hbox {m }(0.5h)\), the ratio between the deflections of MGE Bernoulli–Euler beam theory and the classic beam theory is about 25.90%. The deflections of MGE Bernoulli–Euler beam theory also decrease with the increment of internal length scales in this case.

Fig. 4
figure 4

Deflections of cantilever beam subjected to concentrate force

Full size image

4 Discussion

4.1 The comparison of microbeam models

Based on the couple stress theory or the extended couple stress theory, e.g., [27, 41], various higher-order Bernoulli–Euler beam models have been proposed [27, 28, 31]. The intrinsic length parameter is introduced into constitutive equation by shear modulus and couple stress as:

$$\begin{aligned} m_{ij} =2l^{2}G\chi _{ij} , \end{aligned}$$
(55)

where \(m_{ij}\) is the symmetric part of the couple stress tensor, l is the intrinsic length parameter, G is the shear modulus, and \(x_{ij}\) is the symmetric part of the curvature (or rotation gradient) tensor. Then, even though the shear strains are not considered, the shear modulus G appears in their governing equation, e.g., [27]:

$$\begin{aligned} \Big (EI+GAl^{2}\Big )\frac{\hbox {d}^{4}w}{\hbox {d}x^{4}}=q(x). \end{aligned}$$
(56)

It is a fourth-order partial differential equation.

Different from Eq. (55), the intrinsic length parameters are introduced by the partial derivative of the strain on the strain gradient in MGE Bernoulli–Euler beam model, and the shear modulus does not appear in its governing equation [Eq. (40)]. The governing equation is sixth-order partial differential equation.

A beam model proposed by Lazopoulos in ref [42] has a similar form with MGE Bernoulli–Euler beam model. Even though its constitutive equation contains additional length parameters, i.e., \(l_{k}\) (the direction surface length, \( k=x\), y, z) and g (the intrinsic bulk length), the governing equation of beam model does not include \(l_{k}\):

$$\begin{aligned} EI_y \frac{\hbox {d}^{4}w}{\hbox {d}x^{4}}-EI_y g^{2}\frac{\hbox {d}^{6}w}{\hbox {d}x^{6}}+EAg^{2}\frac{\hbox {d}^{4}w}{\hbox {d}x^{4}}+q(x)=0, \end{aligned}$$
(57)

and the boundary conditions include \(l_{k}\) as:

$$\begin{aligned} {\overline{V}}= & {} E\Big (I_y +g^{2}A\Big )\frac{\hbox {d}^{3}w}{\hbox {d}x^{3}}-EI_y g^{2}\frac{\hbox {d}^{5}w}{\hbox {d}x^{5}}\quad \hbox { or }\quad {\delta }w=0\quad \quad \quad \hbox { at } x=0\hbox { and }x=L, \end{aligned}$$
(58)
$$\begin{aligned} {\overline{M}}= & {} E\Big (I_y +g^{2}A\Big )\frac{\hbox {d}^{2}w}{\hbox {d}x^{2}}-EI_y g^{2}\frac{\hbox {d}^{4}w}{\hbox {d}x^{4}}\quad \hbox { or }\quad \frac{{\hbox {d}\delta }w}{\hbox {d}x}=0\quad \quad \hbox { at }x=0\hbox { and }x=L, \end{aligned}$$
(59)
$$\begin{aligned} \overline{M^{\mathrm {h}}}= & {} EI_y g^{2}\frac{\hbox {d}^{3}w}{\hbox {d}x^{3}}+EI_y l_x \frac{\hbox {d}^{2}w}{\hbox {d}x^{2}}\qquad \qquad \quad \hbox { or }\quad \frac{\hbox {d}^{\mathrm {2}}{\delta }w}{\hbox {d}x^{2}}=0\quad \,\hbox { at } x=0\hbox { and }x=L. \end{aligned}$$
(60)

In Lazopoulos’ beam model, the values of the additional length parameters are restricted as \(0< l_{x} < g^{2}\) [25, 26]. In the MGE Bernoulli–Euler beam model, both of \(l_{x}\) and \(l_{z}\) are included in the governing equation and the boundary conditions, and the values of \(l_{x}\) and \(l_{z}\) have no restriction. Hence, the situation of \(l_{x} < l_{z}\) or \(l_{x} > l_{z}\) can be investigated and the influence of strain gradients on x direction and z direction can be discussed.

4.2 The influence of the internal length scales on deflections

To investigate the influence of \(l_{x}\) and \(l_{z}\) on beam deflection, the beam in Sect. 3 is studied in this section by changing the values of \(l_{x}\) and \(l_{z}\): One remains a constant and the other one changed. Two cases of loading are also considered, respectively. It can be seen from Figs. 5 and 6 that, when \(l_{x}\) remains a constant, the beam deflections decrease obviously with \(l_{z}\) increasing. Different from it, when \(l_{z}\) remains a constant, the beam deflections change slightly with \(l_{x}\) increasing. It confirmed that the influence of \(l_{z}\) on deflections is much greater than that of \(l_{x}\), and the increment of stiffness is mainly controlled by \(l_{z}\).

Fig. 5
figure 5

Deflections of beam subjected to bending moment. a\(l_{z}\) changes only, b\(l_{x}\) changes only

Full size image
Fig. 6
figure 6

Deflections of beam subjected to concentrate force. a\(l_{z}\) changes only, b\(l_{x}\) changes only

Full size image

4.3 Features

The internal length scale parameters contained in MGE Bernoulli–Euler beam model have a clear physical meaning and a brief form [38], so that the internal length scale parameters can be determined not only by the experiments, but also by the microstructure of the materials, and the values of internal length scale parameters are not restricted. It makes the present beam model convenient for engineering applications.

It is easy for MGE Bernoulli–Euler beam model to consider the anisotropy of gradient. The influence of strain gradients along the beam length and thickness direction can be analyzed, and the value of internal length scale can be adjusted by microstructure of materials. So the present beam model can be applied for the design optimization of microbeam and its materials used in engineering applications.

5 Conclusions

A new Bernoulli–Euler beam model within modified gradient elasticity is proposed in this paper. When the internal length scales vanish, MGE Bernoulli–Euler beam model can be simplified to the classical Bernoulli–Euler beam theory. The deflections of the cantilever beams subjected to two typical loadings are analyzed. The deflections decrease with the internal length scales increasing, and the size effect can be captured by MGE Bernoulli–Euler beam model. The influences of strain gradients on x direction and z direction are discussed. The influence of \(l_{z}\) on deflection is much greater than that of \(l_{x}\), and the increment of stiffness is mainly controlled by \(l_{z}\). The internal length scale parameters contained in MGE Bernoulli–Euler beam model have a clear physical meaning and a brief form; thus, MGE Bernoulli–Euler beam model is of great useful in engineering applications and designs.