Keywords

1 Introduction

In recent years, the growing demand on applications of microelectromechanical systems (MEMS) in diverse subjects of sciences and engineering has led to an upsurge of interests in developing microscale beam-type structures. It has been experimentally observed that those tiny-scale structures exhibit significant size-dependent behaviors [1]. Among theories capable of modeling such characteristics, the modified couple stress theory (MCST) [2] has been widely used by many researchers to develop the governing equations of microstructure-dependent beams [3,4,5]. The variational beam formulation based upon the MCST, however, requires C1 or higher-order continuity interpolation functions in the solution procedure, and this strong requirement does not flavor the use of conventional finite element method in the analysis. Such shortcoming has been recently overcome by the development of the isogeometric analysis (IGA) [6], being able to deal with higher-order elements (e.g., [7]). However, an intensive literature survey has indicated that most of existing studies on microscale structures, especially the micro-beams, were limited mainly to the deterministic analysis, which generally ignores inherent uncertainties possibly induced during the fabrication process and throughout their lifespan. Only few investigations to fully integrate the nondeterministic aspect in the simulations have been documented. For instance, Mohammadi et al. [8] studied the influence of the randomness in material properties and geometric parameters on the mechanical response of geometrical nonlinear functionally graded micro-beams using Monte Carlo simulation (MCS). Although the MCS possesses several desirable features including the simplicity and accuracy, the method itself has been found computationally demanding. Recently, the so-called spectral stochastic finite element method (SSFEM) [9], intensively employed to quantify the effects of uncertainties, was extended within the framework of IGA and termed the spectral stochastic isogeometric analysis (SSIGA) [10]. The implemented scheme exhibits not only a powerful ability to model random fields within complex domains and a smooth and effective spectral decomposition of the covariance function of the random fields via Karhunen-Loève (K-L) expansion, but also a high computational efficiency in comparison with the MCS. Due to the attractive advantages of the SSIGA, the technique is implemented, for the first time, to integrate the structural material uncertainty into the analysis of Timoshenko microscale beams based on the MCST.

2 Isogeometric Timoshenko Beam Formulation Based on MCST

Fig. 1
figure 1

Reference coordinate system and geometry of a microscale beam

Full size image

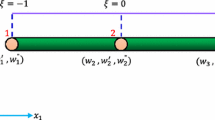
Consider a straight micro-beam of length L and rectangular-cross section \(b \times h\) as shown schematically in Fig. 1. The beam is made of a linear elastic material with Young’s modulus \(E\), shear modulus \(\mu\), and length scale parameter \(\ell\), and loaded by a uniformly distributed transverse load \(q_{z}\). Non-zero components of the displacement vector following Timoshenko beam theory can be expressed as [3]

$$ u_{x} (x,z) = u(x) - z\phi (x), \, u_{y} (x,z) = 0, \, u_{z} (x,z) = w(x) $$
(1)

where \(\{ u,w,\phi \}\) denote the axial displacement, transverse displacement, and rotation of the cross section, respectively. From linearized kinematics and constitutive laws, the non-zero components of the strain \(\{ \varepsilon_{xx} ,\varepsilon_{xz} ,\varepsilon_{zx} \}\) and the curvature \(\{ \chi_{xy} ,\chi_{yx} \}\) are related to the displacements and rotation \(\{ u,w,\phi \}\) and the non-zero components of the force stress \(\{ \sigma_{xx} ,\sigma_{xz} ,\sigma_{zx} \}\) and the couple stress \(\{ m_{xy} ,m_{yz} \}\) by [3]:

$$ \varepsilon_{xx} = \frac{du}{{dx}} - z\frac{d\phi }{{dx}},\varepsilon_{xz} = \varepsilon_{zx} = \frac{1}{2}\left( {\frac{dw}{{dx}} - \phi } \right),\chi_{xy} = \chi_{yx} = - \frac{1}{4}\left( {\frac{d\phi }{{dx}} + \frac{{d^{2} w}}{{dx^{2} }}} \right) $$
(2)
$$ \sigma _{{xx}} = E\varepsilon _{{xx}} ,\sigma _{{xz}} = \sigma _{{zx}} = 2\mu \varepsilon _{{xz}} ,m_{{xy}} = m_{{yx}} = 2\mu {\ell }^{2} \chi _{{xy}} $$
(3)

From the principle of virtual work, the force-stress and couple-stress components must satisfy

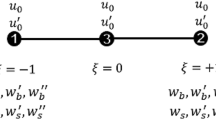
$$ \int\limits_{\Omega }^{{}} {(\sigma_{xx} \delta \varepsilon_{xx} + 2\sigma_{xz} \delta \varepsilon_{xz} + 2m_{xy} \delta \chi_{xy} )d\Omega } = \int\limits_{0}^{L} {q_{z} \delta wdx} $$
(4)

where \(\delta \varepsilon_{xx}\), \(\delta \varepsilon_{xz}\), \(\delta \chi_{xy}\) are the virtual strains and virtual curvature resulting from any virtual displacements and rotation \(\{ \delta u,\delta w,\delta \phi \}\) via the kinematics (2). According to the framework of IGA [6], the B-spline basis functions used to describe the geometry of the beam are also adopted in the discretization of the displacement field:

$$ {\textbf{u}}\left( \xi \right) = [\begin{array}{*{20}c} u & w & \phi \\ \end{array} ]^{T} = \sum\limits_{i = i}^{{N_{cp} }} {N_{i,p} (\xi ){\textbf{u}}_{i} } $$
(5)

where \(N_{i,p} \left( \xi \right)\) is the B-spline basis function of order \(p\) and \({\textbf{u}}_{i}\) is the displacement vector at the control point. Substituting (5) and all involved fields into (4) leads to a system of linear algebraic equations

$$ {\textbf{Ku}} = {\textbf{F}} $$
(6)

where \({\textbf{K}}\) and \({\textbf{F}}\) denote the global stiffness matrix and global force vector, respectively.

3 Spectral Stochastic Isogeometric Analysis

In the present study, the uncertainty on the elastic modulus \(E\) is taken into account by considering its spatial variation as a Gaussian stochastic field which is represented by the K-L expansion of the second kind with the covariance function \(C(x,x^{\prime})\) [10]:

$$ E_{G} (x,\theta ) = \left[ {\mu_{E} + \sum\limits_{j = 1}^{\infty } {\sqrt {\lambda_{j} } \zeta_{j} (\theta )\varphi_{j} (x)} } \right]E $$
(7)
$$ \forall j = 1, \ldots \int\limits_{D}^{{}} {C(x,x^{\prime})\varphi_{j} (x^{\prime})dD_{x^{\prime}} = } \lambda_{j} \varphi_{j} (x) $$
(8)

where \(\mu_{E}\) is the mean of the random field, \(\zeta_{j} (\theta )\) is a set of orthogonal random variables, \(\lambda_{j}\) and \(\varphi_{j} (x)\) are eigenvalues and the corresponding eigenfunctions of the given covariance function \(C(x,x^{\prime})\) of two points \(x\) and \(x^{\prime}\) in the random field domain \(D\), respectively, and \(\theta\) indicates the sample set of the probability space.

To obtain the eigen-solution of Fredholm integral Eq. (8) for arbitrary covariance functions or domains, Galerkin isogeometric method [10] is employed. In particular, each eigenfunction \(\varphi_{j} (x)\) can be represented by

$$ \varphi_{j} (x) = \sum\limits_{i = 1}^{{N_{cp} }} {N_{i,p} (\xi )\upsilon_{i}^{j} } $$
(9)

where \(\upsilon_{i}^{j}\) is the unknown coefficient associated with the ith B-spline basis function. Hence, the random field given by (7) with a constant mean can be discretized by

$$ E_{G} (x,\theta ) = \left[ {\mu_{E} + \sum\limits_{j = 1}^{\infty } {\sqrt {\lambda_{j} } \zeta_{j} (\theta )\left( {\sum\limits_{i = 1}^{{N_{cp} }} {N_{i} (\xi )\upsilon_{i}^{j} } } \right)} } \right]E $$
(10)

Enforcing (10) together with the discretization (5), the weak form Eq. (4) now becomes

$$ \left[ {\sum\limits_{j = 0}^{\infty } {{\textbf{K}}_{j} (\theta )\zeta_{j} (\theta )} } \right] \cdot {\textbf{u}}(\theta ) = {\textbf{F}} $$
(11)

where \(\zeta_{0} (\theta ) = 1\) and

$$ {\textbf{K}}_{0} = \mu_{E} {\textbf{K}} $$
(12)
$$ {\varvec{K}}_{j} (\theta ) = \sqrt {\lambda _{j} } \left( {\sum\limits_{{i = 1}}^{{N_{{cp}} }} {N_{{i,p}} (\xi )\upsilon _{i}^{k} } } \right){\varvec{K}}\;{\text{with}}\;\forall j = 1, \ldots $$
(13)

By adopting the arbitrary polynomial chaos expression (aPCE) [10], the structural displacement of the stochastic linear system (11) can be represented by

$$ {\textbf{u}}(\theta ) = \sum\limits_{k = 0}^{\infty } {{\textbf{u}}_{k} \psi_{k} (\theta )} $$
(14)

where \(\{ \psi_{k} (\theta ), \, k = 0,1, \ldots ,\infty \}\) denotes the polynomial chaos basis function of order \(\overline{p}\). By substituting (14) into (11), it leads to the stochastic governing equation of the micro-beam:

$$ \left[ {\sum\limits_{j = 0}^{\infty } {{\textbf{K}}_{j} (\theta )\zeta_{j} (\theta )} } \right]\left[ {\sum\limits_{k = 0}^{\infty } {{\textbf{u}}_{k} \psi_{k} (\theta )} } \right] = {\textbf{F}} $$
(15)

A finite number of terms are finally retained in both expansions (i.e., \(M\) terms in the K-L expansion and \(P\) terms in the aPCE) leading to a residual of (15) that has to be minimized in the mean square sense in order to obtain the optimal approximation of the exact solution \({\textbf{u}}(\theta )\)[10]. After some algebraic manipulations, the following system is finally obtained:

$$ \sum\limits_{k = 0}^{P - 1} {{\textbf{K}}_{kg} } {\textbf{u}}_{k} = {\textbf{F}}_{g} \, (g = 0, \ldots ,P - 1) $$
(16)

where \({\textbf{K}}_{kg} = \sum\limits_{j = 0}^{M} {c_{jkg} {\textbf{K}}_{j} }\), \(c_{jkg} = \left\langle {\zeta_{j} (\theta )\psi_{k} (\theta ),\psi_{g} (\theta )} \right\rangle\), \({\textbf{F}}_{g} = \left\langle {{\textbf{F}},\psi_{g} (\theta )} \right\rangle\), \(\left\langle \cdot \right\rangle\) denotes the mathematical expectation, and the integer \(P\) is computed by

$$ P = \left( {\begin{array}{*{20}c} {M + \overline{p}} \\ {\overline{p}} \\ \end{array} } \right) = \frac{{(M + \overline{p})!}}{{M!\overline{p}!}} $$
(17)

The approximate stochastic displacement \({\textbf{u}}(\theta )\) can then be obtained by solving the stochastic system (16) together with the approximation (14). Consequently, its mean vector and covariance matrix can be directly determined:

$$ \left\langle {\textbf{u}} \right\rangle = {\textbf{u}}_{0} $$
(18)
$$ COV({\textbf{u}},{\textbf{u}}) = \sum\limits_{k = 1}^{P - 1} {\left\langle {\psi_{k}^{2} } \right\rangle {\textbf{u}}_{k} {\textbf{u}}_{k}^{T} } $$
(19)

4 Preliminary Results

The normalized deterministic mid-span deflections, \(\overline{w} = wEI{/}qL^{4}\), of a simply supported microbeam made from epoxy and subjected to a uniformly distributed transverse load \(q_{0} = 1 \, N{/}m\) are compared with those reported by Reddy [5] in Table 1. The following material and geometric parameters are used in the numerical analysis: \(E = 1.44 \, GPa\), \(\ell = 17.6 \times 10^{ - 6} \, m\), \(v = 0.38\), \(L = 20h\), \(b = 2h\) with \(h{/}\ell = \left\{ {1,5} \right\}\). As can be seen in the Table 1, the polynomial order \(p = 3\) exhibits higher accuracy and convergence rate than \(p = 2\) in comparison with the reported benchmark solutions. Upon the convergence study, the cubic B-spline patch with 20 control points is sufficient to generate accurate results and used in the subsequent analysis.

Table 1 Comparison of normalized mid-span deflections of a simply supported micro epoxy beam
Full size table

Next, preliminary results of the nondeterministic analysis for a representative cantilever micro epoxy beam with the length \(L = 10h\) and \(b = 2h\) subjected to a uniformly distributed transverse load \(q_{0} = 1 \, N{/}m\) are presented and discussed. To demonstrate the accuracy and efficiency of the implemented scheme, the mean and standard deviation (Std. D) of the normalized tip deflection with \(h = \ell\) are compared with those predicted by MCS using 5000 simulation cycles in Table 2. It is noted that the mean and Std. D of the random field and the covariance function are taken as \(\mu_{E} = 1\), \(\sigma_{E} = 0.1\), and \(C(x,x^{\prime}) = \sigma_{E}^{2} \exp (\left| {x - x^{\prime}} \right|{/}2L)\), respectively. Note, in addition, that results of the SSIGA are reported for \(M = 5\) in the K-L expansion and the PCE with various orders. It is seen that the presented results not only exhibit an excellent agreement between the SSIGA and MCS approaches, but also indicate the superior computational efficiency of the SSIGA to the MCS.

Table 2 Comparison of results obtained from the SSIGA and MCS
Full size table

Finally, the influence of the material microstructure and the material uncertainty on the static response of the cantilever microbeam is investigated by using various values of the ratio \(h{/}\ell\) and the Std. D of the random field \(\sigma_{E}\). Numerical results of the mean and Std. D of the normalized tip deflection calculated from \(M = 5\) and the PCE of order 3 are reported in Table 3. Obviously, the obtained results (e.g., the mean and Std. D) exhibit the strong size-dependent behavior when the beam thickness \(h\) is comparable to the material length scale \(\ell\). It is also apparent from results in Table 3 that the randomness of Young’s modulus has a major influence on both mean and Std. D of the predicted normalized tip deflection.

Table 3 Mean and Std. D of the normalized tip deflection with various values of \(h{/}\ell\) and \(\sigma_{E}\)
Full size table

5 Conclusions

A spectral stochastic isogeometric analysis of Timoshenko microbeams based on the modified couple stress theory has been successfully implemented by taking the spatial variation of Young modulus into account in the nondeterministic analysis. The excellent agreement between results obtained in the present study and Monte Carlo simulation employing 5000 random samples through a numerical verification experiment has confirmed the validity of the stochastic analysis scheme. A set of preliminary results have demonstrated the significant role of the randomness of Young’s modulus on the predicted stochastic deflection of the microstructure-dependent beams. It should be remarked that the effect of uncertainties for other material properties and the geometry on the mechanical response of microscale curved beams in both static and dynamic aspects are also of key interest and still under investigation.