1 Introduction

The interest of miniaturized systems is considerable and well established [1]. Based on smart materials like piezoelectric materials, they can change their inherent properties in response to external stimuli in a controllable manner. Taking this advantage, they are widely used in several applications such as: biomedical, optics, fluidics, car industry, energy harvesting, electronics, etc. However, due to their size and density of integration, their design remains challenging because it requires taking into account the coupling between the structure and its mechanisms through a global design strategy. This requirement is induced by smart materials that play a significant role in the technological design of these systems. To address this challenge, various design methodologies have been proposed such as optimal arrangement of actuators/sensors [2,3,4], interval method [5, 6] or blocks method [7, 8]. Nevertheless, most of these methods lack generalization since they act only on the geometric parameters of the structure. This limits efficient shape design of the active mechanisms (actuation and measurement) and consequently that of the resulting structure.

In this regard, topology optimization [9], and particularly the SIMP (Solid Isotropic Material with Penalization) method seems to be a promising solution. Unlike classical optimization methods, it gives rise to efficient structures in response to requirement specifications. Its principle is mainly based on optimal material distribution within a specified design domain. Presented initially by Sigmund et al. [9,10,11], this powerful method is suitable for the design of passive structures. Since becoming a conceptual design tool, it has been particularly applied to design smart structures based on piezoelectric materials [12]. However, it remains challenging to handle due to the non-intuitive and non-unified integration of piezoelectric materials.

To tackle this limitation, the AS2M department has been actively working since 2018 to enhance the SIMP method by extending it to include piezoelectric materials. The objective is to provide a straightforward strategy for integrating the physics of the piezoelectric materials within the SIMP method. This gave rise to several challenges related to: smart materials modeling, finite-elements formulation, computational and numerical implementation. All these challenges have been or are being investigated at AS2M/FEMTO-ST institute.

This paper provides first a comprehensive summary of the research that has been conducted at the AS2M department/FEMTO-ST institute, the works that are currently underway, and the potential directions for future advancements concerning the design of piezoelectric actuators and energy harvesters. Secondly, we present topology optimization of piezoelectric energy harvesters in which the natural frequency of the structure will be tuned with the help of considering the Mass of attachment as an optimization variable. The theoretical aspects in this regard are accompanied by the implementation MATLAB code. The provided MATLAB code is the development of the previously published codes by author for topology optimization of piezoelectric structures [13] that were the first topology optimization MATLAB codes published in the area of piezoelectricity. All the MATLAB codes published in the literature for topology optimization in different physics are reviewed in [14]. The published code in this paper will be the first published MATLAB code in the area of topology optimization of piezoelectric structure with frequency tuning.

In the last part of the paper, we discuss the possibility of multi material topology optimization in which both active (piezo) and passive material will be developed and optimized to obtain more efficient designs.

2 Topology optimization

2.1 SIMP approach

Topology optimization and in particular the SIMP approach is a mathematical design methodology aiming to find an optimal layout within a limited design domain [9]. Based on material distribution, the method allows minimizing or maximizing an objective function while subjected to one or several constraints. Its key principle consists of introducing a density penalization law. The method is largely integrated into several design softwares such as COMSOL, ALTAIR Inspire, Ansys Discovery, SOlIDWORKS, etc. As a global and systematic approach, it is largely used in the engineering and design of passive mechanical structures because it offers several advantages such as weight reduction while enhancing performance and efficiency.

The method has also been applied for the topological design of active structures in particular piezoelectric structures [12]. However, the existing methodology lacks some mathematical development regarding the optimization of the polarity in addition to the topology. These mathematical limitations include the explicit formulation of the sensitivity analysis. Moreover, the realization of the optimized topologies of the piezoelectric structures received a very little attention in the literature. We addressed these limitations by (i) developing analytical and theoretical aspects of topology optimization of piezoelectric structures, (ii) developing algorithms and computer codes and (iii) fabricating and investigating experimentally the obtained structures. The common underlying factors in these developments were piezoelectric material modeling and numerical implementation.

Fig. 1
figure 1

Piezoelectric material sandwiched between two electrodes

Full size image

2.2 Piezoelectric modeling

Our primary investigations focused on planar piezoelectric structures. Thus, the starting design domain consists of a piezoelectric layer sandwiched between two electrodes as illustrated in Fig. 1. Its modeling involves several simplifying assumptions [15, 16] including plan-stress assumption which enable us to derive a 2D model from the IEEE 3D model [17] of piezoelectric material. To discretize the design domain and obtain the finite element modeling, the four-node rectangular element is employed as shown in Fig. 4-(a). With discretization of the design domain, the global finite element equilibrium equation can be derived as [18]

$$\begin{aligned} \left[ \begin{array}{cc} M &{} 0\\ 0 &{} 0 \end{array}\right] \left[ \begin{array}{c} \ddot{U}\\ \ddot{\varPhi } \end{array}\right] +\left[ \begin{array}{cc} K_{uu} &{} K_{u\phi }\\ K_{\phi u} &{} -K_{\phi \phi } \end{array}\right] \left[ \begin{array}{c} U\\ \varPhi \end{array}\right] =\left[ \begin{array}{c} F\\ Q \end{array}\right] \end{aligned}$$
(1)

where \(U\) and \(\phi \) are the vectors of the mechanical displacement and electric potential respectively. \(F\) and \(Q\) are the applied external mechanical force and electrical charge. \(M\), \(K_{uu}\), \(K_{u\phi }\), \(K_{\phi \phi }\) are the global mass matrix, mechanical stiffness matrix, piezoelectric coupling matrix and piezoelectric permittivity matrix respectively. The global matrices are formed by assembling the elemental matrices [13]. The global equilibrium Eq. 1 can be normalized to avoid the numerical instabilities and can be re-written based on the normalization which is provided in Ref. [13]. The normalization starts by factorizing the highest value of each elemental matrix,

$$\begin{aligned} \tilde{k}_{uu}={{k_{uu}}}/k_{0}, \quad \tilde{k}_{u\phi }={{k_{u\phi }}}/\alpha _0\nonumber \\ \tilde{k}_{\phi \phi }=k_{\phi \phi }/\beta _{0}, \quad \tilde{m}=m/m_{0} \end{aligned}$$
(2)

where \(k_{0},\alpha _0,\beta _{0},m_{0}\) are the highest values of the corresponding matrices. Then, the new FEM equation for piezoelectric actuator, can be written as

$$\begin{aligned} \tilde{K}_{uu}\tilde{U}+\tilde{K}_{u\phi }\tilde{\varPhi }=\tilde{F} \end{aligned}$$
(3)

In Eq. 3, \((\tilde{\quad })\) stands for the normalized quantities and

$$\begin{aligned} \tilde{F}=F/f_{0}, \quad \tilde{U}=U/u_{0}, \quad \tilde{\varPhi }=\varPhi /\phi _{0} \nonumber \\ u_{0}=f_{0}/k_{0}, \quad \phi _{0}=f_{0}/\alpha _{0} \end{aligned}$$
(4)

and the new FEM equation for energy harvesting is derived as

$$\begin{aligned} \left[ \begin{array}{cc} \tilde{K}_{uu}-\tilde{M}\tilde{\varOmega }^{2} &{} \tilde{K}_{u\phi }\\ \tilde{K}_{\phi u} &{} -\gamma \tilde{K}_{\phi \phi } \end{array}\right] \left[ \begin{array}{c} \tilde{U}\\ \tilde{\varPhi } \end{array}\right] =\left[ \begin{array}{c} \tilde{F}\\ 0 \end{array}\right] \end{aligned}$$
(5)

where

$$\begin{aligned} \tilde{\varOmega }^{2}=\varOmega ^{2}m_{0}/k_{0}, \quad \gamma =k_{0}\beta _{0}/\alpha _{0}^{2} \end{aligned}$$
(6)

In Eq. 5, \(B\) is a Boolean matrix to apply the equipotential condition on the electrodes with dimension \(N_{e}\times N_{P}\) where \(N_{e}\) is the number of nodes and \(N_{P}\) is the number of potential electrodes where for 2D case \(N_{P}=1\). \(\tilde{\Omega }\) is the normalized excitation frequency (\(\Omega \)), V\(_p\) is the generated voltage by mechanical vibration and \(\gamma \) is the normalized factor that keeps the solution of the system equal before and after applying the normalization.

After solving the FEM , we need to rollback the normalization and calculate the real outputs of the system (i.e. \(\phi \) and U). In actuation mode, the input of the system is potential and hence the value of \(\varPhi _{0}\) is assumed by user a priory. As such, the real value of displacement can be calculated by

$$\begin{aligned} U=U_{0}\tilde{U}=\varPhi _{0}\alpha _{0}\tilde{U}/k_{0} \end{aligned}$$
(7)

In the energy harvesting case, the force is the input and the value of \(f_{0}\) is assumed by user a priory. Therefore, the real value of potential can be calculated by

$$\begin{aligned} \varPhi =\varPhi _{0}\tilde{\varPhi }=f_{0}\varPhi /\alpha _{0} \end{aligned}$$
(8)

With the developed finite element model, it is possible to formulate the optimization problem for piezoelectric actuators and energy harvesters.

3 Piezoelectric micro-actuators

The use of piezoelectric materials to actuate microbotics systems is of particular interest. As a smart material, they have several advantages such as: high displacement resolution, large output force, high dynamics response and significant scaling-down possibilities [19]. However, due to their crystalline arrangement, they provide a low relative deformation (0.1% of actuator’s size) that limits their stroke [20]. To overcome this limitation, we employed topology optimization framework [16] to optimize both the topology and the polarity of the actuator. This simultaneous optimization allows combining material expansion and compression in order to increase the stroke of the actuator without using any passive amplification mechanism. This enables the miniaturization of the optimal design. Two 1D actuators were designed starting from a full domain considered as a basic reference piezoelectric actuator. The first design considered only the optimization of topology while the second one took into account the optimization of the topology and polarization profile simultaneously. This section recaps the problem formulation, the optimization and the main results of this study. To find out more theoretical details, readers can refer to [15, 16].

Fig. 2
figure 2

Topology optimization of a piezoelectric micro-actuators. a) Problem definition, b) Problem formulation, c) Optimized layout without polarity, d) Simulated layout without polarity, e) Optimized layout with polarity, f) Simulated layout with polarity

Full size image

3.1 Problem formulation

To formulate the topology optimization problem, we use the SIMP (Solid Isotropic Material with Penalization) approach. In this approach, optimization variables are attributed to each element in the design domain to relax the physical properties from binary values to continuous values [21]. The extension of SIMP approach for piezoelectric materials known as "Piezoelectric Material with Penalization and Polarization (PEMAP-P)" can be expressed as follows [22, 23]:

$$\begin{aligned} \tilde{k}_{uu}(x)=\left( E_{min}+x^{p_{uu}}(E_{0}-E_{min})\right) \tilde{k}_{uu} \nonumber \\ \tilde{k}_{u\phi }(x,P)=(e_{min}+x^{p_{u\phi }}(e_{0}-e_{min}))(2P-1)^{p_{P}}\tilde{k}_{u\phi } \nonumber \\ \tilde{k}_{\phi \phi }(x)=(\varepsilon _{min}+x^{p_{\phi \phi }}(\varepsilon _{0}-\varepsilon _{min}))\tilde{k}_{\phi \phi } \nonumber \\ \tilde{m}(x)=x\tilde{m} \end{aligned}$$
(9)

where \(E_{min}\), \(e_{min}\) and \(\varepsilon _{min}\) are small numbers to define the minimum values for stiffness, coupling and dielectric matrices while \(E_{0}\), \(e_{0}\) and \(\varepsilon _{0}\) are equal to one to define the maximum values of the respected matrices. The definition of minimum values are provided to avoid the singularities during the optimization iterations. \(x\) is the density ratio of each element which has a value between zero and one. \(P\) is the polarization variable which also has the value between zero and one and determines the direction of polarization. \(p_{uu}\), \(p_{u\phi }\), \(p_{\phi \phi }\) and \(p_{P}\) are penalization coefficients for the stiffness, coupling, dielectric matrices and polarization value respectively. It is obvious that in Eq. 9, the normalized form of piezoelectric matrices are used. However, the interpolation function is true for non-normalized matrices as well.

Now, the optimization problem can be formulated by definition of objective function, constraints and optimization variables. The objective function can be defined using the compliant mechanism analysis in which the goal is to maximize the deflection of a structure in a particular direction. Different objective functions can be considered for compliant mechanisms which are reviewed in [24]. Here, a simple objective function is chosen with a modeled spring to simulate the stiffness of the target object as it is illustrated in the Fig. 2-(a). Moreover, a constraint on the volume of the material can be defined to minimize the consumed material and to increase the flexibility of structure in favor of higher displacement. The optimization variables also defined in the material interpolation scheme Eq. 9. Therefore, the optimization problem for piezoelectric micro-actuators can be formulated as follows

$$\begin{aligned} minimize\quad J_{act}=-L^{T}\tilde{U} \nonumber \\ Subject\,to \quad V(x)=\sum \limits _{i=1}^{NE}x_{i}v_{i}\le V \nonumber \\ 0<x_{i}\le 1 \nonumber \\ 0\le P_{i}\le 1 \end{aligned}$$
(10)

where \(L\) is a Boolean vector with a value of one that corresponds to the output displacement node and zero otherwise. \(V\) is the target volume which is a fraction of the overall volume of the design domain while \(v_{i}\) is the volume of each element and \({NE}\) is the total number of elements and \(i\) is the number of each element in the design domain.

3.2 Sensitivity analysis

To solve the optimization problem, we use the gradient based solvers like Optimality Criteria (OC) and method of moving asymptotes (MMA) [25, 26]. As such, the sensitivity of objective function with respect to optimization variables should be calculated. Based on the material interpolation scheme Eq. 9, we have two optimization variables known as density (x) and polarization (P). The sensitivity with respect to (x) is calculated by using the adjoint method as

$$\begin{aligned} \frac{\partial J}{\partial x_{i}}=\lambda _{i}^{T}\frac{\partial \tilde{k}_{uu}}{\partial x_{i}}\tilde{u_{i}}+\lambda _{i}^{T}\frac{\partial \tilde{k}_{u\phi }}{\partial x_{i}}\tilde{\phi _{i}} \end{aligned}$$
(11)

where \(\lambda \) is the adjoint vector at elemental level. \(\lambda \) is introduced to avoid taking the derivative of displacement with respect to design variable i.e. \(\frac{\partial \tilde{u_{i}}}{\partial x}\). The sensitivity with respect to polarization is

$$\begin{aligned} \frac{\partial J}{\partial P_{i}}=\lambda _{i}^{T}\frac{\partial \tilde{k}_{u\phi }}{\partial P_{i}}\tilde{\phi _{i}} \end{aligned}$$
(12)

The following adjoint equation should be solved to find the adjoint vectores,

$$\begin{aligned} -L^{T}+\Lambda ^{T}\tilde{K}_{uu}=0 \end{aligned}$$
(13)

Where \(\Lambda \) is the adjoint vector at system level (global level).

Based on Eqs. 11 and 12, the derivative of piezoelectric stiffness and coupling matrices with respect to design variables are required which can be derived with the help of Eq. 9 as

$$\begin{aligned} \frac{\partial \tilde{k}_{uu}}{\partial x_{i}}=p_{uu}(E_{0}-E_{min})x_{i}^{p_{uu}-1}\tilde{k}_{uu} \nonumber \\ \frac{\partial \tilde{k}_{u\phi }}{\partial x_{i}}=p_{u\phi }(e_{0}-e_{min})x_{i}^{p_{u\phi }-1}(2P_{i}-1)^{p_{P}}\tilde{k}_{u\phi } \end{aligned}$$
(14)
$$\begin{aligned} \frac{\partial \tilde{k}_{u\phi }}{\partial P_{i}}=2p_{P}(e_{0}-e_{min})(2P_{i}-1)^{p_{P}-1}x_{i}^{p_{u\phi }}\tilde{k}_{u\phi } \end{aligned}$$
(15)

When the sensitivity analysis is provided, the SIMP algorithm can be developed. Beforehand, the design domain and application should be defined.

Table 1 Summary of simulation and experimental results [16]
Full size table
Fig. 3
figure 3

Fabricated prototypes, a) Full plate (reference actuator), b) Prototype without polarity optimization, c) Prototype with polarity optimization

Full size image

3.3 Definition of design domain and application

Figure 2-(a,b) illustrates the definition and the mechanical formulation of 1D piezoelectric actuator. The bottom side of the domain is clamped while the middle point of the top side is considered as the actuator output. In addition, the actuator-object interaction is modeled as a spring that modulates the actuator displacement: a lower stiffness value results in a higher displacement and vice versa. Using this configuration, two optimized designs are obtained where the difference lies in whether or not the polarization is optimized. In both cases, the volume fraction is set to 0.3, meaning that only 30% of the initial domain is used for the optimized designs.

After performing the sensitivity analysis, and defining the constraint, the topology optimization algorithm can be implemented.

3.4 Algorithm, optimization and simulation

Following the modeling and formulation of the problem, an optimization algorithm was developed and implemented under MATLAB [15]. The application of this algorithm leads to the designs depicted in Fig. 2-(c,e). Layout (c) comprises a uniform electrode while layout (e) comprises two different electrodes with opposite polarities. The second design comprises two regions with inverse polarities. When one region retracts the other extends resulting in a considerable improvement of output displacement. This analysis is confirmed by FEA simulations illustrated in Fig. 2-(d,f) where the obtained results show that the displacement of the design with optimized polarity is almost twice the displacement of the design with uniform polarity. More comparison results between the full actuator plate (reference actuator) and the optimized designs are reported in Table 1.

3.5 Fabrication and experimental validation

Starting from a piezoelectric plate, the three prototypes shown in Fig. 3 were fabricated. The fabrication process started by cutting the designs from piezoelectric plates (commercial piezoelectric material PSI-5H4E from Piezo Systems Inc) using a laser machine (Siro Lasertec GmbH, Pforzheim, Germany). Then, the wires are glued to the electrodes of the PZT plates. Moreover, to follow the polarization profile, the top electrode is divided into two sections to avoid charge cancellation. An experimental bench was set and a series of measurements were performed under a maximum excitation voltage of 5V which respects the linear assumption of the piezoelectric model. The resulting average displacements are reported in Table 1. As expected, there is a satisfying agreement between the experimental and the simulation results. In addition, the superiority of the optimized designs versus the full piezoelectric plate in terms of stroke is observed.

3.6 Discussion

The developed algorithm reduces drastically the material amount while enhancing the actuator energy density and stroke. Indeed, only 30% of the material was optimally distributed in order to provide a displacement greater than the displacement of an actuator with a uniform polarization. Although the actuator output force decreased, the optimization led to a compact and economical design. This is particularly interesting in the context of miniaturization since the non-occupied space can be utilized to implement additional functionalities such as sensors or electronic circuits.

4 Piezoelectric energy harvesters

In parallel to actuation, piezoelectric materials are widely used in energy harvesting applications. Converting vibration to electrical energy, these devices, i.e, Piezoelectric Energy Harvesters (PEHs) offer a potential alternative to batteries in low-power-wireless devices such as wireless sensors [27], small-scale robots [28], etc. Thanks to the direct effect of piezoelectricity, they can convert mechanical to electrical energies with a simple mechanism. This simplicity makes the piezoelectric energy harvester more efficient than their rivals like electromagnetic and triboelectric at small scales. At AS2M department, we mainly worked on the optimization of the mechanical structures of PEHs.

Mostly known and still used configuration for the vibrational PEH is the cantilever configuration with tip attachment due to its largely produced strains and feasibility of fabrication. Considering this configuration as the first approach to increase the efficiency of the cantilever PEH, we proposed to have in-span attachments in addition to tip attachment in order to harvest the energy from higher modes and resonance frequencies [31]. Based on an analytical approach to find the output voltage, we proposed a neural network-based genetic algorithm (GA) approach to optimize the placement and geometry of the in-span attachments. However, the major problem with cantilever configuration is that it is one degree of freedom configuration, which can absorb the energy from one direction of excitation. This will restrict the possible applications of the cantilever PEHs, where the excitation can come from different directions. There are some designs for multi-directional PEHs in the literature [32, 33]. However, the miniaturization of these mechanism-based designs is challenging. To tackle this problem, we employed SIMP topology optimization to obtain new and previously unknown configurations for the PEH.

Fig. 4
figure 4

Piezoelectric Energy Harvesters designed by topology optimization. a) single-layer piezo plate modeled by 2D finite element method [29]. b) Optimized topology, c) Optimized polarity, d) Fabricated prototype, e) Bi-morph piezo plate modeled by 3D finite element method [30], f) Optimized topology without polarization optimization, g) Optimized topology with polarization optimization

Full size image

4.1 Single-layer piezoelectric energy harvester

4.1.1 Modeling & problem formulation

Utilizing the piezoelectric constitutive equations, first, a 2D finite element model of a single piezoelectric plate sandwiched between two electrodes (Fig. 1) is developed. The plan-stress assumption is employed to derive the constitutive equation. The normalized equilibrium equation is mentioned in Eq. 5.

TO formulate the problem, objective function is defined as the weighed sum of the mechanical and electrical energy. Similar to actuation case, a constraint is defined on the volume of the material and optimization variables are considered as density and polarization. Therefore, the problem is formulated as follows,

$$\begin{aligned} minimize\quad J_{EH}=w_{j}\Pi ^{S}-(1-w_{j})\Pi ^{E} \nonumber \\ Subject\,to \quad V(x)=\sum \limits _{i=1}^{NE}x_{i}v_{i}\le V \nonumber \\ 0<x_{i}\le 1 \nonumber \\ 0\le P_{i}\le 1 \end{aligned}$$
(16)

\(\Pi ^{E}\) and \(\Pi ^{S}\) are electrical and mechanical energies respectively which are defined in the following form [22, 34]

$$\begin{aligned} \Pi ^{S}=(\frac{1}{2})\tilde{U}^{T}\overline{K_{uu}}\tilde{U}~~,~~ \Pi ^{E}=(\frac{1}{2})V_{p}^{T}\overline{K_{\phi \phi }}V_{p}\nonumber \\ \overline{K_{uu}}=\left[ \tilde{K}_{uu}-\tilde{M}\tilde{\varOmega }^{2}\right] _{bc} ~~,~~ \overline{K_{\phi \phi }}=\gamma B^{T}\tilde{K}_{\phi \phi }B \end{aligned}$$
(17)

In optimization Eq. 16, \(w_{j}\) is the weighing factor which has the value between 0 and 1 and will be found by using trial and error approach. The basis for choosing this value can be the maximum energy conversion factor of the plate under the same force.

4.2 Sensitivity analysis

After defining the mechanical and electrical energies, the sensitivity of each energy with respect to density ratio \(x\) can be found as [29, 30, 34]

$$\begin{aligned} \frac{\partial \Pi ^{S}}{\partial x_{i}}=(\frac{1}{2}\tilde{u}_{i}^{T}+\lambda _{1,i}^{T})\frac{\partial (\tilde{k}_{uu}-\tilde{m}\tilde{\varOmega }^{2})}{\partial x_{i}}\tilde{u}_{i}+\nonumber \\ \lambda _{1,i}^{T}\frac{\partial \tilde{k}_{u\phi }}{\partial x_{i}}\tilde{\phi }_{i}+\mu _{1,i}^{T}\frac{\partial \tilde{k}_{\phi u}}{\partial x_{i}}\tilde{u}_{i}-\mu _{1,i}^{T}\frac{\gamma \partial \tilde{k}_{\phi \phi }}{\partial x_{i}}\tilde{\phi }_{i}\end{aligned}$$
(18)
$$\begin{aligned} \nonumber \\ \frac{\partial \Pi ^{E}}{\partial x_{i}}=\frac{1}{2}\tilde{\phi }_{i}^{T}\frac{\gamma \partial \tilde{k}_{\phi \phi }}{\partial x_{i}}\tilde{\phi }_{i}-\mu _{2,i}^{T}\frac{\gamma \partial \tilde{k}_{\phi \phi }}{\partial x_{i}}\tilde{\phi }_{i}+\nonumber \\ \lambda _{2,i}^{T}\frac{\partial (\tilde{k}_{uu}-\tilde{m}\tilde{\varOmega }^{2})}{\partial x_{i}}u_{i}+\lambda _{2,i}^{T}\frac{\partial \tilde{k}_{u\phi }}{\partial x_{i}}\tilde{\phi }_{i}+\mu _{2,i}^{T}\frac{\partial \tilde{k}_{\phi u}}{\partial x_{i}}\tilde{u}_{i} \end{aligned}$$
(19)

in which \(\mu \) and \(\lambda \) are the elemental adjoint vectors which are calculated by the following global coupled system

$$\begin{aligned} \left[ \begin{array}{cc} \overline{K_{uu}} &{} \overline{K_{u\phi }}\\ \overline{K_{\phi u}} &{} -\overline{K_{\phi \phi }} \end{array}\right] \left[ \begin{array}{c} \Lambda _{1}\\ \Upsilon _{1} \end{array}\right] =\left[ \begin{array}{c} -\overline{K_{uu}}\tilde{U}\\ 0 \end{array}\right] \nonumber \\ \left[ \begin{array}{cc} \overline{K_{uu}} &{} \overline{K_{u\phi }}\\ \overline{K_{\phi u}} &{} -\overline{K_{\phi \phi }} \end{array}\right] \left[ \begin{array}{c} \Lambda _{2}\\ \Upsilon _{2} \end{array}\right] =\left[ \begin{array}{c} 0\\ -\overline{K_{\phi \phi }}V_{p} \end{array}\right] \end{aligned}$$
(20)

where \(\Lambda \) and \(\Upsilon \), are the global adjoint vectors which need to be disassembled to form the elemental adjoint vectors

$$\begin{aligned}{}[\lambda _{1}]_{bc}=\Lambda _{1},[\lambda _{2}]_{bc}=\Lambda _{2} , [\mu _{1}]=B\Upsilon _{1},[\mu _{2}]=B\Upsilon _{2} \end{aligned}$$
(21)

Now, the sensitivities with respect to polarization (\(P\)) is calculated as well [29, 30]

$$\begin{aligned} \frac{\partial \Pi ^{S}}{\partial P_{i}}=\lambda _{1,i}^{T}\frac{\partial \tilde{k}_{u\phi }}{\partial P_{i}}\tilde{\phi }_{i}+\mu _{1,i}^{T}\frac{\partial \tilde{k}_{\phi u}}{\partial P_{i}}\tilde{u}_{i} \nonumber \\ \frac{\partial \Pi ^{E}}{\partial P_{i}}=\lambda _{2,i}^{T}\frac{\partial \tilde{k}_{u\phi }}{\partial P_{i}}\tilde{\phi }_{i}+\mu _{2,i}^{T}\frac{\partial \tilde{k}_{\phi u}}{\partial P_{i}}\tilde{u}_{i} \end{aligned}$$
(22)

Based on sensitivity equations in Eqs. 19 and 22, the derivative of all piezoelectric matrices with respect to the design variables are required. The derivative of stiffness and coupling matrices are found in Eqs. 14 and 15. Here, the derivative of dielectric matrix and mass matrix is also required which are

$$\begin{aligned} \frac{\partial \tilde{k}_{\phi \phi }}{\partial x_{i}}=p_{\phi \phi }(\varepsilon _{0}-\varepsilon _{min})x_{i}^{p_{\phi \phi }-1}\tilde{k}_{\phi \phi } \nonumber \\ \frac{\partial \tilde{m}}{\partial x_{i}}=\tilde{{m}_{i}} \end{aligned}$$
(23)

In addition to derivative of piezoelectric matrices with respect to density, derivation of the piezoelectric coupling matrix with respect to polarization variable is also required

$$\begin{aligned} \frac{\partial \tilde{k}_{u\phi }}{\partial P_{i}}=2p_{P}(2P_{i}-1)^{p_{P}-1}x_{i}^{p_{u\phi }}\tilde{k}_{u\phi } \end{aligned}$$
(24)

After calculation of sensitivities, the optimization variables can be updated in each iteration of optimization with the help of gradient-based optimizers like optimality criteria (OC) and Method Moving Asymptotes (MMA) [26].

For the single layer piezoelectric plate, the goal is to design a two degrees of freedom energy harvester that can harvest the energy from external in-plane harmonic force coming from different directions. In this regard, the configuration of load and boundary conditions in Fig. 4-(a) is proposed. The most challenging problem in this case is the charge cancellation due to a combination of tension and compression in different parts of the plate. However, optimization of polarization profile overcomes the problem of charge cancellation. Moreover, low volume fraction (optimized design volume/full plate volume) decreases the stiffness of the piezoelectric plate against in-plane forces.

4.2.1 Numerical results, simulation & experiment

In panels (b) and (c) of the same figure, the final optimized layout and polarization profile for PZT plate under excitation of two harmonic forces in two directions can be seen [29]. In panel (c), the red color and blue color represent positive and negative polarization in the z direction.

To analyze the performance of the optimized design, COMSOL multiphysics is used to compare the performance of the optimized design with the full plate. The simulation results proved the superiority of the optimized designs over the classical full plate while having less amount of material [29]. On the other hand, the amount of produced voltage and electrical power is not the same for every direction of the force. This is due to the fact that the stiffness of the plate in different directions is not the same. For the sake of brevity, we do not present the simulation results here. Interested readers are referred to the published paper [29].

The fabrication process is similar to what has been explained for the piezoelectric actuators. The difference here is that magnets are attached at the tip of the beam to generate vibrations force when excited by an electromagnet as it is shown in Fig. 4-(d). The magnets are attached in two different directions so they can excite the designs in two different directions.

Experimental results demonstrated that for an excitation frequency equal to 20 Hz, the voltage and power of the optimized design are 8.75 and 7.54 times higher than the full plate. These improvements are due to the fact that the optimized design is having better strain distribution and more importantly, it has separated electrodes that avoid charge cancellation.

4.3 Bi-morph piezoelectric energy harvester

In the next phase of our research, a bi-morph piezoelectric plate instead of the single-layer piezoelectric plate is considered as a design domain to consider out-of-plane forces and deformations [30].

4.3.1 Modeling & problem formulation

Similar objective and constraints from single-layer PEH are considered in the optimization problem of the multi-directional Bi-morph PEH i.e. reduction of weight while maximizing the efficiency of the harvested energy from excitation coming from different directions. In the case of bi-morph PEH, the configuration of the boundary condition remains the same while a 3-load case is applied at the tip of the structure (Fig.  4-(e)). The bi-morph plate consists of 3 electrodes on the top, middle and bottom surfaces of the plate. The finite element modeling of the system is done by discretizing the design domain with a finite number of 3D hexahedron elements.

4.3.2 Algorithm & optimization

The sensitivity analysis and optimization algorithm for 3D and 2D finite element modeling is formulated similarly. However, the implementation MATLAB code changes considerably to include the third dimension and application of electrical boundary conditions regarding the existence of several electrodes.

4.3.3 Numerical results, simulation & experiment

The results of the optimization for two cases are shown in Fig. 4-(f,g) [30]. The optimized design (1) is the result of optimization without optimizing the polarity and design (2) is the result of optimization with optimizing polarity. In design (1), in the case of planar forces, there will be charge cancellation due to compression and tension in different parts of the layer. To remedy, in design (2), the polarity is optimized as well. For the realization of this polarization profile, the top and bottom electrodes are divided into two sections to simulate the polarization profile. As such, the design has 2 electrodes on top, 2 electrodes on bottom and one electrode in the middle.

To assess experimentally the performance of the optimized designs, their electrical to mechanical efficiency is compared with a classical full plate. By COMSOL simulation, we demonstrated how the designs harvested the energy coming from different excitation in 3D space and the superiority of the optimized designs over the full piezoelectric plate is demonstrated. The experimental investigation demonstrated that the optimized design with optimized polarity can have up to 2 times better voltage output than the piezoelectric full plate while having less amount of mass [30].

Finally, although optimized designs are multi-directional harvesters, but they are not excited at their resonance frequency. This is considered in the next stage of our research.

4.4 Frequency tuning & optimization of mass

The best efficiency of a vibrational PEH can be obtained when it is excited at its resonance frequency. Frequency matching is therefore very crucial for every PEH since only 2% deviation of resonance frequency from excitation frequency will drop the electrical output power by 50%. Moreover, the available excitation frequency in real applications is generally between 10 to 30 Hz, which is below the normal resonance frequency of the PEHs. The classical and conventional method to match the resonance frequency with the low excitation frequency is to attach a lumped mass at the tip of the cantilever PEH [38].

In our recently published work [37], we combined topology optimization and frequency tuning technique to raise further the efficiency of PEH. The idea consists to define a constraint on the fundamental frequency of PEH. To tackle the challenges of eigenfrequency tuning within the topology optimization approach, we defined the attachment’s mass as a new optimization variable in addition to the density and polarity. This will be discussed in the next section.

4.4.1 Modeling & problem formulation

The resonance frequency is the natural frequency of the system at short circuit condition. At open circuit condition, the natural frequencies of the system are the anti-resonance frequency [18]. Therefore the fundamental resonance frequency at \( V_{p}=0\) can be calculated,

$$\begin{aligned} \left[ \tilde{K}_{uu}-\tilde{M}\tilde{\omega }_{s}^{2}\right] \Psi _{s}=0 \end{aligned}$$
(25)

in which \(\tilde{\omega }_{s}\) is the natural frequency at short circuit condition and \(\Psi _{s}\) is the related eigenvector. Now, based on the built FEM of the piezoelectric plate and the provided resonance equation, topology optimization algorithm can be applied to maximize the harvested energy of the bi-morph vPEH by optimizing the topology and modifying the resonance frequency.

To define the mass of attachment as an optimization variable, we define the mass matrix of the system as follows,

$$\begin{aligned} \tilde{M}=\sum \limits _{i=1}^{NE}\tilde{m_{i}}+y[\tilde{M}_{mass}]\quad (0\le y\le 1) \end{aligned}$$
(26)

in which \(\tilde{m_{i}}\) is the elemental mass, i is the element number and \(y\) is the optimization variable that stands for the ratio of maximum possible mass of the attachment. By definition of \(y\) here, we give more freedom to the optimization in terms of convergence to a perfect solid void material in the final layout. The reason is that the variable \(y\) can increase or decrease the total mass of the vPEH without changing its stiffness. This optimization variable helps optimization solver to converge to a fully black and white final layout and to avoid the greyness problem which is a common problem in topology optimization with frequency tuning [39].

For tuning the resonance frequency, the first interpolation function defined in Eq. 9 for the stiffness matrix \(K_{uu}\) should be modified to avoid the localized modes at the low density regions [40]. The reason is that, based on the SIMP material interpolation scheme, low density regions are highly flexible (soft) that produce very low and artificial eigenmodes. To remedy, the interpolation function for the stiffness matrix which is proposed by Huang et al. [39] is utilized as follows

$$\begin{aligned} \tilde{k}_{uu}(x_{i})=\left[ \frac{x_{min}-x_{min}^{p_{uu}}}{1-x_{min}^{p_{uu}}}(1-x_{i}^{p_{uu}})+x_{i}^{p_{uu}}\right] \tilde{k}_{uu} \end{aligned}$$
(27)
Fig. 5
figure 5

a) New configuration for frequency tuned piezoelectric energy harvester. b) Topology optimized design [37]

Full size image

Now, to tune the resonance frequency we modify the problem formulation as follows,

$$\begin{aligned} \begin{array}{cc} minimize\quad &{} J_{EH}=w_{j}\Pi ^{S}-(1-w_{j})\Pi ^{E} \\ Subject\,to\quad &{} V(x)=\sum \limits _{i=1}^{NE}x_{i}v_{i}\le V\\ &{} \omega _{1}<\varpi ,\\ &{} 0\le x_{i}\le 1,\quad 0\le P_{i}\le 1,\quad \\ &{} 0\le y\le 1 \end{array} \end{aligned}$$
(28)

where \(y\) is the new optimization variable and \(\varpi \) is the desired resonance frequency. By having the inequality constraint on the resonance frequency, the optimization is more relaxed than having equality constrained. On the other hand, the resonance frequency will finally match the excitation frequency as the structure tends to be more rigid during optimization iterations. To solve the optimization problem with gradient based optimizers like MMA we need to calculate the sensitivity analysis which will be discussed next.

4.4.2 Sensitivity analysis

Since, the objective function in Eq. 28 is the same as Eq. 16, we just calculate here the sensitivity of objective function with respect to the new optimization variable as follows

$$\begin{aligned} \frac{\partial \Pi ^{S}}{\partial y}=(\frac{1}{2}\tilde{u}_{i}^{T}+\lambda _{1,i}^{T})\frac{\partial (\tilde{M}\tilde{\varOmega }^{2})}{\partial y}\tilde{u}_{i} \nonumber \\ \frac{\partial \Pi ^{E}}{\partial y}=\lambda _{2,i}^{T}\frac{\partial (\tilde{M}\tilde{\varOmega }^{2})}{y}u_{i} \end{aligned}$$
(29)

where \(\mu \) and \(\lambda \) are the same elemental adjoint vectors which are calculated in the adjoint Eq. 20.

To apply the constraint on the natural frequency, its gradient with respect to the optimization variables should be calculated. To do so, the fundamental natural frequency of the system can be defined through the Rayleigh quotient [39],

$$\begin{aligned} \tilde{\omega }_{s}^{2}=\frac{\Psi _{s}^{T}\tilde{K}_{uu}\Psi _{s}}{\Psi _{s}^{T}\tilde{M}\Psi _{s}} \end{aligned}$$
(30)

The interpretation of first natural frequency by Rayleigh quotient will result in to more efficient sensitivity analysis. By following the procedure presented in [39], the sensitivities of the natural frequency’s constraints with respect to optimization variables are

$$\begin{aligned} \frac{\partial \omega _{s}}{\partial x_{i}}=\frac{1}{2\omega _{s}\Psi _{s}^{T}\tilde{M}\Psi _{s}}\left[ \Psi _{s}^{T}(\frac{\partial \tilde{k}_{uu}}{\partial x_{i}}-\tilde{\omega }_{s}^{2}\frac{\partial \tilde{M}}{\partial x_{i}})\Psi _{s}\right] \nonumber \\ \frac{\partial \omega _{s}}{\partial y}=-\frac{\tilde{\omega }_{s}}{2\Psi _{s}^{T}\tilde{M}\Psi _{s}}\left[ \Psi _{s}^{T}\frac{\partial \tilde{M}}{\partial y}\Psi _{s}\right] \end{aligned}$$
(31)

Now all the required sensitivities are calculated. However, since we modified the interpolation function of the stiffness matrix in Eq. 27 and the expression for the mass matrix is also changed, their derivatives with respect to density and new mass optimization variable (y) can be calculated as:

$$\begin{aligned} \frac{\tilde{\partial k}_{uu}}{\partial x}=\frac{1-x_{min}}{1-x_{min}^{p}}p_{uu}x_{i}^{p-1}K_{uu} \nonumber \\ \frac{\partial \tilde{m}}{\partial x_{i}}=\tilde{{m}_{i}}, \quad \frac{\partial \tilde{m}}{\partial y}=\tilde{{M}}_{mass} \end{aligned}$$
(32)

Aiming for low weight piezoelectric energy harvester, a new configuration is proposed (Fig. 5-(a)) to minimize the fundamental resonance frequency and the mass of the attachment simultaneously. The obtained result (Fig. 5-(b)) in MATLAB and COMSOL Multiphysics demonstrated that the algorithm successfully restricted the fundamental frequency close to the desired one while respecting the mass and volume constraints of the vPEH.

Simulation results prove the superiority of the optimized design in Fig. 5-(b) in comparison with the previously optimized design of Fig. 4-(g) while having less amount of attachment mass. This is an interesting achievement that we restricted the first resonance frequency while at the same time having a lower amount of weight. On the other hand, the stress analysis reveals a higher amount of stress in the newly proposed configuration (Fig. 5-(a)) in comparison with the previous configuration of the PEH (Fig. 5-(g)).

5 MATLAB code for frequency tuning of PEH with mass optimization

In this section the goal is to provide a MATLAB code for topology optimization of PEH with tuning the resonance frequency and considering the attached mass as an optimization variable. The study of this section is similar to Section 4.4. However, the dimension of study here is 2D and the provided MATLAB code is in 2D as well. It should be noted that, despite the modeling dimension of the system, the analytical calculations of Section 4.4 remain true.

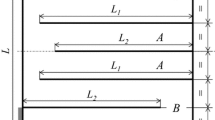
The MATLAB code in this section is developed on the basis of the previously published code from the authors for topology optimization of the PEH [13]. Moreover, the case study of this section is similar to the case study of the published codes [13] with the difference of considering attached mass at the tip of the beam as it has been illustrated in Fig. 6 with mass of attachment as optimization variable. In this case study, the polarization direction is considered to be in the z direction of the coordinate system. However, it is possible to simply consider the polarization direction in the y axis and optimize the structure in the direction of thickness.

Fig. 6
figure 6

a) Piezoelectric energy harvester with tip attachment. The mass of attachment is considered as optimization variable

Full size image

5.1 Description of the code

The implementation topology optimization MATLAB code for case study of Fig. 6 is provided in the appendix. For the sake of brevity, we will only explain here the lines of the code that are different from previously published code [13] to implement the optimization of resonance frequency. Readers are advised to read the paper of previously published codes [13] primarily before reading this section.

5.1.1 Definition of parameters

The provided code starts with the section of GENERAL DEFINITIONS in which the user defines the geometry of the structure, resolution of the mesh, penalty factors, etc. The variable ft defines the filtering type in which the user can choose between two filtering methods including density filter [21, 41] or Heaviside projection suggested by Wang et al. [42]. The complete MATLAB implementation code for this combination of filtering methods is provided by Ferrari et al. [43] and the same lines of codes are utilized in the provided code of this paper. Three parameters in the filtering part should be defined in the first section of the code known as filter radius (rmin), threshold (eta) and sharpness factor (beta). The projection filter is new in this code in comparison to previously published codes and it is more efficient in terms of avoiding the gray elements.

For a better convergence to a clean black and white result, the continuation schemes are applied to the penalties and sharpness factor. To do so, penalCnt, betaCnt are defined similarly to what has been defined by [43]. These parameters accept four values as [istart, maxPar, isteps, deltaPar], which means the continuation starts at iteration = istart and will be increased by deltaPar in each isteps and reaching to maximum value maxPar.

Variable DF determines the maximum desired natural frequency and the Variable MASS determines the maximum allowable attachment mass. These two new variables are defined to integrate the frequency tuning and the optimization of attachment mass.

The sections of MATERIAL PROPERTIES, PREPARE FINITE ELEMENT ANALYSIS, DEFINITION OF BOUNDARY CONDITION, FORCE DEFINITION remain intact in comparison to previously published code [13]. Hence, no descriptions will be given here.

The section of DEFINITION OF ATTACHMENT MASS is new and it is defined to model an attachment mass at the tip of the beam. It should be noted that the code is dynamic and the placement of the mass can be changed easily. The lines of code to model the attached mass are as follows:

figure a

The method to define the mass is to consider elements at the desired location in the design domain to be more heavy than other elements. To do so, we use the sMass which is a Boolean vector with a size of total number of elements. We choose the desired element(s) to place the mass and the rows indexing that element will have the value of 1. In the case study of this paper, since we placed the mass of attachment at the end of the beam as illustrated in Fig. 6, the last element at the tip of the beam in the middle of the width is chosen to be heavier than the rest of the element. To make the element heavier, we modify the density of the elemental mass matrix by ro_M. Finally, this mass will be augmented to the global size mass matrix with the help of the sMMass . The M_Att is a matrix with the size of global mass matrix which only contains the attached mass. As such, it should be augmented to global piezoelectric mass matrix which will be explained later.

The section of PREPARE FILTER is transferred from the code written by Ferrari. et. al [43] to implement the density filter and projection. A detailed explanation can be found in the cited reference. In the section of INITIALIZE ITERATION we defined the ratios for the continuation scheme. These ratios guarantee that the necessary conditions between the penalization factors of piezoelectric matrices will follow the intrinsic conditions suggested by [44] during the continuation scheme of penalization factors. NATD is the normalized desired natural frequency. Ym is the optimization variable for the attachment mass that it has set to zero as the initial value before the optimization.

In the section of MMA Preparation, we set the initial values for the the MMA optimizer. However, the MMA code will not be presented in the paper and these are external codes that are called in our code. To have the MMA code, a request by reader should be sent to the author of the MMA paper [25, 26].

5.1.2 Iteration loop

In the section of START ITERATION, we start the optimization iterations. Iteration loop start by the filter/projection part which is again transferred from the code written by Ferrari et al. [43]. This initial part of iteration loop produce the projected physical densities (xPhys).

The interpolation function mentioned in Eq. 27, is implemented in following line:

figure b

The line after, produces the derivation of (xPhysH) with respect to (xPhys) which is necessary for the sensitivity analysis:

figure c

In the part of (FE-ANALYSIS), the column vectors sM, sKuu, sKup, sKpp will be used to create the mass matrix, stiffness matrix, coupling matrix and permittivity matrix respectively all at the global (system) level.

In the following line, the attachment mass multiplied to optimization variable (Ym), will be augmeneted to the global mass matrix:

figure d

The natural frequency and the related eigenvector of the system are calculated in the following line:

figure e

The variable Freq produces the real natural frequency in Hertz by rolling back the normalization. In next line, eigenvector is normalized with respect to mass matrix:

figure f

The constitution of global matrices and solving the finite element equilibrium equation and adjoint equations remain the same as previous code [13]. In the part of OBJECTIVE FUNCTION AND SENSITIVITY ANALYSIS, the mechanical energy is divided to two parts related to \(k_{uu}\) and \(-m\Omega ^2\).

The sensitivity of objective function related the attachment mass which has been mentioned in Eq. 29, is calculated in the following line:

figure g

The sensitivities of natural frequency with respect to density and mass ratio (y) which are mentioned in Eq. 31 are calculated in following lines:

figure h

All the calculated sensitivities are filtered using the MATLAB built-in function imfilter as suggested by Ferrari et al. [43].

The section of MMA OPTIMIZATION OF DESIGN VARIABLES calls MMA optimizer to update the optimization variables. The external codes which are called in this section are mmasub.m and subsolve.m which should be requested from the author of the papers [25, 26].

After updating the optimization variables, the continuation scheme will be applied to the penalization factor and sharpness factor for the next iteration. The engagement of this continuation scheme will be done in a particular iteration number defined by the user as explained before.

Fig. 7
figure 7

Topology optimization result for PEH energy harvester for different excitation frequency. Desired natural frequency = 2000 (Hz). a-c) Layout results, d-f) Polarization profile, g-j) Numerical plots

Full size image
Fig. 8
figure 8

Topology optimization result for PEH energy harvester for different desired natural frequency. Excitation frequency = 800 (Hz). a-c) Layout results, d-f) Polarization profile, g-j) Numerical plots

Full size image

5.1.3 Presentation of results

The final section of the paper is PLOT DENSITIES & POLARIZATION which show the density and polarization profile in each iteration plus showing the numerical results.

Fig. 9
figure 9

Topology optimization result for PEH energy harvester for different attached mass. Excitation frequency = 800 (Hz) and desired natural frequency = 2000 (Hz). a-c) Layout results, d-f) Polarization profile, g-j) Numerical plots

Full size image

5.2 Case studies

To analyze the efficiency of the code, three case studies are investigated. For all of the case studies the optimization problem is formulated as it is mentioned in Eq. 28 which means the structure in Fig. 6 is under harmonic excitation and while there is a constraint on the fundamental (first) natural frequency, the goal is to maximize the output electrical energy VS mechanical energy. The optimization variables are the density, polarization and attachment’s mass.

5.2.1 Various excitation frequency, constant constraint on the natural frequency

In the first case study, the structure will be excited by three different frequencies while the constraint on the natural frequency is equivalent to 2000 Hz. The results of optimization are illustrated in Fig. 7. As it can be seen in this figure, different optimal layouts are obtained for different excitation frequencies. This was also studied in the previously published code [13]. However, the important points here can be seen in the numerical results. In panel (i) of Fig. 7 it is obvious that in all cases the optimization respected the constraint on the natural frequency precisely. The results are quite satisfactory considering the fact that the optimal layouts are completely steered to fully black and white and gray elements are successfully avoided. Although the filtering and projection were efficient in this case, the major factor is the optimization of the attachment’s mass. As can be seen in panel (j), the optimization variable (y) gradually increased during the optimization to reduce the overall natural frequency of the system. This gives more freedom to the optimization solver to increase the mass of the structure without modifying its stiffness.

5.2.2 Constant excitation frequency, different constraint on the natural frequency

In the next case study, the results of optimization for different constraints on the natural frequency are reported in Fig. 8. In panels (i) and (j) of this figure, it can be seen that the constraint on the natural frequency is respected with different final attachment mass. When the constraint on the natural frequency is very low, higher mass is required to decrease the natural frequency and vice versa.

5.2.3 Different maximum allowable attachment’s mass

In the final case study, the results of optimization for different maximum allowable attachment’s mass are illustrated in Fig. 9. In this case study, a constant constraint on the natural frequency and a constant excitation frequency are considered for three different attachment’s mass. Moreover, the final optimal attachment’s mass (mass ratio times the maximum allowable mass) is the same. However, still, the optimal layouts (panels (a-c)), are different. This can be due to the fact that the maximum allowable jump between the values of optimization variables in two sequences of iteration is limited. Hence, the design with more allowable mass respects the constraint sooner.

The provided MATLAB code in this section can be extended to 3D problem. In this regard, the strategy and structure of the code remains the same. The provided MATLAB code is flexible in terms of considering different case studies i.e. different boundary conditions and force applications, design domain, etc.

6 Toward multi-material topology optimization

In pursuit of advancing the application of topology optimization to piezoelectric structures, AS2M department embarked on a new initiative. Building upon the proven success of topology optimization using single material, particularly in the design of piezoelectric energy harvesters (PEHs) and piezoelectric actuators as summarized in Table 2, this new venture seeks to simultaneously distribute both active and passive materials.

Table 2 Summary of publications regarding topology optimization of piezoelectric structures in AS2M department
Full size table
Fig. 10
figure 10

Piezoelectric multi-material actuator design domain with loading and boundary conditions

Full size image

The research on multi-material has reached a mature stage, as evidenced by several notable works [45,46,47,48]. Multi-material topology optimization (MMTO) involves the integration of soft materials and passive materials, drawing inspiration from natural systems. This innovative design methodology strives to achieve an optimal equilibrium between the flexibility inherent in soft piezoelectric materials and the sturdiness of rigid passive materials.

Leveraging multi-material topology optimization provides an avenue to fully exploit the inherent advantages of using different materials to enhance structural performance. This approach leads to an increase in the degrees of freedom in force, displacement and energy transduction particularly in the context of piezoelectric materials [49]. The process of incorporating multi-material technique into the design of robotic structures as given in the design of Robobee, MiGribot and MilliDelta involves the optimal combination of two distinct materials to leverage their individual inherent characteristics through a unified approach. This integration is crucial for optimizing the overall performance of the robotic systems.

A key technique employed in this endeavor is topology optimization (TO) particularly utilizing the well established Solid Isotropic Materials with Penalization (SIMP) method. The literature primarily addresses cases of combination of multi-material such as passive-passive, active-active and active-passive materials.

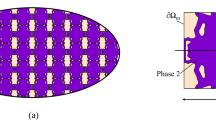
The multi-material scheme is responsible for creation of a design domain comprising of three phases: void and two solid phases corresponding to either void or passive materials as depicted in Fig. 10.

7 Conclusion

This paper primarily summarized and discussed the appro-aches developed at AS2M/FEMTO-ST institute for the topological design of piezoelectric structures. The summary of the publications and the introduced contribution is reported in Table 2. We demonstrated that topology optimization methodology can be employed as a design tool to obtain miniaturized piezoelectric structures with enhanced performances. Moreover, the eigenvalue and mass optimization of the PEH are presented in the paper theoretically and a 2D topology optimization MATLAB code is provided to tune the frequency of a piezoelectric energy harvester by optimizing the mass of the attachment. This is a first and new code in the literature in this context.

Extending the SIMP to piezoelectric material paves the way for promising perspectives. The first perspective would concern multi-material topology optimization including active and passive material. The other perspectives would concern multi-degrees of freedom structures and consideration of large deformations.