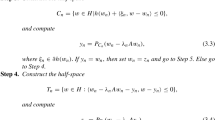Parallel modified methods for pseudomonotone equilibrium problems and fixed point problems for quasi-nonexpansive mappings

Abstract

The paper considers the problem of finding common solutions of a system of pseudomonotone equilibrium problems and fixed point problems for quasi-nonexpansive mappings. The problem covers various mathematical models of convex feasibility problems and the problems whose constraints are expressed by the intersection of fixed point sets of mappings. The main purpose of the paper is to design and improve computations over each step and weaken several assumptions imposed on bifunctions and mappings. Two parallel algorithms for finding of a particular solution of the problem are proposed in Hilbert spaces where each subproblem in the family can be computed simultaneously. The first one is a modified hybrid method which combines three methods including the generalized gradient-like projection method, the Mann’s iteration and the hybrid (outer approximation) method. This algorithm improves the hybrid extragradient method at each computational step where only one optimization problem is solved for each equilibrium subproblem in the family and the hybrid step does not deal with the feasible set of the considered problem. The strong convergence of the algorithm comes from the hybrid method under the Lipschitz-type condition of bifunctions. The second algorithm is a viscosity-like method with a linesearch procedure that aims to avoid the Lipschitz-type condition imposed on bifunctions. With the incorporated viscosity technique, the algorithm also provides strong convergence. Several numerical experiments are performed to illustrate the efficiency of the proposed algorithms and also to compare them with known parallel hybrid extragradient methods.

1 Introduction

Let H be a real Hilbert space and C be a nonempty closed convex subset of H. Let $f:C\times C\rightarrow \mathfrak {R}$ be a bifunction with $f(x,x)=0$ for all $x\in C$. The equilibrium problem (EP) for f on C is to find $x^*\in C$ such that

$$\begin{aligned} f(x^*,y)\ge 0,~\forall y\in C. \end{aligned}$$

(1)

The solution set of EP (1) is denoted by EP(f, C). Mathematically, EP (1) is a generalization of many other mathematical models including variational inequality problems, Nash-Cournot equilibrium point problems, optimization problems and fixed point problems [8, 13, 24]. Some methods for solving EP (1) can be found, for example, in [14,15,16,17,18,19,20, 25, 30, 31, 33,34,35, 38, 40, 41]. The problem of finding common solutions of a system of equilibrium problems has received a lot of attention by many authors in recent years, see for instance [12, 22, 25] and the references therein. This common problem covers in particular various forms of convex feasibility problems [4, 11]. The paper interests in the following problem.

Problem 1.1

Find an element $x^*\in \Omega :=\left( \cap _{i\in I} EP(f_i,C)\right) \bigcap \left( \cap _{j\in J} Fix(S_j)\right)$, where $f_i:C\times C\rightarrow \mathfrak {R},~i\in I=\left\{ 1,2,\ldots ,N\right\}$ are bifunctions and $S_j:C\rightarrow C,~j\in J=\left\{ 1,2,\ldots ,M\right\}$ are quasi-nonexpansive mappings.

The motivation for studying this problem is in its possible application to mathematical models whose constraints can be expressed as the common fixed point set of finitely many mappings. This happens, in particular, in the practical problems as signal processing, network resource allocation, image recovery, for examples [10, 23, 42]. Some algorithms for solving Problem 1.1 can be found in [3, 27, 34, 36] and the references therein. Almost existing methods are designed sequentially and used the proximal method for each equilibrium subproblem in the family. The proximal method for EP (1) consists of solving a strongly monotone regularized equilibrium problem per each iteration, i.e., given $x_0\in C$, find, for all $n\ge 1$, $x_{n+1}\in C$ such that

$$\begin{aligned} f(x_{n+1},y)+\frac{1}{r_n}\left\langle y-x_{n+1},x_{n+1}-x_n\right\rangle \ge 0,~\forall y\in C, \end{aligned}$$

(2)

where $\left\{ r_n\right\}$ is a positive control parameter sequence. In this paper, we focus on the projection methods. In [26], Korpelevich introduced the extragradient projection method for solving saddle point problems in Euclidean spaces. After that this method was extended to solve variational inequality problems (VIP) involving Lipschitz continuous and monotone operators in Hilbert spaces. Recall that the VIP for an operator $A: C \rightarrow H$ is to find $x^* \in C$ such that

$$\begin{aligned} \left\langle Ax^*,x-x^*\right\rangle \ge 0,\,\,\forall x\in C. \end{aligned}$$

(3)

The VIP (3) is known as a special case of the EP (1) when $f(x,y)=\left\langle Ax,y-x\right\rangle$. The extragradient method for the VIP (3) is of the form

$$\begin{aligned} \left\{ \begin{array}{ll} y_n=P_C(x_n-\lambda A(x_n)),\\ x_{n+1}=P_C(x_n-\lambda A(y_n)), \end{array} \right. \end{aligned}$$

(4)

where $\lambda \in \left( 0,\frac{1}{L}\right)$, L is the Lipschitz constant of A, and $P_C$ denotes the metric projection from H onto C.

In 2008, the extragradient method was extended to equilibrium problems by Tran et. al. [35] in Euclidean spaces. In that case, two projections in the extragradient method become two optimization programs

$$\begin{aligned} \left\{ \begin{array}{ll} y_n= \underset{y\in C}{\mathrm{argmin}} \{ \lambda f(x_n, y) +\frac{1}{2}||x_n-y||^2\},\\ x_{n+1} = \underset{y\in C}{\mathrm{argmin}}\{ \lambda f(y_n, y) +\frac{1}{2}||x_n-y||^2\}.\\ \end{array} \right. \end{aligned}$$

(5)

The sequence $\left\{ x_n\right\}$ generated by algorithm  (5) converges to some point in EP(f, C) under the assumptions of pseudomonotonicity and the Lipschitz-type condition of bifunction f. In infinite dimensional Hilbert spaces, the extragradient method, in general, is weakly convergent. A question is how to design an algorithm which provides the strong convergence. The hybrid (outer approximation) method and the viscosity method were sucessfully proposed to answer to the above question. Some strongly convergent algorithms for solving Problem 1.1 with $M=N=1$ in Hilbert spaces can be found in [2, 29, 30, 40, 41]. For solving Problem 1.1 with $M,N>1$, the authors in [22] introduced three parallel hybrid extragradient methods, and one of them [22, Algorithm 1] is designed as follows:

Algorithm 1.1

$$\begin{aligned} \left\{ \begin{array}{ll} y_n^i= \underset{y\in C}{\mathrm{argmin}} \{ \lambda f_i(x_n, y) +\frac{1}{2}||x_n-y||^2\},~i\in I,\\ z_n^i = \underset{y\in C}{\mathrm{argmin}}\{ \lambda f_i(y^i_n, y) +\frac{1}{2}||x_n-y||^2\},~i\in I,\\ \bar{z}_n=\arg \max \left\{ ||z_n^i-x_n||:~i\in I\right\} ,\\ u^j_n=\alpha _n x_n+(1-\alpha _n)S_j\bar{z}_n,~j\in J,\\ \bar{u}_n=\arg \max \left\{ ||u_n^j-x_n||:~j\in J\right\} ,\\ C_{n}=\left\{ z\in C:||\bar{u}_n-z||^2\le ||x_n-z||^2\right\} ,\\ Q_n=\left\{ z\in C:\left\langle x_0-x_n,z-x_n\right\rangle \le 0\right\} ,\\ x_{n+1}=P_{C_n\cap Q_n}(x_0), \end{array} \right. \end{aligned}$$

where $x_0\in C$ and $\lambda >0$, $\left\{ \alpha _n\right\} \subset (0,1)$ are parameters satisfying the following conditions:

$$\begin{aligned} \lim \sup _n\alpha _n<1 ~\text{ and }~0<\lambda <\min \left\{ \frac{1}{2c_1},\frac{1}{2c_2}\right\} \end{aligned}$$

(6)

with $c_1,~c_2$ being two Lipschitz-type constants of f (see, Definition 2.2 (iv) in Sect. 2). Two tasks of Algorithm 1.1 are to solve 2N optimization problems and find the projection $x_{n+1}=P_{C_n\cap Q_n}(x_0)$. The additional computations $\bar{z}_n$ and $\bar{u}_n$ are negligible. It has been proved that the sequence $\left\{ x_n\right\}$ generated by Algorithm 1.1 converges strongly to $P_\Omega (x_0)$ under assumption (6) and the nonexpansiveness of mappings $S_j$. The advantages of the extragradient method are that two optimization problems are solved per each iteration which seems to be numerically easier than nonlinear-inequality (2) in the proximal method and it is used for the class of pseudomonotone bifunctions. Another possible advantage of parallel algorithms, in computations on computing clusters or multi-core computers, is that intermediate approximations can be found simultaneously over each subproblem in the family while sequential ones are not. In this paper, we concern about the followings in Algorithm 1.1 for solving Problem 1.1.

• (a) The number of solved optimization problems per each iteration in Algorithm 1.1 is 2N. This can be costly and it happens if the feasible set C and the bifunctions $f_i,~i\in I$ have complex structures. We want to reduce the number of solved optimization programs in this intermediate step.

• (b) At the last step of Algorithm 1.1, we see that the projection $x_{n+1}=P_{C_n\cap Q_n}(x_0)$ still deals with the feasible set C. In the first proposed parallel algorithm, this projection is a more relaxation without dealing with C.

• (c) The class of mappings is used in Algorithm 1.1 is nonexpansive. We would like to extend this class to the one of quasi-nonexpansive and demiclosed at zero mappings. An example for the class of quasi-nonexpansive mappings $S_j,~j\in J$ is presented in Sect. 5.

• (d) Algorithm 1.1 and the first proposed algorithm (Algorithm 3.1 in Sect. 3) are strongly convergent under the slightly strong assumption of the Lipschitz-type condition of bifunctions. Using the linsearch procedure, we proposed the second parallel algorithm for Problem 1.1 which avoids this strong condition. The proof of the convergence of the second algorithm is based on the obtained ones in the paper [40, Sect. 4].

• (e) The strong convergence of two proposed algorithms comes from the hybrid (outer approximation) method and the viscosity method. The efficiency of the new algorithms is also illustrated by some numerical experiments in comparison with Algorithm 1.1.

This paper is organized as follows: In Sect. 2, we collect some definitions and preliminary results for further use. Sects. 3 and 4 present the proposed algorithms and analyze their convergence. In Sect. 5, we perform some numerical examples to check the convergence of the algorithms and compare them with Algorithm 1.1.

2 Preliminaries

Let C be a nonempty closed convex subset of a real Hilbert space H. The metric projection $P_C$ from H onto C is defined by $P_Cx=\arg \min \left\{ ||x-y||:y\in C\right\} ,~x\in H.$ It is well - known that $P_C$ has the following properties.

Lemma 2.1

Let $P_C:H\rightarrow C$be the metric projection from H onto C. Then

• (i) $\left\langle P_C x-P_C y,x-y \right\rangle \ge \left\| P_C x-P_C y\right\| ^2,~\forall x,~y\in H.$

• (ii) $\left\| x-P_C y\right\| ^2+\left\| P_C y-y\right\| ^2\le \left\| x-y\right\| ^2,~x\in C,~ y\in H$

• (iii) $z=P_C x \Longleftrightarrow \left\langle x-z,z-y \right\rangle \ge 0,~ \forall y\in C.$

Let $\left\{ x_i\right\} _{i=0}^N$ be a finite sequence in H and $\left\{ \gamma _{i}\right\} _{i=0}^N\subset [0,1]$ be a sequence of real numbers such that $\sum _{i=0}^N\gamma _i=1$. By the induction, it is easy to show that the following inequality holds

$$\begin{aligned} ||\sum _{i=0}^N\gamma _i x_i||^2= & {} \sum _{i=0}^N\gamma _i||x_i||^2-\sum _{i\ne j}\gamma _i\gamma _j||x_i-x_j||^2\le {\sum _{i=0}^N\gamma _i||x_i||^2-\sum _{j=1}^N\gamma _0\gamma _j||x_0-x_j||^2 } \end{aligned}$$

(7)

A mapping $S:C\rightarrow C$ is called nonexpansive if $||S(x)-S(y)||\le ||x-y||$ for all $x,~y\in C$. The class of mappings mentioned in Algorithm 1.1 is nonexpansive while certain mappings arising for instance in subgradient-projection techniques are not nonexpansive. In this paper, we consider the following mappings.

Definition 2.1

[29] A mapping $S:C\rightarrow C$ is called:

• (i) quasi-nonexpansive if $Fix(S)\ne \emptyset$ and $||S(x)-x^*||\le ||x-x^*||,~\forall x^*\in Fix(S),~\forall x\in C.$

• (ii) $\beta$ - demicontractive if $Fix(S)\ne \emptyset$, and there exists $\beta \in [0,1)$ such that

  $$\begin{aligned} ||S(x)-x^*||^2\le ||x-x^*||^2+\beta ||x-S(x)||^2,~\forall x^*\in Fix(S),~\forall x\in C. \end{aligned}$$

• (iii) demiclosed at zero if, for each sequence $\left\{ x_n\right\} \subset C$, $x_n\rightharpoonup x$, and $||S(x_n)-x_n||\rightarrow 0$ then $S(x)=x$.

From this definition, we see that each nonexpansive mapping with fixed points is quasi-nonexpansive while the class of demicontractive mappings contains the one of quasi-nonexpansive mappings. Also note that, if $S:C\rightarrow C$ be a $\beta$— demicontractive mapping such that $Fix(S)\ne \emptyset$ then $S_w=(1-w)I+wS$ is a quasi-nonexpansive mapping over C for every $w\in [0,1-\beta ]$ [29, Remark 4.2]. Furthermore,

$$\begin{aligned} ||S_wx-x^*||\le ||x-x^*||^2-w(1-\beta -w)||Sx-x||^2,~\forall x^*\in Fix(S),~\forall x\in C. \end{aligned}$$

It is routine to see that $Fix(S)=Fix(S_w)$ if $w\ne 0$ and Fix(S) is a closed convex subset of C.

In Sect. 4, to find a particular point in the solution set $\Omega$ of Problem 1.1, we focus our attention on an operator $F:C\rightarrow H$ which is $\eta$—strongly monotone and L - Lipschitz continuous, i.e., there exist two positive constants $\eta$ and L such that, for all $x,~y\in C$, $\left\langle F(x)-F(y),x-y\right\rangle \ge \eta ||x-y||^2$ and $||F(x)-F(y)||\le L ||x-y||.$ We need the following result for proving the convergence of our parallel viscosity algorithm.

Lemma 2.2

(cf. [42, Lemma 3.1]) Suppose that $F:C\rightarrow H$is an $\eta$—strongly monotone and L—Lipschitz continuous operator. By using arbitrarily fixed $\mu \in \left( 0,\frac{2\eta }{L^2}\right)$. Define the mapping $G:C\rightarrow H$by $G^\mu (x)=\left( I-\mu F\right) x,~x\in C.$Then

• (i) $G^\mu$is strictly contractive over C with the contractive constant $\sqrt{1-\mu (2\eta -\mu L^2)}$.

• (ii) For all $\nu \in (0,\mu )$,

  $$\begin{aligned} ||G^{\nu }(y)-x||\le \left( 1-\frac{\nu \tau }{\mu }\right) ||y-x||+\nu ||F(x)||, \end{aligned}$$

  where $\tau =1-\sqrt{1-\mu (2\eta -\mu L^2)}\in (0,1)$.

Proof

(i) From the definition of $G^\mu$, the $\eta$—strong monotonicity and L—Lipschitz continuity of F, we obtain

$$\begin{aligned} ||G^\mu (x)-G^\mu (y)||^2= & {} ||(x-y)-\mu (F(x)-F(y))||^2\\= & {} ||x-y||^2-2\mu \left\langle x-y,F(x)-F(y)\right\rangle +\mu ^2||F(x)-F(y)||^2\\\le & {} ||x-y||^2-2\mu \eta ||x-y||^2+\mu ^2L^2||x-y||^2\\= & {} (1-\mu (2\eta -\mu L^2))||x-y||^2. \end{aligned}$$

This yields conclusion (i). Next, we prove claim (ii). From the defition of G and (i), we have

$$\begin{aligned} ||G^{\nu }(y)-x||= & {} ||\left( y-\nu F(y)\right) -\left( x-\nu F(x)\right) -\nu F(x)||\\\le & {} ||\left( y-\nu F(y)\right) -\left( x-\nu F(x)\right) ||+\nu ||F(x)||\\= & {} ||\left( 1-\frac{\nu }{\mu }\right) (y-x)+\frac{\nu }{\mu }\left[ \left( y-\mu F(y)\right) -\left( x-\mu F(x)\right) \right] ||+\nu ||F(x)||\\= & {} ||\left( 1-\frac{\nu }{\mu }\right) (y-x)+\frac{\nu }{\mu }\left[ G^{\mu }(y)-G^{\mu }(x)\right] ||+\nu ||F(x)||\\\le & {} \left( 1-\frac{\nu }{\mu }\right) ||y-x||+\frac{\nu }{\mu }\sqrt{1-\mu (2\eta -\mu L^2)}||y-x||+\nu ||F(x)||\\= & {} \left( 1-\frac{\nu \tau }{\mu }\right) ||y-x||+\nu ||F(x)||. \end{aligned}$$

$\square$

Next, we recall some concepts of monotonicity of a bifunction (see [8]).

Definition 2.2

A bifunction $f:C\times C\rightarrow \mathfrak {R}$ is said to be:

• (i) strongly monotone on C, if there exists a constant $\gamma >0$ such that

  $$\begin{aligned} f(x,y)+f(y,x)\le -\gamma ||x-y||^2,~\forall x,y\in C; \end{aligned}$$

• (ii) monotone on C, if $f(x,y)+f(y,x)\le 0,~\forall x,y\in C;$

• (iii) pseudomonotone on C, if $f(x,y)\ge 0 \Longrightarrow f(y,x)\le 0,~\forall x,y\in C;$

From above definitions, it is clear that a strongly monotone bifunction is monotone and a monotone bifunction is pseudomonotone. We say that a bifunction $f:C\times C\rightarrow \mathfrak {R}$ satisfies a Lipschitz-type condition on C, if there exist two positive constants $c_1,c_2$ such that

$$\begin{aligned} f(x,y) + f(y,z) \ge f(x,z) - c_1||x-y||^2 - c_2||y-z||^2, \quad \forall x,y,z \in C. \end{aligned}$$

The Lipschitz-type condition of a bifunction was introduced by Mastroeni [31]. It is nesessary to prove the convergence of the auxiliary principle method for solving an equilibrium problem. If $A:C\rightarrow H$ is a L—Lipschitz continuous operator then the bifunction $f(x,y)=\left\langle A(x),y-x\right\rangle$ satisfies the Lipschitz-type condition with $c_1=c_2=L/2$.

We need the following technical lemmas for establishing the convergence of the proposed algorithms.

Lemma 2.3

[39, Sec.7.1] Let C be a nonempty closed convex subset of a real Hilbert space H and $g:C\rightarrow \mathfrak {R}$be a convex and subdifferentiable function on C. Then, $x^*$is a solution to the following convex optimization problem $\min \left\{ g(x):x\in C\right\}$if and only if $0\in \partial g(x^*)+N_C(x^*)$, where $\partial g(.)$denotes the subdifferential of g and $N_C(x^*)$is the normal cone of C at $x^*$.

Lemma 2.4

[29, Remark 4.4] Let $\left\{ \epsilon _n\right\}$be a sequence of non-negative real numbers. Suppose that for any integer m, there exists an integer p such that $p\ge m$and $\epsilon _p\le \epsilon _{p+1}$. Let $n_0$be an integer such that $\epsilon _{n_0}\le \epsilon _{n_0+1}$and define, for all integer $n\ge n_0$,

$$\begin{aligned} \tau (n)=\max \left\{ k\in N:n_0\le k\le n, ~\epsilon _k\le \epsilon _{k+1}\right\} . \end{aligned}$$

Then $0\le \epsilon _n \le \epsilon _{\tau (n)+1}$for all $n\ge n_0$. Furthermore, the sequence $\left\{ \tau (n)\right\} _{n\ge n_0}$is non-decreasing and tends to $+\infty$as $n\rightarrow \infty$.

Lemma 2.5

[28] Let $\left\{ \alpha _n\right\}$, $\left\{ \beta _n\right\}$, $\left\{ \gamma _n\right\}$be nonnegative real sequences, $a,~b \in \mathfrak {R}$and for all $n\ge 0$the following inequality holds $\alpha _n\le \beta _n+b \gamma _n-a \gamma _{n+1}.$If $~\sum _{n=0}^\infty \beta _n <+\infty$and $a>b\ge 0$then $\lim _{n\rightarrow \infty }\alpha _n=0$.

3 Parallel modified hybrid method

In this section, we propose a parallel modified hybrid algorithm for solving Problem 1.1. Without loss of generality, we can assume that $M=N$, i.e., $I=J=\left\{ 1,2,\ldots ,N\right\}$. Indeed, if $M>N$ then we can consider additionally $f_i=0$ for all $i=N+1,\ldots ,M$. Otherwise, if $N>M$ then we can set $S_j=I$ for all $j=M+1,\ldots ,N$. In order to obtain the convergence of Algorithm 3.1 below, we assume that the bifunctions $f_i,~i\in I$ satisfy the following conditions.

Condition 1

• A1. $f_i(x,x)=0$ for all $x,y\in C$ and $f_i$ is pseudomonotone on C;

• A2. $f_i$ satisfies Lipschitz-type condition on C with two constants $c_1,~c_2$;

• A3. $\lim \sup _{n\rightarrow \infty }f_i(x_n,y)\le f(x,y)$ for each sequence $\left\{ x_n\right\} \subset C$ converging weakly to x;

• A4.  $f_i(x,.)$ is convex and subdifferentiable on C for every fixed $x\in C$.

If $f_i$ satisfies conditions A1-A4 then $E(f_i,C)$ is closed and convex, see [32, 35]. Thus, the set $\cap _{i\in I} EP(f_i,C)$ is also closed and convex. Hypothesis A3 was used by several authors in [21, 41]. We assume that the bifunctions $f_i,~i\in I$ satisfy Lipschitz-type condition with the same constants $c_1,~c_2$. This assumption does not make a restriction on the considered problem because, if, for each $i\in I$, $f_i$ satisfies Lipschitz-type condition with two constants $c_1^i,~c_2^i$. By putting $c_1=\max \left\{ c_1^i:i\in I\right\}$ and $c_2=\max \left\{ c_2^i:i\in I\right\}$, we see that $f_i,~i\in I$ also satisfy Lipschitz-type condition with two constants $c_1,~c_2$.

The first algorithm is described as follows.

Before analyzing the convergence of Algorithm 3.1, we discuss the differences between Algorithm 3.1 and the hybrid extragradient methods in [2, 21, 22, 33, 40]. Firstly, for $N=M=1$, while the hybrid extragradient methods [2, 33, 40] require solving two optimization programs onto the feasible set C per each iteration, then our Algorithm 3.1 only needs to solve one problem. Besides, the intersection $C_n\cap Q_n$ in the hybrid methods [33, 40] still deals with the feasible set C, in fact, it is the intersection of C with two halfspaces. In contrary to this, $C_n\cap Q_n$ in our algorithm is only the intersection of three halfspaces which is not relative to the feasible set C. Next, for $N,~M>1$, three parallel hybrid extragradient algorithms were proposed in [22] for solving Problem 1.1 where combine the extragradient method [35] and the hybrid projection method. These algorithms require solving 2N optimization programs per each iteration and $C_n\cap Q_n$ is still the intersection of C with two halfspaces. While the main task of our Algorithm 3.1 per each iteration is to solve only N optimization problems. The reason for this is that the constructed sets $C_n^i,~i\in I$ in Step 1.3 (hybrid step) are slightly different to the hybrid projection step in [22, 33, 40]. Moreover, also in Step 1.3 of Algorithm 3.1, $Q_n$ is a halfspace and for each $i\in I$, the set $C_n^i$ is the intersection of two halfspaces, thus $C_n\cap Q_n$ is the intersection of $2N+1$ halfspaces. Since the projection on halfspace is explicit, $x_{n+1}=P_{C_n\cap Q_n}(x_0)$ in Step 2 can be found effectively by Haugazeau’s method [7, Corollary 29.8] or the available methods of convex quadratic programming [9, Chapter 8].

Together with Condition 1, we also assume that each mapping $S_j,~j\in J$ satisfies the following conditions.

Condition 2

• B1. $S_j$ is quasi-nonexpansive on C;

• B2. $S_j$ is demiclosed at zero.

The subgradient—projection mappings presented in Sect. 5 are well—known to satisfy Condition 2. As mentioned above, under Condition 2, the fixed point set $Fix(S_j)$ of $S_j$ is closed and convex. Thus $\Omega$ is closed and convex. In this paper, we assume that $\Omega$ is nonempty. Hence, the projection $P_\Omega (x_0)$ is well-defined. In this section, we also suppose that the two parameters $\lambda ,~k$ and the sequence $\left\{ \gamma _n\right\}$ satisfy the following conditions.

Condition 3

• C1. $0< \lambda <\frac{1}{2(c_1+c_2)},~ k>\frac{1}{1-2\lambda (c_1+c_2)}.$;

• C2. $\lim \inf _{n\rightarrow \infty }\gamma _n(1-\gamma _n)>0$.

Comparing with condition (6) in Algorithm 1.1, we see that the stepsize $\lambda$ in condition C1 is smaller. We have the following lemma which plays a central role in proving the convergence of Algorithm 3.1.

Lemma 3.1

Let $\left\{ x_n\right\} ,\left\{ y_n^i\right\}$and $\left\{ z_n^i\right\}$be the sequences generated by Algorithm 3.1. Then, there hold the following relations for all $i\in I$and $n\ge 1$.

• (i) $\left\langle y_{n+1}^i-x_n,y-y_{n+1}^i\right\rangle \ge \lambda \left( f_i({y}^i_n,y_{n+1}^i)-f_i({y}^i_n,y)\right) ,~\forall y\in C.$

• (ii) $||{z}^i_{n+1}-x^*||^2\le ||y_{n+1}^i - x^*||^2\le ||x_n-x^*||^2+\epsilon _n^i$ for all $x^*\in \Omega$.

Proof

(i) Lemma 2.3 and the definition of $y^i_{n+1}$ imply that

$$\begin{aligned} 0\in \partial _2\left( \lambda f_i(y^i_n,y)+\frac{1}{2}||x_n-y||^2\right) (y^i_{n+1})+N_C(y^i_{n+1}). \end{aligned}$$

Therefore, from $\partial \left( ||x_n-.||^2\right) =2(.-x_n)$, one obtains $\lambda w+y^i_{n+1}-x_n+\bar{w}=0,$ or, equivalently

$$\begin{aligned} y^i_{n+1}-x_n=-\lambda w - \bar{w}, \end{aligned}$$

(8)

where $w\in \partial _2 f_i(y^i_n,y^i_{n+1}):=\partial f_i(y^i_n,.)(y^i_{n+1})$ and $\bar{w}\in N_C(y^i_{n+1})$. From the relation (8), we obtain

$$\begin{aligned} \left\langle y^i_{n+1}-x_n,y-y^i_{n+1}\right\rangle =\lambda \left\langle w,y^i_{n+1}-y\right\rangle +\left\langle \bar{w},y^i_{n+1}-y\right\rangle ,~\forall y\in C \end{aligned}$$

which, from the definition of $N_C$, implies that

$$\begin{aligned} \left\langle y^i_{n+1}-x_n,y-y^i_{n+1}\right\rangle \ge \lambda \left\langle w,y^i_{n+1}-y\right\rangle ,~\forall y\in C. \end{aligned}$$

(9)

Since $w\in \partial _2 f(y^i_n,y^i_{n+1})$, $f_i(y^i_n,y)-f_i(y^i_n,y^i_{n+1})\ge \left\langle w,y-y^i_{n+1}\right\rangle ,~\forall y\in C.$ Thus,

$$\begin{aligned} \left\langle w,y^i_{n+1}-y\right\rangle \ge f_i(y^i_n,y^i_{n+1})-f_i(y^i_n,y),~\forall y\in C. \end{aligned}$$

This together with the relation (9) implies that

$$\begin{aligned} \left\langle y^i_{n+1}-x_n,y-y^i_{n+1}\right\rangle \ge \lambda \left( f_i(y^i_n,y^i_{n+1})-f_i(y^i_n,y)\right) ,~\forall y\in C. \end{aligned}$$

(10)

(ii) By the definition of $z_{n+1}^i$ and the convexity of $||.||^2$, we obtain

$$\begin{aligned} ||z^i_{n+1}-x^*||^2= & {} ||\gamma _n(y^i_{n+1}-x^*)+(1-\gamma _n)(S_{i}y^i_{n+1}-x^*)||^2\nonumber \\= & {} \gamma _n||y^i_{n+1}-x^*||^2+(1-\gamma _n)||S_{i}y^i_{n+1}-x^*||^2-\gamma _n(1-\gamma _n)||S_{i}y^i_{n+1}-y^i_{n+1}||^2\nonumber \\\le & {} \gamma _n||y^i_{n+1}-x^*||^2+(1-\gamma _n)||y^i_{n+1}-x^*||^2-\gamma _n(1-\gamma _n)||S_{i}y^i_{n+1}-y^i_{n+1}||^2\nonumber \\\le & {} ||y^i_{n+1}-x^*||^2-\gamma _n(1-\gamma _n)||S_{i}y^i_{n+1}-y^i_{n+1}||^2 \end{aligned}$$

(11)

$$\begin{aligned}\le & {} ||y^i_{n+1}-x^*||^2. \end{aligned}$$

(12)

From Lemma 3.1(i) we have

$$\begin{aligned} \left\langle y^i_{n}-x_{n-1},y-y^i_{n}\right\rangle \ge \lambda \left( f_i(y^i_{n-1},y^i_{n})-f_i(y^i_{n-1},y)\right) ,~\forall y\in C. \end{aligned}$$

(13)

Substituting $y=y^i_{n+1}\in C$ into (13), we obtain

$$\begin{aligned} \left\langle y^i_{n}-x_{n-1},y^i_{n+1}-y^i_{n}\right\rangle \ge \lambda \left( f_i(y^i_{n-1},y^i_{n})-f_i(y^i_{n-1},y^i_{n+1})\right) . \end{aligned}$$

Thus,

$$\begin{aligned} \lambda \left( f_i(y^i_{n-1},y^i_{n+1})-f_i(y^i_{n-1},y^i_{n})\right) \ge \left\langle y^i_{n}-x_{n-1},y^i_{n}-y^i_{n+1}\right\rangle . \end{aligned}$$

(14)

Substituting $y=x^*$ into (10), we get

$$\begin{aligned} \left\langle y^i_{n+1}-x_n,x^*-y^i_{n+1}\right\rangle \ge \lambda \left( f_i(y^i_n,y^i_{n+1})-f_i(y^i_n,x^*)\right) . \end{aligned}$$

(15)

Since $x^*\in EP(f_i,C)$ and $y^i_n\in C$, $f_i(x^*,y^i_n)\ge 0$. Hence, $f_i(y^i_n,x^*)\le 0$ because of the pseudomonotonicity of $f_i$. This together with (15) implies that

$$\begin{aligned} \left\langle y^i_{n+1}-x_n,x^*-y^i_{n+1}\right\rangle \ge \lambda f_i(y^i_n,y^i_{n+1}). \end{aligned}$$

(16)

Using the Lipschitz-type condition of $f_i$ with $x=y^i_{n-1}$, $y=y^i_{n}$ and $z=y^i_{n+1}$, we get

$$\begin{aligned} f_i(y^i_{n-1},y^i_n)+f_i(y^i_n,y^i_{n+1})\ge f_i(y^i_{n-1},y^i_{n+1})-c_1||y^i_{n-1}-y^i_n||^2-c_2||y^i_n-y^i_{n+1}||^2, \end{aligned}$$

which implies that

$$\begin{aligned} f_i(y^i_n,y^i_{n+1})\ge f_i(y^i_{n-1},y^i_{n+1})-f_i(y^i_{n-1},y^i_n)-c_1||y^i_{n-1}-y^i_n||^2-c_2||y^i_n-y^i_{n+1}||^2. \end{aligned}$$

(17)

Combining (16) and (17), we see that

$$\begin{aligned} \left\langle y^i_{n+1}-x_n,x^*-y^i_{n+1}\right\rangle\ge & {} \lambda \left\{ f_i(y^i_{n-1},y^i_{n+1})-f_i(y^i_{n-1},y^i_n)\right\} \nonumber \\&-\lambda c_1||y^i_{n-1}-y^i_n||^2-\lambda c_2||y^i_n-y^i_{n+1}||^2. \end{aligned}$$

From this and relation (14), we come to the following one,

$$\begin{aligned} \left\langle y^i_{n+1}-x_n,x^*-y^i_{n+1}\right\rangle\ge & {} \left\langle y^i_{n}-x_{n-1},y^i_{n}-y^i_{n+1}\right\rangle -\lambda c_1||y^i_{n-1}-y^i_n||^2\nonumber \\&-\lambda c_2||y^i_n-y^i_{n+1}||^2. \end{aligned}$$

Multiplying both sides of the last inequality by 2, we obtain

$$\begin{aligned} 2\left\langle y^i_{n+1}-x_n,x^*-y^i_{n+1}\right\rangle- & {} 2\left\langle y^i_{n}-x_{n-1},y^i_{n}-y^i_{n+1}\right\rangle \ge -2\lambda c_1||y^i_{n-1}-y^i_n||^2\nonumber \\&-2\lambda c_2||y^i_n-y^i_{n+1}||^2. \end{aligned}$$

(18)

We have the following fact

$$\begin{aligned}&2\left\langle y^i_{n+1}-x_n,x^*-y^i_{n+1}\right\rangle =||x_n-x^*||^2-||y^i_{n+1}-x^*||^2-||x_n-y^i_{n+1}||^2\nonumber \\&\quad = ||x_n-x^*||^2-||y^i_{n+1}-x^*||^2-||x_n-x_{n-1}||^2-2\left\langle x_n-x_{n-1},x_{n-1}-y^i_{n+1}\right\rangle \nonumber \\&\qquad -||x_{n-1}-y^i_{n+1}||^2\nonumber \\&\quad =||x_n-x^*||^2-||y^i_{n+1}-x^*||^2-||x_n-x_{n-1}||^2-2\left\langle x_n-x_{n-1},x_{n-1}-y^i_{n+1}\right\rangle \nonumber \\&\qquad -||x_{n-1}-y^i_{n}||^2-2\left\langle x_{n-1}-y^i_{n},y^i_{n}-y^i_{n+1}\right\rangle -||y^i_{n}-y^i_{n+1}||^2. \end{aligned}$$

(19)

We also have

$$\begin{aligned}&-2\left\langle x_n-x_{n-1},x_{n-1}-y^i_{n+1}\right\rangle \le 2||x_n-x_{n-1}||||x_{n-1}-y^i_{n+1}||\nonumber \\&\quad \le 2||x_n-x_{n-1}||||x_{n-1}-y^i_{n}||+2||x_n-x_{n-1}||||y^i_{n}-y^i_{n+1}||\nonumber \\&\quad \le || x_n-x_{n-1}||^2+||x_{n-1}-y^i_{n}||^2+k|| x_n-x_{n-1}||^2+\frac{1}{k}||y^i_{n}-y^i_{n+1}||^2, \end{aligned}$$

(20)

in which the first inequality follows from the Cauchy-Schwarz inequality, the second one follows from the triangle inequality and the last ones is true by the inequality $2ab\le a^2+b^2$. From the relations (19) and (20), we derive

$$\begin{aligned}&2\left\langle y^i_{n+1}-x_n,x^*-y^i_{n+1}\right\rangle \le ||x_n-x^*||^2-||y^i_{n+1}-x^*||^2+k|| x_n-x_{n-1}||^2\\&\quad +2\left\langle y^i_n-x_{n-1},y^i_{n}-y^i_{n+1}\right\rangle +\left( \frac{1}{k}-1\right) | |y^i_{n}-y^i_{n+1}||^2. \end{aligned}$$

Thus,

$$\begin{aligned}&2\left\langle y^i_{n+1}-x_n,x^*-y^i_{n+1}\right\rangle -2\left\langle y^i_n-x_{n-1},y^i_{n}-y^i_{n+1}\right\rangle \le ||x_n-x^*||^2\\&\quad -||y^i_{n+1}-x^*||^2+k|| x_n-x_{n-1}||^2+\left( \frac{1}{k}-1\right) ||y^i_{n}-y^i_{n+1}||^2, \end{aligned}$$

which, together with (18), leads to the following inequality

$$\begin{aligned} -2\lambda c_1||y^i_{n-1}-y^i_n||^2- & {} 2\lambda c_2||y^i_n-y^i_{n+1}||^2\le ||x_n-x^*||^2-||y^i_{n+1}-x^*||^2\\+ & {} k|| x_n-x_{n-1}||^2+\left( \frac{1}{k}-1\right) ||y^i_{n}-y^i_{n+1}||^2. \end{aligned}$$

Hence,

$$\begin{aligned} ||y^i_{n+1}-x^*||^2\le & {} ||x_n-x^*||^2+k|| x_n-x_{n-1}||^2+2\lambda c_1||y^i_{n-1}-y^i_n||^2\\&-\left( 1-\frac{1}{k}-2\lambda c_2\right) ||y^i_{n}-y^i_{n+1}||^2 \\= & {} ||x_n-x^*||^2+\epsilon ^i_n, \end{aligned}$$

in which the last equality follows from the definition of $\epsilon _n^i$. Combining this with (12), we obtain the desired conclusion. $\square$

Lemma 3.2

Let $\left\{ x_n\right\} ,\left\{ y^i_n\right\}$be the sequences generated by Algorithm 3.1. Then, there hold the following relations:

• (i) $\Omega \subset C_n\cap Q_n$for all $n\ge 0$.

• (ii) The sequence $\left\{ x_n\right\}$is bounded and

  $$\begin{aligned} \lim \limits _{n\rightarrow \infty }||x_{n+1}-x_n||=\lim \limits _{n\rightarrow \infty }||y^i_n-x_n||=\lim \limits _{n\rightarrow \infty }||y^i_{n+1} - y^i_{n}||=\lim \limits _{n\rightarrow \infty }||S_iy^i_{n} - y^i_{n}||=0. \end{aligned}$$

Proof

(i) Lemma 3.1(ii) and the definition of $C_n^i$ ensure that $\Omega \subset C_n^i$ for all $n\ge 0$ and $i\in I$. Thus, $\Omega \subset C_n$ for all $n\ge 0$. It is clear that $\Omega \subset H= C_0\cap Q_0$. Assume that $\Omega \subset C_n\cap Q_n$ for some $n\ge 0$. From $x_{n+1}=P_{C_n\cap Q_n}(x_0)$ and Lemma 2.1(iii), we see that $\left\langle z-x_{n+1},x_0-x_{n+1}\right\rangle \le 0$ for all $z\in C_n\cap Q_n$. Since $\Omega \subset C_n\cap Q_n$,

$$\begin{aligned} \left\langle z-x_{n+1},x_0-x_{n+1}\right\rangle \le 0 \end{aligned}$$

for all $z\in \Omega$. Thus, $\Omega \subset Q_{n+1}$ because of the definition of $Q_{n+1}$ or $\Omega \subset C_{n+1}\cap Q_{n+1}$. By the induction, $\Omega \subset C_n\cap Q_n$ for all $n\ge 0$. Since $\Omega$ is nonempty and the set $C_n\cap Q_n$ is closed and covnex for each $n\ge 0$, we obtain that the projection $P_{C_n\cap Q_n}(x_0)$ is well-defined.

(ii) From the definition of $Q_n$ and Lemma  2.1(iii), we see that $x_n=P_{Q_n}(x_0)$. Thus, by Lemma 2.1(ii), we have

$$\begin{aligned} ||z-x_n||^2\le ||z-x_0||^2-||x_n-x_0||^2,~\forall z\in Q_n. \end{aligned}$$

(21)

Substituting $z=x^\dagger :=P_{\Omega }(x_0)\in Q_n$ into (39), one has

$$\begin{aligned} ||x^\dagger -x_0||^2-||x_n-x_0||^2\ge ||x^\dagger -x_n||^2\ge 0. \end{aligned}$$

(22)

Hence, $\left\{ ||x_n-x_0||\right\}$ is a bounded sequence, and so is $\left\{ x_n\right\}$. Substituting $z=x_{n+1}\in Q_n$ into (39), one also has

$$\begin{aligned} 0\le ||x_{n+1}-x_n||^2\le ||x_{n+1}-x_0||^2-||x_n-x_0||^2. \end{aligned}$$

(23)

This implies that $\left\{ ||x_n-x_0||\right\}$ is non-decreasing. Hence, there exists the limit of $\left\{ ||x_n-x_0||\right\}$. By (23),

$$\begin{aligned} \sum _{n=1}^K||x_{n+1}-x_n||^2\le ||x_{K+1}-x_0||^2-||x_1-x_0||^2,~\forall K\ge 1. \end{aligned}$$

Passing to the limit in the last inequality as $K\rightarrow \infty$, we obtain

$$\begin{aligned} \sum _{n=1}^\infty ||x_{n+1}-x_n||^2<+\infty . \end{aligned}$$

(24)

Thus,

$$\begin{aligned} \lim _{n\rightarrow \infty }||x_{n+1}-x_n||=0. \end{aligned}$$

(25)

Since $x_{n+1}\in C_n=\cap _{i=1}^N C_n^i$, $x_{n+1}\in C^i_n$. From the definition of $C_n^i$,

$$\begin{aligned} ||z^i_{n+1} - x_{n+1}||^2\le ||y^i_{n+1} - x_{n+1}||^2\le ||x_n-x_{n+1}||^2+\epsilon ^i_n. \end{aligned}$$

(26)

Set $M_n^1=||z^i_{n+1} - x_{n+1}||^2$, $M^2_n=||y^i_{n+1} - x_{n+1}||^2$, $N_n=||x_n-x_{n+1}||^2+k||x_n-x_{n-1}||^2$, $P_n=||y^i_n-y^i_{n-1}||^2$, $b=2\lambda c_1$, and $a=1-\frac{1}{k}-2\lambda c_2$. From the definition of $\epsilon ^i_n$, $\epsilon ^i_n=k||x_n-x_{n-1}||^2+b P_n-a P_{n+1}$. Thus, from (26),

$$\begin{aligned} M^1_n\le M^2_n\le N_n+b P_n-a P_{n+1}. \end{aligned}$$

(27)

By the hypothesises of $\lambda , ~k$ and (24), we see that $a>b\ge 0$ and $\sum _{n=1}^\infty N_n<+\infty$. Lemmas  2.5 and (27) imply that $M^1_n,M^2_n\rightarrow 0$, or

$$\begin{aligned} \lim _{n\rightarrow \infty }||z^i_{n+1}- x_{n+1}||=\lim _{n\rightarrow \infty }||y^i_{n+1}- x_{n+1}||=0. \end{aligned}$$

This together with relation (25) and the following inequalities

$$\begin{aligned}&||y^i_{n+1}-y^i_{n}||\le ||y^i_{n+1}-x_{n+1}||+||x_{n+1}-x_n||+||x_{n}-y^i_{n}||,\\&||z^i_{n+1}- y^i_{n+1}||\le ||z^i_{n+1}- x_{n+1}||+|| x_{n+1}-z^i_{n+1}||, \end{aligned}$$

implies that

$$\begin{aligned} \lim _{n\rightarrow \infty }||y^i_{n+1} - y^i_{n}||=\lim _{n\rightarrow \infty }||y^i_{n+1} - z^i_{n+1}||=0,~i\in I. \end{aligned}$$

(28)

In addition, the sequences $\left\{ y^i_{n}\right\}$, $\left\{ z^i_{n}\right\}$ are also bounded because of the boundedness of $\left\{ x_n\right\}$. From relation (11), we obtain

$$\begin{aligned} \gamma _n(1-\gamma _n)||S_{i}y^i_{n+1}-y^i_{n+1}||^2\le & {} ||y^i_{n+1}-x^*||^2-||z^i_{n+1}-x^*||^2\\\le & {} \left( ||y^i_{n+1}-x^*||-||z^i_{n+1}-x^*||\right) \left( ||y^i_{n+1}-x^*||+||z^i_{n+1}-x^*||\right) \\\le & {} ||y^i_{n+1}-z^i_{n+1}|| \left( ||y^i_{n+1}-x^*||+||z^i_{n+1}-x^*||\right) . \end{aligned}$$

This together with (28), the boundedness of $\left\{ y^i_{n}\right\}$, $\left\{ z^i_{n}\right\}$ and the hypothesis of $\left\{ \gamma _n\right\}$ implies that

$$\begin{aligned} \lim _{n\rightarrow \infty }||S_{i}y^i_{n+1}-y^i_{n+1}||=0,~i\in I. \end{aligned}$$

(29)

$\square$

We have the following first main result.

Theorem 3.1

Let C be a nonempty closed convex subset of a real Hilbert space H. Assume that Conditions 1, 2 and 3 hold and the solution set $\Omega$is nonempty. Then, the sequence $\left\{ x_n\right\}$generated by Algorithm 3.1 converges strongly to $P_{\Omega }(x_0)$.

Proof

Assume that p is any weak cluster point of $\left\{ x_n\right\}$. Without loss of generality, we can write $x_n\rightharpoonup p$ as $n\rightarrow \infty$. Since $||x_n-y^i_n||\rightarrow 0$, $y^i_n\rightharpoonup p$. This together with (29) and the demiclosedness at zero of $S_i$, we obtain $p\in \cap _{i\in I}Fix(S_i)$. Next, we show that $p\in \cap _{i\in I}EP(f_i,C)$. From Lemma 3.1(i), we get

$$\begin{aligned} \lambda f_i(y^i_n,y)\ge \lambda f_i(y^i_n,y^i_{n+1})+\left\langle x_n-y^i_{n+1},y-y^i_{n+1}\right\rangle ,~\forall y\in C. \end{aligned}$$

(30)

From relations (14) and (17), we have

$$\begin{aligned} \lambda f_i(y^i_n,y^i_{n+1})\ge \left\langle y^i_{n}-x_{n-1},y^i_{n}-y^i_{n+1}\right\rangle - \lambda c_1||y^i_{n-1}-y^i_n||^2-\lambda c_2||y^i_n-y^i_{n+1}||^2. \end{aligned}$$

(31)

Combining (30) and (31), we obtain

$$\begin{aligned} \lambda f_i(y^i_n,y)\ge & {} \left\langle y^i_{n}-x_{n-1},y^i_{n}-y^i_{n+1}\right\rangle - \lambda c_1||y^i_{n-1}-y^i_n||^2-\lambda c_2||y^i_n-y^i_{n+1}||^2\\&+\left\langle x_n-y^i_{n+1},y-y^i_{n+1}\right\rangle . \end{aligned}$$

Passing to the limit in the last inequality as $n\rightarrow \infty$ and using Lemma 3.2(ii), the bounedness of $\left\{ y^i_n\right\}$, $\lambda >0$ and A3, we obtain

$$\begin{aligned} f_i(p,y)\ge \lim \sup \limits _{n\rightarrow \infty }f_i(y^i_n,y)\ge 0,~\forall y\in C,~i\in I. \end{aligned}$$

Thus, $p\in \cap _{i\in I}EP(f_i,C)$ and $p\in \Omega$. Finally, we show that $x_n\rightarrow x^\dagger := P_\Omega (x_0)$ as $n\rightarrow \infty$. Indeed, from inequality (22), we get $||x_n-x_0||\le ||x^\dagger -x_0||.$ Thus, by the weakly lower semicontinuity of the norm ||.|| and $x_n\rightharpoonup p$, we have

$$\begin{aligned} ||p-x_0||\le \lim _{n\rightarrow \infty }\inf ||x_{n}-x_0||\le \lim _{n\rightarrow \infty }\sup ||x_{n}-x_0||\le ||x^\dagger -x_0||. \end{aligned}$$

By the definition of $x^\dagger$, $p=x^\dagger$ and $\lim _{n\rightarrow \infty }||x_{n}-x_0||=||x^\dagger -x_0||$. Since $x_n\rightharpoonup x^\dagger$, $x_n-x_0\rightharpoonup x^\dagger -x_0$. By the Kadec-Klee property of the Hilbert space H, we have $x_n-x_0\rightarrow x^\dagger -x_0$ or $x_{n}\rightarrow x^\dagger =P_{\Omega }(x_0)$ as $n\rightarrow \infty$. $\square$

4 Parallel viscosity linesearch method

The convergence of Algorithm 3.1 requires the hypothesis A2 of the Lipschitz-type condition of equilibrium bifunction. Actually, this assumption is not easy to check and even if yes, then two Lipschitz-type constants $c_1,~c_2$ can be difficult to approximate. This can make restrictions in implementing numerical experiments of Algorithm 3.1. In this section, we propose a parallel viscosity linesearch algorithm for Problem 1.1 without the assumption A2. The algorithm combines the Armijo linesearch technique [35] with the hybrid steepest descent method [29, 42]. This algorithm is described as follows: at the $n^{th}$ step, given $x_n$, we first split and use the auxiliary principle problem [31] to find component approximations $y_n^i$ on each equilibrium subproblem for $f_i$ in the family. After that, for each equilibrium subproblem, the Armijo linesearch technique is used to find a suitable approximation $v_n^i$ which lies on the segment from $x_n$ to $y_n^i$. Based on $v_n^i$, we construct a halfspace $H_n^i$ which contains the solution set $\Omega$ and splits it with $x_n$. And now we find $z_n^i$ as the projection of the previous iterate $x_n$ on $C\cap H_n^i$. Next, use a convex combination of component approximations $z_n^i,~i\in I$ to compute an intermediate approximation $t_n$ by the hybrid steepest descent method [29, 42]. Finally, the next iterate $x_{n+1}$ is defined as a convex combination of $t_n$ and values $S_jt_n,~j\in J$.

Following the auxiliary problem principle which was introduced by Mastroeni in [31], let us define a bifunction $\mathscr {L}:C\times C\rightarrow \mathfrak {R}$ satisfying the following conditions.

• L1. There exists a constant $\beta >0$ such that $\mathscr {L}(x,y)\ge \frac{\beta }{2}||x-y||^2$ and $\mathscr {L}(x,x)=0$ for all $x,y\in C$;

• L2. $\mathscr {L}$ is weakly continuous; $\mathscr {L}(x,.)$ is differentiable, strongly convex for each $x\in C$ and $\mathscr {L}'_x(y,y)=0$ for all $y\in C$.

Considering the bifunction $\mathscr {L}$ which satisfies the conditions L1 and L2 in this section allowing us a more flexibility. For instance, $\mathscr {L}$ is the Bregman-type distance function as $\mathscr {L}(x,y)=g(x)-g(y)-\left\langle \nabla g(y),x-y\right\rangle$ where $g:C\rightarrow \mathfrak {R}$ is a differentiable, strongly convex function with modulus $\beta >0$. If $g(x)=\frac{1}{2}||x||^2$, then $\mathscr {L}(x,y)=\frac{1}{2}||x-y||^2$. A generalization of this form is $g(x)=\frac{1}{2}\left\langle Mx,x\right\rangle$, where M is a positive definite and self-adjoint linear operator on H, then $\mathscr {L}(x,y)=\frac{1}{2}\left\langle M(x-y),x-y\right\rangle$.

Moreover, from the ideas of Maingé and Moudafi in [30], Yamada in [42], Vuong et al. in [41], we associate the problem of finding a solution $x\in \Omega$ with a variational inequality problem (VIP) on $\Omega$ which is to find $x\in \Omega$ such that

$$\begin{aligned} \left\langle F(x),y-x\right\rangle \ge 0,~\forall y\in \Omega , \end{aligned}$$

(32)

where $F:C\rightarrow H$ is an $\eta$ - strongly monotone and L - Lipschitz continuous operator. Since $\Omega$ is closed, convex and nonempty (assumed), it follows from the hypothesises of F that VIP (32) has the unique solution, denoted $x^*$. In the special case, when $F(x)=x-u$ where u is a suggested point in H, then VIP (32) is equivalent to the problem of finding a solution $x^*$ in $\Omega$ which is the best approximation of u, i.e., $x^*=P_\Omega (u)$. And now, we are in a position to present the second algorithm in details.

The tasks of Algorithm 4.1 are to solve N optimization programs at Step 1, find intermediate approximations $v_n^i$ which are not costly and compute projections for $z_n^i$ and $t_n$ dealing with the feasible set C. If $f_i(x,y)=\left\langle A_i(x),y-x\right\rangle$, where $A_i:C\rightarrow H$ is an operator then the hyperplane $H_n^i$ in Step 3 becomes $H_n^i=\left\{ x\in H:\left\langle A_iv_n^i,v_n^i-x\right\rangle \ge 0 \right\} ,$ which was introduced by Solodov ans Svaiter [37] for solving variational inequality problems. From Remark 4.3 below, we see that $H_n^i$ contains the solution set $\Omega$. Also, like as the remarks of the authors in [37], the computed projection $z_n^i=P_{C\cap H_n^i}(x_n)$ is closer to any solution in $\Omega$ than $x_n$. The projection $t_n=P_C\left( {z}_n-\alpha _n F({z}_n)\right)$ in Step 4 can be replaced by $t_n={z}_n-\alpha _n F({z}_n)$ if $f_i,~\mathscr {L},~S_j$ are defined and satisfy respective conditions on the whole space H.

In order to obtain the convergence of Algorithm 4.1, we install below conditions on the bifunctions and the control parameters. In this section, assumption A2 is redundant, however, hypothesis A3 in Condition 1 is replaced by more slightly restrictive one A3a below.

Condition 4 Hypotheses A1, A4 in Condition 1 hold and

• A3a.  $f_i$ is jointly weakly continuous on the product $\Delta \times \Delta$ where $\Delta$ is an open convex set containing C, in the sense that if $x,y\in \Delta$ and if $\left\{ x_n\right\}$ and $\left\{ y_n\right\}$ are two sequences in $\Delta$ converging weakly to x, y, respectively, then $f_i(x_n,y_n)\rightarrow f_i(x,y)$.

The control parameter sequences in Algorithm 4.1 satisfy the following conditions.

Condition 5

• D1. $\rho _n\rightarrow \rho \in (0,1)$;

• D2. $\sum _{n=1}^{\infty }\alpha _n=\infty$, $\sum _{n=1}^{\infty }\alpha _n^2<\infty$;

• D3. $\sum _{i\in I}w_n^i=1$, $\lim _{n}\inf w^i_n>0$ for all $i\in I$ and $n\ge 0$;

• D4. $\gamma _n^0+\sum _{j\in J}\gamma _n^j=1$, $\lim _{n}\inf \gamma ^0_n\gamma ^j_n>0$ for all $j\in J$ and $n\ge 0$.

An example for the sequence $\left\{ \alpha _n\right\}$ satisfying assumption D2 is $\alpha _n=\frac{1}{n^p}$, where $p\in (\frac{1}{2},1]$. We need the following lemma for proving the convergence of Algorithm 4.1.

Lemma 4.1

Assume that $i\in I_n$for some n. Then

• (i) The linesearch (Step 2) of Algorithm 4.1 is well - defined, $f(v_n^i,x_n)>0$and $0\notin \partial _2 f_i(v_n^i,x_n)$.

• (ii) If $z_n^i=P_{C\cap H_n^i}(x_n)$then $z_n^i=P_{C\cap H_n^i}(u^i_n)$where $u^i_n=P_{H^i_n}(x_n)$.

Proof

See, Propositions 4.1 and 4.5 in [40]. $\square$

Remark 4.1

From Lemma 4.1(i), we see that for each $i\in I_n$ then $g_n^i\ne 0$. Thus, we define $\sigma _n^i$ by

$$\begin{aligned} \sigma _n^i:= {\left\{ \begin{array}{ll} \frac{f_i(v_n^i,x_n)}{||g_n^i||^2} &{}\text{ if }~ i\in I_n,\\ 0&{}\text{ if }~ i\in I\backslash I_n. \end{array}\right. } \end{aligned}$$

(33)

Remark 4.2

$u_n^i=P_{H_n^i}(x_n)=x_n-\sigma _n^ig_n^i$ for all $i\in I$. Indeed, if $i\in I\backslash I_n$ then $v_n^i=x_n$. Thus, from the definition of $H_n^i$ and $f(v_n^i,x_n)=f(x_n,x_n)=0$, we obtain

$$\begin{aligned} H_n^i=\left\{ x\in H:\left\langle g_n^i,x_n-x\right\rangle \ge 0\right\} . \end{aligned}$$

Hence, $x_n\in H_n^i$. This together with the definition of $\sigma ^i_n$ in (33) implies that $u_n^i=P_{H_n^i}(x_n)=x_n=x_n-\sigma _n^ig_n^i$. If $i\in I_n$ then, from Lemma 4.1(i), we obtain $g_n^i\ne 0$ and $f(v_n^i,x_n)>0$. Thus, from the explicit form of the projection onto a half-space and the definition of $\sigma _n^i$, we obtain $u_n^i=P_{H_n^i}(x_n)=x_n-\sigma _n^ig_n^i$.

Remark 4.3

If $x^*\in EP(f_i,C)$ then $\left\langle g_n^i,x_n-x^*\right\rangle \ge \sigma _n^i||g_n^i||^2$ and $x^*\in C\cap H_n^i$ for all $i\in I$ and $n\ge 0$. Indeed, from the facts $x_n \in C$, $y_n^i \in C$ and $v_n^i$ is the convex combination of $x_n$ and $y_n^i$, we obtain that $v_n^i \in C$. Thus, since $x^*\in EP(f_i,C)$, $f_i(x^*,v_n^i)\ge 0$. From the pseudomonotonicity of $f_i$, $f_i(v_n^i,x^*)\le 0$. Thus, by $g_n^i\in \partial _2f_i(v_n^i,x_n)$, we have

$$\begin{aligned} \left\langle g_n^i,x_n-x^*\right\rangle \ge f_i(v_n^i,x_n)-f_i(v_n^i,x^*)\ge f_i(v_n^i,x_n)=\sigma _n^i||g_n^i||^2 \end{aligned}$$

in which the last equality follws from the definitions of $\sigma _n^i$, $v_n^i$ and $f(x,x)=0$ for both two cases $i\in I_n$ and $i\in I\backslash I_n$. So, from the definition of $H_n^i$, we obtain $x^*\in H_n^i$. Thus $x^*\in C\cap H_n^i$ for all $i\in I$ and $n\ge 0$.

Lemma 4.2

Suppose that $x^*\in \Omega$. Then

• (i) $||z_n-x^*||^2\le ||x_n-x^*||^2-\sum _{i\in I}w_n^i(\sigma _n^i ||g_n^i||)^2.$

• (ii)
  $$\begin{aligned} ||x_{n+1}-x^*||^2\le & {} ||x_{n}-x^*||^2-\sum _{j\in J}\gamma _n^0\gamma _n^j||S_{j}t_n-t_n||^2-\sum _{i\in I}w_n^i(\sigma _n^i||g_n^i||)^2\\&-2\alpha _n\left\langle z_n-x^*,Fz_n\right\rangle +\alpha _n^2||Fz_n||^2. \end{aligned}$$

Proof

(i) It follows from the definition of $z_n^i,~\sum _{i\in I}w_n^i=1$, the convexity of $||.||^2$ and Remarks 4.2, 4.3 that

$$\begin{aligned} ||z_n-x^*||^2= & {} ||\sum _{i\in I}w_n^i(z_n^i-x^*)||^2\le \sum _{i\in I}w_n^i||z_n^i-x^*||^2\\= & {} \sum _{i\in I}w_n^i||P_{C\cap H_n^i}(u^i_n)-P_{C\cap H_n^i}(x^*)||^2\\\le & {} \sum _{i\in I}w_n^i||u^i_n-x^*||^2=\sum _{i\in I}w_n^i||x_n-\sigma _n^ig_n^i-x^*||^2\\= & {} \sum _{i\in I}w_n^i||x_n-x^*||^2-2\sum _{i\in I}w_n^i\sigma _n^i\left\langle g_n^i,x_n-x^*\right\rangle +\sum _{i\in I}w_n^i(\sigma _n^i||g_n^i||)^2\\\le & {} ||x_n-x^*||^2-2\sum _{i\in I}w_n^i(\sigma _n^i||g_n^i||)^2+\sum _{i\in I}w_n^i(\sigma _n^i||g_n^i||)^2\\= & {} ||x_n-x^*||^2-\sum _{i\in I}w_n^i(\sigma _n^i||g_n^i||)^2. \end{aligned}$$

(ii) By the definition of $x_{n+1}$, $\gamma _k^0+\sum _{j\in J}\gamma _k^j=1$ and relation (7), we obtain

$$\begin{aligned} ||x_{n+1}-x^*||^2= & {} ||\gamma _n^0(t_n-x^*)+\sum \limits _{j\in J}\gamma _n^j(S_{j}t_n-x^*)||^2\nonumber \\\le & {} \gamma _n^0||t_n-x^*||^2+\sum \limits _{j\in J}\gamma _n^j||S_{j}t_n-x^*||^2-\sum _{j\in J}\gamma _n^0\gamma _n^j||S_{j}t_n-t_n||^2\nonumber \\\le & {} \gamma _n^0||t_n-x^*||^2+\sum \limits _{j\in J}\gamma _n^j||t_n-x^*||^2-\sum _{j\in J}\gamma _n^0\gamma _n^j||S_{j}t_n-t_n||^2\nonumber \\= & {} ||t_n-x^*||^2-\sum _{j\in J}\gamma _n^0\gamma _n^j||S_{j}t_n-t_n||^2. \end{aligned}$$

(34)

$$\begin{aligned}\le & {} ||t_n-x^*||^2. \end{aligned}$$

(35)

From (34), the definition of $t_n$, the nonexpansiveness of the projection and Lemma 4.2(i),

$$\begin{aligned} ||x_{n+1}-x^*||^2\le & {} ||t_n-x^*||^2-\sum _{j\in J}\gamma _n^0\gamma _n^j||S_{j}t_n-t_n||^2\\= & {} ||P_C({z}_n-\alpha _n F({z}_n))-P_C(x^*)||^2-\sum _{j\in J}\gamma _n^0\gamma _n^j||S_{j}t_n-t_n||^2\\\le & {} ||{z}_n-\alpha _n F({z}_n)-x^*||^2-\sum _{j\in J}\gamma _n^0\gamma _n^j||S_{j}t_n-t_n||^2\\= & {} ||{z}_n-x^*||^2-2\alpha _n \left\langle z_{n}-x^*,F({z}_n)\right\rangle +\alpha _n^2||Fz_n||^2-\sum _{j\in J}\gamma _n^0\gamma _n^j||S_{j}t_n-t_n||^2\\\le & {} ||x_n-x^*||^2-\sum _{i\in I}w_n^i(\sigma _n^i ||g_n^i||)^2-2\alpha _n \left\langle z_{n}-x^*,F({z}_n)\right\rangle \\&+\alpha _n^2||Fz_n||^2-\sum _{j\in J}\gamma _n^0\gamma _n^j||S_{j}t_n-t_n||^2. \end{aligned}$$

$\square$

Lemma 4.3

The sequences $\left\{ x_n\right\}$, $\left\{ z_n\right\}$, $\left\{ t_n\right\}$are bounded.

Proof

For a fixed $\mu \in \left( 0,\frac{2\eta }{L^2}\right)$. It follows from hypothesis D2 in Condition 5 that $\alpha _n\rightarrow 0$, thus, without loss of generality, we can assume that $\left\{ \alpha _n\right\} \subset (0,\mu )$. From the definitions of $G^\mu$ in Lemma 2.2 and of $t_n$ in Algorithm 4.1, we have $t_{n}=P_CG^{\alpha _{n}}({z}_{n})$. Using the nonexpansiveness of $P_C$, Lemma 2.2(ii) for $y={z}_{n}$, $x=x^*$, $\nu =\alpha _n$ and Lemma 4.2(i), we obtain

$$\begin{aligned} ||t_n-x^*||= & {} ||P_CG^{\alpha _{n}}({z}_{n})-P_C(x^*)||\le ||G^{\alpha _{n}}({z}_{n})-x^*||\nonumber \\\le & {} \left( 1-\frac{\alpha _{n}\tau }{\mu }\right) ||{z}_{n}-x^*||+\alpha _{n} ||F(x^*)||\nonumber \\\le & {} \left( 1-\frac{\alpha _{n}\tau }{\mu }\right) ||x_{n}-x^*||+\alpha _{n} ||F(x^*)||, \end{aligned}$$

(36)

where $\tau$ is defined as in Lemma 2.2. From relation (35) with $n:=n-1$, we have

$$\begin{aligned} ||x_{n}-x^*||\le ||t_{n-1}-x^*|| \end{aligned}$$

This together with (36) implies that

$$\begin{aligned} ||t_n-x^*||\le & {} \left( 1-\frac{\alpha _{n}\tau }{\mu }\right) ||t_{n-1}-x^*||+\alpha _{n} ||F(x^*)||\\= & {} \left( 1-\frac{\alpha _{n}\tau }{\mu }\right) ||t_{n-1}-x^*||+\frac{\alpha _{n}\tau }{\mu }\left( \frac{\mu }{\tau }||F(x^*)||\right) \\\le & {} \max \left\{ ||t_{n-1}-x^*||,\frac{\mu }{\tau }||F(x^*)||\right\} . \end{aligned}$$

Thus

$$\begin{aligned} ||t_n-x^*||\le \max \left\{ ||t_{0}-x^*||,\frac{\mu }{\tau }||F(x^*)||\right\} ,~\forall n\ge 0. \end{aligned}$$

Hence the sequence $\left\{ t_n\right\}$ is bounded. This together with (35) and Lemma 4.2(i) implies that the sequences $\left\{ x_n\right\}$ and $\left\{ {z}_n\right\}$ are also bounded. $\square$

Lemma 4.4

There exists a subsequence $\left\{ x_m\right\}$of $\left\{ x_n\right\}$converging weakly to $p\in C$and the sequences $\left\{ y^i_m\right\}$, $\left\{ v_m^i\right\}$, $\left\{ g^i_m\right\}$are bounded for all $i\in I$.

Proof

See, Step 4 in the proof of Theorem 4.4 in [40]. $\square$

Lemma 4.5

If there exists a subsequence $\left\{ x_k\right\}$of $\left\{ x_n\right\}$such that $x_k\rightharpoonup t\in C$and $\sigma _k^i||g_k^i||\rightarrow 0, ~\forall i\in I$. Then $t\in \cap _{i\in I}EP(f_i,C)$.

Proof

It follows from Lemma 4.4 that the sequences $\left\{ y^i_k\right\}$, $\left\{ v_k^i\right\}$, $\left\{ g^i_k\right\}$ are bounded for all $i\in I$. Now, without loss of generality, taking a subsequence if necessary, we show that

$$\begin{aligned} \lim \limits _{k\rightarrow \infty }||x_k-y_k^i||\rightarrow 0,~\text{ and } \text{ so }~y_k^i\rightharpoonup t,~\forall i\in I \end{aligned}$$

(37)

Indeed, since $||x_k-y_k^i||=0$ for all $i\in I\backslash I_n$, we can consider $i\in I_n$. From the convexity of $f_i(x,.)$, $f(x,x)=0$ and $v_k^i=(1-\eta ^{m_k^i})x_k+\eta ^{m_k^i}y_k^i$, we have

$$\begin{aligned} 0=f_i(v_k^i,v_k^i)=f_i(v_k^i,(1-\eta ^{m_k^i})x_k+\eta ^{m_k^i}y_k^i)\le (1-\eta ^{m_k^i})f_i(v_k^i,x_k)+\eta ^{m_k^i}f_i(v_k^i,y_k^i). \end{aligned}$$

Thus

$$\begin{aligned} f_i(v_k^i,x_k)\ge \eta ^{m_k^i}\left( f_i(v_k^i,x_k)-f_i(v_k^i,y^i_k)\right) . \end{aligned}$$

This together with the linesearch technique, $f_i(v_k^i,x_k)=\sigma _k^i ||g_k^i||^2$ and $\mathscr {L}(x_k,y_k^i)\ge \frac{\beta }{2}||x_k-y_k^i||^2$ implies that

$$\begin{aligned} \sigma _k^i ||g_k^i||^2= f_i(v_k^i,x_k)\ge \frac{\alpha \eta ^{m_k^i}}{\rho _k}\mathscr {L}(x_k,y_k^i)\ge \frac{\alpha \beta \eta ^{m_k^i}}{2\rho _k}||x_k-y_k^i||^2. \end{aligned}$$

Thus,

$$\begin{aligned} \eta ^{m_k^i}||x_k-y_k^i||^2\le \frac{2\rho _k}{\alpha \beta }\sigma _k^i ||g_k^i||^2=\frac{2\rho _k}{\alpha \beta }||g_k^i||\left( \sigma _k^i ||g_k^i||\right) ,~\forall i\in I_n. \end{aligned}$$

This together with the boundedness of $\left\{ g_k^i\right\}$, the hypotheses $\sigma _k^i||g_k^i||\rightarrow 0$ and $\rho _k\rightarrow \rho$, we have

$$\begin{aligned} \lim _{k\rightarrow \infty }\eta ^{m^i_k}||x_k-y_k^i||^2=0. \end{aligned}$$

(38)

Now, we consider two distinct cases:

Case 1. If $\limsup _{k\rightarrow \infty }\eta ^{m^i_k}>0$ then from (38), without loss of generality, we can conclude that $\lim _{k\rightarrow \infty }||x_k-y_k^i||=0$. Thus, the relation (37) is true in this case.

Case 2. If $\limsup _{k\rightarrow \infty }\eta ^{m^i_k}=0$, and thus $\lim _{k\rightarrow \infty }\eta ^{m^i_k}=0$ then, since $\left\{ y_k^i\right\}$ is bounded, we can assume, taking a subsequence if necessary, that $y_k^i\rightharpoonup {y}^i$ as $k\rightarrow \infty$. From the definition of $y_k^i$, we have

$$\begin{aligned} f_i(x_k, y) +\frac{1}{\rho _k}\mathscr {L}(x_k,y)\ge f_i(x_k, y_k^i) +\frac{1}{\rho _k}\mathscr {L}(x_k,y_k^i),~\forall y\in C. \end{aligned}$$

(39)

Passing to the limit in the last inequality as $k\rightarrow \infty$ and using $\mathrm A3a,~L2,~\rho _k\rightarrow \rho$ with noting that $x_k\rightharpoonup t$, $y_k^i\rightharpoonup y^i$, we obtain

$$\begin{aligned} f_i(t, y) +\frac{1}{\rho }\mathscr {L}(t,y)\ge f_i(t,{y}^i) +\frac{1}{\rho }\mathscr {L}(t,{y}^i),~\forall y\in C. \end{aligned}$$

(40)

Substituting $y=t$ into the relation (40) and employing $\mathrm A1,~L1$, one has

$$\begin{aligned} f_i(t,{y}^i) +\frac{1}{\rho }\mathscr {L}(t,{y}^i)\le 0. \end{aligned}$$

(41)

By $\lim _{k\rightarrow \infty }\eta ^{m^i_k}=0$ (it is obvious that $m^i_k>1$). Since $m_k^i$ is the smallest positive integer number satisfying the linesearch rule,

$$\begin{aligned} f_i((1-\eta ^{m_k^i-1})x_k-\eta ^{m_k^i-1}y^i_k,x_k)-f_i((1-\eta ^{m_k^i-1})x_k-\eta ^{m_k^i-1}y^i_k,y_k^i)-\frac{\alpha }{\rho _k}\mathscr {L}(x_k,y_k^i)< 0. \end{aligned}$$

Letting $k\rightarrow \infty$ in the last inequality, using $\mathrm A3a,~L2$ with noting that $\eta ^{m_k^i-1}=\frac{\eta ^{m_k^i}}{\eta }\rightarrow 0$ and $\rho _k\rightarrow \rho$, we get

$$\begin{aligned} f_i(t,t)-f_i(t,{y}^i)-\frac{\alpha }{\rho }\mathscr {L}(t,{y}^i)\le 0, \end{aligned}$$

which, from $f_i(t,t)=0$, implies that

$$\begin{aligned} -f_i(t,{y}^i)-\frac{\alpha }{\rho }\mathscr {L}(t,{y}^i)\le 0. \end{aligned}$$

(42)

From (41), (42) and $\mathscr {L}(t,y^i)\ge \frac{\beta }{2}||t-y^i||^2$, we obtain

$$\begin{aligned} \frac{(1-\alpha )\beta }{2\rho }||t-y^i||^2\le \frac{1-\alpha }{\rho }\mathscr {L}(t,{y}^i)\le 0. \end{aligned}$$

Thus, from $(1-\alpha )\beta /2\rho >0$, we obtain $t={y}^i$ or $||x_k-y_k^i||\rightarrow 0$ as $k\rightarrow \infty$. Consequently, (37) is also proved in this case.

Finally, note that (39) is true for all $i\in I$. Passing to the limit in the relation (39) as $k\rightarrow \infty$ and using the assumption $x_k\rightharpoonup t$, the relation (37) and $\mathrm A1, L1, A3a,~L2,~\rho _k\rightarrow \rho$, we obtain immediately that

$$\begin{aligned} f_i(t, y) +\frac{1}{\rho }\mathscr {L}(t,y)\ge 0,~\forall y\in C,~i\in I, \end{aligned}$$

which, from the auxiliary principle problem [31, Proposition 2.1], implies that $t\in EP(f_i,C),~i\in I$. Thus, $t\in \cap _{i\in I}i EP(f_i,C)$. $\square$

Theorem 4.1

Let C be a nonempty closed convex subset of a real Hilbert space H. Assume that Conditions 2, 4 and 5 hold and the solution set $\Omega$is nonempty. Then, the sequence $\left\{ x_n\right\}$generated by Algorithm 4.1 converges strongly to $P_{\Omega }(x_0)$.

Proof

In this proof, we consider $x^*$ which is the unique solution of VIP (32). Since F is Lipschitz continuous and $\left\{ z_n\right\}$ is bounded (see, Lemma 4.3), there exist two positive constants $K_1$, $K_2$ such that

$$\begin{aligned} 2|\left\langle z_n-x^*,Fz_n\right\rangle |\le K_1~\text{ and }~ ||Fz_n||\le K_2. \end{aligned}$$

(43)

Set $\epsilon _n=||x_n-x^*||^2$. From Lemma 4.2(ii), we obtain

$$\begin{aligned} \epsilon _{n+1}-\epsilon _{n}+\sum _{j\in J}\gamma _n^0\gamma _n^j||S_{j}t_n-t_n||^2+\sum _{i\in I}w_n^i(\sigma _n^i||g_n^i||)^2\le K_1\alpha _n+K_2^2\alpha _n^2. \end{aligned}$$

(44)

We consider two distinct cases.

Case 1. There exists $n_0\ge 0$ such that $\left\{ \epsilon _n\right\} _{n\ge n_0}$ is decreasing. In this case, since $\epsilon _n\ge 0$ for all $n\ge 0$, there exists the limit $\lim _{n\rightarrow \infty }\epsilon _n=\epsilon \ge 0$ and $\epsilon _{n+1}-\epsilon _{n}\rightarrow 0$. Moreover, since $\sum _{n}\alpha _n^2<+\infty$, $\alpha _n\rightarrow 0$. These together with (44) and the hypotheses $\lim \inf _{n\rightarrow \infty }\gamma _n^0\gamma _n^j>0$, $\lim \inf _{n\rightarrow \infty }w_n^i>0$ imply that

$$\begin{aligned} ||S_{j}t_n-t_n||^2\rightarrow 0~\text{ and }~\sigma _n^i||g_n^i||\rightarrow 0,~\forall i\in I, ~j\in J. \end{aligned}$$

(45)

From the definition of $x_{n+1}$ and the convexity of $||.||^2$, we have

$$\begin{aligned} ||x_{n+1}-t_n||^2= & {} ||\gamma _n^0(t_n-t_n)+\sum _{j\in J}\gamma _n^j(S_jt_n-t_n)||^2\nonumber \\\le & {} \gamma _n^0||t_n-t_n||^2+\sum _{j\in J}\gamma _n^j||S_jt_n-t_n||^2=\sum _{j\in J}\gamma _n^j||S_jt_n-t_n||^2. \end{aligned}$$

(46)

By (45) and (46), we obtain

$$\begin{aligned} \lim _{n\rightarrow \infty }||x_{n+1}-t_n||=0. \end{aligned}$$

(47)

From the definition of $t_n$, $z_n\in C$, the nonexpansiveness of $P_C$ and $\alpha _n\rightarrow 0$, we have

$$\begin{aligned} ||t_n-z_n||= & {} ||P_C(z_n-\alpha _nFz_n)-P_Cz_n||\le ||(z_n-\alpha _nFz_n)-z_n||\nonumber \\= & {} \alpha _n||Fz_n||\le \alpha _nK_2\rightarrow 0. \end{aligned}$$

(48)

Since $\epsilon _{n}=||x_n-x^*||^2\rightarrow \epsilon$, we also have that $\epsilon _{n+1}=||x_{n+1}-x^*||^2\rightarrow \epsilon$. Thus, by the relation (47), we get $||t_n-x^*||^2\rightarrow \epsilon$, which, by the relation (48), follows $||z_n-x^*||^2\rightarrow \epsilon$. Since $\left\{ z_n\right\}$ is bounded, there exists a subsequence $\left\{ z_m\right\}$ of $\left\{ z_n\right\}$ converging weakly to p such that

$$\begin{aligned} \lim \inf _{n\rightarrow \infty }\left\langle z_n-x^*,Fx^*\right\rangle =\lim _{m\rightarrow \infty }\left\langle z_m-x^*,Fx^*\right\rangle . \end{aligned}$$

(49)

From (47), (48) and $z_m\rightharpoonup p$, we obtain $t_n\rightharpoonup p$ and $x_n\rightharpoonup p$. Thus, by (45), the demiclosedness of $S_j$ at zero and Lemma 4.5, we see that $p\in \Omega$. Hence, by $z_m\rightharpoonup p$, relation (49) and $x^*$ solves VIP (32), we obtain

$$\begin{aligned} \lim \inf _{n\rightarrow \infty }\left\langle z_n-x^*,Fx^*\right\rangle =\lim _{m\rightarrow \infty }\left\langle z_m-x^*,Fx^*\right\rangle =\left\langle p-x^*,Fx^*\right\rangle \ge 0. \end{aligned}$$

(50)

From the $\eta$ - strong monotonicity of F, we have

$$\begin{aligned} \left\langle z_{n}-x^*, Fz_{n}\right\rangle =\left\langle z_{n}-x^*, Fz_{n}-Fx^*\right\rangle +\left\langle z_{n}-x^*, Fx^*\right\rangle \ge \eta ||{z}_n-x^*||^2+\left\langle {z}_n-x^*,Fx^*\right\rangle . \end{aligned}$$

Thus, from $||{z}_n-x^*||^2\rightarrow \epsilon$ and (50), we obtain

$$\begin{aligned} \lim _{n\rightarrow \infty }\inf \left\langle z_{n}-x^*, F{z}_n\right\rangle \ge \eta \epsilon +\lim _{n\rightarrow \infty }\inf \left\langle z_{n}-x^*, Fx^*\right\rangle \ge \eta \epsilon . \end{aligned}$$

(51)

Assume that $\epsilon >0$, then there exists a positive integer $N_0$ such that

$$\begin{aligned} \left\langle {z}_n-x^*, F{z}_n\right\rangle \ge \frac{1}{2}\eta \epsilon ,~\forall n\ge N_0. \end{aligned}$$

(52)

It follows from Lemma 4.2(ii), (43) and (52) that, for all $n\ge N_0$,

$$\begin{aligned} ||x_{n+1}-x^*||^2\le ||x_{n}-x^*||^2-2\alpha _n\left\langle z_n-x^*,Fz_n\right\rangle +\alpha _n^2K_2^2\le ||x_{n}-x^*||^2-\alpha _n\eta \epsilon +\alpha _n^2K_2^2. \end{aligned}$$

Thus, from the definition of $\epsilon _n$, we obtain $\epsilon _{n+1}-\epsilon _n\le -\alpha _n\eta \epsilon +\alpha _n^2K_2^2,~\forall n\ge N_0.$ This implies that

$$\begin{aligned} \epsilon _{n+1}-\epsilon _{N_0}\le -\eta \epsilon \sum _{k=N_0}^{n+1}\alpha _k+K_2^2\sum _{k=N_0}^{n+1}\alpha _k^2. \end{aligned}$$

(53)

Since $\eta \epsilon >0$, $\sum _{n=1}^{\infty }\alpha _n=+\infty$ and $\sum _{n=1}^{\infty }\alpha _n^2<+\infty$, it follows from (53) that $\epsilon _n\rightarrow -\infty$. This is absurd. Therefore $\epsilon =0$ or $x_n\rightarrow x^*$.

Case 2. There exists a subsequence $\left\{ \epsilon _{n_i}\right\}$ of $\left\{ \epsilon _n\right\}$ such that $\epsilon _{n_i}\le \epsilon _{n_i+1}$ for all $i\ge 0$. In this case, it follows from Lemma 2.4 that

$$\begin{aligned} \epsilon _{\tau (n)}\le \epsilon _{\tau (n)+1},~\epsilon _n \le \epsilon _{\tau (n)+1},~\forall n\ge n_0. \end{aligned}$$

(54)

where $\tau (n)=\max \left\{ k\in N:n_0\le k\le n, ~\epsilon _k\le \epsilon _{k+1}\right\}$. Furthermore, the sequence $\left\{ \tau (n)\right\} _{n\ge n_0}$ is non-decreasing and $\tau (n)\rightarrow +\infty$ as $n\rightarrow \infty$. It follows from (44) and $\epsilon _{\tau (n)}\le \epsilon _{\tau (n)+1}$ that

$$\begin{aligned} \sum _{j\in J}\gamma _{\tau (n)}^0\gamma _{\tau (n)}^j||S_{j}t_{\tau (n)}-t_{\tau (n)}||^2+\sum _{i\in I}w_{\tau (n)}^i(\sigma _{\tau (n)}^i||g_{\tau (n)}^i||)^2\le K_1\alpha _{\tau (n)}+K_2^2\alpha _{\tau (n)}^2. \end{aligned}$$

Thus, from $\alpha _{\tau (n)}\rightarrow 0$ and the hypotheses $\lim \inf _{n\rightarrow \infty }\gamma _{\tau (n)}^0\gamma _{\tau (n)}^j>0$, $\lim \inf _{n\rightarrow \infty }w_{\tau (n)}^i>0$, we obtain

$$\begin{aligned} ||S_{j}t_{\tau (n)}-t_{\tau (n)}||^2\rightarrow 0~\text{ and }~\sigma _{\tau (n)}^i||g_{\tau (n)}^i||\rightarrow 0,~\forall i\in I,~j\in J. \end{aligned}$$

(55)

From the definition of $x_{\tau (n)+1}$, we have

$$\begin{aligned} ||x_{\tau (n)+1}-t_{\tau (n)}||^2= & {} ||\gamma _{\tau (n)}^0(t_{\tau (n)}-t_{\tau (n)})+\sum _{j\in J}\gamma _{\tau (n)}^j(S_jt_{\tau (n)}-t_{\tau (n)})||^2\nonumber \\\le & {} \gamma _{\tau (n)}^0||t_{\tau (n)}-t_{\tau (n)}||^2+\sum _{j\in J}\gamma _{\tau (n)}^j||S_jt_{\tau (n)}-t_{\tau (n)}||^2\nonumber \\= & {} \sum _{j\in J}\gamma _{\tau (n)}^j||S_jt_{\tau (n)}-t_{\tau (n)}||^2. \end{aligned}$$

(56)

By (55) and (56), we obtain

$$\begin{aligned} \lim _{n\rightarrow \infty }||x_{\tau (n)+1}-t_{\tau (n)}||=0. \end{aligned}$$

(57)

Since $\left\{ {z}_{\tau (n)}\right\}$ is bounded, there exists a subsequence $\left\{ {z}_{\tau (n_k)}\right\}$ of $\left\{ {z}_{\tau (n)}\right\}$ converging weakly to p such that

$$\begin{aligned} \liminf _{n\rightarrow \infty }\left\langle {z}_{\tau (n)}-x^*,F(x^*)\right\rangle =\lim _{k\rightarrow \infty }\left\langle {z}_{\tau (n_k)}-x^*,F(x^*)\right\rangle . \end{aligned}$$

(58)

From the definition of $t_{\tau (n_k)}$, the nonexpansiveness of $P_C$ and $\alpha _{\tau (n_k)}\rightarrow 0$, we have

$$\begin{aligned} ||t_{\tau (n_k)}-z_{\tau (n_k)}||= & {} ||P_C(z_{\tau (n_k)}-\alpha _{\tau (n_k)}Fz_{\tau (n_k)})-P_Cz_{\tau (n_k)}||\le ||(z_{\tau (n_k)}-\alpha _{\tau (n_k)}Fz_{\tau (n_k)})-z_{\tau (n_k)}||\nonumber \\\le & {} \alpha _{\tau (n_k)}||Fz_{\tau (n_k)}||\le \alpha _{\tau (n_k)}K_2\rightarrow 0. \end{aligned}$$

Thus, $t_{\tau (n_k)}\rightharpoonup p\in C$. This together with (55) and the demiclosedness at zero of $S_j$ implies that $p\in \cap _{j\in J}Fix(S_j)$. Moreover, from $t_{\tau (n_k)}\rightharpoonup p$ and (57), one has $x_{\tau (n_k)}\rightharpoonup p$. Thus, from (55) and Lemma 4.5, we also have $p\in \cap _{i\in I}EP(f_i,C)$ or $p\in \Omega$. It follows from (58) and $x^*$ solves VIP (32) that

$$\begin{aligned} \liminf _{n\rightarrow \infty }\left\langle {z}_{\tau (n)}-x^*,F(x^*)\right\rangle =\lim _{k\rightarrow \infty }\left\langle {z}_{\tau (n_k)}-x^*,F(x^*)\right\rangle =\left\langle p-x^*,F(x^*)\right\rangle \ge 0. \end{aligned}$$

(59)

Now, we prove that $x_{\tau (n_k)}\rightarrow x^*$. It follows from Lemma 4.2, the definition of $\epsilon _n$ and $\epsilon _{\tau (n)}\le \epsilon _{\tau (n)+1}$ that

$$\begin{aligned} 2\alpha _{\tau (n)}\left\langle z_{\tau (n)}-x^*,Fz_{\tau (n)}\right\rangle\le & {} \epsilon _{\tau (n)}-\epsilon _{\tau (n)+1}-||x_{\tau (n)+1}-t_{\tau (n)}||^2\\&-\sum _{i\in I}w_{\tau (n)}^i(\sigma _{\tau (n)}^i||g_{\tau (n)}^i||)^2+\alpha _{\tau (n)}^2||Fz_{\tau (n)}||^2\le \alpha _{\tau (n)}^2K^2_2. \end{aligned}$$

Thus, from $\alpha _{\tau (n)}>0$, we obtain

$$\begin{aligned} \left\langle {z}_{\tau (n)}-x^*,F{z}_{\tau (n)}\right\rangle \le \frac{\alpha _{\tau (n)}K_2^2}{2}. \end{aligned}$$

(60)

From the $\eta$—strong monotonicity and the relation (60),

$$\begin{aligned} \eta ||{z}_{\tau (n)}-x^*||^2\le & {} \left\langle {z}_{\tau (n)}-x^*, F{z}_{\tau (n)}-Fx^*\right\rangle =\left\langle {z}_{\tau (n)}-x^*, F{z}_{\tau (n)}\right\rangle -\left\langle {z}_{\tau (n)}-x^*,Fx^*\right\rangle \\\le & {} \frac{\alpha _{\tau (n)}K^2_2}{2}-\left\langle {z}_{\tau (n)}-x^*,Fx^*\right\rangle . \end{aligned}$$

This together with (59) and $\alpha _{\tau (n)}\rightarrow 0$ implies that

$$\begin{aligned} \limsup _{n\rightarrow \infty }\eta ||{z}_{\tau (n)}-x^*||^2\le & {} -\lim \inf _{n\rightarrow \infty }\left\langle {z}_{\tau (n)}-x^*,Fx^*\right\rangle \le 0. \end{aligned}$$

Thus, from $\eta >0$, we obtain

$$\begin{aligned} \lim _{n\rightarrow \infty } ||{z}_{\tau (n)}-x^*||^2=0. \end{aligned}$$

(61)

From the definition of $t_{\tau (n)}$, $z_{\tau (n)}\in C$, the nonexpansiveness of $P_C$ and $\alpha _{\tau (n)}\rightarrow 0$, we have

$$\begin{aligned} ||t_{\tau (n)}-z_{\tau (n)}||= & {} ||P_C(z_{\tau (n)}-\alpha _{\tau (n)}Fz_{\tau (n)}) -P_Cz_{\tau (n)}||\nonumber \\\le & {} ||(z_{\tau (n)}-\alpha _{\tau (n)}Fz_{\tau (n)})-z_{\tau (n)}||=\alpha _{\tau (n)} ||Fz_{\tau (n)}||\le \alpha _{\tau (n)}K_2\rightarrow 0. \end{aligned}$$

This together with (57), (61) and the definition of $\epsilon _n$ implies that $\lim _{k\rightarrow \infty } ||x_{\tau (n)+1}-x^*||^2=0$. Thus, $\epsilon _{\tau (n)+1}\rightarrow 0$. It follows from (54) that $0\le \epsilon _n\le \epsilon _{\tau (n)+1}\rightarrow 0$. Hence, $\epsilon _n\rightarrow 0$ or $x_n\rightarrow x^*$ as $n\rightarrow \infty$. Theorem 4.1 is proved. $\square$

Remark 4.4

If $S_j:C\rightarrow C,~j\in J$ are $\beta _j$ - demicontractive with $\beta _j\in [0,1)$ such that $Fix(S_j)\ne \emptyset$, then $\tilde{S}_j=(1-w_j)I+w_jS_j,~j\in J$ are quasi-nonexpansive and $Fix(S_j)=Fix(\tilde{S_j})$ [29, Remark 4.2], where $w_j\in (0,1-\beta _j)$. Thus, the conclusions of Theorems 3.1 and 4.1 are still true for the family of demicontractive and demiclosed at zero mappings $\left\{ S_j\right\} _{j\in J}$ by replacing $S_j$ in Algorithms 3.1 and 4.1 by $\tilde{S}_j=(1-w_j)I+w_jS_j,~j\in J$.

Remark 4.5

In this paper, we consider Problem 1.1 where, for each $i \in I$ and $j \in J$, the bifunction $f_i$ and the mapping $S_j$ are defined on the feasible set C, and Algorithm 3.1 and Algorithm 4.1 can be applied under Conditions 1 - 5, L1, L2 and the operator $F:C \rightarrow H$ is $\eta$ - strongly monotone and L— Lipschitz continuous on C. The results in this paper is still true if $f_i$, $S_j$, $\mathscr {L}$, and F are defined on the whole space H, and all their respective conditions are satisfied on H.

5 Numerical experiments

In this section, we perform some numerical experiments to illustrate the convergence of Algorithms 3.1 and 4.1 and compare them with Algorithm 1.1 (Parallel Hybrid Extragradient - Mann Method - PHEMM). We consider the bifunctions $f_i:\mathfrak {R}^m \times \mathfrak {R}^m \rightarrow \mathfrak {R}$ which are generalized from the Nash-Cournot equilibrium model in [13, 35] and defined by

$$\begin{aligned} f_i(x,y)=\left\langle P_ix+Q_iy+q_i,y-x\right\rangle ,~i\in I=\left\{ 1,2,\ldots ,N\right\} ,~(N=10), \end{aligned}$$

(62)

where $q_i\in \mathfrak {R}^m$ ($m=5,~10$ or 20) and $P_i,~Q_i$ are matrices of order m such that $Q_i$ is symmetric, positive semidefinite and $Q_i-P_i$ is negative semidefinite. The bifunction $f_i ~(i\in I)$ satisfies Condition 4 and Condition 1 with $c_1^i=c_2^i=||P_i-Q_i||/2$ [35, Lemma 6.2]. We chose two Lipschitz-type constants $c_1=c_2=\max \left\{ c_1^i:i\in I\right\}$, the bifunction $\mathscr {L}(x,y)=\frac{1}{2}||x-y||^2$ and the operator $F(x)=x-x_0$, where $x_0\in \mathfrak {R}^m$ is a suggested point.

Example 1

The feasible set $C\in \mathfrak {R}^m$ is a polyhedral convex set as

$$\begin{aligned}C=\left\{ x\in \mathfrak {R}^m: Ax\le b\right\} , \end{aligned}$$

where $A\in \mathfrak {R}^{l\times m}$$(l=15)$ is a matrix with its entries generated randomly and uniformly in $[-5,5]$ and b is a positive vector in $\mathfrak {R}^l$ with its entries generated uniformly from [1, 5], and so C is nonempty because $0\in C$. Let $g_j:\mathfrak {R}^m\rightarrow \mathfrak {R},~j\in J=\left\{ 1,2,\ldots ,M\right\}$$(M=10)$ be convex functions such that $0\in \cap _{j\in J}\mathrm{lev}_{\le }g_j$, where $\mathrm{lev}_{\le }g_j=\left\{ x\in \mathfrak {R}^m:g_j(x)\le 0\right\}$. We define the subgradient projection relative to $g_j,~j\in J$ by

$$\begin{aligned} S_j(x)= {\left\{ \begin{array}{ll} x-\frac{g_j(x)}{||z_j(x)||^2}z_j(x)&{}\text{ if } ~g_j(x)>0,\\ x&{}\text{ otherwise }, \end{array}\right. } \end{aligned}$$

(63)

where $z_j(x)\in \partial g_j(x),~x\in \mathfrak {R}^m$. The mapping $S_j$ is quasi-nonexpansive and demiclosed at zero [5, Lemma  3.1]. Besides, $Fix(S_j)=\mathrm{lev}_{\le }g_j$. In fact, the mapping $S_j$ does not act from C to C, but it maps from C to $H=\mathfrak {R}^m$. However, the bifunctions $f_i$, $\mathscr {L}$ and the operator F are defined and satisfied their conditions on the whole space $H=\mathfrak {R}^m$. Thus, Algorithms 3.1 and 4.1 can be used to solve our problem. While PHEMM in [22] is not applied because the class of mappings considered in [22] is nonexpansive. We need to solve the following optimization program in $\mathfrak {R}^m$ per each iteration,

$$\begin{aligned} \arg \min \left\{ \frac{1}{2}y^TH_iy+b_i^Ty:Ay\le b\right\} , \end{aligned}$$

(64)

where $H_i=2\lambda Q_i+I$ and $b_i=\lambda (P_i y_n-Q_i y_n+q_i)-x_n$ for Algorithm 3.1 or $H_i=2\rho _n Q_i+I$$b_i=\rho _n (P_i x_n-Q_i x_n+q_i)-x_n$ for Algorithm 4.1. Problem (64) is a convex quadratic program. We use the function quadprog in Matlab 7.0 Optimization Toolbox to solve this problem. The set $C_n\cap Q_n$ in Algorithm 3.1 is the intersection of $2N+1$ halfspaces. Thus, the projection $x_{n+1}=P_{C_n\cap Q_n}(x_0)$ is rewritten equivalently to a convex quadratic optimization program like as (64). The projections onto C and $C\cap H_n^i$ in Algorithm 4.1 are performed similarly.

In the numerical experiments for this example, the matrices $P_i$, $Q_i$ are randomly generated¹ and $q_i$ is chosen as the zero vector for all i. From the property of $Q_i$, we see that $0\in \cap _{i\in I}EP(f_i,C)$. The functions $g_j(x)=\max \left\{ 0, \left\langle c_j,x\right\rangle +d_j\right\}$, where $d_j\in \mathfrak {R}_{-}~(j\in J)$ is a negative number chosen randomly in $[-5,-1]$ and $c_j\in \mathfrak {R}^m~(j\in J)$ is a vector generated randomly with its entries being in $[-5,5]$ and $c_j\ne 0$. Since $0\in \cap _{j\in J}\mathrm{lev}_{\le }g_j=\cap _{j\in J}Fix(S_j)$, $0\in \Omega$. We use $D_n=||x_n-x^*||,~n=0,1,2\ldots$ to check the convergence of the sequence $\left\{ x_n\right\}$. The convergence of $\left\{ D_n\right\}$ to 0 implies that $\left\{ x_n\right\}$ converges to $x^*$. The starting points are $x_0=(1,1,\ldots ,1)^T\in \mathfrak {R}^m$ and $y_0=(0,0,\ldots ,0)^T\in \mathfrak {R}^m$.

We consider four experiments with some different control parameters. Figures 1 and 2 illustrate the behavior of $\left\{ D_n\right\}$ for first 5000 iterations in $\mathfrak {R}^5$ while Figures 3 and 4 are performed in $\mathfrak {R}^{10}$. From these results, we see that the convergence of Algorithm 3.1 is better than the one of Algorithm 4.1 and they also depend on the control parameters. Besides, $\left\{ D_n\right\}$ generated by Algorithm 3.1, in general, is decreasing but not monotone while the one generated by Algorithm 4.1 is stable and monotone decreasing. Moreover, the execution times for Algorithm 3.1 are significantly smaller than those ones for Algorithm 4.1. The reason for this can be from the linesearch step in Algorithm 4.1 which is time-consuming per each iteration for every bifunction.

Fig. 1

Behavior of $D_n=||x_n-x^*||$ in $\mathfrak {R}^5$ for Algorithm 3.1 with $\lambda =1/5c_1,~k=6,~\gamma _n=1/2$ and Algorithm 4.1 with $\alpha =\eta =\rho _n=0.5,~w_n^i=1/N,~\gamma _n^j=1/(M+1),\alpha _n=1/n$ (the execution times for first 5000 iterations are 286.041s, 730.708s, resp.)

Fig. 2

Behavior of $D_n=||x_n-x^*||$ in $\mathfrak {R}^5$ for Algorithm 3.1 with $\lambda =1/10c_1,~k=2,~\gamma _n=n/3(n+3)$ and Algorithm 4.1 with $\alpha =0.01,~\eta =0.99,~\rho _n=9n/(10n+1),~w_n^i=1/N,~\gamma _n^j=1/(M+1),~\alpha _n=1/n^{0.51}$ (the execution times for first 5000 iterations are 379.596s, 825.142s, resp.)

Fig. 3

Behavior of $D_n=||x_n-x^*||$ in $\mathfrak {R}^{10}$ for Algorithm 3.1 with $\lambda =1/10c_1,~k=2,\gamma _n=2n/3(n+3)$ and Algorithm 4.1 with $\alpha =0.8,~\eta =0.01,~\rho _n=8n/(10n+1),~w_n^i=1/N,~\gamma _n^j=1/(M+1),~\alpha _n=1/n^{0.8}$ (the execution times for first 5000 iterations are 184.202s, 488.013s, resp.)

Fig. 4

Behavior of $D_n=||x_n-x^*||$ in $\mathfrak {R}^{10}$ for Algorithm 3.1 with $\lambda =1/4.1c_1,~k=50,~\gamma _n=2n/3(n+3)$ and Algorithm 4.1 with $\alpha =0.8,~\eta =0.01,~\rho _n=9.99n/(10n+1),~w_n^i=1/N,~\gamma _n^j=1/(M+1),~\alpha _n=1/n^{0.8}$ (the execution times first 1000 iterations are 486.317s, 692.574s, resp.)

Example 2

Let $B_p[a_p,r_p]$ be a closed ball centered at point $a_p$ with the radius $r_p$, $p=1,2,\ldots ,P$ ($P=10,~20$ or 40) such that $0\in B_p[a_p,r_p]$ for all p. The feasible set C considered here is the intersection of these balls, i.e., $C=\bigcap _{p=1}^{P} B_p[a_p,r_p]$. Let $H_j$ be a halfspace such that $0\in H_j$ defined by $H_j=\left\{ x\in \mathfrak {R}^m: h_1^j x_1+h_2^j x_2+\ldots +h_m^j x_m\le d_j\right\} , ~j\in J=\left\{ 1,2,\ldots ,M\right\} ~(M=10),$ where $h_k^j$ and $d_j$ are real numbers generated randomly in $[-5,5]$ and [1, 5], respectively. Define the mapping $S_j$ by $S_j=P_{H_j}$. From the property of the metric projection, $S_j$ is nonexpansive (and so quasi-nonexpansive) and $0\in \cap _{j\in J}H_j=\cap _{j\in J}Fix(S_j)$. Thus, Algorithms 3.1, 4.1 and PHEMM [22, Algorithm 1] can be applied in this case. We also chose $q_i$ being the zero vector and the matrices $P_i,~Q_i$ are generated randomly as in Example 1. Hence $0\in \Omega$. From Step 1 of Algorithm 3.1, we need to solve the following optimization problem,

$$\begin{aligned} \arg \min \left\{ \frac{1}{2}y^T\bar{H}_iy+b_i^Ty:y\in C=\bigcap _{p=1}^{P} B_p[a_p,r_p]\right\} , \end{aligned}$$

(65)

where $\bar{H}_i=2\lambda Q_i+I$ and $b_i=\lambda (P_i y_n-Q_i y_n+q_i)-x_n$. We use the function fmincon in Matlab 7.0 Optimization Toolbox to solve problem (65). All other optimization programs and projections dealing with the feasible set C in Algorithm 4.1 and PHEMM are similarly performed as problem (65). Note that the projection $x_{n+1}=P_{C_n\cap Q_n}(x_0)$ in Algorithm 3.1 does not deal with C and is found as in Example 1. In this example, we perform four experiments in $\mathfrak {R}^m$ ($m=5, 10, 20$) and C is the intersection of 2m balls (i.e., $P=2m$) with the same radius $r_p=7$ and the center $a_p$ belongs to the $x_i$—axis such that $||a_p||=4$ ($i=1,2,\ldots ,m$).

Figures 5 and 6 describe the behavior of $\left\{ D_n\right\}$ generated by Algorithms 3.1, 4.1 and PHEMM in $\mathfrak {R}^5$ for first 3000 iterations. Next, it is seen that Algorithm 3.1 and PHEMM in [22] are used for the same class of pseudomonotone and Lipschitz-type bifunctions. However, the stepsize $\lambda$ in Algorithm 3.1 is smaller than that one in PHEMM. Figure 6 is performed with $\lambda =\frac{1}{2(c_1+c_2)}-\epsilon$ for Algorithm 3.1, $\lambda =\min \left\{ \frac{1}{2c_1},\frac{1}{2c_2}\right\} -\epsilon$ for PHEMM and $\rho _n=1-\epsilon$ for Algorithm 4.1, where $\epsilon =10^{-6}$. From these results, we also see that $\left\{ D_n\right\}$ generated by Algorithm 3.1 and PHEMM is not monotone decreasing while that one generated by Algorithm 4.1 is stable. Moreover, the convergence rate of Algorithm 3.1 is the best. The execution times for Algorithms 4.1 and PHEMM are also significantly larger than that one for Algorithm 3.1. This comes from 2N solved optimization problems in PHEMM, the linesearch procedure in Algorithm 4.1 and the projections dealing with the feasible set C in these two algorithms while the main task of Algorithm 3.1 is only to solve N optimization problem per each iteration.

Fig. 5

Behavior of $D_n=||x_n-x^*||$ in $\mathfrak {R}^5$ for Algorithm 3.1 with $\lambda =1/4.1c_1,~k=50,~\gamma _n=2n/3(n+3)$; Algorithm 4.1 with $\alpha =0.01,~\eta =0.01,~\rho _n=9.99n/(10n+1),~w_n^i=1/N,~\gamma _n^j=1/(M+1),~\alpha _n=1/n^{0.8}$ and PHEMM with $\lambda =1/4c_1,~\alpha _n=2n/3(n+3)$ (the execution times for first 3000 iterations are 280.186s, 608.079s and 574.207s, resp.)

Fig. 6

Behavior of $D_n=||x_n-x^*||$ in $\mathfrak {R}^5$ for Algorithm 3.1 with $\lambda =1/2(c_1+c_2)-\epsilon ,~k=1/\epsilon (c_1+c_2),~\gamma _n=2n/3(n+3)$; Algorithm 4.1 $\alpha =0.01,~\eta =0.01,~\rho _n=1-\epsilon ,~w_n^i=1/N,~\gamma _n^j=1/(M+1),~\alpha _n=1/n^{0.8}$ and PHEMM with $\lambda =\min \left\{ 1/2c_1,1/2c_2\right\} -\epsilon ,~\alpha _n=2n/3(n+3)$ (the execution times for first 3000 iterations are 251.222s, 611.694s and 574.234s, resp.), where $\epsilon =10^{-6}$

Finally, Figs. 7 and 8 illustrate the behavior of $\left\{ D_n\right\}$ for mentioned algorithms in $\mathfrak {R}^{10}$ and $\mathfrak {R}^{20}$, respectively. The convergence results are similar, but $\left\{ D_n\right\}$ generated by PHEMM in $\mathfrak {R}^{20}$ seems to be stable and monotone decreasing which is seen in Fig. 8.

Fig. 7

Behavior of $D_n=||x_n-x^*||$ in $\mathfrak {R}^{10}$ for Algorithm 3.1 with $\lambda =1/2(c_1+c_2)-\epsilon ,~k=1/\epsilon (c_1+c_2),~\gamma _n=2n/3(n+3)$; Algorithm 4.1 with $\alpha =0.01,~\eta =0.01,~\rho _n=1-\epsilon ,~w_n^i=1/N,~\gamma _n^j=1/(M+1),~\alpha _n=1/n^{0.8}$ and PHEMM with $\lambda =\min \left\{ 1/2c_1,1/2c_2\right\} -\epsilon ,~\alpha _n=2n/3(n+3)$ (the execution times for first 3000 iterations are 646.246s, 1.7080e+003s and 1.5611e+003s, resp.), where $\epsilon =10^{-4}$

Fig. 8

Behavior of $D_n=||x_n-x^*||$ in $\mathfrak {R}^{20}$ for Algorithm 3.1 with $\lambda =1/2(c_1+c_2)-\epsilon ,~k=1/\epsilon (c_1+c_2),~\gamma _n=2n/3(n+3)$; Algorithm 4.1 with $\alpha =0.01,~\eta =0.01,~\rho _n=1-\epsilon ,~w_n^i=1/N,~\gamma _n^j=1/(M+1),~\alpha _n=1/n^{0.8}$ and PHEMM with $\lambda =\min \left\{ 1/2c_1,1/2c_2\right\} -\epsilon ,~\alpha _n=2n/3(n+3)$ (the execution times for first 3000 iterations are 2.0322e+003s, 1.3127e+004s and 5.4796e+003s, resp.), where $\epsilon =10^{-4}$

From the reported numerical results, we see that the convergence of Algorithm 3.1 is the best. While Algorithm 4.1 is slowly convergent. A reason for this is that at each iteration Algorithm 4.1 uses a linesearch procedure which is time-consuming. However, the advantage of Algorithm 4.1 is that it can be applied for non-Lipschitz-type bifunctions.

6 Conclusion

The paper proposes two parallel algorithms for finding a particular common solution of a system of pseudomonotone equilibrium problems and finitely many fixed point problems for quasi-nonexpansive mappings. The first algorithm is applied to the class of Lipschitz-type bifunctions where only one optimization problem for each bifunction is solved without any extra-step dealing with the feasible set. This comes from constructing slightly different cutting-halfspaces in the hybrid method. The algorithm can be considered as an improvement of hybrid extragradient methods per each computational step. The second algorithm combines the viscosity method and the linesearch procedure which aims to avoid the Lipschitz-type condition. Thanks to the hybrid (outer approximation) method and the viscosity method, the strongly convergent theorems are established. Some numerical experiments are implemented to illustrate the effectiveness of the proposed algorithms in comparison with a known parallel hybrid extragradient method.