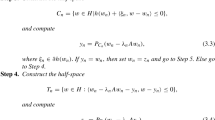Weak and strong convergence of hybrid subgradient method for pseudomonotone equilibrium problem and multivalued nonexpansive mappings

Abstract

In this paper, we introduce a hybrid subgradient method for finding a common element of the set of solutions of a class of pseudomonotone equilibrium problems and the set of fixed points of a finite family of multivalued nonexpansive mappings in Hilbert space. The proposed method involves only one projection rather than two as in the existing extragradient method and the inexact subgradient method for an equilibrium problem. We establish some weak and strong convergence theorems of the sequences generated by our iterative method under some suitable conditions. Moreover, a numerical example is given to illustrate our algorithm and our results.

MSC:47H05, 47H09, 47H10.

1 Introduction

Let H be a real Hilbert space with inner product $〈\cdot ,\cdot 〉$ and norm $\parallel \cdot \parallel$, respectively. Let K be a nonempty closed convex subset of H. Let $F:K\times K\to \mathbb{R}$ be a bifunction, where ℝ denotes the set of real numbers. We consider the following equilibrium problem: Find $x\in K$ such that

$$F(x,y)\ge 0,\mathrm{\forall }y\in K.$$

(1.1)

The set of solution of equilibrium problem is denoted by $EP(F,K)$. It is well known that some important problems such as convex programs, variational inequalities, fixed point problems, minimax problems, and Nash equilibrium problem in noncooperative games and others can be reduced to finding a solution of the equilibrium problem (1.1); see [1–3] and the references therein.

Recall that a mapping $T:K\to K$ is said to be nonexpansive if

$$\parallel Tx-Ty\parallel \le \parallel x-y\parallel ,\mathrm{\forall }x,y\in K.$$

A subset $K\subset H$ is called proximal if for each $x\in H$, there exists an element $y\in K$ such that

$$dist(x,K):=\parallel x-y\parallel =inf\{\parallel x-z\parallel :z\in K\}.$$

We denote by $B(K)$, $C(K)$, and $P(K)$ the collection of all nonempty closed bounded subsets, nonempty compact subsets and nonempty proximal bounded subsets of K, respectively. The Hausdorff metric H on $B(H)$ is defined by

$$H(K_1,K_2):=max\{\underset{x\in K_1}{sup}dist(x,K_2),\underset{y\in K_2}{sup}dist(y,K_1)\},\mathrm{\forall }{K}_1,K_2\in B(H).$$

Let $T:H\to 2^H$ be a multivalued mapping, of which the set of fixed points is denoted by $Fix(T)$, i.e., $Fix(T):=\{x\in Tx:x\in K\}$. A multivalued mapping $T:K\to B(K)$ is said to be nonexpansive if

$$H(Tx,Ty)\le \parallel x-y\parallel ,\mathrm{\forall }x,y\in K.$$

(1.2)

T is said to be quasi-nonexpansive if, for all $p\in Fix(T)$,

$$H(Tx,p)\le \parallel x-p\parallel ,\mathrm{\forall }x\in K.$$

(1.3)

Recently, the problem of finding a common element of the set of solutions of equilibrium problems and the set of fixed points of nonlinear mappings has become an attractive subject, and various methods have been extensively investigated by many authors. It is worth mentioning that almost all the existing algorithms for this problem are based on the proximal point method applied to the equilibrium problem combining with a Mann iteration to fixed point problems of nonexpansive mappings, of which the convergence analysis has been considered if the bifunction F is monotone. This is because the proximal point method is not valid when the underlying operator F is pseudomonotone. Another basic idea for solving equilibrium problems is the projection method. However, Facchinei and Pang [4] show that the projection method is not convergent for monotone inequality, which is a special case of monotone equilibrium problems. In order to obtain convergence of the projection method for equilibrium problems, Tran et al. [5] introduced an extragradient method for pseudomonotone equilibrium problems, which is computationally expensive because of the two projections defined onto the constrained set. Efforts for deducing the computational costs in computing the projection have been made by using penalty function methods or relaxing the constrained convex set by polyhedral convex ones; see, e.g., [6–15].

In 2011, Santos and Scheimberg [15] further proposed an inexact subgradient algorithm for solving a wide class of equilibrium problems that requires only one projection rather than two as in the extragradient method, and of which computational results show the efficiency of this algorithm in finite dimensional Euclidean spaces. On the other hand, iterative schemes for multivalued nonexpansive mappings are far less developed than those for nonexpansive mappings though they have more powerful applications in solving optimization problems; see, e.g., [16–23] and the references therein.

In 2013, Eslamian [21] considered a proximal point method for nonspreading mappings and multivalued nonexpansive mappings and equilibrium problems. To be more precise, they proposed the following iterative method:

$$\{\begin{array}{l}F(u_n,z)+\frac{1}{r_n}〈y-u_n,u_n-x_n〉\ge 0,\mathrm{\forall }y\in K,\\ x_{n+1}={\alpha }_n{u}_n+{\beta }_n{f}_n{u}_n+{\gamma }_n{z}_n,n\ge 1,\end{array}$$

(1.4)

where $T_n=T_{n(modN)}$, $z_n\in T_n{u}_n$, ${\alpha }_n+{\beta }_n+{\gamma }_n=1$ for all $n\ge 1$ and $f_i$, $T_i$ are finite families of nonspreading mappings and multivalued nonexpansive mappings for $i=1,2,\dots ,N$, respectively. Moreover, he further proved the weak and strong convergence theorems of the iterative sequences under the condition of monotone defined on a bifunction F.

In this paper, inspired and motivated by research going on in this area, we introduce a hybrid subgradient method for the pseudomonotone equilibrium problem and a finite family of multivalued nonexpansive mappings, which is defined in the following way:

$$\{\begin{array}{l}{w}_n\in {\partial }_{{ϵ}_n}F(x_n,\cdot )x_n,\\ u_n=P_K(x_n-{\gamma }_n{w}_n),{\gamma }_n=\frac{{\beta }_n}{max\{{\sigma }_n,\parallel w_n\parallel \}},\\ x_{n+1}={\alpha }_n{x}_n+(1-{\alpha }_n)z_n,n\ge 0,\end{array}$$

(1.5)

where $T_n=T_{n(modN)}$, $z_n\in T_n{u}_n$, and $\{{\alpha }_n\}$, $\{{\beta }_n\}$, $\{{ϵ}_n\}$, and $\{{\sigma }_n\}$ are nonnegative real sequences.

Our purpose is not only to modify the proximal point iterative schemes (1.4) for the equilibrium problem to a hybrid subgradient method for a class of pseudomonotone equilibrium problems and a finite family of multivalued nonexpansive mappings, but also to establish weak and strong convergence theorems involving only one projection rather than two as in the extragradient method [5] and the inexact subgradient method [15] for the equilibrium problem. Our theorems presented in this paper improve and extend the corresponding results of [5, 15, 18, 21].

2 Preliminaries

Let K be a nonempty closed convex subset of a real Hilbert space H with inner product $〈\cdot ,\cdot 〉$ and norm $\parallel \cdot \parallel$, respectively. For every point $x\in H$, there exists a unique nearest point in K, denoted by $P_K(x)$, such that

$$\parallel x-P_K(x)\parallel \le \parallel x-y\parallel ,\mathrm{\forall }y\in K.$$

Then $P_K$ is called the metric projection of H onto K. It is well known that $P_K$ is nonexpansive and satisfies the following properties:

$$〈x-P_K(x),P_K(x)-y〉\ge 0,\mathrm{\forall }x\in H,y\in K,$$

(2.1)

$${\parallel x-y\parallel }^2\ge {\parallel x-P_K(x)\parallel }^2+{\parallel y-P_K(x)\parallel }^2,\mathrm{\forall }x\in H,y\in K.$$

(2.2)

Recall also that a bifunction $F:K\times K\to \mathbb{R}$ is said to be

• (i) r-strongly monotone if there exists a number $r>0$ such that

  $$F(x,y)+F(y,x)\le -r{\parallel x-y\parallel }^2,\mathrm{\forall }x,y\in K;$$

• (ii) monotone on K if

  $$F(x,y)+F(y,x)\le 0,\mathrm{\forall }x,y\in K;$$

• (iii) pseudomonotone on K with respect to $x\in K$ if

  $$F(x,y)\ge 0\Rightarrow F(y,x)\le 0,\mathrm{\forall }y\in K.$$

  (2.3)

It is clear that (i) ⇒ (ii) ⇒ (iii), for every $x\in K$. Moreover, F is said to be pseudomonotone on K with respect to $A\subseteq K$, if it is pseudomonotone on K with respect to every $x\in A$. When $A\equiv K$, F is called pseudomonotone on K.

The following example, taken from [15], shows that a bifunction may not be pseudomonotone on K, but yet is pseudomonotone on K with respect to the solution set of the equilibrium problem defined by F and K:

$$F(x,y):=2y|x|(y-x)+xy|y-x|,\mathrm{\forall }x,y\in \mathbb{R},K:=[-1,1].$$

Clearly, $EP(F,K)=\{0\}$. Since $F(y,0)=0$ for every $y\in K$, this bifunction is pseudomonotone on K with respect to the solution $x^{\ast }=0$. However, F is not pseudomonotone on K. In fact, both $F(-0.5,0.5)=0.25>0$ and $F(0.5,-0.5)=0.25>0$.

To study the equilibrium problem (1.1), we may assume that Δ is an open convex set containing K and the bifunction $F:\mathrm{\Delta }\times \mathrm{\Delta }\to \mathbb{R}$ satisfy the following assumptions:

(C1) $F(x,x)=0$ for each $x\in K$ and $F(x,\cdot )$ is convex and lower semicontinuous on K;

(C2) $F(\cdot ,y)$ is weakly upper semicontinuous for each $y\in K$ on the open set Δ;

(C3) F is pseudomonotone on K with respect to $EP(F,K)$ and satisfies the strict paramonotonicity property, i.e., $F(y,x)=0$ for $x\in EP(F,K)$ and $y\in K$ implies $y\in EP(F,K)$;

(C4) if $\{x_n\}\subseteq K$ is bounded and ${ϵ}_n\to 0$ as $n\to \mathrm{\infty }$, then the sequence $\{w_n\}$ with $w_n\in {\partial }_{{ϵ}_n}F(x_n,\cdot )x_n$ is bounded, where ${\partial }_{ϵ}F(x,\cdot )x$ stands for the ϵ-subdifferential of the convex function $F(x,\cdot )$ at x.

Throughout this paper, weak and strong convergence of a sequence $\{x_n\}$ in H to x are denoted by $x_n\rightharpoonup x$ and $x_n\to x$, respectively. In order to prove our main results, we need the following lemmas.

Lemma 2.1 [24]

Let H be a real Hilbert space. For all $x,y\in H$, we have the following identity:

$${\parallel x-y\parallel }^2={\parallel x\parallel }^2-{\parallel y\parallel }^2-2〈x-y,y〉.$$

Lemma 2.2 [25]

Let H be a real Hilbert space and $\alpha ,\beta ,\gamma \in [0,1]$ with $\alpha +\beta +\gamma =1$. For all $x,y,z\in H$, we have the following identity:

$$\begin{array}{rcl}{\parallel \alpha x+\beta y+\gamma z\parallel }^2& =& \alpha {\parallel x\parallel }^2+\beta {\parallel y\parallel }^2+\gamma {\parallel z\parallel }^2-\alpha \beta {\parallel x-y\parallel }^2\\ -\alpha \gamma {\parallel x-z\parallel }^2-\beta \gamma {\parallel y-z\parallel }^2.\end{array}$$

Lemma 2.3 [26]

Let $\{a_n\}$ and $\{b_n\}$ be two sequences of nonnegative real numbers such that

$$a_{n+1}\le a_n+b_n,n\ge 0,$$

where ${\sum }_{n=0}^{\mathrm{\infty }}{b}_n<\mathrm{\infty }$. Then the sequence $\{a_n\}$ is convergent.

Lemma 2.4 [18]

Let K be a nonempty closed convex subset of a real Hilbert space H. Let $T:K\to C(K)$ be a multivalued nonexpansive mapping. If $x_n\rightharpoonup q$ and ${lim}_{n\to \mathrm{\infty }}dist(x_n,T{x}_n)=0$, then $q\in Tq$.

3 Weak convergence

Theorem 3.1 Let K be a nonempty closed convex subset of a Hilbert space H and $F:K\times K\to \mathbb{R}$ be a bifunction satisfying (C1)-(C4). Let ${\{T_i\}}_{i=1}^N:K\to C(K)$ be a finite family of multivalued nonexpansive mappings such that $\mathrm{\Omega }={\bigcap }_{i=1}^{N}Fix(T_i)\cap EP(F,K)\ne \varphi$ and $T_i(q)=\{q\}$ for $i=1,2,\dots ,N$ and $q\in \mathrm{\Omega }$. For a given point $x_0\in K$, $0<c<{\sigma }_n<\sigma$, $\{{\alpha }_n\}$, $\{{\beta }_n\}$, and $\{{ϵ}_n\}$ are nonnegative sequences satisfying the following conditions:

• (i) ${\alpha }_n\in [a,b]\subset (0,1)$;

• (ii) ${\sum }_{n=0}^{\mathrm{\infty }}{\beta }_n=\mathrm{\infty }$, ${\sum }_{n=0}^{\mathrm{\infty }}{\beta }_n^2<\mathrm{\infty }$, and ${\sum }_{n=0}^{\mathrm{\infty }}{\beta }_n{ϵ}_n<\mathrm{\infty }$.

Then the sequence $\{x_n\}$ generated by (1.5) converges weakly to $\overline{x}\in \mathrm{\Omega }$.

Proof First, we show the existence of ${lim}_{n\to \mathrm{\infty }}\parallel x_n-p\parallel$ for every $p\in \mathrm{\Omega }$. It follows from (1.5) and Lemmas 2.1 and 2.2 that

$$\begin{array}{rcl}{\parallel x_{n+1}-p\parallel }^2& =& {\parallel {\alpha }_n(x_n-p)+(1-{\alpha }_n)(z_n-p)\parallel }^2\\ =& {\alpha }_n{\parallel x_n-p\parallel }^2+(1-{\alpha }_n){\parallel z_n-p\parallel }^2-{\alpha }_n(1-{\alpha }_n){\parallel x_n-z_n\parallel }^2\\ =& {\alpha }_n{\parallel x_n-p\parallel }^2+(1-{\alpha }_n)dist{(z_n,T_{n}p)}^2-{\alpha }_n(1-{\alpha }_n){\parallel x_n-z_n\parallel }^2\\ \le & {\alpha }_n{\parallel x_n-p\parallel }^2+(1-{\alpha }_n)H{(T_n{u}_n,T_{n}p)}^2-{\alpha }_n(1-{\alpha }_n){\parallel x_n-z_n\parallel }^2\\ \le & {\alpha }_n{\parallel x_n-p\parallel }^2+(1-{\alpha }_n){\parallel u_n-p\parallel }^2-{\alpha }_n(1-{\alpha }_n){\parallel x_n-z_n\parallel }^2\\ =& {\alpha }_n{\parallel x_n-p\parallel }^2+(1-{\alpha }_n)({\parallel x_n-p\parallel }^2-{\parallel u_n-x_n\parallel }^2+2〈x_n-u_n,p-u_n〉)\\ -{\alpha }_n(1-{\alpha }_n){\parallel x_n-z_n\parallel }^2\\ \le & {\parallel x_n-p\parallel }^2+2(1-{\alpha }_n)〈x_n-u_n,p-u_n〉-{\alpha }_n(1-{\alpha }_n){\parallel x_n-z_n\parallel }^2.\end{array}$$

(3.1)

By $u_n=P_K(x_n-{\gamma }_n{w}_n)$ and (2.1), we have

$$〈x_n-u_n,p-u_n〉\le {\gamma }_n〈w_n,p-u_n〉.$$

(3.2)

Using $u_n=P_K(x_n-{\gamma }_n{w}_n)$ and $x_n\in K$ again, we obtain (note that ${\gamma }_n=\frac{{\beta }_n}{max\{{\sigma }_n,\parallel w_n\parallel \}}$)

$$\begin{array}{rl}{\parallel x_n-u_n\parallel }^2& =〈x_n-u_n,x_n-u_n〉\\ \le {\gamma }_n〈w_n,x_n-u_n〉\\ \le {\gamma }_n\parallel w_n\parallel \parallel x_n-u_n\parallel \\ \le {\beta }_n\parallel x_n-u_n\parallel ,\end{array}$$

(3.3)

which implies that $\parallel x_n-u_n\parallel \le {\beta }_n$. Substituting (3.2) into (3.1) yields

$$\begin{array}{rcl}{\parallel x_{n+1}-p\parallel }^2& \le & {\parallel x_n-p\parallel }^2+2(1-{\alpha }_n){\gamma }_n〈w_n,p-u_n〉-{\alpha }_n(1-{\alpha }_n){\parallel x_n-z_n\parallel }^2\\ =& {\parallel x_n-p\parallel }^2+2(1-{\alpha }_n){\gamma }_n〈w_n,p-x_n〉+2(1-{\alpha }_n){\gamma }_n〈w_n,x_n-u_n〉\\ -{\alpha }_n(1-{\alpha }_n){\parallel x_n-z_n\parallel }^2\\ \le & {\parallel x_n-p\parallel }^2+2(1-{\alpha }_n){\gamma }_n〈w_n,p-x_n〉+2(1-{\alpha }_n){\gamma }_n\parallel w_n\parallel \parallel x_n-u_n\parallel \\ -{\alpha }_n(1-{\alpha }_n){\parallel x_n-z_n\parallel }^2\\ \le & {\parallel x_n-p\parallel }^2+2(1-{\alpha }_n){\gamma }_n〈w_n,p-x_n〉+2(1-{\alpha }_n){\beta }_n^2\\ -{\alpha }_n(1-{\alpha }_n){\parallel x_n-z_n\parallel }^2.\end{array}$$

(3.4)

Since $w_n\in {\partial }_{{ϵ}_n}F(x_n,\cdot )x_n$ and $F(x,x)=0$ for all $x\in K$, we have

$$\begin{array}{rl}〈w_n,p-x_n〉& \le F(x_n,p)-F(x_n,x_n)+{ϵ}_n\\ \le F(x_n,p)+{ϵ}_n.\end{array}$$

(3.5)

On the other hand, since $p\in EP(F,K)$, i.e., $F(p,x)\ge 0$ for all $x\in K$, by the pseudomonotonicity of F with respect to p, we have $F(x,p)\le 0$ for all $x\in K$. Replacing x by $x_n\in K$, we get $F(x_n,p)\le 0$. Then from (3.4) and (3.5), it follows that

$$\begin{array}{rcl}{\parallel x_{n+1}-p\parallel }^2& \le & {\parallel x_n-p\parallel }^2+2(1-{\alpha }_n){\gamma }_{n}F(x_n,p)+2(1-{\alpha }_n){\gamma }_n{ϵ}_n+2(1-{\alpha }_n){\beta }_n^2\\ -{\alpha }_n(1-{\alpha }_n){\parallel x_n-z_n\parallel }^2\\ \le & {\parallel x_n-p\parallel }^2+2(1-{\alpha }_n){\gamma }_n{ϵ}_n+2(1-{\alpha }_n){\beta }_n^2-{\alpha }_n(1-{\alpha }_n){\parallel x_n-z_n\parallel }^2\\ \le & {\parallel x_n-p\parallel }^2+2(1-{\alpha }_n){\gamma }_n{ϵ}_n+2(1-{\alpha }_n){\beta }_n^2.\end{array}$$

(3.6)

Applying Lemma 2.3 to (3.6), by condition (ii), we obtain the existence of ${lim}_{n\to \mathrm{\infty }}\parallel x_n-p\parallel =d$.

Now, we claim that ${lim\hspace{0.17em}sup}_{n\to \mathrm{\infty }}F(x_n,p)=0$ for every $p\in \mathrm{\Omega }$. Indeed, since F is pseudomonotone on K and $F(p,x_n)\ge 0$, we have $-F(x_n,p)\ge 0$. From (3.6), we have

$$\begin{array}{rcl}2(1-{\alpha }_n){\gamma }_n[-F(x_n,p)]& \le & {\parallel x_n-p\parallel }^2-{\parallel x_{n+1}-p\parallel }^2\\ +2(1-{\alpha }_n){\gamma }_n{ϵ}_n+2(1-{\alpha }_n){\beta }_n^2.\end{array}$$

(3.7)

Summing up (3.7) for every n, we obtain

$$\begin{array}{rl}0& \le 2\sum _{n=0}^{\mathrm{\infty }}(1-{\alpha }_n){\gamma }_n[-F(x_n,p)]\\ \le {\parallel x_0-p\parallel }^2+2\sum _{n=0}^{\mathrm{\infty }}{\gamma }_n{ϵ}_n+2\sum _{n=0}^{\mathrm{\infty }}{\beta }_n^2<+\mathrm{\infty }.\end{array}$$

(3.8)

By the assumption (C4), we can find a real number w such that $\parallel w_n\parallel \le w$ for every n. Setting $L:=max\{\sigma ,w\}$, where σ is a real number such that $0<{\sigma }_n<\sigma$ for every n, it follows from (i) that

$$\begin{array}{rl}0& \le \frac{2(1-b)}{L}\sum _{n=0}^{\mathrm{\infty }}{\beta }_n[-F(x_n,p)]\\ \le 2\sum _{n=0}^{\mathrm{\infty }}(1-{\alpha }_n){\gamma }_n[-F(x_n,p)]<+\mathrm{\infty },\end{array}$$

which implies that

$$\sum _{n=0}^{\mathrm{\infty }}{\beta }_n[-F(x_n,p)]<+\mathrm{\infty }.$$

(3.9)

Combining with $-F(x_n,p)\ge 0$ and ${\sum }_{n=0}^{\mathrm{\infty }}{\beta }_n=\mathrm{\infty }$, we can deduced that ${lim\hspace{0.17em}sup}_{n\to \mathrm{\infty }}F(x_n,p)=0$ as desired.

Next, we show that any weak subsequential limit of the sequence of $\{x_n\}$ is an element of $\mathrm{\Omega }={\bigcap }_{i=1}^{N}Fix(T_i)\cap EP(F,K)$. To do this, suppose that $\{x_{n_i}\}$ is a subsequence of $\{x_n\}$. For simplicity of notation, without loss of generality, we may assume that $x_{n_i}\rightharpoonup \overline{x}$ as $i\to \mathrm{\infty }$. By convexity, K is weakly closed and hence $\overline{x}\in K$. Since $F(\cdot ,p)$ is weakly upper semicontinuous for $p\in \mathrm{\Omega }$, we have

$$\begin{array}{rl}F(\overline{x},p)& \ge \underset{i\to \mathrm{\infty }}{lim\hspace{0.17em}sup}F(x_{n_i},p)=\underset{i\to \mathrm{\infty }}{lim}F(x_{n_i},p)\\ =\underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}sup}F(x_n,p)=0.\end{array}$$

(3.10)

By the pseudomonotonicity of F with respect to p and $F(p,\overline{x})\ge 0$, we obtain $F(\overline{x},p)\le 0$. Thus $F(\overline{x},p)=0$. Moreover, by the assumption (C3), we can deduce that $\overline{x}$ is a solution of $EP(F,K)$. On the other hand, it follows from (3.3) and condition (ii) that

$$\underset{n\to \mathrm{\infty }}{lim}\parallel x_n-u_n\parallel =0.$$

(3.11)

From (3.6) and conditions (i)-(ii), we have

$${\alpha }_n(1-{\alpha }_n){\parallel x_n-z_n\parallel }^2\le {\parallel x_n-p\parallel }^2-{\parallel x_{n+1}-p\parallel }^2+2(1-{\alpha }_n){\gamma }_n{ϵ}_n+2(1-{\alpha }_n){\beta }_n^2,$$

taking the limit as $n\to \mathrm{\infty }$ yields

$$\underset{n\to \mathrm{\infty }}{lim}\parallel x_n-z_n\parallel =0,$$

(3.12)

and thus

$$\underset{n\to \mathrm{\infty }}{lim}dist(x_n,T_n{u}_n)\le \underset{n\to \mathrm{\infty }}{lim}\parallel x_n-z_n\parallel =0.$$

(3.13)

Using (1.5) again, we have

$$\underset{n\to \mathrm{\infty }}{lim}\parallel x_{n+1}-x_n\parallel =\underset{n\to \mathrm{\infty }}{lim}(1-{\alpha }_n)\parallel x_n-z_n\parallel =0.$$

(3.14)

It follows that

$$\underset{n\to \mathrm{\infty }}{lim}\parallel x_{n+i}-x_n\parallel =0,i=1,2,\dots ,N.$$

(3.15)

Note that

$$\parallel u_{n+1}-u_n\parallel \le \parallel u_{n+1}-x_{n+1}\parallel +\parallel x_{n+1}-x_n\parallel +\parallel x_n-u_n\parallel .$$

Combining (3.11) and (3.14), we obtain

$$\underset{n\to \mathrm{\infty }}{lim}\parallel u_{n+1}-u_n\parallel =0.$$

(3.16)

This also implies that

$$\underset{n\to \mathrm{\infty }}{lim}\parallel u_{n+i}-u_n\parallel =0,i=1,2,\dots ,N.$$

(3.17)

Observe that

$$\begin{array}{rl}dist(u_n,T_{n+i}{u}_n)& \le \parallel u_n-x_n\parallel +\parallel x_n-x_{n+i}\parallel +dist(x_{n+i},T_{n+i}{u}_{n+i})+H(T_{n+i}{u}_{n+i},T_{n+i}{u}_n)\\ \le \parallel u_n-x_n\parallel +\parallel x_n-x_{n+i}\parallel +dist(x_{n+i},T_{n+i}{u}_{n+i})+\parallel u_{n+i}-u_n\parallel .\end{array}$$

Together with (3.11), (3.13), (3.15), and (3.17), we have

$$\underset{n\to \mathrm{\infty }}{lim}dist(u_n,T_{n+i}{u}_n)=0,i=1,2,\dots ,N,$$

(3.18)

which implies that the sequence

$$\bigcup _{i=1}^N{\{dist(u_n,T_{n+i}{u}_n)\}}_{n\ge 0}\to 0\text{as }n\to \mathrm{\infty }.$$

(3.19)

For $i=1,2,\dots ,N$, we note also that

$$\begin{array}{rl}{\{dist(u_n,T_i{u}_n)\}}_{n\ge 0}& ={\{dist(u_n,T_{n+(i-n)}{u}_n)\}}_{n\ge 0}\\ ={\{dist(u_n,T_{n+i_n}{u}_n)\}}_{n\ge 0}\\ \subset \bigcup _{i=1}^N{\{dist(u_n,T_{n+i}{u}_n)\}}_{n\ge 0},\end{array}$$

where $i-n=i_n(modN)$ and $i_n\in \{1,2,\dots ,N\}$. Therefore, we have

$$\underset{n\to \mathrm{\infty }}{lim}dist(u_n,T_i{u}_n)=0,i=1,2,\dots ,N.$$

(3.20)

Similarly, for $i=1,2,\dots ,N$, we obtain

$$\begin{array}{rl}dist(x_n,T_i{x}_n)& \le \parallel x_n-u_n\parallel +dist(u_n,T_i{u}_n)+H(T_i{u}_n,T_i{x}_n)\\ \le 2\parallel x_n-u_n\parallel +dist(u_n,T_i{u}_n).\end{array}$$

It follows from (3.11) and (3.20) that

$$\underset{n\to \mathrm{\infty }}{lim}dist(x_n,T_i{x}_n)=0,i=1,2,\dots ,N.$$

(3.21)

Applying Lemma 2.4 to (3.21), we can deduce that $\overline{x}\in Fix(T_i)$ for $i=1,2,\dots ,N$ and hence $\overline{x}\in \mathrm{\Omega }$.

Finally, we prove that $\{x_n\}$ converges weakly to an element of Ω. Indeed to verify that the claim is valid it is sufficient to show that ${\omega }_w(x_n)$ is a single point set, where ${\omega }_w(x_n)=\{x\in H:x_{n_i}\rightharpoonup x\}$ for some subsequence $\{x_{n_i}\}$ of $\{x_n\}$. Indeed since $\{x_n\}$ is bounded and H is reflexive, ${\omega }_w(x_n)$ is nonempty. Taking $w_1,w_2\in {\omega }_w(x_n)$ arbitrarily, let $\{x_{n_k}\}$ and $\{x_{n_j}\}$ be subsequences of $\{x_n\}$ such that $x_{n_k}\rightharpoonup w_1$ and $x_{n_j}\rightharpoonup w_2$, respectively. Since ${lim}_{n\to \mathrm{\infty }}\parallel x_n-p\parallel$ exists for all $p\in \mathrm{\Omega }$ and $w_1,w_2\in \mathrm{\Omega }$, we see that ${lim}_{n\to \mathrm{\infty }}\parallel x_n-w_1\parallel$ and ${lim}_{n\to \mathrm{\infty }}\parallel x_n-w_2\parallel$ exist. Now let $w_1\ne w_2$, then by Opial’s property,

$$\begin{array}{rl}\underset{n\to \mathrm{\infty }}{lim}\parallel x_n-w_1\parallel & =\underset{k\to \mathrm{\infty }}{lim}\parallel x_{n_k}-w_1\parallel \\ <\underset{k\to \mathrm{\infty }}{lim}\parallel x_{n_k}-w_2\parallel =\underset{n\to \mathrm{\infty }}{lim}\parallel x_n-w_2\parallel \\ =\underset{j\to \mathrm{\infty }}{lim}\parallel x_{n_j}-w_2\parallel <\underset{j\to \mathrm{\infty }}{lim}\parallel x_{n_j}-w_1\parallel \\ =\underset{n\to \mathrm{\infty }}{lim}\parallel x_n-w_1\parallel ,\end{array}$$

which is a contradiction. Therefore, $w_1=w_2$. This shows that ${\omega }_w(x_n)$ is a single point set, i.e., $x_n\rightharpoonup \overline{x}$. This completes the proof. □

Theorem 3.2 Let K be a nonempty closed convex subset of a Hilbert space H and $F:K\times K\to \mathbb{R}$ be a bifunction satisfying (C1)-(C4). Let $T:K\to C(K)$ be a multivalued nonexpansive mapping such that $\mathrm{\Omega }=Fix(T)\cap EP(F,K)\ne \varphi$ and $T(q)=\{q\}$ for all $q\in \mathrm{\Omega }$. For a given point $x_0\in K$, $0<c<{\sigma }_n<\sigma$, let $\{x_n\}$ be defined by

$$\{\begin{array}{l}{w}_n\in {\partial }_{{ϵ}_n}F(x_n,\cdot )x_n,\\ u_n=P_K(x_n-{\gamma }_n{w}_n),{\gamma }_n=\frac{{\beta }_n}{max\{{\sigma }_n,\parallel w_n\parallel \}},\\ x_{n+1}={\alpha }_n{x}_n+(1-{\alpha }_n)z_n,n\ge 0,\end{array}$$

where $z_n\in T{u}_n$, $\{{\alpha }_n\}$, $\{{\beta }_n\}$, and $\{{ϵ}_n\}$ are nonnegative sequences satisfying the following conditions:

• (i) ${\alpha }_n\in [a,b]\subset (0,1)$;

• (ii) ${\sum }_{n=0}^{\mathrm{\infty }}{\beta }_n=\mathrm{\infty }$, ${\sum }_{n=0}^{\mathrm{\infty }}{\beta }_n^2<\mathrm{\infty }$, and ${\sum }_{n=0}^{\mathrm{\infty }}{\beta }_n{ϵ}_n<\mathrm{\infty }$.

Then the sequence $\{x_n\}$ converges weakly to $\overline{x}\in \mathrm{\Omega }$.

Proof Putting $N=1$, then $T_i=T$, a single multivalued nonexpansive mapping, and the conclusion follows immediately from Theorem 3.1. This completes the proof. □

4 Strong convergence

To obtain strong convergence results, we either add the control condition ${lim}_{n\to \mathrm{\infty }}{\alpha }_n=\frac{1}{2}$, or we remove the condition $T(q)=\{q\}$ for all $q\in \mathrm{\Omega }$ and adjust the nonempty compact subset $C(K)$ to a proximal bounded subset $P(K)$ of K as follows.

Theorem 4.1 Let K be a nonempty closed convex subset of a Hilbert space H and $F:K\times K\to \mathbb{R}$ be a bifunction satisfying (C1)-(C4). Let ${\{T_i\}}_{i=1}^N:K\to C(K)$ be a finite family of multivalued nonexpansive mappings such that $\mathrm{\Omega }={\bigcap }_{i=1}^{N}Fix(T_i)\cap EP(F,K)\ne \varphi$ and $T_i(q)=\{q\}$ for $i=1,2,\dots ,N$ and $q\in \mathrm{\Omega }$. For a given point $x_0\in K$, $0<c<{\sigma }_n<\sigma$, let $\{x_n\}$ be defined by

$$\{\begin{array}{l}{w}_n\in {\partial }_{{ϵ}_n}F(x_n,\cdot )x_n,\\ u_n=P_K(x_n-{\gamma }_n{w}_n),{\gamma }_n=\frac{{\beta }_n}{max\{{\sigma }_n,\parallel w_n\parallel \}},\\ x_{n+1}={\alpha }_n{x}_n+(1-{\alpha }_n)z_n,n\ge 0,\end{array}$$

(4.1)

where $T_n=T_{n(modN)}$, $z_n\in T_n{u}_n$, $\{{\alpha }_n\}$, $\{{\beta }_n\}$, and $\{{ϵ}_n\}$ are nonnegative sequences satisfying the following conditions:

• (i) ${\alpha }_n\in [a,b]\subset (0,1)$ and ${lim}_{n\to \mathrm{\infty }}{\alpha }_n=\frac{1}{2}$;

• (ii) ${\sum }_{n=0}^{\mathrm{\infty }}{\beta }_n=\mathrm{\infty }$, ${\sum }_{n=0}^{\mathrm{\infty }}{\beta }_n^2<\mathrm{\infty }$, and ${\sum }_{n=0}^{\mathrm{\infty }}{\beta }_n{ϵ}_n<\mathrm{\infty }$.

Then the sequence $\{x_n\}$ generated by (4.1) converges strongly to $x^{\ast }\in \mathrm{\Omega }$.

Proof By a similar argument to the proof of Theorem 3.1 and (2.2), we have

$${\parallel z_n-P_{\mathrm{\Omega }}(x_n)\parallel }^2\le {\parallel z_n-x_n\parallel }^2-{\parallel x_n-P_{\mathrm{\Omega }}(x_n)\parallel }^2.$$

(4.2)

It follows from (4.2) that

$$\begin{array}{rl}{\parallel x_{n+1}-P_{\mathrm{\Omega }}(x_{n+1})\parallel }^2& \le {\parallel {\alpha }_n(x_n-P_{\mathrm{\Omega }}(x_n))+(1-{\alpha }_n)(z_n-P_{\mathrm{\Omega }}(x_n))\parallel }^2\\ \le {\alpha }_n{\parallel x_n-P_{\mathrm{\Omega }}(x_n)\parallel }^2+(1-{\alpha }_n){\parallel z_n-P_{\mathrm{\Omega }}(x_n)\parallel }^2\\ \le (2{\alpha }_n-1){\parallel x_n-P_{\mathrm{\Omega }}(x_n)\parallel }^2+(1-{\alpha }_n){\parallel z_n-x_n\parallel }^2.\end{array}$$

(4.3)

Combining (3.12), ${lim}_{n\to \mathrm{\infty }}{\alpha }_n=\frac{1}{2}$, and the boundedness of the sequence $\{x_n-P_{\mathrm{\Omega }}(x_n)\}$, we obtain

$$\underset{n\to \mathrm{\infty }}{lim}\parallel x_{n+1}-P_{\mathrm{\Omega }}(x_{n+1})\parallel =0.$$

(4.4)

By the assumptions (C1) and (C2), the set Ω is convex (see the proof of Theorem 1 in [27]). For all $m>n$, we have $\frac{1}{2}(P_{\mathrm{\Omega }}(x_m)+P_{\mathrm{\Omega }}(x_n))\in \mathrm{\Omega }$, and therefore

$$\begin{array}{rcl}{\parallel P_{\mathrm{\Omega }}(x_m)-P_{\mathrm{\Omega }}(x_n)\parallel }^2& =& 2{\parallel x_m-P_{\mathrm{\Omega }}(x_m)\parallel }^2+2{\parallel x_m-P_{\mathrm{\Omega }}(x_n)\parallel }^2\\ -4{\parallel x_m-\frac{1}{2}(P_{\mathrm{\Omega }}(x_m)+P_{\mathrm{\Omega }}(x_n))\parallel }^2\\ \le & 2{\parallel x_m-P_{\mathrm{\Omega }}(x_m)\parallel }^2+2{\parallel x_m-P_{\mathrm{\Omega }}(x_n)\parallel }^2-4{\parallel x_m-P_{\mathrm{\Omega }}(x_m)\parallel }^2\\ =& 2{\parallel x_m-P_{\mathrm{\Omega }}(x_n)\parallel }^2-2{\parallel x_m-P_{\mathrm{\Omega }}(x_m)\parallel }^2.\end{array}$$

(4.5)

Using (3.6) with $p=P_{\mathrm{\Omega }}(x_n)$, we have

$$\begin{array}{rl}{\parallel x_m-P_{\mathrm{\Omega }}(x_n)\parallel }^2& \le {\parallel x_{m-1}-P_{\mathrm{\Omega }}(x_n)\parallel }^2+2(1-{\alpha }_{m-1}){\gamma }_{m-1}{ϵ}_{m-1}+2(1-{\alpha }_{m-1}){\beta }_{m-1}^2\\ \le {\parallel x_{m-2}-P_{\mathrm{\Omega }}(x_n)\parallel }^2+{\eta }_{m-1}+{\eta }_{m-2}\\ \le \cdots \\ \le {\parallel x_n-P_{\mathrm{\Omega }}(x_n)\parallel }^2+\sum _{j=n}^{m-1}{\eta }_j,\end{array}$$

(4.6)

where ${\eta }_j=2(1-{\alpha }_j){\gamma }_j{ϵ}_j+2(1-{\alpha }_j){\beta }_j^2$. It follows from (4.5) and (4.6) that

$${\parallel P_{\mathrm{\Omega }}(x_m)-P_{\mathrm{\Omega }}(x_n)\parallel }^2\le 2{\parallel x_n-P_{\mathrm{\Omega }}(x_n)\parallel }^2+2\sum _{j=n}^{m-1}{\eta }_j-2{\parallel x_m-P_{\mathrm{\Omega }}(x_m)\parallel }^2.$$

(4.7)

Together with (4.4) and ${\sum }_{j=n}^{m-1}{\eta }_j<\mathrm{\infty }$, this implies that $\{P_{\mathrm{\Omega }}(x_n)\}$ is a Cauchy sequence. Hence $\{P_{\mathrm{\Omega }}(x_n)\}$ strongly converges to some point $x^{\ast }\in \mathrm{\Omega }$. Moreover, we obtain

$$x^{\ast }=\underset{i\to \mathrm{\infty }}{lim}{P}_{\mathrm{\Omega }}(x_{n_i})=P_{\mathrm{\Omega }}(\overline{x})=\overline{x},$$

(4.8)

which implies that $P_{\mathrm{\Omega }}(x_n)\to x^{\ast }=\overline{x}\in \mathrm{\Omega }$. Then, from (3.21), (4.4), and (4.8), we can conclude that $x_n\to x^{\ast }$. This completes the proof. □

Theorem 4.2 Let K be a nonempty closed convex subset of a Hilbert space H and $F:K\times K\to \mathbb{R}$ be a bifunction satisfying (C1)-(C4). Let ${\{T_i\}}_{i=1}^N:K\to P(K)$ be a finite family of multivalued mappings such that $P_{T_i}$ is nonexpansive, where $P_{T_i}:=\{y\in T_{i}x:dist(x,T_{i}x)=\parallel x-y\parallel \}$ and $\mathrm{\Omega }={\bigcap }_{i=1}^{N}Fix(T_i)\cap EP(F,K)\ne \varphi$. For a given point $x_0\in K$, $0<c<{\sigma }_n<\sigma$, let $\{x_n\}$ be defined by

$$\{\begin{array}{l}{w}_n\in {\partial }_{{ϵ}_n}F(x_n,\cdot )x_n,\\ u_n=P_K(x_n-{\gamma }_n{w}_n),{\gamma }_n=\frac{{\beta }_n}{max\{{\sigma }_n,\parallel w_n\parallel \}},\\ x_{n+1}={\alpha }_n{x}_n+(1-{\alpha }_n)z_n,n\ge 0,\end{array}$$

(4.9)

where $T_n=T_{n(modN)}$, $z_n\in P_{T_n}{u}_n$, $\{{\alpha }_n\}$, $\{{\beta }_n\}$, and $\{{ϵ}_n\}$ are nonnegative sequences satisfying the following conditions:

• (i) ${\alpha }_n\in [a,b]\subset (0,1)$;

• (ii) ${\sum }_{n=0}^{\mathrm{\infty }}{\beta }_n=\mathrm{\infty }$, ${\sum }_{n=0}^{\mathrm{\infty }}{\beta }_n^2<\mathrm{\infty }$, and ${\sum }_{n=0}^{\mathrm{\infty }}{\beta }_n{ϵ}_n<\mathrm{\infty }$.

Then the sequence $\{x_n\}$ converges strongly to $x^{\ast }\in \mathrm{\Omega }$.

Proof Taking $p\in \mathrm{\Omega }$, then $P_{T_n}(p)=\{p\}$. By substituting $P_T$ instead of T and similar argument as (3.21) in the proof of Theorem 3.1 we obtain

$$\underset{n\to \mathrm{\infty }}{lim}dist(x_n,T_i(x_n))\le \underset{n\to \mathrm{\infty }}{lim}dist(x_n,P_{T_i}(x_n))=0.$$

(4.10)

By compactness of K, there exists a subsequence $\{x_{n_k}\}$ of $\{x_n\}$ such that ${lim}_{k\to \mathrm{\infty }}{x}_{n_k}=x^{\ast }$, for some $x^{\ast }\in K$. Since $P_{T_i}$ is nonexpansive for $i=1,2,\dots ,N$, we have

$$\begin{array}{rl}dist(x^{\ast },T_i\left(x^{\ast }\right))& \le dist(x^{\ast },P_{T_i}\left(x^{\ast }\right))\\ \le \parallel x^{\ast }-x_{n_k}\parallel +dist(x_{n_k},P_{T_i}(x_{n_k}))+H(P_{T_i}(x_{n_k}),P_{T_i}\left(x^{\ast }\right))\\ \le 2\parallel x^{\ast }-x_{n_k}\parallel +dist(x_{n_k},P_{T_i}(x_{n_k})).\end{array}$$

(4.11)

It follows from (4.10) and (4.11) that

$$\underset{k\to \mathrm{\infty }}{lim}dist(x^{\ast },T_i\left(x^{\ast }\right))=0,$$

(4.12)

which implies that $x^{\ast }\in {\bigcap }_{i=1}^{N}Fix(T_i)$. Since $\{x_{n_k}\}$ converges strongly to $x^{\ast }$ and ${lim}_{n\to \mathrm{\infty }}\parallel x_n-x^{\ast }\parallel$ exists (as in the proof of Theorem 3.1), we find that $\{x_n\}$ converges strongly to $x^{\ast }$. This completes the proof. □

In addition, we supply an example and numerical results to illustrate our method and the main results of this paper.

Example 4.1 Let $H=\mathbb{R}$ and $K:=[0,1]$ with usual metric. Consider the nonsmooth equilibrium problem defined by the bifunction

$$F(x,y)=2xy(y-x)+xy|y-x|,\mathrm{\forall }x,y\in K.$$

Clearly, F is pseudomonotone on K. Note that $F(x,\cdot )$ is convex for $x\in K$ and $\partial F(x,\cdot )x=[x^2,3x^2]$ by taking ${ϵ}_n=0$ for all $n\in \mathbb{N}$.

(i) Let $Tx:=[\frac{x}{6},\frac{x}{2}]$ defined on $K:=[0,1]$. Note that T is a multivalued nonexpansive mapping and $Fix(T)\cap EP(F,K)=\{0\}$. Setting $N=1$, ${\sigma }_n=1$, ${\alpha }_n=\frac{1}{2}$, ${\beta }_n=\frac{1}{n}$, and $\parallel x_n-x^{\ast }\parallel \le {10}^{-4}$ as stop criteria, we obtain the results of algorithm (4.1) with different initial points in Table 1.

Table 1 Numerical results for an initial point ${\mathit{x}}_{\mathbf{0}}\mathbf{=}\mathbf{0.2}\mathbf{,}\mathbf{0.5}\mathbf{,}\mathbf{0.8}$

(ii) Let $Tx:=[-2x,-x]$ defined on $[0,\mathrm{\infty })\to 2^{\mathbb{R}}$. Note that T is not nonexpansive but $P_{T}x=\{-x\}$ is nonexpansive for all $x\in [0,\mathrm{\infty })$. Indeed, for each $u\in Tx$, $u=-ax$, $1\le a\le 2$, choose $v=-ay$. Then

$$|u-v|=|-ax-(-ay)|=a|x-y|\le 2|x-y|=H(Tx,Ty).$$

On the other hand, for any x, we have $0\in [0,\mathrm{\infty })$ and $T0=\{0\}$. It follows that $Fix(T)\cap EP(F,K)=\{0\}$. Setting $N=1$, ${\sigma }_n=1$, ${\alpha }_n=\frac{1}{4}$, ${\beta }_n=\frac{2}{n}$, and $\parallel x_n-x^{\ast }\parallel \le {10}^{-4}$ as stop criteria, we obtain the results of algorithm (4.9) with different initial points to be found in Table 2.

Table 2 Numerical results for an initial point ${\mathit{x}}_{\mathbf{0}}\mathbf{=}\mathbf{0.2}\mathbf{,}\mathbf{0.5}\mathbf{,}\mathbf{0.8}$

The computations are performed by Matlab R2008a running on a PC Desktop Intel(R) Core(TM) i3-2330M, CPU @2.20 GHz, 790 MHz, 1.83 GB, 2 GB RAM.

Remark 4.1 Our hybrid subgradient method improves the extragradient method of Tran et al. [5] and the inexact subgradient algorithm of Santos and Scheimberg [15] for an equilibrium problem in deducing the computational costs of an iterative process.

Remark 4.2 Our results generalize the results of Eslamian [21], a proximal point method for an equilibrium problem, to a hybrid subgradient method for a pseudomonotone equilibrium problem.