1 Introduction

Positive systems effectively model practical dynamic behaviors where state must remain nonnegative [2], such as economics [3] and pharmacokinetics [12]. In recent years, substantial research has been conducted on positive homogeneous-time control methodologies based on state feedback [10, 18], static output feedback [4], and observer-based output feedback (OBOF) [5, 6]. Although sampled-data controllers offer implementation flexibility, their design is structurally complex [7,8,9, 11]. Prompted by these observations, the authors of this study focus on positive sampled-data OBOF control.

  1. (i)

    To ensure the positivity of the OBOF-controlled plant dynamics, the matrices coupled with the system state and estimation error must be Metzler and positive matrices, respectively [6]. However, conventional OBOF controllers may struggle to enforce the Metzler property and positivity simultaneously in each matrix, because controllers typically consist of a single compensation term. A similar challenge arises in the estimation-error dynamics when uncertainties are present in a plant. Shu et al. [14] studied a positive observer with multiple compensation terms without considering uncertainties. Considering that the augmented closed-loop matrix is partitioned, a four-compensation OBOF controller emerges as an effective solution.

  2. (ii)

    Despite the rising prominence of the sampled-data framework in controller design, facilitated by advancements in digital technology, the research on positive sampled-data control has been limited. The hybrid nature of sampled-data control systems, characterized by continuous-time plant dynamics and discrete-time controllers, makes it difficult to establish closed-loop positivity because of the requirement of nonnegativity not only during sampling intervals but also at sampling instants. The existing direct discrete-time design approaches for sampled-data control are limited because they disregard intersampling behavior. The alternate input-delay method, which transforms a sampled-data system into an equivalent continuous-time model [1], incurs a time-varying delay up to one sampling period, which results in conservative design conditions. By contrast, implementing aperiodic sampling provides a novel perspective on positive sampled-data control problems [19]. Zhang and Du [18] constructed an event-triggered positive control strategy for fuzzy systems without uncertainties or disturbances.

  3. (iii)

    In the presence of system model uncertainties, designing the controller and observer separately within the OBOF framework is demanding. Eigenvalue analysis, commonly performed to confirm the separation principle, is ineffective in this case because the closed-loop system matrix no longer retains a triangular form [17]. Additionally, research on separate design of OBOF controllers for disturbance attenuation, even in the absence of model uncertainties, is scant. This is primarily because of the estimation error in closed-loop plant dynamics, which causes an estimation error to appear in the disturbance attenuation performance inequality. Nguyen et al. [13] proposed a separate design scheme by extending the \(\mathcal {H}_{\infty }\) technique without considering uncertainties.

The authors of this paper introduce a separate design methodology for a sampled-data OBOF controller that accomplishes robust positive energy-to-peak (\(\mathcal {L}_{2}\)–\(\mathcal {L}_{\infty }\)) disturbance attenuation—to achieve a finite peak value of controlled outputs for all possible bounded-energy disturbances—in uncertain linear time-invariant (LTI) systems.

The developed controller possesses the following attributes: (i) amplified possibilities for positivity in uncertain closed-loop plants through additional compensations, (ii) utilization of an aperiodic sampling framework, built based on the event-triggering mechanism, to impose a positivity constraint on sampled-data closed-loop systems, and (iii) separate design of the controller and observer, through the introduction of distinct \(\mathcal {L}_{2}\)–\(\mathcal {L}_{\infty }\) disturbance attenuation performances.

Notation: The index set is defined as \(\mathcal {I}_{N}:=\{1,\dots ,n\}\subset \mathbb {N}\). Given a matrix \(A\in \mathbb {R}^{n\times m}\) (or vectors), \((A)_{ij}\) denotes the entry of A located in the ith row and jth column. \(A\geqslant \geqslant B\) or \(A-B\in \mathbb {R}_{\geqslant \geqslant 0}^{n\times m}\) indicates that \((A-B)_{ij}\geqslant 0, \forall (i,j)\in \mathcal {I}_{N}\times \mathcal {I}_{M}\). \(e_{l}\in \mathbb {R}^{n}\) denotes the lth standard unit vector. \(I_{n}\) denotes the identity matrix in \(\mathbb {R}^{n\times n}\). \(\textbf{1}_{n}\) symbolizes the n-dimensional vector whose all entries are equal to 1. The relationship \(P\succ Q\) indicates that the matrix \(P-Q\) is positive definite. The transposed element at symmetric positions is denoted by \(*\) and the shorthand \(\textrm{He}\left\{ X\right\} :=X+X^{\textrm{T}}\) is adopted.

2 Positive Model

We consider the following uncertain LTI model:

$$\begin{aligned} \left\{ \begin{aligned}&\dot{x} = (A+\Delta A)x+Bu+B_{w}w \\&y = Cx \\&z = C_{z}x \end{aligned} \right. \end{aligned}$$
(1)

where \(x\in \mathbb {R}^{n}\) is the state, \(u\in \mathbb {R}^{m}\) is the input, \(w\in \mathbb {R}^{l}\) is the disturbance in \(\mathcal {L}_{2}\), \(y\in \mathbb {R}^{p}\) is the measurement output, \(z\in \mathbb {R}^{q}\) is the controlled output, and \(\Delta A\) denotes the system uncertainty.

Definition 1

(Positivity) Suppose \(u=0\) in (1) for an entire time horizon. System (1) is positive for all \(x(0)\geqslant \geqslant 0\) and \(w\geqslant \geqslant 0\) if \(x\geqslant \geqslant 0\) and \(y\geqslant \geqslant 0, \forall t\in \mathbb {R}_{\geqslant 0}\).

Definition 2

(Metzler) Matrix \(A\in \mathbb {R}^{n\times n}\) is Metzler if \((A)_{ij}\geqslant 0, \forall (i,j)\in \mathcal {I}_{N}\times \mathcal {I}_{N}\ni i \ne j\).

Lemma 1

([10]) System (1) is positive if and only if \(A+\Delta A\) is Metzler, \(B_{w}\geqslant \geqslant 0\), and \(C\geqslant \geqslant 0\).

Assumption 1

\(B_{w}\geqslant \geqslant 0\) and \(C\geqslant \geqslant 0\).

Lemma 2

([6]) Matrix \(A\in \mathbb {R}^{n\times n}\) is Metzler if and only if

$$\begin{aligned} \sum _{l=1}^{n}\textrm{diag}\left\{ e_{l}\right\} A \begin{bmatrix} 0 & 1 \\ I_{n-1} & 0 \end{bmatrix}^{k}\textrm{diag}\left\{ e_{l}\right\} \succcurlyeq 0, \quad k\in \mathcal {I}_{N-1}. \end{aligned}$$

In addition, \(A\geqslant \geqslant 0\) if only if the foregoing inequality holds for \(k\in \mathcal {I}_{N}\).

Assumption 2

There exist known compatible constant matrices D and E and an unknown time-varying diagonal matrix \(\Delta\) satisfying \(\Delta ^{\textrm{T}}\Delta \preccurlyeq I, \forall t\in \mathbb {R}_{\geqslant 0}\) such that

$$\begin{aligned} \Delta A = D\Delta E \end{aligned}$$

with \(DE\geqslant \geqslant 0\).

Remark 1

The imposition of \(DE\geqslant \geqslant 0\) in Assumption 2 is not overly stringent, because \(\Delta A\) typically represents the potential deviation from A. In this case, the following property holds:

$$\begin{aligned} -DE \leqslant \leqslant D\Delta E. \end{aligned}$$

Lemma 3

([15]) Given compatible matrices D, E, \(S=S^{\textrm{T}}\), with \(\Delta \ni \Delta ^{\textrm{T}}\Delta \preccurlyeq I\), there exists \(\epsilon \in \mathbb {R}_{>0}\) such that

$$\begin{aligned} S+\textrm{He}\left\{ D\Delta E\right\} \prec 0 \Longleftrightarrow S+ \begin{bmatrix} D&E^{\textrm{T}} \end{bmatrix} \begin{bmatrix} \epsilon ^{-1}I & * \\ 0 & \epsilon I \end{bmatrix} \begin{bmatrix} D^{\textrm{T}} \\ E \end{bmatrix} \prec 0. \end{aligned}$$

Assumption 3

Matrix B is full column rank and \(B\geqslant \geqslant 0\).

Assumption 4

Only y, rather than x, is available for control.

3 Separate Robust Positive Sampled-Data \(\mathcal {L}_{2}\)–\(\mathcal {L}_{\infty }\) Disturbance Attenuation

In view of Assumption 4, we employ the following event-triggered aperiodic sampled-data OBOF controller:

$$\begin{aligned} \left\{ \begin{aligned}&\dot{\hat{x}} = A\hat{x}+Bu+L(y-\hat{y})+Hy \\&\hat{y} = C\hat{x} \\&u = K\hat{x}_{t_{k}}+Fy_{t_{k}}, \quad t\in [t_{k},t_{k+1}) \end{aligned} \right. \end{aligned}$$
(2)

where \(\hat{x}\) and \(\hat{y}\) are the estimates of x and y, respectively. \(t_{k}\in \mathbb {R}_{\geqslant 0},k\in \mathbb {Z}_{\geqslant 0}\) denotes the sampling instant. The next sampling instant is determined using the following event-triggering mechanism

$$\begin{aligned} t_{k+1}&:= \inf \left\{ t\in \mathbb {R}_{\geqslant 0}:t>t_{k} \right. \\ &\quad \left. \wedge \max \left\{\| \epsilon _{\hat{x}}\| _{1}, \| \epsilon _{{y}}\| _{1}\right\} >\beta \left\| y\right\| _{1} \right\} \end{aligned}$$
(3)

where \(\epsilon _{\hat{x}}:=\hat{x}_{t_{k}}-\hat{x}\), \(\epsilon _{y}:=y_{t_{k}}-y\), and \(\beta \in \mathbb {R}_{>0}\) is a pre-determined threshold.

The problem of interest is summarized as follows.

Problem 1

(positive \(\mathcal {L}_{2}\)–\(\mathcal {L}_{\infty }\)) Find K, F, L, and H such that the uncertain LTI system (1) closed by the aperiodic sampled-data OBOF controller (2) based on the event-triggering mechanism (3) is positive and robustly asymptotically stable against the norm-bounded parametric uncertainties when \(w=0\), and for some attenuation level \(\gamma \in \mathbb {R}_{>0}\), it exhibits the \(\mathcal {L}_{2}\)–\(\mathcal {L}_{\infty }\)-disturbance attenuation performance defined as follows:

$$\begin{aligned} \left\| z\right\| _{\infty } \leqslant \gamma \left\| w\right\| _{2} \end{aligned}$$
(4)

when \(w\in \mathcal {L}_{2}\) and \(w\geqslant \geqslant 0\).

To independently design the controller and observer, we introduce the following two \(\mathcal {L}_{2}\)–\(\mathcal {L}_{\infty }\)-disturbance attenuation performances:

$$\begin{aligned} \left\| z\right\| _{\infty } \leqslant \mu _{1}\left\| e\right\| _{2}+\gamma _{1}\left\| w\right\| _{2} \end{aligned}$$
(5)
$$\begin{aligned} \left\| e\right\| _{\infty } \leqslant \mu _{2}\left\| x\right\| _{2}+\gamma _{2}\left\| w\right\| _{2}. \end{aligned}$$
(6)

Then, we show that the overall closed-loop system satisfies (4), where \(\mu _{1},\mu _{2},\gamma _{2}\), and \(\gamma _{1}\in \mathbb {R}_{>0}\).

We define \(e:=x-\hat{x}\) and \(\xi :=(x,e)\). The closed-loop system of (1) and (2) under (3) is then written as

$$\begin{aligned} \dot{\xi }&= \begin{bmatrix} A+\Delta A+BK+BFC & -BK \\ \Delta A-HC & A-LC \end{bmatrix}\xi + \begin{bmatrix} BK \\ 0 \end{bmatrix}\epsilon _{\hat{x}} \nonumber \\&\quad + \begin{bmatrix} BF \\ 0 \end{bmatrix}\epsilon _{y} + \begin{bmatrix} B_{w} \\ B_{w} \end{bmatrix}w \end{aligned}$$
(7)

for \(t\in [t_{k},t_{k+1})\). In this case, from (3) and Assumption 1, we deduce that the following intervals

$$\begin{aligned} \epsilon _{\hat{x}},\epsilon _{y} \in \left[ -\beta \textbf{1}_{n}\textbf{1}_{p}^{\textrm{T}}y, \beta \textbf{1}_{n}\textbf{1}_{p}^{\textrm{T}}y \right] \end{aligned}$$

hold as long as \(x\geqslant \geqslant 0\). We decompose \(K:=K^{\textrm{L}}+K^{\textrm{U}}\) and \(F:=F^{\textrm{L}}+F^{\textrm{U}}\) such that

$$\begin{aligned} BK^{\textrm{L}}\leqslant \leqslant 0, \quad BK^{\textrm{U}}\geqslant \geqslant 0, \quad BF^{\textrm{L}}C\leqslant \leqslant 0, \quad BF^{\textrm{U}}C\geqslant \geqslant 0. \end{aligned}$$

From Assumption 1, it follows that

$$\begin{aligned} &\beta BK^{\textrm{L}}\textbf{1}_{n}\textbf{1}_{p}^{\textrm{T}}Cx \leqslant \leqslant BK^{\textrm{L}}\epsilon _{\hat{x}} \leqslant \leqslant -\beta BK^{\textrm{L}}\textbf{1}_{n}\textbf{1}_{p}^{\textrm{T}}Cx \\ &-\beta BK^{\textrm{U}}\textbf{1}_{n}\textbf{1}_{p}^{\textrm{T}}Cx \leqslant \leqslant BK^{\textrm{U}}\epsilon _{\hat{x}} \leqslant \leqslant \beta BK^{\textrm{U}}\textbf{1}_{n}\textbf{1}_{p}^{\textrm{T}}Cx \end{aligned}$$

and

$$\begin{aligned} &\beta BF^{\textrm{L}}\textbf{1}_{p}\textbf{1}_{p}^{\textrm{T}}Cx \leqslant \leqslant BF^{\textrm{L}}\epsilon _{y} \leqslant \leqslant -\beta BF^{\textrm{L}}\textbf{1}_{p}\textbf{1}_{p}^{\textrm{T}}Cx \\ &-\beta BF^{\textrm{U}}\textbf{1}_{p}\textbf{1}_{p}^{\textrm{T}}Cx \leqslant \leqslant BF^{\textrm{U}}\epsilon _{y} \leqslant \leqslant \beta BF^{\textrm{U}}\textbf{1}_{p}\textbf{1}_{p}^{\textrm{T}}Cx. \end{aligned}$$

Then we obtain the following differential inequalities:

$$\begin{aligned} &\dot{\xi }\leqslant \leqslant \begin{bmatrix} \Omega _{1} & -BK \\ \Delta A-HC & A-LC \end{bmatrix}\xi + \begin{bmatrix} B_{w} \\ B_{w} \end{bmatrix}w \end{aligned}$$
(8)

and

$$\begin{aligned} &\dot{\xi }\geqslant \geqslant \begin{bmatrix} \Omega _{2} & -BK \\ \Delta A-HC & A-LC \end{bmatrix}\xi + \begin{bmatrix} B_{w} \\ B_{w} \end{bmatrix}w \end{aligned}$$
(9)

where

$$\begin{aligned} &\Omega _{1}:= A+\Delta A+B(K^{\textrm{L}}\Xi _{\hat{x}}^{\textrm{L}}+K^{\textrm{U}}\Xi _{\hat{x}}^{\textrm{U}}+(F^{\textrm{L}}\Xi _{y}^{\textrm{L}}+F^{\textrm{U}}\Xi _{y}^{\textrm{U}})C) \\ &\Omega _{2}:= A+\Delta A +B(K^{\textrm{L}}\Xi _{\hat{x}}^{\textrm{U}}+K^{\textrm{U}}\Xi _{\hat{x}}^{\textrm{L}}+(F^{\textrm{L}}\Xi _{y}^{\textrm{U}}+F^{\textrm{U}}\Xi _{y}^{\textrm{L}})C). \end{aligned}$$

In the above expression, \(\Xi _{\hat{x}}^{\textrm{L}}:=I-\beta \textbf{1}_{n}\textbf{1}_{p}^{\textrm{T}}C\), \(\Xi _{\hat{x}}^{\textrm{U}}:=I+\beta \textbf{1}_{n}\textbf{1}_{p}^{\textrm{T}}C\), \(\Xi _{y}^{\textrm{L}}:=I-\beta \textbf{1}_{p}\textbf{1}_{p}^{\textrm{T}}\), and \(\Xi _{y}^{\textrm{U}}:=I+\beta \textbf{1}_{p}\textbf{1}_{p}^{\textrm{T}}\).

The separate design condition for Problem 1 is summarized as follows.

Theorem 1

(separate positive \(\mathcal {L}_{2}\)–\(\mathcal {L}_{\infty }\) design) Given \(\gamma _{1}\), \(\gamma _{2}\), \(\epsilon _{1}\), \(\epsilon _{2}\), \(\lambda _{1}\), \(\lambda _{2}\), \(\mu _{1}\), and \(\mu _{2}\in \mathbb {R}_{>0}\) such that

$$\begin{aligned} \lambda _{\max }(C_{z}^{\textrm{T}}C_{z})-\mu _{1}^{4}> 0, \quad \lambda _{\max }(C_{z}^{\textrm{T}}C_{z})-\mu _{2}^{4} > 0 \end{aligned}$$
(10)

the uncertain LTI system (1) closed by the aperiodic sampled-data OBOF controller (2) based on the event-triggering mechanism (3) is positive and exhibits the \(\gamma\)-disturbance attenuation performance (4) with asymptotic stability if there exist M, diagonal \(P_{1}=P_{1}^{\textrm{T}}\succ 0\) and \(P_{2}=P_{2}^{\textrm{T}}\succ 0\), and W, \(X^{\textrm{L}}\), \(X^{\textrm{U}}\), \(Y^{\textrm{L}}\), \(Y^{\textrm{U}}\), and Z, such that

$$\begin{aligned}&\begin{bmatrix} (1,1) & * & * & * & * \\ -(X^{\textrm{L}})^{\textrm{T}}B^{\textrm{T}}-(X^{\textrm{U}})^{\textrm{T}}B^{\textrm{T}} & -\mu _{1}^{2}I & * & * & * \\ B_{w}^{\textrm{T}}P_{1} & 0 & -\gamma _{1}^{2}I & * & * \\ D^{\textrm{T}}P_{1} & 0 & 0 & -\epsilon _{1}I & * \\ E & 0 & 0 & 0 & -\epsilon _{1}^{-1}I \end{bmatrix} \prec 0 \end{aligned}$$
(11)
$$\begin{aligned}&P_{1}B-BM = 0 \end{aligned}$$
(12)
$$\begin{aligned}&P_{1}-\lambda _{\max }(C_{z}^{\textrm{T}}C_{z})I \succ 0 \end{aligned}$$
(13)
$$\begin{aligned}&\sum _{l=1}^{n}\textrm{diag}\left\{ e_{l}\right\} (P_{1}A-P_{1}DE+BX^{\textrm{L}}\Xi _{\hat{x}}^{\textrm{U}}+BX^{\textrm{U}}\Xi _{\hat{x}}^{\textrm{L}} \nonumber \\&+BY^{\textrm{L}}\Xi _{y}^{\textrm{U}}C+BY^{\textrm{U}}\Xi _{y}^{\textrm{L}}C) \begin{bmatrix} 0 & 1 \\ I_{n-1} & 0 \end{bmatrix}^{k} \textrm{diag}\left\{ e_{l}\right\} \succ 0, \nonumber \\&\quad k\in \mathcal {I}_{N-1} \end{aligned}$$
(14)
$$\begin{aligned}&\sum _{l=1}^{n}\textrm{diag}\left\{ e_{l}\right\} (BX^{\textrm{L}}+BX^{\textrm{U}}) \begin{bmatrix} 0 & 1 \\ I_{n-1} & 0 \end{bmatrix}^{k}\textrm{diag}\left\{ e_{l}\right\} \prec 0, \nonumber \\&\quad k\in \mathcal {I}_{N} \end{aligned}$$
(15)
$$\begin{aligned}&\begin{bmatrix} -\mu _{2}^{2}I & * & * & * & * \\ -WC & \textrm{He}\left\{ P_{2}A-ZC\right\} & * & * & * \\ 0 & B_{w}^{\textrm{T}}P_{2} & -\gamma _{2}^{2} I & * & * \\ 0 & D^{\textrm{T}}P_{2} & 0 & -\epsilon _{2}I & * \\ E & 0 & 0 & 0 & -\epsilon _{2}^{-1}I \end{bmatrix} \prec 0 \end{aligned}$$
(16)
$$\begin{aligned}&P_{2}-I \succ 0 \end{aligned}$$
(17)
$$\begin{aligned}&\sum _{l=1}^{n}\textrm{diag}\left\{ e_{l}\right\} (P_{2}DE+WC) \begin{bmatrix} 0 & 1 \\ I_{n-1} & 0 \end{bmatrix}^{k}\textrm{diag}\left\{ e_{l}\right\} \prec 0, \nonumber \\&\quad k\in \mathcal {I}_{N-1} \end{aligned}$$
(18)
$$\begin{aligned}&\sum _{l=1}^{n}\textrm{diag}\left\{ e_{l}\right\} (P_{2}A-ZC) \begin{bmatrix} 0 & 1 \\ I_{n-1} & 0 \end{bmatrix}^{k}\textrm{diag}\left\{ e_{l}\right\} \succ 0, \quad k\in \mathcal {I}_{N}. \end{aligned}$$
(19)

Here, \((1,1):=\textrm{He}\left\{ PA+BX^{\textrm{L}}\Xi _{\hat{x}}^{\textrm{L}}+BX^{\textrm{U}}\Xi _{\hat{x}}^{\textrm{U}} +BY^{\textrm{L}}\Xi _{y}^{\textrm{L}}C+BY^{\textrm{U}}\Xi _{y}^{\textrm{U}}\right\} +\lambda _{1}P_{1}\). In this case, the gains are given by \(K^{\textrm{L}}=M^{-1}X^{\textrm{L}}\), \(K^{\textrm{U}}=M^{-1}X^{\textrm{U}}\), \(F^{\textrm{L}}=M^{-1}Y^{\textrm{L}}\), \(F^{\textrm{U}}=M^{-1}Y^{\textrm{U}}\), \(L=P_{2}^{-1}Z\), and \(H=P_{2}^{-1}W\).

Proof

Define the Lyapunov function candidate \(V_{1}:=x^{\textrm{T}}P_{1}x\). Considering (8), the time derivative of \(V_{1}\) is majorized by

$$\begin{aligned} \dot{V}_{1}&\leqslant \begin{bmatrix} \xi \\ w \end{bmatrix}^{\textrm{T}} \bar{\mathcal {M}} \begin{bmatrix} \xi \\ w \end{bmatrix} -\lambda _{1}V_{1}+\mu _{1}^{2}e^{\textrm{T}}e+\gamma _{1}^{2}w^{\textrm{T}}w \end{aligned}$$

where

$$\begin{aligned} \bar{\mathcal {M}}:= \begin{bmatrix} \textrm{He}\left\{ \Omega _{1}^{\textrm{T}}P_{1}\right\} +\lambda _{1}P_{1} & * & * \\ -K^{\textrm{T}}B^{\textrm{T}}P & -\mu _{1}^{2}I & * \\ B_{w}^{\textrm{T}}P_{1} & 0 & -\gamma _{1}^{2}I \end{bmatrix}. \end{aligned}$$

By using Lemma 3 and denoting \(MK^{\textrm{L}}=:X^{\textrm{L}}\), \(MK^{\textrm{U}}=:X^{\textrm{U}}\), \(MF^{\textrm{L}}=:Y^{\textrm{L}}\), and \(MF^{\textrm{U}}=:Y^{\textrm{U}}\), the following implication holds:

$$\begin{aligned} \text{(11) and (12)}&\Longrightarrow \bar{\mathcal {M}} \prec 0 \nonumber \\&\Longrightarrow \dot{V}_{1} < -\lambda _{1}V+\mu _{1}^{2}e^{\textrm{T}}e+\gamma _{1}^{2}w^{\textrm{T}}w. \end{aligned}$$
(20)

Then, from the zero-initial value assumption for the \(\mathcal {L}_{2}\)–\(\mathcal {L}_{\infty }\)-disturbance attenuation performance analysis, we have

$$\begin{aligned} V_{1}&< \int _{0}^{t}\textrm{e}^{-\lambda _{1}(t-\tau )}(\mu _{1}^{2}e^{\textrm{T}}e+\gamma _{1}^{2}w^{\textrm{T}}w)\;\textrm{d}\tau \\&< \mu _{1}^{2}\int _{0}^{\infty }e^{\textrm{T}}e\;\textrm{d}\tau +\gamma _{1}^{2}\int _{0}^{\infty }w^{\textrm{T}}w\;\textrm{d}\tau . \end{aligned}$$

In addition, because (13) reveals the following inequality

$$\begin{aligned}&V_{1}-z^{\textrm{T}}z > 0 \end{aligned}$$

the following expression can be derived for any \(t\in \mathbb {R}_{\geqslant 0}\):

$$\begin{aligned} & \left\| z \right\|^{2} < \mu _{1}^{2} \left\| e \right\|_{2}^{2} + \gamma _{1}^{2} \left\| w \right\|_{2}^{2} \\ & \Longrightarrow \left\| z \right\|<\sqrt {(\mu _{1} \left\| e \right\|_{2} + \gamma _{1} \left\| w \right\|_{2} )^{2} - 2\mu _{1} \gamma _{1} \left\| e \right\|_{2} \left\| w \right\|_{2} } \\ & \Longrightarrow \left\| z \right\| < \mu _{1} \left\| e \right\|_{2} + \gamma _{1} \left\| w \right\|_{2} . \\ \end{aligned}$$

Taking the supremum over \(\mathbb {R}_{\geqslant 0}\) yields (5).

Similarly, for the following time derivative of the Lyapunov function candidate \(V_{2}:=e^{\textrm{T}}P_{2}e\) with (8) and (9)

$$\begin{aligned} \dot{V}_{2} = \begin{bmatrix} \xi \\ w \end{bmatrix}^{\textrm{T}} \bar{\mathcal {N}} \begin{bmatrix} \xi \\ w \end{bmatrix} -\lambda _{2}V_{2}+\mu _{2}^{2}x^{\textrm{T}}x+\gamma _{2}^{2}w^{\textrm{T}}w \end{aligned}$$

the following implication holds:

$$\begin{aligned} (16) \Longrightarrow \bar{\mathcal {N}} \prec 0 \end{aligned}$$
(21)
$$\begin{aligned}\phantom{\text{(16)}}&\Longrightarrow \dot{V}_{2}< -\lambda _{2}V+\mu _{2}^{2}x^{\textrm{T}}x+\gamma _{2}^{2}w^{\textrm{T}}w \nonumber \\&\Longrightarrow V_{2} < \mu _{2}^{2}\int _{0}^{\infty }x^{\textrm{T}}x\;\textrm{d}\tau +\gamma _{2}^{2}\int _{0}^{\infty }w^{\textrm{T}}w\;\textrm{d}\tau \end{aligned}$$
(22)

where

$$\begin{aligned} \bar{\mathcal {N}}:= \begin{bmatrix} -\mu _{2}^{2}I & * & * \\ P_{2}(D\Delta E-HC) & \textrm{He}\left\{ (A-LC)^{\textrm{T}}P_{2}\right\} +\lambda _{2}P_{2} & * \\ 0 & B_{w}^{\textrm{T}}P_{2} & -\gamma _{2}^{2}I \end{bmatrix}. \end{aligned}$$

Similar to the above expression, connecting (22) with the condition

$$\begin{aligned} (17) \Longrightarrow V_{2}-e^{\textrm{T}}e > 0 \end{aligned}$$

implies (6).

Next, by applying Assumption 2, Remark 1, and Lemma 2, we have

$$\begin{aligned} (14)&\Longrightarrow P_{1}(A-DE+B(K^{\textrm{L}}\Xi _{\hat{x}}^{\textrm{U}}+K^{\textrm{U}}\Xi _{\hat{x}}^{\textrm{L}}+ \\&\quad \quad (F^{\textrm{L}}\Xi _{y}^{\textrm{U}}+F^{\textrm{U}}\Xi _{y}^{\textrm{L}})C))\quad \text {Metzler} \\&\Longrightarrow \Omega _{2}\quad \text {Metzler} \end{aligned}$$

because \(P_{1}\succ 0\) is diagonal. Moreover, (19) implies that \(A-LC\) is Metzler. Similar arguments are applied to (15) and (18) to ensure the positivity of \(-BK\) and \(\Delta A-HC\), respectively. According to Assumption 1 and Lemma 1, (9) is positive. Accordingly, the positivity of x in (7) follows.

To demonstrate that the separately designed controller and observer fulfill (4) with respect to (7), we prove the existence of \(\psi _{1}\) and \(\psi _{2}\in \mathbb {R}_{>0}\) such that the following two inequalities for \(V(\xi ):=\psi _{1} V_{1}(x)+\psi _{2} V_{2}(e)\) along the trajectory of (8)

$$\begin{aligned}&\dot{V}+\lambda V-\gamma ^{2} w^{\textrm{T}}w = \begin{bmatrix} \xi \\ w \end{bmatrix}^{\textrm{T}}\bar{\mathcal {O}} \begin{bmatrix} \xi \\ w \end{bmatrix} <0 \nonumber \\&V-z^{\textrm{T}}z = \xi ^{\textrm{T}} \begin{bmatrix} \psi _{1} P_{1}-C_{z}^{\textrm{T}}C_{z} & * \\ 0 & \psi _{2} P_{2} \end{bmatrix}\xi >0 \end{aligned}$$
(23)

hold for some \(\gamma\) and \(\lambda \in \mathbb {R}_{>0}\), where

$$\begin{aligned} \bar{\mathcal {O}}&:= \psi _{1}\bar{\mathcal {M}}+\psi _{2}\bar{\mathcal {N}} + \textrm{diag} \left\{ -\psi _{1}\lambda _{1}P_{1}+\psi _{2}\mu _{2}^{2}I+\lambda \psi _{1}P_{1}, \right. \\&\quad \left. \psi _{1}\mu _{1}^{2}I-\psi _{2}\lambda _{2}P_{2}+\lambda \psi _{2}P_{2}, (\psi _{1}\gamma _{1}^{2}+\psi _{2}\gamma _{2}^{2}-\gamma ^{2})I \right\} . \end{aligned}$$

By using (20) and (21), we only need to show

$$\begin{aligned} -\psi _{1}(\lambda _{1}-\lambda )\lambda _{\min }(P_{1})+\psi _{2}\mu _{2}^{2} < 0 \end{aligned}$$
(24)
$$\begin{aligned} -\psi _{2}(\lambda _{2}-\lambda )\lambda _{\min }(P_{2})+\psi _{1}\mu _{1}^{2} < 0 \end{aligned}$$
(25)
$$\begin{aligned} \psi _{1}\gamma _{1}^{2}+\psi _{2}\gamma _{2}^{2}-\gamma ^{2} < 0 \end{aligned}$$
(26)
$$\begin{aligned} \psi _{1}\lambda _{\min }(P_{1})-\lambda _{\max }(C_{z}^{\textrm{T}}C_{z}) > 0 . \end{aligned}$$
(27)

The inequalities (24) and (25) are true if and only if

$$\begin{aligned}&\exists \psi _{1},\psi _{2},\lambda \in \mathbb {R}_{>0} \ni \nonumber \\&\frac{\mu _{1}^{2}}{\lambda _{\min }(P_{2})(\lambda _{2}-\lambda )}< \frac{\psi _{2}}{\psi _{1}}< \frac{\lambda _{\min }(P_{1})(\lambda _{1}-\lambda )}{\mu _{2}^{2}} \wedge \lambda <\lambda _{1},\lambda _{2} \end{aligned}$$
(28)

which can be expressed as

$$\begin{aligned}&\exists \lambda \in \mathbb {R}_{[0,\lambda _{1}]} \ni \\&f(\lambda ) := \lambda ^{2}-(\lambda _{1}+\lambda _{2})\lambda +\lambda _{1}\lambda _{2}-\frac{\mu _{1}^{2}\mu _{2}^{2}}{\lambda _{\min }(P_{1})\lambda _{\min }(P_{2})} > 0 \end{aligned}$$

assuming \(\lambda _{1}<\lambda _{2}\) without loss of generality. It is straightforward to deduce that

$$\begin{aligned} f(\lambda _{1}) = -\frac{\mu _{1}^{2}\mu _{2}^{2}}{\lambda _{\min }(P_{1})\lambda _{\min }(P_{2})} < 0. \end{aligned}$$

Furthermore, considering (13) and (17),

$$\begin{aligned} (10)&\Longrightarrow \lambda _{\max }(C_{z}^{\textrm{T}}C_{z})-\mu _{1}^{2}\mu _{2}^{2}> 0 \\&\Longrightarrow \lambda _{1}\lambda _{2}\lambda _{\min }(P_{1})\lambda _{\min }(P_{2})-\mu _{1}^{2}\mu _{2}^{2}> 0 \\&\Longleftrightarrow f(0) = \lambda _{1}\lambda _{2}-\frac{\mu _{1}^{2}\mu _{2}^{2}}{\lambda _{\min }(P_{1})\lambda _{\min }(P_{2})} > 0. \end{aligned}$$

This implies that there indeed exists a \(\lambda \in (0,\lambda _{1})\) and a set of pairs of \((\psi _{1},\psi _{2})\) that satisfiy (28). Within this set, the pair \((\psi _{1},\psi _{2})\ni \psi _{1}\geqslant 1\) satisfies (27) through (13). One can identify \(\gamma\) for which (26) is true. When \(w=0, \forall t\in \mathbb {R}_{>0}\), (23) can be expressed as \(\dot{V}+\lambda V<0 \Longrightarrow \dot{V}<0\). The invertibility of M follows from Assumption 3 (for more details, refer to [6]). This concludes the proof. \(\square\)

4 Excluding the Zeno Phenomenon

To exclude the possibility of Zeno behavior in the sampling with (3), we investigate the existence of a nonzero lower bound of the minimum event-triggering interval.

Theorem 2

(no Zeno) The interval between the consecutive sampling instants determined by the event-triggering mechanism (3) is positively lower bounded.

Proof

Because \(\hat{x}_{t_{k}}\) is fixed for \([t_{k}, t_{k+1}), k\in \mathbb {Z}_{\geqslant 0}\), we have the following dynamics:

$$\begin{aligned} \dot{\epsilon }_{\hat{x}}&= \dot{\hat{x}}_{t_{k}}-\dot{\hat{x}} \\&= A\epsilon _{\hat{x}} - \begin{bmatrix} HC&LC \end{bmatrix}\xi - \begin{bmatrix} A+B(K+FC)&-A-BK \end{bmatrix}\xi _{t_{k}}. \end{aligned}$$

By solving the above expression and taking a norm on both sides yields

$$\begin{aligned} \left\| \epsilon _{\hat{x}}\right\|&= \left\| \int _{t_{k}}^{t}\textrm{e}^{A(t-\tau )} \left( \begin{bmatrix} HC&LC \end{bmatrix}\xi \right. \right. \\&\quad \left. \left. + \begin{bmatrix} A+B(K+FC)&-A-BK \end{bmatrix} \xi _{t_{k}} \right) \;\textrm{d}\tau \right\| \\&\leqslant \frac{\rho _{1_{t_{k}}}}{\left\| A\right\| }\left( \textrm{e}^{\left\| A\right\| (t-t_{k})}-1\right) . \end{aligned}$$

Here, we know that

$$\begin{aligned} \rho _{1_{t_{k}}}&:= \sup _{\xi ,\xi _{t_{k}}\in \mathbb {R}_{\geqslant \geqslant 0}^{2n}} \left\| \begin{bmatrix} HC&LC&A+B(K+FC)&-A-BK \end{bmatrix} \right\| \\&\quad \quad \times \left\| \begin{bmatrix} \xi \\ \xi _{t_{k}} \end{bmatrix} \right\| \end{aligned}$$

is finite. Similarly, for the dynamics

$$\begin{aligned} \dot{x}_{t_{k}}-\dot{x}&= (A+\Delta A)(x_{t_{k}}-x) \\&\quad - \left( \begin{bmatrix} A+\Delta A+B(K+FC)&BK \end{bmatrix}\xi _{t_{k}}+B_{w}w \right) \end{aligned}$$

we can derive the following inequality:

$$\begin{aligned} \left\| \epsilon _{y}\right\|&= \left\| Cx_{t_{k}}-Cx\right\| \\&= \left\| C \int _{t_{k}}^{t}\textrm{e}^{(A+\Delta A)(t-\tau )} \right. \\&\quad \left. \times \left( \begin{bmatrix} A+\Delta A+B(K+FC)&BK \end{bmatrix}\xi _{t_{k}}+B_{w}w \right) \;\textrm{d}\tau \right\| \\&\leqslant \frac{\left\| C\right\| \rho _{2_{t_{k}}}}{\left\| A+\Delta A\right\| }\left( \textrm{e}^{\left\| A+\Delta A\right\| (t-t_{k})}-1\right) \end{aligned}$$

where

$$\begin{aligned} \rho _{2_{t_{k}}}&:= \sup _{\xi \in \mathbb {R}_{\geqslant \geqslant 0}^{2n},w\in \mathcal {L}_{2}} \left\| \begin{bmatrix} A+\Delta A+B(K+FC)&BK&B_{w} \end{bmatrix} \right\| \\&\quad \times \left\| \begin{bmatrix} \xi _{t_{k}} \\ w \end{bmatrix}\right\| \end{aligned}$$

is finite as well. Based on (3), the next event may occur at

$$\begin{aligned} t_{k+1}&> \min \left\{ t_{k}+ \frac{1}{\left\| A\right\| }\ln \left( 1+\frac{\beta \left\| y\right\| \left\| A\right\| }{\rho _{1_{t_{k}}}}\right) , \right. \\&\quad \left. t_{k}+ \frac{1}{\left\| A+\Delta A\right\| }\ln \left( 1+\frac{\beta \left\| y\right\| \left\| A+\Delta A\right\| }{\left\| C\right\| \rho _{2_{t_{k}}}}\right) \right\} . \end{aligned}$$

It is clear that \(t_{k+1}-t_{k}>0\) for all \(k\in \mathbb {Z}_{\geqslant 0}\), which excludes the Zeno phenomenon from (3). \(\square\)

5 An Example

Consider the following LTI model, adopted from the pharmacokinetics study of Yin et al. [16]

$$\begin{aligned} A = \begin{bmatrix} -2.25 & 0 & 0 & 0 & 0 \\ 0 & -2.56 & 0 & 0 & 0 \\ 0 & 0 & -3.67 & 0 & 0 \\ 0 & 0 & 3.67 & -3.18 & 0.61 \\ 0 & 0 & 0 & 1.55 & -0.61 \end{bmatrix} \end{aligned}$$

with the parameters defined in Nam et al. [12]. We modify the other state-space data as follows:Footnote 1

$$\begin{aligned} B = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}, \quad C = \begin{bmatrix} 1 & 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 & 1 \end{bmatrix}. \end{aligned}$$

To highlight the advantage of our method, we further introduce

$$\begin{aligned} &\Delta A = \begin{bmatrix} -2.25\delta & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{bmatrix}, \quad B_{w} = \begin{bmatrix} 0 \\ 0 \\ 0.1 \\ 0 \\ 0 \end{bmatrix} \\ &C_{z} = \begin{bmatrix} 0&0&0&1&0 \end{bmatrix} \end{aligned}$$

where \(\delta \in \mathbb {R}_{[-1,1]}\) is the uncertain parameter. According to Assumption 2, \(\Delta A\) is decomposed as

$$\begin{aligned} D = \begin{bmatrix} \sqrt{2.25} \\ 0 \\ 0 \\ 0 \\ 0 \end{bmatrix}, \quad \Delta = \delta , \quad E = \begin{bmatrix} \sqrt{2.25}&0&0&0&0 \end{bmatrix}. \end{aligned}$$

The \(\mathcal {L}_{2}\) disturbance is defined as

$$\begin{aligned} w:= {\left\{ \begin{aligned} &0.1\cos (t)+0.1, \quad t\in \mathbb {R}_{[0,10]} \\ &0, \quad \text {otherwise}. \end{aligned}\right. } \end{aligned}$$

In solving Theorem 1, the controller gain matrices

$$\begin{aligned} &K^{{\text{L}}} = \begin{bmatrix} -0.0206 & -0.0234 & -0.0248 & -0.0267 & -0.0246 \\ -0.0407 & -0.0475 & -0.0472 & -0.0534 & -0.0503 \\ -0.0051 & -0.0055 & -0.0054 & -0.0069 & -0.0097 \end{bmatrix} \\ &K^{{\text{U}}} = \begin{bmatrix} 0.0108 & 0.0102 & 0.0100 & 0.0097 & 0.0100 \\ 0.0211 & 0.0198 & 0.0198 & 0.0190 & 0.0194 \\ 0.0027 & 0.0026 & 0.0026 & 0.0024 & 0.0022 \\ \end{bmatrix} \\ &F^{{\text{L}}} = \begin{bmatrix} -0.0954 & 0.0878 & -0.0200 \\ -0.2814 & 0.2662 & -0.0412 \\ -1.5528 & 1.5509 & -0.0053 \end{bmatrix} \\ &F^{{\text{U}}} = \begin{bmatrix} 0.2149 & -0.0417 & 0.1263 \\ 0.4992 & -0.1452 & 0.2409 \\ 0.0353 & 0.0110 & 0.0314 \end{bmatrix}\end{aligned}$$

and the observer gain matrices

$$\begin{aligned} &L = \begin{bmatrix} -0.8256 & 9.2118 & -0.6981 \\ -0.2180 & 0.0005 & -0.1687 \\ -0.2728 & -0.0022 & -0.2143 \\ 11.6227 & -12.8626 & -0.5654 \\ 1.5048 & -1.5500 & -0.0279 \end{bmatrix} \\ &H = \begin{bmatrix} -0.2103 & -0.1303 & -0.2103 \\ -0.0548 & 0.0176 & -0.0548 \\ -0.0692 & 0.0223 & -0.0692 \\ -0.3144 & 0.1006 & -0.3144 \\ -0.0091 & 0.0030 & -0.0091 \end{bmatrix} \end{aligned}$$

are found independently, where \(\lambda _{\min }(P_{1})=7.0858\) and \(\lambda _{\min }(P_{2})=2.3232\). In this case, the parameters, \(\gamma =2.2937\), \(\lambda =0.3396\), \(\rho =5.2609\), \(\psi _{1}=2.3556\), and \(\psi _{2}=8.3808\) satisfy (24)–(27). Therefore, the separation principle holds for Problem 1.

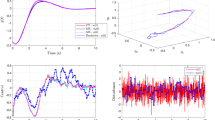
Figure 1 demonstrates the closed-loop time responses, where all the system state variables are nonnegative and well guided to be bounded over the entire simulation time horizon [0, 20] in the presence of parametric uncertainties and the \(\mathcal {L}_{2}\) disturbance. The disturbance attenuation performance is calculated as \(\frac{\left\| z\right\| _{\mathcal {L}_{\infty }}}{\left\| w\right\| _{\mathcal {L}_{2}}}=0.3824<\gamma\). Specifically, the third subfigure on the right depicts the \(\mathcal {L}_{2[0,t_{f}]}\) norm of the applied disturbance (dashed-red) and the \(\mathcal {L}_{\infty [0,t_{f}]}\) norm of the performance output multiplied by \(\gamma\) (solid-blue), where the proposed controller guarantees the disturbance attenuation performance in (4) for all \(t_{f}\). The last subfigure on the right depicts the event-triggering interval versus the event-triggering instant. In this subfigure, the discrete-time signal does not converge to zero, meaning that the proposed OBOF controller operates well in a sampled-data manner without the Zeno behavior affecting the sampling process.

Fig. 1
figure 1

Time response of a Leontief input–output model with uncertainties and disturbances

Full size image

6 Conclusions

We established a robust positive \(\mathcal {L}_{2}\)–\(\mathcal {L}_{\infty }\) disturbance attenuation scheme for uncertain LTI systems by using a sampled-data OBOF. The contributions of this paper are as follows: (i) The proposed controller enhances the likelihood of closed-loop positivity. (ii) The proposed controller guarantees positivity in the sampled-data closed loop free from the effect of Zeno behavior on the sampling process. (iii) The observer and controller can be designed separately in the presence of disturbance system uncertainties. The results of a numerical simulation involving an LTI model adopted from a pharmacokinetics study validated the effectiveness of the proposed technique.