1 Introduction

Dynamic systems in which a nonnegative initial condition excites the nonnegativity of their state are called positive systems. Positive systems have gathered considerable interest because many physical processes involve nonnegative quantities such as the level of liquids [1], population levels [14], and epidemic dynamics [6]. It is worth noting that positive stabilization requires that the closed-loop state is confined within the positive orthant cone rather than the whole state space. However, the state is not entirely measurable in various control processes [7, 8].

It is known that the observer and controller in the observer-based output-feedback (OBOF) framework are very difficult to design separately when the system possesses uncertainties [11]. The uncertain closed-loop system matrix is no longer triangular, and the separation principle is not directly identified from a matrix analysis viewpoint. A non-separate design often provokes a nonconvex optimization problem subject to bilinear matrix inequality (BMI) constraints [15]. Kheloufi et al. [5] recovered the convexity by applying Young’s inequality at the expense of a certain conservatism. Even for systems that do not include uncertainties, studies on the separate design of OBOF controllers aiming at disturbance attenuations are few. In one study, for example, the plant dynamics in an OBOF closed loop includes the estimation error, which hinders the separate design for disturbance attenuation problems [9].

Moreover, imposing closed-loop positivity via an output-feedback controller with a typical Luenberger observer is indeed challenging. This is because a single gain in a controller cannot force the upper-left and upper-right blocks in a closed-loop system matrix to be simultaneously positive, and similarly, a single gain in an observer cannot force the lower-left block in a closed-loop system matrix to be positive because the gain is not placed therein. The positivity of fuzzy observer-control systems was investigated in [3] by regarding the observer system matrix as a decision variable. However, the separation principle was not clearly discussed.

In this paper, we propose a separate OBOF controller design methodology for a discrete-time uncertain linear time-invariant (LTI) system to exhibit closed-loop positivity as well as attenuation performance against \(l_{\infty }\) disturbances and robustness against norm-bounded parametric uncertainties. The contributions of this study are as follows: (i) to ensure that the uncertain closed-loop plant is positive, a novel OBOF controller is used; (ii) to design the controller and observer separately, decoupled \(l_{\infty }\)–\(l_{\infty }\) disturbance attenuation performances are introduced; (iii) the design condition for the controller and observer is formulated as two independent convex optimization problems in terms of linear matrix inequalities (LMI) and linear matrix equalities (LME); (iv) a separation principle is explicitly revealed in the concerned problem. A numerical example of a dynamic Leontief input–output model of a multisector economy [13] demonstrates the efficacy of the proposed method.

Notation: The index set is defined as \({\mathcal {I}}_{N}:=\{1,\dots ,n\}\subset {\mathbb {N}}\). For matrices A and \(B\in {\mathbb {R}}^{n\times m}\), \((A)_{ij}\) denotes the entry of A located in the ith row and jth column. In addition, \(A\geqslant \geqslant B\) indicates that \((A-B)_{ij}\geqslant 0\), \((i,j)\in {\mathcal {I}}_{N}\times {\mathcal {I}}_{M}\). The relation \(P\succ Q\) indicates that the matrix \(P-Q\) is positive definite. The shorthands \({{\mathrm {He}}}\left\{ X\right\} :=X+X^{{\mathrm {T}}}\) and \(XY*:=XYX^{{\mathrm {T}}}\) are adopted, and the transposed element in the symmetric positions is denoted by \(*\). \(e_{l}\in {\mathbb {R}}^{n}\) denotes the lth standard unit vector. \(I_{n}\) denotes the identity matrix in \({\mathbb {R}}^{n\times n}\).

2 Positive Model

Consider the following uncertain discrete-time LTI model:

$$\begin{aligned} \left\{ \begin{aligned}&x_{j+1}= (A+\Delta A)x_{j}+Bu_{j}+B_{w}w_{j} \\&y_{j}=Cx_{j} \\&z_{j}=C_{z}x_{j} \end{aligned} \right. \end{aligned}$$
(1)

where \(x_{j}\in {\mathbb {R}}^{n}\) is the state, \(u_{j}\in {\mathbb {R}}^{m}\) is the input, \(w_{j}\in {\mathbb {R}}^{l}\) is the disturbance in \(l_{\infty }\), \(y_{j}\in {\mathbb {R}}^{p}\) is the measurement output, and \(z_{j}\in {\mathbb {R}}^{q}\) is the controlled output. \(\Delta A\) is the time-varying uncertaint matrix.

Definition 1

(positivity) Suppose \(u_{j}=0\), \(j\in {\mathbb {Z}}_{\geqslant 0}\) in (1). System (1) is positive for all \(x_{0}\geqslant \geqslant 0\) and \(w_{j}\geqslant \geqslant 0\) if \(x_{j}\geqslant \geqslant 0\) and \(y_{j}\geqslant \geqslant 0\) for all \(j\in {\mathbb {Z}}_{\geqslant 0}\).

Lemma 1

([1]) System (1) is positive if and only if \(A+\Delta A\geqslant \geqslant 0\), \(B_{w}\geqslant \geqslant 0\), and \(C\geqslant \geqslant 0\).

Lemma 2

Matrix \(A\in {\mathbb {R}}^{n\times n}\) is positive if and only if

$$\begin{aligned}&\sum _{l=1}^{n}\mathrm {diag}\left\{ e_{l}\right\} A \begin{bmatrix} 0 &{} 1 \\ I_{n-1} &{} 0 \end{bmatrix}^{k}\mathrm {diag}\left\{ e_{l}\right\} \succcurlyeq 0, \quad k\in {\mathcal {I}}_{N}. \end{aligned}$$
(2)

Proof

We define the operator that permutes the first column vector of A and the remaining \(n-1\) vectors as

$$\begin{aligned} T(A):{\mathbb {R}}^{n\times n}\rightarrow {\mathbb {R}}^{n\times n}:=A \begin{bmatrix} 0 &{} 1 \\ I_{n-1} &{} 0 \end{bmatrix}. \end{aligned}$$

The operator that eliminates the off-diagonal entries of A is defined as

$$\begin{aligned} U(A):{\mathbb {R}}^{n\times n}\rightarrow {\mathbb {R}}^{n\times n}:=\sum _{l=1}^{n}\mathrm {diag}\left\{ e_{l}\right\} A(\mathrm {diag}\left\{ e_{l}\right\} ). \end{aligned}$$

Thus, (2) is equivalent to

$$\begin{aligned}&U\circ \underbrace{T\circ \cdots \circ T}_{k}(A) \\&=\mathrm {diag}\left\{ (A)_{1(k+1)},\dots ,(A)_{(n-k)n},(A)_{(n-k+1)1},\dots ,(A)_{nk}\right\} \\&\succcurlyeq 0 \end{aligned}$$

implying \((A)_{ij}\geqslant 0\) for all \((i,j)\in {\mathcal {I}}_{N}\times {\mathcal {I}}_{N}\). \(\square\)

Assumption 1

Matrices \(B_{w}\) and C are positive.

Assumption 2

Matrix B is full column rank.

Assumption 3

There exist known compatible constant matrices D and E and an unknown time-varying matrix \(\Delta\) satisfying \(\Delta ^{{\mathrm {T}}}\Delta \preccurlyeq I\) for all \(j\in {\mathbb {Z}}_{\geqslant 0}\) such that \(\Delta A = D\Delta E\).

Remark 1

Through the appropriate column-row expansion of \(\Delta A\), one can construct \(\Delta\) as a diagonal matrix with \(\left| (\Delta )_{jj}\right| \leqslant 1\) and D and E as positive matrices without loss of generality. Then it follows that

$$\begin{aligned} -DE\leqslant \leqslant D\Delta E. \end{aligned}$$

Assumption 4

Only \(y_{j}\) is available for feedback.

Lemma 3

([12]) Given compatible matrices D, E, \(S=S^{{\mathrm {T}}}\), with \(\Delta \ni \Delta ^{{\mathrm {T}}}\Delta \preccurlyeq I\), there exists \(\epsilon \in {\mathbb {R}}_{>0}\) such that

$$\begin{aligned} S+{{\mathrm {He}}}\left\{ D\Delta E\right\} \prec 0 \iff S+\epsilon ^{-1}D^{{\mathrm {T}}}D+\epsilon EE^{{\mathrm {T}}}\prec 0. \end{aligned}$$

3 Positive \(l_{\infty }\)–\(l_{\infty }\) Disturbance Attenuation and Separation Principle

Considering Assumption 4, the following OBOF controller is adopted:

$$\begin{aligned} \left\{ \begin{aligned}&\hat{x}_{j+1}= A\hat{x}_{j}+Bu_{j}+L(y_{j}-\hat{y}_{j})+Hy_{j} \\&\hat{y}_{j}= C\hat{x}_{j} \\&u_{j}:=K\hat{x}_{j}+Fy_{j}. \end{aligned} \right. \end{aligned}$$
(3)

Define \(e_{j}:=x_{j}-\hat{x}_{j}\) and \(\xi _{j}:=(x_{j},e_{j})\). The closed-loop system is then constructed as

$$\begin{aligned} \xi _{j+1}= \begin{bmatrix} A+\Delta A+BK+BFC &{} -BK \\ \Delta A-HC &{} A-LC \end{bmatrix} \xi _{j}+ \begin{bmatrix} B_{w} \\ B_{w} \end{bmatrix}w_{j}. \end{aligned}$$
(4)

Remark 2

The \(\hat{x}_{j}\) dynamics in (3) has an additional correction through \(Hy_{j}\). By using this term for leverage, one can effectively preserve the positivity of the lower-left block of the closed-loop system matrix in (4). Otherwise, there is no remedy to guarantee the positivity of the \(e_{j}\) dynamics in the presence of uncertainties. This aspect has not been addressed in existing studies, for example, [10]. Similarly, the controller equation in (3) has an additional compensation through \(Fy_{j}\), which increases the possibility that the upper-left and upper-right blocks of the closed-loop system matrix in (4) are simultaneously positive.

We are interested in the following problem.

Problem 1

(\(l_{\infty }\)–\(l_{\infty }\)) Determine K, F, L, and H such that the uncertain LTI system (1) closed by the OBOF controller (3) is positive and robustly asymptotically stable against the norm-bounded parametric uncertainties when \(w_{j}=0\), \(j\in {\mathbb {Z}}_{\geqslant 0}\), and for some attenuation level \(\gamma \in {\mathbb {R}}_{>0}\), it exhibits the \(l_{\infty }\)–\(l_{\infty }\)-disturbance attenuation performance defined as

$$\begin{aligned} \Vert {z_{j}}\Vert _{\infty }\leqslant \gamma \Vert {w_{j}}\Vert _{\infty } \end{aligned}$$
(5)

when \(w_{j}\geqslant \geqslant 0\) and \(w_{j}\in l_{\infty }\).

Remark 3

The separate design of the OBOF controller subject to (5) is challenging. Even if we design the OBOF controller in an integrated way, the synthesis conditions often result in nonconvex BMIs, rather than convex LMIs. The main reason for this is that \(x_{j}\) appears in the \(e_{j}\) dynamics coupled with \(\Delta A\).

To resolve the difficulty mentioned in Remark 3, we regard \(x_{j}\) as a disturbance in the \(e_{j}\) dynamics and define the following \(l_{\infty }\)–\(l_{\infty }\) performance:

$$\begin{aligned} \Vert {e_{j}}\Vert _{\infty } \leqslant \mu _{2}\Vert {x_{j}}\Vert _{\infty }+\gamma _{2}\Vert {w_{j}}\Vert _{\infty } \end{aligned}$$
(6)

where \(\mu _{2}\) and \(\gamma _{2}\in {\mathbb {R}}_{>0}\). Similarly, we consider \(e_{j}\) in the \(x_{j}\) dynamics as a disturbance and introduce the following \(l_{\infty }\)–\(l_{\infty }\) performance:

$$\begin{aligned} \Vert {z_{j}}\Vert _{\infty } \leqslant \mu _{1}\Vert {e_{j}}\Vert _{\infty }+\gamma _{1}\Vert {w_{j}}\Vert _{\infty } \end{aligned}$$
(7)

where \(\mu _{1}\) and \(\gamma _{1}\in {\mathbb {R}}_{>0}\).

Now, we present the separate design condition for Problem 1 based on (7) and (6).

Theorem 1

Given \(\gamma _{1}\), \(\gamma _{2}\), \(\epsilon _{1}\), \(\epsilon _{2}\), \(\lambda _{1}\), \(\lambda _{2}\), \(\mu _{1}\), and \(\mu _{2}\in {\mathbb {R}}_{>0}\), the uncertain LTI system (1) closed by the OBOF controller (3) exhibits the \(\gamma\)-disturbance attenuation performance (5) with asymptotic stability and is positive if there exist M, diagonal \(P_{1}=P_{1}^{{\mathrm {T}}}\succ 0\) and \(P_{2}=P_{2}^{{\mathrm {T}}}\succ 0\), and W, X, Y, and Z, in addition to \(\rho _{1}\), \(\rho _{2}\), \(\phi _{1}\), and \(\phi _{2}\in {\mathbb {R}}_{>0}\) such that

$$\begin{aligned}&\begin{bmatrix} -P_{1} &{} * &{} * &{} * &{} * &{} * \\ (2,1) &{} -P_{1}+\lambda _{1}P_{1} &{} * &{} * &{} * &{} * \\ -X^{{\mathrm {T}}}B^{{\mathrm {T}}} &{} 0 &{} -\phi _{1}I &{} * &{} * &{} * \\ B_{w}^{{\mathrm {T}}}P_{1} &{} 0 &{} 0 &{} -\rho _{1}I &{} * &{} * \\ D^{{\mathrm {T}}}P_{1} &{} 0 &{} 0 &{} 0 &{} -\epsilon _{1} I &{} * \\ E &{} 0 &{} 0 &{} 0 &{} 0 &{} -\epsilon _{1}^{-1}I \end{bmatrix} \prec 0 \end{aligned}$$
(8)
$$\begin{aligned}&P_{1}B-BM=0 \end{aligned}$$
(9)
$$\begin{aligned}&\lambda _{1}P_{1}-\lambda _{\max }(C_{z}^{{\mathrm {T}}}C_{z})I\succ 0 \end{aligned}$$
(10)
$$\begin{aligned}&\mu _{1}^{2}-\phi _{1}\succ 0 \end{aligned}$$
(11)
$$\begin{aligned}&\gamma _{1}^{2}-\rho _{1}\succ 0 \end{aligned}$$
(12)
$$\begin{aligned}&\sum _{l=1}^{n}\mathrm {diag}\left\{ e_{l}\right\} (P_{1}A-P_{1}DE+BX+BYC) \begin{bmatrix} 0 & 1 \\ I_{n-1} & 0 \end{bmatrix}^{k}\nonumber \\ &\times \mathrm {diag}\left\{ e_{l}\right\} \succ 0 \end{aligned}$$
(13)
$$\begin{aligned}&\sum _{l=1}^{n}\mathrm {diag}\left\{ e_{l}\right\} BX \begin{bmatrix} 0 &{} 1 \\ I_{n-1} &{} 0 \end{bmatrix}^{k}\mathrm {diag}\left\{ e_{l}\right\} \prec 0, \quad k\in {\mathcal {I}}_{N} \end{aligned}$$
(14)
$$\begin{aligned}&\begin{bmatrix} \lambda _{\max }(C_{z}^{{\mathrm {T}}}C_{z}) &{} * \\ \phi _{1} &{} \frac{1}{4} \end{bmatrix} \succ 0 \end{aligned}$$
(15)
$$\begin{aligned}&\begin{bmatrix} -P_{2} &{} * &{} * &{} * &{} * &{} * \\ -C^{{\mathrm {T}}}W^{{\mathrm {T}}} &{} -\phi _{2}I &{} * &{} * &{} * &{} * \\ A^{{\mathrm {T}}}P_{2}-C^{{\mathrm {T}}}Z^{{\mathrm {T}}} &{} 0 &{} -P_{2}+\lambda _{2}P_{2} &{} * &{} * &{} * \\ B_{w}^{{\mathrm {T}}}P_{2} &{} 0 &{} 0 &{} -\rho _{2}I &{} * &{} * \\ D^{{\mathrm {T}}}P_{2} &{} 0 &{} 0 &{} 0 &{} -\epsilon _{2} I &{} * \\ E &{} 0 &{} 0 &{} 0 &{} 0 &{} -\epsilon _{2}^{-1}I \end{bmatrix} \prec 0 \end{aligned}$$
(16)
$$\begin{aligned}&\lambda _{2}P_{2}-I\succ 0 \end{aligned}$$
(17)
$$\begin{aligned}&\mu _{2}^{2}-\phi _{2}\succ 0 \end{aligned}$$
(18)
$$\begin{aligned}&\gamma _{2}^{2}-\rho _{2}\succ 0 \end{aligned}$$
(19)
$$\begin{aligned}&\sum _{l=1}^{n}\mathrm {diag}\left\{ e_{l}\right\} (P_{2}DE+WC) \begin{bmatrix} 0 &{} 1 \\ I_{n-1} &{} 0 \end{bmatrix}^{k}\mathrm {diag}\left\{ e_{l}\right\} \prec 0 \end{aligned}$$
(20)
$$\begin{aligned}&\sum _{l=1}^{n}\mathrm {diag}\left\{ e_{l}\right\} (P_{2}A-ZC) \begin{bmatrix} 0 &{} 1 \\ I_{n-1} &{} 0 \end{bmatrix}^{k}\mathrm {diag}\left\{ e_{l}\right\} \succ 0,\quad k\in {\mathcal {I}}_{N} \end{aligned}$$
(21)
$$\begin{aligned}&\begin{bmatrix} \lambda _{\max }(C_{z}^{{\mathrm {T}}}C_{z}) &{} * \\ \phi _{2} &{} \frac{1}{4} \end{bmatrix} \succ 0 \end{aligned}$$
(22)

where \((2,1):=A^{{\mathrm {T}}}P_{1}+X^{{\mathrm {T}}}B^{{\mathrm {T}}}+C^{{\mathrm {T}}}Y^{{\mathrm {T}}}B^{{\mathrm {T}}}\). In this case, the gains are given by \(K=M^{-1}X\), \(F=M^{-1}Y\), \(L=P_{2}^{-1}Z\), and \(H=P_{2}^{-1}W\).

Proof

Let \(V_{1}:=x_{j}^{{\mathrm {T}}}P_{1}x_{j}\) and \(\Delta V_{1}:=x_{j+1}^{{\mathrm {T}}}P_{1}x_{j+1}-x_{j}^{{\mathrm {T}}}P_{1}x_{j}\). We then calculate as

$$\begin{aligned} \Delta V_{1}&= \begin{bmatrix} \xi _{j} \\ w_{j} \end{bmatrix}^{{\mathrm {T}}} \bar{{\mathcal {M}}}*-\lambda _{1}V_{1}+\phi _{1}e_{j}^{{\mathrm {T}}}e_{j}+\rho _{1}w_{j}^{{\mathrm {T}}}w_{j} \end{aligned}$$

where

$$\begin{aligned} \bar{{\mathcal {M}}}&:= \begin{bmatrix} A+\Delta A+BK+BFC&-BK&B_{w} \end{bmatrix}^{{\mathrm {T}}} P_{1}* \\&\quad -\mathrm {diag}\left\{ (1-\lambda _{1})P_{1},\phi _{1}I,\rho _{1}I\right\} . \end{aligned}$$

By using the Schur complement, a congruence transformation, Assumption 3, Remark 1, and Lemma3, and denoting \(MK=:X\) and \(MF=:Y\), the following implication holds:

$$\begin{aligned} (8)~\text{and}~(9) \implies \bar{{\mathcal {M}}} \prec 0. \end{aligned}$$
(23)

Then, the comparison lemma leads to

$$\begin{aligned}&\Delta {V}_{1}+\lambda _{1} V_{1}-\phi _{1}e_{j}^{{\mathrm {T}}}e_{j}-\rho _{1} w_{j}^{{\mathrm {T}}}w_{j}<0 \\&\implies V_{1}\leqslant \frac{1-(1-\lambda _{1})^{j}}{\lambda _{1}} \left( \phi _{1}\Vert {e_{j}}\Vert _{\infty }^{2}+\rho _{1}\Vert {w_{j}}\Vert _{\infty }^{2} \right) . \end{aligned}$$

In addition, from (10)–(12), we can obtain the following inequality:

$$\begin{aligned}&\begin{bmatrix} \xi _{j} \\ w_{j} \end{bmatrix}^{{\mathrm {T}}} \left( \begin{bmatrix} \begin{bmatrix} \lambda _{1}P_{1} & * \\ 0 & (\mu _{1}^{2}-\phi _{1})I \end{bmatrix} & * \\ 0 & (\gamma _{1}^{2}-\rho _{1}) I \end{bmatrix} \right. \\ &\left. - \begin{bmatrix} \begin{bmatrix} C_{z}^{{\mathrm {T}}} \\ 0 \end{bmatrix} \\ 0 \end{bmatrix} I*\right) *>0 \\&\iff \lambda _{1}V_{1}+(\mu _{1}^{2}-\phi _{1})e_{j}^{{\mathrm {T}}}e_{j}+(\gamma _{1}^{2}-\rho _{1})w_{j}^{{\mathrm {T}}}w_{j}-z_{j}^{{\mathrm {T}}}z_{j} >0 \end{aligned}$$

and arrive at

$$\begin{aligned}&\lambda _{1} \left( \frac{1-(1-\lambda _{1})^{j}}{\lambda _{1}} \right) \left( \phi _{1}\Vert {e_{j}}\Vert _{\infty }^{2}+\rho _{1}\Vert {w_{j}}\Vert _{\infty }^{2} \right) \\&+(\mu _{1}^{2}-\phi _{1})\Vert {e_{j}}\Vert _{\infty }^{2}+(\gamma _{1}^{2}-\rho _{1})\Vert {w_{j}}\Vert _{\infty }^{2}> \Vert {z_{j}}\Vert ^{2} \\&\implies \mu _{1}^{2}\Vert {e_{j}}\Vert _{\infty }^{2}+\gamma _{1}^{2}\Vert {w_{j}}\Vert _{\infty }^{2}> \Vert {z_{j}}\Vert ^{2} \\&\implies \sqrt{(\mu _{1}\Vert {e_{j}}\Vert _{\infty }+\gamma _{1}\Vert {w_{j}}\Vert _{\infty })^{2}-2\mu _{1}\gamma _{1}\Vert {e_{j}}\Vert _{\infty }\Vert {w_{j}}\Vert _{\infty }} \\&\quad \quad > \Vert {z_{j}}\Vert _{\infty } \\&\implies (7). \end{aligned}$$

With Lyapunov function candidate \(V_{2}:=e_{j}^{{\mathrm {T}}}P_{2}e_{j}\) and

$$\begin{aligned} \Delta {V}_{2}&=\begin{bmatrix} \xi _{j} \\ w_{j} \end{bmatrix}^{{\mathrm {T}}} \bar{{\mathcal {N}}}*-\lambda _{2}V_{2}+\phi _{2}x_{j}^{{\mathrm {T}}}x_{j}+\rho _{2}w_{j}^{{\mathrm {T}}}w_{j} \end{aligned}$$

along the \(e_{j}\) dynamics in (4), we can derive that:

$$\begin{aligned} (16)&\implies \bar{{\mathcal {N}}} \prec 0 \end{aligned}$$
(24)

where

$$\begin{aligned} \bar{{\mathcal {N}}}&:=\begin{bmatrix} \Delta A-HC&A-LC&B_{w} \end{bmatrix}^{{\mathrm {T}}} P_{2}* \\&\quad -\mathrm {diag}\left\{ \phi _{2}I, (1-\lambda _{2})P_{2}, -\rho _{2}I\right\} . \end{aligned}$$

This implies

$$\begin{aligned}&\Delta {V}_{2}+\lambda _{2} V_{2}-\phi _{2}x_{j}^{{\mathrm {T}}}x_{j}-\rho _{2} w_{j}^{{\mathrm {T}}}w_{j} <0 \\&\implies \lambda _{2}\left( \frac{1-(1-\lambda _{2})^{j}}{\lambda _{2}} \right) \left( \phi _{2}\Vert {x_{j}}\Vert _{\infty }^{2}+\rho _{2}\Vert {w_{j}}\Vert _{\infty }^{2} \right) \\&\quad \quad +(\mu _{2}^{2}-\phi _{2})\Vert {x_{j}}\Vert _{\infty }^{2}+(\gamma _{2}^{2}-\rho _{2})\Vert {w_{j}}\Vert _{\infty }^{2} >\Vert {e_{j}}\Vert ^{2} \\&\implies (6) \end{aligned}$$

under (17)–(18), equivalently,

$$\begin{aligned} \lambda _{2}V_{2}+(\mu _{2}^{2}-\phi _{2})x_{j}^{{\mathrm {T}}}x_{j}+(\gamma _{2}^{2}-\rho _{2})w_{j}^{{\mathrm {T}}}w_{j}-e_{j}^{{\mathrm {T}}}e_{j} > 0. \end{aligned}$$

Next, we demonstrate the closed-loop positivity. By Assumption 3, Remark 1, and Lemma 2,

$$\begin{aligned} (13)&\implies P_{1}(A-DE+BK+BFC) \geqslant \geqslant 0 \\&\implies A+\Delta A+BK+BFC \geqslant \geqslant 0 \end{aligned}$$

because \(P_{1}\succ 0\) is diagonal. Similarly, (20) \(\implies A-LC\geqslant \geqslant 0\), (14) \(\implies -BK\geqslant \geqslant 0\), and (21) \(\Delta A-HC\geqslant \geqslant 0\). According to Assumption 1, and Lemma 1, this guarantees that \(x_{j}\) in (4) is positive.

Finally, we prove the separation principle. To this end, we show that there exist \(\gamma ,\lambda\), and \(\rho \in {\mathbb {R}}_{>0}\) for some \(\psi _{1}\) and \(\psi _{2}\in {\mathbb {R}}_{>0}\) such that the following two inequalities for \(V:=\psi _{1} V_{1}+\psi _{2} V_{2}\) along the closed-loop trajectory of (4) with K, F, L, and H designed above hold:

$$\begin{aligned}&\Delta {V}+\lambda V-\rho w_{j}^{{\mathrm {T}}}w_{j}= \begin{bmatrix} \xi _{j} \\ w_{j} \end{bmatrix}^{{\mathrm {T}}} \bar{{\mathcal {O}}} \begin{bmatrix} \xi _{j} \\ w_{j} \end{bmatrix} <0 \\&\lambda V+(\gamma ^{2}-\rho )w_{j}^{{\mathrm {T}}}w_{j}-z_{j}^{{\mathrm {T}}}z_{j} \nonumber \\&= \begin{bmatrix} \xi _{j} \\ w_{j} \end{bmatrix}^{{\mathrm {T}}} \begin{bmatrix} \mathrm {diag}\left\{ \lambda \psi _{1} P_{1}-C_{z}^{{\mathrm {T}}}C_{z}, \lambda \psi _{2} P_{2}\right\} &{} * \\ 0 &{} (\gamma ^{2}-\rho ) I \end{bmatrix}* \nonumber \\&>0 \nonumber \end{aligned}$$
(25)

where

$$\begin{aligned} \bar{{\mathcal {O}}}&:=\psi _{1}\bar{{\mathcal {M}}}+\psi _{2}\bar{{\mathcal {N}}} +\mathrm {diag}\left\{ \psi _{2}\phi _{2} I-\psi _{1}\lambda _{1}P_{1}+\lambda \psi _{1} P_{1}, \right. \\&\quad \left. \psi _{1}\phi _{1} I-\psi _{2}\lambda _{2}P_{2}+\lambda \psi _{2} P_{2}, (\psi _{1}\rho _{1}+\psi _{2}\rho _{2}-\rho )I\right\} . \end{aligned}$$

Considering (23) and (24), it suffices to show that

$$\begin{aligned} \begin{aligned}&\psi _{2}\phi _{2}-\psi _{1}(\lambda _{1}-\lambda )\lambda _{\min }(P_{1})<0 \\&\psi _{1}\phi _{1}-\psi _{2}(\lambda _{2}-\lambda )\lambda _{\min }(P_{2})<0, \quad \psi _{1}\rho _{1}+\psi _{2}\rho _{2}-\rho <0 \\&\lambda \psi _{1}\lambda _{\min }(P_{1})-\lambda _{\max }(C_{z}^{{\mathrm {T}}}C_{z})>0, \quad \gamma ^{2}-\rho >0. \end{aligned} \end{aligned}$$
(26)

The first two inequalities in (26) hold if and only if there exist \(\psi _{1},\psi _{2}\), and \(\lambda \in {\mathbb {R}}_{>0}\) such that

$$\begin{aligned} 0<\frac{\phi _{1}}{\lambda _{\min }(P_{2})(\lambda _{2}-\lambda )}<\frac{\psi _{2}}{\psi _{1}} <\frac{\lambda _{\min }(P_{1})(\lambda _{1}-\lambda )}{\phi _{2}} \end{aligned}$$
(27)

and equivalently, there exists \(\lambda \in {\mathbb {R}}_{[0,\lambda _{1}]}\) such that

$$\begin{aligned} f(\lambda ) :=\lambda ^{2}-(\lambda _{1}+\lambda _{2})\lambda +\lambda _{1}\lambda _{2} -\frac{\phi _{1}\phi _{2}}{\lambda _{\min }(P_{1})\lambda _{\min }(P_{2})} >0 \end{aligned}$$

assuming \(\lambda _{1}<\lambda _{2}\) without loss of generality. It follows that

$$\begin{aligned} f(\lambda _{1}) =-\frac{\phi _{1}\phi _{2}}{\lambda _{\min }(P_{1})\lambda _{\min }(P_{2})} <0. \end{aligned}$$

In addition, according to (10) and (17)

$$\begin{aligned} (15)~\text{and}~(22)&\implies \lambda _{\max }(C_{z}^{{\mathrm {T}}}C_{z})-4\phi _{1}\phi _{2}>0 \\&\iff \frac{\lambda _{1}\lambda _{2}\lambda _{\max }(C_{z}^{{\mathrm {T}}}C_{z})}{\lambda _{1}\lambda _{2}}-4\phi _{1}\phi _{2}>0 \\&\implies \lambda _{1}\lambda _{2}\lambda _{\min }(P_{1})\lambda _{\min }(P_{2})-4\phi _{1}\phi _{2}>0 \\&\iff f(0) =\lambda _{1}\lambda _{2}-\frac{4\phi _{1}\phi _{2}}{\lambda _{\min }(P_{1})\lambda _{\min }(P_{2})} >0. \end{aligned}$$

This implies that there exist a \(\lambda \in (0,\lambda _{1})\) and a set of all pairs of \((\psi _{1},\psi _{2})\) that meet (27). Within this set, the pair \((\psi _{1},\psi _{2})\ni \psi _{1}:=\frac{\lambda _{1}}{\lambda }\) satisfies the fourth inequality in (26) through (10). It is simple to determine \(\rho\) and \(\gamma\) such that the third and fifth inequalities in (26) are true. When \(w_{j}=0\), \(j\in {\mathbb {Z}}_{\geqslant 0}\), (25) can be expressed as \(\Delta V+\lambda V<0 \implies \Delta V<0\). Therefore, (4) exhibits the \(\gamma\)-disturbance attenuation performance (5) and is robustly asymptotically stable. In (9), Assumption 2 implies M is full rank, and thus invertible. \(\square\)

Remark 4

The compensation through \(Fy_{j}\) in the controller equation of (3) to relax the positivity constraint is designed using the convexification technique in [2]. This scheme also linearizes the bilinear term \(BKP_{1}\) without Young’s inequality [5], serving two ends.

Remark 5

The proposed design condition in Theorem 1 can be solved by using the semidefinite programming or by simply changing (9) into the following LMI

$$\begin{aligned} \begin{bmatrix} -\alpha I &{} * \\ P_{1}B-BM &{} -\alpha I \end{bmatrix} \prec 0 \end{aligned}$$

with a very small \(\alpha \in {\mathbb {R}}_{>0}\), to use the LMI Solvers in MATLAB.

Remark 6

The proposed technique can be applied to real-world research areas such as economic cybernetics. Although the Leontief input–output model is quite efficient to this end, its dynamic behavior needs to imitate the real economic nature like the positivity [4].

4 An Example

A dynamic Leontief input–output model of a multisector economy is described as

$$\begin{aligned} \bar{x}_{j}= L\bar{x}_{j}+V(\bar{x}_{j+1}-\bar{x}_{j})+\bar{u}_{j} \end{aligned}$$
(28)

where \(\bar{x}_{j}\) is the vector of the output levels and \(\bar{u}_{j}\) is the final demand excluding investments. By slightly abusing notations, L and V denote the Leontief input–output matrix satisfying \((I-L)^{-1}\geqslant \geqslant 0\) [4] and the capital coefficient matrix, respectively. Their numerical data

$$\begin{aligned} L=\begin{bmatrix} 0.6 &{} 0.1 &{} 0.1 \\ 0.1 &{} 0.5 &{} 0.2 \\ 0.1 &{} 0.2 &{} 0.4 \end{bmatrix}, \quad V= \begin{bmatrix} 0.1 &{} 0.3 &{} 0.8 \\ 0.5 &{} 0.1 &{} 0.9 \\ 0.8 &{} 0.5 &{} 0.7 \end{bmatrix} \end{aligned}$$

are borrowed from [13]. Let \(A:=I+V^{-1}(I-L)\) and \(B:=V^{-1}\). The minimum demand vector \(r\geqslant \geqslant 0\) is given. The corresponding minimum vector of the output levels is calculated by \(\bar{x}=(I-A)^{-1}Br\geqslant \geqslant 0\). We define \(x_{j}:=\bar{x}_{j}-\bar{x}\). Then, the Leontief input–output model in (28) is equivalently cast into the form of (1), which is absent from uncertainties and disturbances, which is required to be positive because \(\bar{x}_{j}\) should be not less than \(\bar{x}\).

Fig. 1
figure 1

Time response of a Leontief input–output model without uncertainties nor disturbances by the conventional Luenberger OBOF controller

Full size image

Validation is performed through a comparison with the following conventional Luenberger OBOF controller:

$$\begin{aligned} \left\{ \begin{aligned}&\hat{x}_{j+1} =A\hat{x}_{j}+Bu_{j}+L(y_{j}-\hat{y}_{j}) \\&\hat{y}_{j} =C\hat{x}_{j} \\&u_{j} :=K\hat{x}_{j} \end{aligned} \right. \end{aligned}$$

where

$$\begin{aligned} C:=\begin{bmatrix} 1 &{} 1 &{} 0 \\ 0 &{} 1 &{} 1 \end{bmatrix}. \end{aligned}$$

The gain matrices, \(K:=XP_{1}^{-1}\) and \(L:=P_{2}^{-1}Z\) that asymptotically stabilize the equivalent Leontief input–output model are obtained as

$$\begin{aligned} K=\begin{bmatrix} 0.5 &{} 0.2 &{} 0.7 \\ 0.4 &{} 0.6 &{} 0.7 \\ 0.7 &{} 0.3 &{} 1.3 \end{bmatrix}, \quad L=\begin{bmatrix} 0.011 &{} 0.465 \\ -0.512 &{} -0.107 \\ 0.245 &{} 0.278 \end{bmatrix} \end{aligned}$$

by solving

$$\begin{aligned} \begin{bmatrix} -P_{1} &{} * \\ AP+BX &{} -P_{1} \end{bmatrix} \prec 0, \quad \begin{bmatrix} -P_{2} &{} * \\ A^{{\mathrm {T}}}P_{2}-C^{{\mathrm {T}}}Z^{{\mathrm {T}}} &{} -P_{2} \end{bmatrix} \prec 0 \end{aligned}$$

where \(P_{1}\succ 0\) and \(P_{2}\succ 0\). Fig. 1 represents the simulation results with \(x_{0}=(0.2,0.2,0.2)\) and \(\hat{x}_{0}=(0.1,0.1,0.1)\). For \(j\in [0,5]\), the closed-loop state is not positive, even if neither uncertainties nor disturbances are implemented. This phenomenon occurs because the foregoing design condition does not guarantee the positivity of the closed-loop Leontief input–output model. In particular, the computed K and L fails in positifying \(A+BK\), \(-BK\), and \(A-LC\), although they are designed separately.

To highlight the advantage of our method, we introduce

$$\begin{aligned} \Delta A= \begin{bmatrix} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0.09\delta \\ 0 &{} 0 &{} 0 \end{bmatrix}, \quad B_{w}= \begin{bmatrix} 0 \\ 0.0015 \end{bmatrix}, \quad C_{z}= \begin{bmatrix} 0.1 \\ 0.1 \\ 0.1 \end{bmatrix}^{{\mathrm {T}}} \end{aligned}$$

where \(\delta \ni \left| \delta \right| \leqslant 1\) randomly varies in time. The \(l_{\infty }\) disturbance is defined as \(w_{j} := 0.2\cos j+0.2, j \in {\mathbb {Z}}_{\geqslant 0}\). To resolve the difficulty in the validation example, the additional feedback gain, F is introduced to increase the possibility that \(A+\Delta A+BK+BFC\) and \(-BK\) are positive. Moreover, the additional correction gain, H is introduced to ensure that \(\Delta A-HC\) is positive. Let \(\gamma _{1}=\mu _{1}=\gamma _{2}=\mu _{2}=0.6\). According to Assumption 3, \(\Delta A\) is factorized as

$$\begin{aligned} D=\begin{bmatrix} 0&0.3&0 \end{bmatrix}^{{\mathrm {T}}}, \quad \Delta =\delta , \quad E =\begin{bmatrix} 0&0&0.3 \end{bmatrix}. \end{aligned}$$

By solving Theorem 1, the controller gain matrices

$$\begin{aligned} K=\begin{bmatrix} 0.018 &{} 0.016 &{} 0.018 \\ 0.014 &{} 0.013 &{} 0.014 \\ 0.030 &{} 0.026 &{} 0.030 \end{bmatrix}, \quad F=\begin{bmatrix} 0.010 &{} 0.148 \\ 0.148 &{} 0.422 \\ -0.133 &{} 0.363 \end{bmatrix} \end{aligned}$$

and the observer gain matrices

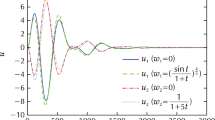
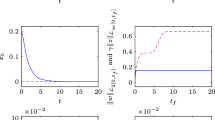
$$\begin{aligned} L=\begin{bmatrix} 0.035 &{} 0.114 \\ 0.820 &{} -1.698 \\ 0.300 &{} 0.209 \end{bmatrix}, \quad H=\begin{bmatrix} -0.096 &{} -0.010 \\ -0.002 &{} -0.003 \\ -0.000 &{} -0.000 \end{bmatrix} \end{aligned}$$

are independently searched. The parameters \(\gamma =1.552, \lambda = 0.378, \rho = 2.410, \psi _{1} = 2.118\), and \(\psi _{2} = 7.793\) with \(\lambda _{\min }(P_{1})=1.369\) and \(\lambda _{\min }(P_{2})=2.078\) satisfy (26), proving the closed-loop stability. This result indicates that the separation principle is established for Problem 1. The closed-loop time responses are shown in Fig. 2. Unlike in the results of the compared method, our results demonstrate that the state is positive and well guided to zero in the presence of parametric uncertainties. As shown in the lower-right subfigure, the proposed controller satisfies the \(l_{\infty }\)–\(l_{\infty }\) disturbance attenuation performance in (5). The specific evaluated value is \(\frac{\Vert {z_{j}}\Vert _{\infty }}{\Vert {w_{j}}\Vert _{\infty }}=0.171<\gamma\) (\(=1.552\)).

Fig. 2
figure 2

Time response of a Leontief input–output model with uncertainties and disturbances

Full size image

5 Conclusions

We present a robust positive OBOF \(l_{\infty }\)–\(l_{\infty }\) disturbance attenuation technique for uncertain LTI systems. The design condition is formulated as a convex optimization problem in terms of LMIs and an LME. Another contribution of this paper is that the separation principle for the concerned design problem is established. The numerical simulation demonstrates that the proposed methodology is successfully applied to the Leontief input–output model.