1 Introduction

As well known, a variety of control problems is concerned with partial cancelation of the dynamics which is achieved by inducing unobservability [1,2,3,4,5,6,7,8]. In the linear case, this is achieved by designing a feedback that assigns the eigenvalues coincident with the zeros of the system so making the corresponding dynamics unobservable. Such an approach is at the basis of feedback linearization which is achieved by maximizing unobservability, that is by canceling the so-called zero dynamics whose stability is thus necessary for guaranteeing feasibility of the control system [9].

In [10], the problem of partial cancelation of the zero dynamics has been introduced and exploited to deal with feedback linearization of nonlinear non-minimum-phase systems (i.e., whose zero dynamics are unstable). The design approach generalizes to the nonlinear context the idea of assigning part of the eigenvalues over part of the zeros of the transfer function of a linear system (partial zero-pole cancelation). As the intuition suggests, when dealing with nonlinear systems, stability of the feedback system can be achieved when only a stable component of the zero dynamics is canceled. Such a stable component can be identified by considering the output associated with the minimum-phase factorization of the transfer function of the linear tangent model at the origin. More in details, a two-step design is proposed: considering the linear tangent model (LTM) of the original system, a dummy output is first constructed via a suitable factorization of the numerator of its transfer function so that the corresponding linearized system is minimum phase; then, classical input–output linearization of the locally minimum-phase nonlinear system is performed with respect to the aforementioned dummy output. Finally, it is proved that when applying the resulting feedback to the original system, input–output linearization still holds with respect to the actual output while guaranteeing stability of the internal dynamics.

In this work, we extend the proposed methodology to the problem of output-disturbance decoupling with internal stability. The problem of decoupling, attenuating or rejecting the effect of the perturbations acting over a nonlinear plant is of paramount importance from both practical and methodological points of view [11,12,13,14,15,16,17,18]. As well known, given a general plant disturbance decoupling is related to generating unobservability so to make the output evolutions independent upon the perturbations acting over the dynamics [19,20,21,22,23]. Starting from the linear time-invariant (LTI) case, the idea we develop makes use of the output factorization introduced in [10] so allowing to: (i) solve the disturbance-decoupling problem for a given action of disturbances while preserving internal stability; (ii) characterize all the actions of disturbances for which disturbance decoupling is solvable while preserving internal stability. As expected, the family of disturbances which can be decoupled in this case is smaller than in the standard one (when canceling out all the zero dynamics). At the best of the authors knowledge, necessary and sufficient conditions for characterizing all the actions of disturbances which can be decoupled from the output while preserving stability are not available. An exception to this is provided by [24], where the problem is solved for classes of nonlinear systems admitting a strict-feedback structure.

The proposed methodology is then applied to the sampled-data context that is when measures of the output (say the state) are available only at some time instants and the control is piecewise constant over the sampling period [25, 26]. In this context, the problem under study is even more crucial because of the further unstable zero dynamics intrinsically arising due to sampling [27]. As a consequence, the minimum-phase property of a given nonlinear continuous-time system is not preserved by its sampled-data equivalent [28,29,30,31]. To overcome those issues, several solutions were proposed based on different sampling procedures [32,33,34,35,36]. Among these, the first one was based on multi-rate sampling in which the control signal is sampled-faster (say r times) than the measured variables. Accordingly, this sampling procedure introduces further degrees of freedom and prevents from the appearance of the unstable sampling zero dynamics while preserving the continuous-time relative degree [28, 37].

In the sampled-data framework, we shall show how multi-rate sampling can be suitable exploited to solve the problem of characterizing all disturbances whose effect can be decoupled by feedback at any sampling instants. In this context, we shall see how sampling induces a more conservative design which requires the disturbance to be measurable and piecewise constant over the sampling period. Related works in the sampled-data and linear contexts have been carried out in [38, 39] under the minimum-phaseness assumptions.

The paper is organized as follows. the classical disturbance-decoupling problem is recalled in Sect. 2 while the problem is settled in Sect. 3. The underlying idea of the proposed approach is discussed in Sect. 4. The solution to the problem for LTI systems is provided in Sect. 5, and the main result is stated in Sect. 6. The case of sampled-data systems is discussed and detailed in Sect. 7 while a simulated example over the TORA system is in Sect. 8. Section 9 concludes the paper with some highlights on future perspectives and current work.

Notations and definitions: All the functions and vector fields defining the dynamics are assumed smooth and complete over the respective definition spaces. \(M_U\) (resp. \(M_U^I\)) denotes the space of measurable and locally bounded functions \(u: \mathbb {R} \rightarrow U\) (\(u: I \rightarrow U\), \(I \subset \mathbb {R}\)) with \(U \subseteq \mathbb {R}\). \(\mathcal {U}_\delta \subseteq M_U\) denotes the set of piecewise constant functions over time intervals of fixed length \(\delta \in ]0, T^*[\); i.e. \(\mathcal {U}_\delta = \{ u \in M_U\ \text {s.t.} \ u(t) = u_k, \forall t \in [k\delta , (k+1)\delta [; k \ge 0\}\). Given a vector field f, \(\mathrm {L}_f\) denotes the Lie derivative operator, \(\mathrm {L}_f = \sum _{i= 1}^n f_i(\cdot )\nabla _{x_i}\) with \(\nabla _{x_i} := \frac{\partial }{\partial x_i}\) while \(\nabla = (\nabla _{x_1}, \dots , \nabla _{x_n})\). Given two vector fields f and g, \(ad_f g = [f, g]\) and iteratively \(ad_{f}^i g = [f, ad_f^{i-1}g]\). The Lie exponent operator is denoted as \(e^{\mathrm {L}_f}\) and defined as \(e^{\mathrm {L}_f}:= \text {Id} + \sum _{i \ge 1}\frac{\mathrm {L}_f^i}{i!}\). A function \(R(x,\delta )= O(\delta ^p)\) is said to be of order \(\delta ^p\) (\(p \ge 1\)) if whenever it is defined it can be written as \(R(x, \delta ) = \delta ^{p-1}\tilde{R}(x, \delta )\) and there exist function \(\theta \in \mathcal {K}_{\infty }\) and \(\delta ^* >0\) such that \(\forall \delta \le \delta ^*\), \(| \tilde{R} (x, \delta )| \le \theta (\delta )\). We shall denote a ball centered at \(x_0 \in \mathbb {R}^n\) and of radius \(\epsilon > 0\) as \(B_\epsilon (x_0)\).

2 Classical DDP for linear and nonlinear systems

In the sequel, we investigate the problem of characterizing the perturbations which can be decoupled under feedback for a given plant of the form

$$\begin{aligned} \dot{x}&= f(x)+g(x)u + p(x) w \end{aligned}$$
(1a)
$$\begin{aligned} y&=Cx \end{aligned}$$
(1b)

with \(x \in \mathbb {R}^n, u \in \mathbb {R}, y \in \mathbb {R}\) and \(w\in \mathbb {R}\) being an external disturbance. We shall refer to such a problem as disturbance decouplability problem (DDP) as a standard revisitation of classical disturbance decoupling.

Consider at first the case of a LTI system of the form

$$\begin{aligned} \dot{x}&= A x + B u + P w \end{aligned}$$
(2a)
$$\begin{aligned} y&= Cx \end{aligned}$$
(2b)

where P defines a family of disturbance actions acting over. The following result concerning DDP for LTI systems is revisited here from [19].

Proposition 1

([19]) Let the system (2) be controllable and possess relative degree \(r\le n\). The disturbance decoupling is solvable for all actions of disturbances such that P verifies the following inclusion

$$\begin{aligned} \text {Im} P \subseteq V^* \end{aligned}$$
(3)

with \(V^*\) being the maximal (A,B)-invariant distribution contained in \(\ker C\) and given by

$$\begin{aligned} V^* = \ker \begin{pmatrix} C \\ CA \\ \vdots \\ CA^{r-1} \end{pmatrix}. \end{aligned}$$
(4)

The feedback ensuring output-disturbance decoupling is given by

$$\begin{aligned} u = \frac{v - CA^r x}{CA^{r-1}B}. \end{aligned}$$
(5)

Whenever P satisfies (3), the feedback solving DDP gets the form (5) which, by construction, makes the closed-loop dynamics maximally unobservable. To see this, introduce the coordinate transformation

$$\begin{aligned} \begin{pmatrix} \zeta \\ \eta \end{pmatrix} = \begin{pmatrix} C \\ CA \\ \vdots \\ CA^{r-1} \\ T_2 \end{pmatrix} x \end{aligned}$$

with \(T_2\) such that \(T_2 B = 0\), putting the closed-loop system in the so-called normal form as

$$\begin{aligned} \dot{\zeta }&= \hat{A} \zeta + \hat{B} v \end{aligned}$$
(6a)
$$\begin{aligned} \dot{\eta }&= Q \eta +R \zeta + \hat{P} w \end{aligned}$$
(6b)
$$\begin{aligned} y&= \hat{C} \zeta \end{aligned}$$
(6c)

with \((\hat{A}, \hat{B})\) being in Brunowski form and \(\hat{C} = (1\ \mathbf {0})\). Accordingly, (6b) corresponds to the component of the system which is made unobservable under feedback coinciding with the zero dynamics as \(w \equiv 0\). It turns out that because \(\sigma (Q)\) coincides with the zeros of (2), stability in closed loop is guaranteed if, and only if, (2) is minimum phase (i.e., \(\sigma (Q)\subset \mathbb {C}^-\)). If this is not the case, the control law (5) is generating unstability of the feedback system. Still, even if necessary and sufficient for the solvability of DDP (regardless of stability), condition (3) is also conservative as it is based on the idea of generating maximal unobservability by canceling all zeros of (2) and making \(V^*\) feedback invariant.

In the nonlinear context, similar arguments hold true. From now on, when dealing with nonlinear systems, all properties are meant to hold locally unless explicitly specified. Assuming that (1) has relative degree \(r\le n\) at the origin (or, for the sake of brevity, relative degreer) that is

$$\begin{aligned}&\hbox {L}_g \hbox {L}_f^i h(x) = 0 \quad \text { for all } i \in [0, r-2] \text { and } x \in B_\epsilon (0) \\&\hbox {L}_g \hbox {L}_f^{r-1} h(0) \ne 0. \end{aligned}$$

with \(h(x) = Cx\), existence of a solution to the DDP is recalled from [9, Proposition 4.6.1].

Proposition 2

([9]) Suppose the system (1) has relative degree \(r \le n\). DDP is solvable for all \(p: \mathbb {R}^n \rightarrow \mathbb {R}^n\) verifying

$$\begin{aligned} \hbox {L}_p \hbox {L}_f^i h(x) = 0 \quad \text { for all } i \in [0, r-1] \text { and } x \in B_\epsilon (0). \end{aligned}$$

In this case, then the DDP feedback is given by

$$\begin{aligned} u = \frac{v - \hbox {L}_f^r h(x)}{\hbox {L}_g \hbox {L}_f^{r-1} h(x)}. \end{aligned}$$
(7)

Remark 1

Along the lines of the linear case, the result above can be interpreted in a differential-geometry fashion by stating that DDP is solvable for all the actions of disturbances verifying the following relation

$$\begin{aligned} \text {Im}p(x) \subseteq \varDelta ^*(x) \end{aligned}$$

with

$$\begin{aligned} \varDelta ^*(x) = \ker \begin{pmatrix} \mathrm {d}h(x)\\ \mathrm {d}\hbox {L}_f h(x) \\ \dots \\ \mathrm {d}\hbox {L}_f^{r-1} h(x) \end{pmatrix} \end{aligned}$$
(8)

being the maximal involutive distribution which is invariant under (1) and contained in \(\ker \mathrm {d} h(x)\).

Whenever DDP is solvable, one deduces the normal form associated to (1) by introducing

$$\begin{aligned} \begin{pmatrix} \zeta \\ \eta \end{pmatrix} = \begin{pmatrix} \mathrm {d}h(x)\\ \mathrm {d}\hbox {L}_f h(x) \\ \dots \\ \mathrm {d}\hbox {L}_f^{r-1} h(x) \\ \phi _2(x) \end{pmatrix} \end{aligned}$$

with \(\phi _2(x)\) such that \(\nabla \phi _2(x) g(x) = 0\). In the new coordinates and under the feedback (7), (1) rewrites as

$$\begin{aligned} \dot{\zeta }&= \hat{A} \zeta + \hat{B} v \end{aligned}$$
(9a)
$$\begin{aligned} \dot{\eta }&= q(\zeta ,\eta ) + \hat{p}(\zeta ,\eta )w \end{aligned}$$
(9b)
$$\begin{aligned} y&= \hat{C} \zeta \end{aligned}$$
(9c)

with \(C = ( 1 \ \mathbf {0})\) and (9b) being the dynamics that is made unobservable under feedback coinciding, when \(\zeta \equiv 0\), with the zero dynamics. Thus, it turns out that a necessary condition for DDP with stability to be solved by (7) is that the zero dynamics are asymptotically stable. If this is not the case, independently of the disturbance, the aforementioned feedback generates unstability by inverting the unstable component of the dynamics so preventing to fulfill design specifications such as output regulations or tracking with boundedness (or input-to-state stability) of the residual internal dynamics.

To summarize, although necessary and sufficient conditions are available for solving DDP, they do not keep into account stability in both the linear and nonlinear settings as generally based on generating maximal unobservability via the cancelation of the zero dynamics. In what follows, we shall present new conditions allowing to state solvability of the disturbance-decoupling problem for linear and nonlinear dynamics while guaranteeing stability.

3 Problem settlement

We consider nonlinear input-affine dynamics with linear output map of the form (1) under the following standing assumptions:

  1. 1.

    when \(w = 0\), the dynamics (1a) is feedback linearizable [9, Theorem 4.2.3];

  2. 2.

    the system (1) has relative degree \(r \le n\) and is partially minimum phase in the sense of the following definition.

Definition 1

Consider a non-minimum-phase nonlinear system (1) with LTM model at the origin (2) whose zeros are the roots of a not Hurwitz polynomial N(s); we say that (1) is partially minimum phase if there exists a factorization of \(N(s) = N_1(s) N_2(s)\) so that \(N_2(s)\) is Hurwitz.

The linear tangent model (LTM) at the origin associated to (1) is of the form (2) and is controllable because (1a) is assumed feedback linearizable. Without loss of generality, we assume (2) exhibits the controllable canonical form that is

$$\begin{aligned} A&=\nabla f(0) =\begin{pmatrix} \mathbf {0} &{} &{}I_{r-1}\\ &{} -\mathbf {a} &{} \end{pmatrix}, \ B = g(0)= \begin{pmatrix} \mathbf {0} \\ 1 \end{pmatrix} \nonumber \\ C&=\begin{pmatrix} b_0&\dots&b_{m}&\mathbf {0} \end{pmatrix}, \quad P = p(0) \end{aligned}$$
(10)

with \(\mathbf {a} = (a_0 \ \dots \ a_{n-1})\) being a row vector containing the coefficients of the associated characteristic polynomial and possessing relative degree coinciding, at least locally, with r.

Remark 2

If (A, B, C) is not in the canonical controllable form (10), one preliminarily applies to (1) the linear transformation

$$\begin{aligned} \xi = T x, \quad T = \begin{pmatrix} \gamma ^{\top }&(\gamma A)^{\top }&\dots (\gamma A^{n-1})^{\top } \end{pmatrix}^{\top } \end{aligned}$$

with \(\gamma = \begin{pmatrix} \mathbf {0}&1 \end{pmatrix} \begin{pmatrix} B&A B&\dots A^{n-1}B \end{pmatrix}^{-1}\) so transforming the system into the required form.

In this setting, one looks for all disturbances which can be input–output decoupled under feedback while preserving stability of (1); namely, given the triplet (f, g, h), we shall characterize the class of disturbances that can be output decoupled under feedback while guaranteeing stability of the internal dynamics. In other words, we shall seek for the maximal subspace of (1) which can be made unobservable under feedback and over which all suitably characterized disturbances can be constrained to act. From now on, we shall refer to such a problem as the Disturbance Decouplability Problem with Stability (DDP-S).

First, the underlying idea of the approach we propose is recalled from [10] in the LTI case. Then, the result is stated for linear time-invariant and nonlinear systems.

4 Partial zero-dynamics cancelation

Let us start discussing how partial cancelation of the zero dynamics can be used to assign the dynamics under feedback. To this end, let (2) be the LTM at the origin of (1) when \(p(\cdot ) \equiv 0\). Since (A, B) is controllable, the transfer function of the system is provided by

$$\begin{aligned} W(s)=C(sI-A)^{-1}B= \frac{N(s)}{D(s)} \end{aligned}$$

with \(N(s) = b_0 + b_1 s + \dots + b_{m} s^m\) and \( D(s) = a_0 + a_1 s + \dots + a_{n-1}s^{n-1} + s^n\) and relative degree \(\hat{r} = n-m\).

Given any factorization of the numerator \(N(s) = N_1(s)N_2(s)\) and fixed D(s), the dummy output \(y_i = C_i x\) with \(C_i = (b_0^i \dots b_{m_i}^i \ \mathbf {0})\) corresponds to the transfer function having

$$\begin{aligned} N_i(s):= b_0^{i} +b_1^{i}s+\dots +b_{m_i}^{i}s^{m_i} \end{aligned}$$

(\(i = 1,2\)) as numerator and relative degree \(r_i=n-m_i\) (\(i = 1,2\)). Accordingly, the outputs y, \(y_1\) and \(y_2\) are related by the differential forms

$$\begin{aligned} y(t)=N_1(\mathrm {d}) y_2(t), \quad y(t)=N_2(\mathrm {d}) y_1(t) \end{aligned}$$

so getting for \(j \ne i\) and \(\mathrm {d} = \frac{\mathrm {d}}{\mathrm {d}t}\)

$$\begin{aligned} y(t)=b_0^j y_i+b_1^j \frac{\mathrm {d}}{\mathrm {d}t}y_i +\dots +b_{m_j}^j \frac{\mathrm {d}^{m_j}}{\mathrm {d} t^{m_j}} y_i. \end{aligned}$$

Remark 3

The feedback

$$\begin{aligned} u_i=\frac{v - C_i A^{r_i}x }{C_i A^{r_i-1}B}, \quad i = 1,2 \end{aligned}$$

transforms (2) into a system with closed-loop transfer function given by

$$\begin{aligned} W^{F_i}(s)&=C(sI-A-BF_i)^{-1}B\\&=\frac{N_j(s)}{s^r_i}=\frac{b_0+ b_1^j s+..+b_{m_j}^j s^{{m_j}}}{s^{r_i}}, \quad j\ne {i}. \end{aligned}$$

The feedback \(u = F_i x + v\) places \(r_i\) eigenvalues of the system coincident with the zeros of \(N_i(s)\) and the remaining ones to 0 so that stabilization in closed loop can be achieved via a further feedback v if and only if \(N_i(s)\) is Hurwitz. The previous argument is the core idea of assigning the dynamics of the system via feedback through cancelation of the stable zeros only. Accordingly, if N(s) is not Hurwitz (i.e., \(N_j(s)\) has positive real part zeros), the closed-loop system will still have non-stable zeros that will play an important role in filtering actions, but that will not affect closed-loop stability. Concluding, given any controllable linear system one can pursue stabilization in closed loop via partial zeros cancelation: starting from a suitable factorization of the polynomial defining the zeros, this is achieved via the definition a dummy output with respect to which the system is minimum phase.

5 DDP-S for LTI systems

Consider the LTI system (2) with relative degree \(r < n\) and being partially minimum phase. Based on the arguments developed in the previous section, the result below provides a characterization of the actions of disturbances which can be decoupled from the output under feedback and with stability. In doing so, we shall show that the problem admits a solution if the disturbance can be constrained onto the largest sub-dynamics of (2) which can be rendered unobservable under feedback while preserving stability; in other words, the problem is solvable if and only if the action of disturbances to be decoupled is contained into the unobservable subspace generated by canceling only the stable zeros of (2).

Theorem 1

Consider the system (2) being controllable and possessing relative degree \(r<n\) and being partially minimum phase. Denote by \(N(s) = b_0 + b_1 s + \dots b_{n-r} s^{n-r} \) the not Hurwitz polynomial identifying the zeros of (2). Consider the maximal factorization of \(N(s) = N_1(s) N_2(s)\) with

$$\begin{aligned} N_i(s) = b_0^i + b_1^i s + \dots b_{n-r_i}^i s^{n-r_i}, \quad i = 1,2 \end{aligned}$$
(11)

such that \(N_2(s)\) is a Hurwitz polynomial of degree \(n-r_2\) and introduce \(C_2 = (b_0^2 \dots b_{m_2}^2 \ \mathbf {0})\). Then, then DDP-S admits a solution for the system (2) for all P verifying

$$\begin{aligned} \text {Im} P \subseteq V_s \end{aligned}$$
(12)

with \(V_s \subseteq V^*\) as in (4) and, for \(r_2 = n - m_2\),

$$\begin{aligned} V_s = \ker \begin{pmatrix} C_2 \\ C_2 A \\ \vdots \\ C_2A^{r_2-1} \end{pmatrix}. \end{aligned}$$

Proof

The proof is straightforward by showing that \(V_s \subseteq V^* \subseteq \ker C\). To this end, one exploits the differential relation \(y = N_1(\mathrm {d})y_2\) by deducing

$$\begin{aligned}&y = C x = N_1(\mathrm {d})C_2x \\&\quad = b_0^1 C_2 x + b_1^1 C_2 A x + \dots + b_{r_2 - r}^1 C_2 A^{r_2 - r} x \\&\dot{y} = CA x = \dot{N}_1(\mathrm {d}) C_2 x\\&\quad = b_0^1 C_2 A x + b_1^1 C_2 A^2 x + \dots + b_{r_2 - r}^1 C_2 A^{r_2 - r +1 } x\\&\dots \\&y^{(r-1)} = CA^{r-1} x= b_0^1 C_2 A^{r-1} x + b_1^1 C_2 A^{r} x + \dots \\&\qquad + b_{r_2-r}^1 C_2 A^{r_2-1} x \end{aligned}$$

for \(r_2> r\) by construction. As a consequence, one gets

$$\begin{aligned}&\underbrace{\begin{pmatrix} C \\ CA \\ \vdots \\ CA^{r-1} \end{pmatrix}}_{:= T^*}= \underbrace{\begin{pmatrix} b_0^1 &{} b_1^1 &{} \dots &{} b_{r_2 - r}^1 &{} 0 &{} \dots &{} 0\\ 0 &{} b_0^1 &{} \dots &{} b_{r_2 - r-1}^1 &{} b_{r_2 - r}^1 &{} \dots &{} 0\\ &{} &{} &{} &{} &{} \ddots &{} \\ 0 &{} 0 &{} \dots &{} * &{} * &{} \dots &{} b_{r_2 - r}^1 \end{pmatrix}}_{:= M}\nonumber \\&\qquad \times \underbrace{\begin{pmatrix} C_2 \\ C_2 A \\ \vdots \\ C_2 A^{r_2 -1}\\ \end{pmatrix} }_{:= T_s} \end{aligned}$$
(13)

so gettingFootnote 1\(V_s \equiv \ker T_s \subseteq \ker T^* \equiv V^*\). As a consequence, one gets that \(V_s \subseteq \ker C\) so getting that all the disturbances that can be made independent on the output are such that \(\text {Im} P \subseteq V_s\). \(\square \)

Remark 4

From the result above, it is clear that the problem is not solvable if \(\{ s \in \mathbb {C} \text { s.t. } N(s) = 0\} \subset \mathbb {C}^+\) that is whenever the system (2) is not partially minimum phase and only the trivial factorization holds with \(N_2(s) = 1\). This pathology also embeds the case of \(r = n-1\) corresponding to the presence of only one zero in (2) that is on the right-hand side of the complex plane.

Remark 5

The previous result shows that whenever (2) is partially minimum phase and DDP-S is solvable, the dimension of the range of disturbances which can be decoupled under feedback while guaranteeing stability is decreasing with respect to the standard DDP problem recalled in Sect. 2 as \(\text {dim}(V_s) < \text {dim} (V^*)\). This is due to the fact that one is constraining the disturbance to act only on the stable lower-dimensional component of the zero dynamics associated to (2) and evolving according to the zeros defined by the Hurwitz sub-polynomial of N(s).

Remark 6

The previous result might be reformulated by stating that DDP-S for (2) is solvable if, and only if the classical DDP is solvable for the minimum-phase system

$$\begin{aligned}&\dot{x} = A x + B u + P w \end{aligned}$$
(14a)
$$\begin{aligned}&y_2 = C_2 x \end{aligned}$$
(14b)

deduced from (2) and having input–output transfer function \(W_2(s) = \frac{N_2(s)}{D(s)}\).

Corollary 1

If DDP-S is solvable for (2), then the disturbance-output decoupling feedback is given by

$$\begin{aligned} u_s = \frac{v - C_2 A^{r_2} x}{C_2 A^{r_2 - 1} B }. \end{aligned}$$
(15)

Proof

First, introduce the coordinate transformation

$$\begin{aligned} \begin{pmatrix} \zeta \\ \eta \end{pmatrix} =\begin{pmatrix} C_2 \\ C_2A \\ \vdots \\ C_2A^{r_2-1} \\ T_2 \end{pmatrix} x, \qquad \zeta = \text {col}(\zeta _1, \dots , \zeta _{r_2} ) \end{aligned}$$

with \(T_2\) such that \(T_2 B = 0\). By exploiting the differential relation

$$\begin{aligned} y = N_1(\mathrm {d})y_2 \end{aligned}$$

with, in the new coordinates, \(y_2 = (1 \ \mathbf {0})\zeta \) and that \(\mathrm {d}\zeta _i = \dot{\zeta }_i = \zeta _{i+1}\) for all \(i = 1, \dots , r_2-r\), the system (2) under the feedback (15) gets the form

$$\begin{aligned} \dot{\zeta }&= \hat{A} \zeta + \hat{B} v \end{aligned}$$
(16a)
$$\begin{aligned} \dot{\eta }&= Q_2 \eta + R_2 \zeta + \hat{P}_2 w \end{aligned}$$
(16b)
$$\begin{aligned} y&= \hat{C} \zeta \end{aligned}$$
(16c)

with \(\hat{C} = \begin{pmatrix} b_0^1&\dots&b_{r_2 - r}^1&\mathbf {0} \end{pmatrix}\) clearly underlying that the disturbance-decoupling problem is solved. As far as stability is concerned, it results that, by construction, \(\sigma (Q_2) \equiv \{s \in \mathbb {C} \text { s.t. } N_2(s) = 0 \} \subset \mathbb {C}^-\) so implying that the unobservable dynamics (16b) are asymptotically stable. \(\square \)

Remark 7

The transfer function of the closed-loop system (16) is provided by

$$\begin{aligned} W_\text {cl}(s) = \frac{N_1(s)}{s^{r_2}} \end{aligned}$$

so emphasizing on the fact that the feedback (15) is canceling only the stable zeros of while leaving the remaining ones unchanged to perform a filtering action that is not compromising the required input–output behavior.

6 DDP-S for nonlinear systems

Consider now the nonlinear system (1) under the standing assumptions detailed in Sect. 3. We shall now investigate on the problem of characterizing the action of disturbances which can be locally decoupled from the output evolutions while ensuring stability in closed loop despite the dynamics (1) is non-minimum phase. To this end, we first recall the auxiliary lemma below from [10].

Lemma 1

Consider the nonlinear system (1) and suppose that its LTM at the origin is controllable in the form (10) and non-minimum phase with relative degree r. Denote by \(N(s) = b_0 + b_1 s + \dots b_{n-r} s^{n-r} \) the not Hurwitz polynomial identifying the zeros of the LTM of (1) at the origin. Consider the maximal factorization of \(N(s) = N_1(s) N_2(s)\)

$$\begin{aligned} N_i(s) = b_0^i + b_1^i s + \dots b_{n-r_i}^i s^{n-r_i}, \quad i = 1,2 \end{aligned}$$
(17)

such that \(N_2(s)\) is a Hurwitz polynomial of degree \(n-r_2\). Then, the system

$$\begin{aligned}&\dot{x} = f(x)+g(x)u + p(x) w\nonumber \\&y_2 =C_2x. \end{aligned}$$
(18)

\(C_2 = \begin{pmatrix} b_0^2&b_1^2&\dots&b_{n-r_2}^2&\mathbf {0} \end{pmatrix}\) has relative degree \(r_2>r\) and is locally minimum phase.

Proof

By computing the linear approximation at the origin of (18), one gets that the matrices \((A, B, C_2)\) are in the form (10) so that the entries of \(C_2\) are the coefficients of \(N_2(s)\) that is the numerator of the corresponding transfer function. By construction, \(N_2(s)\) is a Hurwitz polynomial of degree \(n-r_2\). It follows that, in a neighborhood of the origin, the relative degree of (18) is \(r_2\). Furthermore, since the linear approximation of the zero dynamics of (18) coincides with the zero dynamics of its LTM model at the origin, one gets that (18) is minimum phase. \(\square \)

Remark 8

It is a matter of computations to verify that the zero dynamics of (18) locally coincides with the stable component of the zero dynamics of (1).

In what follows, we show that DDP-S is solvable for the non-minimum-phase system (1) for all disturbances allowing classical DDP to be solved over the auxiliary minimum-phase system (18) in the sense of Proposition 2. In other words, solvability of DDP-S for (1) is equivalent to solvability of DDP for (18).

Theorem 2

Consider the nonlinear system (1) and suppose that its LTM at the origin is controllable in the form (10) and non-minimum phase with relative degree r. Denote by \(N(s) = b_0 + b_1 s + \dots b_{n-r} s^{n-r} \) the not Hurwitz polynomial identifying the zeros of the LTM of (1) at the origin. Consider the maximal factorization of \(N(s) = N_1(s) N_2(s)\)

$$\begin{aligned} N_i(s) = b_0^i + b_1^i s + \dots b_{n-r_i}^i s^{n-r_i}, \quad i = 1,2 \end{aligned}$$
(19)

such that \(N_2(s)\) is a Hurwitz polynomial of degree \(n-r_2\) so deducing the dummy output \(y_2 = h_2(x) = C_2 x\) verifying \(y = N_1(\mathrm {d}) y_2\). Then, DDP-S is solvable for all disturbances for which DDP is solvable for the minimum-phase system (18); namely, DDP-S is solvable for all \(p: \mathbb {R}^n \rightarrow \mathbb {R}^n\) such that

$$\begin{aligned} \hbox {L}_p \hbox {L}_f^i h_2(x) = 0 \quad \text { for all } i \in [0, r] \text { and } x \in B_\epsilon (0). \end{aligned}$$
(20)

In this case, then the DDP-S feedback is given by

$$\begin{aligned} u = \frac{v - \hbox {L}_f^{r_2} h_2(x)}{\hbox {L}_g \hbox {L}_f^{r_2-1} h_2(x)}. \end{aligned}$$
(21)

Proof

First, let us assume that DDP is solvable for the system (18). Thus, consider the closed-loop system (18) under (25) and introduce the coordinate transformation

$$\begin{aligned} \begin{pmatrix} \zeta \\ \eta \end{pmatrix} =\begin{pmatrix} h_2(x) \\ \dots \\ L_{f}^{r_2-1}h_2(x) \\ \phi _2(x) \end{pmatrix} \end{aligned}$$
(22)

with \(\phi _2(x) \) such that \(\nabla \phi _2(x)g(x) =0\) under which it exhibits the normal form

$$\begin{aligned} \dot{\zeta }&= \hat{A} \zeta +\hat{B}v \\ \dot{\eta }&=q_2(\zeta ,\eta ) + p_2(\zeta , \eta )w \\ y_2&=\begin{pmatrix} 1&\mathbf {0} \end{pmatrix} \zeta . \end{aligned}$$

The zero dynamics of (18) is given by

$$\begin{aligned} \dot{\eta }=q_2(0, \eta ) \end{aligned}$$
(23)

which is locally asymptotically stable by Lemma 1. Consider now the original system (1) under the feedback (21). Setting now the transformation (22) to (1) so getting, because \(y = N_1(\mathrm {d}) y_2\)

$$\begin{aligned} \dot{\zeta }&= \hat{A} \zeta +\hat{B}v \end{aligned}$$
(24a)
$$\begin{aligned} \dot{\eta }&=q_2(\zeta ,\eta ) + p_2(\zeta , \eta )w \end{aligned}$$
(24b)
$$\begin{aligned} y&=\begin{pmatrix} b_0^1&b_1^1&\dots&b_{r_2-r}^1&\mathbf {0} \end{pmatrix} \zeta . \end{aligned}$$
(24c)

It turns out that the effect of the disturbance is constrained onto the dynamics (24b) which is made unobservable under feedback coinciding, as \(\zeta = 0\) and \(w = 0\), with the zero dynamics of (18) which is locally stable by assumption so concluding the proof. \(\square \)

Remark 9

The previous result shows that even if a nonlinear system is non-minimum phase, a suitable partition of the output can be performed on its LTM at the origin so that output-disturbance decoupling with stability can be pursued while preserving stability of the internal dynamics. This is achieved by inverting (making unobservable) a lower-dimensional component of the zero dynamics of (1) which is known to possess an asymptotically stable equilibrium at the origin.

Remark 10

As in the standard case, Theorem 2 can be interpreted in a differential-geometry fashion by stating that DDP-S is solvable for all the actions of disturbances verifying the following relation

$$\begin{aligned} \text {Im}p(x) \subseteq \varDelta _s(x) \end{aligned}$$

with

$$\begin{aligned} \varDelta _s(x) = \ker \begin{pmatrix} \mathrm {d}h_2(x)\\ \mathrm {d}\hbox {L}_f h_2(x) \\ \dots \\ \mathrm {d}\hbox {L}_f^{r_2-1} h_2(x) \end{pmatrix} \end{aligned}$$

being such that \(\varDelta _s(x) \subseteq \varDelta ^*(x) \subseteq \ker \mathrm {d}h(x) \) for \(\varDelta ^*(x)\) as in (8) and the feedback (25) being the so-called friend of \(\varDelta _s\).

Once stability of the unobservable dynamics is guaranteed by the decoupling feedback (25), the residual component of the control action can be designed so to guarantee further control specifications with boundedness (or local input-to-state stability) of the residual dynamics (24b). In addition, fixing in (25) the residual control as

$$\begin{aligned} v = -c_0 h_2(x) - \dots - c_{r_2-1} \mathrm {L}_f^{r_2-1} h_2(x) + \bar{v} \end{aligned}$$

with \(c_i\) for \(i = 1, \dots , r_2-1\) being the coefficients of a Hurwitz polynomial, one can conclude [9, Appendix B.2] that for each \(\varepsilon >0\) there exist \(\delta _\varepsilon > 0\) and \(K>0\) such that

$$\begin{aligned} \Vert x(0) \Vert&\le \delta _{\varepsilon } \quad \text { and } \quad | w(t) | \le K, \ | w(t) | \\&\le K \implies \Vert x(t) \Vert \le \varepsilon \text { for all } t\ge 0. \end{aligned}$$

and, thus, boundedness of (1) in closed loop.

Remark 11

Whenever the disturbance w is measurable, the condition (20) in Theorem 2 can be weakened to requiring

$$\begin{aligned}&\hbox {L}_p \hbox {L}_f^i h_2(x) = 0 \quad \text { for all } i \in [0, r_2-2] \text { and } x \in B_\epsilon (0) \\&\quad \hbox {L}_p \hbox {L}_f^{r_2 - 1} h_2(0) \ne 0. \end{aligned}$$

In this case, then the DDP-S feedback is given by

$$\begin{aligned} u = \frac{v - \hbox {L}_f^{r_2} h_2(x) - w\hbox {L}_p \hbox {L}_f^{r_2-1} h_2(x)}{\hbox {L}_g \hbox {L}_f^{r_2-1} h_2(x)} \end{aligned}$$
(25)

aimed at rejecting the effect of the disturbance over the input–output dynamics.

7 DDP-S under sampling

In this section, we are settling the problem of defining the action of disturbances that can be output decoupled under sampling and at any sampling instant \(t = k\delta \) with \(\delta >0\) denoting the sampling period. To this end, we introduce the following requirements over the system (1):

  1. 1.

    the feedback is piecewise constant over the sampling period of length \(\delta >0\) that is \(u(t) \in \mathcal {U}_\delta \);

  2. 2.

    measures are available only at the sampling instants that is \(y(t) = h(x(k\delta ))\) for \(t \in [k\delta , (k+1)\delta [\);

  3. 3.

    the disturbance belongs to the class of piecewise constant signals over the sampling period that is \(w(t) = w_k\) for \(t \in [k\delta , (k+1)\delta [\).

7.1 Sampled-data systems: from single to multi-rate sampling

In this framework, the dynamics of (1) at the sampling instants is described by the single-rate sampled-data equivalent model

$$\begin{aligned} x_{k+1}= & {} F^{\delta }(x_k, u_k, w_k) \nonumber \\ y_k= & {} h(x_k) \end{aligned}$$
(26)

with \(x_{k} := x(k\delta )\), \(y_{k} := y(k\delta )\), \(u_{k} := u(k\delta )\), \(h(x) = Cx\) and

$$\begin{aligned} F^{\delta }(x_k, u_k, w_k) = e^{\delta (\hbox {L}_f + u_k \hbox {L}_g +w_k \hbox {L}_p)}x\big |_{x_k}. \end{aligned}$$

Remark 12

We underline that requiring the disturbance to be a piecewise constant signal might be quite unrealistic. Though, this choice is made for the sake of the sampled-data design. As a matter of fact, if w is continuously varying signal, (26) would be affected by all the time-derivatives of the perturbation (i.e., \(\dot{w}\), \(\ddot{w}\), ...) computed at \(t = k\delta \) so generally preventing from exactly solving DDP-S. In this scenario, the sampled-data design can be pursued in an approximate way by considering only samples of the disturbance and neglecting the derivative terms so applying the feedback strategy to be presented.

Assuming for the time-being \(w = 0\), it is a matter of computations to verify that

$$\begin{aligned} y_{k+1}= & {} h(x_k) + \sum _{i = 1}^{r} \frac{\delta ^i}{i!}\hbox {L}_{f}^i h(x)\big |_{x_k}\\&+\frac{\delta ^r}{r!}u_k \hbox {L}_g \hbox {L}_{f}^{r-1} h(x)\big |_{x_k} + O(\delta ^{r+1}) \end{aligned}$$

so that

$$\begin{aligned} \frac{\partial y_{k+1}}{\partial u_k} = \frac{\delta ^r}{r!} \hbox {L}_g \hbox {L}_{f}^{r-1} h(x)\big |_{x_k} + O(\delta ^{r+1}) \ne 0. \end{aligned}$$

Thus, the relative degree of the sampled-data equivalent model of (1) is always falling to \(r_d = 1\), independently from the continuous-time one. As a consequence, whenever \(r > 1\), the sampling process induces a further zero dynamics of dimension \(r -1\) (i.e., the so-called sampling zero dynamics [27, 28]) that is in general unstable for \(r > 1\). As a consequence, disturbance decoupling under single-rate feedback computed over the sampled-data equivalent model (26) cannot be achieved while guaranteeing internal stability even when the original continuous-time system (1) is minimum phase. In addition, denoting by \(r_w \ge 0\) the first integer such that

$$\begin{aligned} \hbox {L}_p \hbox {L}_f^{r_w-1} h(0) \ne 0 \end{aligned}$$

one also gets that, for \(x \in B_\epsilon (0)\)

$$\begin{aligned} \frac{\partial y_{k+1}}{\partial w_k} = \frac{\delta ^{r_w}}{r_w!} \hbox {L}_p \hbox {L}_{f}^{r_w-1} h(x)\big |_{x_k} + O(\delta ^{r_w+1}) \ne 0. \end{aligned}$$

This imposes, in general, that measures of the disturbance at all \(t = k\delta \) are needed to guarantee output-disturbance decoupling under sampling so making the problem more conservative.

As far as the first pathology is concerned, it was shown in [29] that multi-rate sampling allows to preserve the relative degree and hence avoid the rising of the unstable sampling zero dynamics. Accordingly, one sets \(u(t) = u^i_k\) for \(t \in [(k+i-1)\bar{\delta }, (k+i)\bar{\delta }[\) for \(i = 1, \dots , r\) and \(y(t) = y_k\) for \(t \in [k\delta , (k+1)\delta [\) so that the multi-rate equivalent model of order \(r_2\) of (1) gets the form

$$\begin{aligned} x_{k+1} = F^{\bar{\delta }}_m (x_k, u^1_k, \dots , u^{r_2}_k, w_k) \end{aligned}$$
(27)

where \(\bar{\delta } = \frac{\delta }{r_2}\) and

$$\begin{aligned}&F^{\bar{\delta }}_m(x_k, u^1_k, \dots , u^{r_2}_k, w_k)\\&\quad = e^{\bar{\delta } (\hbox {L}_{f} + u^1_k \hbox {L}_g + w_k \hbox {L}_p)} \dots e^{\bar{\delta } (\hbox {L}_{f} + u^{r_2}_k \hbox {L}_g + w_k \hbox {L}_p)}x\big |_{x_k} \\&\quad = F^{\bar{\delta }}(\cdot , u^{r_2}_k, w_k) \circ \dots \circ F^{\bar{\delta } }(x_k, u^1_k, w_k). \end{aligned}$$

7.2 The DDP-S sampled-data feedback

In the sequel, we shall investigate on the way multi-rate feedback can be suitably employed with the arguments in Theorem 2 to characterize all disturbances whose effect can be output decoupled under multi-rate feedback and at any sampling instants \(t = k\delta \) while preserving stability of the internal dynamics. We shall prove that DDP-S under sampling can be solved via multi-rate under the same hypotheses as in continuous time plus the possibility of measuring the disturbance at any sampling instant.

Accordingly, the multi-rate feedback solving the problem \(\underline{u}_k = \underline{\gamma }(\bar{\delta }, x_k, \underline{v}_k, w_k)\) with \(\underline{u} = \text {col}(u^1, \dots , u^{r_2})\) and \(\underline{v} = \text {col}(v^1, \dots , v^{r_2} \)) is designed so to ensure decoupling with respect to the dummy output \(y_2 = C_2 x\) and, in turn, with respect to the original one \(y = Cx\). This is achieved by considering the sampled-data dynamics (27) with augmented dummy output \(Y_{2k} = H_2(x_k)\) composed of \(y_2 = C_2 x\) and its first \(r_2-1\) derivatives; namely, we consider

$$\begin{aligned} x_{k+1}= & {} F^{\bar{\delta }}_m (x_k, \underline{u}_k, w_k)\nonumber \\ Y_{2k}= & {} H_2(x_k) \end{aligned}$$
(28)

with \(\bar{\delta } = \frac{\delta }{r_2}\) and output vector

$$\begin{aligned} H_2(x) = \begin{pmatrix} h_2(x)&\hbox {L}_{f} h_2(x)&\dots&\hbox {L}_{f}^{r_2 -1}h_2(x) \end{pmatrix}^{\top } \end{aligned}$$

possessing by construction a vector relative degree \(r^{\delta } = (1, \dots , 1)\). Accordingly, the following results can be stated by referring to [37, 41] where these concepts are introduced and similar manipulations detailed with analog motivations.

Theorem 3

Consider the dynamics (1) under the hypotheses of Theorem 2 with \(y_2 = C_2 x\) being the dummy output with respect to which (1a) is minimum phase. Assume the disturbance \(w(t) = w_k\) for \(t \in [k\delta , (k+1)\delta [\) is measured at all sampling instants \(t = k\delta \) and let (27) be the multi-rate sampled-data equivalent model of (1a) of order \(r_2\). Then, DDP-S is solvable under sampling for all piecewise constant disturbances such that \(p: \mathbb {R}^n \rightarrow \mathbb {R}^n\) verifies

$$\begin{aligned} \hbox {L}_p \hbox {L}_f^{i} h_2(x) = 0 \quad \text { for all } i < r_2-1 \quad \text { and } x \in \mathbb {B}_\epsilon (0). \end{aligned}$$

If that is the case, the feedback ensuring DDP-S is the unique solution \(\underline{u} = \underline{u}^{\bar{\delta }} = \text {col}(\gamma ^1(\bar{\delta }, x_k, \underline{v}_k, w_k)\), \(\dots , \gamma ^{r_2}(\bar{\delta }, x_k, \underline{v}_k, w_k))\) to the Input–Output Matching (I–OM) equality

$$\begin{aligned} H_2( F^{\bar{\delta }}_m (x_k, \underline{u}_k, w_k)) = e^{r_2 \bar{\delta } (\hbox {L}_{f} + \gamma (\cdot ,v) \hbox {L}_g + w_k \mathrm {L}_p )}H_2(x) \big |_{x_k} \end{aligned}$$
(29)

for all \(x_k = x(k\delta )\), \(v(t) = v(k\delta ) := v_k\), \(\underline{v}_k = (v_k, \dots , v_k)\) as \(t \in [k\delta , (k+1)\delta [\), \(k\ge 0\) and with

$$\begin{aligned} \gamma (x, v, w) = \frac{v - \hbox {L}_f^{r_{2}}h_2(x) -w \hbox {L}_p\hbox {L}_f^{r_2-1}h_2(x)}{\hbox {L}_g\hbox {L}_f^{r_2-1}h_2(x)}. \end{aligned}$$
(30)

Such a solution exists and is uniquely defined as a series expansion in powers of \(\bar{\delta }\) around the continuous-time feedback \(\gamma (x, v, w)\); i.e., for \(i = 1, \dots , r_2\)

$$\begin{aligned} \gamma ^i(\bar{\delta }, x,\underline{v}, w) {=} \gamma (x, \underline{v}, w) {+}\sum _{j\ge 1} \frac{\bar{\delta }}{(j+1)!} \gamma _j^i(x, \underline{v}, w). \end{aligned}$$
(31)

Proof

First, we rewrite (29) as a formal series equality in the unknown \(\underline{u}^{\bar{\delta }}\); i.e.,

$$\begin{aligned} \begin{pmatrix} {\bar{\delta }^{r_2}}S^{\bar{\delta }}_{1}(x, \underline{u}^{\bar{\delta }}, w)&\dots&\bar{\delta } S^{\bar{\delta }}_{1}(x, \underline{u}^{\bar{\delta }}, w) \end{pmatrix}^{\top } \end{aligned}$$
(32)

with, for \(i = 1, \dots , r_2\),

$$\begin{aligned}&{\bar{\delta }^{i}}S^{\delta }_{i}(x, \underline{u}^{\bar{\delta }}, w)\\&\quad = e^{\bar{\delta } (\hbox {L}_{f} + u^1 \hbox {L}_g + w \hbox {L}_p)} \dots e^{\bar{\delta } (\hbox {L}_{f} + u^1 \hbox {L}_g + w \hbox {L}_p)} \hbox {L}_{f}^{i-1}h_2(x)\\&\qquad - e^{r_2\bar{\delta } (\hbox {L}_{f} +\gamma (\cdot , v, w) \hbox {L}_g +w \hbox {L}_p)}\hbox {L}_{f}^{i-1}h_2(x). \end{aligned}$$

Thus one looks for \(\underline{u} = \underline{\gamma }(\bar{\delta }, x, v, w)\) satisfying

$$\begin{aligned} S^{\bar{\delta }}(x, \underline{u}^{\bar{\delta }}, w) = \begin{pmatrix} S^{\bar{\delta }}_{1}(x, \underline{u}^{\bar{\delta }}, w)&\dots&S^{\bar{\delta }}_{1}(x, \underline{u}^{\bar{\delta }}, w) \end{pmatrix}^{\top } = \mathbf {0} \end{aligned}$$
(33)

where each term rewrites as \(S^{\delta }_{i}(x, \underline{u}^{\bar{\delta }}, w) = \sum _{j\ge 0} \delta ^j S_{ij}(x, \underline{u}^{\bar{\delta }}, w) \) with

$$\begin{aligned}&S_{i0}(x, \underline{u}^{\bar{\delta }}, w)\nonumber \\&\quad = \Big (\varDelta _j \underline{u}^{\bar{\delta }} - r_2^{r_2 - i+1} \gamma (x, v, w) \Big ) \hbox {L}_{g} \hbox {L}_f^{r_{2}-1} h_2(x) \end{aligned}$$
(34)

and \(\frac{\varDelta _j}{j!} = (\frac{j^{r_2-j +1} -(j-1)^{r_2-j+1}}{j!} \ \frac{ (j-1)^{r_2-j +1} - (j-2)^{r_2-j+1}}{j!} \dots \ \frac{1}{j!} ).\) It results that

$$\begin{aligned} \underline{u}^{\bar{\delta }} = \underline{\gamma }( \delta , x, \underline{v}, w) = (\gamma (x,v, w), \dots , \gamma (x,v, w))^{\top } \end{aligned}$$

solves (33) as \(\bar{\delta } \rightarrow 0\). More precisely, as \(\bar{\delta } \rightarrow 0\), one gets the equation

$$\begin{aligned}&S^{\bar{\delta } \rightarrow 0}(x, \underline{u}^{\bar{\delta }}, w)\\&\quad =\Big (\varDelta \underline{u}^{\bar{\delta }} - D \gamma (x, v, w) \Big ) \hbox {L}_{g} \hbox {L}_f^{r_{2}-1} h_2(x) \end{aligned}$$

with \(\varDelta = (\varDelta _1^{\top }, \dots \varDelta _{r_2}^{\top })^{\top }\) and \(D=\text {diag}(r_2^{r_2}, \dots , r_2)\). Furthermore, as \(\bar{\delta }\rightarrow 0\) the Jacobian of \(S^{\bar{\delta }}\) with respect to \(\underline{u}^{\bar{\delta }}\)

$$\begin{aligned} \nabla _{\underline{u}^{\bar{\delta }}} S^{\bar{\delta }}(x, \underline{u}^{\bar{\delta }}, w)\big |_{\bar{\delta } \rightarrow 0} =\varDelta \ \hbox {L}_{g} \hbox {L}_f^{r_{2}-1} h_2(x) \end{aligned}$$

is full rank by definition of the continuous-time relative degree \(r_2\) and because \(\varDelta \) is invertible (see [29] for details) so concluding, from the Implicit Function Theorem, the existence of \(\delta \in ]0, T^*[\) so that (29) admits a unique solution of the form (31) around the continuous-time solution (30). Disturbance decoupling and stability of the zero dynamics are ensured by multi-rate sampling as proven in [29] combined with the arguments of Theorem 2. As a matter of fact, under the coordinate transformation (22), the system (27) with output \(y = Cx\) rewrites as

$$\begin{aligned} \zeta _{k+1}&= \hat{A}^{r_2 \bar{\delta }} \zeta _k + \hat{B}^{\bar{\delta }} v_k \end{aligned}$$
(35a)
$$\begin{aligned} \eta _{k+1}&= Q^{\bar{\delta }}_2(\zeta _k, \eta _k, w_k, v_k) \end{aligned}$$
(35b)
$$\begin{aligned} y_k&= ( C_1 \ \mathbf {0}) \zeta _k \end{aligned}$$
(35c)

with

$$\begin{aligned} \hat{A}^{r_2 \bar{\delta }} = e^{r_2 \bar{\delta } \hat{A}}, \quad \hat{B}^{\bar{\delta }}= \sum _{i = 0}^{r_2-1}\frac{\bar{\delta }^i}{i!} \hat{A}^i \hat{B} \end{aligned}$$

with (\(\hat{A}, \hat{B}\)) being in the Brunowski form. Accordingly, the sampled-data unobservable dynamics (35b) verifies

$$\begin{aligned} \nabla _\zeta Q^{\bar{\delta }}(0, 0, 0, 0) = e^{r_2 \bar{\delta } Q_2} \end{aligned}$$

which is Schur stable as \(Q_2 = \nabla _\zeta q_2(0, 0)\) provided in (23) is Hurwitz by Lemma 1. \(\square \)

The feedback solution of the equality (29) ensures matching, at any sampling instants \(t = k\delta \), of the output evolutions of (18) which are decoupled from the disturbance. Moreover, by matching, one gets that the sampled-data feedback is making the stable component of the \(n-r\) dimensional zero dynamics of (27) with output \(y = Cx\) which locally coincides with the one of the continuos-time original system (1).

Fig. 1
figure 1

\(\delta =0.1\) s

Full size image
Fig. 2
figure 2

\(\delta =0.5\) s

Full size image
Fig. 3
figure 3

\(\delta =0.9\) s

Full size image

7.3 Some computational aspects

The feedback control is in the form of a series expansion in powers of \(\bar{\delta }\). Thus, iterative procedures can be carried out by substituting (31) into (29) and equating the terms with the same powers of \(\bar{\delta }\) (see [41] where the explicit expression for the first terms are given). Unfortunately, only approximate solutions \(\underline{u} = \gamma ^{[p]}(\bar{\delta }, x, \underline{v}, w)\) can be implemented in practice through truncations of the series (31) at finite order p in \(\bar{\delta }\); namely, setting

$$\begin{aligned}&\underline{\gamma }^{[p]}(\bar{\delta }, x, \underline{v}, w)\\&\quad = (\gamma ^{1[p]}(\bar{\delta }, x, \underline{v}, w), \dots , \gamma ^{r_2[p]}(\bar{\delta }, x, \underline{v}, w)) \end{aligned}$$

one gets for \(i = 1, \dots , r_2\)

$$\begin{aligned}&\gamma ^{i[p]}(\bar{\delta }, x,\underline{v}, w)\nonumber \\&\quad =\gamma (x, \underline{v}, w) + \sum _{j=1}^p \frac{\bar{\delta }^j}{(j+1)!} \gamma _j^i(x, \underline{v}, w). \end{aligned}$$
(36)

When \(p = 0\), one recovers the sample-and-hold (or emulated) solution

$$\begin{aligned}&\gamma ^{i[0]}(\bar{\delta }, x_k,\underline{v}_k, w_k)\\&\quad =\gamma (x(k\delta ), v(k\delta ), w(k\delta )), \quad i. =1, \dots , r_2. \end{aligned}$$

The preservation of performances under approximate solutions has been discussed in [42] by showing that although global asymptotic stability is lost, input-to-state stability (ISS) and practical global asymptotic stability can be deduced in closed loop even throughout the inter sampling period.

8 The TORA example

Let us consider the dynamics of the so-called Translational Oscillator with Rotating Actuator (or, for the sake of brevity, TORAFootnote 2 [43]) described by

$$\begin{aligned} \dot{x}_1&= x_2\nonumber \\ \dot{x}_2&= -x_1 + \varepsilon \sin {x_3}\nonumber \\ \dot{x}_3&= x_4\nonumber \\ \dot{x}_4&= \frac{\varepsilon \cos {x_3}(x_1 - \varepsilon x_4^2 \sin {x_3}) + u}{1-\varepsilon ^2 \cos ^2{x_3}}\nonumber \\ y&= \begin{pmatrix} \frac{2(\varepsilon ^2-1)}{\varepsilon }&\frac{2(\varepsilon ^2-1)}{\varepsilon }&1-\varepsilon ^2&1-\varepsilon ^2 \end{pmatrix}x \end{aligned}$$
(37)

with: \(\varepsilon \in ]0, 1[\); \(z_1 = x_1 - \varepsilon \sin x_3\) and \(z_2 = x_2 - \varepsilon x_4 \cos x_3 \) being the displacement and velocity of the platform; \(x_3\) and \(x_4\) being the angle and angular velocity of the rotor carrying the mass; u being the control torque applied to the rotor. It is a matter of computations to verify that (37) has relative degree \(r = 1\) and is not minimum phase as the LTM at the origin possesses transfer function

$$\begin{aligned} W(s) = \frac{(s^2-1)(s+1)}{s^2((1-\varepsilon ^2)s^2 + 1)}. \end{aligned}$$

Suppose now that a disturbance \(w \in \mathbb {R}\) is affecting (37) through the vector

$$\begin{aligned} D = \begin{pmatrix} \frac{2}{\epsilon }(\epsilon ^2 - 1)&0&0&(\epsilon ^2 - 1) \end{pmatrix}^{\top } \end{aligned}$$

so getting the perturbed dynamics

$$\begin{aligned} \dot{x}_1&= x_2 + \frac{\epsilon ^2 - 1}{2} d\nonumber \\ \dot{x}_2&= -x_1 + \varepsilon \sin {x_3}\nonumber \\ \dot{x}_3&= x_4\nonumber \\ \dot{x}_4&= \frac{\varepsilon \cos {x_3}(x_1 - \varepsilon x_4^2 \sin {x_3}) + u}{1-\varepsilon ^2 \cos ^2{x_3}} + (\epsilon ^2 - 1)d\nonumber \\ y&= \begin{pmatrix} \frac{2(\varepsilon ^2-1)}{\varepsilon }&\frac{2(\varepsilon ^2-1)}{\varepsilon }&1-\varepsilon ^2&1-\varepsilon ^2 \end{pmatrix}x. \end{aligned}$$
(38)

It is a matter of computation that classical DDP as in Sect. 2 is solvable for (38) without preserving internal stability as a consequence of the instability of the zero dynamics. According to the arguments of Sect. 6, DDP with stability is still solvable when considering the auxiliary output

$$\begin{aligned} y_2 = \begin{pmatrix} -1&1&0&0 \end{pmatrix} T x = \begin{pmatrix} 0&-\frac{2}{\varepsilon }(\varepsilon ^2 - 1)&1 - \varepsilon ^2&0 \end{pmatrix} x \end{aligned}$$
(39)

with T being computed as in Remark 2 and provided by

$$\begin{aligned} T = (\varepsilon ^2-1)\left( \begin{array}{cccc} -\frac{1}{\varepsilon } &{} 0 &{} 0 &{} 0\\ 0 &{} -\frac{1}{\varepsilon } &{} 0 &{} 0\\ \frac{1}{\varepsilon } &{} 0 &{} -1 &{} 0\\ 0 &{} \frac{1}{\varepsilon } &{} 0 &{} -1 \end{array}\right) . \end{aligned}$$

It is a matter of computations to verify that with respect to the new output (39) the system has relative degree \(r_2 = 2\) and is minimum phase with transfer function of the corresponding LTM at the origin provided by

$$\begin{aligned} W_2(s) = \frac{(s+1)^2}{s^2((1-\varepsilon ^2)s^2 + 1)}. \end{aligned}$$

Moreover, DDP with stability is solvable as the relative degree condition (20) is met so that the feedback (25) with

$$\begin{aligned}&L_{g} L_f h_2(x) \\&\quad = \frac{\epsilon ^2 - 1}{\epsilon ^2\cos ^2(x_3) - 1} \\&L_f^2 h_2(x) \\&\qquad = \frac{2 x_2(\epsilon ^2 - 1)}{\epsilon } - 2 x_4\cos (x_3) (\epsilon ^2 - 1) \\&\qquad + \frac{\epsilon \cos (x3) (\epsilon ^2 - 1) (x_1 - \epsilon \sin (x3)(x_4^2 + 1))}{\epsilon ^2 \cos (x_3)^2 - 1} \end{aligned}$$

fulfills the requirements. Moreover, setting \(v = -k_1 h_2(x) - k_2 L_f h_2(x) \) one gets \(y(t) \rightarrow 0\) as \(t \rightarrow \infty \) whenever \(k_1, k_2 >0\).

To solve the problem under sampling, the multi-rate feedback \(\underline{\gamma }^{[1]}(\delta , x,w ,\underline{v})\) in (36) can be easily deduced for \(p = 1\) with

$$\begin{aligned} \gamma _1^1(x,w ,\underline{v})&= \frac{1}{3} \dot{\gamma }(x,w ,\underline{v}),\\ \gamma _1^2 (x,w ,\underline{v})&= \frac{5}{3} \dot{\gamma }(x,w ,v) \end{aligned}$$

Figures 1, 2 and 3 depict simulations of the aforementioned situations under continuous-time feedback (25) and the sampled-data feedback (36) with one correcting term (i.e., \(p = 1\)) and for several values of the sampling period and different simulating scenario:

  1. 1.

    the full continuous-time case as proposed in Sect. 6 where the disturbance is also continuously varying over time (in red);

  2. 2.

    the ideal sampled-data framework proposed in Sect. 7 where \(w(t) = w_d(t)\) with \(w_d(t) = w_k\) for \(t \in [k\delta , (k+1)\delta [\) (in blue);

  3. 3.

    the realistic sampled-data case in the disturbance is continuously varying over time (and is not piecewise constant) albeit the feedback is computed based on samples of the disturbance at all sampling instants \(t = k\delta \) (in cyan);

  4. 4.

    the emulation-based control scheme where the continuous-time feedback is implemented through mere sample-and-hold devices with no further sampled-data re-design (in magenta).

The disturbance is implemented as a general white noise randomly generated through Simulink–MATLAB.

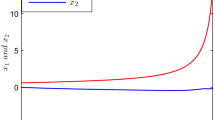
It results from Figs. 1, 2 and 3 that in case of the continuous-time scenario that the proposed feedback computed via partial dynamic inversion succeeds in isolating the effect of the disturbance from the output for the original system as the output goes to zero with an acceptable behavior of the zero dynamics which is still converging to the origin despite the perturbation.

As far as the sampled-data system is concerned, simulations underline that although an approximate feedback is implemented a notable improvement of the performances is achieved with respect to the mere emulation. Moreover, even when the disturbance is continuously varying, the approximate sampled-data feedback yields promising performances that appear even better than the ideal scenario (i.e., when the disturbance affecting the system is piecewise constant). This fact is not surprising as in the latter case, the relative degree of the sampled-data output with respect to the disturbance falls to 1 so compromising the closed-loop behavior. This result motivates and deserves a further formal and general study of this fact which has been empirically illustrated. Finally we note that, as \(\delta \) increases, the proposed multi-rate strategy yields more than acceptable performances even when emulation fails to stabilize the input–output evolutions (Fig. 3).

9 Conclusions and perspectives

In this paper, new conditions for characterizing all the disturbances that can be locally decoupled from the output evolutions of nonlinear systems have been deduced by also requiring preservation of the internal stability. The approach is based on a local factorization of the polynomial defining the zeros of the corresponding linear tangent model at the origin and, thus, on partial dynamics cancelation. Future works are toward the extension of these arguments to the multi-input/multi-output case and to a global characterization of the results possibly combined with input–output stability and related results. Finally, the effect of an approximate sampled-data feedback over a continuously perturbed dynamics (as in the third scenario of the reported simulations) deserves further investigation. The study of zeros of the sampled-data systems in a pure hybrid context [44] is of paramount interest as well.