1 Introduction

In the present era, there occur various new developments in the area of fluid mechanics which are concerned with the flow of fluid in other fluid of immiscible behaviour or fluid droplets of arbitrary shapes. As it efficiently account an idealization of several natural, biological and industrial exercise including formation of raindrop, blood flow problems, extraction of liquid from liquid, prediction of atmospheric conditions and sedimentation processes. In real life, the occurrence of immiscible flow of different fluid flow are found in various situation like the motion of various oils through the bed of rocks, the flow of various industrial fluid in river, the release of dissolved gases from crude oils into the reservoir rock, etc. A significant and powerful technique employed to estimate the impact of particle concentration on the rate of sedimentation of particle is the well known unit cell model. This technique is extensively used for solving problems for particles in dense system. In this approach, the concept involved is to assume the arbitrary cluster of particles to be partitioned into various identical cells, in which every cell contains single particle (spherical, cylindrical, spheroidal etc). And the cell is picked in such a manner that the fractional void volume in the cell becomes identical to the fractional void volume of the entire assemblage. Examination of such problem provides a measure to know information on the wall effects [1]. For the purpose of reporting the impact of neighbouring particles on the particle at the cell, different boundary conditions are proposed at the surface of the fictitious cell [2,3,4,5]. Study of creeping flow past fluid droplets are generally modelled using Stokes equation [1]. Slow motion of fluid drop of spherical geometry in other immiscible fluid was first investigated by Hadamard [6] and Rybczynski [7] by considering the condition of continuity of velocity and tangential stress respectively at the fluid phases interface. With the aim of studying the flow of fluid droplet, Bart [8] analysed the motion of fluid sphere in another viscous fluids by using bipolar spherical coordinate system. Low Reynolds number flow of a sphere filled with fluid in the neighbourhood of other sphere was studied by Wacholde and Weihs [9] and the obtained results agrees with the result of Bart. Bhatt and Shirley [10] analysed the motion of liquid spheres of different viscosities with free outer spherical surface. Flow of non-Newtonian fluid past a droplet of Newtonian fluid sphere contained in a cell was considered by Saad [11].Years later, the quasisteady axisymmetric motion of a fluid sphere contained in a non-concentric spherical cavity was examined by Lee and Keh [12] with the help of boundary collocation method and obtained the wall effect on the fluid droplet. Subsequently, Choudhuri and Padmavati [13] worked on finding a common method for handling the random viscous incompressible Stokes flow either axisymmetric or non-axisymmetric, past a sphere covered with a layer of fluid with different viscosity. Further, Prasad and Kaur [14, 15] analyzed the wall effect on both micropolar flow past a viscous fluid spheroid droplet and viscous flow past a micropolar fluid spheroidal droplet inside a cell.

In recent years, numbers of researches has been carried out solving various real-life problems of industrial, engineering, environmental and also in the biological science. While keeping an eye on the scope of hydrodynamics, various problems related to magnetohydrodynamic (MHD) flows has been investigated by a number of researchers with numerous applications. The motion of conducting fluids under magnetic field are found to be applicable in several physical, geophysical and industrial fields. Therefore, in the recent development, the Hartmann flow has important application including power generators and pumps, polymer technology, the petroleum industry, purification of crude oil, and designing of heat exchangers and various other application can also be found in the books by Cramer and Pai [16] and Davidson [17]. Earlier, Stewartson [18] dealt with the motion of a magneto fluid past a sphere under the influence of a strong magnetic forces. Owing to literature study, several works related to magnetohydrodynamic flow through varying geometry which addresses the consequences of applied magnetic field [19,20,21,22,23]. Verma and Dutta [24] examined the flow through channel of varying viscosity with magnetic force in a direction perpendicular to the flow. Unsteady MHD flow of mixed convective immiscible viscous liquids past a horizontal channel was tackled by Singh et al. [25]. Magnetic effect on the motion of fluid past a porous channel having variable permeability was investigated by Srivastava and Deo [26]. The problem related to MHD flow of immiscible fluid spheres was reported by Jayalakshmamma et al. [27]. In their work, they studied the variation in streamlines pattern. However, they didn’t focused on calculating the hydrodynamic drag. Verma and Singh [28] handled the problem of calculating the impact of magnetic field on the fluid flow rate for the motion of circular channel of porous media. Ansari and Deo [29] demonstrated the MHD effect on the immiscible fluids flow via porous channel.Thereafter, Saad [30] worked on finding the effect of magnetic forces on the flow past porous particles of spherical and cylindrical shapes using Happel and Kuwabara model. Further, Prasad and Bucha [31, 32] studied flow problems for particles of varying shapes including semipermeable sphere and cylindrical shell under magnetohydrodynamics flow and also evaluated the drag force acting on them respectively.

Inspired by the above discussion and its applications, the present work is investigated. The main objective of this analysis is to address the creeping flow of immiscible fluid sphere in cell model under magnetohydrodynamic flow by using Stokes equation modified by Lorentz forces, for studying flow fields. Considered fluids are assumed to be Newtonian and electrically conducting in nature. Boundary condition at the surface of fluid sphere are vanishing of normal velocity component, continuity of tangential components of velocity and stress respectively. At the hypothetical cell surface, Kuwabara model is used. Drag force together with wall correction factor experienced on the sphere filled of fluid are evaluated analytically. Further, the impact of various active parameters involved in the system are discussed through graphs and tables.

2 Problem formulation

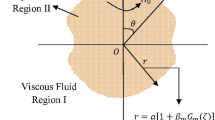
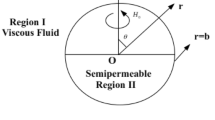
Consider the steady axisymmetric MHD fluid flow past a fluid sphere of radius \(r=b\) bounded by a spherical envelope of radius \(r=a\), which is supposed to be in motion having a uniform velocity U, as shown in Fig 1. Present flow is parted into external and internal fluid regions which are represented as Region I and Region II respectively and for simplicity denoted as i, with \(i=1,2\) respectively.

Fig. 1
figure 1

Visualization of flow past a fluid sphere under magnetic effect

Full size image

The following assumptions are made:

  1. 1.

    A uniform constant magnetic field is applied in a transverse direction of the flow.

  2. 2.

    Exclusion of any applied external electric field.

  3. 3.

    Neglecting induced magnetic field.

The equations governing the flow in external and internal fluid regions are driving by modified Stokes equation given as [1, 30]

$$\nabla \cdot {\mathbf{q}}^{(i)}=0,\,i=1,2.$$
(1)
$$\begin{aligned}&\nabla {p^{(i)}}+\mu _i\nabla \times \nabla \times {\mathbf {q}}^{(i)} \nonumber \\ & \quad -\mu ^2_h\sigma _i\left( {\mathbf {q}}^{(i)}\times {\mathbf {H}}^{(i)}\right) \times {\mathbf {H}}^{(i)}=0, \end{aligned}$$
(2)

where the notation denotes,

  1. 1.

    \({\mathbf {q}}^{(i)}\) as the velocity vector,  \(i=1,2\)

  2. 2.

    \(\sigma _i\) as the electric conductivity,  \(i=1,2\)

  3. 3.

    \({\mathbf {H}}^{(i)}\) as the electromagnetic induction vector,   \(i=1,2\)

  4. 4.

    \({p^{(i)}}\) as the pressure ,  \(i=1,2\)

  5. 5.

    \(\mu _i\) as the coefficient of viscosity ,  \(i=1,2\)

  6. 6.

    \(\mu _h\) the magnetic permeability.

Following non-dimensional variables are chosen, to convert the governing equations into dimensionless form.

$$\begin{aligned}&r=b\,\tilde{r}, {\mathbf {q}}^{(i)}=U\,{\tilde{{\mathbf {q}}}}^{(i)},\,\nabla =\frac{{\tilde{\nabla }}}{b},\,{p^{(i)}}=\frac{\mu _1\, U}{b}{\tilde{p}}^{(i)}, \nonumber \\&{\mathbf {H}}^{(i)}=H_o\, {\tilde{\mathbf {H}}}^{(i)} \end{aligned}$$
(3)

Utilising the above values in Eqs. (1) and (2) and thereafter omitting the tildes, we get

$$\nabla \cdot {\mathbf {q}^{(1)}}=0,$$
(4)
$$\begin{aligned}&\nabla {p^{(1)}}+\nabla \times \nabla \times {\mathbf {q}}^{(1)}\nonumber \\&\quad -\alpha ^2\left( {\mathbf {q}}^{(1)}\times {\mathbf {H}}^{(1)}\right) \times {\mathbf {H}}^{(1)}=0, \end{aligned}$$
(5)
$$\nabla \cdot {{\mathbf {q}}^{\,(2)}}=0,$$
(6)
$$\begin{aligned}&\nabla {p^{\,(2)}}+\gamma ^2\nabla \times \nabla \times {\mathbf {q}}^{(2)}\nonumber \\&\quad -\gamma ^2\beta ^2\left( {\mathbf {q}}^{(2)}\times \mathbf {H}^{\,(2)}\right) \times {\mathbf {H}}^{(2)}=0. \end{aligned}$$
(7)

with \(\alpha =\sqrt{\frac{\mu ^2_hH_o^2\sigma _1b^2}{\mu _1}}\), \(\beta =\sqrt{\frac{\mu ^2_hH_o^2\sigma _2b^2}{\mu _2}}\) are the Hartmann numbers for outer and inner flow respectively, \(\gamma ^2=\frac{\mu _2}{\mu _1}\) as the viscosity ratio. In the work under consideration, dimensionless Hartmann number plays an important role in analyzing the behaviour of fluids. Hartmann number is defined as the ratio of electromagnetic force to the viscous force which comes into play while dealing with magnetohydrodynamic flows. It shows the influence of applied magnetic field on the drag forces.

Consider \((r,\theta ,\phi )\) as the spherical co-ordinate system. The present flow is axially symmetric, leading the physical quantities involved in flow to be independent of \(\phi\). Thus, velocity vectors are given by

$$\begin{aligned} \mathbf {q}^{\,\,(i)}=q_{r}^{(i)}(r,\theta )\,{\mathbf{e}}_{\mathbf r}+q_{\theta }^{(i)}(r,\theta )\,{\mathbf {e}}_{\varvec{\theta}},\,\,i=1,2 \end{aligned}$$
(8)

Expressing velocity components in terms of the stream functions \(\psi ^{(i)}\); \(i=1,2\) which satisfy the continuity Eqs. (4) and (6) as

$$\begin{aligned} q_{r}^{(i)}=-\frac{1}{r^2\sin \theta }\frac{\partial {\psi ^{(i)}}}{\partial \theta },\,\,q_{\theta }^{(i)}=\frac{1}{r\sin \theta }\frac{\partial \psi ^{(i)}}{\partial {r}};\,\,\,i=1,2 \end{aligned}$$
(9)

By substituting Eq. (9) and thereafter eliminating pressure terms from Eqs. (5) and (7), we obtain

$$E^2(E^2-\alpha ^2)\psi ^{(1)}=0$$
(10)

and

$$E^2(E^2-\beta ^2)\psi ^{\,(2)}=0$$
(11)

where \(\displaystyle {E^{2}}=\frac{\partial ^{2}}{\partial {r^{2}}}+\frac{1}{r^{2}}\frac{\partial ^2}{\partial \theta ^2}-\frac{\cot \theta }{r^2}\frac{\partial }{\partial \theta }\) is the axisymmetric Stokesian operator.

3 Boundary conditions

Proper boundary conditions are required at the interface to evaluate the velocity components for the flow in both the regions. As in the classical case, assuming the equilibrium theory [1] of the interfacial tension is to be applicable for the considered flow, which indicates that the occurrence of interfacial tension generates a discontinuity in the normal stresses i.e., \(\tau _{rr}^{(\,1)}\,\ne \,\tau _{rr}^{(\,2)}\) but does not have any effect along the tangential stresses. The latter indicates the continuity of tangential stresses i.e., \(\tau _{r \theta }^{(\,1)}\,=\,\tau _{r\theta }^{(\,2)}\) at the interface. Therefore, we assume vanishing of normal component of velocity, continuity of tangential component of velocity and stress respectively [15]. At the cell surface of the fluid envelope, the condition of vanishing of vorticity i.e., Kuwabara model is considered along with the continuity of radial component of velocity.

Mathematically, at the fluid-fluid interface of the sphere \(r=b\), we have

  1. 1.

    Vanishing of normal components of velocity

    $$q_r^{(i)}=0, \,i=1,2.$$
    (12)
  2. 2.

    Continuity of tangential component of velocity

    $$q_\theta ^{(1)}=q_\theta ^{\,(2)},$$
    (13)
  3. 3.

    Continuity of tangential component of stresses

    $$\tau _{r \theta }^{(1)} =\tau _{r \theta }^{\,(2)},$$
    (14)

At the cell surface \(r=a\):

  1. 1.

    Continuity of radial component of velocity

    $$q_r^{(1)}+ U\cos \theta =0,$$
    (15)
  2. 2.

    Kuwabara model

    $$\nabla \times \mathbf {q}^{(1)}=0.$$
    (16)

In non-dimensional form using stream functions, boundary conditions at the inner fluid surface of sphere \(r=1\) are

$$\frac{\partial \psi ^{(i)}}{\partial \theta }=0,\,i=1,2.$$
(17)
$$\frac{\partial \psi ^{(1)}}{\partial {r}}=\frac{\partial \psi ^{\,(2)}}{\partial {r}},$$
(18)
$$\begin{aligned}&2r\frac{\partial }{\partial r}\left[ \frac{1}{r}\left( \gamma ^2\frac{\partial \psi ^{\,(2)}}{\partial {r}}-\frac{\partial \psi ^{(1)}}{\partial {r}}\right) \right] \nonumber \\&\quad +E^2\left[ \psi ^{(1)}-\gamma ^2\psi ^{\,(2)}\right] =0 , \end{aligned}$$
(19)

Similarly, boundary conditions at the cell surface \(r=\eta ^{-1}\) with \(\eta =b/a\) are

$$\begin{aligned} \frac{\partial \psi ^{(1)}}{\partial \theta }-r^2\,cos\theta \,\sin \theta =0, \end{aligned}$$
(20)

Kuwabara model

$$E^2\psi ^{(1)}=0.$$
(21)

4 Solution part

The expression for the solution for flow in both regions, obtained after solving Eqs. (10) and (11) are

$$\begin{aligned} \psi ^{(1)}= & {} \frac{1}{2}\left[ A\,r^2+\frac{B}{r}+C \sqrt{r}\,K_{3/2}(\alpha r)\right. \nonumber \\ & \left. +\,D \sqrt{r}\,I_{3/2}(\alpha r)\right] \sin ^2\theta , \end{aligned}$$
(22)
$$\psi ^{\,(2)}=\frac{1}{2}\left[ {E\,r^2+F \sqrt{r}\,I_{3/2}(\beta r)}\right] \sin ^2\theta.$$
(23)

where \(I_{3/2}(*)\) and \(K_{3/2}(*)\) represents modified Bessel functions of order 3/2 which are of first and second kind respectively. The arbitrary constants A, B, C, D, E, and F are to be determined.

5 Drag exerted on the fluid sphere

The hydrodynamic resisting force exerted on the sphere of fluid due to the flow of magneto fluid can be obtained by using the formula [1, 30]

$$\begin{aligned} F_D= & {} \pi \mu\, U\,b \nonumber \\&\int _{0}^{\pi }{\left[ r^4\sin ^3\theta \frac{\partial }{\partial r}\left( \frac{E^2\psi ^{(1)}}{r^2\sin ^2\theta }\right) -\alpha ^2r^2\sin \theta \frac{\partial \psi ^{(1)}}{\partial r}\right] }_{r=1}d\theta \end{aligned}$$
(24)

By using Eq. (22) into the integral in Eq. (24), we obtain

$$\begin{aligned} F_D=\frac{2}{3}\pi \mu \,b\,U\alpha ^2\left( B-2A-2CS_2-2DU_2\right) \end{aligned}$$
(25)

After applying the results of A, B, C,and,  D in Eq. (25), we get the required expression for drag on bounded fluid sphere using Kuwabara model as

$$\begin{aligned} F_D=2\pi \mu \,b\,U\left[ \frac{ {\varDelta _1}\, {{\alpha }^{2}}}{{\varDelta _1}\, {{\eta }^{3}}+{\varDelta _2}}\right] \end{aligned}$$
(26)

where the values of \(\varDelta _{1}\) and \(\varDelta _{2}\) are given in “Appendix”.

5.1 Results

5.1.1 Bounded medium using Kuwabara model

Case I

If \(\gamma \rightarrow \infty\) in Eq. (26), it acts as the solid sphere in presence of magnetic forces. Therefore, the drag reduces to

$$\begin{aligned} F_D=2\pi \mu \,b\,U\left[ \frac{(\chi _1\alpha +3\chi _2) {\alpha }^2}{(\chi _1\alpha +3\chi _2 ){{\eta }^{3}}- \chi _{{\textit{1}}} \alpha }\right] \end{aligned}$$
(27)

which is identical to the result obtained by Saad [30].

Case II

If \(\alpha =0,\,\beta =0\) in Eq. (27), we have the result for drag force exerted on solid sphere without magnetic field as

$$F_D=6\pi \mu \,b\,U\left[ \frac{5}{\eta (\eta ^5-5 \eta ^{2}+9) -5}\right]$$
(28)

which is identical to the result given in Saad [33].

5.1.2 Unbounded medium

As \(a\longrightarrow \infty\) or \(\eta =0\) in Eq. (26), the flow in unbounded medium.

Case I

Under magnetic effect, the drag on fluid sphere is given as

$$\begin{aligned} F_{inf}=-2\pi \mu\, b\,U\left[ \frac{ {\varDelta _3}\, {{{\gamma }}^{2}}\,{\chi _5}-{\varDelta _4}\, {\chi _6} }{{\varDelta _5}\, {{{\gamma }}^{2}}-{\varDelta _4}\, \left( \alpha +3\right) }\right] \end{aligned}$$
(29)

Case II

In absence of magnetic field i.e., for \(\alpha =0\) and \(\beta =0\) in Eq. (29), the drag on the fluid sphere is

$$\begin{aligned} F_{inf}=-2\pi \mu\,b\,U\left[ \frac{3{\gamma }^2+2}{{\gamma }^{2}+1}\right] \end{aligned}$$
(30)

which is in agreement with the work of Hadamard [6] and Rybczynski [7].

Case III

If \(\gamma \rightarrow \infty\) in Eq. (29), it acts as flow past solid sphere under magnetic forces and the drag is

$$\begin{aligned} F_{inf}=-2\pi \mu U b({{\alpha }^{2}}+3 \alpha +3) \end{aligned}$$
(31)

which agrees with the work of Prasad and Bucha [31].

Case IV

If \(\gamma \rightarrow \infty\) in Eq. (30), it behaves as solid sphere and the drag is

$$\begin{aligned} F_{inf}=-6\pi \mu \,U\,b \end{aligned}$$
(32)

which agrees with the expression for Stokes drag past a rigid impermeable sphere [1].

6 Graphical representation

The characterisation of wall correction factor \(W_c\) experienced by the bounded fluid sphere in presence of magnetic forces computed for different values of Hartmann numbers \(\alpha ,\,\beta\) for outer fluid and inner fluid region, volume fraction \(\delta =\eta ^3\) (\(0<\delta <1\)), viscosity ratio \(\gamma\) are shown graphically in Figs. 2, 3, 4, 5, 6 and 7 and Table 1. \(W_c\) represents the ratio of drag \(F_D\) acted on the spherical particle in bounded medium to the drag acted on the same in an infinite expanse of fluid \(F_{inf}\) denoted as \(W_c=\frac{F_D}{F_{inf}}\). Hartmann numbers provides a way to analyse the importance of drag forces emerged from magnetic and viscous forces in magnetohydrodynamics.

Table 1 Wall correction factor \(W_c\) against volume fraction \(\delta\) for varying viscosity ratio \(\gamma\) in presence and absence of magnetic field
Full size table
Fig. 2
figure 2

Representing \(W_c\) versus volume fraction \(\delta\) for different \(\alpha\) with \(\beta =10\), \(\gamma =3.5\)

Full size image
Fig. 3
figure 3

Representing \(W_c\) versus volume fraction \(\delta\) for different \(\beta\) with \(\alpha =1.5\), \(\gamma =3.5\)

Full size image
Fig. 4
figure 4

Representing \(W_c\) versus volume fraction \(\delta\) for different \(\gamma\) in both absence and presence of magnetic effect

Full size image
Fig. 5
figure 5

Representing \(W_c\) versus viscosity ratio \(\gamma\) for varying \(\alpha\) with \(\beta =5\), \(\delta =0.5\)

Full size image
Fig. 6
figure 6

Representing \(W_c\) versus viscosity ratio \(\gamma\) for varying \(\beta\) with \(\alpha =1.5\), \(\delta =0.5\)

Full size image
Fig. 7
figure 7

Representing \(W_c\) versus viscosity ratio \(\gamma\) for different \(\delta\) in both absence and presence of magnetic effect

Full size image

Variation of wall factor acting on viscous liquid sphere with \(\delta\) corresponding to increasing value of \(\alpha\) is pictured in Fig. 2. It is depicted that \(W_c\) decreases with an enhance value of \(\alpha\). The nature of increasing Hartmann number \(\beta\) as shown in Fig. 3 indicates a slight increase in the value of \(W_c\). Moreover, both the figure expresses the wall factor to be expanding with the rise in volume fraction. The alteration in values of wall factor is plotted for numerous values of \(\gamma\) in Fig. 4 for both absence  (\(\alpha \rightarrow 0,\beta \rightarrow 0\)) and presence (\(\alpha =2,\beta =5\)) of magnetic fields in the flow. The curves for \(\alpha =2,\beta =5\) is situated below the curves for \(\alpha \rightarrow 0,\beta \rightarrow 0\) which exhibits the decrease in wall correction factor under the action of magnetic fields. Interestingly, magnetic forces has a dominating effect which decreases the overall \(W_c\) acting on the fluid sphere. Demonstration of wall correction \(W_c\) against \(\gamma\) for varying \(\alpha\) is seen in Fig. 5. It is observed that for fixed value of volume fraction \(\delta\), \(W_c\) factor decreases with increasing \(\alpha\). It is also found to be increasing with increasing \(\delta.\) Figure 6 indicates a slight increase in the value of \(W_c\) with increasing \(\beta\). It is illustrated from Fig. 7 that keeping the rest parameters fixed, \(W_c\) is found to be decreasing under magnetic influence. Therefore, applying magnetic forces on the flow of fluid decreases the \(W_c\) acting on the fluid sphere.

Numerical values of wall correction factor for varying \(\delta\) and \(\gamma\) for the case of with and without magnetic forces are illustrated in Table 1. The results for \(\gamma =0\) indicates the case for gaseous bubble whereas \(\gamma \rightarrow \infty\) shows the case of solid sphere. Also \(\gamma =1\) is the case where the viscosity of both the fluids are equal. From the observed values, it is concluded that \(W_c\) decreases with the application of magnetic forces. Moreover, magnitude of wall correction factor are shown to be increasing for increasing volume fraction and viscosity ratio.

7 Conclusions

The major goal pursued in this article is to analyse the Stokes flow of conducting fluid through a fluid sphere surrounded by a spherical envelope, under the magnetic influence. Expression for the drag force on bounded fluid sphere is evaluated in an analytical approach, along with the several useful results in reduction cases. Numerical computation of wall effect and its dependence on various parameters are visualised by graphs. Based on the present work, the dependence of wall effect on magnetic parameters are found to be significant. We also observed a vast change in wall correction factor for varying viscosity ratio and volume fraction on applying magnetic field. It is shown that as the value of Hartmann number \(\alpha\) for outer fluid region increase, a remarkable decrease in the wall correction factor is noticed. A slight increase in wall correction factor is seen by increasing Hartmann number \(\beta\) for the inner fluid region. Overall, applying magnetic field in both the regions shows a decrease in wall correction factor as compared to the case in absence of magnetic effect. Moreover, the wall effect is found to be an increasing with increasing viscosity ratio \(\gamma\) and volume fraction \(\delta.\) As a future aspect of the present work, study of MHD effect on flow of Newtonian and non-Newtonian immiscible fluid with varying geometrical shapes can be considered, via which significant influence on flow may be obtained.