Introduction

With the emergence of nanotechnology, its application in micro/nano-electromechanical systems (MEMS/NEMS) is also developing rapidly. For MEMS/NEMS, due to their unprecedented advantages, they are widely used in high-tech fields such as automobiles, communications, aerospace, energy and national defense areas [1, 2]. The micro-beam resonator is one of the core components in NEMS/MEMS devices, which suffers different energy dissipation modes such as support damping [3, 4], surface damping [5, 6], air damping [7, 8] and thermoelastic damping (TED) [9].

Thermoelastic damping is the main source of energy dissipation [10]. During the micro-beam vibrating process, the tension area first cools down and then the compression area heats up, which induces a temperature gradient inside the structure. Consequently, the temperature transferring from the high-temperature area to the low-temperature area causes energy dissipation, which is accompanied by the production of thermoelastic damping. As early as the middle of the twentieth century, the TED study was first carried out by Zener [11], which triggered a large number of investigations on TED. Then, Lifshitz and Roukes [12] developed a more accurate TED model (L–R model) for rectangular beams using the Fourier’s law. As far as we know, the Zener model and the L–R model are two classical thermoelastic damping models. After that, Prabhakar and Vengallatore [13] conducted a study on the TED model concerning two-dimensional heat conduction along the length and thickness direction of the beam. Then, Chandorkar et al. [14] developed a TED analytical model considering three-dimensional thermal conduction. Many contributions have been devoted to investigating TED in multi-layer beams [15, 16], plates [17, 18], rings [19], non-uniform functionally graded beams [20, 21], continuously graded beams [22, 23] and open-hole resonators for uniform resonant devices [24]. In addition, some typical calculation methods were used to aid the theoretical analysis, for instance, the complex frequency method [11], the finite element method [25], and the thermal energy method [26]. Thermoelastic damping is always present in devices and is unavoidable. The adverse impact on devices can be reduced by optimizing the structural design. Now, due to the pursuit of high-performance NEMS/MEMS, the research on TED of nano-structures and micro-structures has attracted much attention.

It was evidenced that there exists a scale effect in the mechanical behavior of the nano-structures and micro-structures, which can cause significant changes in the performance of the system, such as the stress–strain relationship and TED [27]. Because the classical theory ignores the interactions between the internal units of the structure, the classical theory is incapable of accurately explaining the mechanical behavior of the micro/nano-structures. In general, small-scale effects can be considered by three different theories from different perspectives, namely, the strain gradient theory [28], the nonlocal elasticity theory [29] and the couple stress theory [30]. The classical couple stress theory involves two material length scale parameters. Because it is challenging to obtain the length scale parameters for micro-structures through experiments, Yang et al. [31] proposed a modified couple stress theory (MCST), which only requires one material length scale parameter. The MCST brings convenience to scholars to conduct experimental and theoretical researches. In terms of MCST, Rezazadeh et al. [32] derived an analytical expression of the quality factor for TED in a micro-beam resonator, and Zhong et al. [33] established the TED expression for the micro-plate resonators.

The classic Fourier’s law for heat conduction predicts an infinite heat transfer speed in media. But for heat transfer processes in micro-scale, this law is no longer applicable. To amend such defect, several non-Fourier heat conduction models were proposed, e.g., the Cattaneo–Vernott (C–V) heat wave model [34, 35], the dual-phase-lag (DPL) model [36], the three-phase-lag (TPL) model [37], and the memory-dependent derivative (MDD) model [38]. Accordingly, the generalized thermoelastic theories such as the Lord–Shulman (L–S) theory [39] and the Green–Lindsay (G–L) theory [40] were developed. Based on the L–S theory, Guo et al. [25] derived the TED expression of micro-beams and presented a useful tool in optimization design of micro-beam resonators against thermoelastic damping. Moreover, by employing the MDD heat conduction model, Wang et al. [41] obtained the TED expression for the micro-beam and compared the results with the classical model.

In recent years, only a few literatures considered both the size effect and the heat conduction process to conduct TED research, which hinders the development of high-performance micro/nano-mechanical resonators. Fortunately, scholars are making efforts to forward such researches, e.g., based on the DPL model, Borjalilou et al. [42] established a TED model in the context of the modified couple stress theory and determined the critical thickness in small scales. Shi et al. [43] derived the TED expression of micro-beams based on the surface effect and the DPL model and found that the surface effect has stronger effect than non-Fourier heat conduction on improving TED of nano-resonators. In addition, Kumar et al. [44] created a new type of micro-plate TED model based on the MCST and TPL model and found that the MCST with small values of phase-lag parameters can increase the quality factors of micro-plate resonators.

From the above literature review, it can be realized that the study of scale effect on TED in micro/nano resonators is still insufficient, especially, lacking studies of scale effect on TED based on the combination of MCST and MDD heat conduction model. Thus, the main contribution in present study is to combine MCST and MDD for the first time to lay a foundation for analyzing TED in micro/nano-resonators and then it is used to deal with the TED in Euler–Bernoulli nano-beam resonators by complex frequency method. In calculation, the effects of the nano-beam characteristics on TED, such as aspect ratio, boundary conditions, length scale parameters, temperature, thermal relaxation time etc., are studied and discussed in detail.

Theoretical Backgrounds

The Modified Couple Stress Theory

In accordance with MCST [31], the variation of strain energy \(\delta {\kern 1pt} \Pi\) in isotropic linear elastic material takes the form

$$\delta {\kern 1pt} \Pi = \iiint_{V} {\left( {\sigma_{ij} \delta \varepsilon_{ij} + m_{ij} \delta \eta_{ij} } \right)}{\text{d}}V,$$
(1)

where \(V\) denotes the volume of an elastic medium, \(\sigma_{ij}\) represents the component of the symmetric part of the stress tensor \(\sigma\), \(\varepsilon_{ij}\) is the component of the strain tensor \(\varepsilon\). \(m_{ij}\) and \(\eta_{ij}\) denotes the deviatoric part of the couple stress tensor \(m\) and the symmetric part of the rotation gradient tensor \(\eta\), respectively. These components can be written as

$$\varepsilon_{ij} = \frac{1}{2}\left( {\frac{{\partial u_{i} }}{{\partial x_{j} }} + \frac{{\partial u_{j} }}{{\partial x_{i} }}} \right),$$
(2)
$$\eta_{ij} = \frac{1}{2}\left( {\frac{{\partial \vartheta_{i} }}{{\partial x_{j} }} + \frac{{\partial \vartheta_{j} }}{{\partial x_{i} }}} \right),$$
(3)
$$\vartheta_{i} = \frac{1}{2}\left( {{\text{curl}}\left( u \right)} \right)_{i} ,$$
(4)

where \(u_{i}\) and \(\vartheta_{i}\) are the components of the displacement vector field \(u\) and the components of the infinitesimal rotation vector \(\vartheta\), respectively. The constitutive relationship of linear elastic materials can be defined as

$$\sigma_{ij} = \lambda \varepsilon_{kk} \delta_{ij} + 2\mu \varepsilon_{ij} - (3\lambda + 2\mu )\alpha \theta \delta_{ij} ,$$
(5)
$$m_{ij} = 2\mu l^{2} \eta_{ij} ,$$
(6)

where \(\mu\) and \(\lambda\) are Lame’s constants, which can be represented by Young's modulus \(E\) and Poisson's ratio \(\nu\) as \(\mu = E/2\left( {1 + \nu } \right)\) and \(\lambda = Ev/\left[ {\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)} \right]\). \(\delta_{ij}\) is the Kronecker delta, \(\alpha\) is the linear thermal expansion coefficient, \(\theta = T - T_{0}\) is the temperature increment and \(l\) denotes the material length-scale parameter, which is used to reflect the effect of MCST and seize the size dependency of the Euler–Bernoulli beam model in micro-resonators. Similarly, according to Eq. (5), the component of the strain tensor also can be represented by

$$\varepsilon_{ij} = \frac{1}{E}\left[ {\left( {1 + \nu } \right)\sigma_{ij} - \nu \sigma_{kk} \delta_{ij} } \right] + \alpha \theta \delta_{ij} ,$$
(7)

where \(\sigma_{kk}\) denotes volume stress.

The Memory-dependent (MDD) Heat Conduction Model

According to the MDD heat conduction model, the heat conduction equation proposed by Yu et al. can be written as [38]

$${\varvec{q}} + \tau D_{\omega } {\varvec{q}} = - \kappa \nabla \theta ,$$
(8)
$$D_{\omega } {\varvec{q}}\left( {\vec{r},t} \right) = \frac{1}{\omega }\int_{t - \omega }^{t} {K\left( {t - \xi } \right)} \frac{{\partial {\varvec{q}}\left( {\vec{r},\xi } \right)}}{\partial \xi }{\text{d}}\xi ,$$
(9)
$$K\left( {t - \xi } \right) = \left( {1 - \frac{t - \xi }{\omega }} \right)^{j} ,$$
(10)

where \({\varvec{q}}\) represents the heat flux vector, \(\tau\) and \(\omega\) denote the thermal relaxation time and the memory time period, respectively, \(\kappa\) denotes the thermal conductivity. The memory-dependent derivative of \({\varvec{q}}\) can be expressed as \(D_{\omega } {\varvec{q}}\), the kernel function is represented as \(K\left( {t - \xi } \right)\) and \(j\) represents a real number.

For the isotropic case, the equation of energy conservation can be given by

$$- \nabla \cdot {\varvec{q}} + Q = \rho C_{e} \frac{\partial \theta }{{\partial t}} + T_{0} \beta \frac{{\partial \varepsilon_{kk} }}{\partial t},$$
(11)

where \(Q\) represents the heat supply term. In this work, we consider that \(Q = 0\) which indicates no inner heat source is involved. \(\rho\), \(C_{e}\) and \(\varepsilon_{kk}\) denote the mass density, specific heat and cubic dilation, respectively. Moreover, \(\beta = E\alpha /(1 - 2\nu )\) represents the thermal modulus.

By substituting from Eq. (11) into (8), the heat conduction equation based on the MDD can be yielded as

$$(1 + \tau D_{\omega } )\left( {\rho C_{e} \frac{\partial \theta }{{\partial t}} + \beta T_{0} \frac{{\partial \varepsilon_{kk} }}{\partial t}} \right) = \kappa \nabla^{2} \theta .$$
(12)

Derivation of the Basic Governing Equations

As shown in Fig. 1, an isotropic and homogeneous Euler–Bernoulli beam with length \(L\left( {0 \le x \le L} \right)\), width \(b\left( {{{ - b} \mathord{\left/ {\vphantom {{ - b} 2}} \right. \kern-\nulldelimiterspace} 2} \le y \le {b \mathord{\left/ {\vphantom {b 2}} \right. \kern-\nulldelimiterspace} 2}} \right)\) and thickness \(h\left( {{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-\nulldelimiterspace} 2} \le z \le {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}} \right)\) is considered. For the beam, the displacement components are

$$u_{x} = - z\frac{{\partial w\left( {x,t} \right)}}{\partial x},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} u_{y} = 0,u_{z} = w\left( {x,t} \right),$$
(13)

where \(u_{x}\), \(u_{y}\) and \(u_{z}\) denote the displacements along the axis \(x\), \(y\) and \(z\), respectively.

Fig. 1
figure 1

Schematic diagram of a rectangular nano-beam

Full size image

By substituting from Eq. (13) into Eqs. (2), (3) and (4), the strain component in the x-axis and the components of \(\eta\) can be obtained as

$$\varepsilon_{11} = - z\frac{{\partial^{2} w}}{{\partial x^{2} }},$$
(14)
$$\eta_{12} = \eta_{21} = - \frac{1}{2}\frac{{\partial^{2} w}}{{\partial x^{2} }}.$$
(15)

Substituting from Eq. (15) into Eq. (6) gets

$$m_{12} = m_{21} = - \mu l^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }}.$$
(16)

Based on plane stress condition, we can obtain

$$\sigma_{22} = \sigma_{12} = \sigma_{32} = 0,\sigma_{33} = \sigma_{13} = \sigma_{23} = 0.$$
(17)

Substituting from Eq. (14) into Eq. (7), we get

$$\sigma_{11} = - E\alpha \theta - Ez\frac{{\partial^{2} w}}{{\partial x^{2} }}.$$
(18)

From Eqs. (1) and (14)–(18), we obtain

$$\begin{gathered} \delta {\kern 1pt} \Pi { = }\int_{0}^{L} {\iint_{A} {\left[ {\left( { - Ez\frac{{\partial^{2} w}}{{\partial x^{2} }} - E\alpha \theta } \right)\left( { - z\delta \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)} \right) + \left( { - \mu l^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)\left( { - \delta \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)} \right)} \right]}} {\text{d}}A{\text{d}}x \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} { = }\int_{0}^{L} {\iint_{A} {\left( {Ez^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }} + E\alpha z\theta } \right)}} {\text{d}}A{\text{d}}\delta \left( {\frac{\partial w}{{\partial x}}} \right) + \int_{0}^{L} {\iint_{A} {\left( {\mu l^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)}} {\text{d}}A{\text{d}}\delta \left( {\frac{\partial w}{{\partial x}}} \right) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} { = }\int_{0}^{L} {\left( {EI\frac{{\partial^{2} w}}{{\partial x^{2} }} + M_{T} } \right)} {\text{d}}\delta \left( {\frac{\partial w}{{\partial x}}} \right) + \int_{0}^{L} {\left( {\mu Al^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)} {\text{d}}\delta \left( {\frac{\partial w}{{\partial x}}} \right), \hfill \\ \end{gathered}$$
(19)

where

$$I = \frac{{bh^{3} }}{12},$$
(20)
$$M_{T} = E\alpha b\int_{{ - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}} {\theta z{\text{d}}z} .$$
(21)

By utilizing integration by parts, Eq. (19) can be expressed as

$$\begin{gathered} \delta {\kern 1pt} \Pi { = }\left[ {\left( {EI\frac{{\partial^{2} w}}{{\partial x^{2} }} + M_{T} } \right)\delta \left( {\frac{\partial w}{{\partial x}}} \right)} \right]_{x = 0}^{x = L} - \int_{0}^{L} {\left( {EI\frac{{\partial^{3} w}}{{\partial x^{3} }} + \frac{{\partial M_{T} }}{\partial x}} \right)} \delta \left( {\frac{\partial w}{{\partial x}}} \right){\text{d}}x \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + \left[ {\left( {\mu Al^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)\delta \left( {\frac{\partial w}{{\partial x}}} \right)} \right]_{x = 0}^{x = L} - \int_{0}^{L} {\left( {\mu Al^{2} \frac{{\partial^{3} w}}{{\partial x^{3} }}} \right)} \delta \left( {\frac{\partial w}{{\partial x}}} \right){\text{d}}x, \hfill \\ \end{gathered}$$
(22)
$$\begin{gathered} \delta {\kern 1pt} \Pi { = }\left[ {\left( {EI\frac{{\partial^{2} w}}{{\partial x^{2} }} + M_{T} } \right)\delta \left( {\frac{\partial w}{{\partial x}}} \right)} \right]_{x = 0}^{x = L} - \left[ {\left( {EI\frac{{\partial^{3} w}}{{\partial x^{3} }} + \frac{{\partial M_{T} }}{\partial x}} \right)\delta w} \right]_{x = 0}^{x = L} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + \int_{0}^{L} {\left( {EI\frac{{\partial^{4} w}}{{\partial x^{4} }} + \frac{{\partial^{2} M_{T} }}{{\partial x^{2} }}} \right)} \delta w{\text{d}}x + \int_{0}^{L} {\left( {\mu Al^{2} \frac{{\partial^{4} w}}{{\partial x^{4} }}} \right)} \delta w{\text{d}}x \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + {\kern 1pt} {\kern 1pt} \left[ {\left( {\mu Al^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)\delta \left( {\frac{\partial w}{{\partial x}}} \right)} \right]_{x = 0}^{x = L} - \left[ {\left( {\mu Al^{2} \frac{{\partial^{3} w}}{{\partial x^{3} }}} \right)\delta w} \right]_{x = 0}^{x = L} . \hfill \\ \end{gathered}$$
(23)

Then, the expression of the strain energy can be written as

$$\begin{gathered} \delta {\kern 1pt} \Pi = \left[ {\left( {\left( {EI + \mu Al^{2} } \right)\frac{{\partial^{2} w}}{{\partial x^{2} }} + M_{T} } \right)\delta \left( {\frac{\partial w}{{\partial x}}} \right) - \left( {\left( {EI + \mu Al^{2} } \right)\frac{{\partial^{3} w}}{{\partial x^{3} }} + \frac{{\partial M_{T} }}{\partial x}} \right)\delta w} \right]_{x = 0}^{x = L} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + \int_{0}^{L} {\left[ {\left( {EI + \mu Al^{2} } \right)\frac{{\partial^{4} w}}{{\partial x^{4} }} + \frac{{\partial^{2} M_{T} }}{{\partial x^{2} }}} \right]\delta w{d}x} . \hfill \\ \end{gathered}$$
(24)

Furthermore, the variation of the kinetic energy is denoted as

$$\delta {\kern 1pt} T = \rho A\int_{0}^{L} {\frac{\partial w}{{\partial t}}} \delta {\kern 1pt} \left( {\frac{\partial w}{{\partial t}}} \right){\text{d}}x.$$
(25)

Given Hamilton’s principle [43], the equation of motion in the time interval \(\left[ {t_{1} ,t_{2} } \right]\) is written as

$$\int_{{t_{1} }}^{{t_{2} }} {\left( {\delta {\kern 1pt} \Pi - \delta T} \right)} {d}t = 0.$$
(26)

Conbining Eqs. (24), (25) and (26), the motion equation is obtained as

$$\left( {EI + \mu Al^{2} } \right)\frac{{\partial^{4} w}}{{\partial x^{4} }} + E\alpha b\int_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{{{ + h} \mathord{\left/ {\vphantom {{ + h} 2}} \right. \kern-\nulldelimiterspace} 2}}} {\frac{{\partial^{2} \theta }}{{\partial x^{2} }}z{\text{d}}z} + \rho A\frac{{\partial^{2} w}}{{\partial t^{2} }} = 0.$$
(27)

According to Eqs. (7), (14), and (17), the strain components can be obtained as

$$\varepsilon_{22} = \varepsilon_{33} = \nu z\frac{{\partial^{2} w}}{{\partial x^{2} }} + \left( {1 + \nu } \right)\alpha \theta ,$$
(28)
$$\varepsilon_{kk} = \varepsilon_{11} + \varepsilon_{22} + \varepsilon_{33} = \left( {2\nu - 1} \right)z\frac{{\partial^{2} w}}{{\partial x^{2} }} + 2\left( {1 + \nu } \right)\alpha \theta .$$
(29)

By substituting from (29) into (12), we obtain

$$(1 + \tau D_{\omega } )\left[ {\left( {1 + 2\Delta E\frac{1 + \nu }{{1 - 2\nu }}} \right)\frac{\partial \theta }{{\partial t}} - z\frac{\Delta E}{\alpha }\frac{{\partial^{3} w}}{{\partial x^{2} \partial t}}} \right] = \chi \nabla^{2} \theta ,$$
(30)

where \(\Delta E = E\alpha^{2} T_{0} /\rho C_{e}\) and \(\chi = \kappa /\rho C_{e}\) are called as relaxation strength coefficient and thermal diffusion coefficient, respectively. Since the thermal gradient along the z-direction is much larger than that in other direction [12], \(\nabla^{2} \theta\) can be changed into \({{\partial^{2} \theta } \mathord{\left/ {\vphantom {{\partial^{2} \theta } {\partial z^{2} }}} \right. \kern-\nulldelimiterspace} {\partial z^{2} }}\). Due to \(\Delta E \ll 1\), the Eq. (30) can be reduced to

$$(1 + \tau D_{\omega } )\left( {\frac{\partial \theta }{{\partial t}} - z\frac{\Delta E}{\alpha }\frac{{\partial^{3} w}}{{\partial x^{2} \partial t}}} \right) = \chi \frac{{\partial^{2} \theta }}{{\partial z^{2} }}.$$
(31)

Therefore, Eqs. (27) and (31) compose the governing equations of the nano-beam resonator based on the size-dependent and the memory-dependent influence.

Thermoelastic Damping

The expressions of \(w\) and \(\theta\) are assumed as

$$w\left( {x,t} \right) = w\left( x \right){e}^{{i{\kern 1pt} \Omega {\kern 1pt} t}} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \theta \left( {x,z,t} \right) = \theta \left( {x,z} \right){e}^{{i{\kern 1pt} \Omega {\kern 1pt} t}} ,$$
(32)

where \(\Omega\) denotes the vibration frequency of the beam. Applying the above expressions to Eq. (31), we obtain

$$\Omega \left[ { - \frac{{\tau {\kern 1pt} \Omega }}{\omega }\int_{0}^{\omega } {K\left( s \right)\cos \left( {\Omega s} \right){d}s + i\left( {1 + \frac{{\tau {\kern 1pt} \Omega }}{\omega }\int_{0}^{\omega } {K\left( s \right)\sin \left( {\Omega s} \right){d}s} } \right)} } \right]\left( {\theta - z\frac{\Delta E}{\alpha }\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \chi \frac{{\partial^{2} \theta }}{{\partial z^{2} }}.$$
(33)

For simplification, the following non-dimensional quantities are introduced [41]

$$\begin{gathered} \overline{x} = \frac{x}{L},\overline{z} = \frac{z}{h},\Theta = \frac{\theta }{{T_{0} }},W = \frac{w}{h}, \hfill \\ \left( {\overline{\tau },\overline{\omega },\overline{s}} \right) = \frac{1}{L}\sqrt {\frac{E}{\rho }} \left( {\tau ,\omega ,s} \right),\left( {\overline{\Omega },\overline{\Omega }_{0} } \right) = L^{2} \sqrt {\frac{\rho A}{{EI}}} \left( {\Omega ,\Omega_{0} } \right). \hfill \\ \end{gathered}$$
(34)

By applying the above variables, Eq. (33) turns into

$$\frac{{\partial^{2} \Theta }}{{\partial \overline{z}^{2} }} + k^{2} \Theta - k^{2} a\overline{z}\frac{{\partial^{2} W}}{{\partial \overline{x}^{2} }} = 0,$$
(35)

where

$$k = \zeta \left( {\varphi - i\frac{1}{\varphi }} \right),$$
(36)
$$\zeta = \sqrt {\frac{{\overline{\Omega }h^{2} c}}{2\chi LH}\left( {1 + \frac{{\overline{\tau }{\kern 1pt} \overline{\Omega }}}{H}\int_{0}^{1} {\overline{K}\left( {\overline{s}} \right)\sin \left( {\frac{{\overline{\Omega }\overline{\omega }\overline{s}}}{H}} \right){\text{d}}\overline{s}} } \right)} ,$$
(37)
$$\varphi = \sqrt {\frac{{\frac{{\overline{\tau }{\kern 1pt} \overline{\Omega }}}{H}\int_{0}^{1} {\overline{K}\left( {\overline{s}} \right)\cos \left( {\frac{{\overline{\Omega }\overline{\omega }\overline{s}}}{H}} \right){d}\overline{s}} }}{{1 + \frac{{\overline{\tau }{\kern 1pt} \overline{\Omega }}}{H}\int_{0}^{1} {\overline{K}\left( {\overline{s}} \right)\sin \left( {\frac{{\overline{\Omega }\overline{\omega }\overline{s}}}{H}} \right){d}\overline{s}} }} + \sqrt {\left( {\frac{{\frac{{\overline{\tau }{\kern 1pt} \overline{\Omega }}}{H}\int_{0}^{1} {\overline{K}\left( {\overline{s}} \right)\cos \left( {\frac{{\overline{\Omega }\overline{\omega }\overline{s}}}{H}} \right){d}\overline{s}} }}{{1 + \frac{{\overline{\tau }{\kern 1pt} \overline{\Omega }}}{H}\int_{0}^{1} {\overline{K}\left( {\overline{s}} \right)\sin \left( {\frac{{\overline{\Omega }\overline{\omega }\overline{s}}}{H}} \right){d}\overline{s}} }}} \right)^{2} + 1} } ,$$
(38)
$$\overline{K}\left( {\overline{s}} \right) = \left( {1 - \overline{s}} \right)^{j} ,a = \frac{{\alpha Eh^{2} }}{{\rho C_{e} L^{2} }},c = \sqrt {\frac{E}{\rho }} ,H = L\sqrt{\frac{A}{I}} .$$
(39)

By solving Eq. (35), we obtain the general solution

$$\Theta = A_{1} \sin (k\overline{z}) + A_{2} \cos (k\overline{z}) + a\overline{z}\frac{{\partial^{2} W}}{{\partial \overline{x}^{2} }},$$
(40)

where the two unknown constants \(A_{1}\) and \(A_{2}\) can be determined from the boundary conditions of the top and bottom surfaces. In this paper, the upper and lower surfaces of the beam are adiabatic, which can be expressed as \({{\partial \theta } \mathord{\left/ {\vphantom {{\partial \theta } {\partial z}}} \right. \kern-\nulldelimiterspace} {\partial z}} = 0\left( {z = \pm {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}} \right)\) [41]. Therefore, we obtain

$$A_{1} = - \frac{a}{{k\cos \left( {{k \mathord{\left/ {\vphantom {k 2}} \right. \kern-\nulldelimiterspace} 2}} \right)}}\frac{{\partial^{2} W}}{{\partial \overline{x}^{2} }},{\kern 1pt} {\kern 1pt} {\kern 1pt} A_{2} = 0.$$
(41)

Thus, Eq. (40) is written as

$$\Theta = a\left( {\overline{z} - \frac{{\sin (k\overline{z})}}{{k\cos \left( {{k \mathord{\left/ {\vphantom {k 2}} \right. \kern-\nulldelimiterspace} 2}} \right)}}} \right)\frac{{\partial^{2} W}}{{\partial \overline{x}^{2} }}.$$
(42)

By combining Eqs. (27) and (32), the motion equation can be denoted as

$$\left( {EI + \mu Al^{2} } \right)\frac{{\partial^{4} w}}{{\partial x^{4} }} + E\alpha b\int_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{{{ + h} \mathord{\left/ {\vphantom {{ + h} 2}} \right. \kern-\nulldelimiterspace} 2}}} {\frac{{\partial^{2} \theta }}{{\partial x^{2} }}z{d}z} = \rho A\Omega^{2} w.$$
(43)

According to the non-dimensional quantities, Eq. (43) is written as

$$\left( {1 + B} \right)\frac{{\partial^{4} W}}{{\partial \overline{x}^{4} }} - \overline{\Omega }^{2} W + \alpha T_{0} H^{2} \int_{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} {\frac{{\partial^{2} \Theta }}{{\partial \overline{x}^{2} }}} \overline{z}{d}\overline{z} = 0.$$
(44)

with

$$B = \frac{{\mu Al^{2} }}{EI}.$$
(45)

Substituting Eq. (42) into Eq. (44), we obtain

$$\left[ {1 + B + \Delta E\left( {1 + f\left( {\overline{\Omega }} \right)} \right)} \right]\frac{{\partial^{4} W}}{{\partial \overline{x}^{4} }} - \overline{\Omega }^{2} W = 0,$$
(46)

where

$$f\left( {\overline{\Omega }} \right) = \frac{12}{{k^{2} }}\left( {1 - \frac{2}{k}\tan \frac{k}{2}} \right).$$
(47)

The vibration frequency of the classic Euler–Bernoulli beam can be calculated by

$$\frac{{\partial^{4} W}}{{\partial \overline{x}^{4} }} = \overline{\Omega }_{{{\kern 1pt} {\kern 1pt} 0}}^{2} W,$$
(48)

where \(\overline{\Omega }_{{{\kern 1pt} {\kern 1pt} 0{\kern 1pt} }}\) denotes non-dimensional frequency without thermoelastic damping. For two clamped ends, we know the first three non-dimensional natural frequencies are \(\overline{\Omega }_{{{\kern 1pt} {\kern 1pt} 0}} = \left\{ {22.4,61.7,121} \right\}\). The first non-dimensional natural frequency \(\overline{\Omega }_{{{\kern 1pt} {\kern 1pt} 0}} = \left\{ {15.4,\pi^{2} ,3.52} \right\}\) are for clamped and simply supported ends, two simply supported ends and clamped and free ends, respectively [41].

By combining Eqs. (46) and (48), the non-dimensional natural frequency is represented as

$$\overline{\Omega } = \overline{\Omega }_{{{\kern 1pt} {\kern 1pt} 0}} \sqrt {1{ + }B{ + }\Delta E\left( {1{ + }f\left( {\overline{\Omega }} \right)} \right)} .$$
(49)

Due to \(\Delta E \ll 1\) and the value of TED is very weak, \(f\left( {\overline{\Omega }} \right)\) can be replaced by \(f\left( {\overline{\Omega }_{{{\kern 1pt} {\kern 1pt} 0}} } \right)\), the above equation is written as

$$\overline{\Omega } = \overline{\Omega }_{{{\kern 1pt} {\kern 1pt} 0}} \left[ {\sqrt {1{ + }B} + \frac{{\Delta E\left( {1 + f\left( {\overline{\Omega }_{{{\kern 1pt} {\kern 1pt} 0}} } \right)} \right)}}{{2\sqrt {1 + B} }}} \right].$$
(50)

Now, we can write the real and imaginary parts of \(\overline{\Omega }\) as

$${\text{Re}} \overline{\Omega } = \overline{\Omega }_{{{\kern 1pt} {\kern 1pt} 0}} \left\{ {\sqrt {1{ + }B} + \frac{\Delta E}{{2\sqrt {1{ + }B} }}\left[ {1 + \frac{12}{{\zeta^{2} \left( {\varphi^{2} + \frac{1}{{\varphi^{2} }}} \right)^{2} }}\left( {\varphi^{2} - \frac{1}{{\varphi^{2} }} - 2\frac{{\left( {\varphi^{3} - \frac{3}{\varphi }} \right)\sin \left( {\zeta \varphi } \right) - \left( {3\varphi - \frac{1}{{\varphi^{3} }}} \right)\sinh \left( {\frac{\zeta }{\varphi }} \right)}}{{\zeta \left( {\varphi^{2} + \frac{1}{{\varphi^{2} }}} \right)\left[ {\cos \left( {\zeta \varphi } \right) + \cosh \left( {\frac{\zeta }{\varphi }} \right)} \right]}}} \right)} \right]} \right\},$$
(51)
$${\text{Im}} \overline{\Omega } = \frac{{12\overline{\Omega }_{{{\kern 1pt} {\kern 1pt} 0}} }}{{\sqrt {1{ + }B} }}\frac{\Delta E}{{\zeta^{2} \left( {\varphi^{2} + \frac{1}{{\varphi^{2} }}} \right)^{2} }}\left\{ {1 - \frac{{\left( {3\varphi - \frac{1}{{\varphi^{3} }}} \right)\sin \left( {\zeta \varphi } \right) - \left( {\varphi^{3} - \frac{3}{\varphi }} \right)\sinh \left( {\frac{\zeta }{\varphi }} \right)}}{{\zeta \left( {\varphi^{2} + \frac{1}{{\varphi^{2} }}} \right)\left[ {\cos \left( {\zeta \varphi } \right) + \cosh \left( {\frac{\zeta }{\varphi }} \right)} \right]}}} \right\}.$$
(52)

The thermoelastic damping is denoted in the light of the inverse of the quality factor as [12]

$$Q^{ - 1} = 2\left| {\frac{{{\text{Im}} \overline{\Omega }}}{{{\text{Re}} \overline{\Omega }}}} \right|.$$
(53)

By combining Eqs. (51), (52) and (53), the final expression is obtained by simplifying the result in line with \(\Delta E \ll 1\), which is written as

$$Q^{ - 1} = \frac{24}{{1 + B}}\frac{\Delta E}{{\zeta^{2} \left( {\varphi^{2} + \frac{1}{{\varphi^{2} }}} \right)^{2} }}\left\{ {1 - \frac{{\left( {3\varphi - \frac{1}{{\varphi^{3} }}} \right)\sin \left( {\zeta \varphi } \right) - \left( {\varphi^{3} - \frac{3}{\varphi }} \right)\sinh \left( {\frac{\zeta }{\varphi }} \right)}}{{\zeta \left( {\varphi^{2} + \frac{1}{{\varphi^{2} }}} \right)\left[ {\cos \left( {\zeta \varphi } \right) + \cosh \left( {\frac{\zeta }{\varphi }} \right)} \right]}}} \right\}.$$
(54)

Moreover, when the size-dependent effect and the memory-dependent (MDD) heat conduction model are neglected (\(l = 0,\overline{\tau } = 0\)), the current model of \(Q^{ - 1}\) can be simplified as

$$Q^{ - 1} = \frac{6\Delta E}{{\zeta^{2} }}\left( {1 - \frac{1}{\zeta }\frac{\sinh \zeta + \sin \zeta }{{\cosh \zeta + \cos \zeta }}} \right).$$
(55)

where the TED model is the L–R model under the Fourier heat conduction.

Results and Discussions

In this section, based on the MCST and MDD heat conduction model, we study how the reference temperature, height, boundary conditions and aspect ratios influence the TED in nano-beams. The material constants of silicon are listed in Table 1. Unless otherwise specified, the physical parameter used in the following calculation is \(T_{0} = 300\;{\text{K}}\), \(b = h\), \({L \mathord{\left/ {\vphantom {L b}} \right. \kern-\nulldelimiterspace} b} = 10\), \(\overline{\tau } = 0.5\) and \(\overline{\omega } = 0.5\). For brevity, the reciprocal of the quality factor \(Q^{ - 1}\) is scaled by the relaxation strength coefficient \(\Delta E\).

Table 1 Material parameters of silicon [43]
Full size table

To validate the results obtained from the current model, a comparison is made in Fig. 2. In current TED model, when the length scale parameter \(l = 0\), it will degenerate into the model proposed by Wang et al. [41] that only considers the effect of the memory-dependent heat conduction model. It can be seen from Fig. 2 that the first two curves overlap, which demonstrates the validation of our results. When \(l = 10\;{\kern 1pt} {\kern 1pt} {\text{nm}}\), the value of \({{Q^{ - 1} } \mathord{\left/ {\vphantom {{Q^{ - 1} } {\Delta E}}} \right. \kern-\nulldelimiterspace} {\Delta E}}\) decreases as \(h\) is less than \(400\;{\text{nm}}\), which denotes that the influence of the couple stress theory will weaken TED. These can efficiently prove the validation of the current TED model.

Fig. 2
figure 2

Influence of length scale parameter \(l\) on the variation of \({{Q^{ - 1} } \mathord{\left/ {\vphantom {{Q^{ - 1} } {\Delta E}}} \right. \kern-\nulldelimiterspace} {\Delta E}}\)

Full size image

Figure 3a, b indicate the impact of the length scale parameter \(l\) and thermal relaxation time \(\overline{\tau }\) on TED, respectively. \(\overline{\tau }\) reflects the influence of memory-dependent heat conduction on TED. The effect of modified couple stress on TED is represented by the length scale parameter \(l\). When \(l\) and \(\overline{\tau }\) tend to zero, the case corresponds to that of L–R model [12] as illustrated in Fig. 3a, b, respectively. As shown in Fig. 3a, b, similar to the existing investigation, it can be observed that the peak value of TED decreases with the increase of \(l\) as well as \(\overline{\tau }\). Departing from the peak value, the value of TED on both sides gradually decreases until it disappears. When the height of the nanobeam is about \(10 \sim 10^{3} {\text{nm}}\), the value of TED decreases with the increase of the length scale parameter \(l\) in Fig. 3a. Moreover, in Fig. 3b, it shows that the maximum value of the TED increases with the increase of the thermal relaxation time for nano-beams of thickness of \(10^{2} \sim 10^{4} {\text{nm}}\). However, the critical thickness corresponding to the maximum TED is not affected by the change of the thermal relaxation time.

Fig. 3
figure 3

Influence of a modified couple stress theory, and b memory-dependent heat conduction on variation \({{Q^{ - 1} } \mathord{\left/ {\vphantom {{Q^{ - 1} } {\Delta E}}} \right. \kern-\nulldelimiterspace} {\Delta E}}\)

Full size image

For the variation \({{Q^{ - 1} } \mathord{\left/ {\vphantom {{Q^{ - 1} } {\Delta E}}} \right. \kern-\nulldelimiterspace} {\Delta E}}\) associated with the reference temperature \(T_{0}\), the corresponding variations are shown in Fig. 4. It can be noticed that the reference temperature \(T_{0}\) has no impact on the peak value of TED based on the current model, while, with the increase of the reference temperature \(T_{0}\), the position of the TED peak value changes obviously.

Fig. 4
figure 4

Influence of the reference temperature \({T}_{0}\) on variation \({{Q^{ - 1} } \mathord{\left/ {\vphantom {{Q^{ - 1} } {\Delta E}}} \right. \kern-\nulldelimiterspace} {\Delta E}}\)

Full size image

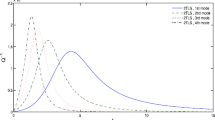
Figure 5a, b demonstrate the effect of length-to-width ratio \({L \mathord{\left/ {\vphantom {L b}} \right. \kern-\nulldelimiterspace} b}\) and modes on TED for various nano-beam thicknesses, respectively. Apparently, with the increase of the length-to-width ratio, the TED peak of the nano-beam decreases. Figure 5a reveals that the lower length-to-width ratio leads to greater value of TED, meanwhile, the nano-beam thickness corresponding to the maximum value of TED also changes with the variation of the length-to-width ratio. It is clear that the TED has a great effect for different modes. It is obvious that the variation of TED with respect to height exists a peak value for each mode. Moreover, based on the first-order mode, it can be observed that the peak value of TED increases significantly compared with the higher order modes.

Fig. 5
figure 5

Variation of \({{Q^{ - 1} } \mathord{\left/ {\vphantom {{Q^{ - 1} } {\Delta E}}} \right. \kern-\nulldelimiterspace} {\Delta E}}\) with the height \(h\) under a different length-to-width ratio \({L \mathord{\left/ {\vphantom {L b}} \right. \kern-\nulldelimiterspace} b}\), and b different modes

Full size image

Figure 6a–c analyze the impact of length scale parameters on TED in nano-resonators with the thickness \(h = 100\;{\text{nm}}\). In the calculation, three different situations, i.e., different reference temperature, length-to-width ratio and modes, and the effect of modified couple stress theory and MDD, are considered. Obviously, when the length scale parameter is less than the thickness, the value of TED increases quickly. These results denote that these factors are significant for high-performance resonator design.

Fig. 6
figure 6

Influence of length scale parameter \(l\) on variation \({{Q^{{ - 1}} } \mathord{\left/ {\vphantom {{Q^{{ - 1}} } {\Delta E}}} \right. \kern-\nulldelimiterspace} {\Delta E}}\) of nano-resonators: a different reference temperature \(T_{0}\), b different length-to-width ratio \({L \mathord{\left/ {\vphantom {L b}} \right. \kern-\nulldelimiterspace} b}\), c different modes

Full size image

Figure 7a, b display the influence of the MDD heat conduction model for a nano-resonator with \(l = 10\;{\text{nm}}\). Apparently, for \(h = 10^{2} \sim 10^{4} \;{\text{nm}}\), Fig. 7a, b represent that the maximum value of \({{Q^{ - 1} } \mathord{\left/ {\vphantom {{Q^{ - 1} } {\Delta E}}} \right. \kern-\nulldelimiterspace} {\Delta E}}\) increases with the increase of the thermal relaxation time and decreases of memory time period for nano-resonator. In addition, for nano-resonators of larger or smaller heights, the thermoelastic damping remains unchanged for any thermal relaxation time and memory time period. Moreover, the critical thickness corresponding to the maximum thermoelastic damping is not affected by changes of the thermal relaxation time and memory time period.

Fig. 7
figure 7

Influence of a thermal relaxation time \(\overline{\tau }\), b memory time period \(\overline{\omega }\) on TED

Full size image

To research the influence of kernel functions on TED, Fig. 8 denotes that the variation of the \({{Q^{ - 1} } \mathord{\left/ {\vphantom {{Q^{ - 1} } {\Delta E}}} \right. \kern-\nulldelimiterspace} {\Delta E}}\) for nano-resonators thickness under different kernel functions, which are ideal kernel with \(j = 0\), linear kernel with \(j = 1\) and nonlinear kernel with \(j = 2\). Obviously, the variation of TED (scaled by \(\Delta E\)) under the ideal kernel is much larger than the nonlinear kernel. When \(j = 2\), the increase of the length scale parameter will weaken the TED of the nano-resonator.

Fig. 8
figure 8

Influence of \({{Q^{ - 1} } \mathord{\left/ {\vphantom {{Q^{ - 1} } {\Delta E}}} \right. \kern-\nulldelimiterspace} {\Delta E}}\) with the beam thickness for different kernel functions

Full size image

Figure 9a, b denote the effect of four types of boundary conditions on TED in nano-resonators. As the restraint stiffness of the nano-resonator increases, the peak value of \({{Q^{ - 1} } \mathord{\left/ {\vphantom {{Q^{ - 1} } {\Delta E}}} \right. \kern-\nulldelimiterspace} {\Delta E}}\) will increase slightly and the critical thickness at the peak position increases with the increase of the length scale parameter. In addition, increasing the length scale parameter also reduces the peak value of \({{Q^{ - 1} } \mathord{\left/ {\vphantom {{Q^{ - 1} } {\Delta E}}} \right. \kern-\nulldelimiterspace} {\Delta E}}\). Therefore, these results provide a basis for the design of high-performance nano-resonators.

Fig. 9
figure 9

Influence of \({{Q^{ - 1} } \mathord{\left/ {\vphantom {{Q^{ - 1} } {\Delta E}}} \right. \kern-\nulldelimiterspace} {\Delta E}}\) with the thickness for different boundary conditions

Full size image

Conclusion

By applying the modified couple stress theory and the memory-dependent derivative heat conduction model, a novel thermoelastic damping model of the nano-beam is established. The exact expression of TED is obtained by means of the complex frequency method. Based on the present model, the effects of the length scale parameter, the thermal relaxation time, reference temperature, aspect ratio, different boundary conditions, etc. on TED of nano-resonators are examined and the results are validated by degrading the current model into L–R model. From the obtained results, it can be concluded that

  1. 1.

    In the present TED model, MCST predicts a smaller value for TED compared to the classical theory. However, when the length scale parameter is smaller than the thickness of the nano-beams, the growth of the thermoelastic damping is very obvious. Moreover, the length scale parameter plays a more significant role in improving the thermoelastic damping of nano-resonators when the thickness of resonators is less than the critical thickness, which indicates that the small size effect has a great influence on the thermoelastic damping of the nano-resonators. It is a phenomenon that the classical L–R model can’t possess. This novel model provides a scientific reference for the design of nano-resonators with high-quality factors.

  2. 2.

    For the nano-resonator, reference temperature has obvious influence on the location of the peak value of the thermoelastic damping. The results denote that high temperature is disadvantageous to high-quality nano-resonators. In addition, the thermoelastic damping decreases with the increase of the memory time period and the exponent of the kernel function.

  3. 3.

    The thermoelastic damping increases with the increase of vibration mode order and end restraint stiffness, or the decrease of aspect ratio for the nano-beam. Therefore, the thermoelastic damping of the nano-resonator can be changed by adjusting the aspect ratio and boundary conditions. Due to the thermal relaxation time, the choice of materials is also an important factor in the design of high-quality nano-resonators.