1 Introduction

With the rapid development of the production of engineering tools in tiny dimensions with micro and nanoscales, the use of micro/nanoelectromechanical systems (MEMS/NEMS) in industrial, engineering, technology and medical applications is growing day by day. MEMS/NEMS devices are utilized in a wide variety of applications like accelerometers [1, 2], gyroscopes [3], inertia sensors, pressure sensors [4], humidity sensors [5], energy harvesters [6,7,8], flow sensors [9], mass sensors [10] and biosensors [11, 12]. The mechanical part of these advanced systems predominantly consists of principal mechanical elements such as beams, plates, shells and rings. Various studies have investigated the effect of size on the behavior of these small-sized elements [13, 14]. Circular and rectangular cross-sectional micro/nanorings are employed for applications with a vast range of purposes in MEMS/NEMS. One of the key issues in the design of MEMS/NEMS is to minimize the energy loss in them in such a way that they can exhibit a performance close to the optimum operation. Various researches have been conducted on concepts such as energy storage and energy dissipation in mechanical systems [15, 16]. Various mechanisms have been identified that bring about energy dissipation in the mechanical elements that constitute MEMS/NEMS, which are generally divided into two categories of intrinsic and extrinsic mechanisms of energy loss. One of the incontrovertible intrinsic sources of energy dissipation in micro/nanostructures, which also has experimental support, is thermoelastic damping (TED) [17,18,19]. The mechanism of this phenomenon is that when a structure oscillates under bending, a non-uniform strain field is formed in it. Due to the coupling of strain and temperature fields, non-uniform temperature distribution occurs across the structure, which causes thermal currents to appear. Given that these heat flows are thermodynamically irreversible, they lead to entropy increase and ultimately energy loss in the structure.

The Fourier model is one of the most famous and oldest heat conduction models, which is impotent to expound the heat transfer process in special situations such as small dimensions or rapid heating due to its simplicity and lack of scale parameters. To obviate the restrictions of the Fourier model, in recent decades and years, many efforts have been made by researchers to provide a proper mathematical model that is qualified to describe the heat transfer process in certain conditions. One of the first of these models is the model proposed by Lord and Shulman (LS model), which can characterize some special states of heat transfer by utilizing a parameter called the relaxation time [20]. Owing to the use of a phase lag parameter, this model is also known as single-phase-lag (SPL) model. By adding a variable called thermal displacement to the Fourier model, Green and Naghdi put forward another non-Fourier model known as Green–Naghdi thermoelasticity theory of type III (GN-III model) [21]. By exploiting the linearized form of Moore-Gibson-Thompson model and combining LS and GN-III models, Quintanilla [22] introduced a more complete model for heat transfer, which is called MGT model in the literature. Guyer and Krumhansl [23] propounded a model (GK model) in which both the nonlocal and phase lagging effects have been taken into account. That’s why this model is also known as the nonlocal single-phase-lag (NSPL) model. By using another phase lag parameter in LS model, Tzou [24] established dual-phase-lag (DPL) model, which can reflect scale effects in both time and space domains.

To theoretically model and compute the amount of TED in different structures, various investigations have been conducted. The first mathematical modeling in this field has been established by Zener [25], in which an analytical relationship was provided to estimate TED value in Euler–Bernoulli beams by applying an approach called the entropy generation (EG) method. By introducing another approach called the complex frequency (CF) method, Lifshitz and Roukes [26] arrived at a mathematical formula to determine the value of TED in small-sized Euler–Bernoulli beams. Both models presented by Zener [25] and Lifshitz and Roukes [26] have been derived in the purview of the Fourier heat conduction model. In the last two decades, based on different models of heat transfer and two EG and CF methods, many articles have been published about TED in various structures, the most prominent of which will be introduced below.

Guo et al. [27] utilized DPL model along with CF method to render a nonclassical theoretical framework for TED calculation in Euler–Bernoulli micro/nanobeams. According to the Fourier model and CF method, Emami and Alibeigloo [28] developed an exact solution for TED in functionally graded (FG) Timoshenko microbeams. In the context of DPL model and nonlocal strain gradient theory (NSGT), Gu et al. [29] analyzed TED in thin beam resonators. With the aid of memory-dependent model of LS model, Wang et al. [30] derived a closed-form solution for TED in slender microbeams. On the basis of EG method and the Fourier model, Li et al. [31] performed a thorough study to extract explicit expressions for TED in rectangular and circular microplates. In the research of Zhou et al. [32], EG method together with GK model have been used to present a three-dimensional (3D) model for TED in rectangular small-sized plates. By utilizing EG method, Fang and Li [33] developed an analytical model for TED in rings with rectangular cross section according to the Fourier model. In a similar investigation, Li et al. [34] provided an analytical solution for TED in circular cross-sectional microring resonators. By employing LS and DPL models, Zhou et al. [35] and Zhou and Li [36] rendered non-Fourier formulations for TED in rectangular cross-sectional miniaturized rings, respectively. Kim and Kim [37], Jalil et al. [38] and Jalil et al. [39] exploited LS, GK and DPL models, respectively, to scrutinize scale effects on TED in small-scaled ring resonators with circular cross section. By implementing EG method in the framework of the Fourier model, Zheng et al. [40] proposed a solution for predicting TED value in circular cylindrical shells with arbitrary boundary conditions. By means of modified couple stress theory (MCST) and DPL model, Borjalilou et al. [41] established a size-dependent model to evaluate TED in Euler–Bernoulli microbeam resonators. Singh et al. [42] utilized MCST and MGT model to appraise size effects on TED in microbeams. In the article of Ge et al. [43], NSGT and GK model have been applied simultaneously to survey TED in rectangular micro/nanoplates. With the help of MCST and fractional DPL model, Wang et al. [44] presented an exact solution for computing TED value in circular microplates. By employing nonlocal theory (NT) in conjunction with DPL model, Li et al. [45] derived an analytical formulation to examine scale effects on TED in thin tubular nanoshells. Ge and Sarkar [46] studied size effects on TED in rectangular cross-sectional rings by making use of MCST and nonlocal DPL (NDPL) model. In the purview of NT and GK model, Li and Esmaeili [47] extracted an explicit solution for TED in circular nanoplates. In addition to the reviewed works, other valuable analytical studies have been conducted on TED in small-sized mechanical elements [48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67].

Attention to the reviewed matters above enlightens that research on thermoelastic damping (TED) in small-sized structures including microrings is of enormous significance. Besides, it was found that the heat transfer process in these microstructures doesn’t comply with the Fourier law and should be modeled through the non-Fourier models of heat conduction. The present paper employs Moore–Gibson–Thompson (MGT) generalized thermoelasticity theory to develop a novel model for TED in circular cross-sectional microrings and provide a formula to calculate its value in such rings. The first step is to extract the temperature field in the ring by solving the equation of heat conduction established on the basis of MGT model. In the next step, the maximum amounts of dissipated thermal energy and strain energy during one cycle of vibration are computed. By using these values in the framework of the entropy generation (EG) method, a mathematical formulation is given for estimation of the amount of TED. The correctness of the provided solution is surveyed by conducting a comparative study. A convergence analysis is also performed to specify how many terms of the obtained infinite series are adequate to achieve accurate results. Lastly, various graphical results are given to scrutinize the influence of momentous parameters on the magnitude of TED.

2 Fundamentals of Moore–Gibson–Thompson (MGT) thermoelasticity theory

According to Moore-Gibson-Thompson (MGT) generalized thermoelasticity theory, the process of heat conduction in isotropic solids is expressed by [22]:

$$\left(1+\tau \frac{\partial }{\partial t}\right){\varvec{q}}=-k\nabla \vartheta -{k}^{*}\nabla \upsilon$$
(1)

in which \({\varvec{q}}\) defines heat flux vector. Also, variable \(\vartheta =T-{T}_{0}\) represents temperature variation in which \(T\) and \({T}_{0}\) refer to the current and surrounding temperature, respectively. Moreover, variable \(\upsilon\) is known as thermal displacement, which is defined via the relation \(\vartheta =\partial \upsilon /\partial t\). Parameters \(k\) and \({k}^{*}\) stand for the thermal conductivity of the material and thermal conductivity rate, respectively. Material constant \(\tau\) is called relaxation time or phase lag of heat flux. One thing to mention here is that when \({k}^{*}\) is set to zero, MGT model corresponds to LS model. In addition, in the absence of \(\tau\), Eq. (1) is converted to equation of heat conduction of GN-III model. Furthermore, by dropping the terms containing parameters \({k}^{*}\) and \(\tau\), the constitutive relation of MGT model reduces to that of the Fourier model.

The equation of conservation of energy is written as follows [24]:

$$-\nabla .\,{\varvec{q}}=\rho {c}_{v}\frac{\partial \vartheta }{\partial t}+\frac{E\alpha {T}_{0}}{1-2\nu }\frac{\partial {\varepsilon }_{mm}}{\partial t}$$
(2)

where \(\rho\) and \({c}_{v}\) are mass density and specific heat per unit mass, respectively. Material constant \(\alpha\) denotes thermal expansion coefficient of the material. Parameters \(E\) and \(\nu\) are also the Young modulus and the Poisson ratio, respectively. Variable \({\varepsilon }_{mm}\) indicates cubical dilatation, which is equal to the trace of strain tensor \({\varvec{\varepsilon}}\). By deleting heat flux \({\varvec{q}}\) from Eqs. (1) and (2), one can achieve the coupled equation of heat conduction corresponding to MGT model as follows:

$$\left(1+\tau \frac{\partial }{\partial t}\right)\left(\rho {c}_{v}\frac{{\partial }^{2}\vartheta }{\partial {t}^{2}}+\frac{E\alpha {T}_{0}}{1-2\nu }\frac{{\partial }^{2}{\varepsilon }_{mm}}{\partial {t}^{2}}\right)={k}^{*}\left(1+{\tau }^{*}\frac{\partial }{\partial t}\right){\nabla }^{2}\vartheta$$
(3)

in which

$${\tau }^{*}=k/{k}^{*}$$
(4)

Moreover, \({\nabla }^{2}\) represents the Laplace operator or Laplacian. As can be seen, Eq. (3) is a hyperbolic differential equation, which guarantees the finite speed of heat transfer, and in addition to temperature change \(\vartheta\), thermal displacement parameter \(\upsilon\) is also involved in it as a constitutive variable. Therefore, MGT-based heat equation has solved the defects of both LS and GN models.

3 Thermoelastic model of rings with circular cross-section according to MGT thermoelasticity theory

In this section, a mathematical framework is developed for thermoelastic modeling of small-scaled circular cross-sectional rings on the basis of MGT heat conduction model. To do so, the following assumptions are applied: (1) Flexural vibrations take place in the plane of the ring without undergoing any extension of the centerline of the ring (in-extensionality assumption), (2) The cross-sectional dimensions of the ring are small compared to the radius of the centerline of the ring (thin ring assumption), and (3) Thermal stresses can be ignored compared to mechanical stresses (weak thermoelastic coupling assumption).

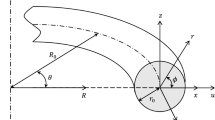
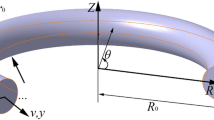
The geometry and coordinate systems of a rectangular cross-sectional ring with the mean radius \({R}_{0}\) and cross-sectional radius \({r}_{0}\) is portrayed in Fig. 1. To define global and local coordinate systems, the symbols \((R, \theta , Z)\) and \((x, y, z)\) are used, respectively. Additionally, independent variable \(\varphi\) represents the angle in local coordinates. Parameter \(u\left(\theta ,t\right)\) stands for the displacement of any arbitrary point of the ring in the radial direction. Also, parameter \(v\left(\theta ,t\right)\) denotes the tangential displacement of the centerline. In the modeling of rings, it is generally assumed that the tangential centerline of the ring is inextensible. Considering this assumption yields the following mathematical relationship [68]:

Fig. 1
figure 1

Schematic view of a ring with circular cross section

Full size image
$$u=-\frac{\partial v}{\partial \theta }$$
(5)

Accordingly, the tangential strain \({\varepsilon }_{\theta \theta }\) at any point of the ring is expressed by [68]:

$${\varepsilon }_{\theta \theta }=-\frac{x}{{R}_{0}^{2}}\left(u+\frac{{\partial }^{2}u}{\partial {\theta }^{2}}\right)$$
(6)

Based on thermoelastic case of Hooke's law in rings, one can write [69]:

$${\sigma }_{\theta \theta }=E\left({\varepsilon }_{\theta \theta }-\alpha \vartheta \right)$$
(7)

Here, \({\sigma }_{\theta \theta }\) denotes the normal tangential stress. Substitution of Eq. (6) into above equation gives:

$${\sigma }_{\theta \theta }=-\frac{Ex}{{R}_{0}^{2}}\left(u+\frac{{\partial }^{2}u}{\partial {\theta }^{2}}\right)-E\alpha \vartheta$$
(8)

According to Hooke's law, the two normal strains \({\varepsilon }_{RR}\) and \({\varepsilon }_{ZZ}\) are given by [70]:

$${\varepsilon }_{RR}={\varepsilon }_{ZZ}=-\nu \frac{{\sigma }_{\theta \theta }}{E}+\alpha \vartheta$$
(9)

By inserting Eq. (8) into Eq. (9), one can arrive at the following relations:

$${\varepsilon }_{RR}={\varepsilon }_{ZZ}=\nu \frac{x}{{R}_{0}^{2}}\left(u+\frac{{\partial }^{2}u}{\partial {\theta }^{2}}\right)+(1+\nu )\alpha \vartheta$$
(10)

Thus, by employing Eqs. (6) and (10), the cubical dilatation \({\varepsilon }_{mm}\) can be obtained by:

$${\varepsilon }_{mm}={\varepsilon }_{RR}+{\varepsilon }_{\theta \theta }+{\varepsilon }_{ZZ}=-(1-2\nu )\frac{x}{{R}_{0}^{2}}\left(u+\frac{{\partial }^{2}u}{\partial {\theta }^{2}}\right)+2(1+\nu )\alpha \vartheta$$
(11)

By placing above equation into Eq. (3) and arranging the result, the following heat conduction equation is derived:

$$\frac{\chi }{{\tau }^{*}}\left(1+{\tau }^{*}\frac{\partial }{\partial t}\right){\nabla }^{2}\vartheta =\left(1+\tau \frac{\partial }{\partial t}\right)\left\{\left[1+\frac{2\left(1+\nu \right)}{1-2\nu }{\Delta }_{E}\right]\frac{{\partial }^{2}\vartheta }{\partial {t}^{2}}-\frac{{\Delta }_{E}}{\alpha }\frac{{\partial }^{2}}{\partial {t}^{2}}\left[\frac{x}{{R}^{2}}\left(u+\frac{{\partial }^{2}u}{\partial {\theta }^{2}}\right)\right]\right\}$$
(12)

with

$$\chi =k/\rho {c}_{v}$$
(13a)
$${\Delta }_{E}=E{\alpha }^{2}{T}_{0}/\rho {c}_{v}$$
(13b)

For most solids, \(\left[2\left(1+\nu \right)/\left(1-2\nu \right)\right]{\Delta }_{E}\ll 1\). By accounting for this point, the heat conduction Eq. (12) becomes:

$$\frac{\chi }{{\tau }^{*}}\left(1+{\tau }^{*}\frac{\partial }{\partial t}\right){\nabla }^{2}\vartheta =\left(1+\tau \frac{\partial }{\partial t}\right)\left\{\frac{{\partial }^{2}\vartheta }{\partial {t}^{2}}-\frac{{\Delta }_{E}}{\alpha }\frac{{\partial }^{2}}{\partial {t}^{2}}\left[\frac{x}{{R}^{2}}\left(u+\frac{{\partial }^{2}u}{\partial {\theta }^{2}}\right)\right]\right\}$$
(14)

To extract temperature distribution at different points of the ring, functions \(\vartheta\) and \(u\) are assumed as follows [71]:

$$\vartheta (R,\theta ,Z,t)={\vartheta }_{0}(R,\theta ,Z){e}^{i{\omega }_{n}t}$$
(15a)
$$u\left(\theta ,t\right)={U}_{n}{\text{sin}}\left(n\theta \right){e}^{i{\omega }_{n}t}$$
(15b)

In the last two relations, \({\omega }_{n}\) stands for the nth natural frequency of the ring, which can be determined by [34, 72]:

$${\omega }_{n}=\frac{n\left({n}^{2}-1\right)}{\sqrt{{n}^{2}+1}}\sqrt{\frac{EI}{\rho A{R}_{0}^{4}}} (n\ge 2)$$
(16)

in which

$$I=\pi {r}_{0}^{4}/4$$
(17a)
$$A=\pi {r}_{0}^{2}$$
(17b)

By placing Eqs. (15a) and (15b) into Eq. (14) and sorting the outcome, one can arrive at the equation below:

$${\nabla }^{2}{\vartheta }_{0}+\frac{{\tau }^{*}{\omega }_{n}^{2}\left(1+i{\omega }_{n}\tau \right)}{\chi \left(1+i{\omega }_{n}{\tau }^{*}\right)}{\vartheta }_{0}=\frac{{\Delta }_{E}}{\alpha }\frac{{\tau }^{*}{\omega }_{n}^{2}\left(1+i{\omega }_{n}\tau \right)}{\chi \left(1+i{\omega }_{n}{\tau }^{*}\right)}\frac{x}{{R}^{2}}\left(1-{n}^{2}\right){U}_{n}{\text{sin}}\left(n\theta \right)$$
(18)

In global coordinate system \((R, \theta , Z)\), the Laplace operator is defined by [34]:

$${\nabla }^{2}=\frac{{\partial }^{2}}{\partial {R}^{2}}+\frac{1}{R}\frac{\partial }{\partial R}+\frac{1}{{R}^{2}}\frac{{\partial }^{2}}{\partial {\theta }^{2}}+\frac{{\partial }^{2}}{\partial {Z}^{2}}$$
(19)

From Fig. 1, it is clear that:

$$x=r{\text{sin}}\varphi$$
(20a)
$$z=r{\text{cos}}\varphi$$
(20b)

In addition:

$$R={R}_{0}+x$$
(21)

By substituting Eqs. (20a), (20b) and (21) in Eq. (19), implementing the chain rule and paying attention to the fact that we have \({R}_{0}\gg x\) in thin rings, the Laplace operator defined in Eq. (19) takes the following form [73]:

$${\nabla }^{2}=\frac{{\partial }^{2}}{\partial {r}^{2}}+\frac{1}{r}\frac{\partial }{\partial r}+\frac{1}{{R}_{0}^{2}}\frac{{\partial }^{2}}{\partial {\theta }^{2}}+\frac{1}{{r}^{2}}\frac{{\partial }^{2}}{\partial {\varphi }^{2}}$$
(22)

Thus, partial differential Eq. (18) can be written in the following form:

$$\frac{{\partial }^{2}{\vartheta }_{0}}{\partial {r}^{2}}+\frac{1}{r}\frac{\partial {\vartheta }_{0}}{\partial r}+\frac{1}{{R}_{0}^{2}}\frac{{\partial }^{2}{\vartheta }_{0}}{\partial {\theta }^{2}}+\frac{1}{{r}^{2}}\frac{{\partial }^{2}{\vartheta }_{0}}{\partial {\varphi }^{2}}+\frac{{\tau }^{*}{\omega }_{n}^{2}\left(1+i{\omega }_{n}\tau \right)}{\chi \left(1+i{\omega }_{n}{\tau }^{*}\right)}{\vartheta }_{0}=\frac{{\Delta }_{E}}{\alpha }\frac{{\tau }^{*}{\omega }_{n}^{2}\left(1+i{\omega }_{n}\tau \right)}{\chi \left(1+i{\omega }_{n}{\tau }^{*}\right)}\frac{x}{{R}^{2}}\left(1-{n}^{2}\right){U}_{n}{\text{sin}}\left(n\theta \right)$$
(23)

Thermal boundary conditions on the outer surface of the ring are considered adiabatic, which can be expressed through the following mathematical relationship:

$$\frac{\partial {\vartheta }_{0}\left(r,\theta ,\varphi \right)}{\partial r}=0 at r={r}_{0}$$
(24)

Moreover, temperature function \({\vartheta }_{0}\) must be periodic in terms of angles \(\theta\) and \(\varphi\). Considering this point and Eq. (24), function \({\vartheta }_{0}\left(r,\theta ,\varphi \right)\) should be in the following form to satisfy both the governing Eq. (23) and the mentioned boundary conditions [34]:

$${\vartheta }_{0}={\sum }_{p=1}^{\infty }{\sum }_{q=1}^{\infty }{A}_{pq}{J}_{1}\left(\frac{{\beta }_{p}}{{r}_{0}}r\right){\text{sin}}(q\theta ){\text{sin}}\varphi$$
(25)

In the above equation, \({J}_{1}\) represents the first order Bessel function of the first kind. The value of unknown coefficients \({\beta }_{p}\) can be determined by applying the adiabatic boundary condition of Eq. (24) to the solution presented in Eq. (25). By doing this and using the properties of Bessel functions of the first kind, the following relationship is finally obtained:

$${J}_{1}\left({\beta }_{p}\right)-{\beta }_{p}{J}_{0}\left({\beta }_{p}\right)=0$$
(26)

By using again the properties of Bessel functions of the first kind, the above equation can also be expressed as follows:

$${J}_{2}\left({\beta }_{p}\right)-{J}_{0}\left({\beta }_{p}\right)=0$$
(27)

By solving one of the transcendental Eqs. (26) or (27), the coefficients \({\beta }_{p}\) in Eq. (25) are determined. Table 1 contains some values for coefficients \({\beta }_{p}\).

Table 1 The value of first ten terms of \({\beta }_{p}\)
Full size table

To calculate the coefficients \({A}_{pq}\) in Eq. (25), the orthogonality property of Bessel and sine functions is exploited, so that first Eq. (25) is inserted into Eq. (23), then the result is multiplied by expression \(r{J}_{1}\left(\frac{{\beta }_{i}}{{r}_{0}}r\right){\text{sin}}(n\theta ){\text{sin}}\varphi\), and the integral is finally taken from the derived expression in the range of the entire ring, i.e. \(0\le r\le {r}_{0}\), \(0\le \theta <2\pi\) and \(0\le \varphi <2\pi\). In this way, the coefficient \({A}_{ij}\) is obtained as follows:

$${A}_{in}=2\frac{{\Delta }_{E}}{\alpha }\frac{{r}_{0}}{{R}_{0}^{2}}\frac{\left({n}^{2}-1\right){U}_{n}}{\left({\beta }_{i}^{2}-1\right){J}_{1}\left({\beta }_{i}\right)}\frac{{\tau }_{i}{\tau }^{*}{\omega }_{n}^{2}\left(1+i{\omega }_{n}\tau \right)}{\left(1+{\psi }_{in}^{2}\right)\left(1+i{\omega }_{n}{\tau }^{*}\right)-{\tau }_{i}{\tau }^{*}{\omega }_{n}^{2}\left(1+i{\omega }_{n}\tau \right)}$$
(28)

with

$${\tau }_{i}=\frac{{r}_{0}^{2}}{\chi {\beta }_{i}^{2}}$$
(29a)
$${\psi }_{in}=\frac{n}{{\beta }_{i}}\frac{{r}_{0}}{{R}_{0}}$$
(29b)

Substitution of Eq. (28) into Eq. (25) yields the following relation for temperature field \({\vartheta }_{0}\):

$$\vartheta_{0} = 2\frac{{\Delta_{E} }}{\alpha }\frac{{U_{n} r_{0} }}{{R_{0}^{2} }}\left( {n^{2} - 1} \right)\sin \left( {n\theta } \right)\sin \varphi \mathop \sum \limits_{i = 1}^{\infty } \frac{{J_{1} \left( {\frac{{\beta_{i} }}{{r_{0} }}r} \right)}}{{\left( {\beta_{i}^{2} - 1} \right)J_{1} \left( {\beta_{i} } \right)}}\frac{{\tau_{i} \tau^{*} \omega_{n}^{2} \left( {1 + i\omega_{n} \tau } \right)}}{{\left( {1 + \psi_{in}^{2} } \right)\left( {1 + i\omega_{n} \tau^{*} } \right) - \tau_{i} \tau^{*} \omega_{n}^{2} \left( {1 + i\omega_{n} \tau } \right)}}$$
(30)

4 MGT-based thermoelastic damping in circular cross-sectional rings

In different structures, the inverse of quality factor (Q-factor) is used to estimate the value of TED. In the context of the entropy generation (EG) method, this value is computed via the following relation [31]:

$${Q}^{-1}=\frac{1}{2\pi }\frac{\Delta W}{{W}_{{\text{max}}}}$$
(31)

In the above equation, \({W}_{{\text{max}}}\) and \(\Delta W\) represent the maximum amount of strain energy per cycle of vibration and the dissipated thermoelastic energy, respectively. In a body with a volume of \(V\), the values of these two terms are computed by [56], [74]:

$${W}_{{\text{max}}}=\frac{1}{2}{\iiint }_{V}{\widehat{\sigma }}_{ij}{\widehat{\varepsilon }}_{ij}{\text{d}}V$$
(32a)
$$\Delta W=-\pi {\iiint }_{V}{\widehat{\sigma }}_{ij}{\text{Im}}\left({\widehat{\varepsilon }}_{ij}^{th}\right){\text{d}}V$$
(32b)

where \({\sigma }_{ij}\) and \({\varepsilon }_{ij}\) denote the components of stress and strain tensors, respectively. The hat symbol represents the peak value of any variable in a cycle of oscillation. Additionally, \({\text{Im}}\left({\varepsilon }_{ij}^{th}\right)\) is the imaginary part of thermal strain tensor. In a circular cross-sectional ring, \({W}_{{\text{max}}}\) and \(\Delta W\) are expressed as follows:

$${W}_{{\text{max}}}=\frac{1}{2}{\iiint }_{V}{\widehat{\sigma }}_{\theta \theta }{\widehat{\varepsilon }}_{\theta \theta }{\text{d}}V$$
(33a)
$$\Delta W=-\pi {\iiint }_{V}{\widehat{\sigma }}_{\theta \theta }{\text{Im}}\left({\widehat{\varepsilon }}_{\theta \theta }^{th}\right){\text{d}}V$$
(33b)

Given faint thermoelastic coupling effect, one can ignore thermal stress in comparison with mechanical stress. Accordingly, on the basis of Eqs. (6), (8) and (15b), the following relations for \({\widehat{\varepsilon }}_{\theta \theta }\) and \({\widehat{\sigma }}_{\theta \theta }\) are obtained:

$${\widehat{\varepsilon }}_{\theta \theta }=-\frac{x}{{R}_{0}^{2}}\left(1-{n}^{2}\right){U}_{n}{\text{sin}}\left(n\theta \right)$$
(34a)
$${\widehat{\sigma }}_{\theta \theta }=-\frac{Ex}{{R}_{0}^{2}}\left(1-{n}^{2}\right){U}_{n}{\text{sin}}\left(n\theta \right)$$
(34b)

In a ring with circular cross section, one can write:

$${\text{d}}V=R{\text{d}}\theta .{\text{d}}r.r{\text{d}}\varphi$$
(35)

By employing Eqs. (20a) and (21) in the above equation, one can arrive at the following relation:

$${\text{d}}V=r\left({R}_{0}+r{\text{sin}}\varphi \right).{\text{d}}r{\text{d}}\theta {\text{d}}\varphi$$
(36)

Substitution of Eqs. (34a), (34b) and (36) into Eq. (33a) leads to:

$${W}_{{\text{max}}}=\frac{1}{2}{\int }_{0}^{2\pi }{\int }_{0}^{2\pi }{\int }_{0}^{{r}_{0}}\frac{E{U}_{n}^{2}}{{R}_{0}^{4}}{\left(1-{n}^{2}\right)}^{2}{r}^{2}{{\text{sin}}}^{2}\varphi .{{\text{sin}}}^{2}\left(n\theta \right).r\left({R}_{0}+r{\text{sin}}\varphi \right).{\text{d}}r{\text{d}}\theta {\text{d}}\varphi$$
(37)

By doing the above integration, one can get the following relationship:

$${W}_{{\text{max}}}=\frac{1}{2}\pi {{\text{EIR}}}_{0}{\left[\frac{\left(1-{n}^{2}\right){U}_{n}}{{R}_{0}^{2}}\right]}^{2}$$
(38)

According to Eq. (15a), one can write \({\widehat{\varepsilon }}_{\theta \theta }^{th}=\alpha {\vartheta }_{0}\). Thus, with the help of Eq. (30), the following relation can be derived:

$${\text{Im}}\left( {\hat{\varepsilon }_{\theta \theta }^{th} } \right) = 2\Delta_{E} \frac{{r_{0} U_{n} }}{{R_{0}^{2} }}\left( {1 - n^{2} } \right)\sin \left( {n\theta } \right)\sin \varphi \mathop \sum \limits_{i = 1}^{\infty } \frac{{J_{1} \left( {\frac{{\beta_{i} }}{{r_{0} }}r} \right)}}{{\left( {\beta_{i}^{2} - 1} \right)J_{1} \left( {\beta_{i} } \right)}}\frac{{\left( {1 + \psi_{in}^{2} } \right)\left( {\tau^{*} - \tau } \right)\tau_{i} \tau^{*} \omega_{n}^{3} }}{{\left( {1 + \psi_{in}^{2} - \tau_{i} \tau^{*} \omega_{n}^{2} } \right)^{2} + \left[ {\left( {1 + \psi_{in}^{2} } \right)\tau^{*} - \tau_{i} \tau^{*} \tau \omega_{n}^{2} } \right]^{2} \omega_{n}^{2} }}$$
(39)

By putting Eqs. (34b), (36) and (39) into Eq. (33b) and performing calculations like what was done to extract \({W}_{{\text{max}}}\), finally the following expression for \(\Delta W\) is obtained:

$$\Delta W={\pi }^{2}{\Delta }_{E}{{\text{EIR}}}_{0}{\left[\frac{\left(1-{n}^{2}\right){U}_{n}}{{R}_{0}^{2}}\right]}^{2}{\sum }_{i=1}^{\infty }\frac{8}{{\beta }_{i}^{2}\left({\beta }_{i}^{2}-1\right)}\frac{\left(1+{\psi }_{in}^{2}\right)\left({\tau }^{*}-\tau \right){\tau }_{i}{\tau }^{*}{\omega }_{n}^{3}}{{\left(1+{\psi }_{in}^{2}-{\tau }_{i}{\tau }^{*}{\omega }_{n}^{2}\right)}^{2}+{\left[\left(1+{\psi }_{in}^{2}\right){\tau }^{*}-{\tau }_{i}{\tau }^{*}\tau {\omega }_{n}^{2}\right]}^{2}{\omega }_{n}^{2}}$$
(40)

At the final stage, by inserting Eqs. (38) and (40) into Eq. (31), one can attain the following relation for TED in circular cross-sectional rings based on MGT equation of heat conduction:

$${Q}^{-1}={\Delta }_{E}{\sum }_{i=1}^{\infty }{C}_{i}\frac{\left(1+{\psi }_{in}^{2}\right)\left({\tau }^{*}-\tau \right){\tau }_{i}{\tau }^{*}{\omega }_{n}^{3}}{{\left(1+{\psi }_{in}^{2}-{\tau }_{i}{\tau }^{*}{\omega }_{n}^{2}\right)}^{2}+{\left[\left(1+{\psi }_{in}^{2}\right){\tau }^{*}-{\tau }_{i}{\tau }^{*}\tau {\omega }_{n}^{2}\right]}^{2}{\omega }_{n}^{2}}$$
(41)

In the above equation, \({C}_{i}\) is the weighting coefficient that can be computed through the following relationship:

$${C}_{i}=\frac{8}{{\beta }_{i}^{2}\left({\beta }_{i}^{2}-1\right)}$$
(42)

5 Results and discussion

In this section, various numerical results are prepared with the aim of conducting validation, convergence and parametric studies. The point to be noted here is that the relation presented for TED in Eq. (41) is for the three-dimensional (3D) case of heat transfer. In the two-dimensional (2D) model, heat transfer in the tangential direction is not considered [34]. Therefore, according to Eqs. (22) and (30), to extract the results corresponding to 2D model, it is sufficient to eliminate term \({\psi }_{{\text{in}}}^{2}\) from Eq. (41).

To validate the developed formulation, the results of this research are compared with those reported by Kim and Kim [37] for the Fourier and LS models. To convert the relationships of MGT model to those of LS model, it is necessary to set \({k}^{*}=0\). Thus, according to Eq. (4), to extract the results based on LS model, relationship \({\tau }^{*}\to \infty\) should be applied in Eq. (41). Moreover, to achieve the results in the framework of the Fourier model, in addition to the relation \({\tau }^{*}\to \infty\), the value of \(\tau\) must be set equal to zero in Eq. (41). With these explanations, in Fig. 2, the diagram of TED changes with respect to the vibrational mode number \(n\) is plotted for a ring with geometrical characteristics \({R}_{0}=50\) μm and \({r}_{0}=1\) μm at \({T}_{0}=293 K\). The properties of the material are as follows: \(E=165.9\, {\text{GPa}}\), \(\rho =2330 \,{\text{kg}}/{{\text{m}}}^{3}\), \({c}_{v}=713 \,{\text{J}}/{\text{kg K}}\), \(k=156 {\text{W}}/{\text{mK}}\), \(\alpha =2.59*{10}^{-6} 1/K\) and \(\tau =3.95649 {\text{ps}}\). The full agreement between the curves extracted via the formulation presented in this work and those published in the research of Kim and Kim [37] betokens the authenticity and exactness of the developed model.

Fig. 2
figure 2

Validation analysis for a circular cross-sectional ring with specifications \({r}_{0}=1\) μm and \({R}_{0}/{r}_{0}=50\)

Full size image

In the following, except for the examples in which the effect of the material of the ring on TED value is discussed, in the rest of the cases, the graphs are drawn for a silicone ring at reference temperature \({T}_{0}=300 K\). Table 2 contains the characteristics of silicon (Si) at this temperature. Figures 3 and 4 are prepared to determine how many terms of the solution derived in this study are sufficient to gain convergent results. Figure 3 is drawn for a ring with specifications \({r}_{0}=1\) μm and \({R}_{0}/{r}_{0}=100\), and Fig. 4 is depicted for a ring with geometrical characteristics \({r}_{0}=2\) μm and \({R}_{0}/{r}_{0}=20\). In these figures, \({Q}_{j}^{-1}\) represents the amount of TED by considering the first \(j\) terms of the obtained solution. As it is evident in these two figures, for both 2D and 3D models, and for all vibrational mode numbers examined (i.e. \(n=2, 100, 200, 500\) and \(1000\)), with the increase of \(j\), the results rapidly approach and converge to TED value estimated by exploiting the first ten terms. This issue is related to the fact that the sequence of the weighting factor introduced in Eq. (42) is sorely descending. All in all, it can be said that the use of first ten terms of the relationship given for TED is adequate to attain highly accurate outcomes.

Table 2 Mechanical and thermal properties of three types of materials at \({T}_{0}=300 K\) [49]
Full size table
Fig. 3
figure 3

Convergence analysis for a Si-ring with characteristics \({r}_{0}=1\) μm and \({R}_{0}/{r}_{0}=100\) a 3D model b 2D model

Full size image
Fig. 4
figure 4

Convergence analysis for a Si-ring with characteristics \({r}_{0}=2\) μm and \({R}_{0}/{r}_{0}=20\) a 3D model b 2D model

Full size image

In Fig. 5, for a ring with geometrical ratio \({R}_{0}/{r}_{0}=20\), the effect of GN-III and MGT models on TED diagram in terms of vibrational mode number \(n\) is examined. Figure 5a, b are drawn for cases \({r}_{0}=1\) μm and \({r}_{0}=10\) μm, respectively. As can be seen, in low vibrational modes, the predictions of MGT and GN-III models are almost the same, but as the vibrational mode number ascends, the difference between the estimations of these two models enlarges, so that MGT model yields a smaller value for TED than GN-III model. Also, these curves reveal that for both MGT and GN-III models, the amount of TED obtained from 3D case of heat conduction is higher than that for 2D case. Another point that can be mentioned is that due to the larger dimensions of the ring in Fig. 5b compared to Fig. 5a, the difference between the outputs of MGT and GN-III models in Fig. 5b is smaller, which is a confirmation of the diminution of size effect in larger dimensions.

Fig. 5
figure 5

TED versus vibrational mode number in the framework of MGT and GN-III models a \({r}_{0}=1\) μm and \({R}_{0}/{r}_{0}=20\) b \({r}_{0}=10\) μm and \({R}_{0}/{r}_{0}=20\)

Full size image

Figure 6 is drawn with the same conditions as Fig. 5, with the only difference being that the geometrical ratio \({R}_{0}/{r}_{0}\) is considered equal to 100. In other words, the size of the ring in Fig. 6 is assumed to be larger than that in Fig. 5. As it is clear in Fig. 6a, the effects of MGT and GN-III models as well as 2D and 3D cases of heat conduction are qualitatively similar to those in Fig. 5, but given the larger dimensions of the ring, the amount of these effects is quantitatively reduced and only in very high vibrational mode numbers are perceptible. In Fig. 6b, where both \({r}_{0}\) and \({R}_{0}/{r}_{0}\) take a large value, the size effect is minimized and it becomes difficult to distinguish between the results of MGT and GN-III models. It was mentioned earlier that the difference between the results of 2D and 3D models is due to the terms including term \({\psi }_{in}^{2}\). According to Eq. (29b), this difference is less in low vibrational mode numbers or high ratios of \({R}_{0}/{r}_{0}\). It is evident in Figs. 5 and 6 that the difference between the estimates of 2D and 3D models augments with the increase of the vibrational mode number \(n\). Also, because of the larger ratio of \({R}_{0}/{r}_{0}\) in Fig. 6 compared to Fig. 5, the difference between the predictions of 2D and 3D models lessens. As it is clear from the diagrams of Fig. 6, the peak amount of TED comes about in a vibrational mode number located in the middle of the studied range. The reason of this outcome can be explained that the temperature field of the ring arrives at balance in a particular time \({\tau }_{0}\). At low vibrational mode numbers that are comparable to small frequencies, one can state \({\tau }_{0}\ll {\omega }_{n}^{-1}\). Consequently, because the period of vibration is long in this case, the oscillating body is isothermal and remains in equilibrium conditions. Therefore, the amount of thermal energy loss is slight. At large vibrational mode numbers or high frequencies (that is \({\tau }_{0}\gg {\omega }_{n}^{-1}\)), a cycle of oscillation happens very quickly, and the vibrating body hasn’t sufficient time to reach equilibrium. Hence, a trivial amount of thermal energy is dissipated. Accordingly, the peak amount of TED occurs at \({\tau }_{0}\sim {\omega }_{n}^{-1}\), which corresponds to intermediate vibrational mode numbers.

Fig. 6
figure 6

TED versus vibrational mode number in the framework of MGT and GN-III models a \({r}_{0}=1\) μm and \({R}_{0}/{r}_{0}=100\) b \({r}_{0}=10\) μm and \({R}_{0}/{r}_{0}=100\)

Full size image

The variations of TED with the cross-sectional radius \({r}_{0}\) are displayed in Fig. 7a, b for vibrational mode numbers \(n=100\) and \(n=200\), respectively. These curves are plotted for a ring with fixed geometrical ratio \({R}_{0}/{r}_{0}=20\). According to these diagrams, the value of TED calculated by MGT model is lower than that anticipated by GN-III model. The physical meaning of this outcome can be that the dispersion velocity of thermal waves in GN-III model is more than that in MGT model. Therefore, the heat induced by the non-uniform stress field in the framework of MGT model has less time to transfer per cycle of vibration, which weakens energy dissipation caused by TED. Consequently, the amount of TED computed by GN-III model is larger than that estimated by MGT model. In addition, for case \(n=200\), the discrepancy between the outcomes of MGT and GN-III models is greater than case \(n=100\). Another point that can be observed in the graphs of Fig. 7 is that with the increase of the value of cross-sectional radius \({r}_{0}\), the results of MGT model approach those of GN-III model, which clearly demonstrates the weakening of size effect with the increase of ring dimensions. One of the things that are very significant in the analytical studies related to TED is to find a characteristic size in which the peak value of TED takes place. For example, the characteristic size in plates and rectangular cross-sectional beams is their thickness (\(h\)) and in circular cross-sectional rings is the radius of their cross section (\({r}_{0}\)), which is known as “critical thickness” or “critical radius”. Depending on the purpose of using the studied structure, TED can have a detrimental or beneficial effect on the performance of that structure, based on which it should be decided whether or not the structure is designed within the critical size range. Considering these explanations, another difference between the results of MGT and GN-III models is that in the range under investigation (i.e. 0.1 μm \(\le {r}_{0}\le 10\) μm), GN-III model predicts a downward trend for TED, but according to MGT model, the peak value of TED occurs at a radius within this range, that is at critical radius.

Fig. 7
figure 7

TED variation with cross-sectional radius according to MGT and GN-III models a \(n=100\) and \({R}_{0}/{r}_{0}=20\) b \(n=200\) and \({R}_{0}/{r}_{0}=20\)

Full size image

Figure 8 is depicted with the same assumptions as Fig. 7, with the only difference being that the geometrical ratio \({R}_{0}/{r}_{0}\) is considered equal to 100. By ascending the value of \({R}_{0}/{r}_{0}\) compared to Fig. 7 and consequently increasing size of the ring, it can be seen that, as expected, the effect of size and consequently the difference between the results of MGT and GN-III models drops noticeably. The noteworthy point in Fig. 8a is that TED value estimated by MGT model is higher than that predicted by GN-III model, although the difference between them is not very large. This implies that although in most cases MGT model anticipates a lower TED value than GN-III model, a different result may occur in some vibrational mode numbers or ratios of \({R}_{0}/{r}_{0}\).

Fig. 8
figure 8

TED variation with cross-sectional radius according to MGT and GN-III models a \(n=100\) and \({R}_{0}/{r}_{0}=100\) b \(n=200\) and \({R}_{0}/{r}_{0}=100\)

Full size image

To survey the impact of the material on TED spectrum, in Fig. 9, the diagram of changes of TED with vibrational mode number \(n\) is displayed for three materials silicon (Si), copper (Cu) and gold (Au). The mechanical and thermal properties of these three materials at reference temperature \({T}_{0}=300 K\) are given in Table 2. To draw these curves, \({r}_{0}=0.5\) μm and \({R}_{0}/{r}_{0}=20\) are considered. In addition, Fig. 9a, b are dedicated to the results of 3D and 2D models, respectively. As it is obvious, the discrepancy between the outcomes of MGT and GN-III models in low vibrational mode numbers is small for all three studied materials, but in high vibration modes, MGT model estimates a lower amount than GN-III model for TED. Although TED value obtained for each material is highly dependent on the vibrational mode number, in general, it can be said that in high vibrational mode numbers (i.e. approximately \(n>100\)), MGT model predicts the highest TED value for Cu-rings and the lowest TED value for Si-rings. Figure 10 is drawn with the same conditions as Fig. 9, but for a ring with a cross-sectional radius of \({r}_{0}=5\) μm. As the dimensions of the ring become larger compared to Fig. 9, it can be observed that the difference between the output of MGT and GN-III models is insignificant in a larger range of \(n\), which indicates the reduction of size effect.

Fig. 9
figure 9

Comparison of TED value for three materials silicon, copper and gold for a ring with geometrical properties \({r}_{0}=0.5\) μm and \({R}_{0}/{r}_{0}=20\) a 3D model b 2D model

Full size image
Fig. 10
figure 10

Comparison of TED value for three materials silicon, copper and gold for a ring with geometrical properties \({r}_{0}=5\) μm and \({R}_{0}/{r}_{0}=20\) a 3D model b 2D model

Full size image

In Fig. 11, the diagram of TED alterations with respect to cross-sectional radius \({r}_{0}\) for the three studied materials in Figs. 9 and 10 is shown. The curves of this figure are extracted for 3D model and geometrical ratio \({R}_{0}/{r}_{0}=40\). Figure 11a, b are drawn for vibrational mode numbers \(n=50\) and \(n=200\), respectively. As it is clear, in Fig. 11a, where the value of \(n\) is relatively small, MGT model predicts a higher value for TED than GN-III model B, but in Fig. 11b, where the vibrational mode number \(n\) is larger, TED value obtained through MGT model is lower than that computed by GN-III model. In both Fig. 11a, b, the convergence of the output of MGT model to that of GN-III model can be clearly seen as the ring size increases. Furthermore, regardless of the vibrational mode number and the value of cross-sectional radius, Si-ring shows the lowest TED value.

Fig. 11
figure 11

TED value obtained by 3D model versus cross-sectional radius for three materials silicon, copper and gold for a ring with \({R}_{0}/{r}_{0}=40\) a \(n=50\) b \(n=200\)

Full size image

For a ring made of lead (Pb) with geometrical ratio \({R}_{0}/{r}_{0}=40\), Fig. 12a, b compare TED values obtained in the context of MGT and DPL models at vibrational mode numbers \(n=50\) and \(n=100\), respectively. According to the findings of Jalil et al. [39], TED relation for small-sized toroidal rings on the basis of DPL model is given by:

$${Q}^{-1}={\Delta }_{E}{\sum }_{i=1}^{\infty }{C}_{i}\frac{{\tau }_{i}{\omega }_{n}\left(1+{\psi }_{in}^{2}-{\tau }_{i}{\tau }_{q}{\omega }_{n}^{2}\right)+{\tau }_{i}{\tau }_{q}{\omega }_{n}^{3}\left[\left(1+{\psi }_{in}^{2}\right){\tau }_{T}+{\tau }_{i}\right]}{{\left(1+{\psi }_{in}^{2}-{\tau }_{i}{\tau }_{q}{\omega }_{n}^{2}\right)}^{2}+{\left[\left(1+{\psi }_{in}^{2}\right){\tau }_{T}+{\tau }_{i}\right]}^{2}{\omega }_{n}^{2}}$$
(43)

where \({\tau }_{q}\) and \({\tau }_{T}\) are the phase lags of heat flux and temperature in DPL model, respectively. Thermomechanical properties of lead at \({T}_{0}=300 K\) are as follows [39, 49]: \(E=16 \,{\text{GPa}}\), \(\rho =11340 \,{\text{kg}}/{{\text{m}}}^{3}\), \({c}_{v}=128 \,{\text{J}}/\mathrm{kg\,K}\), \(k=35.3 {\text{W}}/{\text{mK}}\), \({k}^{*}=150 {\text{W}}/{\text{mK\,s}}\), \(\alpha =28.9*{10}^{-6} 1/K\), \(\tau ={\tau }_{q}=0.1670 {\text{ps}}\) and \({\tau }_{T}=12.097 {\text{ps}}\). As can be seen, in smaller radii, the predicted value for TED in the framework of DPL model is lower than that determined by MGT model, but as the radius increases and the effect of size diminishes, the amount of TED obtained by both models is almost the same.

Fig. 12
figure 12

Comparison of predictions of MGT and DPL models for TED value for a ring made of lead with \({R}_{0}/{r}_{0}=40\) a \(n=50\) b \(n=100\)

Full size image

6 Conclusions

In the present article, by capturing scale effect on thermal field via the Moore-Gibson-Thompson (MGT) generalized thermoelasticity theory, a novel formulation for estimation of the magnitude of thermoelastic damping (TED) in microrings with circular cross section has been developed. By deriving the equation of heat conduction in the context of MGT model, placing the harmonic form of fluctuation temperature and radial displacement in it and finding the solution of extracted partial differential equation (PDE), the distribution of temperature throughout the ring has been derived. By utilizing the obtained temperature distribution in the calculation of the peak values of wasted thermal energy and strain energy and inserting these values in the relationship defined for TED in the entropy generation (EG) method, a mathematical formula in the form of infinite series has been extracted through which TED value can be predicted by taking into account the nonclassical parameters of MGT model. The accuracy of the model has been confirmed via a comparative study. Also, by way of a convergence study, the number of terms necessary to arrive at precise and convergent outcomes has been determined. Finally, through the presentation of various results, a parametric analysis has been done to clarify the way and extent of the impact of different factors on TED. The essential outcomes of this research can be encapsulated as follows:

  • According to the result of convergence analysis, using the first ten terms of the solution obtained in the framework of MGT model is quite enough to reach precise answer.

  • While in low vibrational mode numbers (that is approximately \(n<100\)), the predictions of MGT and GN-III models exhibit little difference, in high vibration modes, GN-III model estimates much more TED value than MGT model.

  • By increasing the dimensions of ring, size effect dwindles and the output of MGT model converges to that of GN-III model.

  • In low vibrational mode numbers and high ratios of \({R}_{0}/{r}_{0}\) (i.e. thin rings), the difference between the results of 2D and 3D models is minimized.

  • Among the three investigated materials (i.e. silicon, copper and gold), Si-rings show the lowest amount of TED, which can be used as a benchmark for optimal design of microring resonators.