Introduction

Linear analysis is very commonly used in the practice of structural dynamics given its relative simplicity and low calculation cost compared to non-linear analyses. However, the assumed linear behaviour is just an approximation of the reality, which involves always to some extent various non-linear effects, making the linear theories valid only in a restricted domain, beyond which they lead to inaccurate results. This occurs in the case of large displacements caused by several dynamic operational conditions. Despite its complexity, and the lack of a unified and complete analytic model allowing a systematic study of the aforementioned phenomenon, non-linear analyses are becoming currently used in different fields such as civil, mechanical or aerospace engineering, to design economic, lightweight, resistant, flexible, and increasingly slender structures. The transverse vibration of multi-span beams carrying concentric elements (rigid and flexible supports, concentric and inertial masses ...), has been the subject of numerous linear studies corresponding to different end conditions [1,2,3,4,5] but relatively less research considers the geometrical non-linearity in the vibration analysis. The steady-state harmonic response of multi-span beams has been studied in Ref. [6], with consideration of the effect of geometrical non-linearity on the beam dynamic behaviour. The mathematical approach was based on the finite element method, the von Karman theory, the Lagrangian formulation and the Ritz method and the obtained non-linear system was solved iteratively. The utility of the method was validated through numerous examples and comparisons with previous works. The perturbation method was used in Ref. [7] to describe the non-linear dynamic behaviour of beams and the results were identical to those obtained by the harmonic balance method. The perturbation technique was also used in Refs. [8, 9], allowing calculation of the eigenfrequencies and determination of the mode shapes and the non-linear frequencies, taking into account the applied force and the damping effects. For the same purpose, in Ref. [10] the problem of free vibrations of an Euler–Bernoulli beam resting on intermediate supports, considering the geometric non-linearity, was investigated using Hamiltons principle and spectral analysis. The analysis performed led to determination of non-linear modes and the amplitude-frequency dependence. In Ref. [11], an Euler–Bernoulli beam resting on an arbitrary number of supports was examined and the forced case was tackled by adopting the single-mode approach. This made it possible to predict the non-linear frequency response in the vicinity of the mode considered but provided no information on the mode amplitude dependence, necessary to estimate the non-linear stress distributions and predict the fatigue life of the studied structure. The present work deals with the problem of geometrically non-linear free and forced vibrations of multi-span Bernoulli beams resting on multiple supports. The theoretical model is based on the Euler–Bernoulli beam theory and the von Kármán geometrical non-linearity assumptions. Harmonic motion is assumed and the beam transverse displacement function is expanded into a series of the linear modes, determined first by solving the linear problem. After discretising the expressions for the beam total strain and kinetic energies, and applying Hamilton’s principle, the problem is reduced to a non-linear algebraic system solved using an approximate method (the so-called second formulation) [12]. Using an approximate multimode approach in the neighbourhood of the predominant mode, numerical results are obtained for a wide range of vibration amplitudes showing the effect of the rigid supports and their positions and number on the dynamic behaviour of the structure. The frequency response function was examined in the non-linear regime for increasing levels and two types of excitation (a centered point force or a uniformly distributed force).

Review of the Mathematical Approach

Determination of the Linear Mode Shapes

Fig. 1
figure 1

Physical model of a multi-span beam resting on arbitrary number of rigid supports

Full size image

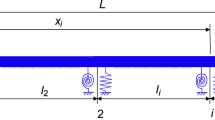
Consider the multi-span beam, shown in Fig. 1, whose geometric and material characteristics, i.e., the length, width, thickness, second moment of area of cross-section, Youngs modulus, area of cross-section and the mass per unit length are, respectively, denoted by: \(L,b,h,I,E,A,\rho.\)

First of all, a linear study is established to determine the system linear mode shapes, to use them as basic functions in the non-linear theory developed below. The transverse displacement function w of the beam shown in Fig. 1 can be defined piece-wise by:

$$\begin{aligned} {w}(x^*)=\left\{ \begin{array}{rl} {w_1}(x^*)\rightarrow ]0,\xi _1[ \\ \cdots \\ {w_j}(x^*)\rightarrow ]\xi _{j-1},\xi _j[ \\ \cdots \\ {w_{n+1}}(x^*)\rightarrow ]\xi _n,1[ \end{array} \right. . \end{aligned}$$
(1)

With \(x^*\) being the non-dimensional coordinate that can be written as: \(x^*=\frac{x}{L}\) and \({\xi _{j}}={\frac{x_{j}}{L}}\) being the non-dimensional position of the support. Using the transfer matrix method as in Ref. [10], a closed form solution to this eigenvalue problem can be obtained. The general solution for transverse vibration at the (j)th span can be written as:

$$\begin{aligned} & {w_{ji}}(x^*) ={c_j} \, \mathrm{cos}h({\beta _i}L(x^*-\xi _{j-1}))+{d_j} \, \mathrm{sin}h({\beta }_{i}L(x^*-\xi _{j-1}))\nonumber \\ & \qquad + {e_j} \, \mathrm{cos} ({\beta _i}L(x^*-\xi _{j-1}))+{g_j} \, \mathrm{sin} ({\beta }_{i}L(x^*-\xi _{j-1})) \\ &\xi _{j-1}\le x^*\le \xi _{j}\nonumber . \end{aligned}$$
(2)

In which \({\beta _i}\) is the eigenvalue parameter of the beam, given by:

$$\begin{aligned} {\beta _i}=\root 4 \of {\frac{\rho A \omega _i^2}{EI}}\ . \end{aligned}$$
(3)

With i varying from 1 to n, n being the number of functions.

The constants \({c_j},{d_j},{e_j},{g_j},\) are determined by the beam end and continuity conditions as follows:

The end conditions (at the left end) [13]:

$$\begin{aligned} \frac{\mathrm{d}^3{w_{1i}}(x^*)}{\mathrm{d}x^{*3}}\Bigr |_{\begin{array}{c} x^*=0 \end{array}}= & {} -K_{t1}{w_{1i}}(x^*)\Bigr |_{\begin{array}{c} x^*=0 \end{array}}, \end{aligned}$$
(4)
$$\begin{aligned} \frac{\mathrm{d}^2{w_{1i}}(x^*)}{\mathrm{d}x^{*2}}\Bigr |_{\begin{array}{c} x^*=0 \end{array}}= & {} K_{\theta 1}\frac{d{w_{1i}}(x^*)}{dx^*}\Bigr |_{\begin{array}{c} x^*=0 \end{array}}. \end{aligned}$$
(5)

The end conditions (at the right end):

$$\begin{aligned} \frac{\mathrm{d}^3{w_{(n+1)i}}(x^*)}{\mathrm{d}x^{*3}}\Bigr |_{\begin{array}{c} {x^*=1} \end{array}}= & {} K_{t2}{w_{(n+1)i}}(x^*)\Bigr |_{\begin{array}{c} x^*=1 \end{array}}, \end{aligned}$$
(6)
$$\begin{aligned} \frac{\mathrm{d}^2{w_{(n+1)i}}(x^*)}{\mathrm{d}x^{*2}}\Bigr |_{\begin{array}{c} {x^*=1} \end{array}}= & {} -K_{\theta 2}\frac{\mathrm{d}{w_{(n+1)i}}(x^*)}{\mathrm{d}x^*}\Bigr |_{\begin{array}{c} {x^*=1} \end{array}}. \end{aligned}$$
(7)

The compatibility conditions at the jth support are given by [13]:

$$\begin{aligned} {w_{ji}}(x^*)\Bigr |_{\begin{array}{c} x^*=\xi _j \end{array}}= & {} {w_{(j+1)i}}(x^*)\Bigr |_{\begin{array}{c} x^*=\xi _j \end{array}}=0, \end{aligned}$$
(8)
$$\begin{aligned} \frac{\mathrm{d}{w_{ji}}(x^*)}{\mathrm{d}x^*}\Bigr |_{\begin{array}{c} x^*=\xi _j \end{array}}= & {} \frac{\mathrm{d}{w_{(j+1)i}}(x^*)}{\mathrm{d}x^*}\Bigr |_{\begin{array}{c} x^*=\xi _j \end{array}}, \end{aligned}$$
(9)
$$\begin{aligned} \frac{\mathrm{d}^2{w_{ji}}(x^*)}{\mathrm{d}x^{*2}}\Bigr |_{\begin{array}{c} x^*=\xi _j \end{array}}= & {} \frac{\mathrm{d}^2{w_{(j+1)i}}(x^*)}{\mathrm{d}x^{*2}}\Bigr |_{\begin{array}{c} x^*=\xi _j \end{array}}, \end{aligned}$$
(10)
$$\begin{aligned} \frac{\mathrm{d}^3{w_{ji}}(x)}{\mathrm{d}x^3}\Bigr |_{\begin{array}{c} x^*=\xi _j \end{array}}= & {} \frac{\mathrm{d}^3{w_{(j+1)i}}(x)}{\mathrm{d}x^3}\Bigr |_{\begin{array}{c} x^*=\xi _j \end{array}}-\frac{R}{EI}. \end{aligned}$$
(11)

The use of the continuity conditions corresponding to each support, the end conditions and the transfer matrix method leads to a homogeneous system. The determinant of the latest must be set equal to zero to obtain the natural frequencies, determined iteratively by the Newton–Raphson method [14].

Formulation of the Non-linear Problem

The total strain energy V of the beam can be written as the sum of the axial strain energy due to the non-linear stretching forces induced by the large deflections \({V_a}\), and the strain energy due to bending \({V_b}\). \({V_a}\), \({V_b}\), and the kinetic energy T can be expressed as [15, 16]:

$$\begin{aligned} {V_a}= & {} \frac{EA}{8L}\left[ \int _{0}^{L}{\left( \frac{\partial {W}}{\partial x}\right) ^2}\mathrm{d}x\right] ^{2}, \end{aligned}$$
(12)
$$\begin{aligned} {V_b}= {} \frac{EI}{2}\int _{0}^{L}\left( \frac{\partial ^2 {W}}{\partial x^2}\right) ^2\mathrm{d}x, \end{aligned}$$
(13)
$$\begin{aligned} {T}= {} \frac{1}{2}\rho A\left[ \int _{0}^{L}\left( \frac{\partial {W}}{\partial t}\right) ^2\mathrm{d}x\right] . \end{aligned}$$
(14)

In this study, the time dependence is assumed to be harmonic and the transverse displacement W is expanded in the form of a finite series of basic spatial functions \({w_i,i=1,2,...,n}\) (which represents the linear modes of the beam) and the time, one may write:

$$\begin{aligned} {W}(x,t)={a_i}{w_i(x)}\mathrm{sin}(\omega t). \end{aligned}$$
(15)

The following expressions can be written for the potential and kinetic energies (as functional involving \({w_i}\)), when W(x, t) is used in the form defined above:

$$\begin{aligned} {V_a}= {} \frac{1}{2}{a_i}{a_j}{a_k}{a_l}{b_{ijkl}}\mathrm{sin}^4(\omega t), \end{aligned}$$
(16)
$$\begin{aligned} {V_b}= {} \frac{1}{2}{a_i}{a_j}{k_{ij}}\mathrm{sin}^2(\omega t), \end{aligned}$$
(17)
$$\begin{aligned} {T}= {} \frac{1}{2}\omega ^2{a_i}{a_j}{m_{ij}}cos^2(\omega t), \end{aligned}$$
(18)

\({b_{ijkl}}\) presents the non-linearity tensor defined as:

$$\begin{aligned} {b_{ijkl}}=\frac{EA}{4L}\int _{0}^{L}\left( \frac{\partial {w_i}}{\partial x}\right) \left( \frac{\partial {w_j}}{\partial x}\right) \mathrm{d}x\int _{0}^{L}\left( \frac{\partial {w_k}}{\partial x}\right) \left( \frac{\partial {w_l}}{\partial x}\right) \mathrm{d}x, \end{aligned}$$
(19)

\({k_{ij}}\) denotes the rigidity matrix:

$$\begin{aligned} {k_{ij}}={EI}\int _{0}^{L}\left( \frac{\partial ^2 {w_i}}{\partial x^2 }\right) \left( \frac{\partial ^2 {w_j}}{\partial x^2}\right) \mathrm{d}x, \end{aligned}$$
(20)

and \({m_{ij}}\) stands for the mass matrix:

$$\begin{aligned} {m_{ij}}=\rho S\int _{0}^{L}{w_i}{w_j}\mathrm{d}x. \end{aligned}$$
(21)

The coefficients \(a_i\) are unknowns as well as the frequency \(\omega.\)

Governing Equation

To examine non-linear forced vibrations, consider a uniform beam excited by the force F(x, t) over the range S(S represents the length of the beam or a part of it). The physical force F(x, t) excites the modes of the structure via a set of generalized forces \({F_i}\) which depend on the expression for F, the excitation point for concentrated forces, the excitation length for distributed forces, and the mode considered. The generalized forces \(F_i(t)\) are given by:

$$\begin{aligned} F_i(t)=\int _{{S}}{{F}(x,t){w}_i(x)\,\mathrm{d}x}. \end{aligned}$$
(22)

The dynamic behaviour of the beam is examined under two types of excitation, a centered point force \({F^c}\) applied at the point \(x_f\), and a distributed harmonic force \({F^d}\) defined by:

$$\begin{aligned} {F^d}(x,t)= {} {f^d}\mathrm{sin}(\omega t), \end{aligned}$$
(23)
$$\begin{aligned} {F^c}(x,t)= {} {f^c}\mathrm{sin}(\omega t)\delta (x-x_f), \end{aligned}$$
(24)

\(\delta\) denotes the Dirac function, \({F_i^d}(t)\) and \({F_i^c}(t)\) are the corresponding generalized forces given by:

$$\begin{aligned} {F_i^d}(t)= {} {F^d}\mathrm{sin}(\omega t)\int _{0}^L{w_i}(x)\mathrm{d}x={f_i^d}\mathrm{sin}(\omega t), \end{aligned}$$
(25)
$$\begin{aligned} {F_i^c}(t)= {} {F^c}\mathrm{sin}(\omega t){w_i}(x_0)\mathrm{d}x={f_i^c}\mathrm{sin}(\omega t). \end{aligned}$$
(26)

It is well known that the dynamic behaviour of a conservative system may be obtained by applying Hamilton’s principle, which, by taking into account the forcing term, may be written as follows [17]:

$$\begin{aligned} \delta \int _{0}^{2\pi /\omega }{({V}-{T}+{W})\mathrm{d}t}, \end{aligned}$$
(27)

where T is the kinetic energy, V is the total stain energy and W is the work done by the external load. After calculations, the following non-linear system is obtained:

$$\begin{aligned} {\mathbf {[K]\{A\}}}+\frac{3}{2}{\mathbf {[B(\{A\})]\{A\}}}-\omega ^2{\mathbf {[M]\{A\}}}={\mathbf {\{F\}}} \end{aligned}$$
(28)

With \({\mathbf {\{A\}}}\) being the column vector of the basic function contribution coefficients.

For obtaining non-dimensional parameters, one puts:

$$\begin{aligned} {w}(x)= {} h{w_i^*}\left( \frac{x}{L}\right) =h{w_i^*}(x^*); \quad \frac{{m_{ij}}}{{m^*_{ij}}}=\rho Sh^2L;\nonumber \\= & {} \frac{{k_{ij}}}{{k^*_{ij}}} \frac{EIh^2}{L^3}; \quad \frac{\omega ^2}{\omega ^{*2}}=\frac{EI}{\rho SL^4}. \end{aligned}$$
(29)

The dimensionless generalized forces \({f_i^{*d}}\) and \({f_i^{*c}}\) are given by:

$$\begin{aligned} {f_i^{*d}}= {} {F^d}\frac{L^4}{EIh}\int _{0}^1{w_i^*}(x^*)\mathrm{d}x^*, \end{aligned}$$
(30)
$$\begin{aligned} {f_i^{*c}}= {} {F^c}\frac{L^3}{EIh}{w_i^*}(x_f). \end{aligned}$$
(31)

Substituting these notations into (27), one obtains the following non-linear algebraic equation:

$$\begin{aligned} \mathbf {[K^*]\{A\}}+\frac{3}{2}\mathbf {[B^{*}(\{A\})]\{A\}}-\omega ^{*2}\mathbf {[M^*]\{A\}}=\mathbf {\{F^*\}}, \end{aligned}$$
(32)

which may be written as:

$$\begin{aligned} a_{i} k_{ir}^{*}-\omega ^{*^{2}}a_{i} m_{ir}^*+\frac{3}{2}a_{i} a_{j} a_{k} b_{ijkr}^{*}=F_{r}^{*}\quad r=1, \ldots , n. \end{aligned}$$
(33)

Considering for example the first non-linear mode, previous works have shown that the contribution of the fundamental mode \(a_1\) remains predominant for the whole range of vibration amplitudes considered. Consequently, the contributions of the other modes are denoted \(\epsilon _2, \ldots \epsilon _n\) instead of \(a_2, \ldots ,a_n\), to indicate that they are small compared to \(a_1\). According to Ref. [12], by separating in the non-linear expression \(a_ia_ja_kb_{ijkr}\) terms proportional to \(a_1^3\), terms proportional to \(a_1^2\epsilon _i\), and by neglecting the terms which are proportional to \(a_1\epsilon _i\epsilon _j\) and terms proportional to \(\epsilon _i\epsilon _j\epsilon _k\) one may write:

$$\begin{aligned} a_i a_j a_k b_{ijkr}=a_1^3 b_{111r}+a_1^2\epsilon _i b_{11ir}\qquad r=1, \ldots ,n. \end{aligned}$$
(34)

In the vicinity of the rth mode, the Eq. (31) can be written as follows:

$$\begin{aligned} ([\mathbf {K}_{\mathbf {r}}^{\mathbf {*}}]_{\mathbf {R}}-\omega ^{*2} [\mathbf {M}_{\mathbf {r}}^{\mathbf {*}}]_{\mathbf {R}}) \{\mathbf {A}_{\mathbf {r}}\}_{\mathbf {R}}+\frac{3}{2} [{\varvec{\alpha }}_{\mathbf {r}}^{\mathbf {*}}]\{\mathbf {A}_{\mathbf {r}}\}_{\mathbf {R}}=\left\{ F_r-\frac{3}{2}a_r^3b_{irrr^*} \right\} . \end{aligned}$$
(35)

With: \([{\alpha _r^*]_R}=[a_r^{*2}b_{ijrr}^*]_R\) Eq. 35 is an approximate linear system, very easy to solve to get the contribution coefficients to the non-linear beam-forced response.

Numerical Results and Discussion

The results presented herein are obtained for a clamped–clamped beam resting on two rigid supports located at \(\eta _1=1/3\), \(\eta _2=2/3\). To obtain both clamped ends, the stiffness of the rotational and translational springs defined in Fig. 1 is given by:

$$\begin{aligned} k_{\varTheta 1}= {} k_{\varTheta 2}=\infty , \end{aligned}$$
(36)
$$\begin{aligned} k_{t1}= {} k_{t2}=\infty . \end{aligned}$$
(37)
Table 1 Eigenvalue parameters of a fully clamped beam resting on two supports
Full size table

Table 1 presents the linear frequencies obtained by the application of the transfer matrix method. The results are compared with those obtained using the finite element method, the theory of which is detailed in Ref. [18]. The results obtained show a very good agreement since the average of the relative difference is of the order of \(0.01 \%\).

Fig. 2
figure 2

Comparison of the frequency ratios of a C-SS-C beam in the vicinity of the first mode

Full size image

Figure 2 illustrates the comparison between the results of the present method and those obtained in Ref. [6], for the first non-linear mode shape. the support positions are selected as: \(\xi _1=2/5\), \(\xi _2=3/5\). It is quite clear that the results obtained by the present approach show a very good agreement with those in Ref. [6] since for amplitudes up to twice the beam thickness, the average of relative difference does not exceed 1 %.

Fig. 3
figure 3

The normalized first non-linear mode (a) and the associated curvature distribution (b) of a C-SS-C beam for various values of the vibration amplitudes

Full size image

Figure 3 corresponds to a beam resting on two supports with \(\xi _1=1/3\) et \(\xi _2=2/3\), the hardening type effect of geometrical non-linearity can be clearly observed for various vibration amplitudes in Fig. 3a. The Fig. 3b shows that the curvatures increase in the vicinity of the clamps. It is quite clear that the effect of the rigid support is accentuated with the increase of the amplitude of vibration.

Fig. 4
figure 4

Backbone curves of a C-SS-C beam, in the vicinity of the first mode for three different number of supports

Full size image

Figure 4 shows that for a given amplitude, the frequency ratio decreases for each added support. This is due to the fact that the denominator, corresponding to the linear frequencies increases by adding new supports, due to the increased rigidity.

Fig. 5
figure 5

Backbone curves in the vicinity of the first mode for the three scenarios considered

Full size image

It can be noticed in Fig. 5, that by moving the support towards the clamps, the linear frequencies decrease significantly, and consequently the corresponding frequency ratio increases.

Fig. 6
figure 6

Comparison between resonance curves obtained for three levels of excitation based on the multimode approach: case of a centered point force

Full size image

Two scenarios are presented, considering two types of excitation: a centered point force applied at the middle of the beam (Fig. 6), and a harmonic force uniformly distributed over the beam length (Fig. 7). These figures illustrate the typical behaviour of the Duffing equation. The hardening type effect of geometrical non-linearity can be clearly observed for the two scenarios, a behaviour that involves the creation of a frequency range in which three amplitudes exist for a single frequency: a phenomenon characteristic of non-linear systems commonly called the jump phenomenon [19]. Another property of the non-linear systems can be noticed: the frequency response functions are not proportional to the level of the force applied, whereas it increases by power of 10.

Table 2 Percentage of generalized forces exciting the first five symmetric modes of a C-SS-C excited by uniformly distributed force along the whole beam
Full size table

Table 2 presents the contributions of the 5 symmetric modes. It can be seen that the force excites predominantly the third mode of vibration. Therefore, an analysis is performed in its neighbourhood based on the multimode approach.

Fig. 7
figure 7

Comparison between resonance curves obtained for three levels of excitation based on the multimode approach: case of uniformly distributed harmonic force

Full size image

Conclusion

Foremost, a linear analysis was performed allowing the determination of the frequencies and linear mode shapes of a multi-span beam. By the use of the transfer matrix method, the problem was generalized to give the exact analytic results for each possible number of supports. The non-linear vibration analysis was established, based on the Euler–Bernoulli beam theory and the von Kármán geometrical non-linearity assumptions. The method was validated through a comparative study with that developed in Ref. [6]. The effect of the supports, their positions and their number were examined. The presence of an additional support increases significantly the linear frequencies, and, consequently, decreases the frequency ratio, which makes it possible to increase the beam rigidity with each additional support. By considering the multimode approach, an analysis of the dynamic behaviour of beams resting on several supports has been established in the vicinity of the predominant mode. The response curves have been illustrated for two scenarios: the first, the beam was excited by a concentric harmonic excitation, in the second, by a uniformly distributed force. The results shows the particular behaviour of non-linear systems such as the jump phenomenon where for the same frequency range, several results are possible, as well as the non-proportional evolution of the frequency response to the intensity of excitation.