An analytical method for vibration analysis of multi-span Timoshenko beams under arbitrary boundary conditions

Abstract

An analytical method for analyzing free vibration of multi-span Timoshenko beams under arbitrary boundary conditions is proposed in this paper. Based on the theoretical model of the Timoshenko beam, linear displacement springs and rotational springs are introduced to simulate the boundary and support forces of multi-span Timoshenko beams. By modifying the springs’ stiffness, different boundary conditions and inter-span coupling conditions can be simulated. To develop the vibration calculation models based on the energy method, the improved Fourier cosine series with four sine series are introduced to represent the displacement functions in order to eliminate the discontinuities or jumps in the solution processes. With the Rayleigh–Ritz method, the Lagrange equations of structures are solved to obtain free vibration characteristics. Using a three-span beam and a four-span beam as examples, this method is applied to calculate the natural frequencies of structures with circular and rectangular cross sections. The correctness and accuracy of the method are verified by comparing the solutions with the results of existing literature. On this basis, the influences of boundary conditions, span ratio and span number on the vibration characteristics of multi-span Timoshenko beams are discussed and analyzed.

1 Introduction

As a traditional beam type, Timoshenko beams are used widely in various fields of engineering, such as aerospace, marine machinery and construction work. Unlike the Euler–Bernoulli beam theory, the Timoshenko beam theory takes the shear deformation into account [1,2,3,4,5,6]. Wide usage in the field of engineering has also led researchers to pay much attention to the study of their vibration characteristics. Based on the theory of Timoshenko beams, Lee and Park [7] introduced an isogeometric approach to develop a thick beam element that allows for transverse shear deformation and rotational inertia effects to accurately identify the natural frequencies and vibration modes of Timoshenko beams, and three refinement schemes were used to verify the rate of convergence. Lee et al. [8] separated the deformation modes to get the bending deflection and shear deflection, which derived gradually the exact stiffness matrix of the Timoshenko beam element. Civalek and Kiracioglu [9] carried out free vibration analysis of Timoshenko beams and used the discrete singular convolution method to solve equations of motion numerically. Lou et al. [10] introduced a modal perturbation method to transform the differential equations of motion for dynamic behavior into nonlinear algebraic equations, in order to solve the dynamic properties of Timoshenko beams with arbitrary boundaries under dynamic loading. Zhou and Cheung [11] proposed static functions of tapered Timoshenko beams under the static load of the Taylor series, and then used the Rayleigh–Ritz method to derive the eigenfrequency equations. Liao and Zhong [12] also analyzed the nonlinear bending vibration of tapered Timoshenko beams. Based on the Timoshenko beam theory, Xiang and Yang [13] analyzed the free and forced vibration effects of functional gradient laminated beams with variable thickness, considering the effects of temperature changing and determining the initial stress state by thermoelastic analysis. Shafiei et al. [14] analyzed the vibration characteristics of rotary tapered axially functionally graded Timoshenko nanobeams in thermal environment based on non-local theory, and discussed the effects of other conditions. Civalek et al. [15] used the first-order shear deformation beam theory and Ritz method to study and analyze the ground forced vibration of carbon nanotube simply supported beams composed of polymer matrix. Similarly, Demir and Civalek [16], based on the Euler–Bernoulli beam theory and combined with the improved Eringen differential model, studied the bending problem of nanobeams under concentrated and distributed loads under various boundary conditions. Based on the Timoshenko beam theory, Numanoğlu [17] combined Hamilton's principle with the stress equation of non-local elastic theory, and analyzed the size-dependent thermal–mechanical vibration properties of nanobeams by using separate variable method and finite element method. Akgöz and Civalek [18] took the size effect into account, modeled the longitudinal microcolumn composed of functionally graded materials theoretically, and solved the eigenvalues, so as to study the buckling problem of microbeams with non-uniform boundary surfaces. Li [19] proposed a unified analysis method for the static and dynamic behaviors of functionally graded beams with the rotary inertia and shear deformation included, which can be used for the calculation of layered Timoshenko beams. Shahba et al. [20] investigated and analyzed free vibration and stability of the axially functionally graded Timoshenko beams, and considered the changes of cross-sectional and mechanical properties. Esen [21] improved the finite element method, based on first-order shear deformation theory to obtain the motion equations of a functionally graded Timoshenko beam exposed to a moving mass, and then investigated the response of the structure under two-parameter elastic foundations. Pradhan and Chakraverty [22] further analyzed the free vibration of functional gradient beams under different boundary conditions based on the classical and first-order shear deformation beam theories. Similarly, Nikrad et al. [23] also studied the influence of parameters on the nonlinear equilibrium path and stability behavior of FG porous curved beams based on the first-order shear deformation theory and nonlinear Green strain, and further discussed the in-plane thermoelastic response of porous material curved beams with different functional gradient porosity. On the basis of the Timoshenko beam theory, Bourada et al. [24] considered the thickness stretching effect and proposed a simple and refined trigonometric higher-order beam theory that can be used for the bending and vibration analysis of functionally graded beams based on the neutral plane concept. Chen et al. [25] studied and analyzed the nonlinear free vibration of shear deformable sandwich porous beams considering the influences of transverse shear deformation and rotary inertia under the theoretical framework of the Timoshenko beam. Based on a modified couple stress theory and Hamilton’s principle, Ma et al. [26] established a microstructure-related Timoshenko beam model that can capture size effect compared with the classical Timoshenko beam theory.

The application of multi-span beams in various engineering fields is also extremely wide, such as in Marine engineering, the structural form of ship deck plate frame can be equivalent to multi-span beam structure: both ends of the longitudinal free support, the beam of the plate frame can be simplified into the elastic support of the longitudinal. Therefore, its mechanical properties have attracted the attention of many scholars. Based on Hamilton’s principle, Zheng et al. [27] modified the beams’ vibration functions to be the assumed modes, so as to analyze the vibration characteristics of multi-span non-uniform beams under dynamic loads. EI-Sayed and EI-Mongy [28] proposed a new method that can solve the complicated free vibration problems with a numeric-symbolic procedure based upon the variational iteration method. Based on the Euler–Bernoulli beam theory and von Kármán geometric nonlinear assumptions, Fakhreddine et al. [29] simplified solving linear problems to nonlinear algebraic systems solved using an approximate method, and obtained a multi-modal method for geometrically nonlinear forced vibrations of multi-span Euler–Bernoulli beams. Dugush and Eisenberger [30] used a combination of the modal analysis and the direct integration method to analyze the vibrations of multi-span non-uniform beams under dynamic loads based on the Euler–Bernoulli beam theory. Abu [31] used the dynamic Green functions to present a method for determining the dynamic response of different types of Euler–Bernoulli beams under load and different boundary conditions. Luo et al. [32] used the generalized function method to analyze and solve the free vibration of discretely supported Euler–Bernoulli beams and Timoshenko beams with an arbitrary number of elastic constraints in between. Using the Green’s functions as the basic solution, Zhao et al. [33] analyzed and solved the forced transverse vibration of a coupled double-beam Timoshenko system under axial compressive load. Ghannadiasl and Khodapanah [34] also used the Green’s function to analyze the dynamic response of a multi-span cracked beam, and combined with tests to verify that cracks on the beam will affect its vibration, and the influence of other parameters is also discussed. Zhu et al. [35] mainly took uniform multi-span beams of finite and infinite length as research objects, and studied the precise responses of free vibration and forced vibration under the premise of rigid lateral constraints and elastic rotation constraints set at the supports of multi-span beams. Lin and Chang [36] based on the Timoshenko beam theory, proposed a hybrid analytical method that can effectively solve the eigensolutions for flexible support of beams with arbitrary number under various boundary conditions. Jin et al. [37] introduced springs to simulate the boundary conditions by adjusting the stiffness values, and analyzed the free vibration characteristics of lattice sandwich beams under various boundary conditions. On this basis, Jin et al. [38] simulated the boundary conditions in the same way, obtained an accurate solution for the free vibration of multi-span lattice sandwich beams under arbitrary boundary conditions with the improved Fourier series introduced to eliminate the discontinuities and jumps in the solution processes. Lin and Tsai [39] used the conventional finite element method to analyze the free vibration characteristics of multi-span beams with multiple spring-mass systems. On this basis, Yesilce and Demirdag [40] considered the influence of multiple spring-mass systems on multi-span Timoshenko beams, and gave accurate solutions of natural frequencies and mode shapes when subjected to axial forces. Subsequently, Yesilce [41] analyzed the free vibration characteristics of Reddy–Bickford multi-span beams carrying multiple spring-mass systems with or without axial forces, and determined the exact solutions of their natural frequencies and modal modes. On this basis, Yesilce [42] also used the Reddy–Bickford beam theory to analyze the free vibration characteristics of Reddy–Bickford multi-span beams with multiple spring-mass systems. In addition, Yesilce [43] analyzed the vibration characteristics of axially loaded multi-span Timoshenko beams bearing several intermediate concentrated masses and/or rotational inertia, and precisely determined their natural frequencies and modal shapes using numerical assembly techniques and differential transformation methods. Borji et al. [44] used the time-weighted residual value approach to store the basic functions of beams in time steps for the first time, and analyzed the forced vibrations of multi-span Timoshenko beams under a wide range of loads. Liu et al. [45] used the first-order shear deformation theory and interpolation functions to analyze and solve the vibration mode of multi-span lattice sandwich beams. Gao et al. [46] used an efficient domain decomposition method to divide the structure, and obtained the free and forced vibration characteristics of multi-span beam structures with Jacobi orthogonal polynomials and the Rayleigh–Ritz method. Xu and Wang [47] applied the discrete singular convolution method to the analysis of the free vibration of Timoshenko beams under free boundary conditions, and proposed a simple method. Shi et al. [48] proposed an accurate solution method for the free vibration of Timoshenko beams with general elastic constraints without modifying algorithms and procedures. In addition to the study of free vibration, scholars have also studied multi-span beams from the perspective of forced vibration. Wang [49] determined the modal frequency and corresponding mode shape functions of multi-span beams based on the analytical method and transfer matrix method, and proposed a modal analysis method to analyze the forced vibration characteristics of multi-span Timoshenko beams. Chen et al. [50] analyzed and solved the free vibration and forced vibration of the hybrid system with multi-step Timoshenko beams coupled with rigid bodies on springs by transfer matrix method. Copetti et al. [51] used the fundamental matrix response to represent eigenanalysis, and analyzed the modal matrix differential equation of an elastically coupled double-beam Timoshenko system. Zhao et al. [52] used the hypothetical mode method to solve the vibration characteristics of multi-span Timoshenko beams, and compared them with the results of software simulation. Based on the Euler–Bernoulli beam theory, Bao and Zhou [53] combined the improved Fourier series method with the Rayleigh–Ritz method to solve the vibration characteristics of multi-span beams with different cross-sectional shapes under elastic support boundary conditions.

In summary, there are many studies on the vibration characteristics of Timoshenko beams and multi-span beams, while the research work on vibration analysis of multi-span Timoshenko beams has more stringent requirements for boundary conditions, inter-span coupling conditions and span number. Therefore, an analytical method is proposed that can be applied to analyze the vibration characteristics of multi-span Timoshenko beams with arbitrary boundary conditions, arbitrary inter-span coupling conditions and arbitrary span number. Firstly, the boundary conditions and inter-span coupling conditions are simulated by transverse displacement springs and rotational constraint springs, and the stiffness values of springs are adjusted to meet any conditions. Secondly, the expressions of the improved Fourier series are used to represent the displacement functions of multi-span Timoshenko beams, and four sine terms are introduced to overcome the jumps or discontinuities in the solution processes. The vibration equations are established based on the energy method and solved by the Rayleigh–Ritz method, so that the problem of solving the vibration characteristics of the structures is transformed into the problem of solving the standard eigenvalues. After comparing with the data of existing literature, the correctness and effectiveness of the proposed method are verified, and other parametric conditions affecting the free vibration characteristics of the structures are studied.

2 Multi-span beam structural model

2.1 Structural model description

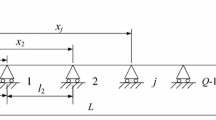
The multi-span Timoshenko beam model (rectangular section as an example) with arbitrary boundary conditions and inter-span coupling conditions is shown in Fig. 1. The total length of the multi-span Timoshenko beam is L, and the section height and width are h and B, respectively. The beam is divided into N spans, and the length of each span from left to right is expressed as l₁, l₂, …, l_i, …, l_N, respectively. Set the coordinate origin of the coordinate axis at the left end of the multi-span beam, x is the transverse coordinate, and the others are shown in Fig. 1.

Fig. 1

The multi-span Timoshenko beam with (N + 1) elastic supports

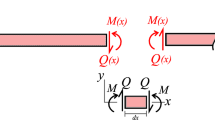
In order to simulate the arbitrary boundary conditions, as shown in Fig. 2, taking the i-th sub-span as an example, transverse displacement springs and rotational restraint springs are set at the left and right ends of each beam, the stiffness values are $\tilde{k}_{i,0}$ and $\tilde{k}_{i,l}$, $\tilde{K}_{i,0}$ and $\tilde{K}_{i,l}$. The boundary conditions of i-th sub-span at $x_{i} = 0$ and $x_{i} = l_{i}$ are simulated by the combination of $\tilde{k}_{i,0}$ and $\tilde{K}_{i,0}$ and the combination of $\tilde{k}_{i,l}$ and $\tilde{K}_{i,l}$.When both ends of i-th sub-span are a fixed supported boundary conditions, $\tilde{k}_{i,0}$ = $\tilde{K}_{i,0}$ = $\tilde{k}_{i,l}$ = $\tilde{K}_{i,l}$ = 1 × 10¹². When both ends of i-th sub-span are a free supported boundary conditions, $\tilde{k}_{i,0}$ = $\tilde{K}_{i,0}$ = $\tilde{k}_{i,l}$ = $\tilde{K}_{i,l}$ = 0. When both ends of ith sub-span are a simple supported boundary conditions, $\tilde{k}_{i,0}$ = $\tilde{k}_{i,l}$ = 1 × 10¹², $\tilde{K}_{i,0}$ = $\tilde{K}_{i,l}$ = 0.

Fig. 2

Calculation model for the multi-span Timoshenko beam with elastic boundary condition

And any other boundary conditions can be easily obtained by changing the stiffness values of displacement springs and rotation springs at both ends of the beam. For arbitrary coupling conditions, the inter-span coupling effects are mainly lateral displacement and transverse bending moment. So the coupling springs are set between the i-th span and the i − 1-th and i + 1-th spans to simulate the arbitrary coupling conditions between spans. For example, symbols $k_{i,i - 1}$ and $K_{i,i - 1}$ represent the coupling spring stiffness values between the i-th sub-span and the i − 1-th sub-span. When $k_{i,i - 1}$ = $K_{i,i - 1}$ = 1 × 10¹², the coupling condition between the i-th and i − 1-th spans is a rigid coupling. When $k_{i,i - 1}$ = $K_{i,i - 1}$ = 0, the coupling condition between the i-th and i − 1-th spans is a free coupling. When 0 < $k_{i,i - 1}$ = $K_{i,i - 1}$ < 1 × 10¹², the coupling condition is an elastic coupling. Therefore, when the boundary conditions and inter-span coupling conditions of the beam change, only the stiffness values of transverse displacement springs and rotational restraint springs need to be changed to simulate arbitrary boundary conditions and coupling conditions.

2.2 Displacement functions representation

According to the Timoshenko beam theory, the displacement functions at any point of the i-th sub-span can be expressed as follows:

$$u_{i} = - z\theta_{i} ,\quad w_{i} = w_{i}$$

(1)

where u_i and w_i represent the axial displacement and lateral displacement of the i-th sub-span, respectively. θ_i represents the rotation angle of the midplane normal of the i-th sub-span.

According to the displacement functions given in Eq. (1), the expressions of the displacement–strain relationship of the i-th sub-span can be expressed as follows:

$$\varepsilon_{i} = - z\frac{{\partial \theta_{i} }}{{\partial x_{i} }},\quad \gamma_{i} = - \theta_{i} + \frac{{\partial w_{i} }}{{\partial x_{i} }}$$

(2)

where ε_i and γ_i represent the normal strain and shear strain of the i-th sub-span.

Based on Hooke’s law, the stress expressions of the i-th sub-span are written as follows:

$$\sigma_{i} = E\varepsilon_{i} ,\quad \tau_{i} = G_{xz} \gamma_{i}$$

(3)

where σ_i and τ_i represent the normal stress and shear stress of the i-th sub-span, respectively. E and G_xz represent the elastic modulus and shear modulus of the beam.

In order to solve the vibration characteristics of multi-span Timoshenko beams under arbitrary boundary conditions, an improved Fourier series and four sine terms are introduced to represent the displacement functions to eliminate the potential discontinuities or jumps of arbitrary boundary conditions during the derivation [54]. Thus, for the i-th sub-span, the lateral displacement functions and the corner displacement functions are expressed by the improved Fourier series are as follows:

$$w_{i} \left( {x_{i} ,t} \right) = \Phi_{i} \left( {x_{i} } \right)e^{j\omega t}$$

(4)

$$\theta_{i} \left( {x_{i} ,t} \right) = \Psi_{i} \left( {x_{i} } \right)e^{j\omega t}$$

(5)

$$\Phi_{i} \left( {x_{i} } \right) = \sum\limits_{m = 0}^{\infty } {A_{i,m} \cos \lambda_{i,m} x_{i} } + \sum\limits_{n = 1}^{4} {A_{i,n}^{a} \sin \lambda_{i,n} x_{i} }$$

(6)

$$\Psi_{i} \left( {x_{i} } \right) = \sum\limits_{m = 0}^{\infty } {B_{i,m} \cos \lambda_{i,m} x_{i} } + \sum\limits_{n = 1}^{4} {B_{i,n}^{a} \sin \lambda_{i,n} x_{i} }$$

(7)

where $\lambda_{i,m} = m\pi /l_{i}$, $\lambda_{i,n} = n\pi /l_{i}$, $0 \le x_{i} \le l_{i}$, and t means time; Φ_i(x_i) and Ψ_i(x_i) are the displacement functions of the i-th sub-span Timoshenko beam, $A_{i,m}$, $B_{i,m}$ are the coefficients of the cosine Fourier series for displacement functions, M is the highest degrees of m, $A_{i,n}^{a}$, $B_{i,n}^{a}$ are supplemented coefficients of the auxiliary functions, where n = 1, 2, 3, 4.

From the formulas (6) and (7), it can be seen that for the i-th sub-span Timoshenko beam, in the entire solution region $R:\left( {0,l_{i} } \right)$, the function expressions contain four single Fourier sine series except the traditional Fourier cosine series, which makes the displacement functions (6) and (7) can be expanded and converged to $f\left( {x_{i} } \right) \in C^{3}$ (C is the convergence value) for $\forall x_{i} \in R:\left( {0,l_{i} } \right)$, that is the improved Fourier trigonometric series can satisfy any boundary conditions and coupling conditions of multi-span Timoshenko beams.

2.3 Energy functions representation and solution

Based on the above all, the kinetic and potential energies of the multi-span Timoshenko beam under arbitrary boundary conditions and coupling conditions are derived and the vibration characteristics are solved with the Rayleigh–Ritz method. The Lagrange energy function L of the multi-span Timoshenko beam can be expressed as follows:

$$L = U - T$$

(8)

where U and T represent the total potential energy and the total kinetic energy of the multi-span Timoshenko beam, respectively.

$$U = U_{P} + U_{{\text{S}}} + U_{{\text{C}}}$$

(9)

$$\begin{aligned} U_{P} & = \sum\limits_{i = 1}^{N} {\frac{1}{2}\int_{0}^{{l_{i} }} {\int_{{A_{i} }} {\left( {\sigma_{i} \cdot \varepsilon_{i} + \tau_{i} \cdot \gamma_{i} } \right){\text{d}}A_{i} {\text{d}}x_{i} } } } \\ & = \sum\limits_{i = 1}^{N} {\frac{{B_{i} }}{2}\int_{0}^{{l_{i} }} {\int_{ - h/2}^{h/2} {\left( {\sigma_{i} \cdot \varepsilon_{i} + \tau_{i} \cdot \gamma_{i} } \right){\text{d}}z{\text{d}}x_{i} } } } \\ \end{aligned}$$

(10)

$$\begin{aligned} U_{{\text{S}}} & = \frac{1}{2}\sum\limits_{i = 1}^{N} {\left[ {\left( {\tilde{k}_{i,0} w_{i}^{2} \left( {x_{i} } \right) + \tilde{K}_{i,0} \left( {\frac{{\partial w_{i} \left( {x_{i} } \right)}}{{\partial x_{i} }}} \right)^{2} + \tilde{K}_{i,0} \theta_{i}^{2} \left( {x_{i} } \right)} \right)_{{x_{i} = 0}} } \right.} \\ & \quad \left. { + \left( {\tilde{k}_{i,l} w_{i}^{2} \left( {x_{i} } \right) + \tilde{K}_{i,l} \left( {\frac{{\partial w_{i} \left( {x_{i} } \right)}}{{\partial x_{i} }}} \right)^{2} + \tilde{K}_{i,l} \theta_{i}^{2} \left( {x_{i} } \right)} \right)_{{x_{i} = l_{i} }} } \right] \\ \end{aligned}$$

(11)

$$\begin{aligned} U_{{\text{C}}} & = \frac{1}{2}\sum\limits_{i = 1}^{N - 1} {\left[ {k_{i,i + 1} \left( {\left. {w_{i} \left( {x_{i} } \right)} \right|_{{x_{i} = l_{i} }} - \left. {w_{i + 1} \left( {x_{i + 1} } \right)} \right|_{{x_{i + 1} = 0}} } \right)^{2} } \right.} \\ & \quad + K_{i,i + 1} \left( {\left. {\frac{{\partial w_{i} \left( {x_{i} } \right)}}{{\partial x_{i} }}} \right|_{{x_{i} = l_{i} }} - \left. {\frac{{\partial w_{i + 1} \left( {x_{i + 1} } \right)}}{{\partial x_{i + 1} }}} \right|_{{x_{i + 1} = 0}} } \right)^{2} \\ & \quad \left. { + K_{i,i + 1} \left( {\left. {\theta_{i} \left( {x_{i} } \right)} \right|_{{x_{i} = l_{i} }} - \left. {\theta_{i + 1} \left( {x_{i + 1} } \right)} \right|_{{x_{i + 1} = 0}} } \right)^{2} } \right] \\ \end{aligned}$$

(12)

where U_P is the total strain energy of each sub-span Timoshenko beam; U_S is the total elastic potential energy stored in the boundary springs of each sub-span beam; U_C is the total elastic potential energy stored in coupling springs connecting two adjacent sub-spans.

$$T = \frac{1}{2}\sum\limits_{i = 1}^{N} {\int_{0}^{{l_{i} }} {\rho \left[ {A\left( {\frac{{\partial w_{i} }}{\partial t}} \right)^{2} + I\left( {\frac{{\partial \theta_{i} }}{\partial t}} \right)^{2} } \right]} {\text{d}}x_{i} }$$

(13)

where ρ is the density of the beam material; A is the cross-sectional area of the beam, A = B·h; I is the cross-sectional moment of the inertia of the beam, I = B·h³/12.

After determining the expression of the Lagrange energy function L, the displacement functions assumed above are brought in, and the Fourier series are variationalized, so as to transform the problem of vibration characteristics into the problem of solving the standard eigenvalues of the matrix. It is included e^jωt in the lateral displacement functions and the corner displacement functions of the multi-span Timoshenko beam, and is still included after calculation. Therefore, for ease of study, the e^jωt in each expression will be omitted in subsequent derivation processes.

After calculating the above equations, the strain potential energy U_P, the elastic potential energy U_S and U_C stored in the structure can be expressed as follows:

$$\begin{aligned} U_{{\text{P}}} & = \sum\limits_{i = 1}^{N} {\frac{{B_{i} }}{2}\int_{0}^{{l_{i} }} {\int_{ - h/2}^{h/2} {\left\{ {E\left( {\frac{{\partial \Psi_{i} \left( {x_{i} } \right)}}{{\partial x_{i} }}} \right)^{2} + G_{xz} \beta \left[ {\left( {\frac{{\partial \Phi_{i} \left( {x_{i} } \right)}}{{\partial x_{i} }}} \right)^{2} } \right.} \right.} } } \\ & \quad \left. {\left. { - \left( {\frac{{\partial \Phi_{i} \left( {x_{i} } \right)}}{{\partial x_{i} }}} \right)\Psi_{i} \left( {x_{i} } \right) - \Psi_{i} \left( {x_{i} } \right)\left( {\frac{{\partial \Phi_{i} \left( {x_{i} } \right)}}{{\partial x_{i} }}} \right) + \Psi_{i}^{2} \left( {x_{i} } \right)} \right]} \right\}{\text{d}}z{\text{d}}x_{i} \\ \end{aligned}$$

(14)

$$\begin{aligned} U_{{\text{S}}} & = \frac{{B_{i} }}{2}\sum\limits_{i = 1}^{N} {\left[ {\left( {\tilde{k}_{i,0} \Phi_{i}^{2} \left( {x_{i} } \right) + \tilde{K}_{i,0} \left( {\frac{{\partial \Phi_{i} \left( {x_{i} } \right)}}{{\partial x_{i} }}} \right)^{2} + \tilde{K}_{i,0} \Psi_{i}^{2} \left( {x_{i} } \right)} \right)_{{x_{i} = 0}} } \right.} \\ & \quad \left. { + \left( {\tilde{k}_{i,l} \Phi_{i}^{2} \left( {x_{i} } \right) + \tilde{K}_{i,l} \left( {\frac{{\partial \Phi_{i} \left( {x_{i} } \right)}}{{\partial x_{i} }}} \right)^{2} + \tilde{K}_{i,l} \Psi_{i}^{2} \left( {x_{i} } \right)} \right)_{{x_{i} = l_{i} }} } \right] \\ \end{aligned}$$

(15)

$$\begin{aligned} U_{{\text{C}}} & = \frac{{B_{i} }}{2}\sum\limits_{i = 1}^{N - 1} {\left[ {k_{i,i + 1} \left( {\left. {\Phi_{i} \left( {x_{i} } \right)} \right|_{{x_{i} = l_{i} }} - \left. {\Phi_{i + 1} \left( {x_{i + 1} } \right)} \right|_{{x_{i + 1} = 0}} } \right)^{2} } \right.} \\ & \quad + K_{i,i + 1} \left( {\left. {\frac{{\partial \Phi_{i} \left( {x_{i} } \right)}}{{\partial x_{i} }}} \right|_{{x_{i} = l_{i} }} - \left. {\frac{{\partial \Phi_{i + 1} \left( {x_{i + 1} } \right)}}{{\partial x_{i + 1} }}} \right|_{{x_{i + 1} = 0}} } \right)^{2} \\ & \quad \left. { + K_{i,i + 1} \left( {\left. {\Psi_{i} \left( {x_{i} } \right)} \right|_{{x_{i} = l_{i} }} - \left. {\Psi_{i + 1} \left( {x_{i + 1} } \right)} \right|_{{x_{i + 1} = 0}} } \right)^{2} } \right] \\ \end{aligned}$$

(16)

where β is the shear correction factor for the beam material.

And the total kinetic energy T of the structure can be written as follows:

$$T = \frac{{\omega^{2} }}{2}\sum\limits_{i = 1}^{N} {\int_{0}^{{l_{i} }} {\rho \left[ {A\Phi_{i}^{2} \left( {x_{i} } \right) + I\Psi_{i}^{2} \left( {x_{i} } \right)} \right]} {\text{d}}x_{i} }$$

(17)

where ω is the circular frequency of the multi-span Timoshenko beam.

Using the Rayleigh–Ritz method, the partial derivatives of the Lagrange energy function for all unknown coefficients $A_{i,m}$, $A_{i,n}^{a}$, $B_{i,m}$ and $B_{i,n}^{a}$ are calculated and the specific calculation formulas are shown as:

$$\frac{\partial L}{{\partial A_{i,r} }} = 0,\quad \frac{\partial L}{{\partial A_{i,s}^{a} }} = 0,\quad \frac{\partial L}{{\partial B_{i,r} }} = 0,\quad \frac{\partial L}{{\partial B_{i,s}^{a} }} = 0$$

(18)

where $m,r = 0\sim \infty$, $n,s = 1,2,3,4$.

After the operation, the vibration characteristic equation of the multi-span Timoshenko beam under arbitrary boundary conditions and elastic coupling conditions can be expressed as follows:

$$\left( {{\mathbf{K}} - \omega^{2} {\mathbf{M}}} \right){\mathbf{A}} = 0$$

(19)

where ${\mathbf{K}}$ is the structural stiffness matrix, ${\mathbf{M}}$ is the structural mass matrix, ${\mathbf{A}}$ is the unknown coefficient matrix, and the specific expressions can be found in the appendix.

Therefore, the natural frequencies and eigenvectors of the multi-span Timoshenko beam under arbitrary conditions and elastic coupling conditions can be solved through Eq. (19). According to these, mode shapes of the structure can be easily obtained.

3 Numerical results and analysis

3.1 Method validation

Based on the multi-span Timoshenko beam theoretical model established above, the natural frequencies of single-span and three-span Timoshenko beams are solved, and the results are compared with the data of the existing literature to verify the correctness and rationality of the proposed method. Firstly, taking the rectangular section single-span Timoshenko beam under arbitrary boundary conditions as an example, the first six non-dimensional frequencies are calculated by the method in this paper and compared with the data calculated by Xu and Wang [47] and Shi [48]. Secondly, taking two three-span Timoshenko beams with different circular section sizes under arbitrary boundary conditions as examples, the first five natural frequencies are calculated by the method, and compared with the data calculated by Zhao [52]. For the convenience of calculation, the geometric dimension and material parameters of sub-span beam are the same except for the length of the following calculation process.

When applying the method to calculate the vibration characteristics of the single-span Timoshenko beam, set the rigid coupling between two adjacent spans and define each intermediate fulcrum as free support, i.e. $k_{i,i + 1}$ = $K_{i,i + 1}$ = 1 × 10¹² and $\tilde{k}_{i,l}$ = $\tilde{K}_{i,l}$ = $\tilde{k}_{i + 1,0}$ = $\tilde{K}_{i + 1,0}$ = 0 (i = 1, …, N − 1), so that the multi-span Timoshenko beam can be degraded to the single-span Timoshenko beam. When the spring stiffness values are $\tilde{k}_{1,0}$ = $\tilde{k}_{N,l}$ = 1 × 10¹², $\tilde{K}_{1,0}$ = $\tilde{K}_{N,l}$ = 1 × 10¹² and $\tilde{k}_{1,0}$ = $\tilde{K}_{1,0}$ = 1 × 10¹², $\tilde{k}_{N,l}$ = $\tilde{K}_{N,l}$ = 0, the boundary conditions are clamped and clamped-free ends, respectively. The material and structural parameters for the single-span Timoshenko beam used in the numerical calculations are: B = 0.02 m, h = 0.02 m, L = 1 m, ρ = 7800 kg/m³, E = 207 GPa, υ = 0.3, G_xz = E/2/(1 + υ), β = 5/6. The calculation results are all listed in Table 1, where η denotes the relative error between the present method and the results of Shi [48].

Table 1 Comparison of the non-dimensional frequencies for a single-span Timoshenko beam under two boundaries (Hz)

When calculating the vibration characteristics of three-span Timoshenko beams with two circular section sizes, the two adjacent spans are rigidly coupled, and each fulcrum is simply supported, the spring stiffness values are $\tilde{k}_{i,0}$ = $\tilde{k}_{i,l}$ = 1 × 10¹², $\tilde{K}_{i,0}$ = $\tilde{K}_{i,l}$ = 0 (i = 1, …, N − 1). For the three-span Timoshenko beam A of the first circular section, the section width and height are 0.05 m (that is the diameter); for the three-span Timoshenko beam B of the second circular section, the diameter are 0.06 m. In addition, the material and structural parameters used are the same: L = 1 m, ρ = 7837 kg/m³, E = 207 GPa, υ = 0.3, G_xz = 7.96 × 10¹⁰, β = 3/4 and the three sub-span’s lengths are 0.3 m, 0.4 m, 0.3 m, respectively. The specific results are listed in Table 2.

Table 2 Comparison of natural frequencies of three-span Timoshenko beams under simple support boundary condition (Hz)

Through the above comparison, it can be seen that whether it is a single-span Timoshenko beam or a multi-span Timoshenko beam, the results calculated by the present method are in good agreement with the results of existing literature, and the errors are less than 1.0%, so the correctness and accuracy can be proved. At the same time, it is shown that the present method is suitable for the analysis of the vibration characteristics of multi-span Timoshenko beams under arbitrary boundary conditions.

3.2 Convergence analysis

After the displacement function is expanded into an improved Fourier series, whether the numerical calculation result of natural frequency converges mainly determines by the value of M. In order to study the convergence of the proposed method, the three-span Timoshenko beam A under simple support boundary condition is selected as the example. Table 3 shows the first eight natural frequencies of the three-span Timoshenko beam A under different truncation terms M.

Table 3 The first eight natural frequencies of multi-span Timoshenko beam A under different truncation terms M (Hz)

By analyzing Table 3, it can be seen that as the number of terms increases, the natural frequency of the multi-span Timoshenko beam shows a downward trend. And the results within a certain accuracy range tend to be stable, indicating that the proposed method has good numerical stability. From the data in the table, the natural frequency of the structure does not change much when the number of terms is greater than 12, so it can be considered that the results of the solution have converged. Therefore, all Fourier series will be truncated to M = 12 in the following numerical calculations.

3.3 Effects of boundary conditions

Theoretically, when changing the stiffness values of multi-span Timoshenko beams, structures will show different supporting effects. For the rigid and free support, the stiffness values of transverse displacement springs and rotational restraint springs need to be set to infinity or infinitesimal. While infinity and infinitesimal are theoretical values, in the actual calculation process, it is necessary to select the maximum or minimum value to substitute. Therefore, this section discusses determining the range of values for the maximum or minimum. On the basis, the stiffness values of springs corresponding to the three different boundary conditions of rigid support, elastic support and free support are determined.

Taking multi-span Timoshenko beam A as the research object under the simply supported boundary condition, it is first assumed that the stiffness value of the displacement spring at each fulcrum remains unchanged at $\tilde{k}_{i,0}$ = $\tilde{k}_{i,l}$ = 1 × 10¹² (i = 1, …, N), the stiffness value of the torsion spring gradually increases from $\tilde{K}_{i,0}$ = $\tilde{K}_{i,l}$ = 10⁰ to 10¹². Secondly, the stiffness changes of two springs are opposite, while the stiffness value of the displacement spring increases from $\tilde{k}_{i,0}$ = $\tilde{k}_{i,l}$ = 10⁰ to 10¹⁴ to make the effect more obvious. The first eight natural frequencies of the structure are calculated by the proposed method and the change curves of the first four natural frequencies are plotted in Figs. 3 and 4, respectively.

Fig. 3

The curve of the first four natural frequencies of the three-span Timoshenko beam A changing with the torsion spring stiffness values

Fig. 4

The curve of the first four natural frequencies of the three-span Timoshenko beam A changing with the displacement spring stiffness values

Through the analysis of Figs. 3 and 4, with the continuous increase in the stiffness, the natural frequencies have the same changing trend. Dividing the stiffness values into three intervals, the natural frequency of the structure firstly remains basically unchanged, gradually increases and stays stable finally. For the torsion spring, when the stiffness is in the range of 0 ≤ $\tilde{K}_{i,0}$ = $\tilde{K}_{i,l}$ ≤ 10⁵, the natural frequency remains basically unchanged, and the supporting effect of the spring is weak, which can be regarded as a free constraint boundary condition.

Fig. 5

The curve of the first six natural frequencies of the three-span Timoshenko beam C changing with the torsion spring stiffness values

When the stiffness is in the range of 10⁵ ≤ $\tilde{K}_{i,0}$ = $\tilde{K}_{i,l}$ ≤ 10⁹, the natural frequency increases, and the supporting effect is gradually obvious, which can be regarded as an elastic constraint boundary condition. When the stiffness is in the range of $\tilde{K}_{i,0}$ = $\tilde{K}_{i,l}$ ≥ 10⁹, the natural frequency increases to the maximum and stays stable, while the supporting effect is the strongest, which can be regarded as a fixed constraint boundary condition. For the transverse displacement spring, the stiffness range of elastic support boundary condition is 10⁶ ≤ $\tilde{k}_{i,0}$ = $\tilde{k}_{i,l}$ ≤ 10¹¹. When the stiffness is $\tilde{k}_{i,0}$ = $\tilde{k}_{i,l}$ ≤ 10⁶, it is a free support boundary condition and when the stiffness is $\tilde{k}_{i,0}$ = $\tilde{k}_{i,l}$ ≥ 10¹¹, it is a fixed support boundary condition. Therefore, for the free support boundary condition, 0 can be used instead of infinitesimal for calculation and 1E12 can be used instead of infinity for the rigid support boundary condition.

In order to further verify and expand the above conclusions, the natural frequencies of the three-span Timoshenko beam C and the single-span Timoshenko beam D are calculated with fulcrum springs change. Compared with the beam C and the beam A, except the span length ratio of beam C is 0.2:0.6:0.2, the other geometric and material parameters are consistent. The geometric and material parameters of the single-span Timoshenko beam D are also consistent with the beam A. For single-span Timoshenko beams, when $\tilde{k}_{1,0}$ = $\tilde{k}_{N,l}$ = 1 × 10¹², $\tilde{K}_{1,0}$ = $\tilde{K}_{N,l}$ = 0, the boundary condition is simple supported. On the basis, the stiffness value of the torsion spring is increased from $\tilde{K}_{i,0}$ = $\tilde{K}_{i,l}$ = 10⁰ to 10¹², and the first eight natural frequency of the structure is calculated. In order to show its change better, the change curves of the first six natural frequencies of the beam C and the first four frequencies of the beam D when the stiffness value of the torsion spring changes are plotted in Figs. 5 and 6.

Fig. 6

The curve of the first four natural frequencies of the single-span Timoshenko beam D changing with the torsion spring stiffness values

In summary, for single-span beams or multi-span beams, when the stiffness value of the torsion spring changes, the change trend of the natural frequency is consistent, and the stiffness range of the elastic support is also the same, that is 10⁵ ≤ $\tilde{K}_{i,0}$ = $\tilde{K}_{i,l}$ ≤ 10⁹. This shows that the simulation of the boundary conditions using lateral displacement springs and rotational constraint springs is not affected by the number of spans. Therefore, it is speculated that regardless of single-span or multi-span beams, the transverse displacement spring stiffness range of the elastic support is still 10⁶ ≤ $\tilde{k}_{i,0}$ = $\tilde{k}_{i,l}$ ≤ 10¹¹. It can be determined that when lateral displacement springs and rotational constraint springs simulate arbitrary boundary condition of multi-span Timoshenko beams, the stiffness values at each fulcrum are shown in Table 4. In Table 4, F represents the free support boundary condition, S represents the simple support boundary condition, C represents the fixed support boundary condition, and E1, E2, E3 represent the elastic support boundary condition. Through analyzing, with the increasing stiffness of the springs at each fulcrum, the constraint effect becomes stronger and stronger, while the lateral displacement and rotation angle will become 0, and the boundary condition converges to rigid support boundary condition. Then, the multi-span Timoshenko beam will be divided into separate single-span beams, and the natural frequencies are the same as that of single-span beams.

Table 4 Simulated spring stiffness values under arbitrary boundary conditions

3.4 Effects of the span ratio

In this paper, the ratio of the length of the sub-span to the total length of a beam is defined as the span length ratio. For multi-span Timoshenko beams, the span ratio has an important influence on mechanical properties. In the section, a three-span and a four-span Timoshenko beams are used as the research objects to explore the influence of the span ratio on the vibration characteristics of multi-span Timoshenko beams. Firstly, assume that the three-span and four-span Timoshenko beams are centrally symmetrical structures, the length is the same and remains unchanged. Different structures are obtained by adjusting the span ratio. The natural frequencies and the modal shapes of structures are calculated by the method, and the influence of the span ratio on the vibration characteristics is studied.

For multi-span Timoshenko beams with different span ratios, the first eight natural frequencies of the three-span and four-span Timoshenko beams under simple support (S–S) are calculated and the mode shape curves are plotted. Secondly, taking three-span Timoshenko beams with different span ratios as examples, the first eight natural frequencies of beams under the two elastic support boundary conditions (S–E2 and E2–E2) are calculated. It is assumed that multi-span Timoshenko beams have the same geometric and material parameters as beam A except for the span ratios. Refer to Table 4, for boundary conditions, the specific values of S–S are $\tilde{k}_{i,0}$ = $\tilde{k}_{i,l}$ = 10¹², $\tilde{K}_{i,0}$ = $\tilde{K}_{i,l}$ = 0; the specific values of S-E2 are $\tilde{k}_{i,0}$ = $\tilde{k}_{i,l}$ = 10¹², $\tilde{K}_{i,0}$ = $\tilde{K}_{i,l}$ = 10⁷; the specific values of E2–E2 are $\tilde{k}_{i,0}$ = $\tilde{k}_{i,l}$ = 10⁹, $\tilde{K}_{i,0}$ = $\tilde{K}_{i,l}$ = 10⁷. The results are recorded in Tables 5 and 6, respectively.

Table 5 Natural frequency of three-span Timoshenko beams with different span ratios under simple support (Hz)

Table 6 Natural frequency of four-span Timoshenko beams with different span ratios under simple support (Hz)

From Table 5, for symmetrical three-span Timoshenko beams with the same length, if the two structures meet the condition that the sum of the span ratios is equal to 1, that is the middle span’s length of one structure is the sum of the first and last spans’ lengths of the other structure, the 2n order natural frequencies of two structures are roughly the same (the error does not exceed 0.3%), where n = 1, 2, 3, …, N. For example, the 2nd, 4th, 6th and 8th natural frequencies of two structures that the span ratios are 0.4:0.2:0.4 and 0.1:0.8:0.1, respectively, are roughly the same.

In order to explore the specific reason, in addition to the structure with span ratio of 0.25:0.5:0.25, the first four mode shapes of the above structures with six different span ratios are plotted in Fig. 7 for comparison. Through comparison, it can be found that the reason: the deformation of the middle span of one structure is equivalent to the deformation combination of the first and last spans of another structure. For example, the middle span of the structure with the span ratio of 0.4:0.2:0.4 is deformed into a straight line, which is equivalent to the combination of two small straight lines, that is the deformation of the first and last spans of the structure with the span ratio of 0.1:0.8:0.1. And the two end spans of the former are deformed into two half-waves, which are combined to a complete wave, that is equivalent to the deformation of the middle span of the latter.

Fig. 7

Diagrams of the first four bending mode of three-span Timoshenko beams with different span ratios

Table 6 shows that for four-span Timoshenko beams, the 1st, 3rd, 5th and 7th natural frequencies of the structures that the span ratios are 0.4:0.1:0.1:0.4, 0.1:0.4:0.4:0.1 and 0.3:0.2:0.2:0.3, 0.2:0.3:0.3:0.2 are roughly the same (the error does not exceed 0.1%). Therefore, it is inferred that for two symmetrical four-span Timoshenko beams with the same length, when the sum of the middle two spans’ lengths of one structure is equal to the sum of the first and last spans’ lengths of the other structure, the 2n − 1 order natural frequencies of two structures are roughly the same, where n = 1, 2, 3, …, N. Similarly, for analysis, taking two structures with span ratios of 0.3:0.2:0.2:0.3 and 0.2:0.3:0.3:0.2 as examples, the first four natural frequencies are calculated and the mode shape curves are drawn in Fig. 8. Through comparing and analyzing, it can be seen that similar to three-span Timoshenko beams, the reason is that the deformation of the middle two spans of one structure is equivalent to the deformation combination of the first and last spans of another structure.

Fig. 8

Diagrams of the first four bending mode of four-span Timoshenko beams with different span ratios

In addition, by comparing and analyzing the data of 0.3:0.4:0.3 and 0.2:0.6:0.2 in Table 5 and 0.3:0.2:0.2:0.3 and 0.2:0.3:0.3:0.2 in Table 6, it can be seen that the 1st, 3rd, 5th and 7th natural frequencies of four-span Timoshenko beams are approximately the same as the 2nd, 4th, 6th and 8th natural frequencies of three-span Timoshenko beams (the error does not exceed 0.1%). Then, it is concluded that when the middle span’s length of a three-span beam is equal to the sum of the middle two spans’ lengths of a four-span beam, the 2n order natural frequency of the three-span Timoshenko beam is basically equal to the 2n − 1 order natural frequency of the four-span Timoshenko beam, where n = 1, 2, 3, …, N.

The above is analysis and discussion under the simple support boundary condition, and the vibration characteristics of three-span Timoshenko beams with different span ratios under two elastic support boundary conditions (S–E2 and E2–E2) will be analyzed, while the first eight natural frequencies are recorded in Tables 7 and 8. By analyzing, it can be seen that under the elastic support boundary conditions, three-span Timoshenko beams don’t have the above conclusion. The reason is that the elastic support changes the symmetry of structures under the simple support. Comparing the data in Tables 5 and 7, it shows that the elastic support boundary condition introduces torsion springs, which increases the binding effect at each fulcrum and the increases the natural frequencies of the structures. With the increasing stiffness values of torsion springs, each fulcrum will become rigid support, and the vibration characteristics of multi-span Timoshenko beams are the same as those of single-span beams with the same length.

Table 7 Natural frequency of three-span Timoshenko beams with different span ratios under elastic support (S–E2) (Hz)

Table 8 Natural frequency of three-span Timoshenko beams with different span ratios under elastic support (E2–E2) (Hz)

In addition to the span length ratio, considering the influence of the slenderness ratio of the short beam, the single-span and multi-span structures are compared, respectively. Under fixed support boundary conditions (C–C), two single-span Timoshenko beams with a total length of 1 m and a total length of 0.2 m are selected for comparison. Other geometric parameters are the same as those of the single-span rectangular cross section Timoshenko beam selected in Sect. 3.1. And the length-to-diameter ratio (L/d) are 20 and 4, respectively. The natural frequencies are recorded in Table 9.

Table 9 Natural frequency of single-span Timoshenko beams with different length under clamped support (Hz)

Under the simply supported boundary condition (S–S), a three-span Timoshenko beam with a total length of 1 m and the span length ratio of 0.1:0.8:0.1 is selected for comparison with a three-span Timoshenko beam with a total length of 0.3 m and the span length ratio of 0.1:0.1:0.1. The other geometric and material parameters are the same as those of the three-span Timoshenko beam A. The length-to-diameter ratio (L/d) are 20 and 6, respectively, and the middle span slenderness ratios are 16 and 2, respectively. The natural frequencies are recorded in Table 10.

Table 10 Natural frequency of three-span Timoshenko beams with different span ratios under simple support (Hz)

As can be seen from the comparison results in the table, when the slenderness ratio is within the range of the short beams, it will greatly affect the natural frequency, resulting in an increase in the natural frequency. This shows that when the beam length is shortened, the length-to-diameter ratio decreases and the stiffness increases, and the short beam is relatively stable to a certain extent.

3.5 Effects of span number

For multi-span Timoshenko beams, the span number is also one of the important factors affecting the vibration characteristics. In order to study the influence of span number on the vibration characteristics of multi-span Timoshenko beams, single-span, double-span, three-span and four-span beams with equal total length are taken as the research objects. Assuming that the length of sub-span in each structure is the same, the method in this paper is used to calculate the first eight natural frequencies of the four structures under five boundary conditions: S–S, C–C, E1–E1, E2–E2 and E3–E3. In the calculation, except for the length of sub-span, the other geometric and material parameters are the same as beam A. The results are listed in Tables 11, 12, 13, 14 and 15, respectively. And the mode shape curves are drawn in Figs. 9, 10, 11, 12 and 13, respectively.

Table 11 Natural frequency of Timoshenko beam with different span number under simple support (S–S) (Hz)

Table 12 Natural frequency of Timoshenko beam with different span number under clamp support (C–C) (Hz)

Table 13 Natural frequency of Timoshenko beam with different span number under elastic support (E1–E1) (Hz)

Table 14 Natural frequency of Timoshenko beam with different span number under elastic support (E2–E2) (Hz)

Table 15 Natural frequency of Timoshenko beam with different span number under elastic support (E3–E3) (Hz)

Fig. 9

Curves of the first four mode shape of beams with different span number under simple support (S–S) (Hz)

Fig. 10

Curves of the first four mode shape of beams with different span number under clamp support (C–C) (Hz)

Fig. 11

Curves of the first four mode shape of beams with different span number under elastic support (E1–E1) (Hz)

Fig. 12

Curves of the first four mode shape of beams with different span number under elastic support (E2–E2) (Hz)

Fig. 13

Curves of the first four mode shape of beams with different span number under elastic support (E3–E3) (Hz)

Through comparing and analyzing, it can be seen that under the same boundary conditions, when the total length remains unchanged, the natural frequency also increases with the increasing of the span number. The reason is that as the number of span increases, the flexibility becomes smaller and stiffness becomes higher, and the natural frequencies of structures increase while the total length and boundary condition remain unchanged. When the span number of structures are the same but boundary conditions are different, the natural frequencies are quite different. The natural frequencies of structures under clamp support are the largest, and the natural frequencies of structures under elastic support E1–E1 are the smallest. Compared with the simple support boundary condition, the other four boundary conditions have rotational constraints. Among the four boundary conditions with lateral displacement and rotational constraints, the greater the stiffness of the springs are, the higher the natural frequencies of structures are. Therefore, it can be seen that for multi-span Timoshenko beams, the stronger boundary constraints at both ends of each span are, the higher the natural frequencies of structures are. Under elastic support boundary condition, torsional constraints have a greater influence on the higher-order natural frequencies of structures.

In order to better study the regularity, the first four mode shape curves of four multi-span beams under five boundary conditions are plotted in Figs. 9, 10, 11, 12 and 13. Through analyzing, it shows that since there are no torsional constraints in simple support boundary condition, the mode shape curves are regular: when the span number is the same, the higher the natural frequencies are, the more the half-wave number of the curves are. For the same order natural frequency, the more the span number is, the more half-wave number of the curves are. Under the clamp support boundary condition, due to the great rigidity of lateral displacement and rotational constraints, a multi-span beam is equivalent to being divided into several single-span beams. The half-wave number of the mode shape curve of a single-span Timoshenko beam is proportional to the order, the one order corresponds to a half-wave number, the natural frequency increases by one order, the half-wave number increases by one. The constraints of elastic support are in a state between free and rigid so that the mode shape curves are complex and have poor regularity. By comparing the data in Tables 12, 13, 14, and 15 and Figs. 9, 10, 11, 12 and 13, it can be found that if the multi-span Timoshenko beam has n similar natural frequencies, there will be n mode shape curves with the same or similar number of half-wave.

4 Conclusion

In this paper, the vibration characteristics of multi-span Timoshenko beams under arbitrary boundary conditions are studied. Based on the improved Fourier series method to represent the displacement functions, two types of constraint springs are used to simulate the boundary conditions and inter-span coupling conditions and the equations are solved by the Rayleigh–Ritz method. At the same time, the correctness of the theoretical method is verified, and the influence of different parameters is analyzed. The following conclusions are summarized:

• (1) For transverse displacement springs and rotational restraint springs, the stiffness range of the elastic support boundary condition are 10⁶ ≤ $\tilde{k}_{i,0}$ = $\tilde{k}_{i,l}$ ≤ 10¹¹ and 10⁵ ≤ $\tilde{K}_{i,0}$ = $\tilde{K}_{i,l}$ ≤ 10⁹, respectively. If the stiffness value of the restraint spring is on the left side of the range, it can be regarded as a free boundary condition; if it is on the right side, it can be regarded as a fixed boundary condition.

• (2) For a three-span beam and a four-span beam, when the length of the middle span is equal to the sum of the length of the side spans, the frequencies of the former 2n order and the latter 2n − 1 order are roughly equal, respectively. When the length of the middle span of two kinds of beams is equal, these frequencies are basically equal.

• (3) When the total lengths are consistent, the more span number is, the greater the natural frequencies are. When the binding effect at both ends of each span become stronger, the natural frequencies get greater. The mode shape curves are related to the natural frequency, and if the multi-span Timoshenko beam has n similar natural frequencies, there will be n mode shape curves with the same or similar number of half-wave.

These conclusions can effectively guide the application of multi-span Timoshenko beams in engineering, such as how to reduce the vibration of the structure under different boundary conditions and how to avoid the resonance phenomenon of the structure.

Appendix

According to the above theoretical derivation process, if the span number is N, and the highest number of terms in the improved Fourier series is M, then the dimension unknown coefficient vector A in Eq. (19) is [2(M + 5) × N] × 1, the specific formula is expressed as follows:

$${\mathbf{A}} = \left\{ {A_{i,0} ,A_{i,1} , \cdots ,A_{i,m} , \cdots ,A_{i,M} ,A_{i,1}^{a} ,A_{i,2}^{a} ,A_{i,3}^{a} ,A_{i,4}^{a} ,B_{i,0} ,B_{i,1} , \cdots ,B_{i,m} , \cdots ,B_{i,M} ,B_{i,1}^{a} ,B_{i,2}^{a} ,B_{i,3}^{a} ,B_{i,4}^{a} } \right\}$$

(20)

Similarly, for an N-span Timoshenko beam, its overall mass matrix ${\mathbf{M}}$ and stiffness matrix ${\mathbf{K}}$ are both [2(M + 5) × N] × [2(M + 5) × N] order matrices. Thus, the specific formulas of the overall mass matrix ${\mathbf{M}}$ and stiffness matrix ${\mathbf{K}}$ in Eq. (19) are expressed as follows:

$${\mathbf{K}} = {\mathbf{K}}_{P} + {\mathbf{K}}_{S} + {\mathbf{K}}_{C}$$

(21)

where ${\mathbf{K}}_{P}$, ${\mathbf{K}}_{S}$ and ${\mathbf{K}}_{C}$ are all [2(M + 5) × N] × [2(M + 5) × N] order matrices.

$${\mathbf{K}}_{P} = \left[ {\begin{array}{*{20}l} {{\mathbf{K}}_{1,P} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & \ddots \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {{\mathbf{K}}_{i,P} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {{\mathbf{K}}_{N,P} } \hfill \\ \end{array} } \right]_{N \times N}$$

(22)

where ${\mathbf{K}}_{i,P}$ is 2(M + 5) × 2(M + 5) order matrices, its specific formula is expressed as follows:

$${\mathbf{K}}_{i,P} = \left[ {\begin{array}{*{20}l} {K_{11}^{i,P} } \hfill & {K_{12}^{i,P} } \hfill & {K_{13}^{i,P} } \hfill & {K_{14}^{i,P} } \hfill \\ {K_{21}^{i,P} } \hfill & {K_{22}^{i,P} } \hfill & {K_{23}^{i,P} } \hfill & {K_{24}^{i,P} } \hfill \\ {K_{31}^{i,P} } \hfill & {K_{32}^{i,P} } \hfill & {K_{33}^{i,P} } \hfill & {K_{34}^{i,P} } \hfill \\ {K_{41}^{i,P} } \hfill & {K_{42}^{i,P} } \hfill & {K_{43}^{i,P} } \hfill & {K_{44}^{i,P} } \hfill \\ \end{array} } \right]$$

(23)

$$K_{11}^{i,P} = GA\beta \lambda_{i,r} \lambda_{i,k} \int_{0}^{{l_{i} }} {\sin \lambda_{i,r} x_{i} \sin \lambda_{i,k} x_{i} {\text{d}}x_{i} }$$

(24)

$$K_{22}^{i,P} = GA\beta \lambda_{i,s} \lambda_{i,j} \int_{0}^{{l_{i} }} {\cos \lambda_{i,s} x_{i} \cos \lambda_{i,j} x_{i} {\text{d}}x_{i} }$$

(25)

$$\begin{aligned} K_{33}^{i,P} & = EI\lambda_{i,r} \lambda_{i,k} \int_{0}^{{l_{i} }} {\sin \lambda_{i,r} x_{i} \sin \lambda_{i,k} x_{i} {\text{d}}x_{i} } \\ & \quad + GA\beta \int_{0}^{{l_{i} }} {\cos \lambda_{i,r} x_{i} \cos \lambda_{i,k} x_{i} {\text{d}}x_{i} } \\ \end{aligned}$$

(26)

$$\begin{aligned} K_{44}^{i,P} & = EI\lambda_{i,s} \lambda_{i,j} \int_{0}^{{l_{i} }} {\cos \lambda_{i,s} x_{i} \cos \lambda_{i,j} x_{i} {\text{d}}x_{i} } \\ & \quad + GA\beta \int_{0}^{{l_{i} }} {\sin \lambda_{i,s} x_{i} \sin \lambda_{i,j} x_{i} {\text{d}}x_{i} } \\ \end{aligned}$$

(27)

$$K_{12}^{i,P} = GA\beta \left( { - \lambda_{i,r} } \right)\lambda_{i,j} \int_{0}^{{l_{i} }} {\sin \lambda_{i,r} x_{i} \cos \lambda_{i,j} x_{i} {\text{d}}x_{i} }$$

(28)

$$K_{13}^{i,P} = GA\beta \lambda_{i,r} \int_{0}^{{l_{i} }} {\sin \lambda_{i,r} x_{i} \cos \lambda_{i,k} x_{i} {\text{d}}x_{i} }$$

(29)

$$K_{14}^{i,P} = GA\beta \lambda_{i,r} \int_{0}^{{l_{i} }} {\sin \lambda_{i,r} x_{i} \sin \lambda_{i,j} x_{i} {\text{d}}x_{i} }$$

(30)

$$K_{21}^{i,P} = GA\beta \lambda_{i,s} \left( { - \lambda_{i,k} } \right)\int_{0}^{{l_{i} }} {\cos \lambda_{i,s} x_{i} \sin \lambda_{i,k} x_{i} {\text{d}}x_{i} }$$

(31)

$$K_{23}^{i,P} = GA\beta \left( { - \lambda_{i,s} } \right)\int_{0}^{{l_{i} }} {\cos \lambda_{i,s} x_{i} \cos \lambda_{i,k} x_{i} {\text{d}}x_{i} }$$

(32)

$$K_{24}^{i,P} = GA\beta \left( { - \lambda_{i,s} } \right)\int_{0}^{{l_{i} }} {\cos \lambda_{i,s} x_{i} \sin \lambda_{i,j} x_{i} {\text{d}}x_{i} }$$

(33)

$$K_{31}^{i,P} = GA\beta \lambda_{i,k} \int_{0}^{{l_{i} }} {\cos \lambda_{i,r} x_{i} \sin \lambda_{i,k} x_{i} {\text{d}}x_{i} }$$

(34)

$$K_{32}^{i,P} = GA\beta \left( { - \lambda_{i,j} } \right)\int_{0}^{{l_{i} }} {\cos \lambda_{i,r} x_{i} \cos \lambda_{i,j} x_{i} {\text{d}}x_{i} }$$

(35)

$$\begin{aligned} K_{34}^{i,P} & = EI\left( { - \lambda_{i,r} } \right)\lambda_{i,j} \int_{0}^{{l_{i} }} {\sin \lambda_{i,r} x_{i} \cos \lambda_{i,j} x_{i} {\text{d}}x_{i} } \\ & \quad + GA\beta \int_{0}^{{l_{i} }} {\cos \lambda_{i,r} x_{i} \sin \lambda_{i,j} x_{i} {\text{d}}x_{i} } \\ \end{aligned}$$

(36)

$$K_{41}^{i,P} = GA\beta \lambda_{i,k} \int_{0}^{{l_{i} }} {\sin \lambda_{i,s} x_{i} \sin \lambda_{i,k} x_{i} {\text{d}}x_{i} }$$

(37)

$$K_{42}^{i,P} = GA\beta \left( { - \lambda_{i,j} } \right)\int_{0}^{{l_{i} }} {\sin \lambda_{i,s} x_{i} \cos \lambda_{i,j} x_{i} {\text{d}}x_{i} }$$

(38)

$$\begin{aligned} K_{43}^{i,P} & = EI\lambda_{i,s} \left( { - \lambda_{i,k} } \right)\int_{0}^{{l_{i} }} {\cos \lambda_{i,s} x_{i} \sin \lambda_{i,k} x_{i} {\text{d}}x_{i} } \\ & \quad + GA\beta \int_{0}^{{l_{i} }} {\sin \lambda_{i,s} x_{i} \cos \lambda_{i,k} x_{i} {\text{d}}x_{i} } \\ \end{aligned}$$

(39)

$${\mathbf{K}}_{S} = \left[ {\begin{array}{*{20}l} {{\mathbf{K}}_{1,S} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & \ddots \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {{\mathbf{K}}_{i,S} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {{\mathbf{K}}_{N,S} } \hfill \\ \end{array} } \right]$$

(40)

where ${\mathbf{K}}_{i,S}$ is 2(M + 5) × 2(M + 5) order matrices, its specific formula is expressed as follows:

$${\mathbf{K}}_{i,S} = \left[ {\begin{array}{*{20}l} {K_{11}^{i,S} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & {K_{22}^{i,S} } \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {K_{33}^{i,S} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right]$$

(41)

$$K_{11}^{i,S} = B_{i} \left( {\tilde{k}_{i,0} + \left( { - 1} \right)^{r + k} \tilde{k}_{i,l} } \right)$$

(42)

$$K_{22}^{i,S} = B_{i} \left( {\lambda_{i,s} \lambda_{i,j} \tilde{K}_{i,0} + \left( { - 1} \right)^{s + j} \lambda_{i,s} \lambda_{i,j} \tilde{K}_{i,l} } \right)$$

(43)

$$K_{33}^{i,S} = B_{i} \left( {\tilde{K}_{i,0} + \left( { - 1} \right)^{r + k} \tilde{K}_{i,l} } \right)$$

(44)

$${\mathbf{\rm K}}_{C} = \left[ {\begin{array}{*{20}l} \ddots \hfill & {{\mathbf{K}}_{i,C}^{11} } \hfill & {{\mathbf{K}}_{i,C}^{12} } \hfill \\ {{\mathbf{K}}_{i,C}^{21} } \hfill & {{\mathbf{K}}_{i,C}^{22} + {\mathbf{K}}_{i + 1,C}^{11} } \hfill & {{\mathbf{K}}_{i + 1,C}^{12} } \hfill \\ {{\mathbf{K}}_{i + 1,C}^{21} } \hfill & {{\mathbf{K}}_{i + 1,C}^{22} } \hfill & \ddots \hfill \\ \end{array} } \right]_{N \times N}$$

(45)

where ${\mathbf{K}}_{i,C}^{11}$, ${\mathbf{K}}_{i,C}^{12}$, ${\mathbf{K}}_{i,C}^{21}$, ${\mathbf{K}}_{i,C}^{22}$ are all 2(M + 5) × 2(M + 5) order matrices, its specific formula are expressed as follows:

$${\mathbf{K}}_{i,C}^{11} = \left[ {\begin{array}{*{20}l} {K_{11,11}^{i,C} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & {K_{11,22}^{i,C} } \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {K_{11,33}^{i,C} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right]$$

(46)

$$K_{11,11}^{i,C} = B_{i} \left( { - 1} \right)^{r + k} k_{i,i + 1}$$

(47)

$$K_{11,22}^{i,C} = B_{i} \lambda_{i,s} \lambda_{i,j} \left( { - 1} \right)^{s + j} K_{i,i + 1}$$

(48)

$$K_{11,33}^{i,C} = B_{i} \left( { - 1} \right)^{r + k} K_{i,i + 1}$$

(49)

$${\mathbf{K}}_{i,C}^{12} = \left[ {\begin{array}{*{20}l} {K_{12,11}^{i,C} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & {K_{12,22}^{i,C} } \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {K_{12,33}^{i,C} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right]$$

(50)

$$K_{12,11}^{i,C} = - B_{i} \left( { - 1} \right)^{s} k_{i,i + 1}$$

(51)

$$K_{12,22}^{i,C} = - B_{i} \lambda_{i,s} \lambda_{i,j} \left( { - 1} \right)^{s} K_{i,i + 1}$$

(52)

$$K_{12,33}^{i,C} = - B_{i} \left( { - 1} \right)^{s} K_{i,i + 1} \left( {A.34} \right)$$

(53)

$${\mathbf{K}}_{i,C}^{22} = \left[ {\begin{array}{*{20}l} {K_{22,11}^{i,C} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & {K_{22,22}^{i,C} } \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {K_{22,33}^{i,C} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right]$$

(54)

$$K_{22,11}^{i,C} = B_{i} k_{i,i + 1}$$

(55)

$$K_{22,22}^{i,C} = B_{i} \lambda_{i,s} \lambda_{i,j} K_{i,i + 1}$$

(56)

$$K_{22,33}^{i,C} = B_{i} K_{i,i + 1}$$

(57)

$${\mathbf{K}}_{i,C}^{21} = \left( {{\mathbf{K}}_{i,C}^{12} } \right)^{T}$$

(58)

$${\mathbf{M}} = \left[ {\begin{array}{*{20}l} {{\mathbf{M}}_{1} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & \ddots \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {{\mathbf{M}}_{i} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {{\mathbf{M}}_{N} } \hfill \\ \end{array} } \right]$$

(59)

$${\mathbf{M}}_{i} = \left[ {\begin{array}{*{20}l} {M_{11}^{i} } \hfill & {M_{12}^{i} } \hfill & {M_{13}^{i} } \hfill & {M_{14}^{i} } \hfill \\ {M_{21}^{i} } \hfill & {M_{22}^{i} } \hfill & {M_{23}^{i} } \hfill & {M_{24}^{i} } \hfill \\ {M_{31}^{i} } \hfill & {M_{32}^{i} } \hfill & {M_{33}^{i} } \hfill & {M_{34}^{i} } \hfill \\ {M_{41}^{i} } \hfill & {M_{42}^{i} } \hfill & {M_{43}^{i} } \hfill & {M_{44}^{i} } \hfill \\ \end{array} } \right]$$

(60)

$$M_{11}^{i} = \rho A\int_{0}^{{l_{i} }} {\cos \lambda_{i,r} x_{i} \cos \lambda_{i,k} x_{i} {\text{d}}x_{i} }$$

(61)

$$M_{22}^{i} = \rho A\int_{0}^{{l_{i} }} {\sin \lambda_{i,s} x_{i} \sin \lambda_{i,j} x_{i} {\text{d}}x_{i} }$$

(62)

$$M_{33}^{i} = \rho I\int_{0}^{{l_{i} }} {\cos \lambda_{i,r} x_{i} \cos \lambda_{i,k} x_{i} {\text{d}}x_{i} }$$

(63)

$$M_{22}^{i} = \rho I\int_{0}^{{l_{i} }} {\sin \lambda_{i,s} x_{i} \sin \lambda_{i,j} x_{i} {\text{d}}x_{i} }$$

(64)

$$M_{12}^{i} = \rho A\int_{0}^{{l_{i} }} {\cos \lambda_{i,r} x_{i} \sin \lambda_{i,j} x_{i} {\text{d}}x_{i} }$$

(65)

$$M_{21}^{i} = \rho A\int_{0}^{{l_{i} }} {\sin \lambda_{i,s} x_{i} \cos \lambda_{i,k} x_{i} {\text{d}}x_{i} }$$

(66)

$$M_{34}^{i} = \rho I\int_{0}^{{l_{i} }} {\cos \lambda_{i,r} x_{i} \sin \lambda_{i,j} x_{i} {\text{d}}x_{i} }$$

(67)

$$M_{43}^{i} = \rho I\int_{0}^{{l_{i} }} {\sin \lambda_{i,s} x_{i} \cos \lambda_{i,k} x_{i} {\text{d}}x_{i} }$$

(68)

$$M_{13}^{i} = M_{14}^{i} = M_{23}^{i} = M_{24}^{i} = M_{31}^{i} = M_{32}^{i} = M_{41}^{i} = M_{42}^{i} = 0$$

(69)

where $r,k = 1,2, \ldots ,M$; $s,j = 1,2,3,4$; $i = 1,2, \ldots ,N$.