Introduction

In engineering practice, elastically supported Euler–Bernoulli beams find numerous applications, for example, in civil engineering, mechanical engineering, aeronautical engineering, and offshore engineering. The transverse vibrations of beams play an important role in the dynamic analysis of structures. Because the development of the exact solutions for the natural frequencies and mode shapes is mathematically complex and is practically significant, the analysis of free vibration of multiple-elastically supported Euler–Bernoulli beams is an ongoing research topic. Although the standard analytical formulas of the frequency equation and the mode shape function for Euler–Bernoulli with simple boundary conditions are taught in the mainstream textbooks (Leissa and Qatu 2011; Rao 2019; Shabana 1991), the vibration analysis of multi-supported Euler–Bernoulli beam is not included, possibly due to the mathematical complexity caused by the intermediate elastic springs (Rončević et al. 2019). The exact solutions play both an important theoretical role and a crucial practical role. For theoretical purposes, mathematical completeness is always an interesting issue. From the perspective of engineering practice, the exact solutions make sensitivity analysis and optimization convenient and convincing as indicated by Banerjee (1999).

Besides, the dynamic responses of beams supported by an arbitrary number of translational elastic springs at arbitrary positions are fundamental problems of mechanical analysis in various fields (Carta and Brun 2015; Connolly et al. 2015; Kukla 1991a, b; Munjal and Heckl 1982; Romeo and Luongo 2002; Rončević et al. 2019), for instance, the vibration analysis of continuous beams in frame structures (Rončević et al. 2019), the dynamic responses of railway tracks (Connolly et al. 2015), and the vibrations of periodically supported panels excited by sound propagation (Legault et al. 2011; Mead and Pujara 1971). Moreover, the vibration analysis of the multi-supported beam plays a crucial role in studying the inverse problem, i.e., detection of weakened supports (Wang et al. 2017). The frequency equation and the mode shape function derived in the analysis of vibrations of the multi-supported beam may be implemented to identify the damaged supports. Therefore, it is an interesting topic to find a general and efficient method for analyzing the vibrations of beams with multiple intermediate supports.

There is much theoretical analysis on the vibrations of elastically supported beams and the investigations of Kukla et al. (Kukla 1991a, b) are some of the representative studies. Implementing Green’s functions (Abu-Hilal 2003; Kukla and Posiadala 1994; Kukla 1997; Mohamad 1994; Sun 2001), Kukla (1991a, b) analyzed the vibration responses of beams with arbitrarily located intermediate translational elastic supports. However, in the study Kukla (1991a, b) only managed to present explicit and exact frequency equations and mode shape functions for one intermediate elastic support under three classical boundary conditions (pinned–pinned, sliding-sliding, and free-free) due to the cumbersome formulation and procedure of the Green’s function method for more than one translational elastic springs.

Recently, Rončević et al. (2019) investigated the vibration of an Euler–Bernoulli beam with multiple translational springs of different stiffness based on the work of Kukla (1991a, b). Implementing the Green’s function method, the natural frequencies, and mode shapes were obtained for 49 different combinations of boundary conditions. According to Rončević et al. (2019), the 49 possible cases of boundary combinations were yielded by combining each of these seven boundary conditions: pinned, fixed, sliding, free, translational spring, rotational spring, and combined translational-rotational spring.

However, there are two limitations in the Green’s function method of Kukla (1991a, b) and Rončević et al. (2019). First, the frequency equation and mode shape function are dependent on the number of the intermediate elastic springs. For a beam with N intermediate elastic springs, the order of the frequency equation is also N. When the number of the elastic springs increases, the computation of the frequencies becomes more computationally demanding. The proposed mode shape function by Rončević et al. (2019) is determined by N− 1 unknown coefficients, which becomes quite cumbersome when the number of the elastic springs increases. Second, the boundary conditions are not incorporated into a unified general form because the Green’s function (Rončević et al. 2019) has to consider the 49 possible combinations of boundary conditions case-by-case. For different combinations of the boundary conditions, varied Green’s functions must be implemented. In the work of Rončević et al. (2019), a table was provided to list the 49 cases of Green’s functions corresponding to the 49 combinations of boundary conditions, which is inconvenient for applications.

As a part of the ongoing research on vibrations of beams, the object of this work is to overcome the above-mentioned limitations of the study of Kukla (1991a, b) and Rončević et al. (2019). The shape function method is proposed to solve the free vibrations of the Euler–Bernoulli beams with an arbitrary number of intermediate elastic supports under arbitrary boundary conditions. This work has two contributions. First, the highest order of the frequency equation is four, which can accommodate an arbitrary number of intermediate elastic supports. Second, the arbitrary boundary conditions could be handled by a system of four homogeneous equations by the proposed shape function method. The frequency equation and the mode shape function in this work are potentially useful for the detection of the weakened (damaged) translational elastic support (Wang et al. 2017) based on the frequency shift or the mode shape variation.

Governing equation of vibration

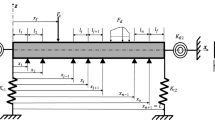
In this section, the fourth-order partial differential equation that governs the free transverse vibration of an Euler–Bernoulli beam with multiple translational supports is formulated. The four conventional boundary conditions in Fig. 1, pinned–pinned (P-P), clamped–clamped (C–C), clamped-free (C-F), and clamped-pinned (C-P), are for demonstration purpose and the general boundary conditions will be addressed in Sect. 4. In the figure, the number and locations of the translational springs are arbitrary, and the stiffness of each of the elastic supports is assumed to be constant. The total length of the beam is assumed to be \(L\).

Fig. 1
figure 1

A Euler–Bernoulli beam supported by multiple translational springs under different boundary conditions: a P–P, b C–C, c C-F, and d C-P

Full size image

According to the Euler–Bernoulli beam theory, the general differential equation governing (Kukla 1991a, b) the free transverse vibration of a beam regardless of the boundary conditions is given as

$$\frac{{\partial }^{2}}{\partial {x}^{2}}\left[E(x)I\left(x\right)\frac{{\partial }^{2}y\left(x,t\right)}{\partial {x}^{2}}\right]+\rho \left(x\right)A\left(x\right)\frac{{\partial }^{2}y\left(x,t\right)}{\partial {t}^{2}}+\sum_{i=1}^{{N}_{s}}{k}_{i}\delta (x-{x}_{i})y\left(x,t\right)=0$$
(1)

where \(y\left( {x,t} \right)\) is the transverse deflection of the beam at time \(t\) and spatial position \(x\), \(I\left(x\right)\) and \(A\left(x\right)\) are the moment of inertia and area of the cross-section at spatial position \(x\), respectively, and \(E(x)\) and \(\rho (x)\) are Young’s modulus and density of the beam at spatial position \(x\), respectively, \({x}_{i}\) is the position of the ith elastic support, \({k}_{i}\) is the translational stiffness of the ith elastic support and \({N}_{s}\) is the total number of elastic supports. In the present work, we assume the flexural stiffness and the mass per unit length of the Euler–Bernoulli beam are constants, i.e., \(E\left(x\right)I\left(x\right)={E}_{0}{I}_{0}\) and \(\rho \left(x\right)A\left(x\right)={\rho }_{0}{A}_{0}\).

In Eq. (1),

$$\delta (x)=\frac{\mathrm{d}H(x)}{\mathrm{d}x}$$
(2)

is the Dirac’s delta function, which is a generalized function, and \(H(x)\) is the Heaviside function.

In this paper, the Heaviside function is defined as

$$H\left(x\right)=\left\{\begin{array}{c}1 (x\ge 0)\\ 0 (x<0)\end{array}\right.$$
(3)

The Dirac’s delta function is different from the conventional functions and has unique properties. In this paper, the following integration property is utilized.

$$\int_{{ - \infty }}^{\infty } {\delta (x - a)f(x){\text{d}}x = f(a)}$$
(4)

where \(f(x)\) is a continuous function.

Assuming the solution \(y\left(x,t\right)\) can be expressed as the product of two functions \(Y(x)\) and \(W(t)\), where \(Y(x)\) depends only on the spatial coordinate \(x\) and \(W(t)\) depends only on the time \(t\), since the free vibration is harmonic,

$$y\left(x,t\right)=Y(x)W(t)$$
(5)

where \(Y(x)\) is the mode shape function to be solved from Eq. (6) and \(W\left(t\right)={e}^{iwt}\) is the harmonic part of the vibration, in which \(\omega\) is the circular frequency to be determined.

Substituting Eq. (5) into the equation of motion Eq. (1), and applying the method of separation of variables, the following fourth-order ordinary differential equation is obtained

$${E}_{0}{I}_{0}{Y}^{\left(iv\right)}\left(x\right)-{{\omega }^{2}\rho }_{0}{A}_{0}Y\left(x\right)+\sum_{i=1}^{{N}_{s}}{k}_{i}\delta (x-{x}_{i})Y(x)=0$$
(6)

where the \((iv)\) indicates taking the fourth derivatives with respect to \(x\).

By introducing the non-dimensional coordinate \(\xi =\frac{x}{L}\) and noticing that \(0\le \xi \le 1\) (Caddemi et al. 2015), the following non-dimensional position parameter is defined

$${\xi }_{i}=\frac{{x}_{i}}{L}$$
(7)

And the dimensionless mode shape function is defined as

$$\phi (\xi )=\frac{Y(\xi )}{L}$$
(8)

After some algebraic operations, Eq. (6) leads to the fourth-order differential equation in terms of the dimensionless parameters

$${\phi }^{\left(iv\right)}\left(\xi \right)-{\beta }^{4}\phi \left(\xi \right)+\sum_{i=1}^{{N}_{s}}{K}_{i}\delta (\xi -{\xi }_{i})\phi \left(\xi \right)=0$$
(9)

where \(\beta =\sqrt[4]{\frac{{{\omega }^{2}\rho }_{0}{A}_{0}{L}^{4}}{{E}_{0}{I}_{0}}}\) is the non-dimensional eigenvalue, and \({\rm K}_{i}=\frac{{k}_{i}{L}^{3}}{{E}_{0}{I}_{0}}\) denotes the dimensionless stiffness of the translational elastic supports. The \(\left(iv\right)\) indicates taking the fourth derivatives with respect to \(\xi\).

Based on the non-dimensional eigenvalue \(\beta\), the circular vibration frequency can be obtained as

$$\omega =\sqrt{\frac{{{\beta }^{4}E}_{0}{I}_{0}}{{\rho }_{0}{A}_{0}{L}^{4}}}$$
(10)

In the next two sections, Eq. (9) is solved first by the variational iteration method and then by the Laplace transform, respectively. Then the exact and explicit solution is presented considering the general of boundary conditions.

Exact and explicit mode shape solution

The exact solution of the differential equation in Eq. (9) is solved by the variational iteration method and the Laplace transform method, based on which the exact and explicit frequency equation and mode shape function are derived in Sect. 5.

Exact solution by the variational iteration method

In this section, the powerful variational iteration method is applied to find the exact solution of the differential equation in Eq. (9). First proposed two decades ago by He (He 1998a, b, 1999a, 2000, 2006, 1997; He et al. 2007), the variational method quickly finds many applications in various scientific fields (Abdou and Soliman 2005; Abulwafa et al. 2006; Momani and Odibat 2006; Wazwaz 2007a, b, c, d, e, f, g, 2008), which can be applied to find the exact solution of linear and nonlinear differential equations.

Assuming a differential equation of the following form,

$$L\phi (\xi )+N\phi (\xi )=f(\xi )$$
(11)

where \(L\) is the linear operator, N is the nonlinear operator, and \(f(\xi )\) is a function.

According to the technique of the variational iteration method, the iteration formula with a correction term can be expressed in the form of

$${\phi }_{n+1}\left(\xi \right)={\phi }_{n}\left(\xi \right)+{\int }_{0}^{\xi }\lambda \left(\tau ;\xi ,\beta \right)\left[L{\phi }_{n}\left(\tau \right)+N{\stackrel{\sim }{\phi }}_{n}\left(\tau \right)-f(\tau )\right]\mathrm{d}\tau$$
(12)

where \(\lambda \left(\tau ;\xi ,\beta \right)\) is the optimal generalized Lagrange’s multiplier and can be identified either as a constant or a function via the variational theory, and \({\stackrel{\sim }{\phi }}_{n}\) is the restricted variation, i.e., \(\delta {\stackrel{\sim }{\phi }}_{n}=0 (n=\mathrm{0,1},2,\dots )\). In the general Lagrange’s multiplier, the letter \(\tau\) is the variable and \(\xi \mathrm{a}\mathrm{n}\mathrm{d} \beta\) are parameters. In the paper, we denote this difference by separating \(\tau\) with the rest two letters with a semicolon.

To solve Eq. (9), the iterative expression with the correction functional and restricted terms according to the variational iteration method is constructed as below

$$\begin{aligned} \phi _{{n + 1}} \left( \xi \right) & = \phi _{n} \left( \xi \right) + \smallint _{0}^{\xi } \lambda \left( {\tau ;\xi ,\beta } \right)[\phi _{n}^{{(iv)}} \left( \tau \right) - \beta ^{4} \phi _{n} \left( \tau \right) \\ & \quad + \sum\limits_{{i = 1}}^{{N_{s} }} {K_{i} } \delta (\tau - \xi _{i} )\mathop \phi \limits^{\sim } _{n} \left( \tau \right)]{\text{d}}\tau \\ \end{aligned}$$
(13)

Taking the variation with respect to \({\phi }_{n}\) on both sides gives

$${\delta \phi }_{n+1}\left(\xi \right)={\delta \phi }_{n}\left(\xi \right)+\delta {\int }_{0}^{\xi }[\lambda (\tau ;\xi ,\beta ){\phi }_{n}^{\left(iv\right)}\left(\tau \right)-\lambda \left(\tau ;\xi ,\beta \right){\beta }^{4}{\phi }_{n}\left(\xi \right)]\mathrm{d}\tau$$
(14)

Solving for the optimal generalized Lagrange multiplier as a function of \(\tau\) and treating \(\xi \mathrm{a}\mathrm{n}\mathrm{d} \beta\) as parameters, the optimal generalized Lagrange multiplier is written as

$$\lambda (\tau ;\xi ,\beta )={S}_{3}(\tau -\xi )$$
(15)

where \({S}_{3}(\tau -\xi )\) is introduced in the next section by the Laplace transform.

Substituting \(\lambda ={S}_{3}(\tau -\xi )\) into the iteration expression in Eq. (13), and eliminating the restrictions results in the following iteration equation with the explicit generalized Lagrange multiplier for the modal shape function

$${\phi }_{n+1}\left(\xi \right)={\phi }_{n}\left(\xi \right)+{\int }_{0}^{\xi }{S}_{3}(\tau -\xi ) \left\{{\phi }_{n}^{(iv)}\left(\tau \right)-{\beta }^{4}{\phi }_{n}\left(\tau \right)+\sum_{i=1}^{{N}_{s}}{K}_{i}\delta (\tau -{\xi }_{i}){\phi }_{n}\left(\tau \right)\right\}\mathrm{d}\tau$$
(16)

Assuming the initial analytical solution has the form

$$\phi_{0} \left( \xi \right) = \phi \left( 0 \right)S_{0} \left( \xi \right) + \phi^{\prime}\left( 0 \right)S_{1} \left( \xi \right) + \phi^{\prime\prime}\left( 0 \right)S_{2} \left( \xi \right) + \phi^{\prime\prime\prime}\left( 0 \right)S_{3} \left( \xi \right)$$
(17)

where \({S}_{0}\left(\xi \right)\), \({S}_{1}\left(\xi \right)\), \({S}_{2}\left(\xi \right)\) and \({S}_{3}\left(\xi \right)\) are four functions to be defined in the last section.

Then the first approximation is obtained as

$${\phi }_{1}\left(\xi \right)={\phi }_{0}\left(\xi \right)+{\int }_{0}^{\xi }{S}_{3}(\tau -\xi )\sum_{i=1}^{{N}_{s}}{K}_{i}\delta (\tau -{\xi }_{i}){\phi }_{0}\left(\tau \right)\mathrm{d}\tau$$
(18)

Applying the integration property of the Dirac’s delta function and substituting Eq. (17), we arrive at

$$ \begin{aligned}\phi _{1} (\xi ) &= \phi (0)S_{0} (\xi ) + \phi ^{\prime } (0)S_{1} (\xi ) + \phi ^{{\prime \prime }} (0)S_{2} (\xi ) \\ &\quad+ \phi ^{{\prime \prime \prime }} (0)S_{3} (\xi ) - \sum\nolimits_{{i = 1}}^{{N_{s} }} {K_{i} S_{3} (\xi - \xi _{i} )\xi _{0} (\xi _{i} )H(\xi - \xi _{i} )}\end{aligned} $$
(19)

in which,

$$\phi_{0} \left( {\xi_{i} } \right) = \phi \left( 0 \right)S_{0} \left( {\xi_{i} } \right) + \phi^{\prime}\left( 0 \right)S_{1} \left( {\xi_{i} } \right) + \phi^{\prime\prime}\left( 0 \right)S_{2} \left( {\xi_{i} } \right) + \phi^{\prime\prime\prime}\left( 0 \right)S_{3} \left( {\xi_{i} } \right)$$
(20)

It should be noticed that the deflection accompanying the \({i}^{th}\) translational elastic support at \({\xi }_{i}\) should be \({\phi }_{1}\left({\xi }_{i}\right)\) in Eq. (19), instead of the approximate value \({\phi }_{0}\left({\xi }_{i}\right)\). Therefore, replacing \({\phi }_{0}\left({\xi }_{i}\right)\) in Eq. (19) by \({\phi }_{1}\left({\xi }_{i}\right)\) and removing the sub-index, the exact solution of the equation of motion is written as

$$\begin{aligned} \phi \left( \xi \right) & = \phi \left( 0 \right)S_{0} \left( \xi \right) + \phi ^{\prime } \left( 0 \right)S_{1} \left( \xi \right) + \phi ^{{\prime \prime }} \left( 0 \right)S_{2} \left( \xi \right) + \phi ^{{\prime \prime \prime }} \left( 0 \right)S_{3} \left( \xi \right) \\ & \quad - \sum\limits_{{i = 1}}^{{N_{s} }} {K_{i} } S_{3} \left( {\xi - \xi _{i} } \right)\phi \left( {\xi _{i} } \right)H\left( {\xi - \xi _{i} } \right) \\ \end{aligned}$$
(21)

To find the exact solution of the equation of motion in Eq. (9), the optimal generalized Lagrange multiplier is first solved according to the theory of variational calculus. Then the iteration expression is constructed by removing the restriction on the nonlinear term in Eq. (12). It is worth mentioning that for linear problems after the optimal generalized Lagrange multiplier is obtained, the exact solution of the differential equation concerned can be obtained in one iteration. In this work, one iteration is required to get the exact solution in Eq. (21).

Exact solution by the Laplace transform method

The analytical solution can also be obtained by the Laplace transform, which is a powerful tool for solving a differential equation with Dirac’s delta function.

Performing the forward Laplace transform \(\mathcal{L}\) on Eq. (9), we arrive at

$$\begin{aligned} s^{4} \Phi \left( s \right) & - s^{3} \phi \left( 0 \right) - s^{2} \phi ^{\prime}\left( 0 \right) - s\phi ^{\prime\prime}\left( 0 \right) - \phi ^{\prime\prime\prime} - \beta ^{4} \Phi \left( s \right) \\ & + \sum\limits_{{i = 1}}^{{N_{s} }} {K_{i} } \phi \left( {\xi _{i} } \right)e^{{ - s\xi _{i} }} = 0 \\ \end{aligned}$$
(22)

Or equivalently,

$$\Phi (s) = \frac{{s^{3} \phi (0) + s^{2} \phi ^{{(0)}} + s\phi ^{{\prime \prime }} \left( 0 \right) + \phi ^{{\prime \prime \prime }} \left( 0 \right) - \sum\limits_{{i = 1}}^{{N_{s} }} {K_{i} } \phi \left( {\xi _{i} } \right)e^{{ - s\xi _{i} }} }}{{s^{4} - \beta ^{4} }}$$
(23)

where \(\Phi \left(s\right)\) is the Laplace transform of \(\phi (\xi )\), \(s\) is the frequency domain parameter, which is generally a complex number, and \(\phi \left(0\right),{\phi }^{{^{\prime}}}\left(0\right),{\phi }^{{^{\prime}}{^{\prime}}}\left(0\right)\) and \({\phi }^{{^{\prime}}{^{\prime}}{^{\prime}}}\left(0\right)\) are four unknown constants evaluated at \(\xi =0\), which can be determined by imposing the boundary conditions of the problem. In fact, \(\phi \left(0\right),{\phi }^{{^{\prime}}}\left(0\right),{\phi }^{{^{\prime}}{^{\prime}}}\left(0\right)\) and \({\phi }^{{^{\prime}}{^{\prime}}{^{\prime}}}\left(0\right)\) are directly related to the deflection, slope, moment and shear force at \(\xi =0\), respectively. It is worth noting that the technique for deriving Eq. (22) can be found in the reference (Zhao 2019).

Defining the inverse Laplace transform of the terms in Eq. (23) as follows

$${\mathcal{L}}^{-1}\left\{\frac{{s}^{3}}{{s}^{4}-{\beta }^{4}}\right\}=\frac{cos\left(\beta \xi \right)+cosh(\beta \xi )}{2}{\stackrel{\scriptscriptstyle\mathrm{def}}{=}S}_{0}\left(\xi \right)$$
(24)
$${\mathcal{L}}^{-1}\left\{\frac{{s}^{2}}{{s}^{4}-{\beta }^{4}}\right\}=\frac{sin\left(\beta \xi \right)+sinh(\beta \xi )}{2\beta }{\stackrel{\scriptscriptstyle\mathrm{def}}{=}S}_{1}\left(\xi \right)$$
(25)
$${\mathcal{L}}^{-1}\left\{\frac{s}{{s}^{4}-{\beta }^{4}}\right\}=\frac{cosh(\beta \xi )-cos\left(\beta \xi \right)}{2{\beta }^{2}}{\stackrel{\scriptscriptstyle\mathrm{def}}{=}S}_{2}\left(\xi \right)$$
(26)
$${\mathcal{L}}^{-1}\left\{\frac{1}{{s}^{4}-{\beta }^{4}}\right\}=\frac{sinh(\beta \xi )-sin\left(\beta \xi \right)}{2{\beta }^{3}}{\stackrel{\scriptscriptstyle\mathrm{def}}{=}S}_{3}\left(\xi \right)$$
(27)

where \({S}_{0}\left(\xi \right),{S}_{1}\left(\xi \right),{S}_{2}\left(\xi \right)\) and \({S}_{3}\left(\xi \right)\) are arbitrarily differentiable functions that are frequently utilized in the vibration analysis of Euler–Bernoulli beams under various boundary conditions. In this work, we name these four functions as the shape functions of the intact uniform Euler–Bernoulli beam, because the mode shape functions of the intact uniform beam can be completely determined with them when boundary conditions are given.

Performing the inverse Laplace transformation \({\mathcal{L}}^{-1}\) on Eq. (23), the exact modal shape function of the beam supported by multiple translational elastic supports at arbitrary positions is obtained

$$\begin{aligned} \phi \left( \xi \right) & = \phi \left( 0 \right)S_{0} \left( \xi \right) + \phi ^{\prime}\left( 0 \right)S_{1} \left( \xi \right) + \phi ^{\prime\prime}\left( 0 \right)S_{2} \left( \xi \right) + \phi ^{\prime\prime\prime}\left( 0 \right)S_{3} \left( \xi \right) \\ & \quad - \sum\limits_{{i = 1}}^{{N_{s} }} {K_{i} } S_{3} \left( {\xi - \xi _{i} } \right)\phi \left( {\xi _{i} } \right)H\left( {\xi - \xi _{i} } \right) \\ \end{aligned}$$
(28)

which is the same as the solution from the variational iteration method in Eq. (21).

Exact and explicit solution

As can be seen from the mode shape solution in Eq. (28), the exact solution of the differential equation governing the vibration of the elastically supported beam is not explicit, since the deflections at each of the translational springs are unknown in the right-hand side. Therefore, additional manipulations are required to convert Eq. (28) into the explicit form.

First, substituting \(\xi ={\xi }_{i}\) into both sides of Eq. (28) gives

$$ \begin{aligned}& \phi \left({\xi }_{i}\right)+\sum_{j=1,i\ne j}^{{N}_{s}}{K}_{j}{S}_{3}\left({\xi }_{i}-{\xi }_{j}\right)\phi \left({\xi }_{j}\right)H\left({\xi }_{i}-{\xi }_{j}\right)\\ &\quad=\phi \left(0\right){S}_{0}\left({\xi }_{i}\right)+{\phi }^{{^{\prime}}}\left(0\right){S}_{1}\left({\xi }_{i}\right)+{\phi }^{{^{\prime}}{^{\prime}}}\left(0\right){S}_{2}\left({\xi }_{i}\right)+{\phi }^{{^{\prime}}{^{\prime}}{^{\prime}}}\left(0\right){S}_{3}\left({\xi }_{i}\right)\end{aligned} $$
(29)

Rewriting the above equation into a compact form yields,

$${\varvec{\Omega}}{\varvec{\phi}}=\mathbf{\varphi }$$
(30)

where \(\Omega\) is a square non-singular lower-triangle matrix of the size \({N}_{s}\times {N}_{s}\), \(\phi ={[\phi \left({\xi }_{1}\right),\phi \left({\xi }_{2}\right),...,\phi \left({\xi }_{{N}_{s}}\right)]}^{T}\) is a column vector of size \({N}_{s}\times 1\) and \({\varphi }={[{\varphi }\left({\xi }_{1}\right),{\varphi }\left({\xi }_{2}\right),...,{\varphi }\left({\xi }_{{N}_{s}}\right)]}^{T}\) is a column vector of size \({N}_{s}\times 1\) and the superscript \(T\) indicates transpose of the vector.

In element form,

$${\Omega }_{ij}=\left\{\begin{array}{ll}1\\ {K}_{j}{S}_{3}\left({\xi }_{i}-{\xi }_{j}\right)H\left({\xi }_{i}-{\xi }_{j}\right) \end{array}\begin{array}{c}if\,\, i=j\\ if\,\, i\ne j\end{array}\right.$$
(31)

Equation (31) indicates that the matrix \(\Omega\) is a matrix of scalars, provided that the location and the stiffness of the translational elastic supports are known.

Then the deflection at each of the ith elastic support can be obtained as

$$\phi ={\Omega }^{-1}\varphi$$
(32)

Defining

$${\phi }_{i}=\phi \left({\xi }_{i}\right)$$
(33)

and

$${\varphi }_{i}=\phi \left(0\right){S}_{0}\left({\xi }_{i}\right)+{\phi }^{{^{\prime}}}\left(0\right){S}_{1}\left({\xi }_{i}\right)+{\phi }^{{^{\prime}}{^{\prime}}}\left(0\right){S}_{2}\left({\xi }_{i}\right)+{\phi }^{{^{\prime}}{^{\prime}}{^{\prime}}}\left(0\right){S}_{3}\left({\xi }_{i}\right)$$
(34)

Then in element form and adopting the Einstein convention, we obtain the deflection of the beam at each of the translations supports as

$${\phi }_{i}={\Omega }_{ij}^{-1}{\varphi }_{j}$$
(35)

Substituting the obtained deflection at \({\xi }_{i}\) into the mode shape function in Eq. (28), the exact mode shape is obtained as

$$ \begin{aligned}{\varvec{\phi}}\left(\xi \right)&=\,\phi \left(0\right){S}_{0}\left(\xi \right)+{\phi }^{{^{\prime}}}\left(0\right){S}_{1}\left(\xi \right)+{\phi }^{{^{\prime}}{^{\prime}}}\left(0\right){S}_{2}\left(\xi \right)\\ &\quad+{\phi }^{{^{\prime}}{^{\prime}}{^{\prime}}}\left(0\right){S}_{3}\left(\xi \right)-\sum_{i=1}^{{N}_{s}}{K}_{i}{S}_{3}\left(\xi -{\xi }_{i}\right){\Omega }_{ij}^{-1}{\varphi }_{j}H\left(\xi -{\xi }_{i}\right)\end{aligned} $$
(36)

Collecting the terms by the constant coefficients \(\phi \left(0\right),{\phi }^{{^{\prime}}}\left(0\right),{\phi }^{{^{\prime}}{^{\prime}}}\left(0\right)\) and \({\phi }^{{^{\prime}}{^{\prime}}{^{\prime}}}\left(0\right)\), respectively, yields the exact solution of the mode shape function below,

$$ \begin{aligned}\phi \left(\xi \right)&=\,\phi \left(0\right)[{S}_{0}\left(\xi \right)-\sum_{i=1}^{{N}_{s}}{K}_{i}{S}_{3}\left(\xi -{\xi }_{i}\right){\Omega }_{ij}^{-1}{S}_{0}\left({\xi }_{j}\right)H\left(\xi -{\xi }_{i}\right)]\\ &\quad+{\phi }^{{^{\prime}}}\left(0\right)[{S}_{1}\left(\xi \right)-\sum_{i=1}^{{N}_{s}}{K}_{i}{S}_{3}\left(\xi -{\xi }_{i}\right){\Omega }_{ij}^{-1}{S}_{1}\left({\xi }_{j}\right)H\left(\xi -{\xi }_{i}\right)]\\ &\quad+{\phi }^{{^{\prime}}{^{\prime}}}\left(0\right)[{S}_{2}\left(\xi \right)-\sum_{i=1}^{{N}_{s}}{K}_{i}{S}_{3}\left(\xi -{\xi }_{i}\right){\Omega }_{ij}^{-1}{S}_{2}\left({\xi }_{j}\right)H\left(\xi -{\xi }_{i}\right)]\\ &\quad+{\phi }^{{^{\prime}}{^{\prime}}{^{\prime}}}\left(0\right)[{S}_{3}\left(\xi \right)-\sum_{i=1}^{{N}_{s}}{K}_{i}{S}_{3}\left(\xi -{\xi }_{i}\right){\Omega }_{ij}^{-1}{S}_{3}\left({\xi }_{j}\right)H\left(\xi -{\xi }_{i}\right)\end{aligned} $$
(37)

As suggested by the exact explicit solution in Eq. (37), the exact explicit mode shape solution of the multi-supported Euler–Bernoulli beam is completely determined by the unknown constants \(\phi \left(0\right),{\phi }^{{^{\prime}}}\left(0\right),{\phi }^{{^{\prime}}{^{\prime}}}\left(0\right)\) and \({\phi }^{{^{\prime}}{^{\prime}}{^{\prime}}}\left(0\right)\) regardless of the number and location of the translational elastic supports, assuming the position and the stiffness parameters of the elastic supports are known.

Boundary conditions

The non-conventional boundary conditions (Rončević et al. 2019) of a beam (see Fig. 2) with translational and rotational elastic supports at the two ends (\(x=0 or L\)) can be written as

$$Q\left(0,t\right)=-{k}_{0t}y(0,t)$$
(38)
$$M\left(0,t\right)={k}_{0r}{y}^{^{\prime}}(0,t)$$
(39)
$$Q\left(L,t\right)={k}_{Lt}y(L,t)$$
(40)
$$M\left(L,t\right)=-{k}_{Lr}{y}^{^{\prime}}(L,t)$$
(41)

where \(Q\) and \(M\) are the shear force and moment, respectively, \({k}_{0t},{k}_{0r},{k}_{Lt} \mathrm{a}\mathrm{n}\mathrm{d}{ k}_{Lr}\) are the translational and rotational stiffness of the spring at \(x=0\) and \(x=L\), respectively. By specifying the stiffness level, a wide range of boundary conditions can be represented.

Fig. 2
figure 2

A beam with intermediate elastic supports with variable translational-rotational boundary conditions

Full size image

The shear force and the bending moment in the Euler–Bernoulli beam are defined as

$$Q\left(x,t\right)={E}_{0}{I}_{0}{y}^{\prime\prime\prime}(x,t)$$
(42)
$$M\left(x,t\right)={E}_{0}{I}_{0}{y}^{\prime\prime}(x,t)$$
(43)

And the sign convention for the shear force and bending moment adopted in this paper is: the positive shear force rotates the beam segment clockwise and the positive bending moment stretches the bottom fiber of the beam.

In terms of the non-dimensional coordinate (\(\xi =0 or 1\)), the general boundary conditions can be rewritten as

$${\phi }^{\prime\prime\prime}\left(0\right)=-{K}_{0t}\phi (0)$$
(44)
$${\phi }^{\prime\prime}\left(0\right)={K}_{0r}{\phi }^{^{\prime}}(0)$$
(45)
$${\phi }^{\prime\prime\prime}\left(1\right)={K}_{1t}\phi (1)$$
(46)
$${\phi }^{\prime\prime}\left(1\right)=-{K}_{1r}{\phi }^{^{\prime}}(1)$$
(47)

where \({K}_{0t}=\frac{{k}_{0t}{L}^{3}}{{E}_{0}{I}_{0}}, {K}_{0r}=\frac{{k}_{0r}L}{{E}_{0}{I}_{0}},{K}_{1t}=\frac{{k}_{Lt}{L}^{3}}{{E}_{0}{I}_{0}}, \text{and}\, {K}_{1r}=\frac{{k}_{Lr}L}{{E}_{0}{I}_{0}}\). In this work, the 0 and 1 in the sub-indices of the non-dimensional spring stiffness \({K}_{0t}\), \({K}_{0r}\), \({K}_{1t}\), and \({K}_{1r}\) indicate the left end and the right end supports, respectively; while the letter \(t\) and \(r\) indicate the translational and rotational elastic supports, respectively.

Specifically, the classical boundary conditions for the pinned support, clamped support, free end and sliding restraint in terms of the non-dimensional coordinate (\(\xi =0 or 1\)) are presented below

$$\mathrm{P}\mathrm{i}\mathrm{n}\mathrm{n}\mathrm{e}\mathrm{d}: \phi =0 \,\,\mathrm{a}\mathrm{n}\mathrm{d}\,\, {\phi }^{\prime\prime}=0$$
(48)
$$\mathrm{C}\mathrm{l}\mathrm{a}\mathrm{m}\mathrm{p}\mathrm{e}\mathrm{d}: \phi =0 \,\,\mathrm{a}\mathrm{n}\mathrm{d} \,\,{\phi }^{^{\prime}}=0$$
(49)
$$\mathrm{F}\mathrm{r}\mathrm{e}\mathrm{e} \,\,\mathrm{e}\mathrm{n}\mathrm{d}: {\phi }^{\prime\prime}=0 \,\,\mathrm{a}\mathrm{n}\mathrm{d} \,\,{\phi }^{\prime\prime\prime}=0$$
(50)
$$\mathrm{S}\mathrm{l}\mathrm{i}\mathrm{d}\mathrm{i}\mathrm{n}\mathrm{g} \,\,\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}\mathrm{t}: {\phi }^{^{\prime}}=0\,\, \mathrm{a}\mathrm{n}\mathrm{d}\,\, {\phi }^{\prime\prime\prime}=0$$
(51)

where the primes indicate taking derivatives with respect to the non-dimensional coordinate \(\xi\).

Frequency equation and mode shape function

In this section, the general form of the frequency equation and the mode shape function for the general boundary conditions are presented.

Based on the exact explicit mode shape solution in Eq. (37), it is observed that the mode shape of the beam with multiple translational elastic supports takes the form of

$$\phi \left(\xi \right)=\phi \left(0\right){\Psi }_{0}\left(\xi \right)+{\phi }^{^{\prime}}\left(0\right){\Psi }_{1}\left(\xi \right)+{\phi }^{\prime\prime}\left(0\right){\Psi }_{2}\left(\xi \right)+{\phi }^{\prime\prime\prime}\left(0\right){\Psi }_{3}\left(\xi \right)$$
(52)

where \({\Psi }_{0}\left(\xi \right)\), \({\Psi }_{1}\left(\xi \right)\), \({\Psi }_{2}\left(\xi \right)\) and \({\Psi }_{3}\left(\xi \right)\) are four functions in terms of the non-dimensional coordinate \(\xi\). The functions \({\Psi }_{j}\left(\xi \right) (j=0, 1, 2 \mathrm{a}\mathrm{n}\mathrm{d} 3)\) are linearly independent and serves as the basic set of solutions of the mode shapes. When there is no intermediate translational elastic support, \({\Psi }_{j}\left(\xi \right)={S}_{j}\left(\xi \right) (j=0, 1, 2 \mathrm{a}\mathrm{n}\mathrm{d} 3)\). In explicit forms, they are written as

$${\Psi }_{0}\left(\xi \right)={S}_{0}\left(\xi \right)-\sum_{i=1}^{{N}_{s}}{K}_{i}{S}_{3}\left(\xi -{\xi }_{i}\right){\Omega }_{ij}^{-1}{S}_{0}\left({\xi }_{j}\right)H\left(\xi -{\xi }_{i}\right)$$
(53)
$${\Psi }_{1}\left(\xi \right)={S}_{1}\left(\xi \right)-\sum_{i=1}^{{N}_{s}}{K}_{i}{S}_{3}\left(\xi -{\xi }_{i}\right){\Omega }_{ij}^{-1}{S}_{1}\left({\xi }_{j}\right)H\left(\xi -{\xi }_{i}\right)$$
(54)
$${\Psi }_{2}\left(\xi \right)={S}_{2}\left(\xi \right)-\sum_{i=1}^{{N}_{s}}{K}_{i}{S}_{3}\left(\xi -{\xi }_{i}\right){\Omega }_{ij}^{-1}{S}_{2}\left({\xi }_{j}\right)H\left(\xi -{\xi }_{i}\right)$$
(55)
$${\Psi }_{3}\left(\xi \right)={S}_{3}\left(\xi \right)-\sum_{i=1}^{{N}_{s}}{K}_{i}{S}_{3}\left(\xi -{\xi }_{i}\right){\Omega }_{ij}^{-1}{S}_{3}\left({\xi }_{j}\right)H\left(\xi -{\xi }_{i}\right)$$
(56)

In this work, we call the above four functions the shape functions of the Euler–Bernoulli beam with multiple translational elastic supports, which is a modification of the shapes functions of the uniform Euler–Bernoulli beams without translational springs.

Substituting the general translational and rotational boundary conditions in Eqs. (44)–(47) and considering the mode shape function in Eq. (52), a system of four linear homogeneous equations in terms of the four constants \(\phi \left(0\right),{\phi }^{{^{\prime}}}\left(0\right),{\phi }^{{^{\prime}}{^{\prime}}}\left(0\right)\) and \({\phi }^{{^{\prime}}{^{\prime}}{^{\prime}}}\left(0\right)\) are yielded

$$\left[\begin{array}{c}{\Psi }_{0}^{\prime\prime\prime}\left(0\right)+{K}_{0t}\\ {\Psi }_{0}^{\prime\prime}\left(0\right)\\ {\Psi }_{0}^{\prime\prime\prime}\left(1\right)-{{\Psi }_{0}\left(1\right)K}_{1t}\\ {\Psi }_{0}^{\prime\prime}\left(1\right)+{\Psi }_{0}^{\prime}\left(1\right){K}_{1r}\end{array}\begin{array}{c}{\Psi }_{1}^{\prime\prime\prime}\left(0\right)\\ {\Psi }_{1}^{\prime\prime}\left(0\right)-{K}_{0r}\\ {\Psi }_{1}^{\prime\prime\prime}\left(1\right)-{\Psi }_{1}\left(1\right){K}_{1t} \\ {\Psi }_{1}^{\prime\prime}\left(1\right)+{\Psi }_{1}^{\prime}\left(1\right){K}_{1r}\end{array}\begin{array}{c}{\Psi }_{2}^{\prime\prime\prime}\left(0\right) \\ {\Psi }_{2}^{\prime\prime}\left(0\right)\\ {\Psi }_{2}^{\prime\prime\prime}\left(1\right)-{\Psi }_{2}\left(1\right){K}_{1t} \\ {\Psi }_{2}^{\prime\prime}\left(1\right)+{\Psi }_{2}^{\prime}\left(1\right){K}_{1r}\end{array}\begin{array}{c}{\Psi }_{3}^{\prime\prime\prime}\left(0\right)\\ {\Psi }_{3}^{\prime\prime}\left(0\right)\\ {\Psi }_{3}^{\prime\prime\prime}\left(1\right)-{\Psi }_{3}\left(1\right){K}_{1t}\\ {\Psi }_{3}^{\prime\prime}\left(1\right)+{\Psi }_{3}^{\prime}\left(1\right){K}_{1r}\end{array}\right]\left(\begin{array}{c}\phi \left(0\right)\\ {\phi }^{\prime}\left(0\right)\\ \genfrac{}{}{0pt}{}{{\phi }^{\prime\prime}\left(0\right)}{{\phi }^{\prime\prime\prime}\left(0\right)}\end{array}\right)=\left(\begin{array}{c}0\\ 0\\ 0\\ 0\end{array}\right)$$
(57)

From linear algebra theory, to achieve a non-trivial solution, the determinant of the coefficient matrix must be zero. Setting the determinant of the square matrix in Eq. (57) equal to zero leads to the frequency equation of a beam with elastic supports at the ends:

$$\left|\begin{array}{c}{\Psi }_{0}^{\prime\prime\prime}\left(0\right)+{K}_{0t}\\ {\Psi }_{0}^{\prime\prime}\left(0\right)\\ {\Psi }_{0}^{\prime\prime\prime}\left(1\right)-{{\Psi }_{0}\left(1\right)K}_{1t}\\ {\Psi }_{0}^{\prime\prime}\left(1\right)+{\Psi }_{0}^{^{\prime}}\left(1\right){K}_{1r}\end{array}\begin{array}{c}{\Psi }_{1}^{\prime\prime\prime}\left(0\right)\\ {\Psi }_{1}^{\prime\prime}\left(0\right)-{K}_{0r}\\ {\Psi }_{1}^{\prime\prime\prime}\left(1\right)-{\Psi }_{1}\left(1\right){K}_{1t} \\ {\Psi }_{1}^{\prime\prime}\left(1\right)+{\Psi }_{1}^{^{\prime}}\left(1\right){K}_{1r}\end{array}\begin{array}{c}{\Psi }_{2}^{\prime\prime\prime}\left(0\right) \\ {\Psi }_{2}^{\prime\prime}\left(0\right)\\ {\Psi }_{2}^{\prime\prime\prime}\left(1\right)-{\Psi }_{2}\left(1\right){K}_{1t} \\ {\Psi }_{2}^{\prime\prime}\left(1\right)+{\Psi }_{2}^{^{\prime}}\left(1\right){K}_{1r}\end{array}\begin{array}{c}{\Psi }_{3}^{\prime\prime\prime}\left(0\right)\\ {\Psi }_{3}^{\prime\prime}\left(0\right)\\ {\Psi }_{3}^{\prime\prime\prime}\left(1\right)-{\Psi }_{3}\left(1\right){K}_{1t}\\ {\Psi }_{3}^{\prime\prime}\left(1\right)+{\Psi }_{3}^{^{\prime}}\left(1\right){K}_{1r}\end{array}\right|=0$$
(58)

As suggested by Eqs. (48) and (58), the exact explicit mode shape solution of the multi-supported Euler–Bernoulli beam is completely determined by four unknown constants \(\phi \left(0\right),{\phi }^{{^{\prime}}}\left(0\right),{\phi }^{{^{\prime}}{^{\prime}}}\left(0\right)\) and \({\phi }^{{^{\prime}}{^{\prime}}{^{\prime}}}\left(0\right)\) regardless of the boundary conditions, assuming the positions and the stiffness parameters of the elastic supports are known. Besides, considering the combination of the boundary conditions, the highest rank of the coefficient matrix in Eq. (57) is four, making the proposed method more computationally efficient when the number of elastic supports is large.

In the work of Rončević et al. (2019), a total of 49 cases of combinations of boundary condition is tabulated, whereas in the represent investigation they were accommodated by a system of four homogeneous equations in Eq. (57). The computational efficiency and practical convenience are obvious. As can be seen from the above equations, the proposed solution is consistent for all boundary conditions and is more convenient to apply, compared with the Green’s function method (Kukla 1991a, b; Rončević et al. 2019).

It is worth noting that the general equation in Eq. (57) can be further simplified for the conventional boundary conditions. In this study, we also present the mode shapes and frequency equations of four frequently encountered boundary conditions in civil engineering, namely, pinned on both ends, clamped on both ends, clamped at \(\xi =0\) and free at \(\xi =1\), and clamped at \(\xi =0\) and pinned at \(\xi =1\). The corresponding frequency equation and mode shape function are given below.

Case I: pinned–pinned (P-P).

The frequency equation is

$$\left|\begin{array}{cc}{\Psi }_{1}\left(1\right)& {\Psi }_{3}\left(1\right)\\ {\Psi }_{1}^{\prime\prime}\left(1\right)& {\Psi }_{3}^{\prime\prime}\left(1\right)\end{array}\right|=0$$
(59)

The mode shape is written as

$$\phi \left(\xi \right)={\phi }^{^{\prime}}\left(0\right){\Psi }_{1}\left(\xi \right)+{\phi }^{\prime\prime\prime}\left(0\right){\Psi }_{3}\left(\xi \right)$$
(60)

Case II: clamped–clamped (C-C).

The frequency equation is

$$\left|\begin{array}{cc}{\Psi }_{2}\left(1\right)& {\Psi }_{3}\left(1\right)\\ {\Psi }_{2}^{^{\prime}}\left(1\right)& {\Psi }_{3}^{^{\prime}}\left(1\right)\end{array}\right|=0$$
(61)

The mode shape is written as

$$\phi \left(\xi \right)={\phi }^{\prime\prime}\left(0\right){\Psi }_{2}\left(\xi \right)+{\phi }^{\prime\prime\prime}\left(0\right){\Psi }_{3}\left(\xi \right)$$
(62)

Case III: clamped-free (C-F).

The frequency equation is

$$\left|\begin{array}{cc}{\Psi }_{2}^{\prime\prime}\left(1\right)& {\Psi }_{3}^{\prime\prime}\left(1\right)\\ {\Psi }_{2}^{\prime\prime\prime}\left(1\right)& {\Psi }_{3}^{\prime\prime\prime}\left(1\right)\end{array}\right|=0$$
(63)

The mode shape is written as

$$\phi \left(\xi \right)={\phi }^{\prime\prime}\left(0\right){\Psi }_{2}\left(\xi \right)+{\phi }^{\prime\prime\prime}\left(0\right){\Psi }_{3}\left(\xi \right)$$
(64)

Case IV: clamped-pinned (C-P).

The frequency equation is

$$\left|\begin{array}{cc}{\Psi }_{2}\left(1\right)& {\Psi }_{3}\left(1\right)\\ {\Psi }_{2}^{\prime\prime}\left(1\right)& {\Psi }_{3}^{\prime\prime}\left(1\right)\end{array}\right|=0$$
(65)

The mode shape is written as

$$\phi \left( \xi \right) = \phi ^{\prime\prime}\left( 0 \right)\Psi _{2} \left( \xi \right) + \phi ^{{\prime \prime \prime }} \left( 0 \right)\Psi _{3} \left( \xi \right)$$
(66)

For most of the classical boundary conditions, the order of the frequency equation is two, as is demonstrated in the above four cases.

Illustrating examples

Example 1: double springs

The clamped beam with two intermediate elastic supports and a translational-rotational support in Fig. 3 is studied and demonstrated in this example, which was also investigated by Rončević et al. (2019). The two intermediate springs are located at \({\xi }_{1}=0.6\) and \({\xi }_{2}=0.8\), respectively. The left end of the beam is clamped, and the right end is supported by a translational spring (\({K}_{1\mathrm{t}}\)) and a rotational spring (\({K}_{1\mathrm{r}}\)). The magnitudes of the two intermediate elastic supports are \({K}_{1}=233.429\) and \({K}_{2}=2{K}_{1}\), respectively.

Fig. 3
figure 3

A clamped beam with double intermediate elastic springs and a translational-rotational support

Full size image

Applying the frequency equation in Eq. (58), the first three non-dimensional natural frequencies corresponding to all seven different combinations of boundary conditions at the right end are tabulated in Table 1. The frequencies by the Green’s functions method Rončević et al. (2019) are also presented in the table, together with the percentage error. It is observed in Table 1 that very encouraging agreement between the shape function method and the Green’s function method is achieved. Besides, the normalized mode shapes of the first three modes by both the shape function method in Eq. (52) and the Green’s function method are graphed in Fig. 4, and excellent agreement between the two methods are obtained, justifying the validity of the shape function method.

Table 1 Non-dimensional frequency comparison between the proposed shape function method (SFM) and the Green’s function method (GFM) in the literature for seven combinations of B.C.s
Full size table
Fig. 4
figure 4figure 4

The first three mode shapes by the shape function method (━: first mode; ━ ━: Second mode; ━•: third mode) and the Green’s function method (Rončević et al. 2019) (❋: first mode; square: second mode; star: third mode) for a beam with a\({K}_{1\mathrm{t}}={K}_{1\mathrm{r}}=\infty\), b\({K}_{1\mathrm{t}}=\infty , {K}_{1\mathrm{r}}=0\), c\({K}_{1\mathrm{t}}=0, {K}_{1\mathrm{r}}=\infty\), d\({K}_{1\mathrm{t}}={K}_{1\mathrm{r}}=0\), e\({K}_{1\mathrm{t}}=233, {K}_{1\mathrm{r}}=0\), f\({K}_{1\mathrm{t}}=0, {K}_{1\mathrm{r}}=15\), and g\({K}_{1\mathrm{t}}=233, {K}_{1\mathrm{r}}=15\)

Full size image

Example 2: 100 springs

It is known that when the number of the elastic supports is sufficiently large (100), the frequencies and the mode shapes of the beam in Fig. 5 are approaching that of the pinned–pinned beam on an elastic foundation with equivalent stiffness \({K}_{f}\) as shown Fig. 6, respectively. In this example, the beam with 100 intermediate elastic supports in Fig. 5 is investigated to show that the proposed method could accommodate a large number of elastic supports.

Fig. 5
figure 5

A pinned–pinned beam with 100 intermediate elastic supports

Full size image
Fig. 6
figure 6

A pinned–pinned beam on an elastic foundation

Full size image

The governing equation of vibration of a beam on an elastic foundation is formulated as

$${\phi }^{\left(iv\right)}\left(\xi \right)-({\beta }^{4}-{K}_{f})\phi \left(\xi \right)=0$$
(67)

the solution of which can be obtained by the Laplace transform method as presented in Sect. 3.2.

It is noticed that

$${K}_{i}={K}_{f}\Delta (i=\mathrm{1,2},...,100)$$
(68)

where \({K}_{i}\) is the stiffness of each elastic support (Fig. 5), \(\Delta\) is the space between the elastic supports as shown in Fig. 5, assuming the stiffness of the elastic foundation \({K}_{f}\) is given.

Applying Eq. (59), the first three vibration frequencies of the beam with 100 intermediate elastic supports in Fig. 5, and the vibration frequency of the beam on an elastic foundation (see Fig. 6) are tabulated in Table 2, together with the percentage error. The typical normalized vibration mode shapes for the beam with 100 intermediate elastic springs by the shape function method and the solution of the beam on an elastic foundation is graphed in Fig. 7.

Table 2 Non-dimensional frequency comparison between a pinned–pinned beam with 100 intermediate elastic supports and a pinned–pinned beam on an elastic foundation with equivalent stiffness
Full size table
Fig. 7
figure 7

The first three mode shapes by the shape function method for a pinned–pinned beam with 100 intermediate springs (━: first mode; ━ ━: Second mode; ━ •: third mode) and the mode shapes of a pinned–pinned beam on an elastic foundation (❋: first mode; square: second mode; star: third mode)

Full size image

It is observed in Table 2 and Fig. 7 that the frequency responses and mode shapes of the proposed shape function method are in excellent agreement with the solution of the vibration of a beam on an elastic foundation, justifying that the shape function method could handle a large number of elastic supports.

Parametric study

In this section, the influences of two parameters, i.e., the spring position and the magnitude of spring stiffness, on the frequency responses of a beam with an intermediate elastic support are demonstrated and the four cases of boundary conditions in Fig. 8 are considered. Applying the frequency equations for the conventional boundary conditions in Eqs. (59), (61), (63), and (65), the non-dimensional frequency responses of the beam corresponding to the different positions of the spring \(\xi\) under the P–P, C–C, C-F, and C-P boundary conditions are shown in Figs. 9, 10, 11 and 12, respectively. This parametric study is intended to show that there is a strong link between the frequency change and the weakening of the stiffness of the intermediate translational support, which may be useful for the inverse problem, i.e., weakened supports detection.

Fig. 8
figure 8

A beam with an intermediate translational support under different boundary conditions (Up-down: P–P, C–C, C-F, and C-P)

Full size image
Fig. 9
figure 9

Non-dimensional frequency responses versus the spring position for varied spring stiffness under P-P boundary conditions

Full size image
Fig. 10
figure 10

Non-dimensional frequency responses versus the spring position for varied spring stiffness under C–C boundary conditions

Full size image

The following key observations are made based on Figs. 9, 10, 11 and 12. First, when the stiffness of the elastic support decreases from \(K={10}^{4}\) to 10, the first four natural frequencies drop considerably for the four combinations of boundary conditions, suggesting that there is a strong link between the spring stiffness and the frequency change.

Second, along the beam, the frequency responses of the lower modes (first and second) are relatively sensitive to the weak stiffness (\(K\) < 5000) for all four cases of conventional boundary conditions and the higher modes (third and fourth) are relatively sensitive to strong stiffness (\(K\) > 5000). This observation can be applied to the inverse problem to identify the stiffness of the elastic support if the frequencies are obtained. For instance, to detect the damaged supports with high residual elastic stiffness, the higher modes (third and fourth) should be utilized while the lower modes (first and second) should be implemented to identify the supports with low residual stiffness. As far as the first mode is concerned, it should be pointed out that the spring position of the maximum frequency drop is influenced by the boundary conditions. For the P-P beam and the C–C beam, the maximum frequency drop for the first mode occurs at the middle-point of the beam. For the C-F beam and the C-P beam, the maximum frequency drops are achieved at \(\xi =0.78\) and \(\xi =0.56\), respectively.

Third, when the stiffness of the elastic support decreases, the vibration frequency of the beam also decreases. However, for a beam with the same boundary conditions, the different modes are separated by the asymptotic lines. This indicates that when the stiffness of the elastic support is decreased to zero the frequency will infinitely approach the frequency of the immediate lower mode with an elastic support of infinite stiffness, as suggested in Figs. 9, 10, 11 and 12.

Besides, it is also noticed that for the clamped-free beam (Fig. 11) when the spring is located close to the right end (\(\xi\)=1) and the increasing the spring stiffness to infinity, the frequencies for all four modes are approaching to the corresponding frequencies of the clamped-pinned beam (Fig. 12) with no elastic support, suggesting that the conventional pinned boundary condition can be simulated by the elastic support with infinite stiffness.

Fig. 11
figure 11

Non-dimensional frequency responses versus the spring position for varied spring stiffness under C-F boundary conditions

Full size image
Fig. 12
figure 12

Non-dimensional frequency responses versus the spring position for varied spring stiffness under C-P boundary conditions

Full size image

Conclusion

Vibrations of Euler–Bernoulli beams with multiple translational elastic supports are of theoretical and practical importance. In this paper, the problem of free vibrations of beams supported by multiple translational elastic supports under the elastic boundary conditions is solved. The locations and the stiffnesses of the intermediate supports are arbitrary. The Dirac’s delta function is introduced to formulate the equation of motion, which is solved by the variational iteration method and the Laplace transform method. Four novel shape functions are introduced, based on which the exact and explicit solutions of the characteristic frequencies and mode shapes for the general boundary conditions are obtained. The derived solution is verified with the Green’s function method in the literature and encouraging agreements are demonstrated.

The resulted mode shape function is completely determined by four shape functions and four constants, the latter of which can be determined by considering the boundary conditions. Both the frequency equation and the mode shape function could accommodate all 49 possible boundary conditions in the literature in one consistent form. The parametric study shows that the weakening of elastic supports is reflected by the vibration frequencies and suggests that it is applicable to identify the stiffness of the elastic support based on the frequency responses of the beam. Two main contributions are made in this work. First, the highest order of the frequency equation is four for an arbitrary number of elastic spring supports and arbitrary boundary conditions, which is independent of the number of elastic supports. Second, a much more compact and efficient solution is presented to incorporate all 49 possible cases of combinations of boundary conditions in the literature. Compared with the methods in the literature, the present paper is more efficient and convenient to implement. This paper mainly deals with the forward problem (vibration analysis) and is potentially useful for attacking the inverse problem, i.e., detection of the weakened supports.