Queueing-Inventory System with Two Commodities

Abstract

A two-commodity inventory system with a single server is considered in this paper. We assume that the capacity of the buffers (to store the two types of commodities) to be finite. Customers (or demands) arrive according to a Poisson Process and the requirement for either type or both type of commodities are modelled using certain probabilities. Customers are lost when their demands are not met due to shortage only at the time of service offerings as opposed to getting lost when the inventory level is zero at the time of arrival. This is to allow the possibility of inventory being replenished prior to offering services to those who arrive when the inventory level is zero. A customer’s demand for both items may be met with only one item should a situation in which there is only one type of inventory is positive and the other is zero at the time of initiating a service occurs. The processing time for meeting the demands are random and modelled using exponential distribution with parameters depending on the type of demands being processed. We adopt (s, S)-type replenishment policy which depends on the type of commodity. Assuming the lead times to be exponentially distributed with parameters depending on the type of commodity, we employ matrix-analytic methods to study the queueing inventory system and report interesting results including an optimization dealing with various costs.

1 Introduction

Inventory systems dealing with several/distinct commodities are very common, (see for example Miller 1971, Agarwal 1984). Such systems are more complex than single commodity system which could be attributed to the reordering procedures. Whether the ordering policies of joint, individual or some mixed type are superior will depend on the particular problem at hand.

For commodities which are clearly of distinct types and which are supplied by different vendors, the individual strategies would be given top priority. The individual order policy consists of the calculation of optimum order quantities and/or time periods from item to item, disregarding any economic interaction between them. This policy has considerable flexibility in selecting the individually best inventory models for each single item, as well as in the possibility of modifying independently any constant entering the calculations. For this reason, believers of the concept of management by exception and designers of computer controlled large multi-item inventory systems seem to prefer individual order policies in applications (General Information Manual 1962).

In contrast, the joint policies may have advantages in situations where a procurement is made from the same suppliers/ items produced on the same machine/ items have to be delivered using the same transport facility. In such cases, the joint ordering policy might be superior with regard to cost efficiency. The modelling of multi-item inventory systems is getting more attention now-a-days. In the following we will use the terminology item or commodity interchangeably.

Balintfy (1964) compared multi-item inventory problems where joint order of several items may significantly reduce the total set up cost. The comparisons call for the necessity of a new policy for reorder point-triggered random output multi-item systems. This policy, the “random joint order policy” operates through the determination of a reorder range within which several items can be ordered. The existence of an optimum reorder range is proved, and a computational technique is demonstrated with the help of a machine-interference type queueing model.

Federgruen et al. (1984) considered a continuous review multi-item inventory system with compound Poisson demand processes; excess demands are backlogged and each replenishment requires a lead time. There is a major setup cost associated with any replenishment of the family of items, and a minor (item dependent) setup cost when including a particular item in this replenishment. Moreover, there are holding and penalty costs. An algorithm which searches for a simple coordinated control rule which minimizes the long run average cost per unit time subject to a service level constraint per item on the fraction of demand satisfied directly from on hand inventory is presented. This algorithm is based on a heuristic decomposition procedure and a specialized policy-iteration method to solve the single-item subproblems generated by the decomposition procedure.

Two-commodity continuous review inventory system without lead time is considered by Krishnamoorthy et al. (1994) where each demand is for one unit of the first commodity or one unit of the second commodity or one unit each of both commodities with a pre-determined probability. Krishnamoorthy and Varghese (1994) considered a two-commodity inventory problem without any lead time and with Markovian shift in demand for first commodity, second commodity and both commodities. Using results from Markov renewal theory Sivasamy and Pandiyan (1998) derived various results by the application of filtering techniques for the same problem.

A two-commodity continuous review inventory system with independent Poisson demands is considered by Anbazhagan and Arivarignan (2001). Here the maximum inventory level for $i\mathrm{{th}}$ commodity is fixed as $S_i, i=1,2$ and net inventory level at time t for the $i\mathrm{{th}}$ commodity is denoted by $I_i(t),i=1,2$. If the total net inventory level $I(t)=I_1(t)+I_2(t)$ drops to a prefixed level, s [$\le \frac{S_1-2}{2}$ or $\frac{S_2-2}{2}$ ] an order is placed for $(S_i-s)$ units of $i\mathrm{{th}}$ commodity $(i=1,2)$. Here the probability distribution for inventory level and mean reorders and shortage rates in the steady state are computed. Two-commodity continuous review inventory system with renewal demands and ordering policy as a combination of individual and joint ordering policies is considered by Sivakumar et al. (2007). Two-commodity stochastic inventory system with lost sales, Poisson arrivals with joint and individual ordering policies is considered by Yadavalli et al. (2004).

Two-commodity continuous review inventory system with substitutable items and Markovian demands is considered by Anbazhagan et al. (2012). Here reordering for supply is initiated as soon as the sum of the on-hand inventory levels of the two commodities reaches a certain level s.

In the present paper we consider a two-commodity queueing inventory system in which the customer arrivals form a Poisson process, the service times are exponentially distributed, and the lead times are exponentially distributed. We assume all the underlying random variables are independent of each other. Customers demand either one of the commodities or both with some pre-determined probabilities. The customers’ requirements are revealed only at the time of offering services. If the item demanded is not available, the customer leaves the system for ever. If both items are demanded when only one of the commodity is available, the available item is served to the customer. The model under study is always stable due to the fact that the customers finding zero inventory at the beginning of a service are all lost (i.e., cleared) from the system. We adopt individual replenishment policy.

The motivation for our study is as follows. Typically customers arrive to a service area to buy one or more (distinct) items or products. Suppose that there are n different items and that the customers shop for product i with probability, $p_i, 1 \le i \le n$. With probability, $p_{i_1,\ldots ,i_k},$ where $\{i_1,\ldots , i_k\}$ is a subset of the set of integers $\{1,2,\ldots ,n\}$, the customers shop for products $i_1,\ldots ,i_k$, for $2 \le k \le n$. If the requested distinct products are not all in stock, the customers will be served with only those in stock among the requested ones. If a customer cannot be served with any product, then that customer will be lost. Note that there are $2^n - 1$ distinct possibilities for a customer to shop for the products. As it can be seen, the dimension of the problem grows exponentially with n. In this paper, we will focus on the case when $n = 2$. The study of a multi-server queueing-inventory problem is similar to the one studied here for the single server case; however, the dimension of the problem increases with the number of servers.

The rest of the paper is arranged as follows. In Sect. 2, the mathematical formulation of the problem under investigation is given. The structure of the infinitesimal generator of the underlying continuous time Markov chain is shown to be of the GI / M / 1 type. Section 3 investigates in detail the system stability. In Sect. 4 we provide several system performance indices. The expected loss rate of customers demanding only one of $C_1$ and $C_2$ or both $C_1$ and $C_2$ are evaluated. These are numerically illustrated in Sect. 5. Also, analysis of cycle time of commodity $C_i, i=1,2$ is performed. An optimization problem related to the model under investigation is presented in Sect. 6. Concluding remarks including future work are given in Sect. 7.

2 Model Description

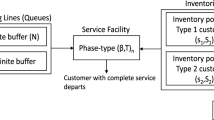
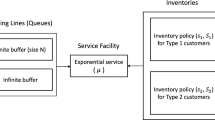
Consider a two-commodity inventory system with a single server. The maximum storage capacity for the $i\mathrm{{th}}$ commodity is $S_i$ units for $i=1,2$. Demands arrive according to a Poisson Process of rate $\lambda$ and demand for each commodity is of unit size. Customers are not allowed to join the system when inventory levels of both commodities are zero. However, customers join the system even when the server is busy with no excess inventory available at hand. This is with the hope that during the current service the replenishment of the items would take place, so that at the epoch when taken for service, the item demanded by the customer can be provided. Also customers are lost when no item of the commodity demanded by them is available at the time of offering service. At the time when taken for service the customer demands item $C_i$ with probability $p_i$, for $i=1,2$ or both $C_1$ and $C_2$ with probability $p_3$ such that $p_1+p_2+p_3=1$ . The demanded item is delivered to the customer after a random duration of service. The service times for processing orders for $C_1$, $C_2$ or both $C_1$ and $C_2$ are exponentially distributed with parameters $\mu _1$, $\mu _2$ and $\mu _3$ respectively. We adopt $(s_i,S_i)$ replenishment policy for commodity $C_i$, $i=1,2$. That is, whenever the inventory level of commodity $C_i$ falls to $s_i$ an order is placed for that alone to bring the inventory level back to $S_i$, $i=1,2$ at the time of replenishment. The time till replenishment from the epoch at which order is placed(lead time) is exponentially distributed with parameters $\beta _i$ for $C_i. i=1,2$

The above problem can be modelled as a continuous time Markov chain of the GI / M / 1 type

$$\begin{aligned} \{(N(t),I_1(t),I_2(t),J(t)), \quad t\ge 0\} \end{aligned}$$

where N(t) denotes the number of customers in the queue

$I_{i}(t)$ denotes the excess inventory level of commodity $C_i$ , $i=1,2$

J(t) denotes the state of the server at time t, where

$$\begin{aligned} J(t)= \left\{ \begin{array}{ll} 0 &{}\quad \hbox {if \ server \ is \ idle;} \\ 1 &{}\quad \hbox {if \ server \ is \ busy \ processing} \ C_1; \\ 2 &{} \quad \hbox {if \ server \ is \ busy \ processing } \ C_2; \\ 3 &{} \quad \hbox {if \ server \ is \ busy \ processing } \ C_1\hbox { and }C_2. \end{array}^{} \right. \end{aligned}$$

The state space of the above process is ${\varvec{\Omega }} =\bigcup _{n=0}^{\infty }\varvec{\ell (n)}$ where $\varvec{\ell (n)}$ denotes level n, $\varvec{\ell (0)}$={$(0,j_1,j_2,r): 0\le j_1 \le S_1, 0\le j_2 \le S_2, 0 \le r \le 3$}

and $\varvec{\ell (n)}$ ={$(n,j_1,j_2,r): 0\le j_1 \le S_1, 0\le j_2 \le S_2, 1 \le r \le 3$}, $n \ge 1$ Thus, the infinitesimal generator matrix of the Markov chain has the form

$$\begin{aligned} \mathcal {Q}=\left[ \begin{array}{cccccc} B_{1} &{}\quad B_{0} &{} &{} &{} &{} \\ B_{2} &{}\quad A_{1} &{}\quad A_{0} &{} &{} &{} \\ B_{3}&{}\quad A_{2} &{}\quad A_{1} &{}\quad A_{0} &{} &{} \\ B_{4} &{}\quad A_{3} &{}\quad A_{2} &{}\quad A_{1} &{}\quad A_{0} &{} \\ \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \ddots &{} \quad \ddots &{}\quad \ddots \\ \end{array} \right] \end{aligned}$$

(1)

where

$B_{n+1}, n \ge 0$ contains transitions from $\varvec{\ell (n)}$ to $\varvec{\ell (0)}$,

$B_{0}$ contains the transition from $\varvec{\ell (0)}$ to $\varvec{\ell (1)}$,

$A_1$ contains the transitions within $\varvec{\ell (n)}$ $n \ge 1$,

$A_0$ contains transitions from $\varvec{\ell (n)}$ to $\varvec{\ell (n+1)}$ $i \ge 1$

and $A_{k+1}$ contains transitions from $\varvec{\ell (n)}$ to $\varvec{\ell (n-k)}$, $1 \le k \le n-1, n \ge 2$.

Then $A_0$, $A_1$, $A_2$, $\ldots$ are square matrices of dimension a, where $a= 3(S_1+1)(S_2+1)$. $B_1$ is a square matrix of dimension b, $b=4(S_1+1)(S_2+1)$. $B_0$, $B_i$, $i \ge 2$, are of dimensions $b\times a$, $a \times b$, respectively.

Transitions in the Markov chain and the corresponding rates are described below: The matrix $B_1$ governs,

• 1. $(0,j_1,j_2,r)\rightarrow (0,j_1,j_2,0)$ with rate $\mu _r$ for $1 \le r \le 3$, $0 \le j_1 \le S_1$, $0 \le j_2 \le S_2$

• 2. $(0,j_1,j_2,r)\rightarrow (0,S_1,j_2,r)$ with rate $\beta _1$ for $0\le r \le 3$ $0 \le j_1 \le s_1$, $0 \le j_2 \le S_2$

• 3. $(0,j_1,j_2,r)\rightarrow (0,j_1,S_2,r)$ with rate $\beta _2$ for $0\le r \le 3$ $0 \le j_1 \le S_1$, $0 \le j_2 \le s_2$

• 4. $(0,0,0,r)\rightarrow (1,0,0,r)$ with rate $\lambda$ for $1\le r \le 3$

• 5. $(0,0,j_2,0)\rightarrow (0,0, j_{2}-1,2)$ with rate $\lambda (p_2+p_3)$ for $1 \le j_2 \le S_2$

• 6. $(0,j_1,0,0)\rightarrow (0,j_{1}-1,0,1)$ with rate $\lambda (p_1+p_3)$ for $1 \le j_1 \le S_1$

• 7. $(0,j_1,j_2,0)\rightarrow (0, j_{1}-1, j_2,1)$ with rate $\lambda p_1$ for $1\le j_1 \le S_1, 1 \le j_2 \le S_2$

• 8. $(0,j_1,j_2,0)\rightarrow (0,j_1,j_{2}-1,2)$ with rate $\lambda p_2$ for $1\le j_1 \le S_1, 1 \le j_2 \le S_2$

• 9. $(0,j_1,j_2,0)\rightarrow (0,j_{1}-1, j_{2}-1,3)$ with rate $\lambda p_3$ for $1\le j_1 \le S_1, 1 \le j_2 \le S_2$

The matrix, $B_{n+1}, n \ge 1$, governs

• 1. $(n,0,0,r)\rightarrow (0,0,0,0)$ with rate $\mu _r$ for $1\le r \le 3$

• 2. $(n,0,j_2,r)\rightarrow (0,0,j_2,0)$ with rate $\mu _r p_1^{n}$ for $1 \le j_2 \le S_2$, $1\le r \le 3$

• 3. $(n,0,j_2,r)\rightarrow (0,0,,j_{2}-1,2)$ with rate $\mu _rp_1^{n-1}(p_2+p_3)$ for $1 \le j_2 \le S_2$, $1\le r \le 3$

• 4. $(n,j_1,0,r)\rightarrow (0,j_1,0,0)$ with rate $\mu _r p_2^{n}$ for $1 \le j_1 \le S_1$,$1\le r \le 3$

• 5. $(n,j_1,0,r)\rightarrow (0,j_{1}-1,0,1)$ with rate $\mu _r p_2^{n-1}(p_1+p_3)$ for $1 \le j_1 \le S_1$, $1\le r \le 3$

• 6. $(1,j_1,j_2,r) \rightarrow (0,j_1-1,j_2,1)$ with rate $\mu _r p_1$ for $1 \le j_1 \le S_1$,$1 \le j_2 \le S_2$,$1\le r \le 3$

• 7. $(1,j_1,j_2,r) \rightarrow (0,j_1,j_2-1,2)$ with rate $\mu _r p_2$ for $1 \le j_1 \le S_1$,$1 \le j_2 \le S_2$, $1\le r \le 3$

• 8. $(1,j_1,j_2,r) \rightarrow (0,j_1-1,j_2-1,3)$ with rate $\mu _r p_3$ for $1 \le j_1 \le S_1$,$1 \le j_2 \le S_2$, $1\le r \le 3$

The matrix, $A_{k+1}, 1\le k \le n-1, n \ge 3$, governs

• 1. $(n,0,j_2,r) \rightarrow (n-k,0,j_2-1,2)$ with rate $\mu _r p_1^{k-1}(p_2+p_3)$ for $1 \le j_2 \le S_2$, $1\le r \le 3$

• 2. $(n,j_1,0,r) \rightarrow (n-k, j_1-1,0,1)$ with rate $\mu _r p_2^ {k-1} (p_1+p_3)$ for $1 \le j_1 \le S_1$, $1\le r \le 3$

• 3. $(n, j_1,j_2,r) \rightarrow (n-1,j_1-1,j_2,1)$ with rate $\mu _r p_1$ for $1 \le j_1 \le S_1$, $1 \le j_2 \le S_2$, $1\le r \le 3$

• 4. $(n, j_1,j_2,r) \rightarrow (n-1,j_1,j_2-1,2)$ with rate $\mu _r p_2$ for $1 \le j_1 \le S_1$, $1 \le j_2 \le S_2$, $1\le r \le 3$

• 5. $(n, j_1,j_2,r) \rightarrow (n-1,j_1-1,j_2-1,3)$ with rate $\mu _r p_3$ for $1 \le j_1 \le S_1$, $1 \le j_2 \le S_2$, $1\le r \le 3$

The entries of matrix, $A_1$ are:

• 1. $(n,j_1,j_2,r) \rightarrow (n,S_1,j_2,r)$ with rate $\beta _1$ for $0\le j_1 \le s_1, 0\le j_2 \le S_2, 1 \le r \le 3$

• 2. $(n,j_1,j_2,r) \rightarrow (n, j_1,S_2,r)$ with rate $\beta _2$ for $0\le j_1 \le S_1, 0\le j_2 \le s_2, 1 \le r \le 3$

Thus, the elements of the matrices can be described as

$$\begin{aligned}&B_0(n,i_1,i_2,r; \ m,j_1,j_2,l)\\&\quad =\left\{ \begin{array}{ll} \lambda , &{}\quad m=n+1, \ 0\le i_1\le S_1, \ 0\le i_2\le S_2, \ r=l=1,2,3; \\ &{}\quad j_1=i_1, j_2=i_2, l=r;\\ 0, &{}\quad \hbox {otherwise.} \end{array} \right. \\&B_{2}(n,i_1,i_2,r; \ m,j_1,j_2,l)\\&\quad =\left\{ \begin{array}{ll} \mu _r, &{}\quad m=n-1, \ i_1=i_2=j_1=j_2=0, \ r=1,2,3, \ l=0; \\ \mu _r (p_2+p_3), &{}\quad m=n-1, \ i_1=j_1=0, \ 1 \le i_2\le S_2,\\ &{}\quad j_2=i_{2}-1, \ r=1,2,3, \ l=2 ;\\ \mu _r p_1, &{}\quad m=n-1, \ i_1=j_1=0, \ 1 \le i_2\le S_2,\\ &{}\quad j_2=i_{2}, \ r=1,2,3, \ l=0 ;\\ \mu _r (p_1+p_3), &{}\quad m=n-1, \ 1 \le i_1\le S_1, \ i_2=j_2=0,\\ &{}\quad j_1=i_{1}-1, \ r=1,2,3, \ l=1 ; \\ \mu _r p_2, &{}\quad m=n-1, \ 1 \le i_1\le S_1, \ i_2=j_2=0,\\ &{}\quad j_1=i_{1}, \ r=1,2,3, \ l=0 ; \\ \mu _r p_1, &{}\quad m=n-1, \ 1 \le i_1\le S_1,\\ &{}\quad 1 \le i_2\le S_2, \ j_1=i_{1}-1, \ r=1,2,3, \ l=1; \\ \mu _r p_2, &{}\quad m=n-1, \ 1 \le i_1\le S_1,\\ &{}\quad 1 \le i_2\le S_2, \ j_2=i_{2}-1, \ r=1,2,3, \ l=2; \\ \mu _r p_3, &{}\quad m=n-1, \ 1 \le i_1\le S_1,\\ &{}\quad 1 \le i_2\le S_2, \ j_1=i_{1}-1, \ j_{2}=i_{2}-1, \ r=1,2,3, \ l=3;\\ 0, &{}\quad \hbox {otherwise.} \end{array} \right. \\&A_0(n,i_1,i_2,r; \ m,j_1,j_2,l)\\&\quad =\left\{ \begin{array}{ll} \lambda , &{}\quad m=n+1, \ 0\le i_1\le S_1, \ 0\le i_2\le S_2, \ r=1,2,3, \\ &{}\quad j_1=i_1, \ j_2=i_2, \ l=r;\\ 0, &{}\quad \hbox {otherwise.} \end{array} \right. \end{aligned}$$

For $1\le k \le i-1$, $i\ge 3$,

$$\begin{aligned}&A_{k+1}(n,i_1,i_2,r; \ m,j_1,j_2,l)\\&\quad =\left\{ \begin{array}{ll} \mu _r p_1^{k-1}(p_2+p_3), &{}\quad m=i-k,\ 1\le i_2\le S_2,\\ &{}\quad i_1=j_1=0, \ r=1,2,3, \ l=2; \\ \mu _r p_2^{k-1}(p_1+p_3), &{}\quad m=i-k, \ 1\le i_1\le S_1,\\ &{}\quad i_2=j_2=0, \ r=1,2,3, \ l=1; \\ 0, &{}\quad \hbox {otherwise.} \end{array} \right. \\&B_1(n,i_1,i_2,r; \ m,j_1,j_2,l)\\&\quad = \left\{ \begin{array}{ll} -\,(\beta _1+\beta _2),&{}\quad n=m=0,\ i_1=i_2=j_1=j_2=0, \ k=l=0; \\ \mu _r,&{}\quad n=m=0, \ 0\le i_1, \ j_1\le S_1,\\ &{}\quad 0\le i_2, \ j_2\le S_2, \ r=1,2,3, \ l=0;\\ \beta _2,&{}\quad n=m=0, \ 0\le i_1, \ j_1\le S_1,\\ &{}\quad 0\le i_2\le s_2,j_2=S_2, \ r=l=0,1,2,3; \\ \beta _1, &{}\quad n=m=0, \ 0\le i_1\le s_1, \ j_1=S_1,\\ &{}\quad 0\le i_2, \ j_1\le 1,2,\ldots S_2, \ r=l=0,1,2,3; \\ \lambda (p_2+p_3)&{}\quad n=m=0, \ i_1=j_1=0, \ 1\le i_2\le S_2,\\ &{}\quad j_{2}=i_{2}-1, \ r=0, \ l=2;\\ \lambda (p_1+p_3)&{}\quad n=m=0, \ 1\le i_{1}\le S_1, \ j_{1}=i_{1}-1,\\ &{}\quad i_{2}=j_{2}=0, \ r=0, \ l=1;\\ \lambda p_1&{}\quad n=m=0, \ 1\le i_1\le S_1, \ j_{1}=i_{1}-1,\\ &{}\quad 1 \le i_2, \ j_2\le S_2,\ r=0,\ l=1;\\ \lambda p_2&{}\quad n=m=0, \ 1\le i_1, \ j_1\le S_1,\\ &{}\quad 1\le i_2\le S_2, \ j_{2}=i_{2}-1, \ r=0, \ l=2;\\ \lambda p_3&{}\quad n=m=0,1 \le i_1\le S_1,1 \le i_2\le S_2,\\ &{}\quad j_{1}=i_{1}-1, \ j_{2}=i_{2}-1, \ r=0, \ l=3;\\ -\,(\lambda +\mu _r+\beta _1+\beta _2)&{}\quad n=m=0, \ 0\le i_1, \ j_1\le s_1,\\ &{}\quad 0\le i_2, \ j_2\le s_2, \ r=l=1,2,3;\\ -\,(\lambda (p_2+p_3)+\beta _1+\beta _2)&{}\quad n=m=0, \ i_{1}=j_{1}=0,\\ &{}\quad 0\le i_2, \ j_2\le s_2, \ r=l=0;\\ -\,(\lambda (p_1+p_3)+\beta _1+\beta _2)&{}\quad n=m=0, \ i_{2}=j_{2}=0,\\ &{}\quad 0\le i_1, \ j_1\le s_2, \ r=l=0;\\ -\,(\lambda +\beta _1+\beta _2)&{}\quad n=m=0, \ 1\le i_1, \ j_1\le s_1,\\ &{}\quad 1\le i_2, \ j_2\le s_2, \ r=l=0;\\ -\,(\lambda +\mu _r+\beta _1) &{}\quad n=m=0, \ 1\le i_1\le s_1,\\ &{}\quad s_{2}+1\le i_2\le S_2, \ r=l=1,2,3;\\ -\,(\lambda +\mu _r+\beta _2)&{}\quad n=m=0, \ s_{1}+1\le i_1\le S_1,\\ &{}\quad 1\le i_2\le s_2, \ r=l=1,2,3;\\ \,-(\lambda +\beta _2)&{}\quad n=m=0, \ s_{1}+1\le i_1\le S_1,\\ &{}\quad 1\le i_2\le s_2, \ r=l=0;\\ -\,(\lambda +\beta _1)&{}\quad n=m=0, \ 1\le i_1\le s_1,\\ &{}\quad s_{2}+1\le i_2\le S_2, \ r=0;\\ -\,\lambda &{}\quad n=m=0, \ s_{1}+1\le i_1\le S_1, \ j_1=i_1,\\ &{}\quad s_{2}+1\le i_2\le S_2, \ j_2=i_2, \ r=0=l;\\ 0, &{}\quad \hbox {otherwise.} \end{array} \right. \end{aligned}$$

For $i \ge 2$

$$\begin{aligned}&B_{i+1}(n,i_1,i_2,r; \ m,j_1,j_2,l)\\&\quad =\left\{ \begin{array}{ll} \mu _r, &{}\quad m=0, \ i_1=i_2=j_1=j_2=0, \ r=1,2,3,l=0; \\ \mu _r p_1^{i}, &{}\quad m=0, \ i_1=j_1=0,\\ &{}\quad 1 \le i_2, \ j_2 \le S_2, \ r=1,2,3, \ l=0 ;\\ \mu _r p_1^{i-1}(p_2+p_3), &{}\quad m=0, \ i_1=j_1=0,\\ &{}\quad 1 \le i_2\le S_2, \ j_2=i_{2}-1, \ r=1,2,3, \ l=2 ;\\ \mu _r p_2^{i-1} (p_1+p_3), &{}\quad m=0, \ 1 \le i_1\le S_1,\\ &{}\quad j_1=i_{1}-1, \ i_2=j_2=0, \ r=1,2,3, \ l=1; \\ \mu _r p_2^{i}&{}\quad m=0, \ 1 \le i_1\le S_1, \ i_2=j_2=0,\\ &{}\quad r=1,2,3, \ l=0; \\ 0, &{}\quad \hbox {otherwise.} \end{array} \right. \\&A_{2}(n,i_1,i_2,r; \ m,j_1,j_2,l)\\&\quad =\left\{ \begin{array}{ll} \mu _r (p_2+p_3), &{}\quad m=n-1, \ i_1=0, \ 1\le i_2\le S_2,\\ &{}\quad j_2=i_{2}-1, \ r=1,2,3, \ l=2; \\ \mu _r (p_1+p_3), &{}\quad m=n-1,1\le i_1\le S_1,\\ &{}\quad i_2=0, j_1=i_{1}-1, \ r=1,2,3, \ l=1; \\ \mu _r p_1, &{}\quad m=n-1, \ 1\le i_1\le S_1,\\ &{}\quad 1\le i_2\le S_2, \ j_1=i_{1}-1, \ r=1,2,3, \ l=1; \\ \mu _r p_2, &{}\quad m=n-1, \ 1\le i_1\le S_1,\\ &{}\quad 1\le i_2\le S_2, \ j_2=i_{2}-1, \ r=1,2,3, \ l=2; \\ \mu _r p_3, &{}\quad m=n-1, \ 1\le i_1\le S_1,\\ &{}\quad 1\le i_2\le S_2, \ j_1=i_{1}-1, \ j_2=i_{2}-1, \ r=1,2,3, \ l=3; \\ 0, &{}\quad \hbox {otherwise.} \end{array} \right. \\&A_{1}(n,i_1,i_2,r;\ m,j_1,j_2,l)\\&\quad =\left\{ \begin{array}{ll} \beta _2,&{}\quad n=m, \ 0\le i_1, \ j_1\le S_1,\\ &{}\quad 0\le i_2\le s_2, \ j_2=S_2, \ r=l=1,2,3; \\ \beta _1, &{}\quad n=m, \ 0\le i_1\le s_1, \ j_1=S_1,\\ &{}\quad 0\le i_2, \ j_2\le 1,2,\ldots S_2, \ r=l=0,1,2,3; \\ -\,(\lambda +\mu _r+\beta _1+\beta _2)&{}\quad n=m, \ 0\le i_1, \ j_1\le s_1,\\ &{}\quad 0\le i_2, \ j_2\le s_2, \ r=l=1,2,3;\\ -\,(\lambda +\mu _r+\beta _1) &{}\quad n=m, \ 0\le i_1, \ j_1\le s_1,\\ &{}\quad s_{2}+1\le i_2, \ j_2\le S_2, \ r=l=1,2,3;\\ -\,(\lambda +\mu _r+\beta _2)&{}\quad n=m, \ s_{1}+1\le i_1, \ j_1\le S_1,\\ &{}\quad 0\le i_2, \ j_2\le s_2, \ r=l=1,2,3;\\ -\,(\lambda +\mu _r)&{}\quad n=m, \ s_{1}+1\le i_1, \ j_1\le S_1,\\ &{}\quad s_{2}+1\le i_2, \ j_2\le S_2, \ r=1,2,3;\\ 0, &{}\quad \hbox {otherwise.} \end{array} \right. \end{aligned}$$

3 Steady-State Analysis

A necessary condition for $\mathcal {Q}$ to be irreducible is $B_1$ and $A_1$ are nonsingular. Consider the matrix $A= \sum _{k=0}^ {\infty } A_k$. Let the unique stationary distribution of A be $\varvec{\pi }$. Under the condition (Neuts (1981)),

$$\begin{aligned} \varvec{\pi } A_0 \mathbf e < \sum _{k=2}^{\infty } (k-1) \varvec{\pi } A_k \mathbf e , \end{aligned}$$

an irreducible Markov chain with generator $\mathcal {Q}$ possesss a unique stationary solution vector $\mathbf {x}= (\mathbf {x}_0, \mathbf {x}_1, \mathbf {x}_2, \ldots )$ satisfying

$$\begin{aligned}\mathbf {x} \mathcal Q=0, \mathbf {x}\mathbf {e}=1.\end{aligned}$$

Partitioning $\mathbf {x}$ as $\mathbf {x} = (\mathbf {x}_0, \mathbf {x}_1, \mathbf {x}_2, \ldots )$ where

$$\begin{aligned} \mathbf {x}_0= & {} (x_0(j_1,j_2,r): 0 \le j_1\le S_1, \ 0 \le j_2 \le S_2, \ 0 \le r \le 3),\\ \mathbf {x}_i= & {} (x_{i}(j_1,j_2,r): 0 \le j_1\le S_1, \ 0 \le j_2 \le S_2, \ 1\le r \le 3), \ \mathrm{{for}} \ i\ge 1, \end{aligned}$$

where $\mathbf {x}_0$ is of dimension $1\times b$ and $\mathbf {x}_i$ for $i \ge 1$, is of dimension $1\times a$ Then $\mathbf {x}$ is obtained from

$$\begin{aligned} \mathbf {x}_i= \mathbf {x}_1R^{i-1}, \quad i \ge 2 \end{aligned}$$

where R is the minimal non negative solution of the matrix equation $\sum _{k=0}^{\infty }X^k A_k=0$. The boundary equations are given by

$$\begin{aligned} \sum _{r=0}^{\infty }\mathbf {x}_r B_{r+1}= & {} 0\\ \mathbf {x}_0 B_0+\sum _{r=1}^{\infty }\mathbf {x}_r A_r= & {} 0 \end{aligned}$$

The normalizing condition $\mathbf {x} \mathbf {e} = 1$ gives

$$\begin{aligned} \mathbf {x}_0 \mathbf {e}+ \mathbf {x}_1 [I-R]^{-1} \mathbf {e}=1 \end{aligned}$$

R matrix is obtained using the algorithm:

$$\begin{aligned} R(0)= & {} 0\\ R(n+1)= & {} -A_0A_1^{-1}-R^2(n)A_2A_1^{-1}-R^3(n)A_3A_1^{-1}-\ldots , n\ge 0\end{aligned}$$

Theorem 3.1

The Markov chain with infinitesimal generator $\mathcal {Q}$ given in (1) is always stable.

Proof

Consider a service completion epoch at which stock of both commodities or at least one commodity drops to zero. Suppose n customers are waiting in the queue at this epoch. When both the inventory becomes zero, then all the customers waiting in the queue will be lost. Suppose that, if one inventory is positive and the other one is empty. If all of them ask for the same commodity which is not available in stock then all these customers leave the system instantly. Otherwise, the service will be offered to a waiting customer (after removing, if any, all those customers who request the item for which the inventory level is zero) and we repeat this process. Thus, we can think of this queueing-inventory model as some kind of a catastrophic model in which all waiting customers will be cleared. Thus, from any level the queue size may drop to zero with positive probability, however small(as n becomes very large), in a very short time following a service completion. $\square$

4 System Characteristics

Next we proceed to compute measures that are indications of the system performance.

• Expected number of customers in the system, $\displaystyle E_N= \sum \nolimits _{n=1}^{\infty }n \sum \nolimits _{j_{1}=0}^{S_{1}}\sum \nolimits _{j_{2}=0}^{S_{2}}\sum \nolimits _{r=1}^{3}x_n(j_{1},j_{2},r).$

• Expected number of customers demanding $C_1$ alone, $\displaystyle E_{C1} = p_1 E_N.$

• Expected number of customers demanding $C_2$ alone, $\displaystyle E_{C2} = p_2 E_N.$

• Expected number of customers demanding both $C_1$ and $C_2$, $\displaystyle E_{C12}= p_3 E_N.$

• Expected number of item $C_1$ in the system, $\displaystyle E_{I_{1}}= \sum \nolimits _{n=0}^{\infty } \sum \nolimits _{j_{1}=1}^{S_{1}}\sum \nolimits _{j_{2}=0}^{S_{2}}\sum \nolimits _{r=0}^{3}j_{1}x_n(j_{1},j_{2},r).$

• Expected number of item $C_2$ in the system, $\displaystyle E_{I_{2}}= \sum \nolimits _{n=0}^{\infty } \sum \nolimits _{j_{1}=0}^{S_{1}}\sum \nolimits _{j_{2}=1}^{S_{2}}\sum \nolimits _{r=0}^{3}j_{2}x_n(j_{1},j_{2},r).$

• Probability that server is busy processing a demand for $C_1$ alone,

  $\displaystyle P_{C_{1}}= \sum \nolimits _{n=1}^{\infty } \sum \nolimits _{j_{1}=0}^{S_{1}}\sum \nolimits _{j_{2}=0}^{S_{2}}x_n(j_{1},j_{2},1).$

• Probability that server is busy processing a demand for $C_2$ alone,

  $\displaystyle P_{C_{2}}= \sum \nolimits _{n=1}^{\infty } \sum \nolimits _{j_{1}=0}^{S_{1}}\sum \nolimits _{j_{2}=0}^{S_{2}}x_n(j_{1},j_{2},2).$

• Probability that server is busy processing a demand for both $C_1$ and $C_{2}$,

  $\displaystyle P_{C_{12}}= \sum \nolimits _{n=1}^{\infty } \sum \nolimits _{j_{1}=0}^{S_{1}}\sum \nolimits _{j_{2}=0}^{S_{2}}x_n(j_{1},j_{2},3).$

• Probability that server is busy, $\displaystyle P_{busy}= \sum \nolimits _{n=1}^{\infty } \sum \nolimits _{j_{1}=0}^{S_{1}}\sum \nolimits _{j_{2}=1}^{S_{2}}\sum \nolimits _{r=1}^{3}x_n(j_{1},j_{2},r)+ \sum \nolimits _{n=1}^{\infty } \sum \nolimits _{j_{1}=1}^{S_{1}}\sum \nolimits _{r=1}^{3}x_n(j_{1},0,r).$

• Probability that inventory $C_1$ alone is zero,

  $\displaystyle P_{C_{10}}= \sum \nolimits _{n=0}^{\infty } \sum \nolimits _{j_{2}=0}^{S_{2}} \sum \nolimits _{r=0}^{3}x_n(0,j_2,r).$

• Probability that inventory $C_2$ alone is zero,

  $\displaystyle P_{C_{20}}= \sum \nolimits _{n=0}^{\infty } \sum \nolimits _{j_{1}=0}^{S_{1}} \sum \nolimits _{r=0}^{3}x_n(j_1,0,r).$

• Probability that both inventory $C_1$ and $C_2$ equal to zero,

  $\displaystyle P_{00}= \sum \nolimits _{n=0}^{\infty } \sum \nolimits _{r=0}^{3}x_n(0,0,r).$

• Probability that customer demanding $C_1$ alone is lost,

  $\displaystyle P_{C_{1}lost}= p_1\sum \nolimits _{n=1}^{\infty } \sum \nolimits _{j_{2}=0}^{S_{2}}\sum \nolimits _{r=1}^{3} \mu _{r}x_n(0,j_{2},r).$

• Probability that customer demanding $C_2$ alone is lost,

  $\displaystyle P_{C_{2}lost}= p_2\sum \nolimits _{n=1}^{\infty } \sum \nolimits _{j_{1}=0}^{S_{1}}\sum \nolimits _{r=1}^{3}\mu _{r} x_n(j_{1},0,r).$

• Probability that customer demanding both $C_1$ and $C_2$ is lost, $\displaystyle P_{C_{12}lost}= p_3\sum \nolimits _{n=1}^{\infty } \sum \nolimits _{r=1}^{3}\mu _{r}x_n(0,0,r).$

• Probability that customer demanding both $C_1$ and $C_2$ is met with $C_1$,

  $\displaystyle P_{C_{121}}= p_3\sum \nolimits _{n=1}^{\infty } \sum \nolimits _{j_{1}=1}^{S_{1}} \sum \nolimits _{r=1}^{3}\mu _{r}x_n(j_1,0,r).$

• Probability that customer demanding both $C_1$ and $C_2$ is met with $C_2$,

  $\displaystyle P_{C_{122}}= p_3\sum \nolimits _{n=1}^{\infty } \sum \nolimits _{j_{2}=1}^{S_{2}} \sum \nolimits _{r=1}^{3}\mu _{r}x_n(0,j_2,r).$

• Expected rate of replenishments for item $C_1$,$\displaystyle E_{RC1}=\beta _1\sum \nolimits _{n=0}^{\infty } \sum \nolimits _{j_{1}=0}^{s_{1}}\sum \nolimits _{j_{2}=0}^{S_{2}}\sum \nolimits _{r=0}^{3}x_n(j_1,j_{2},r).$

• Expected rate of replenishments for item $C_2$, $\displaystyle E_{RC2}=\beta _2\sum \nolimits _{n=0}^{\infty } \sum \nolimits _{j_{1}=0}^{S_{1}}\sum \nolimits _{j_{2}=0}^{s_{2}}\sum \nolimits _{r=0}^{3}x_n(j_1,j_{2},r).$

• Expected reorder rate of commodity C1,$\displaystyle E_{R1}= \mu _1 \sum \nolimits _{n=0}^{\infty }\sum \nolimits _{j_{2}=0}^{S_{2}}x_n(s_{1}+1,j_2,1).$

• Expected reorder rate of commodity C2,$\displaystyle E_{R2}= \mu _2 \sum \nolimits _{n=0}^{\infty }\sum \nolimits _{j_{1}=0}^{S_{1}}x_n(j_1,s_{2}+1,2).$

• Expected reorder rate of commodity C1 and C2,$\displaystyle E_{R12}= \mu _3 \sum \nolimits _{n=0}^{\infty }x_n(s_{1}+1,s_{2}+1,3).$

We now look for additional information needed to optimally design the system.

4.1 Expected Loss Rate of Customers in the Queue Demanding $C_1$ Alone

In order to compute the expected loss rate of customers in the queue demanding $C_1$ alone, consider the Markov chain

$$\begin{aligned} \{(N(t), \ I_1(t), \ I_2(t), \ J(t)), \ t\ge 0\} \end{aligned}$$

where N(t), $I_1(t)$, $I_2(t)$,J(t)) were as defined in Sect. 2. The state space of the above process is $\{(n,0,j_2,r): 1\le n\le K, 0\le j_2 \le S_2, 1 \le r \le 3\}\bigcup \varvec{\{\Delta \}}$ where $\varvec{\{\Delta \}}$ is the absorbing state which represents the state that number of customers in the queue becomes zero and K( the size of the queue). It is the maximum value to which the queue size can grow. Thus we have a finite state space Markov chain. The possible transitions and corresponding rates are:

• (n, 0, 0, r) $\rightarrow$ (0, 0, 0, 0) at the rate $\mu _{r}$ for $r=1,2,3$

• $(n,0,j_2,r)$ $\rightarrow$ $(0,0,j_2,0)$ at the rate $\mu _{r}p_1^n$ for $r=1,2,3$

• $(n,0,j_2,r)$ $\rightarrow$ $(n+1,0,j_2,r)$ at the rate $\lambda$ for $r=1,2,3$

• $(n,0,j_2,r)$ $\rightarrow$ $(n,0,S_2,r)$ at the rate $\beta _2$ for $r=1,2,3$

The infinitesimal generator $\mathcal {G}$ of the above Markov chain is of the form

$$\begin{aligned} \mathcal {G}_1 = \left[ {\begin{array}{*{20}c} {T_1 } &{}\quad {T_1^0 } \\ \mathbf 0 &{}\quad 0 \\ \end{array}} \right] \end{aligned}$$

with initial probability vector

$$\begin{aligned} \varvec{\alpha }=(cx_1(0,j_2,r), \ cx_2(0,j_2,r),\ldots , cx_K(0,j_2,r):0 \le j_2 \le S_2, \ 1 \le r \le 3), \end{aligned}$$

where

$$\begin{aligned} c=\left\{ \sum _{n=1}^{K}\sum _{j_2=0}^{S_2}\sum _{r=1}^{3}x_n(0,j_2,r)\right\} ^{-1}; \end{aligned}$$

$T_1$ is a matrix of order $3K (S_2+1)$ and $T_1^0$ is a column vector of order $3K (S_2+1)$ such that $T_1 \mathbf e + T_1^0=0$.

Hence we arrive at

Theorem 4.1

The expected loss rate of customers in the queue demanding $C_1$ alone is,

$$\begin{aligned} \displaystyle E_{L1}=\left\{ -\varvec{\alpha } T_1^{-1}{} \mathbf e \right\} ^{-1} \end{aligned}$$

On similar lines we can compute the expected loss rate of customers in the queue demanding $C_2$ alone and both $C_1$ and $C_2$. The following results are arrived at, the details of which are omitted.

Theorem 4.2

The expected loss rate of customers in the queue demanding $C_2$ alone is

$$\begin{aligned}\displaystyle E_{L1}=\{-\varvec{\alpha _1} T_2^{-1}{} \mathbf e \}^{-1}\end{aligned}$$

where initial probability vector

$$\begin{aligned}\varvec{\alpha _1}=(cx_1(j_1,0,r), \ cx_2(j_1,0,r),\ldots , cx_K(j_1,0,r):0 \le j_1 \le S_1, \ 1 \le r \le 3),\end{aligned}$$

and

$$\begin{aligned}c=\left\{ \sum _{n=1}^{K}\sum _{j_1=0}^{S_1}\sum _{r=1}^{3}x_n(j_1,0,r)\right\} ^{-1};\end{aligned}$$

and $T_2$ is a matrix of order $3K (S_{1}+1)$ and $T_2^0$ is a column vector of order $3K (S_{1}+1)$ such that $T_2 \mathbf e + T_2^0=0$.

Theorem 4.3

The expected loss rate of customers demanding both $C_1$ and $C_2$ is,

$$\begin{aligned} \displaystyle E_{L12}=\{-\varvec{\alpha _2} T_3^{-1}{} \mathbf e \}^{-1}\times \sum _{n=1}^{K}\sum _{r=1}^{3}x_n(0,0,r) \end{aligned}$$

with initial probability vector

$$\begin{aligned}\varvec{\alpha _2}=(cx_1(0,0,r), \ cx_2(0,0,r),\ldots , cx_K(0,0,r): 1 \le r \le 3),\end{aligned}$$

$$\begin{aligned}c=\left\{ \sum _{n=1}^{K}\sum _{r=1}^{3}x_n(0,0,r)\right\} ^{-1};\end{aligned}$$

$T_3$ is a matrix of order 3K and $T_3^0$ is a column vector of order 3K such that $T_3 \mathbf e + T_3^0=0$.

4.2 Analysis of $C_1$ Cycle Time

The cycle time of item $C_1$ is defined as the time interval between two consecutive instants at which its inventory level hits $S_1$ due to replenishment. We assume that with at most M demands the first return to $S_1$ of $C_1$ takes place. Let us consider a Markov chain $\{(N(t),I_1(t),I_2(t),J(t), D(t)), t\ge 0\}$ where D(t) denotes the type of the demand of the commodity; the rest of the notations are as defined in Sect. 2. The state space of the above process is $\{(n,j_1,j_2,r,d): 0\le n\le K, 0\le i_1 \le S_1, 0\le j_2 \le S_2, 1 \le r \le 3, 1 \le d\le M\}\bigcup \varvec{\{\Delta \}}$ where $\varvec{\{\Delta \}}$ is the absorbing state which represents the state that level of $C_1$ returns to $S_1$ and K, the maximum size the queue can grow up. Thus we have a finite state space Markov chain. The possible transitions and corresponding rates are:

• $(n,S_1,j_2,r,d)\rightarrow (n-1,S_{1}-1,j_2,1,d)$ with rate $\mu _r p_1$

• $(n,0,j_2,r,d)\rightarrow (0,0,j_2,0,d)$ with rate $\mu _r p_1^{n}$ or $(0,0,,j_{2}-1,2,d)$ with rate $\mu _r p_1^{n-1}(p_2+p_3)$

• $(n,j_1,0,r,d)\rightarrow (0,j_1,0,0,d)$ with rate $\mu _r p_2^{n}$ or $(0,j_{1}-1,0,1,d)$ with rate $\mu _r p_2^{n-1}(p_1+p_3)$

• $(n,j_1,j_2,r,d) \rightarrow (n-1,j_1-1,j_2,1,d)$ with rate $\mu _r p_1$, or to $(n-1,j_1,j_2-1,2,d)$ with rate $\mu _r p_2$ or to $(n-1,j_1-1,j_2-1,3,d)$ with rate $\mu _r p_3$

• $(n,0,j_2,r,d) \rightarrow (n-k,0,j_2-1,2,d)$ with rate $\mu _r p_1^{k-1}(p_2+p_3)$

• $(n,j_1,0,r,d) \rightarrow (n-k, j_1-1,0,1,d)$ with rate $\mu _r p_2^ {k-1} (p_1+p_3)$

• $(n,j_1,j_2,r,d) \rightarrow (n,S_1,j_2,r,d)$ with rate $\beta _1$ for $0\le j_1 \le s_1, 0 \le j_2 \le S_2, 1 \le r \le 3$

• $(n,j_1,j_2,r,d) \rightarrow (n+1,j_1,j_2,r,d)$ with rate $\lambda$ for $0\le n \le K-1$ for $0 \le j_1 S_1$, $0 \le j_2 \le S_2$, $1 \le r \le 3$, $1 \le d \le M$

The infinitesimal generator $\mathcal {C}$ of the above Markov chain is of the form

$$\begin{aligned} \mathcal {C} = \left[ {\begin{array}{*{20}c} {D } &{}\quad {D^0 } \\ \mathbf 0 &{}\quad 0 \\ \end{array}} \right] \end{aligned}$$

with initial probability vector

$$\begin{aligned} \varvec{\gamma }=(cx_0(S_1,j_2,r), \ cx_1(S_1,j_2,r),\ldots , cx_K(S_1,j_2,r),0,0,\ldots ):0 \le j_2 \le S_2, \ 1 \le r \le 3), \end{aligned}$$

where

$$\begin{aligned} c=\left\{ \sum _{n=0}^{K}\sum _{j_2=0}^{S_2}\sum _{r=1}^{3}x_n(S_1,j_2,r)\right\} ^{-1}; \end{aligned}$$

D is a matrix of order $3(K+1)(S_{1}+1)(S_2+1)$ and $D^0$ is a column vector of order $3 (K+1)(S_{1}+1)(S_2+1)$ such that $D \mathbf e + D^0=0$. Hence, the expected cycle length is

$$\begin{aligned}\{-\varvec{\gamma } D^{-1}{} \mathbf e \}.\end{aligned}$$

Similarly the cycle time of item $C_2$ has expected value

$$\begin{aligned}\{-\varvec{\gamma _{1}} D_1^{-1}{} \mathbf e \}\end{aligned}$$

where

$$\begin{aligned} \varvec{\gamma _1}=(cx_0(j_1,S_2,r), \ cx_1(j_1,S_2,r),\ldots , cx_K(j_1,S_2,r),0,0,\ldots ):0 \le j_1\le S_1, \ 1 \le r \le 3), \end{aligned}$$

where

$$\begin{aligned} c=\left\{ \sum _{n=0}^{K}\sum _{j_1=0}^{S_1}\sum _{r=1}^{3}x_n(j_1,S_2,r)\right\} ^{-1}; \end{aligned}$$

$D_1$ is a matrix of order $3(K+1)(S_{1}+1)(S_2+1).$

5 Numerical Illustration

In this section we provide numerical illustration of the system performance with variation in values of underlying parameters.

5.1 Effect of $\lambda$ on Various Performance Measures

Table 1 indicates that increase in $\lambda$ value results in increase in expected number of customers in the queue, expected loss rate of customers demanding $C_1$ alone, $C_2$ alone, both $C_1$ and $C_2$. As $\lambda$ increases there is a decrease in the expected number of items in the inventory. Also, as $\lambda$ increases reorder rates for $C_1$ alone, $C_2$ alone, both $C_1$ and $C_2$ also increase. These are all natural consequences of increase in arrival rate.

Table 1 Effect of $\lambda$: Fix $S_1=10, S_2=15, s_1=3,s_2=4,\mu _1=2, \mu _2=3, \mu _3=4, \beta _1=2, \beta _2=3, p_1=0.1, p_2=0.1,p_3=0.8$

Table 2 Effect of $\mu _1$: Fix $S_1=10, S_2=15, s_1=3,s_2=4, \lambda =1, \mu _2=2, \mu _3=3,\beta _1=2, \beta _2=3, p_1=0.1, p_2=0.1,p_3=0.8$

5.2 Effect of $\mu _1$ on Various Performance Measures

Table 2 indicates that increase in service rate$\mu _1$ for processing commodity 1, makes decrease in expected number of customers in the system. As $\mu _1$ increases there is a slight decrease initially in the expected number of $C_1$, then it shows increasing tendency. There is increase in expected loss rate of customers demanding $C_1$ alone initially and then remains constant and then it increases. Reorder rates for $C_1$ alone, $C_2$ alone, for both $C_1$ and $C_2$ remains constant. Expected value of $C_2$ decreases. Expected loss rate of customers demanding $C_2$ alone increases and loss rate demanding both $C_1$ and $C_2$ decreases.

Similarly we can see the effect of $\mu _2$ and $\mu _3$ on various performance measures.

5.3 Effect of $\beta _1$ on Various Performance Measures

Table 3 indicates that as the replenishment rate for the first commodity increases expected number of customers in the queue increases and then remains constant. Expected number of items $C_1$ increases but that of $C_2$ remains constant. Expected loss rate of customers demanding $C_1$ alone is constant, but those for $C_2$ alone and both $C_1$ and $C_2$ decrease. Reorder rates for $C_1$ alone and both $C_1$ and $C_2$ increases and for $C_2$ alone decreases and then remains constant. Similarly effect of $\beta _2$ on various performance measures can be seen.

Table 3 Effect of $\beta _1$: Fix $S_1=10, S_2=15, s_1=3,s_2=4, \lambda =1, \mu _1=2, \mu _2=3, \mu _3=3, \beta _2=3, p_1=0.1, p_2=0.1,p_3=0.8$

Table 4 Value of cost function for various $(S_1,S_2)$: Fix $s_1=4, s_2=5, h=3,c_1=5,c_2=8,c_3=15,c_4=20, c_5=10,c_6=100,c_7=150,c_8=200$

6 Optimization Problem

We now construct an optimization problem involving costs for holding, procurement and due to loss of demands when the item asked for is not available. Consider the cost function,

$$\begin{aligned} hE_C+c_1 E_{I_1}+c_2 E_{I_2}+c_3E_{L1}+c_4E_{L2}+c_5 E_{L12}+c_6 E_{R1}+c_7 E_{R2}+c_8 E_{R12} \end{aligned}$$

where

h : holding cost per customer per unit time,

$c_i$: per unit holding cost of $C_i$ per unit time,for $i=1,2$,

$c_i$, for $i=3,4,5$: cost due to loss of customer demanding $C_1$ alone, $C_2$ alone and both $C_1$ and $C_2$ respectively,

$c_i$ for $i=6,7,8$: fixed procurement cost for $C_1$, $C_2$, and both $C_1$ and $C_2$ respectively.

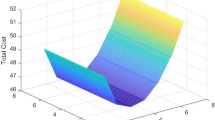
In the absence of analytical expressions for system state distribution, discussions on global optimum is impossible. However, cost for various $(s_i,S_i)$ for $i=1,2$ is given below (Table 4):

7 Conclusion

We analyzed a two-commodity queueing inventory problem with Poisson arrival of demands. Customers reveal their requirement at the time when taken for service. If item demanded is not available, the customer leaves the system forever. If both items are demanded when taken for service and only one item is available, then the customer is served that item. Service times are exponentially distributed with parameter depending on the type of demand. The lead times for $i\mathrm{{th}}$ commodity is exponentially distributed with parameter $\beta _i, 1=1,2$. The continuous time Markov chain is seen to be of GI/M/1 type. The system is shown to be stable. Several system performance indices are derived and numerical illustration provided. An optimization problem is set up and its numerical investigation is carried out.

Extension of the model discussed to $n-$ commodity system with MAP and PH type service time with representation depending on the commodity served is proposed. If ’emergency purchase’ is made whenever inventory level of an item drops to zero without cancelling replenishment order seems to produce product form solution. This is also proposed to be investigated.