Abstract
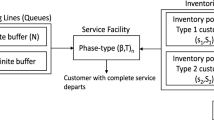
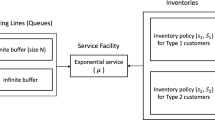
In this paper, we consider a two commodity queueing inventory system with random common lifetimes for each commodity, positive service time, positive lead time, and individual ordering policy. Inventory is managed by the continuous review \((s_{i}, S_{i})\) policy for the commodity \(i, i=1, 2\). On realization of the common lifetime or inventory level less than or equal to \(s_{i}, i=1,2\) by service completions, a replenishment order is placed for \(S_{i}, i=1,2\) items to bring the inventory level back to \(S_{i}, i=1,2\). There are two types of customers called priority and non-priority. Customers arrive according to two independent Poisson processes. A single server processes the inventory before delivery. Lifetimes and lead times of each commodity and service time for each customer category follow an independent exponential distribution with different rates. No customer will be allowed to join when the inventory levels become zero. System performance measures are derived. We also examine the effect of the lead time parameters and common lifetime parameters on the system performance measures. The model was examined in the steady state by using the matrix geometric approach. Further, we analyzed an associated optimization problem and carried out numerical illustrations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Accurate inventory management is key to running a successful product business. Inventory control is the most important control technique having direct relationships with manufacture, purchase, marketing and financial policies. Inventory models play a very crucial role in operations research and management science. They are classified based on a number of factors such as the type of demands (deterministic or random), the shelf time (infinite, finite random, or finite deterministic) of the inventory items, and the replenishing time (zero or finite deterministic or random).
The term “perishable inventory” describes goods with a short shelf life or expiration date. A form of inventory known as perishable inventory with a common lifetime (CLT) consists of goods that have a finite shelf life and will all expire at the same time. This can include things like dairy products, fresh produce, and specific kinds of medicines. Businesses that deal with perishable goods need to have mechanisms in place to make sure they can sell or use the items before they perish. A tremendous amount of work has been seen in the literature on stochastic inventory systems with perishable items. In all those works mentioned, researchers assumed that each item fail randomly and independently of others. Review papers focusing on perishable inventory management started with the work of Nahmias who studied the literature for ordering policies of perishable products with fixed lifetimes and with continuous exponential decay. But in perishable inventory systems, items with finite lifetimes can be divided into two categories. Each item has an independent lifetime and the items that survive a random common lifetime in inventory. In the second category, when the random common lifetime realizes, all items of that commodity perish.
There are several applications in retail industries where existing inventory items, if any, are all replaced after a random amount of time. For example, analyzing inventory systems involving food items such as vegetables, fresh fruits, meats, drugs, photographic materials, and even electronic items such as memory chips, fall under perishable inventory models and need replacement as a batch when the lifetime expires. Hence it necessitates the study of perishable inventory systems with the random common lifetime of items.
In this paper, we study a two-commodity perishable inventory system, in which both commodities have independent random common shelf time, two demand classes of customers, called priority and non-priority, occur according to two independent Poisson processes, positive service time, random lead time and individual ordering policy. Inventory is monitored under continuous review (s, S) type policy. There is a finite capacity buffer for the priority customers and an infinite pool for the non-priority customers and assumed a non-preemptive priority for the customers in service. The objective of this study is to analyze the effect of the common lifetime parameters, and lead-time parameters on the measures of performance, such as the expected inventory levels of both commodities, expected number of priority and non-priority customers, expected loss rate of priority and non-priority customers etc.
The rest of the paper is organized as follows: Sect. 2 gives literature review. Model formation and analysis and steady state system size probability vectors are given in Sect. 3. Section 4 provides system performance measures such as expected number of customers, expected reorder rates, average waiting time of a priority customer and cycle time analysis for two types of commodities. In Sect. 5, cost analysis is carried out and numerical illustrations are provided.
2 Literature review
In this section we provide some of the important studies appeared in the two commodity inventory problems. Stochastic models that appeared in two commodity stochastic inventory systems with non perishable items in the literature are as follows. Krishnamoorthy and Varghese [1, 2] have analyzed two commodity inventory problems with zero lead time and positive lead time in which the change in demand for an item at each demand epoch is according to a discrete Markov chain. Yadavalli et al. [3] studied the system with substitutable items and also considered an arbitrary distributed lead time for replenishment of items. Sivakumar et al. [4] analyzed a two-commodity inventory system with individual and joint ordering policies and renewal demands and [5] studied a two commodity inventory system with retrial demand for the unsatisfied customers who arrive during the inventory dry period. Benny et al. [6] have analyzed a two-item queueing inventory system with a single server and individual ordering policy. Ozkar and Uzunoglu Kocer [7] have studied the system with two types of customers and individual ordering policies. Recently, Jeganathan et al. [8] studied a two commodity Markovian demands inventory system with queue-dependent services and an optional retrial facility.
In the above literature, inventories are not perishable. As mentioned earlier, most of the studies in perishable inventory literature, one can refer to the review paper and the monograph on perishable inventory systems by Nahmias [9, 10] respectively. Later [11, 12] studied a two commodity perishable stochastic inventory system under continuous review. In that paper, authors assumed that the lifetime of items of each commodity is exponentially distributed and items are supposed to be substitutable. Also joint re-ordering policy is adopted with a random lead time for the replenishment of orders with exponential distribution. Yadavalli et al. [13] considered a two commodity continuous review perishable inventory system with three types of customers. The arrivals of all three types of customers are assumed to be a Markovian arrival process. The lifetime of each commodity is exponentially distributed and the lead time is assumed to have a phase-type distribution. Bakker et al. [14] provide an extensive literature on the modeling of deteriorating inventory since 2001. Jeganathan [15] analyzed a stochastic perishable inventory system with two different items and the demands originate from a finite population. Duong et al. [16] analyzed products that possess a multi-period lifetime, positive lead time, and required customer service level. Later, Suganya et al. [17] analyzed a perishable inventory system that has an (s, Q) ordering policy, along with a finite waiting hall.
In all the models mentioned above, they have assumed a random lifetime for each item. In this paragraph, we discuss models with a random common lifetime for items. A discrete-time (s, S) inventory model in which the stored items have a random common lifetime with a discrete phase-type distribution was analyzed by Lian et al. [18]. The first reported work in continuous time inventory systems with a random common lifetimes for items was by Chakravarthy [19]. They have studied a single commodity inventory system Markovian demands, phase type distributions for perishability and replenishment. Later [20, 21] analyzed single server queueing inventory systems in which items in the inventory have a random common lifetime. But in the context of two commodity inventory systems, random common lifetime models have not been studied in the literature. In (2022), Dissa and Ushakumari studied a two-commodity queueing inventory system with perishable items having a random common lifetime for each of the commodities and zero lead time for replenishment of items.
3 Model description and analysis
We consider a two-commodity queueing inventory system in which the maximum inventory level for commodity-i is \(S_{i},i=1,2\). There are two types of customers coming to the system called non-priority(type-1) and priority(type-2). The arrival process of these customers follows independent Poisson processes with rates \(\lambda _{1}\) and \(\lambda _{2}\) respectively. A non-priority customer demands items from commodity-1 alone and a priority customer demands items from commodity-2 alone. Items are served only after processing by a single server. Service times for commodity-1 and 2 follow independent exponential random variables with parameters \(\mu _{1}\) and \(\mu _{2}\) respectively. There is a positive lead time for the replenishment of commodities and for the ith commodity it is exponentially distributed with parameter \(\beta _{i},i = 1, 2\) and are independent of each other. Also for each of the commodities, a random common lifetime is assumed. The lifetime for the ith commodity is exponentially distributed with parameter \(\gamma _{i}, i=1, 2\) and the lifetime of commodity-1 and 2 are independent of each other. Inventory is monitored by continuous review \((s_i, S_i), i = 1, 2\) type policy. On realization of the common lifetime or inventory level less than or equal to \(s_i, i = 1, 2\) by a service completion, and a replenishment order will be given for \(S_i\) units \(i = 1, 2\). That is, a replenishment order for \(S_i\) items is triggered under the following circumstances:
i) When the common lifetime is reached, indicating that all items of a particular commodity have been depleted from the stock, or
ii) When the inventory level falls below or equal to a threshold value \(s_i\) due to service completion.
Once the common lifetime is realized or replenishment occurs, all items of that commodity are removed from the stock. In other words at the time of replenishment of items in stock, all items are assumed as fresh. If the server is busy at the time of arrival of a priority customer, then that customer can join in a finite capacity buffer of size M, \(M>0\). If the buffer is full, that customer is assumed to be lost. A non-priority customer can opt for service and join in a pool with probability p or leave the system with probability \((1-p),0<p<1\) if the server is busy at the arrival epoch. Customers from the pool will be selected for service if no priority customer is waiting for service. The selection of customers for service is on a FCFS basis. Also assumed non-pre-emptive priority for service.
3.1 Notations and explanations
Throughout the paper, we use the following notations.
-
\(S_{i}^{*}\) denote a temporary state which indicates the replenishment due to the realization of CLT and \(S_{i}^{*}=S_{i}\)
-
e = Column vector of 1’s with appropriate order.
-
\(\varvec{0}\) = Zero matrix of appropriate order.
-
\(I_{a}\) = Identity matrix of order a.
-
\(\bigotimes\) denotes the Kronecker product of matrices.
-
\(B^{T}\) represents the transpose of the matrix B.
3.2 Analysis
For the mathematical formulation of the model, we define the following: At time t,
\(N_{1}(t)\): the number of customers in the pool including the one in service
\(N_{2}(t)\): the number of customers in the buffer including the one in service
\(J_{1}(t)\): the residual inventory level of commodity -1
\(J_{2}(t)\): the residual inventory level of commodity -2 and
L(t) : the state of the server at time t, where
\(L(t)={\left\{ \begin{array}{ll}0 ,\hspace{5 pt} if \, the \, server \, idle \, at \, time \, t\\ 1 \hspace{5 pt},\hspace{5 pt} if \, the \, server \, busy \, with \, a \, type-1 customer \, at \, time \, t \\ 2 ,\hspace{5 pt} if \, the \, server \, busy \, with \, a type-2 \, customer \, at \, time \, t \end{array}\right. }\)
Let \(Z(t)=(N_{1}(t),N_{2}(t),J_{1}(t),J_{2}(t),L(t))\). Then \(\{Z(t);t\ge 0\}\) forms a continuous time Markov chain over the state space \(E= E_{0} \bigcup E_{1} \bigcup E_{2}\bigcup E_{3}\), where
\(E_{0}=\{(n_{1},n_{2},0,0,0); n_{1}\ge 0; 0\le n_{2}\le M; M\ge 1\},\)
\(E_{1}=\{(0,0,j_{1},j_{2},0); j_{1}=0,1,2,\ldots , S_{1},S_{1}^{*}; j_{2}=0,1,2,\ldots , S_{2},S_{2}^{*} \},\)
\(E_{2}=\{(n_{1},n_{2},j_{1},j_{2},1); j_{1}=0,1,2,\ldots , S_{1},S_{1}^{*}; j_{2}=0,1,2,\ldots , S_{2},S_{2}^{*}; n_{1}\ge 0; 0\le n_{2}\le M; M\ge 1\},\)
\(E_{3}=\{(n_{1},n_{2},j_{1},j_{2},2); i_{1}=0,1,2,\ldots , S_{1},S_{1}^{*}; j_{2}=0,1,2,\ldots , S_{2},S_{2}^{*}; n_{1}\ge 0; 0\le n_{2}\le M; M\ge 1\}\) and \(S_{i}^{*}~,~i=1,2\) denote the inventory level due to replenishment of commodity-i after the realization of common lifetime. This is same as \(S_{i}~,~i=1,2\). However to distinguish the begining of the next cycle due to realization of common lifetime, we use it as a purely temporary notation. Here we consider the number of customers in the pool as the level of the process. By the above assumptions and notations, \(\{Z(t),t\ge 0\}\) forms a level independent Quasi-Birth and Death (LIQBD) process over E. The infinitesimal generator matrix of the system is of the form
Let us denote \(a_{1}=(S_{1}+2) (S_{2}+2); a_{2}=(S_{1}+2) (S_{2}+2)(M+1); a_{3}=2a_{2}; a_{4}=2a_{2}+(M+1);a_{5}=2a_{2}+a_{1}+M; b=(S_{2}+2);{\bar{a}}_{4}=2a_{2}+M\)
With these notations, the sub matrices of Q are as follows:
The sub matrices are
where T stands for the transpose of a matrix.
\(D_{00}\) is a square matrix of dimension \(M\times M. B_{21}\) is a zero matrix of order \((a_{2}\times a_{2})\).
where T stands for the transpose of a matrix.
\(D_{11}\) is a square matrix of order \((M+1)\).
\(\hat{R}_{k},\hat{\hat{R}}_{k}\) are of order \((M+1)\times a_{1}\) and \(\tilde{\hat{\hat{R}}}_{k}\) is of order \(M\times a_{1}. \hat{C}_{k},\hat{\hat{C}}_{k}\) are of order \((a_{1}\times (M+1)).\) The elements of matrices \(\hat{\hat{R_{k}}}, \hat{R_{k+1}},\tilde{\hat{\hat{R_{k}}}}, \hat{C_{k+1}}, \hat{\hat{C_{k+1}}}, \tilde{ \hat{C_{k+1}}}, \tilde{\hat{\hat{C_{k+1}}}}\) represents the transitions from \((n_{1},n_{2},j_{1},j_{2},l)\xrightarrow \;(n_{1},n_{2},j_{1},j_{2},l)\) where \(n_{1},n_{2}\) represents the number of customers in the pool and in the buffer. \(j_{1},j_{2}\) represents the residual inventory level of commodity-1 and commodity-2. l represents the state of the server.
The elements of matrix H represents the transitions from \((n_{1},0,i_{1},i_{2},l) \xrightarrow (n_{1}-1,0,j_{1},j_{2},l)\) where \(n_{1}, (n_{1}-1)\) represents the number of customers in the pool and ’0’ represents there is no customers in the buffer. \(i_{1},j_{1}\) represents the residual inventory level of commodity-1 and \(i_{2},j_{2}\) represents the residual inventory level of commodity-2. l represents the state of the server.
Define \(F= I_{S_{1}+2}\bigotimes F_{1};G=I_{S_{1}+2}\bigotimes G_{1}\) and \(E_{1}=(\lambda _{1}p)I_{b}\)
F, G, E all are square matrices of order \(a_1\times a_1\) and \(I_a\) is an identity matrix of order a.
\(V_{0}=\beta _{1}I_{b}; V_{1}=\gamma _{1}I_{b}; Z_{i},i=0,1,\ldots , (S_{1}+1)\) are of order \(b\times b; Z_{i}=Z_{S_{1}+1}-V_{1}-V_{0};i=1,2,\ldots ,s_{1}; Z_{i}=Z_{S_{1}+1}-V_{1};i=s_{1}+1,s_{1}+2,\ldots ,S_{1}; Z_{a}=Z_{S_{1}+1}-2V_{0}+(\lambda _{1}p)I_{b}; D_{a}=D_{2a}+C_{1}-G-M_{1}; D_{1a}=D_{a}+F; D_{0}=D_{2a}^{'}+C_{1}; D_{2a}^{'}=D_{2a};Z_{b}=Z_{a}+\hat{M_{1}}-\hat{M_{2}}; D_{b}=D_{2b}-G+C_{1}-M_{1}+M_{2}; D_{1b}=D_{b}+F; D_{2b^{'}}=D_{2b}+C_{1}-M_{1}+M_{2}-C_{2};C_{1}=\mu _{1}I_{a_{1}};C_{2}=\mu _{2}I_{a_{1}}\)
The elements of matrix \(Z_{S_{1}+1}\) represents the transitions from \((n_{1},n_{2},S_{1}^{*},j_{2},l) \xrightarrow \; (n_{1},n_{2},S_{1}^{*},j_{2},l)\) where \(n_{1},n_{2}\) represents the number of customers in the pool and in the buffer. \(S_{1}^{*},j_{2}\) represents the residual inventory level of commodity-1 and commodity-2. l represents the state of the server.
3.3 Steady state analysis
To obtain the stability condition, we examine the Markov chain \(\{Y(t);t\ge 0\} =\{(N_{2}(t),J_{1}(t),J_{2}(t),L(t));t\ge 0\}\) on the finite state space \(\{(n_{2},0,0,0); 0\le n_{2}\le M; M\ge 1\} \bigcup \{(0,j_{1},j_{2},0); j_{1}=0,1,2,\ldots , S_{1},S_{1}^{*}; j_{2}=0,1,2,\ldots , S_{2},S_{2}^{*}\} \bigcup \{(n_{2},j_{1},j_{2},l);j_{1}=0,1,2,\ldots , S_{1},S_{1}^{*}; j_{2}=0,1,2,\ldots , S_{2},S_{2}^{*};0\le n_{2}\le M; M\ge 1;l=1,2\}\). Let \(y=(y_{0}, y_{1}, y_{2},\ldots ,y_{2(M+1)})\) represent the steady state probability vector of this Markov chain, and \(y_{0}=(y_{0}(1),\ldots , y_{0}(M+1)), y_{i}=(y_{i}(1), y_{i}(2),\ldots , y_{i}(a_{1}))\),for \(i=1,2,\ldots , 2(M+1)\). Infinitesimal generator of \(\{Y(t);t\ge 0\}\) is \(B=B_{0}+B_{1}+B_{2}\) where
Then y satisfies
where e is a column vector of 1’s.
Substituting the values of y and B in equation (2), we get the following sets of equations.
Solving the above set of equations, (4) and (5), we get
where,
for \(i=3,4,\ldots ,M;\)
We get all values of \(y_{i},i=2,3,\ldots ,2(M+1)\) in terms of \(y_{1}\) and \(y_{0}\).
From equation (3), we get \(y_{0}=-y_{1}({\mathcal {A}}_{1}{\mathcal {A}}^{-1}_{0}),\) where
\({\mathcal {A}}_{0}=D_{11}+\sum ^{M+1}_{i=2} K_{i}{\hat{C}}_{i}+\sum ^{2(M+1)}_{i=M+2} K_{i}\hat{{\hat{C}}}_{i}\) and
\({\mathcal {A}}_{1}={\hat{C}}_{1}+\sum ^{M+1}_{i=2} L_{i}{\hat{C}}_{i}+\sum ^{2(M+2)}_{i=M+2} L_{i}\hat{{\hat{C}}}_{i}\) and \(y_{1}\) can be determined from the normalizing condition \(ye=1,\) and we have
\(y_{1}[-{\mathcal {A}}_{1}{\mathcal {A}}^{-1}_{0}+I+\sum ^{2\,M+2}_{i=2} (-{\mathcal {A}}_{1}{\mathcal {A}}^{-1}_{0})K_{i}+L_{i})]e=1\)
3.4 Condition of stability
In this section we provide an implicit stability condition of the system which is given in the following lemma.
3.4.1 Lemma
The queueing inventory system described above is stable if and only if
Proof: The LIQBD description of the model shows that the queueing inventory system is stable (see [22]) if and only if \(yB_{0}e<yB_{2}e\). From the value of y computed from the previous section, we can see that this condition reduces to (7).
3.5 Steady state probability vector
In this section we compute the steady state probability vectors of the system. Assume that the stability condition in Sect. 3.4.1 is satisfied, we give an outline of the calculation of the steady state probability vector of the sytem. Let z denotes the steady state probability vector of the generator Q. Then z satisfies the condition
Partition \(z = (z_{0}, z_{1},z_{2},\ldots ).\) Then the subvectors in z are, \(z_{n_{1}} = \{z_{n_{1}}(n_{2},0,0,0);0\le n_{2}\le M;\) except for the case both \(n_{1}=0\) and \(n_{2}=0\}\bigcup \{z_{n_{1}} (0,j_{1},j_{2},0);0\le j_{1}\le S_{1},S^{*}_{1}; 0\le j_{2}\le S_{2},S^{*}_{2} \} \bigcup \{z_{n_{1}} (n_{2},j_{1},j_{2},l);0\le n_{2}\le M;0\le j_{1}\le S_{1},S^{*}_{1}; 0\le j_{2}\le S_{2},S^{*}_{2}; M\ge 1;l=1,2\}\) for \(n_{1}\ge 0.\) We see that, the steady state probability vector \(z=(z_{0},z_{1},z_{2},\ldots )\) satisfies the matrix geometric solution \(z_{n_{1}}= z_{1} R^{n_{1}-1}; n_{1}\ge 2\). One can refer [22] for details. Here R is the minimal non-negative solution to the matrix quadratic equation: \(R^2B_{2}+RB_{1}+B_{0}=0\) and the vectors \(z_{0}\) and \(z_{1}\) are given by the boundary equations:
\(z_{0}B_{00}+z_{1}B_{10}=0 z_{0}B_{01}+z_{1}B_{1}+z_{2}B_{2}=0.\) The normalizing condition (8) gives
\(z_{0}[I-B_{01}(B_{1}+RB_{2})^{-1}(I-R)^{-1}e] = 1\)
4 System performance measures
In this section, we derive performance measures of the system under the steady state.
1) Expected number of type-I (non priority) customers in the system
2) Expected number of type-II ( priority) customers in the system
3) Expected inventory level of commodity-1
4) Expected inventory level of commodity-2
5) Probability that the server is busy processing a demand of commodity-1 alone
6) Probability that the server is busy processing a demand of commodity-2 alone
7 (a) Server idle probability
7 (b) Probability that the server is busy
8 (a) Expected loss rate of non priority customers in the system
8 (b) Expected loss rate of priority customers in the system
9 (a) Expected number of old items removed on replenishment due to realization of common lifetime of commodity-1,
9 (b ) Expected number of old items removed on replenishment due to realization of lead time of commodity-1,
10 (a) Expected number of old items removed on replenishment due to realization of common lifetime of commodity-2,
10 (b ) Expected number of old items removed on replenishment due to realization of leadtime of commodity-2,
11(a) Expected reorder rate of commodity-1
11(b) Expected reorder rate of commodity-2
4.1 Analysis of cycle time for commodity-1
A cycle time for commodity-1 is defined as the time starting from maximum inventory level \(S_{1}\) at an epoch, untill the next epoch of replenishment. That is, duration between two consecutive \(S_{1}\) to \(S_{1}\) or \(S_{1}^{*}\) transitions. For the computation of the expected duration of a cycle, we assume that the pool capacity is \(K>0\) (Sufficiently large). Now consider the Markov Chain \(Z_{1}(t)=\{(N_{4}(t),N_{2}(t),I_{1}(t),I_{2}(t),L(t)); t\ge 0\}\) over the finite state space \(\{(n_{4},n_{2},j_{1},j_{2},l); 0\le n_{4}\le K; 0\le n_{2}\le M; M\ge 1; 0\le j_{1}\le S_{1},S^{*}_{1} \;; 0\le j_{2}\le S_{2},S^{*}_{2}; l=1,2\}\bigcup \{(n_{4},n_{2},0,0,0); 0\le n_{4}\le K; 0\le n_{2}\le M \}\bigcup \{(0,0,j_{1},j_{2},0); 0\le j_{1}\le S_{1},S^{*}_{1}; 0\le j_{2}\le S_{2},S^{*}_{2} \} \bigcup \Delta \beta _{1}.\) Here \(N_{4}(t)\) is the number of customers in the finite pool and \(\Delta \beta _{1}\) is an absorbing state due to realization of lead time of commodity-1. Let \(a_{6}= K a_{4}+ a_{5}.\) The infinitesimal generator of \(\{Z_{1}(t)\;;t\ge 0\}\) is of the form \(Z_{1}=\begin{bmatrix}\ {\hat{\tau }}_{1}&{}{\hat{\tau }}_{1}^{0}&{} \\ \varvec{0}&{}\varvec{0}\end{bmatrix}\) where
Here \(A_{c}\) is a zero column vector with dimension \(M\times 1, A_{e}\) is a zero column vector with dimension \((S_{2}+2)(S_{1}-s_{1}+1)\times 1. A_{h}\) is a column vector with elements \(\beta _{1}\) and its dimension is \((M+1)\times 1\).
(a) The distribution of the cycle time of commodity-1 is of phase type with representation \((\alpha ,\hat{\tau _{1}})\) where \(\alpha =(\alpha _{S_{1}},0,0,\ldots ,0); \alpha _{S_{1}}= \{(C{z_{0}}(n_{2},S_{1},j_{2},0),C{z_{1}}(n_{2},S_{1},j_{2},l),\ldots ,C{z_{K}}(n_{2},S_{1},j_{2},l)); 0\le j_{2} \le S_{2},S^{*}_{2}; 0 \le n_{2} \le M; l=1,2\}\) and \(C= [ \sum ^{K}_{n_{1}=0}\sum ^{M}_{n_{2}=0} \sum ^{S^{*}_{2}}_{j_{2}=0}\sum ^{2}_{l=1}z_{n1}(n_{2},S_{1},j_{2},l) ]^{-1}\) (b) The mean cycle length of commodity-1 is\(\eta _{1}= -\alpha \hat{\tau _{1}}^{-1}e,\) where e is a column vector of \(1^{'}s\) with appropriate order.
In a similar way we can write the cycle time for commodity-2.
4.2 Average waiting time of a priority (type-2) customer
Here, we calculate the average waiting time of a priority customer. We consider the Markov process \(Z_{2}(t)=\{(N^{'}_{2}(t), I_{2}(t)); t\ge 0 \}\), where \(N^{'}_{2}(t)\) is the rank of the tagged customer in the buffer at time t. The rank \(N^{'}_{2}(t)\) of the tagged customer is j (finite) if he is the jth customer in the queue at time t. His rank decreases to one as the customers ahead of him leave the system after completing service. The statespace of the process is \(\{(n,i_{2}); 1\le n\le j\;;j\le M\;;0\le i_{2} \le S_{2},S^{*}_{2}\}\bigcup \{\Delta \}\), where \(\{\Delta \}\) is the absorbing state which shows that the marked customer is selected for service. The infinitesimal generator of\(\{Z_{2}(t);t\ge 0 \}\) is of the form \(Z_{2}=\begin{bmatrix}\ {\tau }_{2}&{}{\tau }^{0}_{2} \\ \varvec{0}&{}\varvec{0}\end{bmatrix}\) where
\(W_{2}=W+W_{1}; W_{3}\) is a column vector of order \((S_{2}+1) \times 1\) whose elements are \(\mu _{2}\). The elements of matrix W represents the transitions from \((r,i_{2}) \xrightarrow \;(r,j_{2})\), where r is the rank of the tagged customer in the buffer, \(i_{2}, j_{2}\) represents the residual inventory level of commodity-2.
Now, the waiting time of a type-2 customer, who enters the queue as the pth customer is the time until absorption of the Markov chain\(\{Z_{2}(t); t\ge 0\}\). This random duration follows a phase type distribution. Thus the average waiting time of the pth customer is a column vector \(\eta _{p}=-\tau _{2}^{-1}e.\)
Hence the average waiting time of a general (type-2) customer in the system is
\(E_{W_{2}}= \sum ^{\infty }_{n_{1}=0}\sum ^{M}_{p=1} y_{n_{1}}(p)\eta _{p},\) where
4.3 Expected time to reach zero inventory level of commodity-1 in a cycle
Here we compute the expected time to reach zero inventory of commodity-1 in a cycle. Starting from the maximum inventory level \(S_{1}\), the inventory level of commodity-1 becomes zero, either by service completion when the inventory is left with a single unit or by common lifetime realization. We consider the Markov chain \(Z_{3}(t)=\{(N_{4}(t),N_{2}(t),I_{1}(t),I_{2}(t),l);t\ge 0 \}.\) Its state space is \(\{(n_{4},n_{2},i_{1},i_{2},l);0 \le n_{4}\le K;0 \le n_{2}\le M; 0\le i_{1}\le S_{1},S^{*}_{1};0\le j_{2}\le S_{2},S^{*}_{2};l=1,2 \}\bigcup \{(n_{4},n_{2},0,0,0); 0 \le n_{4}\le K; 0\le n_{2} \le M\} \bigcup \{(0,0,j_{1},j_{2},0); 0\le j_{1}\le S_{1},S^{*}_{1}; 0\le j_{2}\le S_{2},S^{*}_{2} \}\bigcup \Delta \mu _{1} \bigcup \Delta _{CLT-1},\) where \(\Delta \mu _{1}\) is an absorbing state consequent to the replenishment order placed for commodity-1 due to service completion and \(\Delta _{CLT-1}\) is an absorbing state consequent to the replenishment order placed due to realization of common lifetime of commodity-1. The infinitesimal generator of \(\{Z_{3}(t); t \ge 0\}\) is of the form \(Z_{3}=\begin{bmatrix}\tau _{3}&{}\tau ^{o}_{\mu _{1}}&{}\tau ^{o}_{CLT-1}\\ \varvec{0} &{}\varvec{0}&{}\varvec{0}\end{bmatrix}\) where
,where T stands for the transpose of a matrix.
Let the initial distribution of the chain is \(\gamma = (\gamma _{S_{1}},0,0,\ldots ,0),\) where \(\gamma _{S_{1}}=\{(C{z_{0}(n_{2},0,j_{2},0),C{z_{1}}(n_{2},0,j_{2},l),\ldots C{z_{K}}(n_{2},0,j_{2},l));0\le j_{2}\le S_{2},S^{*}_{2};0\le n_{2}\le M};l=1,2\}\) and \(C =[ \sum ^{K}_{n_{1}=0}\;\;\sum ^{M}_{n_{2}=0} \sum ^{S^{*}_{2}}_{j_{2}=0} \sum ^{2}_{l=1}z_{n_{1}}(n_{2},0,j_{2},l)]^{-1}\). The distribution of time till absorption to state zero starting from a replenishment epoch is of phase type with representation \((\gamma , \tau _{3}).\)
(a) Probability that the inventory level becomes zero before realization of common lifetime
\(=-\gamma \tau ^{-1}_{3} \tau ^{0}_{\mu _{1}}\)
(b) Probability that the common lifetime realizes before inventory level becomes zero
\(=-\gamma \;\tau ^{-1}_{3} \; \tau ^{0}_{CLT-1}\)
(c) Expected time to reach zero inventory level of commodity-1 in a cycle
=\(-\gamma \tau ^{-1}_{3}e\)
In a similar way we can find the expected time to reach zero inventory level of commodity-2 in a cycle
5 Numerical illustrations
5.1 Sensitivity analysis on performance measures
In this section, some numerical examples are presented to show the impact of some parameters on the performance measures of the system (i.e. sensitivity analysis).
5.1.1 Effect of \(\beta _{1}\) and \(\beta _{2}\) on various performance measures
We fix the values of the parameters as \(\beta _{2}=6;\mu _{1}=3.2;\mu _{2}=2.1;\gamma _{1}=7;\gamma _{2}=5; p=1/3;\lambda _{1}=1.5;\lambda _{2}=3.5;M=3; (s_{1}, S_{1})=(6,8)\;;(s_{2}, S_{2})=(5,8)\) and examine the effect of \(\beta _{1}\) on various performance measures. From Table 1, we can see that when lead time parameter of commodity-1 increases, the expected number of non-priority customers and their average loss rate decreases. Similarly fixing the values of the parameters as \(\beta _{1}=4;\mu _{1}=3.2; \mu _{2}=2.1;\gamma _{1}=7;\gamma _{2}=5; p=1/3;\lambda _{1}=1.5;\lambda _{2}=3.5;M=3;(s_{1}, S_{1})=(6,8);(s_{2}, S_{2})=(5,8)\), from Table 2 we can see that when lead time parameters of commodity-2 increases, the expected number of priority customers, and their average loss rate decreases.
5.1.2 Effect of \(\gamma _{1}\) and \(\gamma _{2}\) on various performance measures
Fixing the values of the parameters as \(p=1/3; (s_{1},S_{1})=(6, 8);(s_{2},S_{2})=(5,8);M=3;\beta _{1}=3;\beta _{2}=2; \mu _{1}=3.2; \mu _{2}=2.1;\lambda _{1}=1.5;\gamma _{2}=2;\lambda _{2}=5.2,\) we can see from Table 3that the CLT parameter \(\gamma _{1}\) increases, the expected reorder rate of commodity-1 increases, as expected. Similarly fixing the values of the parameters as \(p=1/3; (s_{1},S_{1})=(6, 8);(s_{2},S_{2})=(5,8);M=3;\beta _{1}=3;\beta _{2}=2; \mu _{1}=3.2; \mu _{2}=2.1;\lambda _{1}=1.5;\gamma _{1}=2;\lambda _{2}=5.2\), we can see from Table 4 that the re-order rate of commodity-2 increases.
5.1.3 Effect of \(\lambda _{1}\) and \(\lambda _{2}\) on various performance measures
Fix the values of the parameters as \(p=1/3; (s_{1},S_{1})=(6, 8);(s_{2},S_{2})=(5,8);M=3;\beta _{1}=5;\beta _{2}=7; \mu _{1}=3.2; \mu _{2}=2.1;\gamma _{1}=8;\gamma _{2}=7;\lambda _{2}=3\), we can see from Table 5 that as \(\lambda _{1}\) increases, the expected number of non priority customers and their loss rate increases. Similary to see the effect of the arrival rate of priority customers, we fix the values of the parameters as \(p=1/3; (s_{1},S_{1})=(6, 8);(s_{2},S_{2})=(5,8);M=3;\beta _{1}=5;\beta _{2}=12; \mu _{1}=3.3; \mu _{2}=2.5;\lambda _{1}=3\;;\;\gamma _{1}=7;\gamma _{2}=8\). Then from Table 6, we can see that the expected number of non-priority customers decreases and the expected loss rate increases as \(\lambda _2\) increases, and also, the expected loss rate of priority customers increases.
5.1.4 Effect of \(\mu _{1}\) and \(\mu _{2}\) on various performance measures
Here we study the effect of the service time parameters on the system performance measures. Fixing the parameter values as \(p=1/3; (s_{1},S_{1})=(6, 8);(s_{2},S_{2})=(5,8);M=3;\beta _{1}=5;\beta _{2}=12; \lambda _{1}=1.5; \mu _{2}=2.5\;;\gamma _{1}=7\;;\;\gamma _{2}=8;\lambda _{2}=3.5\) and observing the effect of \(\mu _{1}\) on the performance measures, from Table 7 we can see that the expected number of non-priority customers and their average loss rate decreases. Similarly, if we fix \(p=1/3; (s_{1},S_{1})=(6, 8);(s_{2},S_{2})=(5,8);M=3;\beta _{1}=5;\beta _{2}=12; \mu _{1}=3.2; \lambda _{2}=3.5\;;\lambda _{1}=1.5\;;\;\gamma _{1}=7;\gamma _{2}=8\) then from Table 8 we can see that as \(\mu _{2}\) increases the expected number of non-priority customers and their average loss rate increases as expected.
5.2 Cost analysis
In this section we analyze a cost function related with the model under study to obtain the optimal values of the control parameters. Here our objective is to find the optimal values of the control parameters \(s_{i}, i=1, 2.\) For that we construct a total expected cost function with the following costs in to consideration.
\(\psi _{1}\)—Cost of holding a type-1 customer per unit per unit of time in the pool.
\(\psi _{2}\)—Cost of holding a type-2 customer per unit per unit of time in the buffer.
\(\chi _{i}\)—Cost of holding inventory per unit of time for commodity-\(i, i=1, 2.\)
\(\phi _{i}\)—Cost due to type-i customer loss per unit of time, \(i= 1, 2.\)
\(\theta _{i}\)—Cost due to removal of commodity \(-i,i=1, 2.\)
\(\delta _{i}\)—Purchase price per unit for commodity-\(i, i=1, 2.\)
The total expected cost per unit time is given by
\(T(s_{1},s_{2}) = \psi _{1}.E_{1}+\psi _{2}.E_{2}+\chi _{1}.EI_{1}+\chi _{2}.EI_{2}+\phi _{1}.EL_{1}+\phi _{2}.EL_{2}+\theta _{1}.(EO_{C1}+EO_{L1})+\theta _{2}.(EO_{C2}+EO_{L2})+\delta _{1}.ER_{1}+\delta _{2}.ER_{2}.\)
This function is not easy to analyze analytically, we look the convexity of the cost function numerically. For the given fixed values of the parameters \(\beta _{1}=5;\beta _{2}=12;\mu _{1}=3.2; \mu _{2}=2.1;\gamma _{1}=7;\gamma _{2}=8; p=1/3;\lambda _{1}=1.5;\lambda _{2}=5.2;M=3,\) fixed costs \(\psi _{1}= 2;\psi _{2}=3;\chi _{1}=1.5;\chi _{2}=2.5;\phi _{1}=1.5;\phi _{2}=2;\theta _{1}=3;\theta _{2}=4;\delta _{1}=1;\delta _{2}=1.2\) and different values of \(s_{i}, i=1,2.\) we obtained the total expected cost, and are given in the Table 9. The numerical values shows that \(T(s_{1},s_{2})\) is minimum when \((s_{1},S_{1})=(3,8)\) and \((s_{2},S_{2})=(3,8).\) We can observe this from Fig. 1.
5.3 Sensitivity analysis of the cost function
In this section we analyze the effect of the CLT parameters and the lead time parameters on the cost function. To examine this, we fix the costs as \(\psi _{1}= \$2;\psi _{2}=\$3;\chi _{1}=\$1.5;\chi _{2}=\$2.5;\phi _{1}=\$1.5;\phi _{2}=\$2;\theta _{1}=\$3;\theta _{2}=\$4;\delta _{1}=\$1;\delta _{2}=\$1.2\)
5.3.1 Effect of CLT parameters and Lead time parameters on the cost function
Here, we study the effect of common lifetime parameters \(\gamma _{i}, i=1,2\) on total expected cost function. We fix the parameters of the model as \(p=1/3; (s_{1},S_{1})=(6,8);(s_{2},S_{2})=(5,8);M=3;\beta _{1}=5;\beta _{2}=12; \mu _{1}=3.2; \mu _{2}=2.1;\lambda _{1}=1.5;\gamma _{2}=8;\lambda _{2}=5.2\)
and examined the effect of \(\gamma _{1}\), we can see from Table 10 that as \(\gamma _{1}\) increases, the total expected cost per unit time increases. Similarly we fix \(p=1/3; (s_{1},S_{1})=(6,8);(s_{2},S_{2})=(5,8);M=3;\beta _{1}=5;\beta _{2}=12; \mu _{1}=3.2; \mu _{2}=2.1;\lambda _{1}=1.5;\gamma _{1}=8;\lambda _{2}=5.2,\) from Table 11, we can see that as \(\gamma _{2}\) increases, the total expected cost per unit time increases. Similarly, fixing the parameters as \(p=1/3; (s_{1},S_{1})=(6,8);(s_{2},S_{2})=(5,8);M=3;\beta _{2}=12; \mu _{1}=3.2; \mu _{2}=2.1;\lambda _{1}=1.5;\gamma _{1}=7;\gamma _{2}=8;\lambda _{2}=5.2\) and observing the effect of \(\beta _{1}\), from Table 12 we can see that, \(\beta _{1}\) increases the total expected cost per unit time increases. Similary fixing the parameters as \(p=1/3; (s_{1},S_{1})=(6, 8);(s_{2},S_{2})=(5,8);M=3;\beta _{1}=3; \mu _{1}=3.2; \mu _{2}=2.1;\lambda _{1}=1.5;\gamma _{1}=2;\gamma _{2}=4;\lambda _{2}=5.2\) and observing the effect of \(\beta _{2}\), from Table 13 we can see that, \(\beta _{2}\) increases the total expected cost per unit time increases.
6 Conclusion
In this paper, we have studied a two commodity queueing inventory system at a service facility with a random common lifetime, random lead time for each of the commodities, positive service time, and two classes of customers. Also, there is a finite capacity buffer for the priority customers and an infinite pool for the non-priority customers. Matrix geometric method is used for finding steady-state system size probability vectors. We have studied various system characteristics such as expected number of customers, expected loss rate of customers, expected waiting time of priority customers, expected inventory levels, expected reorder rates for commodities, expected time to reach zero inventory in a cycle and also analyzed the mean cycle time for both commodities. A cost function is constructed and analyzed numerically to find the optimum values of the control parameters \(s_{i}\), i = 1, 2. Also, we have presented numerical illustrations to show the effect of common lifetime parameters and lead time parameters on the cost function. The present work can be extended by using general distributions for lead time and common lifetime.
References
Krishnamoorthy, A., Varghese, T.: A two commodity inventory problem. Int. J. Inf. Manage. Sci. 5(3), 55–70 (1994)
Krishnamoorthy, A., Varghese, T.: On a two-commodity inventory problem with markow shift in demand. OPSEARCH-New Delhi 32(2), 44–44 (1995)
Yadavalli, V.S., Van Schoor, C.D.W., Udayabaskaran, S.: A substitutable two-product inventory system with joint-ordering policy and common demand. Appl. Math. Comput. 172(2), 1257–1271 (2006)
Sivakumar, B., Anbazhagan, N., Arivarignan, G.: Two-commodity inventory system with individual and joint ordering policies and renewal demands. Stoch. Anal. Appl. 25(6), 1217–1241 (2007)
Sivakumar, B.: Two-commodity inventory system with retrial demand. Eur. J. Oper. Res. 187(1), 70–83 (2008)
Benny, B., Chakravarthy, S., Krishnamoorthy, A.: Queueing-inventory system with two commodities. J. Indian Soc. Probab. Stat. 19(2), 437–454 (2018)
Ozkar, S., Uzunoglu Kocer, U.: Two-commodity queueing-inventory system with two classes of customers. Opsearch 58(2), 234–256 (2021)
Jeganathan, K., Reiyas, M.A., Selvakumar, S., Anbazhagan, N., Amutha, S., Joshi, G.P., Jeon, D., Seo, C.: Markovian demands on two commodity inventory system with queue-dependent services and an optional retrial facility. Mathematics. 10(12), 2046 (2022)
Nahmias, S.: Perishable inventory theory: a review. Oper. Res. 30(4), 680–708 (1982)
Nahmias, S.: Perishable Inventory Systems. Springer, Boston (2011)
Goyal, S.K., Giri, B.C.: Recent trends in modeling of deteriorating inventory. Eur. J. Oper. Res. 134(1), 1–16 (2001)
Sivakumar, B., Anbazhagan, N., Arivarignan, G.: A two-commodity perishable inventory system. ORiON. 21(2), 157–172 (2005)
Yadavalli, V.S.S., Adetunji, O., Sivakumar, B., Arivarignan, G.: Two-commodity perishable inventory system with bulk demand for one commodity articles. S. Afr. J. Ind. Eng. 21(1), 137–155 (2010)
Bakker, M., Riezebos, J., Teunter, R.H.: Review of inventory systems with deterioration since 2001. Eur. J. Oper. Res. 221(2), 275–284 (2012)
Jeganathan, K.: Two commodity perishable inventory system with negative and impatient customers, postponed demands and a finite population. Int. J. Appl. Sci. Eng. Res. 3(1), 265–280 (2014)
Duong, L.N., Wood, L.C., Wang, W.Y.: A multi-criteria inventory management system for perishable and substitutable products. Procedia Manuf. 2(2), 66–76 (2015)
Suganya, R., Nkenyereye, L., Anbazhagan, N., Amutha, S., Kameswari, M., Acharya, S., Joshi, G.P.: Perishable inventory system with n-policy, map arrivals, and impatient customers. Mathematics. 9(13), 1514 (2021)
Lian, Z., Liu, L., Neuts, M.F.: A discrete-time model for common lifetime inventory systems. Math. Oper. Res. 30(3), 718–732 (2005)
Chakravarthy, S.R.: An inventory system with markovian demands, phase type distributions for perishability and replenishment. Opsearch 47(4), 266–283 (2010)
Shajin, D., Benny, B., Deepak, T., Krishnamoorthy, A.: A relook at queueing-inventory system with reservation, cancellation and common life time. Commun. Appl. Anal. 20(2), 545–574 (2016)
Krishnamoorthy, A., Benny, B., Shajin, D.: A revisit to queueing-inventory system with reservation, cancellation and common life time. Opsearch 54(2), 336–350 (2017)
Neuts, M.: Matrix Geometric Solutions in Stochastic Models: An Algorithmic Approach. The John Hopkins University Press, Baltimore (1981)
Funding
No funding was receieved for conducting this study.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no relevant financial or non-financial interests to disclose.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Dissa, S., Ushakumari, P.V. Two commodity perishable queueing inventory system with random common lifetime of commodities and positive lead time. OPSEARCH 61, 809–834 (2024). https://doi.org/10.1007/s12597-023-00707-3
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12597-023-00707-3