Two-commodity queueing-inventory system with phase-type distribution of service times

Abstract

A two-commodity queueing-inventory system with phase-type service times and exponential lead times is considered. There are two types of customers; Type 1 and Type 2. Demands from each customer type occur independently according to a Poisson process with different rates whereas the service times follow a phase-type distribution. Type 1 customers have a non-preemptive priority over Type 2 customers. We assume a finite waiting space for Type 1 customers whereas there is no limit on the waiting room for Type 2 customers. Type i customers demand only commodity i, $i=1,2$. For the ith commodity, $S_i$ and $s_i$ represent, respectively, the maximum inventory level and the reorder level. Whenever the inventory level of ith commodity drops to $s_i$, an order is placed from retailer-i to make the inventory level $S_i$. The lead times of the commodities are exponentially distributed with different parameters. When there is a Type i customer waiting in the queue, if the inventory level of ith commodity is zero (or reaches zero), a decision of immediate purchase is made so as not to lose the waiting customer. The queueing-inventory model in the steady-state is analyzed using the matrix-geometric method. The system performance is examined for different values of parameters. Besides, an optimization study is performed for some system parameters.

1 Introduction

Multi-commodity inventory systems are commonly encountered in many real-life situations and are complex systems due to the multitude of items stocked and their coordinated actions. The main problem is the interaction of the reorder points and reorder times for each individual item. The individual ordering policy and the joint ordering policy are commonly used in the inventory systems depending on whether the items share the same storage space and also the same transportation facilities. We refer to the papers in Balintfy (1964), Federgruen et al. (1984), Kalpakam and Arivarignan (1993) and Silver (1974) for the multi-item inventory systems and the ordering policies.

A two-commodity inventory system is discussed by Krishnamoorthy et al. (1994). The shortage is not allowed in the system with zero lead time. Demand occurs either one unit of commodity-1 with probability $p_1$ or one unit of commodity-2 with probability $p_2$ or one unit each of commodities 1 and 2 with probability $p_{12}$. The inventory problem is formulated by using the semi-Markov process. Krishnamoorthy and Varghese (1994) examines the problem in Krishnamoorthy et al. (1994) with Markov-shift in demand for the type of commodity. They use Markov renewal theory for the analysis and perform an optimization study. Using the results from the Markov renewal theory, Sivasamy and Pandiyan (1998) examines the problem defined by Krishnamoorthy and Varghese (1994) with the application of the filtering technique. The similar three-type-of-demand for the two commodities is considered also by Yadavalli et al. (2010). They investigate the inventory system with perishable items where the lead times are phase-type distributed. All three types of demands occur according to a Markovian arrival process. The lifetime of each commodity has an exponential distribution with different parameters. The system is characterized by a continuous-time Markov chain and a steady-state analysis is presented. Anbazhagan and Arivarignan (2000) analyzes a two-commodity inventory system where demands for each commodity occur according to independent Poisson processes with parameters $\lambda _1$ and $\lambda _2$. They consider a coordinated ordering policy in which the reorder level is fixed as $s_i$ ($i=1,2$) for the commodity-i and an order is placed for $Q_i (=S_i-s_i)$ items for the commodity-i when both inventory levels are less than or equal to their respective reorder levels. A two-commodity inventory system with the same demand process is examined by Anbazhagan and Arivarignan (2001). They propose a joint replenishment policy in which an order is placed for both the commodities when the total net available inventory is equal to s and the ordering quantity occurs $Q_i (=S_i-s)$ items for the commodity-i. In Anbazhagan and Kumaresan (2012) and Yadavalli et al. (2004), it is also considered a two-commodity inventory system with fixed individual and joint reorder levels. A combination of individual and joint ordering policies is examined by Sivakumar et al. (2007) where demands occur according to the renewal process.

In Anbazhagan and Vigneshwaran (2010), Anbazhagan et al. (2012) and Anbazhagan et al. (2015), it is considered that commodities are substitutable. That is, if the inventory level of one commodity reaches zero, then any demand for this commodity will be satisfied by the item of the other commodity. Yadavalli et al. (2006) discusses a two-commodity inventory system where demands occur according to Poisson processes with different parameters. However, it is assumed that the demand for the first commodity requires one unit of the second commodity in addition to the first commodity, with probability $p_1$. Similarly, the demand for the second commodity requires one unit of the first commodity in addition to the second commodity with probability $p_2$. Sivakumar (2008) and Anbazhagan and Jeganathan (2013) analyze two-commodity retrial inventory systems with different ordering policies in which demands for each commodity occur to independent Poisson processes with different parameters. In both studies, the constant retrial policy is considered. When there are i demands in the orbit, a signal is sent out according to an exponential distribution which does not depend on the number of the orbit. Sivakumar (2008) consider that two commodities are substitutable. That is, at the time of zero stock of any one commodity, the other one is used to meet the demand. If the inventory level of both commodities is zero then any primary demand arrival enters into the orbit of infinite size. Anbazhagan and Jeganathan (2013) assumes that if the demand occurs for the first commodity, then one unit of the second commodity is supplied as a gift to the customer who ordered a unit of the first commodity. However, the opposite case is not valid; that is no first commodity is supplied as a gift for ordering a second commodity. If the inventory level of the first commodity is zero, thereafter any arriving primary demand for the first commodity enters into the orbit of finite size. In Sivakumar et al. (2006), it is investigated a two-commodity perishable inventory system with the Poisson demand process. The lifetime of each commodity is exponentially distributed with different parameters. Jeganathan (2014) examines a perishable inventory system with postponed demand with two different items; a major item (first commodity) and a gift item (second commodity). A two-commodity substitutable inventory system with postponed demand is also studied by Jeganathan et al. (2018). When the inventory level is zero, a customer takes in the offer of postponement with an independent Bernoulli trial.

The inventory problems have different types of customers are also of great importance. The following studies examine inventory systems with a single commodity and two-type of customers. Sapna Isotupa (2006) considers an inventory system with two types of customers; prioritized and ordinary. Demands from each type of customer arrive according to independent Poisson processes with different parameters. When inventory level is below s, demand for ordinary customers is not satisfied and lost. Also, when inventory levels are zero, demands due to both types of customers are assumed to be lost. The inventory system is analyzed by a continuous-time Markov chain. Liu et al. (2014) introduces a priority parameter distinctly from the study in Sapna Isotupa (2006). When the ordinary customers arrive, the system decides whether or not to offer service whereas when the prioritized customers arrive, they get service immediately. That is if $0<p<1$, when on-hand inventory drops to the predefined safety level, the ordinary customers will receive service with probability p. In Sapna Isotupa (2011) and Sapna Isotupa and Samanta (2013), there is a high priority customer class. When the inventory level is below a threshold level, the demands from high-priority customers are only satisfied and low priority demands are not met. An inventory system with two types of customers, high priority customers and low priority customers, is also studied by Sapna Isotupa (2015). A threshold rationing policy is employed, that is, if the on-hand inventory level is less than or equal to a critical level, k, and a demand occurs by a low priority customer, the demand is not met and results in a lost sale. The lost of a demand by a high priority customer is only occurs when inventory level is zero. They prove that there is an optimal policy where differentiating between customers and using a threshold rationing policy yields lower costs for the supplier and provides better service levels to both classes of customers when compared to the case of not differentiating between customers.

In most of the inventory models considered in the literature, demanded items are directly delivered from stock (if available). Demand occurred during stock-out periods either results in lost sales or is satisfied only after the arrival of the replenishments. Moreover, in classical inventory problems, the amount of time required for service is negligible. In contrast, in most real-life situations, a positive amount of time to serve the inventory is needed. Up to now, we have mentioned the two-commodity (or multi-commodity) inventory systems under different assumptions, but without queueing aspect. In queueing analysis, if the server is idle at the time of arrival, the customer is served immediately and leaves the system after the service. On the other hand, queueing-inventory systems deal with both an inventory problem and a queueing problem. If there is not enough inventory at the time of arrival, even the server is idle, the customer may leave the system without being served or may have to wait in the queue. These systems must take into account the inventory problems in the queueing concept. Queuing-inventory systems can be handled according to many features such as arrival/service processes, inventory policy implemented, shortage or lost sale assumption, if there is queue capacity or not, service interruption or vacation assumption, or perishability of items in inventory. We can put forward some important studies as follows. Schwarz et al. (2006) analyze the model with exponentially distributed service time and lead time and Poisson input of customers. The authors suggest the product form solution for the system state distribution under the assumption that customers do not join when the inventory level is zero. In their model, customers are provided an item from the inventory on completion of service. On the other hand, it can be some situations where the customer may not be served the item on completion of service. The situation is modelled by Krishnamoorthy et al. (2015). That is, the item is served with probability $\gamma$ at the end of a service and with probability $1-\gamma$ the item is not delivered to the customer. The model reduces to Schwarz et al. (2006) when $\gamma =1$. A queueing-inventory system with two parallel service facilities is examined in Deepak et al. (2008). Customers arrive to the system according to two independent Poisson processes and demand exactly one item from the inventory. There are two service counters manned by one server each. Server at counter i serves according to exponentially distributed time with different parameter. At both counters the same (s, S)-inventory policy is adopted and the lead time at counter i is exponentially distributed with different parameter. When the difference between the number of customers in the two queues reaches the quantity L, a batch of K customers transferred from the longer to the shorter queue. Simultaneously with the transfer of customers the authors also transfer inventoried items subject to its availability. Krishnamoorthy et al. (2016) suggest the a queueing-inventory system applicatiable in railway and airline reservation systems. An arrival customer is immediately taken for service or he joins the buffer with capacity S (also S is the maximum inventory level) depending on number of items in the inventory. If there is no item in the inventory, the arriving customer first queue up in a finite waiting space. When it overflows an arrival goes to an orbit of infinite capacity with probability p or is lost forever with probability $1-p$. Cancellation of sold items before its expiry is permitted. Inventory gets added through cancellation of purchased items, until the expiry time. Melikov et al. (2017) is one of the significant studies from the ordering policy point of view. The policy they propose enables variable order size, different from the classical (s, S) policy. They suppose that order size is variable and depends on the available inventory level. One customer class is assumed and joint distribution of inventory level and queue length is derived. For queueing-inventory systems we refer to the some interesting studies in Amirthakodi et al. (2015), Chakravarthy et al. (2017), Manuel et al. (2007) and Nair et al. (2015). Also, one can examine the brief review articles in Karthikeyan and Sudhesh (2016), Krishnamoorthy et al. (2011) and Krishnamoorthy et al. (2020).

Sivakumar et al. (2005) investigates a two-commodity perishable inventory system at a service facility and with a finite waiting room. The commodities are assumed both perishable and substitutable. The arrival of customers is considered to constitute a Poisson process with parameter $\lambda$. At the starting time of service, the arriving customer requires a single item of the first commodity with probability $p_1$ or a single item of the second commodity with probability $p_2$. The service times of both commodities are independent and exponentially distributed with parameters $\mu _i$ $(i = 1, 2)$. The reorder level for the commodity-i is fixed as $s_i$ and an order is placed for both commodities when both inventory levels are less than or equal to their respective reorder levels. The ordering quantity for the commodity-i is $Q_i~(= S_i-s_i)$ items. The lead time is assumed to be exponentially distributed. A two-commodity inventory system with a service facility and a finite waiting room is also examined by Gomathi et al. (2012). The arrivals occur according to a Poisson process with a parameter $\lambda$. An arrival may be an ordinary customer with probability p or a negative customer with probability of $q~(=1-p)$. The demands occur either one unit from the first commodity or one unit from the second commodity or one unit from each commodity. The service time and the lead time are assumed to be exponentially distributed. Benny et al. (2018) considers a two-commodity queueing inventory system in which the customers arrive according to a Poisson process, the service times and the lead times are exponentially distributed. Customers may require either one of the commodities or both commodities with some pre-determined probabilities. If the item demanded is not available, the customer leaves the system forever. If both items are demanded when only one of them is available, the available item is served to the customer. The queueing-inventory problem is modeled as a continuous-time Markov chain of the GI/M/1-type. A multi-commodity queueing inventory system with one essential and a set of m optional item(s) is introduced by Shajin et al. (2021). Once the service of an essential item is completed, the customer either departs from the system with probability p or goes for optional item(s) with probability $(1-p)$.

Considering that there are two types of customers, queueing-inventory systems are examined in the literature are include the assumption of a single commodity. Sivakumar and Arivarignan (2008) discusses a system in which the Type-1 customers are willing to wait for the delivery of their demanded items but the Type-2 customers are not. When the stock level is above s, the customers are not distinguished according to their type and their demanded items are delivered immediately. Once the inventory level drops to s, an order for $Q~(=S-s)$ items is placed, and only Type-2 customer demands are satisfied. Type-1 customers are asked to wait until the ordered items are received and their demand is satisfied immediately when the ordered items are received. The maximum number of Type-1 customers allowed to wait is fixed. Once the number of customers of Type-1 reaches a prefixed level, all Type-1 customers who are arriving thereafter are lost. Karthick et al. (2015) generalizes the system examined by Sivakumar and Arivarignan (2008). Once the inventory level drops to s, an order for $Q~(=S-s)$ items is placed, and only Type-2 customer demands are satisfied. Type-1 customers are sent to an orbit of infinite size. Zhao and Lian (2011) introduces an optimal service rule. When two classes of customers are present in the queue, the server needs to make a decision on who to serve first. Each customer requires exactly one item in the inventory for service and the service time follows an exponential distribution with parameter $\mu _i~(i=1,2)$.

To the best of our knowledge, the existing studies in the literature related to two-commodity queueing-inventory systems include only one type of customer. Moreover, only single commodity is assumed in the existing studies that examine the queueing-inventory systems with two types of customers. So far no study is encountered about the queueing-inventory systems including both two-commodity and two types of customers except Ozkar and Uzunoglu Kocer (2021). They analyze a two-commodity queueing-inventory system with two types of customers where Type-1 is a priority customer and Type-2 is the ordinary customer. Customers arrive according to a Poisson process with different parameters. The service times are exponentially distributed. The lead times are ignored, namely, the orders are immediately supplied. They adopt $(s_i,S_i)$, $i=1,2$, type replenishment policy for each commodity type, individually. That is, when the inventory level of Type-i customers drops to $s_i$, the order is given and the inventory level becomes $S_i$. The inventory levels in the system never becomes less than $s_i$. In other words, the shortage is not allowed in the system with zero lead time. The matrix geometric method is employed to analyze the system.

This study improves the paper in Ozkar and Uzunoglu Kocer (2021) as follows. (i) the service times follow a phase-type distribution; (ii) the lead times of the commodities are exponentially distributed with possibly different parameters; (iii) If an arriving Type-i customer in the idle system finds that the inventory level of the ith commodity is zero, the customer becomes lost. On the other hand, the Type-i customer joins in the queue even though his inventory level is zero when the server is busy with any customer; (iv) If the inventory of the customer to be taken into service is zero at time of the service completion, one purchase is made in order not to lose the customer waiting in the queue.

Chakravarthy (2020) considers queueing-inventory models with exponential service times where batch demands follow a Poisson process. The two models are discussed in Chakravarthy (2020). In Model 1, if any arriving customer finds the inventory level to be zero, he is be lost. In Model 2, the loss of customers is performed in the two ways. First, if an arriving customer in the idle system finds the inventory level to be zero, the customer is be lost, and secondly, the customers present at time of a service completion with zero inventory are all be lost. Chakravarthy and Rumyantsev (2020) analyzes the two models in Chakravarthy (2020) by considering MAP demands in batches and phase type service times. In sense of the loss of customers we pay attention to the Model 2 mentioned in Chakravarthy (2020) and Chakravarthy and Rumyantsev (2020). That is, whereas the first way keep in the item (iii), we change the second way by considering a local purchase to not lose the waiting customer in the item (iv).

We believe that the model described and the analysis provided in this study will be useful for various industrial companies since two types of customers, as well as two types of commodities, and also phase-type service times can be frequently observed in practice. Let us assume that a company will earn more from Type-1 customers compared to Type-2 customers. On the other hand, it will be more expensive to have items in the warehouse for these customers. So, it is important for the company to control the two types of commodities separately in the warehouse. Also, considering a service policy such that “the Type-1 customer who wants the commodity-1 has service priority over the Type-2 customer who wants the commodity-2” will not wrong. Since different type of customers pay different prices for the requested product, the management has an incentive to meet the demand of the customer who pays a higher price. The management’s objective is to meet the service requirements of the different customer classes while keeping costs low (maximizing profits).

• Customers can be considered in two classes as follows: Companies that make special production (Type-1) and companies that make ordinary production (Type-2). Type-1 customers can request new technology products (top quality, special product) from the warehouse, while Type-2 customers can request outdated products (medium quality, ordinary product).

• A firm that produces furniture may produce in two different types. Specially designed products (commodity-1) in line with customer demand and ordinary products for general buyers (commodity-2)

• A firm may produce items in two types of quality for sending to domestic and international companies. Therefore, international markets (export departments) can be considered as Type-1 customers and domestic markets (distribution company) as Type-2 customers.

The rest of the paper is organized as follows. In Sect. 2 the model description is presented. The steady-state analysis of the model is performed and some key system performance measures are derived in Sect. 3. Illustrative numerical examples, including an optimization problem, are discussed in Sect. 5. Finally, some concluding remarks are given in Sect. 6.

2 Model description

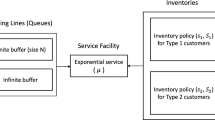
In this study, we analyze a queueing-inventory system with two-commodity and two classes of customers. Figure 1 describes the structure of the system.

Fig. 1

A two-commodity queueing-inventory system with two classes of customers

The assumptions of the queueing-inventory system under study are as follows.

• The queueing-inventory system includes two classes of customers; Type-1 customers are priority ones and Type-2 customers are ordinary ones.

• Type-1 customers have a non-preemptive priority over Type-2 customers. Upon completion of a service, the empty server offers service to a Type-1 customer; however, when there are no Type-1 customers waiting, the server serves a Type-2 customer if there is one present in the queue.

• There is a single server in the system and the customers are served on the basis of the first come first served (FCFS) without ignoring the priority relationship among the types of customers.

• There are two different inventory levels for each commodity class. Each customer in the queue requires one item for service from the related inventory. A served customer leaves the system and the inventory level decreases by one unit. It should be noted that the items in the inventory for Type-1 customers (commodity-1) are more expensive than those for Type-2 customers (commodity-2). Hence, setting priority to Type-1 customers will increase the earning.

• Demands from each customer class arrive independently according to a Poisson process with rates $\lambda _1$ and $\lambda _2$.

• Customers are not allowed to join the system when the inventory level of the demanded commodity is zero and the server is idle. However, customers join the system when the server is busy even though no excess inventory is available on hand. The reason is that during the service time of the customer even though the stock level reaches zero, there is a probability that the replenishments may arrive until the next customer is served.

• There is a local purchase option in order not to lose the customer waiting in the queue. That is if the inventory level reaches zero upon service is completed (or if the inventory level is zero), a local purchase is made for the next customer waiting in line. It is also assumed that replenishment of orders is made instantaneously and the order size is one when a local purchase is made.

• It is assumed a finite waiting space for Type-1 customers whereas the waiting space for Type-2 customers is infinite. Thus, it is possible for a Type-1 customer to be lost at the time of arrival due to the buffer being full. The buffer size is N.

• Service times follow a phase-type distribution with representation $({\varvec{\beta }},{\varvec{T}})$ of order n. The service rate is given by $\mu =[{{\varvec{\beta }}}(-{\varvec{T}})^{-1}{\varvec{e}}]^{-1}$.

• The inventory policy $(s_i,S_i)$ is adopted for the commodity-i, $i=1,2$, where $S_i$ and $s_i$ represent, respectively, the maximum inventory level and the reorder level, $s_i<S_i$. Once the inventory level for commodity-1 (commodity-2) drops to $s_1$ ($s_2$), an order is placed from the retailer-1 (the retailer-2), to make the inventory level reach its maximum level $S_1$ ($S_2$). This policy is also referred to as order up to S in Krishnamoorthy et al. (2015).

• The lead times follow an exponential distribution with parameters $\eta _1$ and $\eta _2$ for commodity-1 and commodity-2, respectively.

3 The steady-state analysis

The steady-state analysis of the queueing-inventory model described in Sect. 2 is performed in this section. Let $N_2(t), N _1(t), I_2(t), I_1(t)$, J(t) and K(t) denote, respectively, the number of Type-2 customers in the queue, the number of Type-1 customers in the queue, the inventory level of commodity-2, the inventory level of commodity-1, the state of the server and the phase of the service (if any), at time t. The state of the server is given by

$$\begin{aligned} J(t) = \left\{ \begin{array}{ll} 0 &{} \text {, if the server is idle,}\\ 1 &{} \text {, if the server is busy with Type-1 customer,}\\ 2 &{} \text {, if the server is busy with Type-2 customer.}\\ \end{array} \right. \end{aligned}$$

The process $\{ (N_2(t), N_1(t), I_2(t),I_1(t), J(t)), K(t),~~ t \ge 0 \}$ is a continuous-time Markov chain with state space given by

$$\begin{aligned} \Omega&=\{(0,0,i_2,i_1,0): 0\le i_2\le S_2,~0 \le i_1\le S_1 \} \\&\cup \{(n_2,n_1,i_2,i_1,1,k): n_2 \ge 0,~ 0 \le n_1 \le N,~ 0\le i_2\le S_2,~1\le i_1\le S_1,~ 1\le k \le n \} \\&\cup \{(n_2,n_1,i_2,i_1,2,k): n_2 \ge 0,~ 0 \le n_1 \le N,~ 1\le i_2\le S_2,~0\le i_1\le S_1,~ 1\le k \le n \} . \end{aligned}$$

The level $(0,0,i_2,i_1,0)$, of dimension $(S_1+1) (S_2+1)$, corresponds to the case when the server is idle, there is no waiting customer in the queue and the inventory level of the commodity-2 is $i_2$ whereas the inventory level of the commodity-1 is $i_1$.

The level $(n_2,n_1,i_2,i_1,1,k)$, of dimension $S_1(S_2+1)(N+1)n$, corresponds to the following case: there is a Type-1 customer in the servicing, there are $n_2$ Type-2 customers and $n_1$ Type-1 customers waiting in the queue, the inventory levels for the commodity-2 and the commodity-1 are $i_2$ and $i_1$, respectively, and the service is in one of n phases.

Similarly, the level $(n_2,n_1,i_2,i_1,2,k)$, of dimension $S_2 (S_1+1) (N+1)n$, corresponds to the case that a Type-2 customer is being served, there are $n_2$ Type-2 customers and $n_1$ Type-1 customers waiting in the queue, the inventory levels for the commodity-2 and the commodity-1 are $i_2$ and $i_1$, respectively, and the service is in one of n phases.

The transitions rates are listed as following:

• (1) Transitions due to the arrival of Type-1 customers.

  • (a) $(0,0,i_2,i_1,0)\rightarrow (0,0,i_2,i_1,1)$ with rate $\lambda _1\beta$ for $0\le i_2\le S_2$, $1\le i_1 \le S_1$.

  • (b) $(n_2,n_1,i_2,i_1,1)\rightarrow (n_2,n_1+1,i_2,i_1,1)$ with rate $\lambda _1 I_n$ for $n_2\ge 0$, $0\le n_1\le N-1$, $0\le i_2\le S_2$, $1\le i_1 \le S_1$.

  • (c) $(n_2,n_1,i_2,i_1,2)\rightarrow (n_2,n_1+1,i_2,i_1,2)$ with rate $\lambda _1 I_n$ for $n_2\ge 0$, $0\le n_1\le N-1$, $1\le i_2\le S_2$, $0\le i_1 \le S_1$.

• (2) Transitions due to the arrival of Type-2 customers.

  • (a) $(0,0,i_2,i_1,0)\rightarrow (0,0,i_2,i_1,2)$ with rate $\lambda _2\beta$ for $1\le i_2\le S_2$, $0\le i_1 \le S_1$.

  • (b) $(n_2,n_1,i_2,i_1,1)\rightarrow (n_2+1,n_1,i_2,i_1,1)$ with rate $\lambda _2 I_n$ for $n_2\ge 0$, $0\le n_1\le N$, $0\le i_2\le S_2$, $1\le i_1 \le S_1$.

  • (c) $(n_2,n_1,i_2,i_1,2)\rightarrow (n_2+1,n_1,i_2,i_1,2)$ with rate $\lambda _2 I_n$ for $n_2\ge 0$, $0\le n_1\le N$, $1\le i_2\le S_2$, $0\le i_1 \le S_1$.

• (3) Transitions due to the service of Type-1 customers.

  • (a) $(0,0,i_2,i_1,1)\rightarrow (0,0,i_2,i_1-1,0)$ with rate $T^0$ for $0\le i_2\le S_2$, $1\le i_1 \le S_1$.

  • (b) $(n_2,0,i_2,i_1,1)\rightarrow (n_2-1,0,i_2,i_1-1,2)$ with rate $T^0\beta$ for $n_2\ge 1$, $1\le i_2\le S_2$, $1\le i_1 \le S_1$.

  • (c) $(n_2,n_1,i_2,i_1,1)\rightarrow (n_2,n_1-1,i_2,i_1-1,1)$ with rate $T^0\beta$ for $n_2\ge 0$, $1\le n_1 \le N$, $0\le i_2\le S_2$, $2\le i_1 \le S_1$.

• (4) Transitions due to the service of Type-2 customers.

  • (a) $(0,0,i_2,i_1,2)\rightarrow (0,0,i_2-1,i_1,0)$ with rate $T^0$ for $1\le i_2\le S_2$, $0\le i_1 \le S_1$.

  • (b) $(n_2,0,i_2,i_1,2)\rightarrow (n_2-1,0,i_2-1,i_1,2)$ with rate $T^0\beta$ for $n_2\ge 1$, $2\le i_2\le S_2$, $0\le i_1 \le S_1$.

  • (c) $(n_2,n_1,i_2,i_1,2)\rightarrow (n_2,n_1-1,i_2-1,i_1,1)$ with rate $T^0\beta$ for $n_2\ge 0$, $1\le n_1 \le N$, $1\le i_2\le S_2$, $1\le i_1 \le S_1$.

• (5) Transitions due to the purchase for Type-1 customer.

  • (a) $(n_2,n_1,i_2,1,1)\rightarrow (n_2,n_1-1,i_2,1,1)$ with rate $T^0\beta$ for $n_2\ge 0$, $1\le n_1 \le N$, $0\le i_2\le S_2$.

  • (b) $(n_2,n_1,i_2,0,2)\rightarrow (n_2,n_1-1,i_2-1,1,1)$ with rate $T^0\beta$ for $n_2\ge 0$, $1\le n_1 \le N$, $1\le i_2\le S_2$.

• (6) Transitions due to the purchase for Type-2 customer.

  • (a) $(n_2,0,0,i_1,1)\rightarrow (n_2-1,0,1,i_1-1,2)$ with rate $T^0\beta$ for $n_2\ge 1$, $1\le i_1 \le S_1$.

  • (b) $(n_2,0,1,i_1,2)\rightarrow (n_2-1,0,1,i_1,2)$ with rate $T^0\beta$ for $n_2\ge 1$, $0\le i_1 \le S_1$.

• (7) Transitions due to replenishments of Commodity-1

  • (a) $(0,0,i_2,i_1,0)\rightarrow (0,0,i_2,S_1,0)$ with rate $\eta _1$ for $0\le i_2 \le S_2$, $0\le i_1 \le s_1$.

  • (b) $(n_2,n_1,i_2,i_1,1)\rightarrow (n_2,n_1,i_2,S_1,1)$ with rate $\eta _1I_n$ for $n_2\ge 0$, $0\le n_1 \le N$, $0\le i_2 \le S_2$, $1\le i_1 \le s_1$.

  • (c) $(n_2,n_1,i_2,i_1,2)\rightarrow (n_2,n_1,i_2,S_1,2)$ with rate $\eta _1I_n$ for $n_2\ge 0$, $0\le n_1 \le N$, $1\le i_2 \le S_2$, $0\le i_1 \le s_1$.

• (8) Transitions due to replenishments of Commodity-2

  • (a) $(0,0,i_2,i_1,0)\rightarrow (0,0,S_2,i_1,0)$ with rate $\eta _2$ for $0\le i_2 \le s_2$, $0\le i_1 \le S_1$.

  • (b) $(n_2,n_1,i_2,i_1,1)\rightarrow (n_2,n_1,S_2,i_1,1)$ with rate $\eta _2I_n$ for $n_2\ge 0$, $0\le n_1 \le N$, $0\le i_2 \le s_2$, $1\le i_1 \le S_1$.

  • (c) $(n_2,n_1,i_2,i_1,2)\rightarrow (n_2,n_1,S_2,i_1,2)$ with rate $\eta _2I_n$ for $n_2\ge 0$, $0\le n_1 \le N$, $1\le i_2 \le s_2$, $0\le i_1 \le S_1$.

The infinitesimal generator matrix of the Markov chain governing the system has a block-tridiagonal matrix structure and is given by

$$\begin{aligned} {\varvec{Q}}=\left( \begin{array}{cccccccccccccc} {\varvec{B}}_0&{} {\varvec{A}}_0 \\ {\varvec{C}}_0&{} {\varvec{B}}&{} {\varvec{A}} \\ &{} {\varvec{C}}&{}{\varvec{B}}&{} {\varvec{A}}\\ &{} &{} {\varvec{C}}&{} {\varvec{B}} &{} {\varvec{A}} \\ &{} &{} &{}\ddots &{}\ddots &{}\ddots \\ \end{array} \right) . \end{aligned}$$

(1)

In the sequel, we need the following notations. $d_1=(S_1+1)(S_2+1)$, $d_2= S_1 (S_2+1)n$, $d_3=d_2 (N+1)$, $d_4=S_2 (S_1+1)n$, $d_5=d_4 (N+1)$ and $d=d_3+d_5$ are the scalars which will be used to define the dimensions of the sub-matrices in the matrix ${\varvec{Q}}$; ${\varvec{e}}_i$ is a unit column vector with 1 in the $i^{th}$ position and 0 elsewhere; ${\varvec{e}}(j)$ shows that a unit column vector is of dimension j; ${\varvec{I}}_{k}$ is an identity matrix of order k and the symbol $\otimes$ represents the Kronecker product of two matrices.

$$\begin{aligned} {\varvec{A}}_{0}=\left( \begin{array}{ccc|cc} {\varvec{A}}_{01}&{} {\textbf {0}} &{}{\textbf {0}}&{}{\textbf {0}}&{}{\textbf {0}}\\ {\textbf {0}} &{} ({\varvec{I}}_{S_2} \otimes {\varvec{A}}_{01})&{}{\textbf {0}}&{} ({\varvec{I}}_{S_2} \otimes {\varvec{A}}_{02})&{}{\textbf {0}}\\ \end{array} \right) _{d_1\times d}, \end{aligned}$$

with

$$\begin{aligned}&{\varvec{A}}_{01}=\left( \begin{array}{cccccccccccccc} {\textbf {0}}\\ {\varvec{I}}_{S_1} \otimes \lambda _1 {{\varvec{\beta }}}\\ \end{array} \right) _{(S_1+1)\times nS_1} ~~\text {and}~~~~ {\varvec{A}}_{02}=\left( \begin{array}{cccccccccccccc} {\varvec{I}}_{S_1+1} \otimes \lambda _2 {{\varvec{\beta }}} \end{array} \right) _{(S_1+1)\times n(S_1+1)}.\\&{\varvec{B}}_{0}=\left( \begin{array}{cccccccccccccc} {\varvec{B}}_{01}&{}&{} {\textbf {0}}&{}&{}&{}{\varvec{e}}'_{S_2-s_2}(S_2-s_2)\otimes {\varvec{B}}_{04}\\ {\textbf {0}}&{}&{} {\varvec{I}}_{s_2}\otimes {\varvec{B}}_{02}&{}&{}&{}{\varvec{e}}'_{S_2-s_2}(S_2-s_2)\otimes [{\varvec{e}}(s_2)\otimes {\varvec{B}}_{04}] \\ {\textbf {0}}&{}&{}{\textbf {0}}&{}&{}&{}{\varvec{I}}_{S_2-s_2}\otimes {\varvec{B}}_{03}\\ \end{array} \right) _{d_1\times d_1}, \end{aligned}$$

with

$$\begin{aligned}&{\varvec{B}}_{01}=\left( \begin{array}{cccccccccccccc} -(\eta _1+\eta _2)&{} {\textbf {0}} &{}&{}{\varvec{e}}'_{S_1-s_1}(S_1-s_1)\eta _1\\ {\textbf {0}}&{} -(\lambda _1+\eta _1+\eta _2){\varvec{I}}_{s_1} &{}&{}{\varvec{e}}'_{S_1-s_1}(S_1-s_1)\otimes {\varvec{e}}(s_1)\eta _1\\ {\textbf {0}}&{}{\textbf {0}}&{}&{}-(\lambda _1+\eta _2){\varvec{I}}_{S_1-s_1}\\ \end{array} \right) ,\\&{\varvec{B}}_{02}={\varvec{B}}_{01}-\lambda _2{\varvec{I}}_{(S_1+1)},~~~~ {\varvec{B}}_{03}={\varvec{B}}_{02}+\eta _2{\varvec{I}}_{(S_1+1)}~~\text {and}~~{\varvec{B}}_{04}=\eta _2{\varvec{I}}_{(S_1+1)}.\\&{\varvec{C}}_{0}=\left( \begin{array}{cccccccccccccc} ({\varvec{I}}_{S_2} \otimes {\varvec{C}}_{01})&{}{\textbf {0}}\\ {\textbf {0}}&{} {\varvec{C}}_{01}\\ {\textbf {0}}&{}{\textbf {0}}\\ \hline ({\varvec{I}}_{S_2} \otimes {\varvec{C}}_{02})&{} {\textbf {0}}\\ {\textbf {0}}&{}{\textbf {0}}\\ {\textbf {0}}&{}{\textbf {0}}\\ \end{array} \right) _{d\times d_1}, \end{aligned}$$

with

$$\begin{aligned}&{\varvec{C}}_{01}=\left( \begin{array}{cccccccccc} ({\varvec{I}}_{S_1} \otimes {\varvec{T}}^0)&{}&{}{\textbf {0}}\\ \end{array} \right) _{nS_1\times (S_1+1)} ~~\text {and}~~ {\varvec{C}}_{02}=\left( \begin{array}{cccccccccccccc} {\varvec{I}}_{S_1+1} \otimes {\varvec{T}}^0 \end{array} \right) _{n(S_1+1)\times (S_1+1)}.\\&{\varvec{A}}=\left( \begin{array}{c|c} \lambda _2{\varvec{I}}_{d_3}&{}{\textbf {0}}\\ \hline {\textbf {0}}&{}\lambda _2{\varvec{I}}_{d_5}\\ \end{array} \right) _{d \times d}.\\&{\varvec{C}}=\left( \begin{array}{cc|cc} {\textbf {0}}&{}{\textbf {0}}&{} {\varvec{C}}_1&{}{\textbf {0}}\\ {\textbf {0}}&{}{\textbf {0}}&{}{\textbf {0}}&{}{\textbf {0}}\\ \hline {\textbf {0}}&{}{\textbf {0}}&{}{\varvec{C}}_2&{}{\textbf {0}}\\ {\textbf {0}}&{}{\textbf {0}}&{}{\textbf {0}}&{}{\textbf {0}}\\ \end{array} \right) _{d \times d}, \end{aligned}$$

with

$$\begin{aligned}&{\varvec{C}}_1=\left( \begin{array}{c} {\varvec{e}}'_{1}(S_2) \otimes {\varvec{C}}_{11}\\ {\varvec{I}}_{S_2} \otimes {\varvec{C}}_{11}\\ \end{array} \right) ,~~{\varvec{C}}_{11}=\left( \begin{array}{ccc} ({\varvec{I}}_{S_1} \otimes {\varvec{T}}^0{{\varvec{\beta }}})&{}\quad &{}\quad {\textbf {0}}\\ \end{array} \right) _{nS_1 \times n(S_1+1)}~~\text {and}\\&{\varvec{C}}_2=\left( \begin{array}{c} {\varvec{e}}'_{1}(S_2) \otimes {\varvec{C}}_{21}\\ {\varvec{I}}_{S_2} \otimes {\varvec{C}}_{21}\\ \end{array} \right) ,~~{\varvec{C}}_{21}=\left( \begin{array}{c} {\varvec{I}}_{(S_1+1)} \otimes {\varvec{T}}^0{{\varvec{\beta }}} \end{array} \right) _{n(S_1+1) \times n(S_1+1)}.\\&{\varvec{B}}=\left( \begin{array}{ccccc|ccccccccc} {\varvec{B}}_1&{}\quad {\varvec{B}}_2&{}\quad &{}\quad &{}\quad \\ {\varvec{B}}_3&{}\quad {\varvec{B}}_1&{}\quad {\varvec{B}}_2&{}\quad &{}\quad \\ &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad \\ &{}\quad &{}\quad {\varvec{B}}_3&{}\quad {\varvec{B}}_1&{}\quad {\varvec{B}}_2\\ &{}\quad &{}\quad &{}\quad {\varvec{B}}_3&{}\quad ({\varvec{B}}_1+ \lambda _1{\varvec{I}}_{d_2})\\ \hline {\textbf {0}}&{}\quad &{}\quad &{}\quad &{}\quad &{}\quad {\varvec{B}}_4&{}\quad {\varvec{B}}_5&{}\quad &{}\quad \\ {\varvec{B}}_6&{}\quad &{}\quad &{}\quad &{}\quad &{}\quad &{}\quad {\varvec{B}}_4&{}\quad {\varvec{B}}_5&{}\quad \\ &{}\quad \ddots &{}\quad &{}\quad &{}\quad &{}\quad &{}\quad &{}\quad \ddots &{}\quad \ddots \\ &{}\quad &{}\quad {\varvec{B}}_6&{}\quad &{}\quad &{}\quad &{}\quad &{}\quad &{}\quad {\varvec{B}}_4&{}\quad {\varvec{B}}_5\\ &{}\quad &{}\quad &{}\quad {\varvec{B}}_6&{}\quad {\textbf {0}}&{}\quad &{}\quad &{}\quad &{}\quad &{}\quad ({\varvec{B}}_4+\lambda _1{\varvec{I}}_{d_4}) \end{array} \right) _{d \times d}, \end{aligned}$$

where

$$\begin{aligned}&{\varvec{B}}_{1}=\left( \begin{array}{cccccccccccccc} {\varvec{I}}_{(s_2+1)}\otimes \hat{{\varvec{B}}}_{1}&{}\quad &{}\quad &{}\quad &{}\quad {\varvec{e}}'_{S_2-s_2}(S_2-s_2)\otimes [{\varvec{e}}(s_2+1)\otimes ({\varvec{I}}_{S_1} \otimes \eta _2{\varvec{I}}_{n})] \\ {\textbf {0}}&{}\quad &{}\quad &{}\quad &{}\quad {\varvec{I}}_{S_2-s_2}\otimes [\hat{{\varvec{B}}}_{1}+({\varvec{I}}_{S_1} \otimes \eta _2{\varvec{I}}_{n})]\\ \end{array} \right) _{d_2\times d_2}~~\text {with} \\&\hat{{\varvec{B}}}_{1}=\left( \begin{array}{cccccccccccccc} {\varvec{I}}_{s_1}\otimes [{\varvec{T}}-(\lambda _1+\lambda _2+\eta _1+\eta _2){\varvec{I}}_{n}]&{}\quad &{}\quad &{}\quad &{}\quad {\varvec{e}}'_{S_1-s_1}(S_1-s_1)\otimes [{\varvec{e}}(s_1)\otimes \eta _1{\varvec{I}}_{n}] \\ {\textbf {0}}&{}\quad &{}\quad &{}\quad &{}\quad {\varvec{I}}_{S_1-s_1}\otimes [{\varvec{T}}-(\lambda _1+\lambda _2+\eta _2){\varvec{I}}_{n}]\\ \end{array} \right) _{nS_1\times nS_1}, \\&{\varvec{B}}_{4}=\left( \begin{array}{cccccccccccccc} {\varvec{I}}_{s_2}\otimes \hat{{\varvec{B}}}_{4}&{}\quad &{}\quad &{}\quad &{}\quad {\varvec{e}}'_{S_2-s_2}(S_2-s_2)\otimes [{\varvec{e}}(s_2)\otimes ({\varvec{I}}_{(S_1+1)} \otimes \eta _2{\varvec{I}}_{n})] \\ {\textbf {0}}&{}\quad &{}\quad &{}\quad &{}\quad {\varvec{I}}_{S_2-s_2}\otimes [\hat{{\varvec{B}}}_{4}+({\varvec{I}}_{(S_1+1)} \otimes \eta _2{\varvec{I}}_{n})]\\ \end{array} \right) _{d_4\times d_4}~~\text {with} \\&\hat{{\varvec{B}}}_{4}=\left( \begin{array}{cccccccccccccc} {\varvec{I}}_{s_1+1}\otimes [{\varvec{T}}-(\lambda _1+\lambda _2+\eta _1+\eta _2){\varvec{I}}_{n}]&{}\quad &{}\quad &{}\quad &{}\quad {\varvec{e}}'_{S_1-s_1}(S_1-s_1)\otimes [{\varvec{e}}(s_1+1)\otimes \eta _1{\varvec{I}}_{n}] \\ {\textbf {0}}&{}\quad &{}\quad &{}\quad &{}\quad {\varvec{I}}_{S_1-s_1}\otimes [{\varvec{T}}-(\lambda _1+\lambda _2+\eta _2){\varvec{I}}_{n}]\\ \end{array} \right) , \\&{\varvec{B}}_2=\left( \begin{array}{cc} \lambda _1{\varvec{I}}_{d_2}\\ \end{array} \right) ,~~ {\varvec{B}}_5=\left( \begin{array}{c} \lambda _1{\varvec{I}}_{d_4}\\ \end{array} \right) , \\&{\varvec{B}}_3=\left( \begin{array}{c} {\varvec{I}}_{S_2+1} \otimes \hat{{\varvec{B}}}_3 \end{array} \right) _{d_2\times d_2}~~\text {with}~~\hat{{\varvec{B}}}_3=\left( \begin{array}{ccc} {\varvec{e}}'_{1}(S_1-1) \otimes {\varvec{T}}^0{{\varvec{\beta }}}&{}\quad &{}\quad {\textbf {0}}\\ {\varvec{I}}_{S_1-1} \otimes {\varvec{T}}^0{{\varvec{\beta }}}&{}\quad &{}\quad {\textbf {0}}\\ \end{array} \right) _{nS_1 \times nS_1}, \\&{\varvec{B}}_6=\left( \begin{array}{ccc} {\varvec{I}}_{S_2} \otimes \hat{{\varvec{B}}}_6&\quad&\quad {\textbf {0}} \end{array} \right) _{d_4\times d_4}~~\text {with}~~\hat{{\varvec{B}}}_6=\left( \begin{array}{c} {\varvec{e}}'_{1}(S_1) \otimes {\varvec{T}}^0{{\varvec{\beta }}}\\ {\varvec{I}}_{S_1} \otimes {\varvec{T}}^0{{\varvec{\beta }}}\\ \end{array} \right) _{n(S_1+1) \times nS_1}. \end{aligned}$$

3.1 Stability condition

Let ${{\varvec{\pi }}}$ be the steady-state probability vector of the finite generator matrix ${\varvec{D}}={\varvec{A}}+{\varvec{B}}+{\varvec{C}}$. That is, ${{\varvec{\pi }}}$ satisfies

$$\begin{aligned} {{\varvec{\pi }}}{\varvec{D}}={\textbf {0}}~~\text {and}~~{{\varvec{\pi }}}{\varvec{e}}=1. \end{aligned}$$

(2)

Let ${{\varvec{\pi }}}=({{\varvec{\pi }}}_1,{{\varvec{\pi }}}_2)$ with ${{\varvec{\pi }}}_1=({{\varvec{\pi }}}_{01},{{\varvec{\pi }}}_{11},\ldots ,{{\varvec{\pi }}}_{N1})$ and ${{\varvec{\pi }}}_2=({{\varvec{\pi }}}_{02},{{\varvec{\pi }}}_{12},\ldots ,{{\varvec{\pi }}}_{N2})$. The steady-state equations in (2) can be rewritten as

$$\begin{aligned} \begin{array}{rrr} {{\varvec{\pi }}}_{01}[{{\varvec{e}}} \otimes ({{\varvec{T}}}-\lambda _1{{\varvec{I}}_n})]+{{\varvec{\pi }}}_{11}({{\varvec{e}}}\otimes {{\varvec{T}}}^0{{\varvec{\beta }}})+{{\varvec{\pi }}}_{12}({{\varvec{e}}}\otimes {{\varvec{T}}}^0{{\varvec{\beta }}})&{}={{\textbf {0}}} &{}\\ {{\varvec{\pi }}}_{i-1,1}({{\varvec{e}}}\otimes \lambda _1 {{\varvec{I}}}_n)+{{\varvec{\pi }}}_{i1}[{{\varvec{e}}} \otimes ({{\varvec{T}}}-\lambda _1{{\varvec{I}}_n})]+{{\varvec{\pi }}}_{i+1,1}({{\varvec{e}}}\otimes {{\varvec{T}}}^0{{\varvec{\beta }}})\\ +{{\varvec{\pi }}}_{i+1,2}({{\varvec{e}}}\otimes {{\varvec{T}}}^0{{\varvec{\beta }}})&{}={{\textbf {0}}}&{},1\le i \le N-1\\ {{\varvec{\pi }}}_{N-1,1}({{\varvec{e}}}\otimes \lambda _1 {{\varvec{I}}}_n)+{{\varvec{\pi }}}_{N1}({{\varvec{e}}}\otimes {{\varvec{T}}})&{}={{\textbf {0}}} &{}\\ {{\varvec{\pi }}}_{01}({{\varvec{e}}}\otimes {{\varvec{T}}}^0{{\varvec{\beta }}})+{{\varvec{\pi }}}_{02}[{{\varvec{e}}} \otimes ({{\varvec{T}}}-\lambda _1{{\varvec{I}}_n}+{{\varvec{T}}}^0{{\varvec{\beta }}})]&{}={{\textbf {0}}} &{}\\ {{\varvec{\pi }}}_{i-1,2}({{\varvec{e}}}\otimes \lambda _1 {{\varvec{I}}}_n)+{{\varvec{\pi }}}_{i2}[{{\varvec{e}}} \otimes ({{\varvec{T}}}-\lambda _1{{\varvec{I}}_n})]&{}={{\textbf {0}}} &{},1\le i \le N-1\\ {{\varvec{\pi }}}_{N-1,2}({{\varvec{e}}}\otimes \lambda _1 {{\varvec{I}}}_n)+{{\varvec{\pi }}}_{N2}({{\varvec{e}}}\otimes {{\varvec{T}}})&{}={{\textbf {0}}} &{}\\ \end{array} \end{aligned}$$

(3)

with the normalizing condition

$$\begin{aligned} \sum _{i=0}^{N} {{\varvec{\pi }}}_{i1}{{\varvec{e}}}+\sum _{i=0}^{N} {{\varvec{\pi }}}_{i2}{{\varvec{e}}}=1. \end{aligned}$$

(4)

Lemma 1

We have

$$\begin{aligned} \sum _{i=0}^{N} {{\varvec{\pi }}}_{i1}({{\varvec{e}}}\otimes {{\varvec{I}}_n})+\sum _{i=0}^{N} {{\varvec{\pi }}}_{i2}({{\varvec{e}}}\otimes {{\varvec{I}}_n})=\mu {{\varvec{\beta }}} (-{{\varvec{T}}})^{-1}. \end{aligned}$$

(5)

Proof

Adding the equations in (3) we obtain

$$\begin{aligned} \left[ \sum _{i=0}^{N} {{\varvec{\pi }}}_{i1}({{\varvec{e}}}\otimes {{\varvec{I}}_n})+\sum _{i=0}^{N} {{\varvec{\pi }}}_{i2}({{\varvec{e}}}\otimes {{\varvec{I}}_n})\right] ({{\varvec{T}}}^0{{\varvec{\beta }}}+{{\varvec{T}}})={\textbf {0}}. \end{aligned}$$

(6)

Now from the uniqueness of the steady-state vector of the generator $({{{\varvec{T}}}+{\varvec{T}}}^0{{\varvec{\beta }}})$ and the normalizing condition in (4), it can be obtained the result in Lemma 1. $\square$

Lemma 2

We have

$$\begin{aligned} \sum _{i=1}^{N} {{\varvec{\pi }}}_{i1}({{\varvec{e}}}\otimes {{\varvec{T}}^0})+\sum _{i=1}^{N} {{\varvec{\pi }}}_{i2}({{\varvec{e}}}\otimes {{\varvec{T}}^0})=\lambda _1 (1-{{\varvec{\pi }}}_{N1}{\varvec{e}}-{{\varvec{\pi }}}_{N2}{\varvec{e}}). \end{aligned}$$

(7)

Proof

Post-multiplying the equations in (3) by ${{\varvec{e}}}$ and then adding iteratively we obtain

$$\begin{aligned} \begin{array}{ccl} {{\varvec{\pi }}}_{i1}({{\varvec{e}}}\otimes {{\varvec{T}}^0})&{}=&{}{{\varvec{\pi }}}_{i-1,1}({{\varvec{e}}}\otimes \lambda _1 {{\varvec{e}}})+\displaystyle \sum _{j=i+1}^{N}{{\varvec{\pi }}}_{j,2}({{\varvec{e}}}\otimes {{\varvec{T}}^0}),~1\le i\le N-1\\ {{\varvec{\pi }}}_{N1}({{\varvec{e}}}\otimes {{\varvec{T}}^0})&{}=&{}{{\varvec{\pi }}}_{N-1,1}({{\varvec{e}}}\otimes \lambda _1 {{\varvec{e}}})\\ {{\varvec{\pi }}}_{02}({{\varvec{e}}}\otimes \lambda _1 {{\varvec{e}}})&{}=&{}{{\varvec{\pi }}}_{01}({{\varvec{e}}}\otimes {{\varvec{T}}^0})\\ {{\varvec{\pi }}}_{i2}({{\varvec{e}}}\otimes \lambda _1 {{\varvec{e}}})&{}=&{}\displaystyle \sum _{j=i+1}^{N}{{\varvec{\pi }}}_{j,2}({{\varvec{e}}}\otimes {{\varvec{T}}^0}),~0\le i \le N-1\\ \end{array} \end{aligned}$$

(8)

Adding the equations given in (8) and using the normalizing condition in (4) we get the result in Lemma 2. $\square$

The two-commodity queueing-inventory system under study has the QBD-type generator in (1) and so it is stable if and only if ${{\varvec{\pi }}}{\varvec{A}} {\varvec{e}}<{{\varvec{\pi }}}{\varvec{C}} {\varvec{e}}$ (see, e.g., Neuts (1981)). That is, the stability condition becomes

$$\begin{aligned} \begin{array}{ll} {{\varvec{\pi }}}{\varvec{A}} {\varvec{e}}=\lambda _2< {{\varvec{\pi }}}{\varvec{C}} {\varvec{e}}={{\varvec{\pi }}}_{01}({{\varvec{e}}}\otimes {{\varvec{T}}^0})+{{\varvec{\pi }}}_{02}({{\varvec{e}}}\otimes {{\varvec{T}}^0}).\\ \end{array} \end{aligned}$$

(9)

From Lemma 1, it can be seen that $\sum _{i=0}^{N} {{\varvec{\pi }}}_{i1}({{\varvec{e}}}\otimes {{\varvec{T}}^0})+\sum _{i=0}^{N} {{\varvec{\pi }}}_{i2}({{\varvec{e}}}\otimes {{\varvec{T}}^0})=\mu .$ Using the fact and the result in Lemma 2, the following theorem is established.

Theorem 3

The defined queuing-inventory system is stable if and only if the following condition is satisfied:

$$\begin{aligned} \begin{array}{lll} \lambda _2 < \mu -\lambda _1(1-{{\varvec{\pi }}}_{N1}{\varvec{e}}-{{\varvec{\pi }}}_{N2}{\varvec{e}}). \\ \end{array} \end{aligned}$$

(10)

3.2 The steady-state probability vector of ${\varvec{Q}}$

Let ${{\varvec{x}}}=({{\varvec{x}}}^*,~{{\varvec{x}}}(0),~ {{\varvec{x}}}(1),~\cdots )$ denote the steady-state probability vector of the generator matrix ${\varvec{Q}}$ in (1). That is, ${{\varvec{x}}}$ satisfies

$$\begin{aligned} {{\varvec{x}}}~ {\varvec{Q}}= \mathbf{0}~~\text {and}~~{{\varvec{x}}}~{{\varvec{e}}} = 1. \end{aligned}$$

(11)

The vector ${{\varvec{x}}}^*=x_0(0,0,i_2,i_1)$, of dimension $d_1=(S_1+1)(S_2+1)$, gives the steady-state probability that the server is idle and no customer in the queue. $i_2,~0\le i_2 \le S_2$, and $i_1,~0\le i_1 \le S_1$, are the inventory levels of commodities for Type-2 customers and Type-1 customers, respectively.

The probability vector ${{\varvec{x}}}(n_2)$, of dimension $d=d_3+d_5$, is partitioned as ${{\varvec{x}}}(n_2) = [ {{\varvec{x}}}_1(n_2),~{{\varvec{x}}}_2(n_2)],~n_2\ge 0$. The subvector ${{\varvec{x}}}_1(n_2)$, of dimension $d_3=d_2(N+1)$, is further partitioned into the vectors represented as ${{\varvec{x}}}_1(n_2) = [{{\varvec{x}}}_{1}(n_2,0),~{{\varvec{x}}}_{1}(n_2,1),\cdots ,{{\varvec{x}}}_{1}(n_2,N)]$ and the dimension of the each vector is $d_2=S_1(S_2+1)n$. The vector ${{\varvec{x}}}_{1}(n_2,n_1),~n_1=0,1,\ldots ,N,$ gives the steady-state probability that there is a Type-1 customer in the server, there are $n_2$ Type-2 customers and $n_1$ Type-1 customers waiting in the queue, the inventory levels of the commodities for Type-2 customers and Type-1 customers are $i_2,~0 \le i_2\le S_2$, and $i_1,~1\le i_1 \le S_1$, respectively, and the service is in one of n phases. Similarly, the subvector ${{\varvec{x}}}_2(n_2)$, of dimension $d_5=d_4(N+1)$, is further partitioned into vectors as ${{\varvec{x}}}_2(n_2) = [{{\varvec{x}}}_{2}(n_2,0),~{{\varvec{x}}}_{2}(n_2,1),\cdots ,{{\varvec{x}}}_{2}(n_2,N)]$ and the dimension of the each vector is $d_4=S_2(S_1+1)n$. The vector ${{\varvec{x}}}_{2}(n_2,n_1)$, $n_1=0,1,\ldots ,N,$ gives the steady-state probability of a Type-2 customer is being served, there are $n_2$ Type-2 customers and $n_1$ Type-1 customers waiting in the queue, the inventory levels of commodities for Type-2 customers and Type-1 customers are $i_2,~1 \le i_2\le S_2$, and $i_1,~0 \le i_1 \le S_1$, respectively, and the service is in one of n phases.

Under the stability condition given in (10) the steady-state probability vector ${{\varvec{x}}}$ is obtained (see Neuts (1981)) as

$$\begin{aligned} {{\varvec{x}}}(i) = {{\varvec{x}}}(0) {\varvec{R}}^i,~~i \ge 1, \end{aligned}$$

(12)

where the matrix ${\varvec{R}}$ is the minimal nonnegative solution to the following matrix quadratic equation

$$\begin{aligned} {\varvec{R}}^2 {\varvec{C}} + {\varvec{R}} {\varvec{B}} + {\varvec{A}}={\textbf {0}}, \end{aligned}$$

(13)

and the vectors, ${{\varvec{x}}}^*$ and ${{\varvec{x}}}(0)$ are obtained by solving

$$\begin{aligned} \begin{array}{ccccccc} {{\varvec{x}}}^*{\varvec{B}}_0 + {{\varvec{x}}}(0) {\varvec{C}}_0 = {{\textbf {0}}},\\ {{\varvec{x}}}^*{\varvec{A}}_0+{{\varvec{x}}}(0)[{\varvec{B}}+ {\varvec{R}} {\varvec{C}}] = {{\textbf {0}}},\\ \end{array} \end{aligned}$$

(14)

subject to the normalizing condition

$$\begin{aligned} {{\varvec{x}}}^*{{\varvec{e}}}+{{\varvec{x}}}(0)({\varvec{I}}-{\varvec{R}})^{-1}{{\varvec{e}}} = 1. \end{aligned}$$

(15)

For the computation of the matrix ${\varvec{R}}$ in (13) it can be carried out using logarithmic reduction algorithm given in Latouche and Ramaswami (1999) or successive substitution method that is used in this study.

Successive substitution method for ${\varvec{R}}$:

• Step 0 : ${\varvec{R}} \leftarrow {\textbf {0}}~~$ and $~~{\varvec{R}}_b \leftarrow [{\varvec{A}}(-{\varvec{B}})^{-1}+{\varvec{R}}^2 {\varvec{C}}(-{\varvec{B}})^{-1}]$.

• Step 1 : ${\varvec{R}} \leftarrow {\varvec{R}}_b$,

  $~~~~~~~~~~~~~~{\varvec{R}}_b \leftarrow [{\varvec{A}}(-{\varvec{B}})^{-1}+{\varvec{R}}^2 {\varvec{C}}(-{\varvec{B}})^{-1}]$

• Continue Step 1 until $\Vert {\varvec{R}}_b-{\varvec{R}}\Vert _\infty < \varepsilon$.

• Step 2 : ${\varvec{R}}={\varvec{R}}_b$.

3.3 Performance measures

Some performance measures are computed representing the system and summarized below.

The probability that there is no customer in the system

$$\begin{aligned} P_{idle}={{\varvec{x}}}^*{{\varvec{e}}_{d_1}}. \end{aligned}$$

The probability that an arriving Type-1 customer is lost because of the finite capacity

$$\begin{aligned} P_{lost}=\sum _{n_2=0}^{\infty }{{\varvec{x}}}_{1}(n_2,N){{\varvec{e}}_{d_2}}+\sum _{n_2=0}^{\infty }{{\varvec{x}}}_{2}(n_2,N){{\varvec{e}}_{d_4}}. \end{aligned}$$

The probability that an arriving Type-1 customer is lost because of no inventory

$$\begin{aligned} P_{lost1}=\sum _{i_2=0}^{S_2}x_0(0,0,i_2,0). \end{aligned}$$

The probability that an arriving Type-2 customer is lost because of no inventory

$$\begin{aligned} P_{lost2}=\sum _{i_1=0}^{S_1}x_0(0,0,0,i_1). \end{aligned}$$

Mean number of Type-1 customers in the queue

$$\begin{aligned} EN_{Q1}=\sum _{n_2=0}^{\infty }\sum _{n_1=1}^{N} n_1~{{\varvec{x}}}_{1}(n_2,n_1){{\varvec{e}}_{d_2}}+\sum _{n_2=0}^{\infty }\sum _{n_1=1}^{N} n_1~{{\varvec{x}}}_{2}(n_2,n_1){{\varvec{e}}_{d_4}}. \end{aligned}$$

Mean number of Type-2 customers in the queue

$$\begin{aligned} EN_{Q2}={{\varvec{x}}}(0){{\varvec{R}}}({{\varvec{I}}}-{{\varvec{R}}})^{-2}{{\varvec{e}}_d}. \end{aligned}$$

Mean number of commodities in the inventory for Type-1 customers

$$\begin{aligned} EN_{I1}= & {} \sum _{i_2=0}^{S_2}\sum _{i_1=1}^{S_1}i_1~x_0(0,0,i_2,i_1)\\&+ \sum _{n_2=0}^{\infty }\sum _{n_1=0}^{N}\left[ \left( \sum _{i_2=0}^{S_2}\sum _{i_1=1}^{S_1}i_1~{{\varvec{x}}}_{1}(n_2,n_1,i_2,i_1){{\varvec{e}}_{n}} \right) +\left( \sum _{i_2=1}^{S_2}\sum _{i_1=1}^{S_1}i_1~{{\varvec{x}}}_{2}(n_2,n_1,i_2,i_1){{\varvec{e}}_{n}} \right) \right] . \end{aligned}$$

Mean number of commodities in the inventory for Type-2 customers

$$\begin{aligned} EN_{I2}= & {} \sum _{i_2=1}^{S_2}i_2~\sum _{i_1=0}^{S_1}x_0(0,0,i_2,i_1)\\&+ \sum _{n_2=0}^{\infty }\sum _{n_1=0}^{N}\left[ \left( \sum _{i_2=1}^{S_2}i_2~\sum _{i_1=1}^{S_1}{{\varvec{x}}}_{1}(n_2,n_1,i_2,i_1){{\varvec{e}}_{n}} \right) +\displaystyle \left( \sum _{i_2=1}^{S_2}i_2~\sum _{i_1=0}^{S_1}{{\varvec{x}}}_{2}(n_2,n_1,i_2,i_1){{\varvec{e}}_{n}} \right) \right] . \end{aligned}$$

Mean replenishment rate for commodity-1

$$\begin{aligned} E_{R1}= & {} \eta _1 \sum _{i_2=0}^{S_2}\sum _{i_1=0}^{s_1}x_0(0,0,i_2,i_1)\\&+\eta _1 \sum _{n_2=0}^{\infty }\sum _{n_1=0}^{N}\left[ \left( \sum _{i_2=0}^{S_2}\sum _{i_1=1}^{s_1}{{\varvec{x}}}_{1}(n_2,n_1,i_2,i_1){{\varvec{e}}_{n}} \right) + \left( \sum _{i_2=1}^{S_2}\sum _{i_1=0}^{s_1}{{\varvec{x}}}_{2}(n_2,n_1,i_2,i_1){{\varvec{e}}_{n}} \right) \right] . \end{aligned}$$

Mean replenishment rate for commodity-2

$$\begin{aligned} E_{R2}= & {} \eta _2 \sum _{i_2=0}^{s_2}\sum _{i_1=0}^{S_1}x_0(0,0,i_2,i_1)\\&+\eta _2 \sum _{n_2=0}^{\infty }\sum _{n_1=0}^{N}\left[ \left( \sum _{i_2=0}^{s_2}\sum _{i_1=1}^{S_1}{{\varvec{x}}}_{1}(n_2,n_1,i_2,i_1){{\varvec{e}}_{n}} \right) + \left( \sum _{i_2=1}^{s_2}\sum _{i_1=0}^{S_1}{{\varvec{x}}}_{2}(n_2,n_1,i_2,i_1){{\varvec{e}}_{n}} \right) \right] . \end{aligned}$$

Mean purchase rate for commodity-1

$$\begin{aligned} \begin{array}{ccccccc} E_{P1}=\mu \displaystyle \sum _{n_2=0}^{\infty }\sum _{n_1=1}^{N}\Bigg [ \sum _{i_2=0}^{S_2}{{\varvec{x}}}_{1}(n_2,n_1,i_2,1){{\varvec{e}}_{n}}+\sum _{i_2=1}^{S_2}{{\varvec{x}}}_{2}(n_2,n_1,i_2,0){{\varvec{e}}_{n}} \Bigg ]. \end{array} \end{aligned}$$

Mean purchase rate for commodity-2

$$\begin{aligned} E_{P2}= & {} \mu \displaystyle \sum _{n_2=1}^{\infty }\left[ \sum _{i_1=1}^{S_1}{{\varvec{x}}}_{1}(n_2,0,0,i_1){{\varvec{e}}_{n}}+\sum _{i_1=0}^{S_1}{{\varvec{x}}}_{2}(n_2,0,1,i_1){{\varvec{e}}_{n}} \right] . \end{aligned}$$

4 Stationary waiting time distribution of an admitted Type-1 customer

We discuss that the stationary waiting time distribution in the queue of an admitted Type-1 customer at an arrival epoch follows a phase type distribution. For this purpose, we define the row vector ${\varvec{a}}$ of order $d=[S_1(S_2+1)+S_2(S_1+1)](N+1)n$ in partitioned form as

$$\begin{aligned} {\varvec{a}}=\big [\hat{{\varvec{a}}}_0,\hat{{\varvec{a}}}_1...,\hat{{\varvec{a}}}_N,\tilde{{\varvec{a}}}_0,\tilde{{\varvec{a}}}_1...,\tilde{{\varvec{a}}}_N \big ],~~\text {where}~~{\varvec{a}}={\varvec{x}}(0)({\varvec{I}}-{\varvec{R}})^{-1}. \end{aligned}$$

Theorem 4

Suppose X denotes the waiting time in the queue of an admitted Type-1 customer in steady-state. Then X follows a phase-type distribution with representation $({{\varvec{\alpha }}},{\varvec{S}})$ of order Nn, where

$$\begin{aligned} {{\varvec{\alpha }}}=({{\varvec{\alpha }}}_1,{{\varvec{\alpha }}}_2,\ldots ,{{\varvec{\alpha }}}_N ),~~{\varvec{S}}=\left( \begin{array}{cccccccccccccc} {\varvec{T}}&{}\quad &{}\quad &{}\quad \\ {\varvec{T}}^0 {{\varvec{\beta }}}&{}\quad {\varvec{T}} &{}\quad \\ &{}\quad {\varvec{T}}^0 {{\varvec{\beta }}}&{}\quad {\varvec{T}}&{}\quad \\ &{}\quad &{}\quad \ddots &{}\quad \ddots &{}\quad \\ &{}\quad &{}\quad &{}\quad {\varvec{T}}^0 {{\varvec{\beta }}}&{}\quad {\varvec{T}} \\ \end{array} \right) , \end{aligned}$$

(16)

where

$$\begin{aligned} {{\varvec{\alpha }}}_k=\frac{1}{(1-P_{lost}-P_{lost1})}\big [\hat{{\varvec{a}}}_{k-1}({\varvec{e}}_{S_1(S_2+1)}\otimes {\varvec{I}}_n)+\tilde{{\varvec{a}}}_{k-1}({\varvec{e}}_{S_2(S_1+1)}\otimes {\varvec{I}}_n)\big ],~~1\le k \le N. \end{aligned}$$

Proof

There is no need to keep track of the type of customer in service due to the nature of (identical) services for Type 1 and Type 2 customers. The $j^{th}$ component of the n dimensional vector ${{\varvec{\alpha }}}_k$ gives the probability that an admitted Type-1 customer finds $(k-1)$ Type-1 customers waiting in the queue and the current service phase is in j. Since Type-1 customers have non-preemptive priority over Type-2 customers, there is no need to keep track of the number of Type-2 customers in the queue as well as any future arrivals. The result follows immediately from the law of total probability. The probability that the waiting time in the queue is zero is given by $(1-{{\varvec{\alpha }}}{\varvec{e}})$. $\square$

The mean waiting time in the queue of an admitted Type-1 customer can be calculated by using $EW_{Q1}= {{\varvec{\alpha }}}(-{\varvec{S}})^{-1}$. By using the Little’s law, one can calculate $EN_{Q1}=\lambda _1(1-P_{lost}-P_{lost1})EW_{Q1}$ as an accuracy check.

5 Numerical examples

In this section, illustrative numerical examples are performed to see the effects of various parameters on the system performance measures. Also, we discuss some optimization problems about inventory policies, service rate and buffer size by using a constructed profit function.

For the service times, we consider three phase-type distributions with parameter $({{\varvec{\beta }}},{\varvec{T}})$. The distributions are normalized at a desired value for the service rate $\mu$.

Erlang distribution (ERLS):

$$\begin{aligned} {{\varvec{\beta }}}=\left( \begin{array}{cc} 1,&{} \quad 0\\ \end{array} \right) ,~~{\varvec{T}}=\left( \begin{array}{cc} -1&{}\quad 1\\ 0&{}\quad -1\\ \end{array} \right) . \end{aligned}$$

Exponential distribution (EXPS):

$$\begin{aligned} {{\varvec{\beta }}}=\left( \begin{array}{cc} 1\\ \end{array} \right) ,~~{\varvec{T}}=\left( \begin{array}{cc} -1 \end{array} \right) . \end{aligned}$$

Hyperexponential distribution (HEXS):

$$\begin{aligned} {{\varvec{\beta }}}=\left( \begin{array}{cc} 0.9,&{} \quad 0.1\\ \end{array} \right) ,~~ {\varvec{T}}=\left( \begin{array}{cc} -10&{}\quad 0\\ 0&{}\quad -1\\ \end{array} \right) . \end{aligned}$$

Example 1

The purpose of this example is to examine how some of the performance measures such as $P_{idle}$, $P_{lost}$, $P_{lost1}$, $P_{lost2}$, $EN_{Q1}$ and $EN_{Q2}$, are affected by the increasing values of arrival rates. The changes in the performance measures are illustrated in Fig. 2 and Fig. 3 for the increasing values of $\lambda _1$ and $\lambda _2$, respectively.

When the computations are performed, the inventory policy is assumed $(s_1,S_1)=(s_2,S_2)=(3,5)$; the lead time rates are assumed $\eta _1=\eta _2=0.2$; the buffer size of Type-1 customers is assumed $N=3$ and the service rate is assumed $\mu =3$. Also, we specified $\lambda _2=1.2$ for the increasing values of $\lambda _1$ in Fig. 2 and $\lambda _1=1.2$ for the increasing values of $\lambda _2$ in Fig. 3.

As the arrival rate $\lambda _1$ increases, there is an increase in the expected number of both types of customers in the queue denoted by $EN_{Q1}$ and $EN_{Q2}$. Also, the loss probability of an arriving Type-1 customer ($P_{lost}$) increases as well since the waiting space has a finite capacity in Fig.2. It can be seen from Fig.3 that a similar increment occurs for the increasing values of $\lambda _2$. Moreover, the probability that the system is idle, $P_{idle}$, decreases as the arrival rates increase for both levels of the arrival rate. These are expected consequences of the increase in the arrival rates. At this point, we should note that HEXS services are significantly separated from the other service time distributions, especially for the systems where the traffic intensity is high.

Fig. 2

Some performance measures for the increasing values of $\lambda _1$

Fig. 3

Some performance measures for the increasing values of $\lambda _2$

As an interesting observation, there is an increase in the loss probability of Type-1 customers, $P_{lost1}$, in the idle system because there is no inventory on hand. With the increasing values of $\lambda _1$, this probability tends to decrease in Fig. 2. The reason is the buffer capacity of Type-1 customers. A similar conclusion can be made for the change of the probability $P_{lost2}$ with respect to the arrival rate in Fig. 3.

Example 2

The effect of service rate on the performance measures is examined in this example. It can be noted that variation in the service time distributions has a great effect on some performance measures, depending on lead time rate. This effect can be seen from Fig. 4. Computations are performed with the lead time rates $\eta _1=\eta _2=0.2$ and in Fig. 5 additionally is considered with the lead time rates $\eta _1=\eta _2=0.7$ while the inventory levels are fixed and taken as $(s_1,S_1)=(s_2,S_2)=(3,5)$; the buffer size of Type-1 customers is assumed $N=3$; the arrival rates are $\lambda _1=1.2$ and $\lambda _2=1$ for Type-1 and Type-2 customers, respectively.

The probability $P_{idle}$ increases with the increasing service rate $\mu$ whereas the other performance measures in Fig. 4 decrease, as expected. For $EN_{Q2}$, we conclude that the variation in the service time distribution is effective when the system traffic intensity is high.

An increase in service rate results in a decrease in the expected number of items in the inventory, besides an increase in the probability $P_{idle}$. So, $P_{lost1}$ increases normally but the increment is dramatic when the replenishment rates are relatively low (equal to 0.2) in Fig. 5.

Fig. 4

Some performance measures for the increasing values of $\mu$

Fig. 5

Some performance measures under different lead time for the increasing values of $\mu$

Example 3

This example studies the change in performance measures with respect to different arrival rates, for the increasing values of lead time rates. These are illustrated in Figs. 6 and 7. In these figures, the assumed inventory policies are $(s_1,S_1)=(s_2,S_2)=(3,5)$; the buffer size of Type-1 customers is taken as $N=3$ and the service rate is assumed $\mu =3$. Figure 6 presents the effect of the increasing values of $\eta _1$ on the performance measures for fixed $\lambda _2=1.2$, and for the two arrival rates, $\lambda _1=1,1.2$. Similarly, the effect of the increasing values of $\eta _2$ on the performance measures is indicated in Fig. 7 by using fixed $\lambda _1=1.2$ and for the arrival rates $\lambda _2=1,1.2$.

As the lead time rate of the commodity-1 items, $\eta _1$, increases, the mean arrival time of the orders will decrease, hence a decrease is observed for the values of the performance measures given in Fig. 6. This is an expected result. When the mean arrival rate increases, the system traffic intensity will increase (for $\lambda _1=1.2$). For the high-intensity traffic case, HEXS service time distribution results in different values of the performance measures with respect to the ones with the ERLS and EXPS service times.

Fig. 6

Some performance measures for the increasing values of $\eta _1$

Figure 7 illustrates the effect of the variation in service time distribution on the performance measures, for the increasing values of $\eta _2$. When Figs. 6 and 7 are compared, we would like to draw attention to the expected purchase rates for commodity-i, $E_{Pi}$. In the figures when the service time is hyper-exponential (HEXS), $E_{P1}$ has lower values than ones in ERLS and EXPS service time. On the other hand, $E_{P2}$ in the HEXS service time has higher values than the others in Fig. 7.

Fig. 7

Some performance measures for the increasing values of $\eta _2$

5.1 Optimization

For the described system, the expected total profit per unit of time, ETP, is constructed and an optimization discussion is provided for some specific parameters. The profit function includes the terms related to the revenue earned by precessing the customers and the cost terms related to the customer loss, waiting, inventory holding, replenishment, and instant local purchase.

$$\begin{aligned} ETP&= r_1\lambda _1(1-P_{lost} -P_{lost1} )+r_2\lambda _2 (1-P_{lost2})-c_{lost}\lambda _1 P_{lost} \\&\quad -c_{L1}\lambda _1 P_{lost1}-c_{L2}\lambda _2 P_{lost2} -c_{w1} EW_{Q1}-c_{w2} EW_{Q2}\\&\quad -c_{h1} EN_{I1}-c_{h2} EN_{I2} -c_{r1} E_{R1}-c_{r2} E_{R2} -c_{p1} E_{P1}-c_{p2} E_{P2} \end{aligned}$$

where

$r_i:$:

Revenue per Type i customer processed per unit of time, $i=1,2$

$c_{lost}:$:

Cost incured due to the loss of Type 1 customer, $i=1,2$

$c_{Li}:$:

Cost incured due to the loss of customer because of no inventory, $i=1,2$

$c_{wi}:$:

Waiting cost of a Type i customer in the queue, per unit time, $i=1,2$

$c_{hi}:$:

Inventory holding cost per commodity i, per unit time, $i=1,2$

$c_{ri}:$:

Replenishment cost for commodity i, per unit time, $i=1,2$

$c_{pi}:$:

Local purchase cost for commodity i, $i=1,2$.

Towards finding the optimum values, we fixed the unit values for the revenues and costs as follows: $r_1=250$, $r_2=50$, $c_{lost}=50$, $c_{L1}=10$, $c_{L2}=5$, $c_{w1}=100$, $c_{w2}=50$, $c_{h1}=10$, $c_{h2}=2$, $c_{r1}=15$, $c_{r2}=8$, $c_{p1}=9$ and $c_{p2}=4$.

Example 4

Optimum inventory policy $(s_1^*,S_1^*)$ for Type-1 customers is presented in Table 1. The values for Type-2 customer are assumed to be $\lambda _2=1$, and $(s_2,S_2)=(3,5)$. Optimum policy for Type-1 customer is searched with respect to two arrival and two service rates, i.e. $\lambda _1=2.5,3.5$, $\mu =4.4,5.4$. Similarly, the optimum inventory policy $(s_2^*,S_2^*)$ for Type-2 customers are given in Table 2 by using the values $\lambda _1=1$, $(s_1,S_1)=(3,5)$, $\lambda _2=1.3, 2.1$, $\mu =3.8,4.6$. Note that we fix $\eta _1=0.8$, $\eta _2=0.4$ and $N=3$ for the two tables.

Table 1 Optimum values of $s_1^*$ and $S_1^*$

Table 2 Optimum values of $s_2^*$ and $S_2^*$

Comparing the tables, it is clearly seen that the value of expected profit, ETP, is affected by the variation in service time distribution. That is, the lowest expected profit is obtained when the service times are hyper-exponential (HEXS) in both tables. In other words, as the variation in the service time distribution is increased, the profit decreases under the examined cases in Tables 1 and 2.

Example 5

Optimum service rates, $\mu ^*$, are examined with respect to other parameters and results are summarized in Table 3. For this purpose, the following parameter values are used: $\eta _1=0.8$, $\eta _2=0.4$, $(s_1,S_1)=(2,5)$, $(s_2,S_2)=(3,5)$. Optimal service rate is found for two different arrival rate values for both customer type; $\lambda _1=3.5,4.5$, $\lambda _2=1.5,2,2.5,3$. Also two different buffer values are used; $N=3,4$.

Table 3 gives the optimum service rates that maximize the expected profit function. The more variation in service time distribution results in lower profit.

When the arrival rate $\lambda _1$ is increased from 3.5 to 4.5, it is necessary to use higher service rates for ERLS and EXPS service time distribution. On the other hand, for the HEXS service time distribution, the increment in $\lambda _1$ causes decrement in service rate.

Table 3 Optimum values of $\mu ^*$

Example 6

Optimum buffer sizes, $N^*$, are given for different phase type service times in Table 4. The following values of the parameters are used: $\eta _1=0.8$, $\eta _2=0.4$, $(s_1,S_1)=(2,5)$, $(s_2,S_2)=(2,5)$, $\lambda _2=2$, $\lambda _1=1.6,2$ and $\mu =4.5,5,6$.

Table 4 shows that when the traffic intensity is low, more Type-1 customers are allowed to wait in the queue. It is also seen from Table 4 that the variation in the service time distribution is more effective when the traffic intensity is low. In other words, the HEXS service times clearly depart from the other two service times when the traffic intensity is low.

Table 4 Optimum values of $N^*$

6 Conclusion

We have discussed a two-commodity queueing-inventory system with two types of customers. Type-1 customers have the waiting room with capacity whereas Type-2 customers have the one with no capacity. Each type of customer demand occurs related to one type of commodity. So, two inventory policies have been separately considered for the two commodities.

The quasi birth-and-death structure of the studied model has been constructed and the steady-state analysis has been performed by using the matrix geometric method. The sensitivity analysis of the parameters has been provided, besides optimization studies have been performed, as well. By maximizing the structured profit function, the optimum inventory policy has been obtained for each commodity. Also, the optimum buffer size and the optimum service rate are, separately, examined with respect to the different values of parameters. The optimum values obtained are affected by the variation in the service time distribution.

For future works, the model studied can be extended by considering arrivals according to the Markovian arrival process or/and more types of customers or/and more types of commodities. Also, one possible extention of this study is the analysis of time-related quantities by adding the distribution of the waiting time in the queue for Type-2 customers. We refer to studies in Razumchik and Telek (2016) and Chakravarthy and Dudin (2017) for related analysis.