Analysis, Synchronization and Microcontroller Implementation of a New Quasiperiodically Forced Chaotic Oscillator with Megastability

Abstract

Periodically and quasiperiodically forced nonlinear oscillators are in the group of systems which can exhibit chaotic behavior. Chaotic systems could be characterized by their strange attractor’s properties into one or more subtypes, e.g., chaotic systems with hidden attractors, megastability or extreme multistability. In this article, we propose a new quasiperiodically forced chaotic system, which has megastability. The statistical properties, bifurcation diagram, Lyapunov exponents and entropy analysis are considered to study this new system. Furthermore, for the first time, the bidirectional and unidirectional coupling schemes between two quasiperiodically forced chaotic systems with megastability have been studied. As it is observed, when the value of the coupling coefficient is increased in both coupling schemes, the coupled systems undergo a transition from desynchronization mode to complete synchronization. Also, the simulation results reveal the richness of the coupled system’s dynamical behavior. In particular, in the bidirectional coupling case, interesting nonlinear dynamics, such as a transition from a chaotic to quasiperiodic desynchronization and finally to a complete synchronization via an intermittent phenomenon, are observed. Furthermore, in the unidirectional coupling case, in which the system passes from the desynchronization to complete synchronization through a region where the chaotic attractor of the second coupled system is shifted and decreased, is also observed. Finally, the system’s realization has been done by using a microcontroller.

1 Introduction

Periodically forced nonlinear oscillators are in the group of systems which can exhibit chaotic behavior, e.g., periodically forced form of the van der Pol oscillator (Sprott 2010). Furthermore, the driving term could be a quasiperiodic forcing function, which makes the system show more complex behavior. Designing chaotic differential equations and oscillators with desired properties has been an attractive topic recently, especially designing and analyzing chaotic systems with predefined number of equilibria (Pham et al. 2014, 2016), predefined attractors’ structure (Wang et al. 2017), delayed chaotic systems (Li and Fu 2011; Li and Rakkiyappan 2013; Li et al. 2015a, 2018), hidden attractors (Kuznetsov et al. 2010; Leonov et al. 2011; Dudkowski et al. 2016) and multistable attractors (Li and Sprott 2014; Li et al. 2017a, b; Li and Sprott 2018).

Systems with megastability (Sprott et al. 2017; Li and Song 2017; Wang et al. 2018; Tang et al. 2018a, b; He et al. 2018; Wei et al. 2018) and extreme multistability (Bao et al. 2016, 2017a, b; Chen et al. 2018), recently categorized and studied by researchers, are two subtypes of multistable systems, which have infinite number of coexisting attractors.

In 2017, for the first time, the term megastability was introduced by Sprott et al., which is defined by coexistence of a countable infinity of attractors in a system. Their proposed system is a periodically forced oscillator with a spatially periodic damping term (Sprott et al. 2017). This system has coexisting attractors including limit cycles, tori and chaotic attractors which form a layered cabbage-like structure. Wang et al. (2018) proposed a new oscillator which has infinite coexisting asymmetric attractors and hence is in the group of systems with megastability property. In this system, some attractors are in the group of hidden and the others are in the group of self-excited attractors. A new two-dimensional nonlinear oscillator with infinite coexisting whirlpool-like-structure limit cycles was proposed in Tang et al. (2018a). Tang et al. (2018b) proposed a megastable system whose coexisting attractors form a carpet-like structure.

There are some linear and nonlinear methods to investigate the properties of the complex system, especially chaotic systems. Considering the phase space of the system for different initial conditions is one of the basic approaches to show the multistability of a system. Also, considering the bifurcation diagram and Lyapunov exponents (LEs) for different initial conditions can exhibit coexisting attractors as the control parameter of the system changes. Entropy is another measure that has the potential to show the complexity of the systems. Many entropy measures have been proposed in recent years, such as Kolmogorov, approximate (ApEn), permutation (also modified permutation) entropies.

In the past 3 decades, the phenomenon of synchronization between coupled nonlinear systems and especially systems with chaotic behavior has attracted the interest of the research community due to the broad range of applications, such as in various complex biological, physical and chemical systems (Szatmári and Chua 2008; Tognoli and Kelso 2009; Mosekilde et al. 2002; Holstein-Rathlou et al. 2001; Pikovsky et al. 2003), in secure and broadband communication system (Kocarev et al. 1992; Jafari et al. 2010; Feki et al. 2003; Wu and Chua 1993; Sheng-Hai and Ke 2004; Cuomo et al. 1993; Dmitriev et al. 2006) and in cryptography (Dachselt and Schwarz 2001; Khan et al. 2018; Baptista 1998; Volos et al. 2006; Klein et al. 2005; Alvarez and Li 2006; Annovazzi-Lodi et al. 1997; Grassi and Mascolo 1999). However, having two chaotic systems being synchronized is a major surprise, due to the exponential divergence of the nearby trajectories of the systems. A great number of researches based on synchronization of nonlinear systems have been carried out. Complete or full chaotic synchronization, phase synchronization, lag synchronization, generalized synchronization, antisynchronization, anti-phase synchronization, projective, anticipating, inverse lag synchronization and fractional-order synchronization are the most interesting synchronization types which have been investigated numerically and experimentally by many research groups (Voss 2000; Cao and Lai 1998; Kim et al. 2003; Tolba et al. 2017; Li 2009; Kyprianidis and Stouboulos 2003; Dykman et al. 1991). However, the most interesting and the most studied case of synchronization is the complete or full synchronization. In this case, the interaction between two coupled identical nonlinear circuits leads to a perfect coincidence of their chaotic trajectories, i.e.,

$$x_{1} \left( t \right) = x_{2} \left( t \right),\quad {\text{as}}\,t \to \infty$$

(1)

Furthermore, chaotic systems are used today in many applications due to their interesting characteristics, such as highly sensitive dependence on initial conditions and system’s parameters, non-periodicity, unpredictability, wide spectrum (as well as noise) and limited orbits in the phase space (Azzaz et al. 2013; Liu and Zhang 2013; Yu 2011). So, it is necessary to have real circuits for the purpose of using chaotic systems in engineering applications. Therefore, the realization of chaotic systems with analog electronic devices (resistance, capacitor, operational amplifier) is often used. On the other hand, embedded digital devices, such as field-programmable gate array (FPGA) (Shah et al. 2017; Tlelo-Cuautle et al. 2015; Alçın et al. 2016), field-programmable analog array (FPAA) (Caponetto et al. 2005; Kilic and Dalkiran 2009; Dalkiran and Sprott 2016), digital signal processor (DSP) (Guglielmi et al. 2009) and microcontroller (Kaçar 2016; Zambrano-Serrano et al. 2017; Volos 2013; Acho 2015), are used in the digital design of chaotic systems. Digital designs have advantages over analog designs due to some features, such as the lower energy consumption, small physical dimensions and the easy way of making changes.

In this article, we first introduce our proposed quasiperiodically forced chaotic oscillator with megastability and its statistical properties in Sect. 2. Dynamical behavior of this novel system is analyzed using Lyapunov exponents (LEs), bifurcation diagram and entropy in Sect. 3. In Sect. 4, the study of the synchronization between bidirectionally or unidirectionally coupled dynamical systems with megastability is presented for the first time as far as we know. The proposed system’s realization by using a microcontroller is introduced in Sect. 5. The paper is concluded in the last section.

2 Quasiperiodically Forced Oscillator (QFO)

Let us consider the following oscillator which is discussed in Kahn and Zarmi (2014):

$$\begin{aligned} \dot{x} & = y \\ \dot{y} & = - x + y\cos \left( x \right) \\ \end{aligned}$$

(2)

Modifying system (2) by forcing it with a quasiperiodic function gives a system as:

$$\begin{aligned} \dot{x} & = y \\ \dot{y} & = - \cos (ax) - by\cos \left( x \right) + A\left( {\sin \left( {ct} \right) + \sin \left( {dt} \right)} \right) \\ \end{aligned}$$

(3)

If the ratio $\frac{c}{d}$ is irrational, the forcing term is quasiperiodic. System (3) is a nonautonomous system; hence, calculating fixed points for this system is not possible. Therefore, we consider unforced form of the system, $A = 0$, and thus this system has infinite number of equilibrium points in $\left[ {\left( {2n - 1} \right)\frac{\pi }{2a},0} \right]$ where $n$ is an integer number.

The Jacobian of the above system in its equilibria is:

$$\left[ {\begin{array}{*{20}c} 0 & 1 \\ {a\sin \left( {ax} \right) + by\sin \left( x \right)} & { - b\cos \left( x \right)} \\ \end{array} } \right]$$

(4)

The characteristic polynomial can be derived as:

$$\lambda^{2} + b\cos \left( {\left( {2n - 1} \right)\frac{\pi }{2a}} \right)\lambda - a\sin \left( {\left( {2n - 1} \right)\frac{\pi }{2}} \right)$$

(5)

So, the eigenvalues will be:

$$\begin{aligned} \lambda_{1,2} = \frac{{ - B \pm \left( {B^{2} - 4C} \right)^{0.5} }}{2} \hfill \\ B = b\cos \left( {\left( {2n - 1} \right)\frac{\pi }{2a}} \right) \hfill \\ C = - a\sin \left( {\left( {2n - 1} \right)\frac{\pi }{2a}} \right) \hfill \\ \end{aligned}$$

(6)

For a specific value of $a$ and $b$, it can be concluded that if $b {\text{cos}}\left( {\left( {2n - 1} \right)\frac{\pi }{2a}} \right) < 0$, the corresponding equilibrium is unstable and when $b {\text{cos}}\left( {\left( {2n - 1} \right)\frac{\pi }{2a}} \right) > 0$, it is stable. Considering that $b, a > 0$, the equilibrium is unstable if $\frac{a + 1}{2} < n < \frac{3a + 1}{2}$ and is stable if $n < \frac{a + 1}{2}$ or $\frac{3a + 1}{2} < n < \frac{4a + 1}{2}$.

As per Routh–Hurwitz criterion, all the principal minors need to be positive in order to have stable equilibrium. The principal minors are,

$$\delta_{0} > 0,\quad \Delta_{1} = \delta_{1} > 0,\quad \Delta_{2} = \delta_{1} \delta_{2} > 0$$

(7)

where $\delta_{0} = 1$, $\delta_{1} = b\cos \left( {\left( {2n - 1} \right)\frac{\pi }{2a}} \right)$ and $\delta_{2} = - a\sin \left( {\left( {2n - 1} \right)\frac{\pi }{2a}} \right)$. Again we can conclude from the Routh–Hurwitz criterion that the equilibrium is stable if $\frac{3a + 1}{2} < n < \frac{4a + 1}{2}$ and is unstable otherwise.

Now our interest is finding chaotic solutions in system (3), and it should be noted that the system shows chaotic solutions for various combinations of $A,a,b,c$ and $d$. The forcing term is quasiperiodic when the ratio $\frac{c}{d}$ is irrational; hence, we choose $c = \sqrt {0.5}$ and $d = \sqrt {0.2}$. The other parameters are taken as $A = 0.07,a = 0.3$ and $b = 0.55$. The different nested attractors of the system for various initial conditions are shown in Fig. 1. It should be noted that $t$ in Eq. (3) is considered as state variable and $t_{0} = 0$ as initial condition.

Fig. 1

QFO coexisting attractors when initial conditions ($\left[ {x_{0} , y_{0} ,t_{0} } \right]$) are, respectively, [0, 0, 0], [0.5, 0, 0], [1, 0, 0], [1.3, 0, 0], [1.5, 0, 0], [2, 0, 0], [3, 0, 0], and [3.5, 0, 0] in plot₁ to plot₈

3 Dynamical Behavior of the QFO

To analyze the complete dynamical behavior of the QFO, we derive the bifurcation diagrams of the system by considering $b$ as the control parameter. The QFO shows chaotic oscillations for $0.0595 \le b \le 0.06$, $0.175 \le b \le 0.2148$, $0.335 \le b \le 0.34$, $0.528 \le b \le 0.595$, $0.607 \le b \le 0.787$ and $0.8423 \le b \le 1$ as shown in Fig. 2a. These intervals are confirmed by the Lyapunov spectrum given in Fig. 2b. To show the effect of initial conditions on the QFO, we have also derived the bifurcation-like diagram of the system when the initial condition x_o changes (Fig. 3a). Actually, as this system shows infinite coexisting attractors, we can conclude that it is in the group of systems with megastability property. Also, this figure shows that this system has the state variable $x$ as offset boostable and the DC offset of this variable can boost the system to any level (Li et al. 2015b; Li and Sprott 2016). We could see alternative regions of chaotic attractor and attracting tori which are confirmed by the corresponding Lyapunov exponents shown in Fig. 3b.

Fig. 2

a Bifurcation diagram of the QFO system as parameter $b$ increases and the other parameters are taken as $A = 0.07, a = 0.3$, $c = \sqrt {0.5}$, $d = \sqrt {0.2}$ and initial condition $\left[ {0, 0, 0} \right]$. b corresponding Lyapunov exponents

Fig. 3

a Bifurcation diagram of the QFO when the initial condition $x_{0}$ changes and the other parameters are taken as $A = 0.07, a = 0.3$, $b = 0.55$, $c = \sqrt {0.5}$, $d = \sqrt {0.2}$ and $y_{0} = 0$. Existence of these coexisting attractors shows the megastability of this system. b Corresponding Lyapunov exponents

Approximate entropy is also used to measure the complexity of the system as the control parameter changes. Considering a series of data $u\left( 1 \right), u\left( 2 \right), \ldots , u\left( N \right)$, for each control parameter, forms a sequence vector $x\left( 1 \right), x\left( 2 \right), \ldots , x\left( {N - m + 1} \right) \in R^{m}$ in which $m$ is a positive integer. This vector is defined by,

$$x\left( i \right) = \left[ {u\left( i \right), u\left( {i + 1} \right), \ldots , u\left( {i + m - 1} \right)} \right],\quad 1 \le i \le N - m + 1$$

(8)

For each $i$, we have

$$d\left[ {x\left( i \right),x\left( j \right)} \right] = \mathop {\hbox{max} }\limits_{k = 1,2, \ldots ,m} \left( {\left| {u\left( {i + k - 1} \right) - u\left( {j + k - 1} \right)} \right|} \right)$$

(9)

To measure the similarity of other sequences ($x\left( j \right)$) to $x\left( i \right)$, $c_{i}^{m} \left( r \right)$ is defined as,

$$c_{i}^{m} \left( r \right) = ({\text{number}}\,{\text{of}}\,j\,{\text{which}}\,{\text{satisfies}}\,d[x(i),x(j)] \le r)/\left( {N - m + 1} \right)$$

(10)

$$\phi^{m} \left( r \right) = \frac{{\mathop \sum \nolimits_{j = 1}^{N - m + 1} \log C_{i}^{m} \left( r \right)}}{N - m + 1}$$

(11)

where $r$ is the tolerance of this similarity and is defined by $r = k \times {\text{std}}\left( {u\left( t \right)} \right)$ and $0.1 \le k \le 0.2$. Finally, approximation entropy is defined as

$${\text{ApEn}}\left( {m,r,N} \right) = \phi^{m} \left( r \right) - \phi^{m + 1} \left( r \right)$$

(12)

Figure 4 shows the corresponding approximation entropy of the QFO as the parameters are the same as Fig. 2 and $m$ and $r$ are chosen as 8 and 0.1, respectively. Comparing Figs. 4 and 2, we claim that ApEn can distinguish quasiperiodic attractor from chaotic as it assigns positive values to chaotic responses. The equivalent ApEn of Fig. 3 is shown in Fig. 5 which approves previous results.

Fig. 4

ApEn of system (2) as the control parameter, $b$, changes. Other parameters are taken as $A = 0.07, a = 0.3$, $b = 0.55$, $c = \sqrt {0.5}$, $d = \sqrt {0.2}$ and initial condition $\left[ {0, 0, 0} \right]$. Also, $m$ and $r$ are chosen 8 and 0.1, respectively

Fig. 5

ApEn of system (2) as the control parameter, $x_{0}$, changes and the other parameters are taken as $A = 0.07, a = 0.3$, $b = 0.55$, $c = \sqrt {0.5}$, $d = \sqrt {0.2}$ and $y_{0} = 0$. Also, $m$ and $r$ are chosen 8 and 0.1, respectively

4 The Coupling Schemes

Generally, there are various methods of coupling between coupled nonlinear systems available in the literature. However, two are the most interesting. In the first method due to Pecora and Carroll (1990), a stable subsystem of a chaotic system could be synchronized with a separate chaotic system under certain suitable conditions. In the second method, chaos synchronization between two nonlinear systems is achieved due to the effect of coupling without requiring any stable subsystem be constructed (Kyprianidis and Stouboulos 2003; Chua et al. 1992).

The second method can be divided into two classes: drive response or unidirectional coupling and bidirectional or mutual coupling. In the first case, one system drives another one called the response or slave system. The system of two unidirectional coupled identical systems is described by the following set of differential equations:

$$\begin{aligned} \dot{\varvec{x}} & = F\left( \varvec{x} \right) \\ \dot{\varvec{y}} & = F\left( \varvec{y} \right) + \xi \left( {\varvec{x} - \varvec{y}} \right) \\ \end{aligned}$$

(13)

where F is a vector field in a phase space of dimension n and ξ is the coupling factor, which describes the nature and strength of the coupling between the oscillators. It is obvious from (13) that only the first system influences the dynamic behavior of the other.

In the second case, both the coupled systems are connected and each one influences the dynamics of the other. This is the reason for which this method is called mutual (or bidirectional). The coupled system of two mutually coupled chaotic oscillators is described by the following set of differential equations:

$$\begin{aligned} \dot{\varvec{x}}_{1} & = F\left( {\varvec{x}_{1} } \right) + \xi \left( {\varvec{x}_{2} - \varvec{x}_{1} } \right) \\ \dot{\varvec{x}}_{2} & = F\left( {\varvec{x}_{2} } \right) + \xi \left( {\varvec{x}_{1} - \varvec{x}_{2} } \right) \\ \end{aligned}$$

(14)

In this work, the study of the dynamic behavior of the bidirectionally and unidirectionally coupled systems of Eq. (3) has been investigated numerically by employing the fourth-order Runge–Kutta algorithm. It is the first time, as far as we know, that the synchronization between coupled chaotic systems with megastability has been investigated.

So, the system of differential equations that describes the bidirectionally coupled systems’ dynamics is:

$$\begin{aligned} \dot{x}_{1} & = y_{1} + \xi \left( {x_{2} - x_{1} } \right) \\ \dot{y}_{1} & = - \cos (ax_{1} ) - by\cos \left( {x_{1} } \right) + A\left( {\sin \left( {ct} \right) + \sin \left( {dt} \right)} \right) \\ \dot{x}_{2} & = y_{2} + \xi \left( {x_{1} - x_{2} } \right) \\ \dot{y}_{2} & = - \cos (ax_{2} ) - by\cos \left( {x_{2} } \right) + A\left( {\sin \left( {ct} \right) + \sin \left( {dt} \right)} \right) \\ \end{aligned}$$

(15)

The first two equations of system (15) describe the first of the two coupled identical systems with megastability, while the other two describe the second one. Also, the parameter ξ is the coupling coefficient and it is present in the equations of both systems since the coupling between them is mutual.

In the case of unidirectionally coupled systems (3), the following system of differential equations is produced:

$$\begin{aligned} \dot{x}_{1} & = y_{1} \\ \dot{y}_{1} & = - \cos (ax_{1} ) - by\cos \left( {x_{1} } \right) + A\left( {\sin \left( {ct} \right) + \sin \left( {dt} \right)} \right) \\ \dot{x}_{2} & = y_{2} + \xi \left( {x_{1} - x_{2} } \right) \\ \dot{y}_{2} & = - \cos (ax_{2} ) - by\cos \left( {x_{2} } \right) + A\left( {\sin \left( {ct} \right) + \sin \left( {dt} \right)} \right) \\ \end{aligned}$$

(16)

The coupling coefficient ξ is present only in the second coupled system since only the first system affects the dynamics of the second.

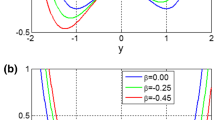
The parameters of the system are chosen as: $A = 0.07, a = 0.3$, $b = 0.55$, $c = \sqrt {0.5}$, $d = \sqrt {0.2}$. So, by solving numerically the coupled systems’ Eqs. (15) and (16), the bifurcation diagrams of the signal’s difference (y₂ − y₁) versus the coupling factor ξ are produced. These diagrams are produced by increasing the coupling factor ξ, from ξ = 0 (uncoupled systems) with step Δξ = 4 × 10⁻⁵, by using the same initial conditions in each iteration (x₁, y₁, x₂, y₂)₀ = (0, 0, 3.5, 0). With these initial conditions, the two coupled systems have different chaotic attractors, as they are depicted in Fig. 1.

4.1 Bidirectional Coupling

The bifurcation diagram of the bidirectionally coupling system (15) in Fig. 6 shows that the coupled system undergoes from full desynchronization, for ξ < 0.00356 (Fig. 7a), where each system is in a chaotic state and lies on its own manifold to complete chaotic synchronization for ξ ≥ 0.05836 (Fig. 7f), where their manifolds coincide through an intermediate region where the system shows a more complex dynamic behavior. This is an interesting transition from full desynchronization to complete synchronization.

Fig. 6

Bifurcation diagram of (y₂ − y₁) versus ξ of the bidirectionally coupling system (15), with the same initial conditions in each iteration. The parameters are: $A = 0.07, a = 0.3$, $b = 0.55$, $c = \sqrt {0.5}$, $d = \sqrt {0.2}$ and initial conditions (x₁, y₁, x₂, y₂)₀ = (0, 0, 3.5, 0)

Fig. 7

Simulation phase portraits of y₂ versus y₁ of the bidirectionally coupled system (15) with $A = 0.07, a = 0.3$, $b = 0.55$, $c = \sqrt {0.5}$, $d = \sqrt {0.2}$ and initial conditions (x₁, y₁, x₂, y₂)₀ = (0, 0, 3.5, 0), for aξ = 0.002 (chaotic desynchronization), bξ = 0.0095 (complete synchronization), cξ = 0.015 (quasiperiodic desynchronization), dξ = 0.0433 (chaotic desynchronization), eξ = 0.05 (quasiperiodic desynchronization), fξ = 0.065 (complete synchronization)

So, the intermediate region of the bifurcation diagram of Fig. 6 is more complicated and it can be divided into two discrete regions:

• Region I: 0.00356 ≤ ξ < 0.03724 (quasiperiodic desynchronization). This type of behavior (Fig. 7c) is interrupted by small regions of chaotic desynchronization as well as a small region of complete synchronization (Fig. 7b).

• Region II: 0.03724 ≤ ξ < 0.05836 (intermittent synchronization). Intermittent synchronization has been observed in a variety of different experimental settings in physics and beyond and is an established research topic in nonlinear dynamics (Pomeau and Manneville 1980). When coupled oscillators exhibit relatively weak, intermittent synchrony, the trajectory in the phase space spends a substantial fraction of time away from a vicinity of a synchronized state. Thus, to describe and understand the observed dynamics, one may consider both synchronized episodes and desynchronized episodes (the episodes when oscillators are not synchronous). Briefly, the desynchronized episodes in these cases can be either chaotic or quasiperiodic, as it is depicted in Fig. 7d, e, respectively.

So, in this case of coupling, a sudden transition from the extended quasiperiodic desynchronization region to the also extended intermittent synchronization region, which is very rare in the literature, has been reported.

4.2 Unidirectional Coupling

In the case of unidirectionally coupling system (16), the bifurcation diagram, which has been obtained numerically, is depicted in Fig. 8. From this diagram, another interesting system’s (3) behavior can be observed. The coupled system undergoes full desynchronization for ξ < 0.00248 (Fig. 9a), where each system is in a chaotic state and lies on its own manifold to complete chaotic synchronization for ξ ≥ 0.1075 (Fig. 9d), where their manifolds coincide, through an intermediate region where the system shows a more complex dynamic behavior. In this region, the chaotic attractor of the first coupled system keeps its features, while the chaotic attractor of the second coupled system, as the coupling factor ξ is increased, is slightly shifted and its dimensions are decreased in the phase plane (Fig. 10). As a consequence, a shift in the plane of y₁–y₂ (Fig. 9b) and a decrease (Fig. 9c) in the direction of y₂ are also observed, as the coupling factor ξ is increased, which is a very interesting phenomenon. Finally, for ξ ≥ 0.1075, the system enters the region of a complete chaotic synchronization state.

Fig. 8

Bifurcation diagram of (y₂ − y₁) versus ξ of the unidirectionally coupling system (16), with the same initial conditions in each iteration. The parameters are: $A = 0.07, a = 0.3$, $b = 0.55$, $c = \sqrt {0.5}$, $d = \sqrt {0.2}$ and initial conditions (x₁, y₁, x₂, y₂)₀ = (0, 0, 3.5, 0)

Fig. 9

Simulation phase portraits of y₂ versus y₁ of the unidirectionally coupled system (16) with $A = 0.07, a = 0.3$, $b = 0.55$, $c = \sqrt {0.5}$, $d = \sqrt {0.2}$ and initial conditions (x₁, y₁, x₂, y₂)₀ = (0, 0, 3.5, 0), for aξ = 0.002 (chaotic desynchronization), bξ = 0.01 (chaotic desynchronization), cξ = 0.06 (chaotic desynchronization), dξ = 0.12 (complete synchronization)

Fig. 10

Simulation phase portraits of y₂ versus x₂ of the unidirectionally coupled system (16) with $A = 0.07, a = 0.3$, $b = 0.55$, $c = \sqrt {0.5}$, $d = \sqrt {0.2}$ and initial conditions (x₁, y₁, x₂, y₂)₀ = (0, 0, 3.5, 0), for ξ = 0.06

5 Experimental Setup

The feature of megastability of system (3) makes it attractive for an electronic realization using discrete electronics, like microcontroller units, in order to be used in a variety of chaos-based applications, like cryptography or random generators. Today, microcontrollers are found in a huge number of applications in automotive, consumer, communications and industrial manufacturing (Predko 2000). The microcontrollers are also important because they make electronic circuits cheaper and easier to build (Bates 2011). The objective of this paper is to use system (3) and a low-cost microcontroller-based device (Chaos Generator), which has been constructed at the Laboratory of Nonlinear Systems, Circuits & Complexity, in order to produce chaos by using C language.

Many well-known development platforms, like Arduino, have been used in such implementations. However, demands on computational power and data memory require a microcontroller from the latest series. For this reason, the Microchip Microcontroller which belongs to the MZ series microcontrollers has been chosen. Also, the ARM series microcontroller, with corresponding performance, as well as the Raspberry Pi development board could also be used for development because they meet the above requirements.

In brief, the implemented device consists of two boards (Fig. 11): a small board with a relatively new microcontroller from MZ series of Microchip Corp., namely PIC32MZ2048EFH144. It is a 32-bit microcontroller with FPU (floating-point unit) for 32-bit and 64-bit floating-point math, running at 250 MHz with large flash memory (2 Mbytes), large static RAM (512 Kbytes) and up to 120 I/O pins, to name only a few of the features of this microcontroller. On the same small board, there is also a crystal oscillator working at 12 MHz some anti-coupling capacitors and a LED indicator. On the main board, there is a 16-key keypad, a 2 × 16 (two lines of 16 characters per line) LCD, a USB type B connector, an SD card socket and a reset button. On the back side of the main board (solder side), there are two DACs which consist of resistors with R2R configuration, driving two BNC connectors. The device can numerically solve the QFO, by using the fourth-order Runge–Kutta algorithm. Two output signals produced by the DACs correspond to the state variables (x and y) of the system. The device can produce three of the most well-known diagrams from nonlinear theory: the bifurcation diagram, the phase portrait and the Poincaré map. The obtained data are displayed on an oscilloscope (digital or analog) or can also be stored on an SD card as time-series data. Figure 12 shows the place of all aforementioned parts of the chaos generator device. By using different initial conditions, the megastability of the system implemented with the device has been highlighted in the phase portraits of Fig. 13. It should be noted that the value of the parameters is the same as Fig. 1 (c = $\sqrt {0.5}$, d = $\sqrt {0.2}$, A = 0.07, a = 0.3 and b = 0.55). Comparing Figs. 1 and 13, the accuracy of our implemented device in generating different attractors of the system for different initial conditions is observed.

Fig. 11

“Chaos Generator” device (front side)

Fig. 12

Main parts of the “Chaos Generator” device as they have been placed inside the custom board

Fig. 13

QFO coexisting attractors, produced by the device, when initial conditions ($\left[ {x_{0} , y_{0} ,t_{0} } \right]$) are: a [0, 0, 0], b [0.5, 0, 0], c [1, 0, 0], d [1.5, 0, 0], e [2, 0, 0], f [2.5, 0, 0], g [3, 0, 0], and h [3.5, 0, 0]. Also, the other parameters are c = $\sqrt {0.5}$, d = $\sqrt {0.2}$, A = 0.07, a = 0.3 and b = 0.55

In Fig. 14, the bifurcation diagram of system (3), by considering $b$ as the control parameter, produced by the microcontroller device, which is obtained in an analog oscilloscope, is depicted. By comparing this bifurcation diagram with the respective diagram produced in MATLAB (Fig. 2), a divergence is observed. This divergence occurred due to the different way of calculation of the trigonometric functions between the MATLAB and microcontroller compiler library. However, in this case, the aforementioned divergence is not essential because the use of microcontroller highlights the main feature of the system, which is the megastability. So, we could also see regions of chaotic attractors and attracting tori which are confirmed by the phase portraits shown in Fig. 15, for various values of parameter b.

Fig. 14

Bifurcation diagram of the QFO system, produced by the microcontroller-based device, as parameter b increases and the other parameters are taken as $A = 0.07, a = 0.3$, $c = \sqrt {0.5}$, $d = \sqrt {0.2}$ and initial condition [0, 0, 0]

Fig. 15

QFO attractors, produced by the microcontroller-based device, when initial conditions are [0, 0, 0], for ab = 0.06, bb = 0.25, cb = 0.45, db = 0.73, eb = 0.86 and fb = 0.93

To verify the effect of initial conditions on the QFO, the bifurcation-like diagram of the system when the initial condition x_o changes has been obtained by using the analog oscillator (Fig. 16). Alternative regions of chaotic attractors and attracting tori are confirmed by the phase portraits in x–y plane for various values of the initial condition $x_{0}$ (Fig. 17).

Fig. 16

Bifurcation diagram of the QFO, produced by the microcontroller-based device, when the initial condition $x_{0}$ changes and the other parameters are taken as: $A = 0.07, a = 0.3$, $b = 0.55$, $c = \sqrt {0.5}$, $d = \sqrt {0.2}$ and $y_{0} = 0$

Fig. 17

QFO attractors, produced by the microcontroller-based device, when parameters are taken as $A = 0.07, a = 0.3$, $b = 0.55$, $c = \sqrt {0.5}$, $d = \sqrt {0.2}$ and $y_{0} = 0$ and initial condition of x₀ is ax₀ = 5, bx₀ = 30, cx₀ = 40, dx₀ = 50, ex₀ = 60, fx₀ = 70, gx₀ = 90 and fx₀ = 99

6 Conclusion

To search for the coexistence of infinite countable attractors, megastability, it is necessary to examine different initial conditions as the control parameters are fixed. In this paper, we design a quasiperiodic forced nonlinear oscillator which is chaotic and megastable. State space, bifurcation diagram, Lyapunov exponents and basin of attraction of the proposed system were investigated. Furthermore, the phenomenon of synchronization of two bidirectionally and unidirectionally coupled quasiperiodic forced nonlinear systems with megastability was studied for the first time. In the case of bidirectional coupling, interesting dynamics such as a transition from a region of chaotic desynchronization to quasiperiodic desynchronization and finally to a complete synchronization via an intermittent phenomenon was observed. On the other hand, in the unidirectional coupling case, the coupled system passed from the desynchronization to complete synchronization through a region where the chaotic attractor of the second coupled system was shifted and decreased. Also, the proposed system’s realization was done by using a microcontroller-based device. The feature of the megastability was also observed making the device with the quasiperiodically forced oscillator capable of using it in chaos-based applications, like cryptography and random number generators. The proposed schemes of coupling (unidirectional and bidirectional), between chaotic oscillator with megastability, implemented with integrated nonlinear circuits, for a communication over the Internet, could be an interesting subject of a future study. In this direction, practical problems related to noise and mismatches, which may affect the chaotic synchronization, could be studied.