Coupled van der Pol and Duffing oscillators: emergence of antimonotonicity and coexisting multiple self-excited and hidden oscillations

Abstract

Due to its fundamental and technological relevance, the system formed by a van der Pol oscillator coupled to a Duffing oscillator is the subject of increasing research interest. In this contribution, we study the dynamics of a system composed of a van der Pol oscillator coupled to a Duffing oscillator with two asymmetric potential wells. In the considered coupling scheme, the van der Pol oscillator is disturbed by a signal proportional to the difference of position while the Duffing oscillator is driven by a signal proportional to the speed difference. We use analytical and numerical methods to shed light on the complex behaviors exhibited by the coupled system. We highlight striking phenomena such as hysteresis, parallel bifurcation branches, the coexistence of multiple (i.e., three, four or five) self-excited and hidden attractors, and the coexistence of symmetric and asymmetric bifurcation bubbles depending on the numerical values of initial conditions and parameters. An in-depth study of the coexistence of solutions is carried out by constructing basins of attraction. Sample experimental results captured from STM32F407ZE microcontroller-based digital implementation of the coupled system verify the striking dynamics features observed during the theoretical analysis. It should be noted that the coexistence of a hidden attractor with self-excited others is unique for the coupled oscillators system considered in the context of this work and thus deserves dissemination.

1 Introduction

In the field of nonlinear dynamical systems, the terms mono-stability, bi-stability and multistability refer to situations for which a dynamical system has one, two, or more than two attractors [1]. Extreme multistability is used in the case of an infinity of attractors. When there are more than two solutions (i.e., attractors) for the same rank of parameters, the state space is partitioned so that each of the competing attractors is associated with a domain of initial conditions giving rise to the underlined attractor (i.e., basin of attraction). The number and types of competing attractors vary with system parameters. The multistable system can involve attractors of the same type (self-excited or hidden) or of both types (self-excited and hidden attractors) [2, 3]. This latter situation is very little documented. We would like to quote that a hidden attractor has a basin of attraction which does not intercede with the vicinity of an unstable equilibrium point. Otherwise, the attractor is said to be self-excited. From another point of view, a distinction is made between homogeneous multistability and heterogeneous multistability [4, 5]. Heterogeneous multistability means that with the same values of parameters, the chaotic system possesses several chaotic attractors with different topology, while homogenous multistability refers to the case where the chaotic system can generate attractors with the same topology, but the amplitudes and state space locations of the various attractors can be different. At this point, it should be noted that in view of recent publications, multistability undoubtedly represents one of the most discussed research themes in nonlinear science. For example, multistability is the subject of many works in laser systems, electronic circuits, ecological models, chemical processes, biological models as well as economic models, just to name a few [6].

In this contribution, we focus on the dynamics of a system made of a van der Pol oscillator [7] coupled to a Duffing oscillator [8] with particular emphasis on the occurrence of multistable dynamics. Before we proceed, a brief review on previous studies related to the dynamics of these type of system is necessary. Literature [9] focusses on the dynamics of a system formed by a van der Pol oscillator coupled (elastically and dissipatively) to a Duffing oscillator described by the following couple of second-order equations:

$$ \frac{{{\text{d}}^{2} x}}{{{\text{d}}t^{2} }} - \varepsilon_{1} \left( {1 - x^{2} } \right)\frac{{{\text{d}}x}}{{{\text{d}}t}} + \omega_{1}^{2} x + cx^{3} = c_{1} y + c_{2} \frac{{{\text{d}}y}}{{{\text{d}}t}} $$

(1a)

$$ \frac{{{\text{d}}^{2} y}}{{{\text{d}}t^{2} }} + \varepsilon_{2} \frac{{{\text{d}}y}}{{{\text{d}}t}} + \omega_{2}^{2} y + c_{0} y^{3} = c_{1} x + c_{2} \frac{{{\text{d}}x}}{{{\text{d}}t}} $$

(1b)

where ε₁ and ε₂ represent positive real parameters and c and c₀ are the coefficients controlling the nonlinearity in both oscillators. c₁ and c₂ denote, respectively, the elastic and dissipative coupling parameters. ω₁ and ω₂ refer to the natural frequencies of the oscillators. An example of a physical system with practical interest connected to system (1) is a nonlinear oscillator operating under the action of a self-sustained electrical oscillator [9]. The analytic solutions are derived in the resonant and non-resonant regime of operation. The chaotic dynamics is examined by utilizing the Shilnikov theorem complemented by a direct numerical integration of the coupled evolution equations. Literature [10] further investigates with analog simulators the complex behavior of a system (1). Amplitude response curves are derived in the internal resonance mode. Hysteretic dynamics and jump phenomenon are highlighted. Sudden chaos, period-adding and torus break down scenarios to chaos are revealed. Both experimental results the numerical solutions present a very good agreement. In Ref.3 also considers the dynamics of a system composed of a van der Pol oscillator elastically coupled to a double-well Duffing oscillator [11] governed by the following coupled system of second-order nonlinear differential equations:

$$ \frac{{{\text{d}}^{2} x}}{{{\text{d}}t^{2} }} - \mu \left( {1 - x^{2} } \right)\frac{{{\text{d}}x}}{{{\text{d}}t}} + x - k\left( {y - x} \right) = 0 $$

(2a)

$$ \frac{{{\text{d}}^{2} y}}{{{\text{d}}t^{2} }} + \alpha \frac{{{\text{d}}y}}{{{\text{d}}t}} - y + \delta y^{2} + \varepsilon y^{3} - k\left( {x - y} \right) = 0 $$

(2b)

where μ and ε indicate positive real parameters that control the model nonlinearities. α measures the dissipation while k denotes the coupling coefficient. It is shown that the existence of different attractors in the system engenders rich dynamic patterns when changing both parameters and the coupling strength. The transitions between the various dynamic regimes are illustrated by resorting to 1D and 2D bifurcation diagrams produced for specific values of the coupling coefficient. The author also examined the synchronization of the coupled system when monitoring its parameters. Further results related to the complex behavior of the coupled system (2) are reported in [12] where complementary information related to the numerical analysis, the circuit simulation and the synchronization system (2) are provided. In particular, the authors studies the stability of the equilibrium points analytically by using the Routh stability criterion. The bifurcation mechanism of the coupled system (2) is investigated with particular attention on the effects induced by the nonlinearity. Hardware experimental measurements based on a suitable analog simulator of the system confirm the theoretical predictions. The problem of synchronization of the coupled system (2) is also addressed by resorting to recent results on adaptive control theory. In [13], the authors consider the dynamics of a self-driven electromechanical transducer governed by the following coupled van der Pol and Duffing equations:

$$ \frac{{{\text{d}}^{2} x}}{{{\text{d}}t^{2} }} - \varepsilon_{1} \left( {1 - x^{2} } \right)\frac{{{\text{d}}x}}{{{\text{d}}t}} + \omega_{1}^{2} x + f\frac{{{\text{d}}^{2} y}}{{{\text{d}}t^{2} }} = 0 $$

(3a)

$$ \frac{{{\text{d}}^{2} y}}{{{\text{d}}t^{2} }} + \varepsilon_{2} \frac{{{\text{d}}y}}{{{\text{d}}t}} + \omega_{2}^{2} y + cy^{3} - {\text{d}}x = 0 $$

(3b)

where f and d control the gyroscopic and elastic coupling of both oscillators. Other parameters are defined as previously. The authors investigate the stability of the equilibrium points by making use of the analytic Routh–Hurwitz criterion. They derived analytic oscillatory solutions for the resonant and nonresonant cases as well. The chaotic mechanism is studied by resorting to the Shilnikov theorem complemented by a direct numerical integration of the evolution equations. Literature [14] further investigates the complex dynamics of system (3) by providing several bifurcation diagrams and related graphs of 1D largest Lyapunov exponent. Period doubling, sudden transitions, torus breakdown and period adding routes to chaos are reported. The sensitivity of the self-driven electromechanical system with respect to changes in both initial conditions and the coupling strengths is also described. A suitable electronic analog of the self-excited electromechanical system is designed and used for investigations. The abovementioned studies, thus very enriching and interesting, restrict on coupled systems with ideal symmetry, and the influence of both initial states and parameters (e.g., multistable dynamics) is not sufficiently analyzed. Also, in order to provide additional insight on the complex behavior exhibited by such class of systems, the main contributions and innovations of the presents work can be listed as follows:

• 1. We consider the dynamics of a system composed of a van der Pol oscillator coupled elastically (i.e., via solutions) and dissipatively (i.e., via velocity) to an asymmetric double-well Duffing oscillator;

• 2. Domains of hysteretic behaviors and multistability are identified by monitoring both the parameters and initial conditions in both symmetric and asymmetric regimes of operation;

• 3. We evaluate how the explicit symmetry break modifies the location and nature of the equilibrium points, the bifurcation modes, the topology and number of coexisting attractors, and the structure of the basins of attraction as well.

• 4. An experimental study based on STM32F407ZE microcontroller digital implementation of the coupled system is carried out to verify the striking dynamics features observed during the theoretical investigations.

The rest of our presentation is articulated in our sections. Section 2 presents the evolution equation of the system of formed by linear connection a van der Pol oscillator to an asymmetric Duffing oscillator. We discuss the stability and nature of the equilibrium points based on the classic Routh–Hurtwitz criterion. The numerical study of the coupled oscillator system is described in Sect. 3 by resorting to 1D and 2D Lyapunov diagrams, 1D bifurcation plots, state space trajectories plots and basins of attraction as well. We report attractive and complex features such as coexisting asymmetric self-excited and hidden dynamics, coexisting asymmetric period-doubling reversals, hysteresis, and basin collapse (i.e., critical event) when the coupled system parameters are changed. An experimental study based on STM32F407ZE microcontroller digital implementation of the coupled system is carried out in Sect. 4. The conclusion of whole work is included in Sect. 5.

2 Evolution equations and basic properties

2.1 Evolution equations

The evolution equation of the system made of a van der Pol oscillator mutually coupled to a Duffing oscillator which is the material of the present work consists of the following two coupled second-order nonlinear ordinary differential equations:

$$ \frac{{{\text{d}}^{2} x}}{{{\text{d}}t^{2} }} - \mu \left( {1 - x^{2} } \right)\frac{{{\text{d}}x}}{{{\text{d}}t}} + x - k\left( {y - x} \right) = 0 $$

(4a)

$$ \frac{{{\text{d}}^{2} y}}{{{\text{d}}t^{2} }} + \alpha \frac{{{\text{d}}y}}{{{\text{d}}t}} - y + \beta y^{2} + \varepsilon y^{3} - k\left( {\frac{{{\text{d}}x}}{{{\text{d}}t}} - \frac{{{\text{d}}y}}{{{\text{d}}t}}} \right) = 0 $$

(4b)

where k denotes the coupling coefficient. μ and ε stand as positive real parameters which models the nonlinearities of the relevant oscillators. α represents the dissipation coefficient of the Duffing oscillator. The quadratic term (β) in the Duffing equation is introduced in order to perform an explicit symmetry breaking of the whole coupled system. Notice that in the underlined coupling scheme, the van der Pol oscillator is excited by a signal proportional to the difference of position while the Duffing oscillator is driven by a signal proportional to the speed difference [15]. System (4) is connected to diverse physical processes including a system made up of a nonlinear oscillator functioning under the action of a self-sustained electrical oscillator (i.e., electromechanical system [9]) whose general model reads:

$$ \frac{{{\text{d}}^{2} x}}{{{\text{d}}t^{2} }} - \varepsilon_{1} \left( {1 - x^{2} } \right)\frac{{{\text{d}}x}}{{{\text{d}}t}} + \omega_{1}^{2} x + cx^{3} = c_{1} y + c_{2} \frac{{{\text{d}}y}}{{{\text{d}}t}} $$

(5a)

$$ \frac{{{\text{d}}^{2} y}}{{{\text{d}}t^{2} }} + \varepsilon_{2} \frac{{{\text{d}}y}}{{{\text{d}}t}} - \omega_{2}^{2} y + c_{0} y^{3} = c_{3} x + c_{4} \frac{{{\text{d}}x}}{{{\text{d}}t}} $$

(5b)

Hence, the correspondence between the parameters of the coupled systems (4) and (5) can be easily identified (in the absence of perturbed quadratic term) as follows: c = 0; c₀ = ε, c₁ = k, c₂ = c₃ = 0, c₄ = k, ε₁ = μ, ε₂ = α + k, $\omega_{1}^{2} = 1 + k,\omega_{2}^{2} = 1$. Another mathematical representation of system (4a)-(4b) is defined in the following way:

$$ \frac{{{\text{d}}^{2} x}}{{{\text{d}}t^{2} }} - \mu \left( {1 - x^{2} } \right)\frac{{{\text{d}}x}}{{{\text{d}}t}} + \frac{{\partial U_{1} \left( x \right)}}{\partial x} - k\left( {y - x} \right) = 0 $$

(6a)

$$ \frac{{{\text{d}}^{2} y}}{{{\text{d}}t^{2} }} + \alpha \frac{{{\text{d}}y}}{{{\text{d}}t}} + \frac{{\partial U_{2} \left( y \right)}}{\partial y} - k\left( {\frac{{{\text{d}}x}}{{{\text{d}}t}} - \frac{{{\text{d}}y}}{{{\text{d}}t}}} \right) = 0 $$

(6b)

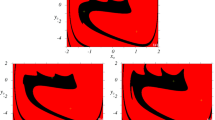
where $U_{1} \left( x \right) = \frac{1}{2}x^{2}$ represents the potential function related to the van der Pol oscillator and $U_{2} \left( y \right) = - \frac{1}{2}y^{2} + \frac{1}{3}\beta y^{3} + \frac{1}{4}\varepsilon y^{4}$ the potential function connected to the Duffing oscillators. Figure 1a, b displays the plots of the potential functions related to the Duffing oscillator obtained with ε = 1.0. We consider two different sets of values for the symmetry breaking parameter for the Duffing oscillator, namely β = 0.00, β = ±0.25 and β = ±0.45. With the definitions of variables $\frac{{{\text{d}}x}}{{{\text{d}}t}} = u$ and $\frac{{{\text{d}}y}}{{{\text{d}}t}} = v$, system (1) takes the form:

$$ \frac{{{\text{d}}x}}{{{\text{d}}t}} = u $$

(7a)

$$ \frac{{{\text{d}}u}}{{{\text{d}}t}} = \mu \left( {1 - x^{2} } \right)u - x + k\left( {y - x} \right) $$

(7b)

$$ \frac{{{\text{d}}y}}{{{\text{d}}t}} = v $$

(7c)

$$ \frac{{{\text{d}}v}}{{{\text{d}}t}} = - \alpha v + y - \beta y^{2} - \varepsilon y^{3} + k\left( {u - v} \right) $$

(7d)

For the uncoupled mode (i.e., k = 0.0), the van der Pol oscillator develops a limit cycle attractor, whereas the Duffing oscillator undergoes a fixed-point behavior. In case of a zero value of β-parameter, there is an important symmetry in the coupled system (7). In fact, if we replace $\left( {x(t),u(t),y(t),v(t)} \right)^{{\text{T}}}$ by $\left( { - x(t), - u(t), - y(t), - v(t)} \right)^{{\text{T}}}$, the equations stay the same. Hence if $\left( {x(t),u(t),y(t),v(t)} \right)^{{\text{T}}}$ is a solution, then $\left( { - x(t), - u(t), - y(t), - v(t)} \right)^{{\text{T}}}$ is also a solution regardless the values of parameters. In other words, all solutions are either symmetric themselves or owns a symmetric partner. The practical implication of the latter feature is the occurrence of multiple coexisting dynamics found in the coupled system. For any β ≠ 0, the symmetry of the coupled system is explicitly broken which is manifested by the presence of more complex dynamics in the parameter space.

Fig. 1

Plots of the potential functions (a, b) related to the Duffing oscillator obtained with ε = 1.0. We consider two different sets of values for the symmetry breaking parameter for the Duffing oscillator, namely β = 0.00, β = ±0.25 and β = ±0.45

2.2 The equilibrium points and their nature

The classic approach [16, 17] of searching for the equilibrium points by setting all the derivative to zero in the state equations and solving the corresponding nonlinear algebraic systems leads to the conclusion that the coupled system (7) owns three static solutions (i.e., equilibrium points): $M_{0} = \left( {0,0,0,0} \right)^{{\text{T}}} ,M_{1} = \left( {x_{1} ,0,y_{1} ,0} \right)^{{\text{T}}}$ and $M_{2} = \left( {x_{2} ,0,y_{2} ,0} \right)^{{\text{T}}}$ with x₁, x₂, y₁ and y₂ expressed in the following way:

$$ x_{1,2} = \frac{{k\left( { - \beta \pm \sqrt {\beta^{2} + 4\varepsilon } } \right)}}{{2\varepsilon \left( {1 + k} \right)}} $$

(7a)

$$ y_{1,2} = \frac{{ - \beta \pm \sqrt {\beta^{2} + 4\varepsilon } }}{2\varepsilon } $$

(7b)

In case of ideal symmetry (i.e., β = 0), M₁ and M₂ share symmetrical state space positions with respect to the original point M₀ and display the same dynamic property accordingly. From the linear perturbation of the coupled system (7) in the neighborhood of any point $N\left( {x_{0} ,u_{0} ,y_{0} ,v_{0} } \right)^{{\text{T}}}$ results in the following Jacobian matrix [5, 6]:

$$ M_{J} = \left[ {\begin{array}{llll} 0 \quad& 1 \quad& 0 \quad& 0 \\ { - 1 - k - 2\mu u_{0} x_{0} } \quad\quad & {\mu \left( {1 - x_{0}^{2} } \right)} \quad\quad& k \quad& 0 \\ 0 \quad& 0\quad & 0 \quad& 1 \\ 0 \quad& k \quad& {1 - 2\beta y_{0} - 3\varepsilon y_{0}^{2} } \quad\quad& { - \alpha - k} \\ \end{array} } \right] $$

(8)

Thus the characteristic polynomial ($Q\left( \eta \right) = \det \left( {M_{J} - \eta I_{d} } \right) = 0$) connected to the Jacobian matrix [17] computed at any state space point $M\left( {x_{0} ,0,y_{0} ,0} \right)^{{\text{T}}}$ is yielded as follows:

$$ Q\left( \eta \right) = \eta^{4} + m_{3} \eta^{3} + m_{2} \eta^{2} + m_{1} \eta + m_{0} $$

(9a)

with the real coefficients $m_{j} \left( {j = 0,1,2,3} \right)$ expressed as follows:

$$ m_{0} = \left( {1 + k} \right)\left( {1 - 2\beta y_{0} - 3\varepsilon y_{0}^{2} } \right) $$

(9b)

$$ m_{1} = - k^{2} + \left( {\alpha + k} \right)\left( {1 + k} \right) + \mu \left( {1 - 2\beta y_{0} - 3\varepsilon y_{0}^{2} } \right)\left( {1 - x_{0}^{2} } \right) $$

(9c)

$$ m_{2} = - 1 - k - \left( {1 - 2\beta y_{0} - 3\varepsilon y_{0}^{2} } \right) - \mu \left( {\alpha + k} \right)\left( {1 - x_{0}^{2} } \right) $$

(9d)

$$ m_{3} = \alpha + k - \mu \left( {1 - x_{0}^{2} } \right) $$

(9e)

After simple algebraic calculations based on the Routh–Hurwitz criterion, it turns out that for all the roots of the characteristic polynomial Q(η) to present negative real parts, the following set of four conditions must to be fulfilled:

$$ m_{j} > 0\left( {j = 0,1,2,3} \right) $$

(10a)

$$ m_{3} m_{2} - c_{j} > 0 $$

(10b)

$$ m_{3} \left( {m_{1} m_{2} - m_{0} m_{3} } \right) - m_{1}^{2} > 0 $$

(10c)

Regardless the values of parameters, we notice that $M_{0} \left( {0,0,0,0} \right)^{{\text{T}}}$ is always an unstable equilibrium point as the corresponding coefficient $m_{2} = - 2 - k - \mu \left( {\alpha + k} \right)$ is negative (i.e., presence of coefficients with opposite sign). Table 1 presents the sstability and nature of the three equilibrium points evaluated for a specific set of parameters’ values of the coupled system. The dynamic regime of the coupled systems and related figures are also provided.

Table 1 Stability and nature of the three equilibrium points evaluated for two specific sets of parameter values of the coupled system

3 Numerical experiment

3.1 Lyapunov diagrams and routes to chaos

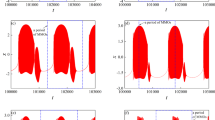
A suitable method of uncovering changes in the model dynamics resulting to parameter variation consists of computing two-parameter diagrams connected to the evolution of the largest Lyapunov exponent [18]. Plotted with different initial conditions, Lyapunov diagrams can be exploited to detect domains of hysteresis and multiple competing dynamics. On this line, Fig. 2 presents 2D Lyapunov diagrams showing the variation of the maximum Lyapunov exponent when a couple of parameters are considered, namely in the k–μ, k–α and k–ε planes (see caption for details). The system is always started from the same initial state (0.1,0,0,0) for the right panel (Fig. 2a1–b1–c1) and (3,0,0,0) for the left panel (Fig. 2a2–b2–c2). The interpretation of the maximum Lyapunov exponent is done using the color bar. Considering a 1D path, we provide in Fig. 3 downward continuation of the coupled system (blue and green) from the initial states (± 0.1,0,0,0) when considering two different values of the dissymmetry (see Fig. 3a1–b1) parameter. The graphs of associated 1D maximum Lyapunov exponent (MLE) are provided in Fig. 3a2–b2. The red branch was obtained by scanning the parameter upward starting from initial state (5,0,0,0). Other parameters are: μ = 0.8, ε = 1.2, k = 3.0. It clearly appears from Fig. 3 that the model follows a period doubling route to chaos when decreasing α-parameter. Notice a very good coincidence between the bifurcation diagrams and the associated plots of largest Lyapunov exponent provided in Fig. 3b1–b2. In case of an ideal symmetry (β = 0.0), the blue and green bifurcation trees are perfectly symmetric and owns the same maximum Lyapunov exponent accordingly. In contrast, for a nonzero value of β (eg. β = 0.05), the blue and green bifurcation trees displays a horizontal shift which results in the occurrence of asymmetric competing solutions. Interestingly, in the latter situation, the green bifurcation three collapses as a result of a crisis event when α is decreased in tiny steps (see Fig. 3a1). We present in Fig. 4 several coexisting phase portraits for both oscillators confirming route to chaos for varying α using the parameters of Fig. 3a1, namely α = 0.80; α = 0.60; α = 0.55; and α = 0.50. A hidden attractor (see Fig. 4e1–e2) coexists with those in Fig. 4c1–c2–d1–d2.

Fig. 2

Two-parameter Lyapunov diagrams showing the variation of the largest Lyapunov exponent when a couple of parameter are considered: a in the k–μ plane for α = 0.4, ε = 1.0, β = 0; b in the k–α plane for μ = 0.8, ε = 1.0, β = 0. c in the k–ε plane for μ = 0.8, α = 0.5, β = 0. The system is always started from the same initial state (0.1,0,0,0) for the right panel (a1–b1–c1) and (3,0,0,0) for the left panel (a2–b2–c2)

Fig. 3

Downward continuation of the coupled system (blue and green) from the initial states (± 0.1,0,0,0) computed for two different values of the dissymmetry (a1–b1) parameter. The graphs of corresponding 1D largest Lyapunov exponent (MLE) are provided in (a2–b2). The red branch is obtained by scanning the parameter upward starting from initial state (5,0,0,0). Other parameters are: μ = 0.8, ε = 1.2, k = 3.0

Fig. 4

Computer generated phase portraits for both oscillators showing route to chaos for varying α using the parameters of Fig. 2a1: a α = 0.80; b α = 0.60; c α = 0.55; d α = 0.50. The hidden attractor (e) that coexists with those in c and d

Considering the asymmetric set up, Fig. 5 displays several coexisting attractors of both oscillators showing the transition to chaos for varying α using the parameters of Fig. 3a2, namely α = 0.650; α = 0.585; α = 0.545; and α = 0.50. A hidden attractor (see Fig. 4e1–e2 coexists with those in Fig. 5c1–c2–d1–d2. Consequently, multistability of multiple coexisting self-excited and hidden attractors occurs in system (7) and represents the topic of the next section.

Fig. 5

Computer generated attractors for both oscillators showing route to chaos for varying α using the parameters of Fig. 2a2: a α = 0.650; b α = 0.585; c α = 0.545; d α = 0.50. A hidden attractor (see Fig. 4e) coexists with those in c and d

3.2 Coexisting self-excited and hidden oscillations

As mentioned in the introduction part of the present work, multistability [19, 20] is listed among the most attracting features of the system made of a van der Pol oscillator coupled a Duffing oscillator investigated in this article. The numerical exploration highlights several parameter ranges associated to the coexistence of two, three, four and five competing solutions. On this line, we present in Fig. 6a several coexisting bifurcation diagrams of the system for varying k in the range 0.1 ≤ k ≤ 5.0 calculated using three different numerical procedures (see Table 1). The magnification of the diagrams in Fig. 6a is provided in the graph in Fig. 6b in the range 0.7 ≤ k ≤ 1.1. For these computations, we fix other parameters as: α = 0.40, μ = 0.80, ε = 1.0, δ = 0.0. Exploiting the results gathered in Fig. 6a, b, we present in Fig. 7a, b the coexistence of a chaotic attractor with a period-3 cycle arising at k = 0.89 when considering two different initial conditions (see caption). Cross sections of the basins of attraction (see Fig. 7b) of the respective attractors on the plane u = v = 0 are depicted using the attractors’ colors. Figure 8a, b displays a situation where coexists a chaotic attractor with a pair of period-3 cycle for k = 0.85 considering two different initial conditions (see caption). Once more, cross sections of the basins of attraction (see Fig. 8c) of the respective attractors on the plane u = v = 0 are depicted using the attractors’ colors. On the same line, Fig. 9a, b shows the coexistence of a pair chaotic attractors with a pair of period-3 cycle computed for k = 0.93 using two different initial condition (see caption). Additional insight connected to these competing solutions is provided in the form of cross sections of the basins of attraction of the respective attractors onto the plane u = v = 0 using the attractors’ colors. Up to four coexisting attractors (i.e., a pair of period-4 cycles and a pair of chaotic attractors) are depicted Fig. 10a1–a2 to b1–b2 when setting the parameters as: α = 0.572, μ = 0.80, ε = 1.2, k = 3.0, β = 0.0. Corresponding cross sections of the basins of attraction (e) are depicted using the attractors’ colors (see Fig. 10c). The presence of parallel bifurcation branches is better illustrated in Fig. 10c where the range of α-values 0.57 ≤ α ≤ 0.59 is considered keeping other values of parameters as above. The case of multistability reported so far involves only self-excited attractors. In contrast, the coexistence of a hidden attractor with self-excited others can be found by exploiting the results in Fig. 11. Figure 12a, b presents two bifurcation diagrams of the system for values of k in the ranges 4.5 ≤ k ≤ 4.75 for (a) and 0.5 ≤ k ≤ 1.0 for (b); other parameters are as follows: α = 0.50; μ = 0.80; ε = 1.2; δ = 0.0. In fact, the numerical techniques utilized to produce the various diagrams are explained in Table 1. Exploiting the results of Fig. 11, we present in Fig. 12 the coexistence of a chaotic attractor with a hidden period-1 cycle computed for k = 3.5 using two different initial conditions (see caption). Cross sections of the basins of attraction (see Fig. 12c) of the respective attractors onto the plane u = v = 0 are depicted using the attractors’ colors. On the same line, Fig. 13a, b concerns the case where two mutually symmetric chaotic attractors coexist with a hidden period-1 cycle for k = 4.5 using two different initial states (see caption). Cross sections of the basins of attraction (Fig. 13c) of the relevant attractors onto plane u = v = 0 are displayed using the attractors’ colors. Finally, Fig. 14a1–a2 to b1–b2 depicts a situation involving five attractors (i.e., a hidden period-1 cycle and a pair of period-2 cycles a pair of chaotic attractors) computed for k = 4.665 using different initial conditions (see caption). Figure 15a, b highlights metamorphoses in the bifurcation diagrams of Figs. 6b and 12b computed for β = 0.010 with numerical procedures detailed in Table 2.

Fig. 6

Coexisting bifurcation diagrams (a) of the system for varying k in the range 0.1 ≤ k ≤ 5.0 computing using three different numerical procedures (see Table 1). The enlargement of the diagrams in a is provided in the graph in b in the range 0.7 ≤ k ≤ 1.1. We fix other parameters as: α = 0.40, μ = 0.80, ε = 1.0, δ = 0.0

Fig. 7

Coexistence of a chaotic attractor with a period-3 cycle computed for k = 0.89 using two different initial conditions, (5,0,0.1,0) and (0.1,0,0.1,0), respectively. Cross sections of the basins of attraction of the respective attractors on the plane u = v = 0 are depicted using the attractors’ colors. The rest of parameters are defined in Fig. 6

Fig. 8

Coexistence of a chaotic attractor with a pair of period-3 cycle computed for k = 0.85 using two different initial conditions, (0.1,0,0,0) and (± 0.1,0, ± 0.1,0), respectively. Cross sections of the basins of attraction of the respective attractors on the plane u = v = 0 are depicted using the attractors’ colors. The rest of parameters are defined in Fig. 6

Fig. 9

Coexistence of a pair chaotic attractors with a pair of period-3 cycle computed for k = 0.93 using two different initial conditions, (± 0.1,0,0,0) and (± 0.1,0, ± 0.1,0), respectively. Cross sections of the basins of attraction of the respective attractors on the plane u = v = 0 are depicted using the attractors’ colors. The rest of parameters are defined in Fig. 6

Fig. 10

Coexistence of four different attractors obtained with: α = 0.572, μ = 0.80, ε = 1.2, k = 3.0, β = 0.0: a a pair of period-4 cycles with initial state (± 0.1,0, ± 0.1,0); b a pair of chaotic attractors with initial state (± 1,0, ± 1,0). Corresponding cross sections of the basins of attraction e are depicted using the attractors’ colors. The presence of parallel bifurcation branches is better illustrated in e where the range of α-values 0.57 ≤ α ≤ 0.59 is considered keeping other values of parameters as above

Fig. 11

Bifurcation diagrams of the system for values of k in the ranges 4.5 ≤ k ≤ 4.75 for a and 0.5 ≤ k ≤ 1.0 for b. The numerical techniques utilized to produce the various diagrams are explained in Table 2. The rest of parameters are: α = 0.50; μ = 0.80; ε = 1.2; δ = 0.0

Fig. 12

Coexistence of a chaotic attractor with a hidden period-1 cycle computed for k = 3.5 using two different initial conditions, (5,0,0.1,0) and (0.1,0,0.1,0), respectively. Cross sections of the basins of attraction (BA) of the respective attractors on the plane u = v = 0 are depicted using the attractors’ colors. The rest of parameters are defined in Fig. 11. In the zoom of BA provided in d, the three fixed points are represented in magenta color

Fig. 13

Coexistence of two mutually symmetric chaotic attractors with a hidden period-1 cycle computed for k = 4.5 using two different initial conditions, (5,0,0.1,0) and (± 0.1,0, ± 0.1,0), respectively. Cross sections of the basins of attraction (BA) of the respective attractors on the plane u = v = 0 are depicted using the attractors’ colors. The rest of parameters are defined in Fig. 11. In the zoom of BA provided in (d), the three fixed points are represented in magenta color

Fig. 14

Coexistence of five attractors computed for k = 4.665 using different initial conditions: (a1–a2) a hidden period-1 cycle and a pair of period-2 cycles for (5,0,0.1,0) and (± 1,0, ± 1,0), respectively; (b1–b2) a pair of chaotic attractors for (± 0.1,0, ± 0.1,0). The rest of parameters are defined in Fig. 11

Fig. 15

Metamorphoses in the bifurcation diagrams of Figs. 5b and 6b computed for β = 0.010. The numerical procedures employed to obtain the relevant diagrams are detailed in Table 2

Table 2 Numerical techniques employed to obtain the bifurcation diagrams depicted in Figs. 6 and 11

Before we proceed, it is important to quote that multistability (discussed in this work) has also been reported in many other nonlinear problems. The type and number of coexisting solutions depend on the form of nonlinearity and the numerical values of parameters as well. In case the nonlinearity is in the form of a trigonometric function, the system can develop periodic solutions which results in an infinite number of coexisting attractors [21,22,23,24,25].

3.3 Coexistence of period doubling reversals

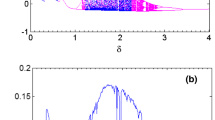
The period doubling cascade followed by the reverse scenario (i.e., antimonotonicity) denotes a special nonlinear behavior commonly uncovered by varying a couple of parameters in a nonlinear system [26, 27]. In the case of a system possessing at least a symmetry property as the model studied in this article, the bubbles occur in symmetric pairs. Concerning the 4D system formed by a van der Pol oscillator coupled to a double-well Duffing oscillator described by system (1), Fig. 16 presents coexisting pairs of mutually symmetric bubbles computed for α = 0.5; μ = 1.0; β = 0 for five discrete values of ε-parameter. We observe a pair of period-2 bubbles (Fig. 16a); period-4 bubbles (Fig. 16b); period-4 bubbles (Fig. 16c); and a chaotic bubbles (Fig. 16d, e) for ε = 0.43, ε = 0.450, ε = 0.455, ε = 0.460 and ε = 0.475, respectively. We produced these plots by scanning the k-parameter downward in the range 0.5 ≤ k ≤ 2.5, starting from initial state (± 0.1,0,0,0). This latter feature is related to the perfectly symmetric operation mode while coexisting asymmetric bubbles are reported for a nonzero value of the symmetry parameter β. For example, we present in Fig. 17, for ε = 0.470 (the rest of parameters being the same as in Fig. 16), the coexistence of a chaotic bubble with a chaotic bubble for β = 0.005 (a); another chaotic bubbles for β = 0.020 (b); period-8 bubbles for ε = 0.027 (c); period-4 bubbles for β = 0.030 (d). Interestingly, a zoom (not shown for the sake of brevity) of the bifurcation diagram of Fig. 1 in the range 0.9 ≤ k ≤ 2.1 highlights the striking phenomenon of coexisting symmetric reverse bubbles of bifurcation (blue and green colors) for β = 0. The graphs were obtained by sweeping the parameter downward without resetting the initial conditions beginning from the initial states (± 0.1,0,0,0). At this point, we would like to point out that the coexistence of asymmetric bubbles of bifurcations reported above represents one of the most striking manifestations of symmetry perturbation of the coupled van der Pol and Duffing oscillators analyzed in this article. For the reader’s guidance, remark antimonotonicity behavior has been previously discussed in previous works related to several other nonlinear systems such as memristive Chua circuit[28, 29], the memristive Twin-T-based oscillator [30], and third-order RLCM chaotic circuit [31], just to mention a few.

Fig. 16

Coexisting pairs of mutually symmetric bubbles computed for α = 0.5; μ = 1.0; β = 0: a period-2 bubbles for ε = 0.43; b period-4 bubbles for ε = 0.450; c period-4 bubbles for ε = 0.455; d chaotic bubbles for ε = 0.460; e chaotic bubbles for ε = 0.475

Fig. 17

For ε = 0.470, we observe a the coexistence of a chaotic bubble with: a a chaotic bubble for β = 0.005; b another chaotic bubbles for β = 0.020; c period-8 bubbles for ε = 0.027; d period-4 bubbles for β = 0.030. The rest of parameters are: α = 0.5, μ = 1.0

4 Microcontroller-based implementation

This section is devoted to the experimental study of the system composed of a Duffing oscillator coupled to a van der Pol oscillator considered in this work. It should be recalled that the hardware implementation of chaotic differential models opens the way to technological applications of these models. Moreover, the hardware implantation represents an alternative approach to verify and validate the results of the theoretical analysis. Three tools are traditionally used for the hardware implementation of chaotic systems: (1) the analog computer [32]; (2) the FPGA module [33, 34]; and (3) the microcontroller board [35,36,37,38]. The latter approach is considered in the present work for the experimental study of system (1). Mention that an interesting aspect of digital hardware platform is that the initial conditions and parameters can be selected in advance, whereas in the analog computing scheme, initial capacitor voltages are randomly achieved by switching on/off repeatedly power supply. The STM32F407ZE Black Board card with an ARM Cortex M4 32bits RISC processor is used to build our digital computer. Figure 18a presents the block diagram of Black Board STM32F407ZE based on ARM microcontroller (digital computer), whereas the experimental setup of our system composed of STM32 microcontroller and a digital oscilloscope whose screen displays a chaotic attractor is provided in Fig. 18b. Based on the (Runge–Kutta method) discrete-time model of the coupled system (3), the writing of the program, compilation and the downloading of codes in the STM32F407ZE processor were done by Arduino software using the programming language C/C++. As sample experimental results, Fig. 19a1–a3 and (b1–b3) shows eexperimental phase portraits of the coexistence of three self-excited attractors corresponding to the numerical results of Fig. 9. Left and right panels correspond to the van der Pol and Duffing oscillators, respectively. These results were obtained with the same sets of parameter values and initial states provided in Fig. 9. On the same line, experimental results showing the coexistence of two self-excited attractors and a hidden limit cycle corresponding to the numerical results of Fig. 13 are provided in Fig. 19a1–a3 and b1–b3. These results were obtained with the same sets of parameters values and initial states provided in Fig. 13. Notice a very good agreement between the experimental phase portraits and those obtained during the theoretical analysis.

Fig. 18

a Block diagram of Black Board STM32F407ZE based on ARM microcontroller (digital computer); b experimental setup of our system based on STM32 microcontroller and visualization of a chaotic attractor using a digital oscilloscope

Fig. 19

Experimental results showing the coexistence of three self-excited attractors corresponding to the numerical results of Fig. 9. Left and right panels correspond to the van der Pol and Duffing oscillators, respectively. These results were obtained with the same sets of parameter values and initial states provided in Fig. 9

5 Conclusions and outlook

To summarize, this work has analyzed the dynamics of a system formed by coupling a van der Pol oscillator to an asymmetric double-well Duffing oscillator. In the underlined coupling scheme, the van der Pol and the Duffing oscillators are driven by a signal proportional to the difference of their position and velocity, respectively. Both analytical and numerical tools were followed to shed light on the complex behaviors exhibited by the coupled system. We reported striking phenomena such as chaos, hysteresis, parallel bifurcation branches, the coexistence of multiple (i.e., three, four or five) self-excited and hidden attractors, the coexistence of symmetric and asymmetric bifurcation bubbles depending on the location in parametric space. An in-depth study of the presence of multiple competing dynamics was carried out by constructing 2D basins of attraction. Sample experimental results captured from STM32F407ZE microcontroller-based digital implementation of the coupled system present a very good agreement with the theoretical predictions. It is important to point out that the coexistence of a hidden attractor with self-excited others discussed in the present work represents the first report of this type of phenomenon for a system of coupled van der Pol and Duffing oscillators (Fig. 20).

Fig. 20

Experimental results showing the coexistence of two self-excited attractors and a hidden limit cycle corresponding to the numerical results of Fig. 13. Left and right panels correspond to the van der Pol and Duffing oscillators, respectively. These results were obtained with the same sets of parameters values and initial states provided in Fig. 13

Concerning the practical exploitation of the results of the present work, we would like to quote that one of the primary motivations is to shed light on the dynamics of any process governed by the coupled system (4). There are ranges of system parameters where the model experiences a single chaotic attractor. Such parameter ranges are suited for chaos based communication (i.e., domains of multistability should be avoided). A suitable control technique can be used for attractor selection in case of multistability [39]. This latter issue is out of the scope of the present manuscript. However, numerous benefits of multistability have been identified recently and research efforts have been devoted to artificially creating multistability for a wide range of applications, such as signal processing, energy harvesting, composite structures and metamaterials, and micro-/nano-electromechanical actuators. For further discussion along this line, the reader is referred to the review work of Shitong Fang and colleagues [40].

As future work, the extension of the present study to the more complex case where the Duffing oscillator possesses a triple well potential [41] represents an interesting problem under consideration. On the same line, mention that the trial-and-error method was used to detect the combinations of parameters for which the coupled system exhibits interesting behaviors [42]. In particular, concerning the coexistence of hidden attractors reported in this article, the development of analytical–numerical algorithms [2, 3] could shed more light on this type of behavior in our coupled system. These aspects will probably be the topic of our next investigations.