1 Introduction

The fluctuation of the time-varying mesh stiffness is one of the main excitations leading to vibration and noise problems of gear transmission systems (Kiekbusch et al. 2011; Chang et al. 2015). Localized tooth defects may also affect gear dynamic responses by reducing tooth flexibility and gear mesh stiffness (Chen and Shao 2011). Therefore, the determination of gear mesh stiffness should be one of the priority issues in gear dynamic analysis. Many researchers have considered gear mesh stiffness as an important indication of the conditions of tooth engagement and used it to reflect the working conditions of gear transmission systems in the presences of some localized defects (Wan et al. 2015; Yu et al. 2015; Han et al. 2017; Liu et al. 2012, 2017; Liu and Shao 2017a, b; Ma et al. 2014).

The calculation methodologies for the mesh stiffness of spur gears are abundant in the literature, which can be summarized as finite element (FE) methods (Kiekbusch et al. 2011; Ma et al. 2016a, 2016b; Vijayakar 1991), analytical methods based on the potential energy principle (Wan et al. 2015; Yu et al. 2015; Han et al. 2017), FE-analytical hybrid methods (Chang et al. 2015; Vijayakar 1991), empirical formula (Umezawa and Suzuki 1985; Umezawa et al. 1986; Cai 1995) and approximations based on ISO 6336-1 standard (Velex 2012; ISO 6336-1 2006). The literature also reports a few investigations using experimental method to calculate the gear mesh stiffness. However, these experimental studies are rare due to the difficulty in correctly measuring the tooth deformation (Ma et al. 2015). Munro et al. (2001) have tried using high-resolution (360 000 line per rotation) encoders to obtain the mesh stiffness of a single spur gear tooth pair through the measurement of the gear transmission error. However, the accuracies were limited. One of the challenges in the measurement was that the large force needed to deflect the teeth by a significant amount will also deflect other components (shafts, bearings) in the test rig, which will cause non-tooth deflections in the measurement. Some other indirect measurement techniques, such as the modal analysis on the vibration signal (Yesilyurt et al. 2003) and the digital photoelasticity analysis (Pandya and Parey 2013), were also reported. To the authors’ knowledge, the applications of these experimental techniques still face significant challenges in accurately measuring the gear tooth stiffness. Thus, FE methods and analytical methods are still the two main tools to accurately calculate the gear mesh stiffness up till now.

Although the calculation methodologies for the mesh stiffness of spur gears are abundant in the literature, studies about the mesh stiffness calculation of helical gears are comparatively limited. FE methods are still the primary tool used to yield the mesh stiffness of helical gears (Hedlund and Lehtovaara 2008), which requires a three-dimensional (3D) helical gear model with refined nonlinear contact elements near contact regions, making the calculation time-consuming. ISO 6336-1 (2006) provides equivalent formula to transform the mesh stiffness values of the spur gear case into those of helical gear case. However, this standard only provides the maximum value of the single mesh stiffness (mesh stiffness of a single tooth pair) and mean value of the gear mesh stiffness. Currently, analytical methods based on the potential energy principle and the “thin-slice” approach (or slicing principle) are becoming popular. The basic idea is that a cylindrical gear can be considered as a series of staggered infinitesimal (thin) spur gears along the face width direction and the contact line between a meshing tooth surface is sliced accordingly. The mesh stiffness of the cylindrical gear pair can, thus, be obtained by integrating the individual stiffness of each staggered spur gear pair along the face width direction. This methodology has been adopted by Chen and Shao (2011, 2013), Chen et al. (2016), Wan et al. (2015), Yu et al. (2015), Han et al. (2017) and Wang et al. (2014), to evaluate the mesh stiffness of helical gears or spur gears with friction, misalignment, tooth profile error and localized crack defects. Recently, Feng et al. (2017) proposed an improved analytical method for calculating the mesh stiffness of helical gears based on the slicing principle by considering the fillet-foundation correction effect and nonlinear Hertzian contact effect, which were first introduced by Ma et al. (2016a, b) for a more accurate mesh stiffness calculation of spur gears with tip relief. In almost all the above-reviewed work, the tooth fillet-foundation stiffness is derived based on the formula proposed by Sainsot and Velex (2004). Chen et al. (2017) recently proposed a more general method to calculate the tooth fillet-foundation stiffness even in the presence of tooth root crack.

The first limitation in the current analytical methodologies based on the slicing principle for the mesh stiffness calculation of helical gears is that most research work considers only one type of helical gear pair, i.e. the helical gear pair with a transverse contact ratio larger than its overlap ratio (Type I) so that the maximum effective contact face width is always the tooth face width for whatever the helix angle. However, for the helical gear pair with a transverse contact ratio smaller than its overlap ratio (Type II), its maximum effective contact face width will be smaller than the tooth face width, and will be reduced for increased helix angle. More importantly, the convective effect (or elastic coupling effect) between sliced tooth pieces can be influential for this type of gear.

Besides, there is confusion and inconsistency in evaluating the total mesh stiffness based on the slicing principle. One strategy yields the total mesh stiffness by integrating the mesh stiffness of the staggered spur gear pair along the face width (Feng et al. 2017; Ma et al. 2016a, b), and the other is by combining individual stiffness components (tooth beam stiffness, tooth fillet-foundation stiffness and tooth contact stiffness), which are obtained through integrating corresponding stiffness components of the staggered spur pair along the face width (Chen and Shao 2011; Wan et al. 2015; Yu et al. 2015; Han et al. 2017; Wang et al. 2014). Comparisons and discussions about these two strategies have not been made in the literature so far.

Finally, in most of the existing analytical methodologies using the slicing principle, the sliced tooth pieces are considered to be independent from each other, meaning that the inter-tooth elastic couplings (or convective effects) are neglected. This assumption is valid for Type I helical gear pairs (normally narrow-faced, small helix angle) as such effect is normally negligible (Wang et al. 2014). However, for Type II helical gear pairs (normally wide faced, large helix angle), Ajmi and Velex (2005), and Umezawa (1973) have shown such coupling can be influential to the load distribution along the contact line. This brings a challenge to the traditional analytical methodologies using the slicing principle, which assumes an even load distribution along the contact line when calculating the mesh stiffness for each sliced thin tooth piece.

In this paper, two types of the helical gear pairs are first defined based on the relationship between the transverse contact ratio and overlap contact ratio. The two integration strategies used to evaluate the total mesh stiffness based on the slicing principle are mathematically expressed and compared. An improved analytical model based on the slicing principle is introduced for the consideration of the convective effects among neighbouring tooth pieces. The calculation results for the single mesh stiffness of two types of helical gear pairs obtained from various methods are compared and discussed, which validates the accuracy of the proposed analytical model compared with the traditional analytical model, especially for the helical gears with wide face and large helix angle.

2 Mesh Stiffness Calculation

2.1 Analytical Methods

According to Weber (1949), three contributing factors need to be considered when analytically calculating the tooth deformation (or deflection) in the line of action (LOA) at the contact point j subjected to a certain mesh force F: (1) the local deformation caused by the Hertzian contact; (2) the deflection caused by the tooth beam itself; and (3) the deflection caused by the flexibility of the foundation (gear body).

2.1.1 For Spur Gear Tooth Pair

The Hertzian contact deformation δh between the meshing tooth surfaces of a mating tooth pair is generally nonlinear. Some researchers (Feng et al. 2017; Ma et al. 2016a, 2016b) used the following nonlinear formula for the evaluation of Hertzian contact stiffness kh of the ith spur tooth pair:

$$k_{h}^{i} = \frac{{E_{e}^{0.9} L_{i}^{0.8} F_{i}^{0.1} }}{1.275}$$
(1)

where L is the length of contact line between the meshing tooth surfaces of the ith tooth pair, Fi is the meshing force of the ith tooth pair, which can be obtained by:

$$F_{i} = F*LSR_{i}$$
(2)

where F is the total mesh force of the spur gear pair, and LSRi is the load sharing ratio of the ith tooth pair. Ee in Eq. (1) is the effective elastic modulus. According to (Feng et al. 2017), its value can be expressed as:

$$E_{e} = \left\{ {\begin{array}{*{20}c} {E/\left( {1 - \nu^{2} } \right)} & {R \ge 5} \\ E & { R < 5} \\ \end{array} } \right.$$
(3)

where E and ν are the Young’s modulus and the Poisson ratio of the gear material, respectively. R = 2L/(πm) determines whether the gear teeth are wide (R ≥ 5) or narrow (R < 5), and m is the gear module.

For the tooth beam stiffness, the potential energy method is usually used in the literature. The key idea of this method is to divide the total energy stored in the tooth beam subjected to a mesh force into three parts: bending energy, shear energy and axial compressive energy. Therefore, the tooth beam stiffness kt consists of three parts: bending stiffness kb, shear stiffness ks and compressive stiffness ka:

$$k_{t} = \frac{1}{{\frac{1}{{k_{b} }} + \frac{1}{{k_{s} }} + \frac{1}{{k_{a} }}}}$$
(4)

where

$$\frac{1}{{k_{b} }} = \mathop \int \limits_{0}^{l} \frac{{\left[ {\left( {l - y} \right)\cos \alpha_{p} - h\sin \alpha_{p} } \right]^{2} }}{{EI_{y} }}{\text{d}}y,\quad \frac{1}{{k_{s} }} = \mathop \int \limits_{0}^{l} \frac{{1.2\cos^{2} \alpha_{p} }}{{GA_{y} }}{\text{d}}y,\quad \frac{1}{{k_{a} }} = \mathop \int \limits_{0}^{l} \frac{{\sin^{2} \alpha_{p} }}{{EA_{y} }}{\text{d}}y,$$
(5)

where l, h, αp and y are shown in Fig. 1a. G is shear modulus of the gear material, and:

$$I_{y} = \frac{1}{12}\left( {2h_{y} } \right)^{3} L,\quad A_{y} = \left( {2h_{y} } \right)L$$
(6)

are the effective area moment of inertia and area of the integral section, respectively, as shown in Fig. 1b. According to the geometry of the involute profile, d and h are related to the mesh angle αp by:

$$l = R_{b} \left[ {\cos \alpha_{p} + \left( {\alpha_{p} + \alpha_{2} } \right)*\sin \alpha_{p} - \cos \alpha_{2} } \right],\quad h = R_{b} \left[ {\left( {\alpha_{p} + \alpha_{2} } \right)*\cos \alpha_{p} - \sin \alpha_{p} } \right],$$
(7)

where Rb is the base radius, and α2 is the half base angle as shown in Fig. 1b. Detailed discussions can be found in (Chen and Shao 2011; Wan et al. 2015; Yu et al. 2015).

Fig. 1
figure 1

Model of spur gear tooth a geometric parameters for gear body, b geometric parameters for single tooth

Full size image

The tooth fillet-foundation stiffness kf can be acquired based on the work of Sainsot and Velex (2004):

$$\frac{1}{{k_{f} }} = \frac{{\cos^{2} \alpha_{p} }}{LE}\left\{ {L^{*} \left( {\frac{{u_{f} }}{{s_{f} }}} \right)^{2} + M^{*} \left( {\frac{{u_{f} }}{{s_{f} }}} \right) + P^{*} \left( {1 + Q^{*} *\tan^{2} \alpha_{p} } \right)} \right\}$$
(8)

where uf and sf are shown in figure. The coefficients L*, M*, P* and Q* can be obtained by polynomial functions proposed by Sainsot and Velex (2004).

Therefore, the equivalent mesh stiffness of the ith tooth pair in mesh can be expressed as:

$$k^{i} = \frac{1}{{\frac{1}{{k_{t, 1}^{i} }} + \frac{1}{{k_{t, 2}^{i} }} + \frac{1}{{k_{h}^{i} }} + \frac{1}{{k_{f, 1}^{i} }} + \frac{1}{{k_{f, 2}^{i} }}}}$$
(9)

where k i t, j and k i f, j denote the tooth beam stiffness and tooth fillet-foundation stiffness, respectively, and subscript j = 1, 2 represent the driving gear tooth and driven gear tooth of the ith tooth pair in mesh, respectively.

2.1.2 For Helical Gear Tooth Pair

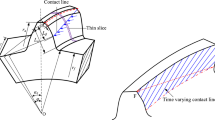
For helical gear tooth pair, the contact line between the meshing surfaces of a mating tooth pair inclines by the helix angle β. Besides, the length of contact line changes gradually as shown in Fig. 2. The classic “thin-slice” approach (slicing principle) is usually applied. This is achieved by slicing the helical gear into a series of thin gear pieces with equal width δz along the tooth face width direction (Z-direction as shown in Fig. 2), so that each thin gear piece can be treated as spur gear. Therefore, the stiffness of the ith helical tooth pair Ki can be calculated by integration along the face width (Wan et al. 2015):

$$K^{i} = \mathop \int \limits_{0}^{W} k^{i} \left( z \right)$$
(10)

where ki (z) is the stiffness of the spur tooth pair piece at coordinate z. It can be obtained from Eqs. (1)–(9) by changing the contact length L with δz. W is the face width of gear meshing. Besides, l, h and αp in Eqs. (1)–(5) are also z-coordinate dependent, i.e. l(z), h(z) and αp(z) (or lz, hz, and αpz shown in Fig. 3), as these three parameters are changing for different helical gear tooth thin pieces along the face width. Besides,

$$l\left( z \right) = R_{b} \left[ {\cos \alpha_{p} \left( z \right) + \left( {\alpha_{p} \left( z \right) + \alpha_{2} } \right)*\sin \alpha_{p} \left( z \right) - \cos \alpha_{2} } \right]$$
(11)
$$h\left( z \right) = R_{b} \left[ {\left( {\alpha_{p} \left( z \right) + \alpha_{2} } \right)*\cos \alpha_{p} \left( z \right) - \sin \alpha_{p} \left( z \right)} \right]$$
(12)

where αp(z) is assumed as a linear change (Wan et al. 2015):

$$\alpha_{p} \left( z \right) = \alpha_{p1} + \left( {\alpha_{p2} - \alpha_{p1} } \right)*\frac{z}{{W_{e} }}$$
(13)

where αp1 and αp2 are the mesh angles of the two tooth pieces at the two ends of the contact line, as shown in Fig. 2. The effective contact face width We is defined as the length of line along the face width direction where the contact happens (as illustrated in Fig. 4). Depending on the relationship between the transverse contact ratio εα and overlap contact ratio εβ, a helical gear pair can be classified as two types: Type I where the transverse contact ratio εα is larger than the overlap contact ratio εβ, and Type II where the transverse contact ratio εα is smaller than the overlap contact ratio εβ, as described in Fig. 3.

Fig. 2
figure 2

Helical gear tooth model

Full size image
Fig. 3
figure 3

Classification of helical gear pairs

Full size image
Fig. 4
figure 4

Variation of contact line in the plane of action a Type I, b Type II

Full size image

For these two types of helical gear pair, the variations of the We are different as the contact line moves along the plane of action as shown in Fig. 4. It can be expressed as:

  1. ①

    For Type I Helical gear pair (εα> εβ)

    $$W_{e} = \left\{ {\begin{array}{*{20}c} {\mu \cot \beta_{b} } & {\mu < L_{\beta } } \\ W & {L_{\beta } \le \mu \le L_{\alpha } } \\ {W - \left( {\mu - L_{\alpha } } \right)\cot \beta_{b} } & {L_{\alpha } < \mu } \\ \end{array} } \right.$$
    (14)
  2. ②

    For Type II Helical gear pair (εα< εβ)

    $$W_{e} = \left\{ {\begin{array}{*{20}c} {\mu \cot \beta_{b} } & {\mu < L_{\beta } } \\ {L_{\alpha } \cot \beta_{b} } & {L_{\alpha } \le \mu \le L_{\beta } } \\ {W - \left( {\mu - L_{\alpha } } \right)\cot \beta_{b} } & {L_{\beta } < \mu } \\ \end{array} } \right.$$
    (15)

where μ is the distance between the mesh point on the back face and the initial mesh point F0, Lα is the length of line of action (LOA) in the transverse plane of helical gear pair, and Lβ is the length of LOA due to the overlap of tooth action in the axial direction, and:

$$L_{\alpha } = \varepsilon_{\alpha } P_{bt} ,\quad L_{\beta } = \varepsilon_{\beta } P_{bt} ,\quad \tan \beta_{b} = \tan \beta *\cos \alpha_{t} ,\quad \tan \alpha_{t} = \tan \alpha_{n} /\cos \beta ,\quad m_{t} = m_{n} /\cos \beta ,$$
(16)

where Pbt is the base pitch in the transverse plane, βb is the base helix angle, αt and αn are the transverse and normal pressure angles, respectively, mt and mn are the transverse and normal gear modules, respectively.

Based on Eqs. (11)–(15), the stiffness of each thin tooth piece can be obtained, and the mesh stiffness of the helical tooth pair can be evaluated through integration along the face width as shown in Eq. (12).

  1. ①

    Traditional analytical (TA) method

In the traditional analytical method, the helical gear is considered as a series of independent staggered spur gears with no elastic coupling among them (Feng et al. 2017; Ma et al. 2016a, b). The mesh stiffness of the helical gear pair is evaluated through the integration of the mesh stiffness of the staggered spur gears along the face width. This strategy is mathematically expressed as:

$$k^{i} = \mathop \sum \limits_{j = 1}^{Nc} k^{i,j} = \mathop \sum \limits_{j = 1}^{Nc} \frac{1}{{\frac{1}{{k_{t, 1}^{i,j} }} + \frac{1}{{k_{t, 2}^{i, j} }} + \frac{1}{{k_{h}^{i,j} }} + \frac{1}{{k_{f, 1}^{i, j} }} + \frac{1}{{k_{f, 2}^{i,j} }}}}$$
(17)

where Nc is the total number of staggered spur gears. k i j is the mesh stiffness of the jth staggered spur tooth pair. \(k_{t, 1}^{i, j}\) and \(k_{t, 2}^{i, j}\) are the tooth beam stiffness of the jth staggered driving gear and driven gear, respectively. \(k_{f, 1}^{i, j}\) and \(k_{f, 2}^{i, j}\) are the tooth foundation stiffness of the jth staggered driving gear and driven gear, respectively. \(k_{h}^{i, j}\) is the contact stiffness between the jth staggered spur tooth pair. There is a slight difference in this strategy compared with that used by Ma et al. (2016a, b), which used Ee = E/(1− μ2) to calculate the contact stiffness k i h of the staggered spur tooth pair for a wide-faced helical gear pair. However, since the staggered spur teeth are naturally narrow, the effective elastic modulus Ee should always be E no matter if the helical gear pair considered is wide or narrow.

It should be mentioned that there is another integration strategy in some literature (Chen and Shao 2011; Wan et al. 2015; Yu et al. 2015; Han et al. 2017; Wang et al. 2014), where the mesh stiffness of the helical gear pair is evaluated through Eq. (9), and each stiffness component (tooth beam stiffness, tooth fillet-foundation stiffness and tooth contact stiffness) is obtained through the integration of that stiffness component of the spur tooth pieces along the face width. This strategy is mathematically expressed as:

$$k^{i} = \frac{1}{{\frac{1}{{k_{t, 1}^{i} }} + \frac{1}{{k_{t, 2}^{i} }} + \frac{1}{{k_{h}^{i} }} + \frac{1}{{k_{f, 1}^{i} }} + \frac{1}{{k_{f, 2}^{i} }}}}$$
(18)

where

$$k_{t, 1}^{i} = \mathop \sum \limits_{j = 1}^{{N_{c} }} k_{t, 1}^{i,j} ,\quad k_{t,2}^{i} = \mathop \sum \limits_{j = 1}^{{N_{c} }} k_{t, 2}^{i,j} ,\quad k_{h}^{i} = \mathop \sum \limits_{j = 1}^{{N_{c} }} k_{h}^{i,j} ,\quad k_{f,1}^{i} = \mathop \sum \limits_{j = 1}^{{N_{c} }} k_{f, 1}^{i,j} ,\quad k_{f,2}^{i} = \mathop \sum \limits_{j = 1}^{{N_{c} }} k_{f, 2}^{i,j}$$
(19)

Note the difference between these two integration strategies.

  1. ②

    Improved analytical (IA) method

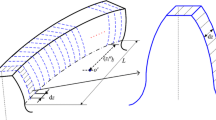
In the traditional method using the slicing principle, it is assumed that the effect of elastic couplings (or convective effects) among adjacent spur gear pieces after slicing the helical gear can be neglected. This assumption may be valid for narrow-faced gears. For wide-faced gears, Ajmi and Velex (2005) proposed a Pasternak’s elastic foundation model which is made of the superposition of bending and shearing elements lying on independent springs (i.e. spur tooth pieces in the traditional method). The bending and shearing elements couple the spring stiffnesses and convey deflections from any loaded point to the neighbouring points. Based on this model, Ajmi and Velex (2005) obtained the tooth structural deflection curves of contact lines across the face width when submitted to a point load at various positions on the tooth flank. One example is shown in Fig. 5. It should be noted that the tooth structural deflection includes components due to the tooth bending, shearing and tooth foundation effects, which is normally linear with the point load.

Fig. 5
figure 5

Tooth structural deflection curves (Ajmi and Velex 2005)

Full size image

As can be found in Fig. 5, a point load will deflect the loaded point, as well as the its neighbouring unloaded points, which demonstrates the convective effect between neighbouring thin tooth pieces. The deflection curves look like normal distribution curves. Besides, the peak amplitude when the loaded point is on the tooth edge is larger than that on the middle of the tooth face width, which is due to the edge effect (Ajmi and Velex 2005). These shapes agree coincidentally well with the effect functions of bending moments along the fillet when a concentrated load acts on the middle and free edge of a tooth provided by Umezawa (1973). Ajmi and Velex (2005) also obtained the tooth contact deflection curves and found that the contact deflections are far less convective than the structural ones. Thus, it can be assumed that the contact deflections are nonlinear, and non-convective compared with the structural ones. The total tooth deflection is the combination of the structural deflection and contact deflection and should still be nonlinear and convective.

In order to quantify these effects on the calculation of mesh stiffness based on the slicing principle, we assign a non-uniform weighting distribution on the sliced tooth pieces along the face width direction, and the stiffness of each tooth piece is associated with a weighting factor WF between 0 and 1. The non-uniform weighting distribution can be approximated by summing all the normal distribution curves when a point load is applied on each tooth piece, and normalizing the result within the region between 0 and 1. It should be noted that the peak amplitude of the normal curve at the tooth edge should be larger than that at the middle.

Figure 6 shows a simulated summation of all the normal distribution curves (the blues lines in Fig. 6) based on the above requirements. It can be found that the resulting summation line (the red line in Fig. 6) along the tooth face width resembles a parabolic-like curve with the maximum value at the middle, and minimum value at the tooth edges. This means when an uniform-distributed mesh force is applied along the tooth contact line (equivalent to point loads applied on tooth pieces with the same amplitude), the tooth deformation curve along the contact line is parabolic meaning the deformations at the tooth edges are small whereas the deformation at the tooth middle is large, instead of having the same deformations as assumed by the traditional model without considering the convective effect. Thus, we assume that the weighting factor distribution along the contact line is also parabolic-like, and the weighting factor WFj for the jth tooth piece at zj can be approximated as:

$$WF^{j} = \frac{{4\left( {WF_{\hbox{min} } - WF_{\hbox{max} } } \right)}}{{W^{2} }} \times \left( {z_{j} - \frac{W}{2}} \right)^{2} + WF_{\hbox{max} }$$
(20)

where WFmin is the minimum weighting factor at the tooth edge, and WFmax is the maximum weighting factor at the tooth middle. Therefore, the improved equation for the calculation of the mesh stiffness of the ith helical tooth pair is:

$$k^{i} = CF \times \mathop \sum \limits_{j = 1}^{Nc} k^{i,j} WF^{i, j} = \mathop \sum \limits_{j = 1}^{Nc} \frac{{CF \times WF^{i, j} }}{{\frac{1}{{k_{t, 1}^{i,j} }} + \frac{1}{{k_{t, 2}^{i, j} }} + \frac{1}{{k_{h}^{i,j} }} + \frac{1}{{k_{f, 1}^{i, j} }} + \frac{1}{{k_{f, 2}^{i,j} }}}}$$
(21)

where CF is a correction factor slightly larger than 1 in order to raise the value of mesh stiffness to account for the decrease in the mesh stiffness caused by the weighting factor being always smaller than 1. Normally we make WFmax = 1, and 0 ≤ WFmin ≤ 1, which should be dependent on the helix angle and tooth face width. The higher the helix angle and the tooth face width, the smaller the WFmin. The correction factor CF can be approximated by assuming that the area under the weighting factor distribution curve is always constant and the same with the area under a constant line WFj = 1. For instance, the area under a constant line WFj = 1 is:

$$A = WF^{j} *W = W$$
(22)

where W is the face width. For a parabolic curve described by Eq. (20) at a given WFmin, the area under the parabolic curve is:

$$A_{0} = \mathop \int \limits_{0}^{W} WF^{j} *dW = \left( {\frac{2}{3} + \frac{1}{3}WF_{\hbox{min} } } \right)*W$$
(23)

where WFj is described by Eq. (20). In order to make the area under the parabolic curve A0 equal with the A, the parabolic curve should be raised by a factor of:

$$CF = \frac{A}{{A_{0} }} = {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\left( {\frac{2}{3} + \frac{1}{3}WF_{\hbox{min} } } \right)}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\left( {\frac{2}{3} + \frac{1}{3}WF_{\hbox{min} } } \right)}$}}$$
(24)

Comparing Eqs. (17) and (21), it can be concluded that in the traditional analytical method using the slicing principle, each tooth piece is considered as being associated with an equal weighting factor (WFj = 1), and has equal influence on the total mesh stiffness. In the proposed analytical method, a parabolic weighting factor distribution is assigned to the tooth pieces, and the central tooth pieces have higher influences on the total mesh stiffness, whereas the tooth pieces at the edges have lower influences.

Fig. 6
figure 6

Simulated weighting factor distribution

Full size image

2.2 ISO Standard

Sometimes, it is interesting to have orders of magnitude of the approximate values of the mesh stiffness (Velex 2012; Yu 2017). The ISO 6336-1 standard (2006) defined a single stiffness, c’, as the maximum stiffness of a cylindrical tooth pair in single pair contact. For gear made of steel, an expression for c’ is provided as:

$$c^{\prime} \cong \frac{{C_{M} C_{R} C_{B} \cos \beta }}{q}$$
(25)

where CM is the correction factor accounting for the difference between the measured values and the theoretical calculated values, CR is the gear blank factor accounting for the flexibility of gear rims and webs, CB is the basic rack factor accounting for the deviations of the actual basic rack profile of the gear from the standard basic rack profile. Their values can be determined by expressions and graphs provided by ISO 6336-1 standard (2006). In addition:

$$q = C_{1} + \frac{{C_{2} }}{{Zn_{1} }} + \frac{{C_{3} }}{{Zn_{2} }} + C_{4} x_{1} + C_{5} \frac{{x_{1} }}{{Zn_{1} }} + C_{6} x_{2} + C_{7} \frac{{x_{2} }}{{Zn_{2} }} + C_{8} x_{1}^{2} + + C_{9} x_{2}^{2}$$
(26)

where Zni = Zi/(cos3β), Zi are the number of teeth of the driving gear (i = 1) and driven gear (i = 2), xi are the profile shift coefficients on the driving gear and driven gear. Coefficients C1, …, C9 have been tabulated and are listed in Table 1.

Table 1 Values of coefficients in Eq. (24) (ISO 6336-1 2006)
Full size table

It should be noted that the mesh stiffness formula (Eq. (25)) in the ISO standard 6336 stems from Weber’s analytical formulae (Weber 1949) which were modified to bring the analytical results into closer agreement with the experimental results.

It should also be mentioned that the ISO 6336-1 defined the stiffness as “The requisite load over 1 mm face width, directed along the line of action to produce, in line with the load, the deformation amounting to 1 μm of one or more pairs of deviation-free teeth in contact”. Therefore, the unit of c’ is N/(μm mm). Previous researchers got confused when transforming the c′ (N/(μm mm)) into the mesh stiffness ki (N/mm) of a tooth pair. Maatar and Velex (1996), Ajmi and Velex (2005) and Gu et al. (2015) got the ki by directly multiplying c’ with the time-varying length of contact line (L in Fig. 4), whereas Chang et al. (2015), Wan et al. (2015) and Feng et al. (2017) obtained the maximum mesh stiffness k imax of a single tooth pair by multiplying c’ with the face width (W in Fig. 4), which is valid for Type I gears, as the maximum mesh stiffness happens when the contact line is along the whole tooth face width. However, for Type II gears, only part of the tooth face width is in contact when the maximum mesh stiffness happens. Therefore, the correct multiplying factor is the maximum of the effective contact face width We:

$$k_{\hbox{max} }^{i} = c^{\prime}*\hbox{max} \left( {W_{e} } \right)$$
(27)

For Type I gear, max(We) = W. For Type II gear, max(We) = Lαcosβb.

2.3 FE Method

FE models are the primary tools used to obtain gear mesh stiffness due to their significant advantage in representing the crucial tooth contact behaviour (Vijayakar 1991). Three-dimensional (3D) FE models were built in the ANSYS Workbench for the helical gear pairs shown in Table 2. Each gear has only one tooth in the FE models in order to simulate the single stiffness of a helical tooth pair during its mesh cycle. The inner hubs of the driven gears are completely constrained from motion. The inner hubs of the driving gears are only allowed rotation along its axis. In addition, the end faces of the driving gear and driven gear are constrained from motion in the axial direction. The input torque T1 is applied on the inner hubs of the driving gears. The contact behaviour between teeth faces is simulated by the contact elements. The high-order tetrahedron elements with 10 nodes were considered for the FE modelling. The element size in the contact region is significantly smaller than the size in the other regions. A convergence study has been conducted, which justifies that a 1 mm element size in the tooth contact region is suitable to reach accurate results without increasing the computation burden significantly.

Table 2 Parameters of the gear pairs
Full size table

Figure 7 shows a 3D FE model for gear pair #2 in Table 2 with a helix angle of 20°. By adjusting the angular positions of the gears, the time-varying rotational deformation θ1(t) of the driving gear at each roll angle can be determined once the gear deformation field is evaluated. The single mesh stiffness of the tooth pair is then calculated by:

$$k^{i} = \frac{{(T_{1} /R_{b1} )}}{{R_{b1} \theta_{1} }} = \frac{{T_{1} }}{{R_{b1}^{2} \theta_{1} }}$$
(26)

where Rb1 is the base radius of the driving gear.

Fig. 7
figure 7

FE model of a helical gear pair: a 3D model, b close-up plot near the contact region

Full size image

3 Comparisons and Discussion

In this section, two types of helical gear pairs are used to compare the mesh stiffness results obtained from the ISO standard, traditional analytical (TA) method, the improved analytical (IA) method, FE models and some calculation results provided in the literature. The main parameters of the first helical gear pair (narrow-faced) are from (Kubur et al. 2004), which belong to Type I helical gears defined in Fig. 4. The main parameters of the second helical gear pairs (wide faced) are provided by Chang et al. (2015), which belong to Type II helical gears defined in Fig. 4.

Figure 8 shows the variations of the effective contact face width We for the two types of helical gear pairs with different helix angles listed in Table 2. It can be found that the effective contact face width changes linearly from zero to maximum, remains at the maximum for a moment, and then linearly decreases from maximum to zero. The higher the helix angle, the steeper the linearly increasing and decreasing slope. For Type I helical gear pairs, the maximum effective contact face width is the tooth face width, whereas for Type II helical gear pairs, the maximum effective contact face width decreases with the increase in the helix angle.

Fig. 8
figure 8

Variations of effective contact face width in a mesh cycle for a helical gear pair #1, b helical gear pair #2

Full size image

3.1 Gear Pair #1

Figure 9 shows the single mesh stiffness curves of the helical tooth pairs (Type I) with different helix angles yielded by different methods. The value of WFmin = 0.25 is used when using the proposed method to calculate the stiffness, which is a suggested value by comparing with the FE results for the helical gear pairs considered. It can be found that the single mesh stiffness curves look like a parabola which changes quite smoothly and has its peak at the 0.5 mesh cycle, which is the moment when the contact line passes through the pitch point at the tooth middle of face with (Umezawa et al. 1986). Based on this feature, Umezawa et al. (1986) proposed a cubic polynomial expression to approximate the single mesh stiffness. The helix angle has a similar influence on the single mesh stiffness with that on the effective contact face width shown in Fig. 8a.

Fig. 9
figure 9

Comparisons of the single stiffness curves with different helix angles calculated by various methods a FE method, b traditional analytical method based on Eq. (17), c traditional analytical method based on Eq. (18), d proposed analytical method based on Eq. (21) using WFmin = 0.25 (Note: the solid dots blue circle, red square and green triangle in each figure represent the maximum single stiffness values provided by ISO 6336-1 for each helical angle case)

Full size image

However, there are obvious discrepancies between the results yielded from Eq. (18) and results from the other methods, as we notice that the maximum single mesh stiffnesses yielded from the latter decrease slightly with the increase in the helix angle. This is brought by the term cosβ in Eq. (25), as the ISO 6336-1 (2006) explained, which was used to transform the normal into transverse theoretical single stiffness of the helical gear teeth. This demonstrates that the integration strategy used in Eqs. (17) and (21), which evaluates the mesh stiffness of the helical gear pair through the integration of the mesh stiffness of the staggered spur gears along the face width, is more accurate than the integration strategy used in Eq. (18), which evaluates the mesh stiffness of the helical gear pair through combining each stiffness component, and each stiffness component (tooth beam stiffness, tooth fillet-foundation stiffness and tooth contact stiffness) is obtained through the integration of that stiffness component of the spur tooth pieces along the face width.

Compared with the traditional analytical method, the proposed analytical method considering the convective effects among tooth pieces seems to yield a single mesh stiffness curve having little difference with that of the traditional analytical method, except making the curve smoother, especially when the helix angle is higher, which is consistent with the FE results in Fig. 9a. This proves that for Type I helical gears, the convective effect among neighbouring tooth pieces is negligible.

3.2 Gear Pair #2

Figure 10 shows the single mesh stiffness curves of the helical tooth pairs (Type II) with different helix angles yielded by different methods. It should be noted that in Chang’s method (2015), the mesh stiffness provided is stiffness per unit face width (W), whereas in ISO 6336-1 method (2006), the maximum mesh stiffness value provided is stiffness per unit effective contact face width (We). Therefore, the stiffness curves in Fig. 10b are obtained by multiplying the stiffness curves in (Chang et al. 2015) with face width W, and the stiffness values for all dots are obtained by multiplying the single stiffness c′ provided by ISO 6336-1 (2006) with the corresponding maximum effective face width We shown in Fig. 8b. Compared with the Type I helical gear pairs, it can be found that the single mesh stiffness decreases more abruptly as the helix angle increases for Type II helical gear pair. Apart from the reduction of single stiffness c’ introduced by the term cosβ in Eq. (25), the abrupt reductions of the maximum effective contact face width We with the increase in helix angle β for type II gear (see Figs. 8b and 11) are the main reason leading to it.

Fig. 10
figure 10

Comparisons of the single stiffness curves with different helix angles calculated by various methods a FE method, b Chang’s method (2015), c traditional analytical method based on Eq. (17), d proposed analytical method based on Eq. (21) using WFmin = 0.5 (Note: the solid dots blue circle, red square, green triangle and pink inverted triangle, and in each figure represent the maximum single stiffness values provided by ISO 6336-1 (2006) for each helical angle case)

Full size image
Fig. 11
figure 11

Maximum effective contact face width We for each helix angle of gear pair #2 in Table 2

Full size image

As can be seen in Fig. 10, except those obtained from the traditional analytical method, the single mesh stiffness curves from all the other methods look like a parabola which changes quite smoothly and has its peak when the contact line passes through the pitch point at the tooth middle of face with (Chang et al. 2015; Umezawa et al. 1985). The single mesh stiffness curves yielded from the TA method change abruptly from a gradual steep line to a flat one (region where the length of contact line keeps constant). Figure 12a illustrates the single mesh stiffness curves during the flat curve region (A–B region in Fig. 12) from different methods when the helix angle is 24°, which clearly shows the discrepancies between the traditional analytical method and other methods. The reason that a strange flat curve happens using the TA method for type II helical gear pair, is that the TA method assumes that the sliced tooth pieces are independent from each other, and each tooth piece has the same influence as that of the total tooth mesh stiffness. Therefore, during the A-B region, the single mesh stiffness remains constant as the length of the contact line and its position relative to gear tooth involute flank does not change at all. This demonstrates one of the shortcomings of the traditional analytical method using slicing principle to evaluate the mesh stiffness of helical gear pair. The proposed analytical method can yield a quite similar parabolic-shaped, smooth curve with that yielded by FE method and Chang’s method (2015).

Fig. 12
figure 12

Single mesh stiffness in the flat curve region using different methods when the helix angle is 24°: a single mesh stiffness curves in the flat curve region, b corresponding flat curve region in the plane of action

Full size image

On the other hand, in terms of the maximum single mesh stiffness k i max , the results from traditional analytical method agree well with the ISO 6336-standard. This is reasonable as the stiffness formula provided by ISO 6336 stems from Weber’s analytical formulae, which is the basis of the TA method. The maximum single mesh stiffness evaluated from different methods and the percentage error relative to the FE results are listed in Table 3. It can be found that when the helix angle is small, the results yielded by all methods show negligible discrepancies. However, as the helix angle increases, there are comparatively large percentage errors from the ISO 6336 and the traditional analytical method. This demonstrates that the proposed analytical method considering a parabolic weighting factor distribution on the tooth pieces has a higher accuracy compared with the traditional analytical method which assumes no coupling effects among tooth pieces.

Table 3 Maximum single mesh stiffness evaluated from different methods
Full size table

4 Conclusions

This paper classified two types of helical gear pair based on the relationship between its transverse contact ratio and overlap contact ratio. An improved analytical method considering the elastic couplings between neighbouring tooth pieces is introduced. This is achieved by assigning a parabola-like weighting factor distribution on the sliced tooth pieces along the tooth width. The calculation results from various methods (mainly FE method, traditional analytical method, proposed analytical method and the ISO standard) for the single mesh stiffness of two gear pair cases provided in the literature are compared and discussed in terms of the stiffness curve shape and maximum stiffness value. The main conclusions of this study include:

  1. 1.

    For Type I helical gear pairs, the maximum single mesh stiffness decreases slightly with the increase in the helix angle by an approximate term of cosβ. For Type II helical gear pairs, the maximum single mesh stiffness decreases abruptly with the increase in the helix angle, which is due to the abrupt reductions of the maximum effective contact face width.

  2. 2.

    The integration strategy that evaluates the mesh stiffness of the helical gear pair through the integration of the mesh stiffness of the staggered spur gears along the face width (Eq. (17)), is more accurate than the strategy that evaluates the mesh stiffness of the helical gear pair through combining each stiffness component (Eq. (18)), which is obtained through the integration of that stiffness component of the spur tooth pieces along the face width.

  3. 3.

    Compared with the traditional analytical method, the proposed analytical method yields more accurate results in terms of the shape of the single mesh stiffness curve in a mesh cycle, and the maximum value of single mesh stiffness, especially for the helical gears with wide face and large helix angle.