Keywords

1 Introduction

In recent years, the constraints in gear design process are concentrated on lightweight and defined size of gears thus to reach—efficient gear power transmission system. To achieve this objective, it is essential to understand the dynamic behaviour of gears. In general, a pair of gears is simulated with two disks coupled with non-linear mesh stiffness and mesh damping, (Umezawa et al. 1986; Parker et al. 2000). Many authors confirmed this simplified dynamic model and focus their investigation resources on various influence factors (Walha et al. 2011; Atanasovska et al. 2012). Moradi and Salarieh (2012) in their latest paper point out the importance of studying the nonlinear oscillations of gears from aspect of competitive limitations of noise level and vibrations in last decade. However, solution for helical gears oscillations can be obtained only if non-linear functions of stiffness and load are known.

In the literature, the tooth stiffness and mesh stiffness are treated in different ways. In the simpler models, the gear mesh stiffness is assumed to be constant. In last decade, authors overcame this simplification and presented various methods for teeth deformation teeth stiffness and load calculation. Thus, Andersson and Vedmar (2003) determined the dynamic load between two elastic helical gears with excitation from new incoming contacts and calculated the total deformation of contact teeth as sum of numerical calculated (with Finite Element Method) teeth bending deformations and analytical calculated Hertz’s teeth contact deformations. But, they neglected influence of load value on contact deformations. The importance of determination of variable contact area in simulation of contact problems in gears is discussed by Ulaga et al. (1999). They presented a new Finite element technique for more accurate contact stress predictions, while Pedrero et al. (2007, 2011) described minimum elastic potential criterion as method for calculation of load distribution in involute gears mesh. But they still used Hertz’s formulae for contact in one point and neglected influence of load value. This is not appropriate calculation methods for teeth total deformations, because contact deformation depends of the magnitude of load and must be determined through iterative procedure (Atanasovska et al. 2010).

In two new series of papers, Li (2007, 2008) and Atanasovska and Nikolić (2007b; Atanasovska et al. 2008, 2010) have been confirmed the Finite Element Method (FEM) as out of competition method for investigations of deformations and load distribution for spur gears. Pimsarn and Kazerounian (2002) present comparative analysis that give one more confirmation for FEM usage in evaluation of spur gear tooth mesh load.

The main objective of this paper is to present a method to determine the load in a helical gear pair considering the actual positions of the contacts and the actual deformations of the gear teeth. With this method, the transient loading and unloading is avoided. In the presented analysis, the positions of the contacts and the actual deformations of the gear teeth can be determined. This analysis is carried out each time the contact force changes, i.e., in every time increment in the dynamic simulation process and give quasi-static analysis of helical gears motion. The obtained deformations are then used to determine the mesh stiffness and load distribution between the meshed teeth pairs.

2 Theoretical Considerations

2.1 Teeth Stiffness and Mesh Stiffness

In general, stiffness is the force that causes unit deformation. There are different variables that describe stiffness for helical gears. In this paper, the few of them are used. The tooth stiffness for helical gears can be defined as ratio of differential of unit normal load in tooth face plane section \( d\left( {F_{bt} /b} \right) \) and appropriate elastic deformation:

$$ c = \frac{{d\left( {F_{bt} /b} \right)}}{du} $$
(1)

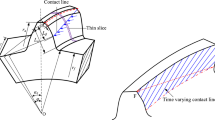
The tooth stiffness depends of many influence factors (gears geometry, load value, material characteristics etc.) and varies along length of action, as well as along line of contact of a teeth pair. Determination of tooth stiffness function is very important point in helical gears investigations. The complex helical gears geometry and variable length and position of teeth contact lines during mesh period require complex study of teeth contact. During meshing period for helical gears lines of contact are not parallel to gears axis. Therefore, teeth pairs coming in mesh gradually. Contact starts at pinion tooth root on one face of gears and propagates through face width towards pinion tooth top on another face of gears. This leads to continuously changing of contact line length and makes load distribution calculation very complex. Zone of action (contact zone) for involute parallel-axis gears with helical teeth is the rectangular area in the plane of action bounded by the length of action and the effective face width, Fig. 1.

Fig. 1
figure 1

Zone of action for involute parallel-axis gears with helical teeth

Full size image

The tooth stiffness at each point of line of teeth pair contact is called specific tooth stiffness and can be obtained as ratio of unit load and tooth deformation for any specific point:

$$ c_{sp} = q/u $$
(2)

For calculation of unit stiffness for ith teeth pair (when m teeth pair are simultaneously in contact), contact is simulated with serially connected springs, which is in accordance with contact modelling in mechanics. So, the specific teeth pair stiffness for any contact point when unit specific tooth stiffness for pinion tooth c sp1, and wheel tooth c sp2 are known has following form:

$$ c_{sp(i)} = \frac{{c_{sp1} \cdot c_{sp2} }}{{c_{sp1} + c_{sp2} }} $$
(3)

In many theoretical calculations, the assumption of constant teeth stiffness along line of contact exists. The average teeth pair stiffness along line of contact is used as constant teeth stiffness and for helical gears can be calculated for every of m teeth pair in contact as average value of specific teeth pair stiffness along line of contact:

$$ c^{\prime } = \overline{q/u} $$
(4)

The previous mentioned dynamic models of helical gears motion (Walha et al. 2011; Atanasovska et al. 2012), use simplified stiffness variable called total mesh stiffness c 0 that is sum of total teeth pair stiffness for all simultaneously meshed teeth pairs. For involute helical gears, that means:

$$ \begin{aligned} c_{0} & = \sum {(c_{i}^{\prime } \cdot B_{i} } ),\;i = 1, 2 {\text{ for two teeth pair in contact}} \\ c_{0} & = \sum {(c_{i}^{\prime } \cdot B_{i} } ),\;i = 1, 2, 3 {\text{ for three teeth pair in contact}} \\ \end{aligned} $$
(5)

where: c i ’ is average teeth pair stiffness for ith teeth pair in contact and B i is length of line of contact for ith teeth pair.

2.2 Analytical Model for Load Distribution

The load distribution is more complex task for involute cylindrical gears with helical teeth in comparison with the same task for the involute straight spur gears, and could not been solved with procedures published so far. Lines of teeth contact for helical gears are inclined and are not parallel with gear axis of rotation and length of contact line varies along length of contact, Fig. 1. Also, for one particular contact position contact points lie on different radius and have different deformations and stiffness. The nonlinear load distribution in helical gear mesh could be solved only by resolving the load distribution between simultaneously meshed teeth pairs and the load distribution along each of teeth pair contact line, at the same time. In this paper, for analytical definition of load distribution in helical gear mesh, the expanded procedure for load distribution over gear facewidth for involute spur gear have been used (Atanasovska and Nikolic 2006).

For every moment (contact position P) during helical gears mesh m tooth pairs are simultaneously in contact. System of integral equations, which consists of the contact equation and balance equation, can be defined for each ith of m simultaneously meshed teeth pairs for the contact position. This system can be presented in the following form:

$$ \int\limits_{0}^{{B_{i} }} {q_{i} \left( z \right)} \cdot K_{i} \left( {z,u} \right)dz = \Updelta_{i} + F_{\beta i} \left( z \right);\;\int\limits_{0}^{{B_{i} }} {q_{i} \left( z \right)dz = F_{bti} } $$
(6)

where: q i (z)—is function of unit load change along the ith teeth pair contact line, B i —is length of ith teeth pair contact line for position P, K i (z,u)—is influence function, which defines relation between u (elastic deformation at one particular point on the contact pattern) and q i (z)dz (unit concentrated load at the same point), z—is coordinate of studied point along contact pattern, Δ i —is total teeth pair deformation in the direction normal to teeth pair contact pattern, F βi (z)—is mesh initial misalignment (deviation between pinion tooth face width direction and wheel tooth face width direction when the gear pair is unloaded), F bti —is total normal load value for ith teeth pair in mesh. Systems of Eq. (6) for all m simultaneously meshed tooth pairs and equation of load balance

$$ F_{bt1} + F_{bt2} + \ldots + F_{btm} = F_{bt} $$
(7)

yield the (2m + 1) equation system for load distribution solution. It’s very hard or almost impossible to determine real values for many factors and variables that have crucial influence on accurate form of the function q i (z), as well as on value of real teeth pair bearing pattern length B i . Therefore, this equation system can be solved only by numerical methods with same simplification and assumptions.

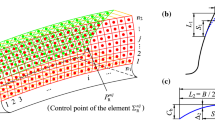
The discrete method is a simplification model chosen for solving the load distribution in gear mesh, (Atanasovska and Nikolic 2007b). The main principle of this method defines teeth pairs contact lines like finale number of equal segments. A length of these segments is nearly a value of gear pair module and the n i is the number of segments on the ith teeth pair contact line, so the Eq. (7) takes the following form:

$$ \sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{{n_{i} }} {q_{ij} \cdot } } B_{ij} = F_{bn} $$
(8)

where q ij —is normal unit load along the jth segment of ith teeth pair contact line; B ij —is length of the contact line segment. The numerical Finite Element Method is used for calculation of these values. In this way the nonlinear load distribution in helical gears mesh can be solved with some assumptions and simplifications: only normal load acts on teeth flanks, friction is neglected, deformations of shafts and bearings are neglected and the initial misalignment is neglected in the first step of the load distribution calculation.

3 Results and Discusion

3.1 Finite Element Analysis

The precise calculation of helical gear teeth deformations can be carried out by three-dimensional Finite Element Model (FEM) only. To develop such a model, authors defined the procedure of numerical calculations (Atanasovska et al. 2009). The commercial software Ansys 11.0 has been used. With the analysis of different models, and with emphasize on balance between accuracy and FEM calculation time, the physical models of gear segments with three teeth were adopted. The verification of FEM models is performed by strain gauges experiment on the tooth root and analytical contact stress calculation, and explained in paper Atanasovska et al. 2007a.

3D iso-parametric structural solid element defined by eight points (for 3D gear modelling) and 3D point to surface contact element (for teeth contact modelling) are used for 3D FEM helical gear pair model developing. Quasi static numerical model of helical gears are chosen for Finite Element Analysis (FEA). For every simulated contact position P two models are developed: one for the pinion, Fig. 2a and second for the wheel, sl.2.b. Figure 2 shows models for one particular contact position through period with three teeth pairs in contact. Results of FEA for this contact position are shown in Figs. 3 and 4. Figure 3 is the contour plot of deformation vector for pinion and for wheel, and Fig. 4 shows the reaction forces in teeth contacts (normal load distribution). Such results are obtained for all modelled contact position and total deformations of pinion teeth and wheel teeth are read from them. Also, the distribution of normal load is obtained for all modelled contact line positions. The obtained results are then used for determination of mesh stiffness and load distribution in accordance with procedure explained in following chapter.

Fig. 2
figure 2

FEM models for pinion and wheel

Full size image
Fig. 3
figure 3

Contour plot of deformation vectors for the pinion and the wheel

Full size image
Fig. 4
figure 4

Contact forces on the pinion tooth and the wheel tooth

Full size image

3.2 Calculation of Mesh Stiffness and Load Distribution

The appropriate investigations (Atanasovska et al. 2010) showed that gear teeth stiffness and load distribution in mesh depend on the magnitude of normal contact load. So, the iteration procedure is used for determination of teeth pair stiffness and load distribution. In the first step (iteration), total normal load for each teeth pair contact position is divided on simultaneously meshed teeth pairs in proportion of appropriate length of teeth pair contact lines, which are scanned from FEM model. After nonlinear FEA calculation, specific teeth pair stiffness of every jth segment on ith line of contact is calculated:

$$ c_{ij} = \frac{{F_{ij} }}{{u_{ij}^{\prime } \cdot B_{ij} }} $$
(9)

Total teeth pair deformation on jth segment of ith line of contact u ij ’, length of jth segment on ith line of contact—B ij and total contact force (sum of all reactions) on jth segment of ith line of contact—F ij are scanned from FEA results. Then average teeth pair stiffness for all lines of contact and total mesh stiffness for all calculated contact positions P in zone of action could be calculated.

For any next iteration normal load is divided on teeth pairs in mesh following the fact that continuous contact is possible only when total teeth deformations in contact point of all teeth pairs in contact in direction of normal load are equal. The equations for calculation of normal loads on m meshed teeth pairs for next iteration have following form:

$$ F_{bti} = \frac{{c_{i}^{\prime } \cdot F_{bt} }}{{\sum\limits_{i = 1}^{m} {(c_{i}^{\prime } \cdot B_{i} )} }} \cdot B_{i} ,\;i = 1,m $$
(10)

The final results for the modelled gear pair are given in diagrams in Fig. 5.

Fig. 5
figure 5

Specific teeth pair stiffness and normal load distribution in zone of action

Full size image

The total mesh stiffness and normal load distribution calculated with this procedure can be used for helical gears load capacity calculations and for modelling of nonlinear dynamic behaviour of helical gears.

4 Conclusion

A new approach for calculation of mesh teeth stiffness and load distribution for helical gears takes in consideration real gear teeth contact without usage of traditional Hertz’s solution for two cylinders in contact. The tooth deformation and mesh teeth pair stiffness are calculated in time and along contact lines at the same time. Helical gears transfer load with low noise and wear compare with spur gears. In coming years, efficiency will be one of the most important reasons for gear power transmission systems design and the application of helical gears will be increased. The research presented in this paper can help to gear researchers and green engineers to calculate helical gears with optimal parameters. The goal is to obtain gears with high level of both reliability and efficiency. In addition, the improved calculations of helical gears dynamics may lead to decrease of transmission systems vibrations and their longer life cycles.