1 Introduction

The helical gears are widely used in industrial applications to transmit motion and power with the advantages of high load capability and smooth transmission. The time-varying gear mesh stiffness (TVMS), which is the relationship between the load of the tooth and its deformation and fluctuates due to the alternating single pair of teeth and double pairs of teeth in engagement during the meshing process, constitutes the main excitation sources of vibration in gear systems [1, 2]. Simultaneously, elastic deformation, manufacturing error and assemble error of gear pairs are inevitable in practical gear transmissions. These factors result in mesh fluctuation and transmission error causing vibration during gear meshing [3, 4]. Appropriate tooth profile modification can reduce the mesh fluctuations and the associated internal excitations of time-varying mesh stiffness and transmission error [5,6,7,8]. Consequently, a large number of research work have been done on the tooth profile modification and its role on the TVMS and dynamic behavior of gear system.

The idea of tooth profile correction and the application to reduce gear mesh fluctuations can date back to the work by Harris [5]. Later on, Lin et al. [6] studied the effect of tooth profile modification on the transmission error and dynamic load of spur gears, in which the mesh stiffness was calculated using the empirical tooth deformation expressions. Kahraman and Blankenship [8] experimentally studied the effect of tooth profile modifications on the dynamic transmission error and vibration amplitude of a spur gear pair. Tesfahunegn et al. [9] investigated the influence of profile shape modifications on the transmission error and contact stress of a spur gear pair using finite element method. Chen and Shao [10] developed a general analytical formulation for mesh stiffness prediction of spur gears involving the effect of tooth errors. Ma et al. [11] developed an improved analytical model for the TVMS calculation of spur gear pairs with tooth profile modification by considering the effects of nonlinear contact stiffness and revised fillet-foundation stiffness. Xie et al. [12] further proposed a TVMS model for spur gear pair with tooth profile error by considering the effects of tooth and body flexibility. Sánchez et al. [13] studied the influence of different profile modifications on the mesh stiffness and transmission error of spur gears. The symmetric linear tip-relief was suggested to be the optimum to induce minimum dynamic load. Fernandez et al. [14] established a nonlinear dynamic model of spur gear transmissions to study the effects of profile deviation and support flexibility on the dynamic responses. These previously work on profile modification are all for spur gears.

As for the helical gear, the contact of gear tooth surface is in three-dimensional space with the helix angle, and the calculation of TVMS is different from that of a spur gear pair. The method based on the slicing principle is the most widely used analytical approach to calculate the TVMS of helical gears currently. The basic idea of the slicing method is that the helical gear tooth can be assumed as the superposition of sliced spur gear teeth along the tooth width direction. Accordingly, the mesh stiffness of the helical gear pair can be obtained by integrating the stiffness of each sliced spur gear pair. Based on this principle, Wan et al. [15] proposed an accumulated integral potential energy method to calculate the mesh stiffness of helical gears. Yu and Mechefske [16] proposed an improved analytical TVMS model of helical gears to consider the coupling effect between neighboring sliced tooth pieces using the introduced weighting factor. Feng et al. [17] proposed an improved TVMS of helical gears by including the effects of the fillet-foundation correction coefficient and the nonlinear Hertzian contact for the sliced spur gear. Wang and Zhu [18] developed an improved mesh stiffness model of helical gear pair by considering the axial mesh force and friction force influenced by surface roughness under elastohydrodynamic lubrication (EHL) condition. Benatar et al. [19] experimentally measured the transmission error for a series of helical gear pairs with different tooth profile modifications. The results show that the tooth modifications are directly related to the dynamic performances.

Although the studies on the TVMS of helical gears are abundant in the literature, investigations on the TVMS of helical gear with tooth profile modification are limited. Wang and Zhang [20] developed an analytical TVMS model for a helical gear with tooth profile errors based on the slicing method. The total mesh stiffness was determined as functions of mesh stiffness of sliced tooth pairs in ideal involute profile and the minimum tooth profile error in the meshing sliced tooth pairs. It is necessary to determine the mesh state of the sliced tooth pairs and to calculate the stiffness and tooth profile error of each sliced tooth pair in mesh, as well as to find the sliced tooth pair with the minimum tooth profile error. The calculation process is relatively complicated.

In this work, a novel analytical method is proposed to calculate the mesh stiffness of helical gears with tooth profile modification based on the slicing principle. Four types of helical gears are classified based on the geometry characteristics of the gear. The mesh stiffness of the corresponding single spur tooth pair with tooth profile modification is calculated firstly. Then, the mesh stiffness of helical gear pairs with tooth profile modification for the defined four types are obtained by integrating the mesh stiffness of a sliced modified spur gear pair with the contact line. The total mesh stiffness of helical tooth pairs with tooth profile modification can be obtained by summation of the single-tooth stiffness with the number of tooth pairs in mesh simultaneously.

2 Proposed mesh stiffness model

2.1 Model description

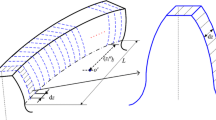
The contact line between the engaging surfaces of a helical gear inclines to the axes of the gears with a helix angle β, which moves its operating location from the root of one end B to the tip of the other end F during the mesh process, as shown in Fig. 1. The length of the contact line is time-varying between zero to maximum during the mesh process and therefore avoiding the sudden loading and unloading associated with the full tooth width contact in spur gears. Gear tooth profile modification, namely tip relief, is adjustment of the addendum by removing part of the surface material from the tooth tip and the tooth profile is not the theoretical profile any more, as that shown in Fig. 2. This modification can compensate for manufacturing errors and tooth deflections during meshing process and reduce the mesh impact and transmission error of gear system [8].

Fig. 1
figure 1

Helical gear tooth model and the varying contact line

Full size image
Fig. 2
figure 2

Gear with tooth profile modification

Full size image

The amount and length of the modification can be the same for both the pinion and the gear, which is defined by the maximum magnitude of the tip relief (Ca), the length of the relief (La) and the shape. The amount of modification in the mesh position along the horizontal direction can be expressed as

$$C(x) = C_{a} \left( {\frac{x}{{L_{a} }}} \right)^{s}$$
(1)

where x is the distance between the profile point and the starting point (SP) of the modification, s denotes the shape of tip relief curve and a linear tip relief with s = 1 is adopted. The maximum amount of tip modifications is generally in the microscale of order μm, which are suggested to be Ca_max = 0.02Mt and La_max = 0.6Mt according to the standards [10], where Mt is the face module of the helical gear with Mt = M/(1 + cosβ), M is the module of the helical gear and β is the helix angle.

According to the slicing principle, the helical gear can be divided into thin pieces with equal width along the tooth width direction, and each thin piece can be regarded as spur gear due to the negligible helix angle, as shown in Fig. 1. The mesh stiffness of a helical gear pair with tooth profile modification khm can be obtained by integrating the mesh stiffness of a sliced modified spur gear pair with the contact line of the helical gear, which can be expressed as

$$k_{hm} = \int_{0}^{{L_{t\max } }} {\left( {\frac{{k_{sm} }}{W}\cos^{2} \beta } \right){\text{d}}L_{t} }$$
(2)

where W is the width of the gear, ksm is the mesh stiffness of the corresponding single spur tooth pair with tooth profile modification, ksm/W is the mesh stiffness of the single spur tooth pair with tooth profile modification per unit width, β is the helix angle, Lt is the length of contact line of the helical tooth pair.

The total mesh stiffness of helical gears with tooth profile modification can be obtained as

$$K_{hm} = \sum\limits_{j = 1}^{{N_{h} }} {k_{hmj} ,\begin{array}{*{20}c} {} & {} \\ \end{array} N_{h} = \left[ {\varepsilon_{a} + \varepsilon_{b} } \right]}$$
(3)

where Nh is the maximum number of helical tooth pairs in simultaneous mesh with Nh = [εα + εβ], εα and εβ are the transverse contact ratio and overlap contact ratio of the helical gear, respectively. The notation [] means round a number upwards to the nearest integer.

Therefore, to determine the mesh stiffness of helical gears with tooth profile modification Khm, it is necessary to obtain the mesh stiffness of the corresponding single spur tooth pair with tooth profile modification ksm firstly.

2.2 Mesh stiffness of a single spur tooth pair with tooth profile modification

The total mesh stiffness of spur gear pair with microscale tooth profile modification can be expressed as [10]

$$K_{m} = \frac{{\sum\nolimits_{i = 1}^{{N_{s} }} {k_{i} } }}{{1 + \sum\nolimits_{i = 1}^{{N_{s} }} {k_{i} E_{pg} /F} }}$$
(4)

where F is the total mesh force, Epg is the total tooth profile error, Ns is the number of teeth pairs in engagement, ki is the single tooth-meshing stiffness of the ith gear pair with standard involute profile and is expressed as [10, 12, 16]

$$k_{i} = \frac{1}{{\left( {\frac{1}{{k_{b1} }} + \frac{1}{{k_{s1} }} + \frac{1}{{k_{a1} }} + \frac{1}{{k_{f1} }} + \frac{1}{{k_{b2} }} + \frac{1}{{k_{s2} }} + \frac{1}{{k_{a2} }} + \frac{1}{{k_{f2} }} + \frac{1}{{k_{h} }}} \right)}}$$
(5)

where kb, ks, ka, kf and kh are the bending stiffness, shear stiffness, compressive stiffness, base foundation stiffness and contact stiffness, respectively. The symbols 1 and 2 denote the driving gear and driven gear, respectively. Each stiffness component can be computed using the following expressions [16, 21, 22]

$$\frac{1}{{k_{b} }} = \int_{0}^{d} {\frac{{\left[ {\left( {d - x} \right)\cos \alpha - h_{g} \sin \alpha } \right]}}{{EI_{x} }}} {\text{d}}x$$
(6)
$$\frac{1}{{k_{s} }} = \int_{0}^{d} {\frac{{1.2\cos^{2} \alpha }}{{GA_{x} }}} {\text{d}}x$$
(7)
$$\frac{1}{{k_{a} }} = \int_{0}^{d} {\frac{{\sin^{2} \alpha }}{{EA_{x} }}} {\text{d}}x$$
(8)
$$\frac{1}{{k_{f} }} = \frac{{\cos^{2} \alpha }}{EW}\left[ {L^{*} \left( {\frac{{U_{f} }}{{S_{f} }}} \right)^{2} } \right. + \left. {P^{*} \left( 1 \right. + Q^{*} \tan^{2} \alpha } \right)\left. { + M^{*} \left( {\frac{{U_{f} }}{{S_{f} }}} \right)} \right]$$
(9)
$$k_{h} = \frac{{E^{0.9} L^{0.8} F^{0.1} }}{1.275}$$
(10)

where E and G are the elastic modulus and shear modulus, respectively, α is the pressure angle, hg is the half tooth thickness at the action point, d denotes the distance between the action point and the tooth root circle, Ix and Ax are the equivalent cross-sectional modulus and equivalent cross-sectional area, respectively. The parameters of L*, M*, P*, Q*, Uf and Sf are constants [22].

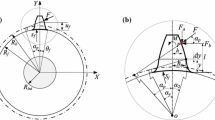
The total tooth profile error is related to the meshing states of the gear pairs. Assuming the meshing process starts from the double-tooth engagement and the tooth pair 1 and tooth pair 2 are in mesh, as the stage I shown in Fig. 3a, the tooth pair 1 is in the standard profile range and the pair 2 is in the profile modification range A2B2. The total tooth profile error is the summation of the profile error for the two meshing pairs. As the gear rotates, the tooth pair 1 exits meshing and the tooth pair 2 comes into engagement in the single tooth-meshing with standard profile, as the stage II shown in Fig. 3b. There is no tooth profile error at this stage. At the third stage III shown in Fig. 3c, the tooth pair 2 and tooth pair 3 are in double-tooth engagement. The tooth pair 2 is exiting mesh and is in the profile modification range A2B2 again. The tooth pair 3 comes into mesh in the standard profile range. The total tooth profile error is the sum of the profile error for the two pairs again.

Fig. 3
figure 3

Meshing process of the helical gear pairs a stage I, b stage II, c stage III

Full size image

Figure 4 shows the relative position relationships between the three tooth pairs and the tooth profile error of the gear pairs in the meshing process. At stage I, tooth pair 1 and tooth pair 2 are in mesh and the profile errors of the two pairs are E1 and E2, respectively. At stage II, only tooth pair 2 is in mesh with the standard profile and there is no profile error. At stage III, tooth pair 2 and tooth pair 3 are in mesh and the profile errors are E2 and E3, respectively. For the double-single-double tooth engagement period, the total tooth profile error has the expression as follows

$$E_{pg} = \left\{ {\begin{array}{*{20}l} {\left| {E_{2} - E_{1} } \right|,} \hfill & {0 < \theta < \theta_{1} {,}} \hfill & {\text{double - tooth}} \hfill \\ {0,} \hfill & {\theta_{1} \le \theta \le \theta_{2} - \theta_{1} {,}} \hfill & {\text{single - tooth}} \hfill \\ {\left| {E_{3} - E_{2} } \right|,} \hfill & {\theta_{2} - \theta_{1} < \theta \le \theta_{2} {,}} \hfill & {\text{double - tooth}} \hfill \\ \end{array} } \right.$$
(11)

where Ei (i = 1, 2, 3) is the profile error of the ith meshing tooth pair, θ is the rotating angle of the pinion, θ1 is the rotating angle for the double-tooth engagement period, θ2 is the total rotating angle for the double-single-double tooth engagement period, which has the expressions of

$$\theta_{1} { = }\frac{2\pi }{N}\left( {\varepsilon_{\alpha } - 1} \right),\begin{array}{*{20}c} {} \\ \end{array} \theta_{2} { = }\frac{{{2}\pi \varepsilon_{\alpha } }}{N}$$
(12)

where εα is the transverse contact ratio, N is the tooth number of the pinion. For the double-tooth engagement of stage I, the tooth profile error of each component and the total tooth profile error can be expressed as

$$E_{1} = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {0 \le \theta \le \theta_{1} - \theta_{0} } \hfill \\ {\frac{{C_{a} }}{{\theta_{0} }}\left[ {\theta - (\theta_{1} - \theta_{0} )} \right],} \hfill & {\theta_{1} - \theta_{0} \le \theta \le \theta_{0} } \hfill \\ {\frac{{C_{a} }}{{\theta_{0} }}\left[ {\theta - (\theta_{1} - \theta_{0} )} \right],} \hfill & {\theta_{0} \le \theta \le \theta_{1} } \hfill \\ \end{array} } \right.$$
(13)
$$E_{2} = \left\{ {\begin{array}{*{20}l} {C_{a} - \frac{{C_{a} \theta }}{{\theta_{0} }},} \hfill & {0 \le \theta \le \theta_{1} - \theta_{0} } \hfill \\ {C_{a} - \frac{{C_{a} \theta }}{{\theta_{0} }},} \hfill & {\theta_{1} - \theta_{0} \le \theta \le \theta_{0} } \hfill \\ {0,} \hfill & {\theta_{0} \le \theta \le \theta_{1} } \hfill \\ \end{array} } \right.$$
(14)
$$E_{pg(12)} = \left\{ {\begin{array}{*{20}l} {C_{a} - \frac{{C_{a} \theta }}{{\theta_{0} }},} \hfill & {0 \le \theta \le \theta_{1} - \theta_{0} } \hfill \\ {C_{a} + \left( {\theta_{1} - \theta_{0} } \right)\frac{{C_{a} }}{{\theta_{0} }},} \hfill & {\theta_{1} - \theta_{0} \le \theta \le \theta_{0} } \hfill \\ {\left[ {\left( {\theta_{1} - \theta_{0} } \right) - \theta } \right]\frac{{C_{a} }}{{\theta_{0} }},} \hfill & {\theta_{0} \le \theta \le \theta_{1} } \hfill \\ \end{array} } \right.$$
(15)

where θ0 is the rotating angle corresponding to the length of the tip relief with θ0 = La/rb, rb is the base circle radii of the pinion. For the double-tooth engagement of stage III, the tooth profile error of each component and the total tooth profile error can be expressed as

$$E_{2} = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {\theta_{2} - \theta_{1} \le \theta < \theta_{2} - \theta_{0} } \hfill \\ {\frac{{C_{a} }}{{\theta_{0} }}\left[ {\theta - \left( {\theta_{1} - \theta_{0} } \right)} \right],} \hfill & {\theta_{2} - \theta_{0} \le \theta \le \theta_{2} - \theta_{1} + \theta_{0} } \hfill \\ {\frac{{C_{a} }}{{\theta_{0} }}\left[ {\theta - \left( {\theta_{1} - \theta_{0} } \right)} \right],} \hfill & {\theta_{2} - \theta_{1} + \theta_{0} \le \theta \le \theta_{2} } \hfill \\ \end{array} } \right.$$
(16)
$$E_{3} = \left\{ {\begin{array}{*{20}l} {C_{a} - \left[ {\theta - \left( {\theta_{2} - \theta_{1} } \right)} \right]\frac{{C_{a} }}{{\theta_{0} }},} \hfill & {\theta_{2} - \theta_{1} \le \theta \le \theta_{2} - \theta_{0} } \hfill \\ {\frac{{C_{a} }}{{\theta_{0} }}\left[ {C_{a} - \left( {\theta - (\theta_{1} - \theta_{3} )} \right)} \right],} \hfill & {\theta_{2} - \theta_{0} \le \theta \le \theta_{2} - \theta_{1} + \theta_{0} } \hfill \\ {0,} \hfill & {\theta_{2} - \theta_{1} + \theta_{0} \le \theta \le \theta_{2} } \hfill \\ \end{array} } \right.$$
(17)
$$E_{pg(23)} = \left\{ {\begin{array}{*{20}l} {C_{a} - \left[ {\theta - \left( {\theta_{2} - \theta_{1} } \right)} \right]\frac{{C_{a} }}{{\theta_{0} }},} \hfill & {\theta_{2} - \theta_{1} \le \theta \le \theta_{2} - \theta_{0} } \hfill \\ {C_{a} + \left[ {2\theta_{2} - 2\theta - \theta_{1} - \theta_{0} } \right]\frac{{C_{a} }}{{\theta_{0} }},} \hfill & {\theta_{2} - \theta_{0} \le \theta \le \theta_{2} - \theta_{1} + \theta_{0} } \hfill \\ {\left[ {\left( {\theta_{2} - \theta_{0} } \right) - \theta } \right]\frac{{C_{a} }}{{\theta_{0} }},} \hfill & {\theta_{2} - \theta_{1} + \theta_{0} \le \theta \le \theta_{2} } \hfill \\ \end{array} } \right.$$
(18)
Fig. 4
figure 4

Tooth profile error of the gear pairs in different mesh states

Full size image

Combining Eq. (4), Eq. (5), Eq. (15) and (18), the total mesh stiffness of a spur gear pair with tooth profile modification Km can be determined.

The total mesh stiffness of spur gear pairs with tooth profile modification Km can be also obtained by combining the corresponding mesh stiffness of a modified single spur tooth pair ksm with the contact ratio. Accordingly, the mesh stiffness of a single spur tooth pair with tooth profile modification ksm can be determined by subtracting the single tooth-meshing stiffness from the total mesh stiffness Km.

The mesh stiffness of a modified single spur tooth pair consists of three stages corresponding to the meshing states of the gears, as shown in Fig. 3. In the first stage I, the pair 1 is in the standard profile range and the pair 2 is in the profile modification range. Accordingly, the mesh stiffness of tooth pair 2 can be obtained by subtracting the single mesh stiffness of tooth pair 1 from the total mesh stiffness. In the second stage II, the mesh stiffness of tooth pair 2 is the single tooth-meshing stiffness with standard profile. In the third stage III, the mesh stiffness of tooth pair 2 can be obtained by subtracting the single mesh stiffness of tooth pair 3 from the total mesh stiffness. Consequently, the mesh stiffness of a single spur tooth pair with tooth profile modification can be determined as

$$k_{sm} = \left\{ {\begin{array}{*{20}l} {k_{sm1} = K_{m} - k_{i - 1} ,} \hfill & {0 \le \theta < \theta_{0} } \hfill \\ {k_{sm2} = k_{i} ,} \hfill & {\theta_{0} \le \theta \le \theta_{2} - \theta_{0} } \hfill \\ {k_{sm3} = K_{m} - k_{i + 1} ,} \hfill & {\theta_{2} - \theta_{0} \le \theta \le \theta_{2} } \hfill \\ \end{array} } \right.$$
(19)

where Km is the total mesh stiffness of spur gear considering tooth profile modification in Eq. (4), ki is the single tooth-meshing stiffness of the ith gear pair with standard profile in Eq. (5).

2.3 Mesh stiffness of helical gears with tooth profile modification

Substituting Eq. (19) into Eq. (2) and recalling the relationship between the length of contact line and the rotating angle

$$dL_{t} = \frac{W/\cos \beta }{{\theta_{3} }} \cdot d\theta$$
(20)

where θ3 is the rotating angle along the line of action when the helical gears coincide in the normal direction with θ3 = 2πεβ/N. The mesh stiffness of the jth single helical tooth pair considering tooth profile modification of Eq. (2) can be rewritten as

$$k_{hmj} = \int_{{\theta_{sj} }}^{{\theta_{ej} }} {k_{smb} d\theta }$$
(21)

where θsj and θej are the rotating angles corresponding to the start position and end position of the contact line for the jth helical tooth pair, respectively, and ksmb has the expressions of

$$\begin{gathered} k_{smb} = \left\{ {\begin{array}{*{20}l} {k_{smb1} = \left( {K_{m} - k_{i - 1} } \right)\frac{\cos \beta }{{\theta_{3} }},} \hfill & {0 \le \theta < \theta_{0} } \hfill \\ {k_{smb2} = k_{i} \frac{\cos \beta }{{\theta_{3} }},} \hfill & {\theta_{0} \le \theta \le \theta_{2} - \theta_{0} } \hfill \\ {k_{smb3} = \left( {K_{m} - k_{i + 1} } \right)\frac{\cos \beta }{{\theta_{3} }},} \hfill & {\theta_{2} - \theta_{0} \le \theta \le \theta_{2} } \hfill \\ \end{array} } \right. \hfill \\ \hfill \\ \end{gathered}$$
(22)

The range of integration for θsj and θej are determined by the geometric dimensions of the helical gear. Depending on the relationship between the length of the relief (La), the transverse length of line of action (LOA) Lp (= 2πrbεα/N) and the axial length of LOA Lβ (= 2πrbεβ/N), a helical gear pair can be classified into four types:

  1. 1.

    Type I: the length of the relief La is larger than the length Lβ and smaller than the length Lp with Lβ < La < Lp;

  2. 2.

    Type II: the length Lβ is larger than the length of the relief La and smaller than the length of Lp—La with La < Lβ < Lp − La;

  3. 3.

    Type III: the length Lβ is larger than the length of Lp − La and smaller than the length Lp with Lp—La < Lβ < Lp;

  4. 4.

    Type IV: the length Lβ is larger than the length Lp with Lβ > Lp.

Figure 5 shows the plane of action for the four helical types. The point F0 on the front face indicates the starting position of the meshing process, and point B1 on the back face indicates the endpoint of meshing. The solid lines in the rectangle B0B1F1F0 represent the instant contact lines which moves along the plane of action. F0F2 is the distance moving along the base cylinder during the engagement. For the four types of helical gear pair, the start position and end position of the contact line are different, and accordingly the range of integration for θsj and θej in Eq. (21) is different.

Fig. 5
figure 5

Plane of action of a helical gear for the four types a Lβ < La (θ3 < θ0), b La < Lβ < Lp − La (θ0 < θ3 < θ2 − θ0), c Lp − La < Lβ < Lp (θ2 − θ0 < θ3 < θ2), d Lβ > Lp (θ3 > θ2). The dash line indicates the extension of the contact line

Full size image

Incorporating the rotating angles, the mesh stiffness of the jth single helical tooth pair considering tooth profile modification of Eq. (21) can be further written as.

(1) For type I with Lβ < La (θ3 < θ0),

$$k_{hmj} = \left\{ {\begin{array}{*{20}l} {\int_{0}^{\theta } {k_{smb1} {\text{d}}\theta ,} } \hfill & {0 \le \theta < \theta_{3} } \hfill \\ {\int_{{\theta - \theta_{3} }}^{\theta } {k_{smb1} {\text{d}}\theta ,} } \hfill & {\theta_{3} \le \theta \le \theta_{0} } \hfill \\ {\int_{{\theta - \theta_{3} }}^{{\theta_{0} }} {k_{smb1} {\text{d}}\theta } + \int_{{\theta_{0} }}^{\theta } {k_{smb2} {\text{d}}\theta ,} } \hfill & {\theta_{0} < \theta \le \theta_{3} + \theta_{0} } \hfill \\ {\int_{{\theta - \theta_{3} }}^{\theta } {k_{smb2} {\text{d}}\theta ,} } \hfill & {\theta_{3} + \theta_{0} < \theta \le \theta_{2} - \theta_{0} } \hfill \\ {\int_{{\theta - \theta_{3} }}^{{\theta_{2} - \theta_{0} }} {k_{smb2} {\text{d}}\theta } + \int_{{\theta_{2} - \theta_{0} }}^{\theta } {k_{smb3} {\text{d}}\theta } ,} \hfill & {\theta_{2} - \theta_{0} < \theta \le \theta_{2} + \theta_{3} - \theta_{0} } \hfill \\ {\int_{{\theta - \theta_{3} }}^{\theta } {k_{smb3} {\text{d}}\theta ,} } \hfill & {\theta_{2} + \theta_{3} - \theta_{0} < \theta \le \theta_{2} } \hfill \\ {\int_{\theta - \theta 3}^{{\theta_{2} }} {k_{smb3} {\text{d}}\theta ,} } \hfill & {\theta_{2} < \theta \le \theta_{2} + \theta_{3} } \hfill \\ \end{array} } \right.$$
(23)

(2) For type II with La < Lβ < Lp − La (θ0 < θ3 < θ2 − θ0),

$$k_{hmj} = \left\{ {\begin{array}{*{20}l} {\int_{0}^{\theta } {k_{smb1} {\text{d}}\theta } ,} \hfill & {0 \le \theta \le \theta_{0} } \hfill \\ {\int_{0}^{{\theta_{0} }} {k_{smb1} {\text{d}}\theta } + \int_{{\theta_{0} }}^{\theta } {k_{smb2} {\text{d}}\theta } ,} \hfill & {\theta_{0} \le \theta \le \theta_{3} } \hfill \\ {\int_{{\theta - \theta_{3} }}^{{\theta_{0} }} {k_{smb1} {\text{d}}\theta } + \int_{{\theta_{0} }}^{\theta } {k_{smb2} {\text{d}}\theta } ,} \hfill & {\theta_{3} \le \theta \le \theta_{0} + \theta_{3} } \hfill \\ {\int_{{\theta - \theta_{3} }}^{\theta } {k_{smb2} {\text{d}}\theta } ,} \hfill & {\theta_{0} + \theta_{3} \le \theta \le \theta_{2} - \theta_{0} } \hfill \\ {\int_{{\theta - \theta_{3} }}^{{\theta_{2} - \theta_{0} }} {k_{smb2} {\text{d}}\theta } + \int_{{\theta_{2} - \theta_{0} }}^{\theta } {k_{smb3} {\text{d}}\theta } ,} \hfill & {\theta_{2} - \theta_{0} \le \theta \le \theta_{2} } \hfill \\ {\int_{{\theta - \theta_{3} }}^{{\theta_{2} - \theta_{0} }} {k_{smb2} {\text{d}}\theta } + \int_{{\theta_{2} - \theta_{0} }}^{{\theta_{2} }} {k_{smb3} {\text{d}}\theta } ,} \hfill & {\theta_{2} \le \theta \le \theta_{2} + \theta_{3} - \theta_{0} } \hfill \\ {\int_{{\theta - \theta_{3} }}^{{\theta_{2} }} {k_{smb3} {\text{d}}\theta ,} } \hfill & {\theta_{2} + \theta_{3} - \theta_{0} \le \theta \le \theta_{2} + \theta_{3} } \hfill \\ \end{array} } \right.$$
(24)

(3) For type III with Lp − La < Lβ < Lp (θ2 − θ0 < θ3 < θ2),

$$k_{hmj} = \left\{ {\begin{array}{*{20}l} {\int_{0}^{\theta } {k_{smb1} d\theta } ,} \hfill & {0 \le \theta \le \theta_{0} } \hfill \\ {\int_{0}^{{\theta_{0} }} {k_{smb1} d\theta } + \int_{{\theta_{0} }}^{\theta } {k_{smb2} d\theta } ,} \hfill & {\theta_{0} \le \theta \le \theta_{2} - \theta_{0} } \hfill \\ {\int_{0}^{{\theta_{0} }} {k_{smb1} d\theta } + \int_{{\theta_{0} }}^{{\theta_{2} - \theta_{0} }} {k_{smb2} d\theta } + \int_{{\theta_{2} - \theta_{0} }}^{\theta } {k_{smb3} d\theta } ,} \hfill & {\theta_{2} - \theta_{0} \le \theta \le \theta_{3} } \hfill \\ {\int_{{\theta - \theta_{3} }}^{{\theta_{0} }} {k_{smb1} d\theta } + \int_{{\theta_{0} }}^{{\theta_{2} - \theta_{0} }} {k_{smb2} d\theta } + \int_{{\theta_{2} - \theta_{0} }}^{\theta } {k_{smb3} d\theta } ,} \hfill & {\theta_{3} \le \theta \le \theta_{2} } \hfill \\ {\int_{{\theta - \theta_{3} }}^{{\theta_{0} }} {k_{smb1} d\theta } + \int_{{\theta_{0} }}^{{\theta_{2} - \theta_{0} }} {k_{smb2} d\theta } + \int_{{\theta_{2} - \theta_{0} }}^{{\theta_{2} }} {k_{smb3} d\theta } ,} \hfill & {\theta_{2} \le \theta \le \theta_{2} + \theta_{0} } \hfill \\ {\int_{{\theta - \theta_{3} }}^{{\theta_{2} - \theta_{0} }} {k_{smb2} d\theta } + \int_{{\theta_{2} - \theta_{0} }}^{{\theta_{2} }} {k_{smb3} d\theta ,} } \hfill & {\theta_{2} + \theta_{0} \le \theta \le \theta_{2} + \theta_{3} - \theta_{0} } \hfill \\ {\int_{{\theta - \theta_{3} }}^{{\theta_{2} }} {k_{smb3} d\theta ,} } \hfill & {\theta_{2} + \theta_{3} - \theta_{0} \le \theta \le \theta_{2} + \theta_{3} } \hfill \\ \end{array} } \right.$$
(25)

(4) For type IV with Lβ > Lp (θ3 > θ2),

$$k_{hmj} = \left\{ {\begin{array}{*{20}l} {\int_{0}^{\theta } {k_{smb1} d\theta ,} } \hfill & {0 \le \theta \le \theta_{0} } \hfill \\ {\int_{0}^{{\theta_{0} }} {k_{smb1} d\theta } + \int_{{\theta_{0} }}^{\theta } {k_{smb2} d\theta ,} } \hfill & {\theta_{0} \le \theta \le \theta_{2} - \theta_{0} } \hfill \\ {\int_{0}^{{\theta_{0} }} {k_{smb1} d\theta } + \int_{{\theta_{0} }}^{{\theta_{2} - \theta_{0} }} {k_{smb2} d\theta } + \int_{{\theta_{2} - \theta_{0} }}^{\theta } {k_{smb3} d\theta } ,} \hfill & {\theta_{2} - \theta_{0} \le \theta \le \theta_{2} } \hfill \\ {\int_{0}^{{\theta_{0} }} {k_{smb1} d\theta } + \int_{{\theta_{0} }}^{{\theta_{2} - \theta_{0} }} {k_{smb2} d\theta } + \int_{{\theta_{2} - \theta_{0} }}^{{\theta_{2} }} {k_{smb3} d\theta } ,} \hfill & {\theta_{2} \le \theta \le \theta_{3} } \hfill \\ {\int_{{\theta - \theta_{3} }}^{{\theta_{0} }} {k_{smb1} d\theta } + \int_{{\theta_{0} }}^{{\theta_{2} - \theta_{0} }} {k_{smb2} d\theta } + \int_{{\theta_{2} - \theta_{0} }}^{{\theta_{2} }} {k_{smb3} d\theta } ,} \hfill & {\theta_{3} \le \theta \le \theta_{3} + \theta_{0} } \hfill \\ {\int_{{\theta - \theta_{3} }}^{{\theta_{2} - \theta_{0} }} {k_{smb2} d\theta } + \int_{{\theta_{2} - \theta_{0} }}^{{\theta_{2} }} {k_{smb3} d\theta } ,} \hfill & {\theta_{3} + \theta_{0} \le \theta \le \theta_{2} + \theta_{3} - \theta_{0} } \hfill \\ {\int_{{\theta - \theta_{3} }}^{{\theta_{2} }} {k_{smb3} d\theta ,} } \hfill & {\theta_{2} + \theta_{3} - \theta_{0} \le \theta \le \theta_{2} + \theta_{3} } \hfill \\ \end{array} } \right.$$
(26)

Consequently, the total mesh stiffness of helical gears with tooth profile modification can be obtained by summarizing the obtained mesh stiffness of the single modified helical tooth pair in Eq. (23) to Eq. (26) with the maximum number of tooth pairs in mesh simultaneously using Eq. (3). Figure 6 shows the flowchart of the proposed method.

Fig. 6
figure 6

Flowchart of the proposed method

Full size image

Accordingly, the loaded static transmission error (LSTE) of the helical gears can be expressed as

$${\text{LSTE}} = \frac{{F_{N} }}{{K_{hm} }} + E_{pg\_\min }$$
(27)
$$E_{pg\_\min } = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {\theta \le \frac{{\theta_{1} }}{2}} \hfill \\ {\min (E_{1} ,E_{2} ,E_{3} ),} \hfill & {\frac{{\theta_{1} }}{2} \le \theta \le \theta_{1} } \hfill \\ \end{array} } \right.$$
(28)

where FN is normal mesh force with \(F_{N} = {T \mathord{\left/ {\vphantom {T {\left( {r_{b} \cos \alpha \cos \beta } \right)}}} \right. \kern-0pt} {\left( {r_{b} \cos \alpha \cos \beta } \right)}}\), Khm is the total mesh stiffness of helical gears with tooth modification, Epg_min is the minimum tooth profile error of the helical gears in mesh.

3 Results and discussion

3.1 Model verification

In order to validate the proposed method for the mesh stiffness of helical gears with tooth profile modification, the mesh stiffness of a single spur tooth pair with tooth profile modification in Eq. (19) is validated firstly. The time-varying mesh stiffness of spur gears with tooth profile modification can be obtained by superimposing the mesh stiffness of a single tooth in Eq. (19) with the contact ratio, which is then compared with the corresponding mesh stiffness calculated using the published formulation of Eq. (4). Two sets of spur gear pair models in references [10, 23] are used. The parameters are presented in Table 1. The magnitude of the tip relief and the length of the relief are Ca = 32 μm, La = 960 μm, and Ca = 8 μm, La = 600 μm for the two models, respectively. The comparison results are shown in Fig. 7. It can be seen that the time-varying mesh stiffness of spur gears with tooth profile modification obtained by the two methods are completely the same, which verify the accuracy of the developed mesh stiffness of single spur tooth pair considering tooth profile modification.

Table 1 Parameters of the spur gears used in calculation [10, 23]
Full size table
Fig. 7
figure 7

Comparison of the total mesh stiffness for spur gears with tooth profile modification calculated using the developed method and the method in reference a Model I [10], b Model II [23]

Full size image

To further validate the proposed method for the total mesh stiffness of helical gears with tooth profile modification, the predicted results using the developed method are compared with the results presented in reference [20]. The parameters of Model III listed in Table 2 from reference [20] are used for calculation. The comparison results are shown in Fig. 8. The maximum magnitude of the tip relief is Ca = 52 μm with the length of the relief varies as La = 932 μm, 1600 μm, 2200 μm and 2800 μm. It can be seen that the results calculated using the developed method are consistent with the results presented in reference. Table 3 shows the extracted maximum value and average value of the total mesh stiffness obtained using the developed method and that in reference. The maximum relative error is 3.8%. The differences in the results can be attributed to the following two reasons. Firstly, the mesh stiffness in the developed method is derived based on the relationship between contact length and rotating angle, and the effect of profile modification on the instant length of contact line is ignored, while the profile modification is included in the tooth profile error of sliced tooth pairs in the reference but with a relatively complicated calculation process. Secondly, the linear contact stiffness was employed for the mesh stiffness calculation in the reference, while the nonlinear Hertzian contact stiffness varying with contact force is considered in this work.

Table 2 Parameters of the helical gears used in calculation
Full size table
Fig. 8
figure 8

Comparison of the total mesh stiffness for helical gears with tooth profile modification calculated using the developed method and the results in reference [20]. The maximum magnitude of the tip relief is Ca = 52μm with different modification lengths as a La = 932 μm, b La = 1600 μm, c La = 2200 μm, d La = 2800μm

Full size image
Table 3 Error analysis of the results shown in Fig. 8
Full size table

3.2 Effect of tooth profile modification

Effects of the length and amount of tooth profile modification on the total mesh stiffness and loaded static transmission error are studied. The two sets of helical gear pair models listed in Table 2, with low contact ratio (LCR) as ε = 1.85 and high contact ratio (HCR) as ε = 4.9, are used for calculations. The transverse contact ratio is similar for both cases, but the overlap ratio is very different. The tip relief limitations are determined as Ca_max = 50μm, La_max = 1524μm, and the non-dimensional profile modification parameters are calculated using [10, 24]

$$C_{n} = \frac{{C_{a} }}{{C_{{a\_\max }} }},\quad L_{n} = \frac{{L_{a} }}{{L_{{a\_\max }} }}$$
(29)

where Cn and Ln are the normalized tip relief parameters representing the amount of actual relief relative to the limit values.

The mesh stiffness of the corresponding single spur tooth pair with tooth profile modification is obtained firstly with the helix angles set to be zero. An example is shown in Fig. 9 for non-dimensional tooth profile modification parameters Cn = 1 and Ln = 0.4. As seen, there are at most two pairs of teeth engaged simultaneously for the corresponding spur gears because the values of transverse contact ratio are εα = 1.58 and εα = 1.71 for the two models, as listed in Table 2. The mesh stiffness of the helical tooth pairs with tooth profile modification for the two models is shown in Fig. 10. For Model III, the contact ratio is ε = 1.85, and there are at most two pairs of teeth engaged simultaneously. For Model IV, there are five tooth pairs in mesh simultaneously as the contact ratio is ε = 4.9. It can be also seen that the variation of mesh stiffness during the periodical engagement decreases with the increase of contact ratio.

Fig. 9
figure 9

Mesh stiffness of the corresponding single spur tooth pair with tooth profile modification for a Model III (LCR), b Model IV (HCR)

Full size image
Fig. 10
figure 10

Mesh stiffness of the helical tooth pair with tooth profile modification for a Model III (LCR), b Model IV (HCR)

Full size image

The total mesh stiffness and loaded static transmission error for helical gears with different length and amount of tooth profile modification are presented in Figs. 11 and 12, respectively. The cases of Ln = 0 or Cn = 0 correspond to gears in standard involute profile with no profile modification. The proportion of double-tooth engagement and five-tooth engagement in one mesh cycle for the two models are both significantly affected by the length and amount of the profile modification. The transition of mesh stiffness between single- to double-tooth engagement or the four- to five-tooth engagement is smoothed with the growth of tooth profile modification. In addition, the variation of mesh stiffness and loaded transmission error during the periodical engagement decreases with the length and the amount of tooth profile modification. For helical gears with HCR (Figs. 11b, 12b), the introduction of large length or amount of profile modification can lead to almost constant mesh stiffness and transmission error. However, the average mesh stiffness decreases. The small variation of mesh stiffness and loaded transmission error indicates weaker mesh fluctuations and is beneficial for vibration and noise reduction, but the resulted small average mesh stiffness exerts negative impact on the load capacity ability. These two aspects should be both considered in applying tooth profile modification.

Fig. 11
figure 11

Effect of tooth profile modification length on the total mesh stiffness and loaded transmission error of helical gears for a, c Model III (LCR), b, d Model IV (HCR)

Full size image
Fig. 12
figure 12

Effect of profile modification amount on the total mesh stiffness and loaded static transmission error of helical gears for a, c Model III (LCR), b, d Model IV (HCR)

Full size image

4 Conclusions

In this work, a novel mesh stiffness model of helical gear pairs with tooth profile modification has been developed based on the slicing principle. Four types of helical gears are classified based on the geometry characteristics of the gear. The corresponding single gear mesh stiffness and total mesh stiffness are determined. The proposed method is convenient without the need to determine the mesh state of each sliced tooth pairs and to calculate the stiffness and tooth profile error of each sliced tooth pair in mesh. The accuracy of the proposed method is validated by comparing with the previously reported results. Effects of tooth profile modification on the total mesh stiffness and loaded static transmission error are studied for helical gear pair models with both low contact ratio and high contact ratio. The presence of tooth profile modification smooths the transition of mesh stiffness and loaded transmission error in the periodical mesh engagement, whilst also reduces the average mesh stiffness. The variation of mesh stiffness during the periodical engagement decreases with the increase of contact ratio. A proper tooth profile modification should be considered in respect of both the vibration and noise deduction and load capacity. The developed model can be further used for the mesh stiffness and dynamic performance evaluation of helical gears with different types of tooth errors.