1 Introduction

The uncertainty associated with geotechnical structures can be broadly classified into three categories: (1) the inherent variability associated with the soil properties, (2) the variability in sampling and testing processes, and (3) the uncertainty related to the model transformation (Phoon and Kulhawy 1999). To incorporate these uncertainties into the structure, engineers have historically used the conventional deterministic-based approach, considering the factor of safety (FOS). However, this concept does not ensure that the structure is completely safe against failure, and it often leads to the under-prediction or over-prediction of the responses of the structure (Gong et al. 2015). The rationality of using the failure probability concept in the structure can be justified as it helps in considering the inherent variability associated with the soil parameters using the probabilistic statistics and distribution type of these parameters (Cherubini 2000; Mollon et al. 2009; Nazeeh and Sivakumar Babu 2021; Luo and Luo 2022). The concept of soil spatial variability has been incorporated into several geotechnical problems (Fenton and Griffiths 2002; Griffiths et al. 2002; Griffiths and Fenton 2004; Haldar and Sivakumar Babu 2008; Luo et al. 2012; Kasama and Whittle 2016; Halder and Chakraborty 2020) using the random field theory introduced by Vanmarcke (1983). Several studies on the shallow foundation have taken into account the effect of soil spatial variability (Fenton and Griffiths 2003; Griffiths et al. 2006; Cho and Park 2010; Johari and Sabzi 2017; Wu et al. 2019; Johari et al. 2019; Krishnan and Chakraborty 2022). However, these studies were restricted to two-dimensional strip footings. Reliability-based studies on three-dimensional shallow foundations (e.g., rectangular, square) considering soil spatial variability are limited, as the analyses of these foundations are computationally expensive. Nevertheless, such probabilistic analyses are essential, because these foundations are constructed to carry massive super-structural loads, and the failure associated with them must be appropriately assessed (Kawa and Puła 2020). Fenton and Griffiths (2005) produced the pioneering work on the probabilistic assessment of individual and two closely spaced square footings considering the spatial variability effect of the elastic modulus to determine the total and differential settlements, respectively. Al-Bittar and Soubra (2014) carried out a reliability-based study on the bearing capacity of square footing, considering cohesion and friction angle as the spatially variable random fields. Ahmed and Soubra (2014) conducted probability-based analyses of a three-dimensional circular footing under inclined loading. Their study aimed to determine the reliability index and the correlated failure modes under ultimate and serviceability limit states. However, the spatial variability effect was not taken into account in their study. Kawa and Pula (2020) studied the spatial variability effect of cohesion and friction angle on the load-carrying capacity of a square footing resting on cohesive-frictional (c–ϕ) soil. The aim of their paper was to study the effect of the horizontal scale of fluctuation on the probabilistic characteristics of the load-carrying capacity. Several other researchers (Simões et al. 2013; Kawa and Puła 2020; Chwała and Kawa 2021) have explored the effect of spatial variability on the three-dimensional bearing capacity of strip footing, considering the modeled length in the out-of-plane direction. Recently, Choudhuri and Chakraborty (2022) conducted probability-based analyses of the three-dimensional bearing capacity of a circular footing resting on a spatially variable two-layer c-ϕ soil system.

Circular footing on sandy soil is a classical geotechnical problem which has been used worldwide over the decades. Several researchers (Manoharan and Dasgupta 1995; Erickson and Drescher 2002; Loukidis and Salgado 2009) have conducted deterministic analyses on the bearing capacity of circular footing on sandy soil, exploring the effect of both associativity and non-associativity. Erickson and Drescher (2002) carried out a two-dimensional axisymmetric analysis of a circular footing having D = 12 m for ϕ = 20°, 35°, 40°, and 45° and corresponding ψ = 0°, ϕ/2, and ϕ, considering mass density (ρm) = 1500 kg/m3, cohesion (c) = 0.1 kPa and ρm = 2500 kg/m3, c = 100 kPa. The ultimate bearing capacity of the circular footing was found to increase with the increase in dilation angle for a particular ϕ value. Ornek et al. (2012) carried out a numerical study using finite-element software to predict the scale effect of circular footing supported by partially replaced granular fill on natural clay deposits. A two-dimensional axisymmetric model was generated in their study, and the numerical analysis results were validated with small-scale field tests. It was observed that the ultimate bearing capacity increased with the increase in footing diameter. The present study compares the results obtained by Erickson and Drescher (2002) for the cases of ϕ = 20ο, 35ο, and 40ο and corresponding ψ = 0°, ϕ/2, and ϕ, considering ρm = 1500 kg/m3, and c = 0.1 kPa, and the comparison is presented in Table 1. Similarly, this study compares the field test results obtained by Ornek et al. (2012), considering the diameter of the footing, D = 0.12 m, and the thickness of the granular layer, Hgr = 0.333D. The comparison is illustrated in Fig. 1. It can be seen that the results obtained from the present study closely resemble those in the literature.

Table 1 Comparison of qud (in kPa) of circular footing between the present study and Erickson and Drescher (2002)
Full size table
Fig. 1
figure 1

Comparison of bearing pressure versus settlement ratio curve for the circular footing between the present study and Ornek et al. (2012)

Full size image

From the extensive literature survey, it is found that no reliability-based study is available on the three-dimensional circular surface footing resting on sandy soil, considering the spatial variability effect of the soil friction angle. Hence, the present study tries to provide a general perspective of the problem. The primary objective of this paper is to study the variations in μq and pf of the system for different θx/D = θy/D. In this study, the friction angle (ϕ) is characterized as the spatially variable random field. Since the dilation angle (ψ) is assumed to be the function of friction angle, it is also simulated as the random field. The soil cohesion is assumed to be a non-random parameter in the study. However, the effect of cross-correlation between cohesion and friction angle (ρc-tanϕ) is also explored in the present study as a representative case where the soil cohesion is characterized as a random field. The changes in pf for different FOS and θx/D = θy/D are explored in the study. Design charts are provided, illustrating the variations in the FOSreq for different pf_tgt. The qad of the footing is evaluated based on a few standard reliability indices (β), and the variations in qad are also shown for different coefficients of variation of tan (COVtanϕ) and θx/D = θy/D.

2 Details of Finite-Difference Numerical Modeling

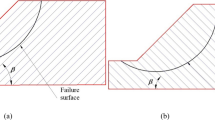
A three-dimensional rigid circular footing with a rough base placed on the surface of sandy soil is represented by a schematic diagram shown in Fig. 2a. The diameter of the footing is represented by D. FLAC3D software (Itasca 2012) is used to model the footing and the soil domain and to execute all the numerical analyses. In the probabilistic analysis, a full model domain is considered where the stretch of the model domain in both horizontal directions is assumed to be 10D, whereas the stretch of the model in the vertical direction is considered to be 5D. The model domain is chosen after several trials to avoid boundary effects. The horizontal and vertical movements are restricted at the bottom boundary, whereas only the vertical movement is allowed at the outer side boundaries by the provision of the lateral restriction. Radially graded mesh around a cylindrical tunnel with a solid core is incorporated for discretization of the soil domain. Finer mesh is generated adjacent to the footing area where the high-stress gradient is expected, whereas the mesh size becomes coarser as it approaches the boundary. Total elements of the domain are selected as 18,144 to maintain the balance between efficiency and accuracy. The finite-difference discretized mesh is shown in Fig. 2b. The sandy soil is assumed to obey the elastic-perfectly plastic Mohr–Coulomb yield criterion. Three different friction angles (ϕ = 30°, 35°, and 40°) are considered in the present study. As per Sloan (2013), the ψ of the soil varies from 0ο to ϕ/3. Hence, three different dilation angles, ψ = 0°, ϕ/6, and ϕ/3, are considered in this study to correspond to ϕ = 30°, 35°, and 40°, respectively. Young's modulus (E) and Poisson's ratio (υ) of the soil are assumed to be 30 MPa and 0.3, respectively (as per Johari and Sabzi 2017). After mesh generation and allocation of soil properties to all the elements, the whole model is analyzed under gravity loading. The footing roughness is ensured by providing lateral resistance to the footing nodes. An optimum and very small amount of controlled downward displacement of magnitude 5 \(\times\) 10–6 m (per step) is applied at the specified nodes. Then the model undergoes a certain number of steps until the limiting value of bearing capacity is achieved (Halder and Chakraborty 2020; Kawa and Puła 2020). It should be noted that a small amount of cohesion (c = 0.5 kPa) is considered in all the analyses to achieve numerically stable results. For this reason, the results are presented using the ultimate bearing capacity of footing (qu) instead of the bearing capacity factor, Nγ.

Fig. 2
figure 2

Circular footing on sandy soil: a schematic diagram, b finite-difference discretization

Full size image

3 Deterministic Analysis

Deterministic analyses are carried out for three different combinations of friction and dilation angles (i.e., ϕ = 30°, ψ = 0°; ϕ = 35°, ψ = ϕ/6; and ϕ = 40°, ψ = ϕ/3) and three different diameters (D = 0.5 m, 1 m, and 2 m) of the circular footing. The importance of deterministic analyses is justified as the results obtained can be used as a reference to calculate the pf of the system. Both ϕ and ψ are considered to be spatially constant during the deterministic analyses. The bearing pressure–settlement ratio (q versus s/D) curves for three different ϕ, ψ, and D are illustrated in Fig. 3a, b, and c. The bearing capacity of the footing increases with the increase in ϕ and ψ, which is a very intuitive observation. In the present study, the qud of the footing is expressed as the footing pressure for a particular settlement ratio (s/D) of 6%. However, in the case of ϕ = 40ο, ψ = ϕ/3 for D = 0.5 m and 1 m, and for all the combinations of ϕ and ψ for D = 2 m, the stable value of footing pressure has yet to be reached. According to Eurocode 7 (CEN 2013), the permissible settlement of a typical footing for a normal residential building can be considered as 75–135 mm, and the settlement value of 6% of D (even for D = 2 m) falls within this range. Hence, the qud of the footing is defined based on the settlement criterion. The qud of the footing corresponding to s/D = 6% for different ϕ, ψ, and D is shown in Fig. 3d, where it is observed that the qud of the footing (at s/D = 6%) increases as the footing diameter increases, irrespective of the change in ϕ and ψ.

Fig. 3
figure 3

Bearing pressure versus settlement ratio curves for circular footing with a D = 0.5 m, b D = 1 m, c D = 2 m, and d variation in qud with respect to D corresponding to s/D = 6%

Full size image

4 Probabilistic Analyses

4.1 Random Fields for ϕ and ψ

Generally, soil is highly complex in nature, depending on its mineralogical components, physicomechanical behavior, and loading history. Hence, layer-wise variations in soil properties may be observed in nature, in which the variation can also be observed within a single layer of soil (Johari et al. 2017). In the present study, ϕ is characterized by a random field. Since the dilation angle for ϕ = 35º and 40° is a function of ϕ, the dilation angles for these two friction angles can also be defined by the random fields. However, due to the very small cohesion value (i.e., c = 0.5 kPa), it is considered homogeneous throughout the study. Similarly, this study considers E and υ as spatially constant. The random field for tanϕ is assumed to be lognormally distributed, as it always gives non-negative random numbers. The tanϕ is chosen as a random field instead of ϕ, as it ensures that the randomly initiated ϕ values are between 0° and 90° (Griffiths et al. 2011; Krishnan and Chakraborty 2022).

In the present study, a three-dimensional Markov exponential autocorrelation function, \(\rho (\varsigma )\) , is used to define the correlation structure of the randomly generated friction field. The three-dimensional Markov function uses the scales of fluctuation (SOFs) in both the horizontal (θx, θy) and vertical (θz) directions and can be expressed as follows:

$$\rho (\varsigma_{x} ,\varsigma_{y} ,\varsigma_{z} ) = \exp \left( {\frac{{ - 2|\varsigma_{x} |}}{{\theta_{x} }} + \frac{{ - 2|\varsigma_{y} |}}{{\theta_{y} }} + \frac{{ - 2|\varsigma_{z} |}}{{\theta_{z} }}} \right)$$
(1)

In the above equation, \(\varsigma_{x} = (x_{k} - x_{l} )\), \(\varsigma_{y} = (y_{k} - y_{l} )\), and \(\varsigma_{z} = (z_{k} - z_{l} )\) are the centroidal distances between the kth and lth elements, where k = 1, 2, 3, …, En, and l = 1, 2, 3, …, En (En is the total number of elements in the generated mesh). θx, θy, and θz are the SOFs in the x, y, and z directions, respectively. The SOF defines the distance over which the randomly generated values of a soil parameter are strongly correlated with each other. Lower SOF values define ragged fields, whereas higher SOF values define smoothly varying random fields (Griffiths et al. 2002). The present study considers the SOFs in the x and y directions as equal (i.e., θx = θy), following the literature (Kawa and Puła 2020; Choudhuri and Chakraborty 2021). Considering the soil deposition process in nature, θx = θy is generally assumed to be greater than θz (Jamshidi Chenari and Mahigir 2014). Hence, the anisotropic random field is considered in the present study where θx = θy \(>\) θz. However, it should be noted that there are a few cases where θz is considered to be greater than θx = θy to explore the effect of θz on the probabilistic characteristics of bearing capacity. The parameters used in the probabilistic study are outlined in Table 2.

Table 2 Parameters used in probabilistic analyses
Full size table

The spatially variable random field of ϕ is generated using the Cholesky decomposition method (Haldar and Sivakumar Babu 2008; Kasama and Whittle 2016). Since the obtained autocorrelation matrix \(\rho (\varsigma )\) is positive definite, the matrix can be factorized into the lower triangular matrix (Q) and its transpose (QT), as follows:

$$\rho (\varsigma ) = QQ^{{\text{T}}}$$
(2)

The spatially correlated standard normal random field for friction angle \(\left( {G_{{\ln \tan \overline{\phi } }} } \right)\) can be evaluated using the lower triangular matrix (Q) as follows:

$$G_{\ln \tan \overline{\phi } } = \sum\limits_{j = 1}^{i} {Q_{ij} (G_{\ln \tan \phi \;}})_{j},i = { 1},{ 2},{ 3}, \, \ldots ,E_{n}$$
(3)

where \(G_{\ln \tan \phi }\) denotes the column vector of the uncorrelated standard normal variable with zero mean and unit standard deviation. As tanϕ of the soil is assumed to be lognormally distributed, the spatially varied random fields for ϕ can be expressed as follows:

$$\phi (\xi ) = \tan^{ - 1} [\exp \{ \mu_{\ln \tan \phi } + \sigma_{\ln \tan \phi } G_{\ln \tan \overline{\phi } }\} ]$$
(4)

In the above equation, \(\xi\) = \(\xi\)(x, y, z) denotes the spatial location of a point where the friction field is required. The underlying normal distribution parameters \(\mu_{\ln \tan \phi }\) and \(\sigma_{\ln \tan \phi }\) are evaluated using the following transformations:

$$\sigma_{\ln \tan \phi }^{2} = \ln \left( {1 + \frac{{\sigma_{\tan \phi }^{2} }}{{\mu_{\tan \phi }^{2} }}} \right) = \ln (1 + {\text{COV}}_{\tan \phi }^{2} )$$
(5)
$$\mu_{\ln \tan \phi } = \ln \mu_{\tan \phi } - \frac{1}{2}\sigma_{\ln \tan \phi }^{2}$$
(6)

To extract the centroidal coordinates of all the elements of the discretized mesh as a text file, an in-house FISH subroutine is written in FLAC3D. After extracting those coordinates into the text files, the files are loaded into MATLAB (The MathWorks Inc. 2020). The spatially varied random fields for ϕ and ψ are generated in MATLAB using the parameters provided in Table 2. Then the obtained random fields are taken back to FLAC3D as the text file and assigned to each element of the discretized mesh using the FISH subroutine. The exemplary random fields for different ϕ for the constant values of θx/D = θy/D, θz/D, COVtanϕ, and D are illustrated in Fig. 4. Cross-sectional views of the friction field along the centroid of the footing are also depicted in that figure. It should be noted that the illustrated fields correspond to a particular Monte Carlo realization. The μq and COVq of qu for the given sets of probabilistic parameters are evaluated using the Monte Carlo simulation (MCS) technique. In addition, the probabilistic qu is evaluated at s/D = 6%. The coefficient of variation of the failure probability (COVpf) of the footing is evaluated to check the performance of the MCS (Cheng et al. 2018). This is essential, because as the number of MCS increases, the numerical accuracy increases. However, the probabilistic analyses of the three-dimensional problem under the MCS framework require substantial computational effort. Hence, a trade-off between the computational efficiency and accuracy of the obtained solution should be established. Following the central limit theorem, the estimated pf can be used to determine the accuracy of the chosen MCS. The COVpf is evaluated using the following equation:

$${\text{COV}}_{{p{\text{f}}}} = \sqrt {\frac{{1 - p_{{\text{f}}} }}{{N_{{{\text{mcs}}}} p_{{\text{f}}} }}}$$
(7)
Fig. 4
figure 4

Spatially variable random fields of friction angle (ϕ) for a ϕ = 30ο, b ϕ = 35°, and c ϕ = 40°

Full size image

In the above equation, Nmcs denotes the number of Monte Carlo simulations. As per the literature (Cheng et al. 2018), the reasonable value of the COVpf can be set as 10%. The variations in pf and COVpf for different MCS and COVtanϕ are illustrated in Fig. 5. It is observed that the pf of the system is almost stable after 300 Monte Carlo realizations. The obtained COVpf values for different COVtanϕ are also well below 10% after the 300 MC realizations. Hence, all the probabilistic analyses are carried out for the 300 MC realizations. All analyses were performed on a PC with 12 GB RAM and a single Intel Core i5 processor with a clock speed of 1.80 GHz, and around 22 h of computational time was required to complete the 300 MCSs for a particular set of probabilistic input statistics.

Fig. 5
figure 5

Variations in a pf and b COVpf of the footing with respect to MCS for different COVtanϕ

Full size image

4.2 Failure Probability

A footing is said to fail under the ultimate limit state of collapse when the stress applied to the footing (i.e., qapp) exceeds the qu of the underlying soil. Following the existing literature (Griffiths et al. 2002; Haldar and Sivakumar Babu 2008; Krishnan and Chakraborty 2022), the present study considers the qud as the stress applied to the footing. Since tanϕ is assumed to be lognormally distributed, the distribution of the probabilistic ultimate bearing capacity (qu) will most likely follow the lognormal distribution. However, the actual distribution of qu is compared with the assumed hypothetical cumulative lognormal distribution having the parameters μq and COVq (Fig. 6a). The plot is constructed for the case of ϕ = 30ο, ψ = 0ο, D = 1, θx/D = θy/D = 2.5, θz/D = 1, and COVtanϕ = 20%. The observed distribution of qu closely matches the theoretical distribution. The distribution of qu is further confirmed using the Kolmogorov–Smirnov test (Massey 1951), which is performed for three different significance levels (i.e., α = 1%, 5%, and 20%). For each significance level, the maximum absolute difference between the actual and theoretical distribution is well below the critical value. Thus, the lognormal distribution is acceptable at the given significance levels. Along with this cumulative distribution function (CDF) plot, the actual distribution of qu is expressed through the histogram illustrated in Fig. 6b. It is observed that the histogram of qu closely resembles the lognormal fit. Hence, the pf of the system can be estimated as the probability for which the evaluated qu is less than the qud, as follows:

$$p_{{\text{f}}} = P(q_{u} < q_{{{\text{app}}}} ) = P(q_{u} < q_{{{\text{ud}}}} ) = \Phi \left( {\frac{{\ln (q_{{{\text{ud}}}} ) - \mu_{{\ln q_{u} }} }}{{\sigma_{{\ln q_{u} }} }}} \right) = \Phi ( - \beta )$$
(8)

where \(\Phi (.)\) is the cumulative normal distribution function. \(\mu_{{\ln q_{u} }}\) and \(\sigma_{{\ln q_{u} }}\) are the transformed normal distribution parameters, and β defines the reliability index. It should be noted that in this section, the obtained pf is for FOS = 1.

Fig. 6
figure 6

a Comparison of actual distribution with the assumed theoretical lognormal distribution of qu, b histogram of qu with lognormal fit for D = 1 m, ϕ = 30ο, ψ = 0°, c = 0.5 kPa, COVtanϕ = 20%, θx/D = θy/D = 2.5, and θz/D = 1

Full size image

5 Results Obtained from the Probabilistic Analyses

This section is devoted to the detailed discussion on the variation in μq and pf with respect to different θx/D = θy/D. The effect of θz/D on μq and pf is also scrutinized in this section for the particular values of ϕ and ψ, COVtanϕ, and D. The next sub-section illustrates the failure mechanism of the spatially variable random soil under the footing for different ϕ and ψ. Then, the changes in CDF and PDF of qu for different COVtanϕ, θx/D = θy/D, and θz/D are discussed. The impacts of different FOS on the pf for different COVtanϕ and θx/D = θy/D are also discussed in this section, and based on this, the plots of pf_tgt versus FOSreq are provided for different COVtanϕ and θx/D = θy/D. Finally, the qad of the footing is evaluated for different β, COVtanϕ, and θx/D = θy/D.

5.1 Variations in μ q and p f for Different θ x/D = θ y/D, ϕ, and ψ

The variations in μq for different θx/D = θy/D, ϕ, and ψ with constant values of D = 1 m, COVtanϕ = 20%, and θz/D = 1 are illustrated in Fig. 7a. Similarly, the variations in pf for the same set of parameters are shown in Fig. 7e. For ϕ = 30ο, ψ = 0ο and ϕ = 35ο, ψ = ϕ/6, the μq increases as θx/D = θy/D increases, whereas for ϕ = 40°, ψ = ϕ/3, μq decreases with an increase in θx/D = θy/D. However, the variation in μq with respect to θx/D = θy/D is restricted to a very small range. The pf of the system decreases with the increase in θx/D = θy/D irrespective of the change in magnitude of ϕ and ψ. For a particular value of θx/D = θy/D, the pf of the system increases remarkably as ϕ increases from 30° to 35°, and ψ increases from 0ο to ϕ/6. However, a marginal increase in pf is observed as ϕ increases from 35° to 40°, and ψ increases from ϕ/6 to ϕ/3. It is also observed that the rate of change in both μq and pf with respect to θx/D = θy/D decreases as θx/D = θy/D increases. Halder and Chakraborty (2020) and Kawa and Pula (2020) reported a similar observation.

Fig. 7
figure 7

Variations in µq with respect to θx/D = θy/D corresponding to different a ϕ and ψ, b COVtanϕ, c θz/D and d D; variations in pf with respect to θx/D = θy/D corresponding to different e ϕ and ψ, f COVtanϕ, g θz/D, and h D

Full size image

5.2 Variations in μ q and p f for Different θ x/D = θ y/D and COV tanϕ

Figure 7b and f illustrate the variations in μq and pf, respectively, for different θx/D = θy/D and COVtanϕ corresponding to the constant values of ϕ = 30°, ψ = 0°, D = 1 m, and θz/D = 1. The μq of the footing decreases as the COVtanϕ increases, whereas the pf increases with an increase in COVtanϕ. These observations can be attributed to the increase in the randomness of generated ϕ values with the increase in COVtanϕ. Hence, the chances of producing weaker strength zones under the footing increase as the COVtanϕ increases, which leads to failure of the soil under the footing when the load is applied to the footing. It is also observed that the rate of change in μq with respect to θx/D = θy/D decreases as the COVtanϕ decreases.

5.3 Variations in μ q and p f for Different θ x/D = θ y/D and θ z/D

Figure 7c and g illustrate the variations in μq and pf, respectively, for different θx/D = θy/D and θz/D corresponding to the constant values of ϕ = 35°, ψ = ϕ/6, COVtanϕ = 20%, and D = 1 m. The μq and pf of the system increase and decrease, respectively, as θz/D increases, irrespective of θx/D = θy/D. Krishnan and Chakraborty (2022) reported a similar observation when the mean bearing capacity factor (μNγ) is varied with θz/D. Similarly, for each set of θz/D, the μq of the system increases as θx/D = θy/D increases. However, the pf of the system decreases as θx/D = θy/D increases.

5.4 Variations in μ q and p f for Different θ x/D = θ y/D and D

Figure 7d and h illustrate the variations in μq and pf, respectively, for different θx/D = θy/D and D corresponding to constant values of ϕ = 30°, ψ = 0ο, COVtanϕ = 20%, and θz/D = 1. For D = 0.5 m and 1 m, the μq of the system increases as θx/D = θy/D increases, whereas for D = 2 m, μq decreases as θx/D = θy/D increases. In the case of pf, it increases with the increase in D for constant values of θx/D = θy/D. However, the pf of the system decreases as θx/D = θy/D increases, irrespective of the change in D. It should be noted that the results obtained for different D are based on non-dimensionalized parameters such as θx/D = θy/D and θz/D, and the domain of the model is also considered based on the footing diameter. Hence, a particular value of θx/D = θy/D and θz/D provides the different values of θx = θy and θz for different D, which can be attributed to the decreasing trend of μq with respect to θx/D = θy/D for D = 2 m.

5.5 Effect of Cross-Correlation Between c and tanϕ

The soil shear strength parameters (i.e., c and ϕ) show the degree of interdependence between them. The present study considers the cross-correlation between c and tanϕ instead of ϕ, and it is represented as the cross-correlation coefficient ρc-tanϕ. For this reason, the soil cohesion is characterized as the lognormally distributed random field with a mean (μc) = 0.5 kPa and coefficient of variation (COVc) = 50%. In general, the soil cohesion and friction angle are negatively correlated, and the cross-correlation coefficient varies from −0.70 to −0.24 (Cherubini 2000; Johari et al. 2017). The typical value of ρc-tanϕ is considered as −0.5 for this study following Johari et al. (2017), to generate the cross-correlated random fields for c and tanϕ. The obtained μq and pf of the system for ρc-tanϕ = −0.5 are compared with the results for ρc-tanϕ = 0.

The cross-correlation between c and tanϕ can be described using the following matrix:

$$\it A_{{{\text{cr}}}} = \left[ {\begin{array}{*{20}c} 1 & {\rho_{{{\text{c}} - \tan \phi }} } \\ {\rho_{{{\text{c}} - \tan \phi }} } & 1 \\ \end{array} } \right]$$
(9)

Since the cross-correlation matrix is positive definite, it can be decomposed into lower and upper triangular matrices using the Cholesky decomposition method given in the following equation:

$$\it A_{{{\text{cr}}}} = \overline{Q} \overline{Q}^{{\text{T}}}$$
(10)

Hence, the cross-correlated standard normal random fields for c and tanϕ can be evaluated using the following expression:

$$\left( {\begin{array}{*{20}c} {G_{{\ln \tan \overline{\phi } }}^{{{\text{cr}}}} } \\ {G_{{\ln \overline{\it c} }}^{cr} } \\ \end{array} } \right) = \left[ {\begin{array}{*{20}c} {\overline{Q}_{11} } & 0 \\ {\overline{Q}_{21} } & {\overline{Q}_{22} } \\ \end{array} } \right]\left( {\begin{array}{*{20}c} {G_{{\ln \tan \overline{\phi } }}^{{}} } \\ {G_{{\ln \overline{\it c} }}^{{}} } \\ \end{array} } \right)$$
(11)

Here, \(G_{{\ln \overline{{\text{c}}} }}^{{}}\) is the auto-correlated standard normal field for cohesion which can be evaluated using the following equation:

$$G_{{\ln \overline{{\text{c}}} }} = \sum\limits_{j = 1}^{i} {Q_{ij} \left( {G_{{\ln {\text{c}}}} } \right)_{j} } \,,i\, = \,{1},{ 2},{ 3}, \, \ldots ,E_{n}$$
(12)

where \(G_{\ln c}^{{}}\) is the uncorrelated standard normal random field for cohesion with zero mean and unit standard deviation.

Since the lognormal distribution is considered for both c and tanϕ, the cross-correlated random fields for c and ϕ can be evaluated using the following equations:

$$\phi (\xi ) = \tan^{ - 1} [\exp (\mu_{\ln \tan \phi } + \sigma_{\ln \tan \phi } G_{{\ln \tan \overline{\phi } }}^{cr} )]$$
(13)
$$c(\xi ) = \tan^{ - 1} [\exp (\mu_{{\ln {\text{c}}}} + \sigma_{\ln c} G_{{\ln \overline{{\text{c}}} }}^{cr} )]$$
(14)

The underlying normal distribution parameters for cohesion, i.e., \(\mu_{\ln c}\) and \(\sigma_{\ln c}\) are evaluated using the following transformations:

$$\sigma_{{\ln {\text{c}}}}^{2} = \ln \left( {1 + \frac{{\sigma_{{\text{c}}}^{2} }}{{\mu_{{\text{c}}}^{2} }}} \right) = \ln (1 + {\text{COV}}_{{\text{c}}}^{2} )$$
(15)
$$\mu_{\ln c} = \ln \mu_{c} - \frac{1}{2}\sigma_{\ln c}^{2}$$
(16)

Figure 8a, b, and c illustrate the respective variations in μq, COVq, and pf with respect to θx/D = θy/D for ρc-tanϕ = 0 and −0.5 corresponding to constant values of ϕ = 30°, ψ = 0°, COVtanϕ = 20%, θz/D = 1, and D = 1 m. The μq of the footing for ρc-tanϕ = −0.5 shows higher values as compared to that for ρc-tanϕ = 0, whereas the COVq of the footing for ρc-tanϕ = −0.5 is observed to be less than that for ρc-tanϕ = 0. The negative cross-correlation between c and tanϕ indicates that the increase in the tanϕ value is associated with the decrease in c value and vice versa. Hence, the averaging effect is present, which increases the μq and reduces the COVq for ρc-tanϕ = −0.5. The pf of the system is also found to be smaller for ρc-tanϕ = −0.5. However, the difference between pf for ρc-tanϕ = 0 and −0.5 is only marginal for θx/D = θy/D = 1.25 and 2.5, and an observable difference is present for θx/D = θy/D > 2.5.

Fig. 8
figure 8

Variations in a µq, b COVq, and c pf of the circular footing with respect to θx/D = θy/D for ρc-tanϕ = 0 and −0.5

Full size image

5.6 Failure Patterns

This study illustrates the failure mechanisms of the underlying spatially variable soil using the maximum shear strain rate contour plots. The comparisons of these failure patterns for different ϕ and ψ corresponding to the constant values of COVtanϕ = 10%, θx/D = θy/D = 10, θz/D = 1, and D = 1 m are shown in Fig. 9. For a better understanding of the failure mechanism of the soil under the footing, the cross-sectional views of the failure patterns along the centroidal point of the footing in the x–z plane are illustrated in Fig. 9. Despite having identical probabilistic statistics of underlying soil friction angle (for a particular value of ϕ), different spatial orientations of ϕ are expected for different Monte Carlo realizations. Therefore, different bearing pressure–settlement responses are achieved for different realizations, where the bearing capacities reach their ultimate state for some of the realizations but they have yet to reach their limiting values for other realizations. Hence, the failure patterns illustrated in the figure correspond to a particular Monte Carlo realization. It is evident from the figure that the developed plastic regions are asymmetric for all the cases, as the generated ϕ (as well as ψ except ϕ = 30°) values are different at different spatial coordinates. It is also observed that the plastic regions are well developed and reach the ground surface for all ϕ, indicating that the system is failing under the general shear failure mechanism in that particular realization. It is also evident from the figures that both ϕ and ψ have profound effects on the failure pattern. With the increase in ϕ and ψ, the resistance offered by the underlying soil increases, and the ϕ and ψ of the large volume of soil mass get mobilized during load transfer. Hence, the extent of the plastic zones in the depth direction as well as beyond the edge of the footing increase with the increase in ϕ and ψ. For example, the maximum depths of the bottom of the asymmetric failure zone (from the ground surface) are found to be 0.84 m, 1.2 m, and 1.71 m for (1) ϕ = 30°, ψ = 0°, (2) ϕ = 35ο, ψ = ϕ/6, and (3) ϕ = 40°, ψ = ϕ/3, respectively (for the particular realization). It is also observed that the maximum shear strain rate value increases with the increase in ϕ and ψ.

Fig. 9
figure 9

Maximum shear strain rate (Max. SSR) contour plots of the underlying spatially variable soil for a ϕ = 30ο, ψ = 0° b ϕ = 35°, ψ = ϕ/6, and c ϕ = 40°, ψ = ϕ/3

Full size image

5.7 Variations in CDF and PDF for Different COV tanϕ, θ x/D = θ y/D, and θ z/D

The variations in CDF and PDF for different values of COVtanϕ corresponding to the specific values of ϕ = 30°, ψ = 0°, θx/D = θy/D = 10, θz/D = 1, and D = 1 m are presented in Fig. 10a and d, respectively. It is clear from the CDF plot that for the lower values of the probabilistic qu, the cumulative probability or the pf of the system increases with the increase in COVtanϕ. Similarly, at the qud, the pf also increases with the increase in COVtanϕ, although for higher values of qu, pf decreases as the COVtanϕ increases. The PDF plot clearly shows that the qu of the footing at the maximum probability of occurrence is less than the qud, and it decreases as the COVtanϕ increases, suggesting that when the COVtanϕ value increases, a significant reduction in qu occurs as compared to qud. It is also observed that the maximum probability of occurrence decreases as the COVtanϕ increases, whereas the skewness of the PDF curve increases as the COVtanϕ increases.

Fig. 10
figure 10

Variations in CDF of qu for different values of a COVtanϕ, b θx/D = θy/D, and c θz/D; variations in PDF of qu for different values of d COVtanϕ, e θx/D = θy/D and f θz/D

Full size image

The variations in CDF and PDF for different θx/D = θy/D corresponding to the particular values of ϕ = 30°, ψ = 0°, COVtanϕ = 20%, θz/D = 1, and D = 1 m are illustrated in Fig. 10b and e, respectively. Similarly, the variations in cumulative and probability density plots for different θz/D corresponding to the particular values of ϕ = 30°, ψ = 0°, COVtanϕ = 20%, θx/D = θy/D = 10, and D = 1 m are represented in Fig. 10c and f, respectively. It is observed from the CDF plot that for the lower values of qu, the cumulative probability increases as θx/D = θy/D increase. However, at the qud and for higher values of qu, the cumulative probability decreases as θx/D = θy/D increases. From the PDF plot, it can be clearly stated that the maximum probability of occurrence decreases as θx/D = θy/D increases, and at qud, the probability of occurrence also decreases as θx/D = θy/D increases. However, for the lower and higher values of qu, the probability of occurrence increases as θx/D = θy/D increases. A similar observation is observed for the variations in CDF and PDF with respect to θz/D. However, for the lower values of qu, the segments of CDF and PDF curves fall within a very tight band for θz/D.

5.8 Variation in p f with Respect to FOS

The significance of probabilistic analyses is justified in the Introduction section as it helps calculate the pf, which is found to be a more robust concept as compared to the FOS. However, pf and FOS are strongly correlated, which can be defined using the following expression:

$$p_{{\text{f}}} = P(q_{u} < q_{{{\text{ud}}}} /{\text{FOS}}) = \Phi \left( {\frac{{\ln (q_{{{\text{ud}}}} /{\text{FOS}}) - \mu_{{\ln q_{u} }} }}{{\sigma_{{\ln q_{u} }} }}} \right) = \Phi ( - \beta )$$
(17)

Figure 11a, b demonstrate the variations in pf with respect to the FOS for different COVtanϕ and θx/D = θy/D, respectively. Both figures show a drastic reduction in pf with the increase in FOS. However, the observed trend is very obvious. For COVtanϕ = 5%, the pf of the system tends to zero when the FOS approaches 1.7. Similarly, for COVtanϕ = 10%, the pf of the system tends to zero when the FOS approaches 2.3, whereas for COVtanϕ = 20%, the system is not completely safe at FOS = 3, as pf is found to be 1.5% at FOS = 3. Hence, designing a typical footing considering FOS = 3 can overestimate the allowable bearing capacity (qa) for COVtanϕ = 5% and 10%, whereas it can underestimate qa for COVtanϕ = 20%. It is found that for FOS = 1, the pf of the system decreases as the θx/D = θy/D increases, although the variation is very small. However, for the FOS values \(\ge\) 1.1, pf increases as θx/D = θy/D increases. The significant variation in pf for different θx/D = θy/D is observed as the FOS increases from 1.3 to 2.5. As the FOS increases beyond 2.5, the variation in pf for different θx/D = θy/D decreases. It is also observed that for θx/D = θy/D = 1.25, pf tends to zero when the FOS approaches 2.6, whereas the system pf is found to be 1.5% for θx/D = θy/D = 10 at FOS = 3. Hence, at FOS = 3, qa is slightly overestimated for θx/D = θy/D = 1.25, whereas it is underestimated for θx/D = θy/D = 10. Based on these observations, Fig. 11c and d are plotted, estimating the required factor of safety  (FOSreq) to achieve a specific target failure probability (pf_tgt). The FOSreq corresponding to a specific pf_tgt can be evaluated by rearranging Eq. (17) as follows:

$${\text{FOS}}_{{{\text{req}}}} = \frac{{q_{{{\text{ud}}}} }}{{\exp [\mu_{{\ln q_{u} }} + \sigma_{{\ln q_{u} }} \{ \Phi^{ - 1} (p_{{{\text{f}}\_{\text{tgt}}}} )\} ]}}$$
(18)
Fig. 11
figure 11

Variations in pf with respect to FOS for different values of a COVtanϕ, b θx/D = θy/D; variations in pf_tgt with respect to FOSreq for different values of c COVtanϕ, d θx/D = θy/D

Full size image

Figure 11c, d represents pf_tgt versus FOSreq for different COVtanϕ and θx/D = θy/D, respectively. For a given pf_tgt (say pf_tgt = 0.1%), the FOSreq increases with the increase in COVtanϕ. A similar trend is observed for θx/D = θy/D. For example, FOSreq increases from 1.53 to 4.45 as the COVtanϕ increases from 5 to 20% to achieve a pf_tgt = 0.1% for the particular values of ϕ = 30ο, ψ = 0ο, θx/D = θy/D = 10, θz/D = 1, and D = 1 m. Similarly, the FOSreq is observed to increase from 2.75 to 4.45 as θx/D = θy/D increases from 1.25 to 10 for the particular values of ϕ = 30°, COVtanϕ = 20%, θz/D = 1, and D = 1 m.

5.9 Variations in q ad of Footing for Different β, COV tanϕ, and θ x/D = θ y/D

The present study also attempts to evaluate the qad of the footing by modifying Eq. (8) as follows:

$$\Phi \left( {\frac{{\ln (q_{{{\text{ad}}}} ) - \mu_{{\ln q_{{\text{u}}} }} }}{{\sigma_{{\ln q_{{\text{u}}} }} }}} \right) = \Phi ( - \beta )$$
(19)

By rearranging the above equation, the qad of the footing can be obtained directly as follows:

$$q_{{{\text{ad}}}} = \exp (\mu_{{\ln q_{u} }} - \beta \sigma_{{\ln q_{u} }} )$$
(20)

Four different reliability indices are used in this study to obtain qad: (1) β = 3.0902, corresponding to the target failure probability (pf_tgt) of 0.1%; (2) β = 3.8, which corresponds to the RC2 reliability class structures (residential and office buildings and their typical foundations) having medium consequences of failure, and 50 years of design working life (CEN 2002); (3) β = 3.0 for the average performance and (4) β = 4.0 for the good performance of the geotechnical structures provided by USACE (1997). The variations in qad with respect to β for different COVtanϕ and θx/D = θy/D are shown in Fig. 12a and b, respectively. As illustrated in the figures, the qad decreases with the increase in β. Similarly, a drastic decrease in qad is also seen with the increase in COVtanϕ for the constant values of β and θx/D = θy/D (Fig. 12a). Likewise, a lower value of θx/D = θy/D provides a higher value of qad, whereas for higher values of θx/D = θy/D, the qad obtained is quite low (Fig. 12b). However, the qad values approach stable solutions as θx/D = θy/D increases. Kawa and Pula (2020) observed a similar trend.

Fig. 12
figure 12

Variations in qad of the footing with respect to β for different values of a COVtanϕ, b θx/D = θy/D

Full size image

6 Remarks

The present study primarily estimates the probabilistic bearing capacity of circular footing. However, while estimating the bearing capacity of the footing, it is also necessary to calculate the probabilistic allowable settlement of the foundation. For this reason, the elastic modulus (E) and Poisson's ratio (υ) of the foundation soil need to be considered as the random field. Hence, the cross-correlated random fields for the elastic modulus (E) and Poisson's ratio (υ) are generated, and the probabilistic allowable foundation settlement (δall) is evaluated corresponding to an allowable bearing pressure (qa) of 150 kPa, considering both E and υ as lognormally distributed, with μE = 30 MPa, μυ = 0.3, COVE = 30%, COVυ = 5%, and ρE-υ = −0.5 (following Johari and Sabzi 2017). As a representative case, the CDF and histogram fit of probabilistic allowable settlements are plotted for θx/D = θy/D = 10 and θz/D = 1 (Fig. 13). It is clear from Fig. 13 that the probabilistic allowable settlement of the foundation follows the Weibull distribution. The distribution of the probabilistic allowable settlement is further confirmed using the Kolmogorov–Smirnov goodness-of-fit test. It is also found that the obtained absolute difference between the actual distribution and the theoretical Weibull distribution is well below the critical value of the difference for the given significance levels (i.e., α = 1%, 5%, and 20%). Hence, the assumed theoretical distribution is acceptable at those given significance levels, and the pf of the system in terms of the allowable settlement can be estimated as the probability for which the evaluated δall is greater than the deterministic allowable settlement (δall_det), as follows:

$$p_{f} = P(\delta_{{{\text{all}}}} > \delta_{{{\text{all}}\_\det }} ) = 1 - P(\delta_{{{\text{all}}}} \le \delta_{{{\text{all}}\_\det }} ) = 1 - \left( {1 - e^{{ - \left( {\frac{{\delta_{{{\text{all}}\_\det }} }}{A}} \right)^{B} }} } \right) = e^{{ - \left( {\frac{{\delta_{{{\text{all}}\_\det }} }}{A}} \right)^{B} }}$$
(21)
Fig. 13
figure 13

a Comparison of actual distribution with the assumed theoretical Weibull distribution of δall, b histogram of δall with the Weibull-distribution fit for D = 1 m, ϕ = 30°, ψ = 0°, c = 0.5 kPa, μE = 30 MPa, μυ = 0.3, COVE = 30%, COVυ = 5%, ρE-υ = −0.5, θx/D = θy/D = 10, and θz/D = 1 

Full size image

In the above equation, A and B denote the respective scale and shape parameters for the Weibull distribution.

The variations in the mean, coefficient of variation of allowable settlement (µδall and COV_δall), and the failure probability (pf) of the footing in terms of allowable settlement for different θx/D = θy/D are presented in Fig. 14a, b, and c, respectively. The µδall of the footing decreases with the increase in θx/D = θy/D. However, the variation in µδall is very insignificant beyond θx/D = θy/D = 2.5. In contrast to µδall, the COV_δall increases with the increase in θx/D = θy/D because of the averaging effect. The failure probability of the system is found to be decreasing with the increase in θx/D = θy/D.

Fig. 14
figure 14

Variations in a µδall, b COV_δall, and c pf of the circular footing with respect to θx/D = θy/D for D = 1 m, θz/D = 1, ϕ = 30°, ψ = 0°, c = 0.5 kPa

Full size image

7 Conclusions

The present study explores the spatial variability effect of soil friction and dilation angles on the bearing capacity of a three-dimensional circular surface footing resting on sandy soil. Deterministic analyses are carried out for three different combinations of ϕ and ψ (ϕ = 30°, ψ = 0°; ϕ = 35°, ψ = ϕ/6; and ϕ = 40°, ψ = ϕ/3) and three different D (D = 0.5 m, 1 m, and 2 m). In the case of probabilistic analyses, the tanϕ is assumed to be lognormally distributed instead of ϕ. The main focus of the study is to investigate the effect of θx/D = θy/D on the μq and pf of the system for different values of ϕ, ψ, COVtanϕ, θz/D, and D. The probabilistic allowable settlement of the footing corresponding to the allowable bearing pressure of 150 kPa is also evaluated considering the E and υ as the lognormally distributed cross-correlated random fields. The essential conclusive remarks drawn from the present study are listed below:

  1. (1)

    Higher values of ϕ, ψ, COVtanϕ, and D have a notable impact on the μq and the pf of the system. ϕ = 40°, ψ = ϕ/3 (for D = 1 m, COVtanϕ = 20%, θz/D = 1, and FOS = 1) shows the opposite trend of μq (with respect to θx/D = θy/D) which is observed for ϕ = 30ο, ψ = 0° and ϕ = 35°, ψ = ϕ/6. Similarly, D = 2 m (for ϕ = 30ο, ψ = 0°, COVtanϕ = 20%, θz/D = 1, and FOS = 1) shows the opposite trend of μq which is observed for D = 0.5 m and 1 m. Additionally, ϕ = 40°, ψ = ϕ/3, and D = 2 m give the highest value of pf as compared to the other cases.

  2. (2)

    The negative cross-correlation between c and tanϕ shows higher values of μq and lower values of COVq and pf than the case without cross-correlation, irrespective of the change in θx/D = θy/D. In the case of pf, the change in it is only marginal up to θx/D = θy/D = 2.5, beyond which there is an observable difference.

  3. (3)

    The use of the FOS concept may overestimate the qa of the footing for lower values of COVtanϕ, whereas it may underestimate the qa for higher values of COVtanϕ. Similarly, the qa gets overestimated for lower θx/D = θy/D and underestimated for higher θx/D = θy/D.

  4. (4)

    Estimating the FOSreq is essential, as higher values of FOS do not ensure that the system is entirely safe against failure. Hence, the FOSreq is calculated based on the fundamental concept of failure probability to achieve a target pf of the system. It is found that to achieve a pf_tgt of 0.1%, the FOSreq increases as the COVtanϕ and θx/D = θy/D increase.

  5. (5)

    The qad of the footing decreases significantly as β, COVtanϕ, and θx/D = θy/D increase. However, the variation in qad decreases as θx/D = θy/D approaches a higher value.

  6. (6)

    The probabilistic allowable settlement (δall) is observed to follow the Weibull distribution. The µδall and pf associated with the allowable settlement is found to decrease with the increase in θx/D = θy/D, whereas COV_δall increases with the increase in θx/D = θy/D.

  7. (7)

    The primary focus of the present study is on estimating the probabilistic bearing capacity of circular footing. The probabilistic allowable settlement of the footing corresponding to a specific allowable bearing pressure is also evaluated. However, it is also essential to evaluate the probabilistic allowable differential settlement of two closely spaced circular footings, which is beyond the scope of the study and can be considered in a future study.

The trend of using the spatial variability concept in the geotechnical fields has grown rapidly over the past few decades. The present analysis of the probabilistic bearing capacity of circular footing, considering the inherent spatial variability of the soil shear strength parameters under vertical loading, provides a general perspective of the problem. The risk associated with the potential failure of the footing is also discussed in the study. Hence, the authors hope the present study will help engineers working on this type of problem.