Reliability Analyses at Ultimate and Serviceability Limit States of Obliquely Loaded Circular Foundations

Abstract

This paper aims at determining the failure probability and the corresponding most predominant failure mode at both ultimate (ULS) and serviceability (SLS) limit states of a circular foundation resting on a (c, φ) soil and subjected to an inclined loading. The failure modes at ULS are the footing sliding and the soil punching while those at SLS are the exceedance of tolerable horizontal and vertical footing displacements. The probabilistic results based on the response surface methodology have shown that at both ULS and SLS, there is a load inclination where neither mode of failure is predominant. This inclination corresponds to the loading configurations situated on the line joining the origin and the maximal point of the interaction diagram. In a second stage, the results of a sensitivity analysis showing the effect of the different statistical parameters of the uncertain variables on the value of the failure probability were presented and discussed.

1 Introduction

Previous reliability analyses on shallow foundations focused on the reliability analysis of strip footings subjected to a central vertical load (Cherubini 2000; Griffiths and Fenton 2001; Griffiths et al. 2002; Low and Phoon 2002; Fenton and Griffiths 2002, 2003; Popescu et al. 2005; Przewlocki 2005; Sivakumar Babu and Srivastava 2007; Youssef Abdel Massih et al. 2008; Youssef Abdel Massih and Soubra 2008; Srivastava and Sivakumar Babu 2009; Soubra and Youssef Abdel Massih 2010).

To the authors knowledge, the reliability analysis of footings subjected to an inclined, an eccentric or a complex loading (as is the case of offshore structures) has received little attention in the literature. Notice that contrary to the vertical load case where only a punching failure mode may occur at the ultimate limit state (ULS), the (H, V, M) complex loading (where H, V and M are respectively the horizontal, vertical and moment applied to the footing) may involve different failure modes such as footing sliding, soil punching and footing overturning. Similar to the ULS, the serviceability limit state (SLS) should involve the study of three performance functions. These performance functions are defined with respect to the exceedance of tolerable horizontal and vertical displacements and rotation of the footing.

This paper deals with the reliability analysis of a circular foundation subjected to an inclined load. It aims at determining the failure probability and the corresponding most predominant failure mode at both ULS and SLS. It also aims at performing a sensitivity analysis at ULS showing the effect of the different statistical parameters of the uncertain variables on the value of the failure probability. The deterministic models are based on three-dimensional (3D) numerical simulations using the Lagrangian explicit finite difference code FLAC^3D. Hasofer–Lind reliability index is used for the computation of the footing reliability. The response surface methodology (RSM) is used to find an approximation of the limit state surface.

The paper is organized as follows: The basic reliability concepts and the RSM are briefly described. They are followed by the probabilistic analyses and the corresponding numerical results.

2 Basic Reliability Concepts and Response Surface Methodology

The reliability index of a geotechnical structure is a measure of the safety that takes into account the inherent uncertainties of the input parameters. The Hasofer–Lind reliability index (Hasofer and Lind 1974) defined in matrix formulation is given by:

$$ \beta_{HL} = \mathop {\hbox{min} }\limits_{G\left( x \right) = 0} \sqrt {(x - \mu )^{T} C^{ - 1} (x - \mu )} $$

(1)

in which x is the vector representing the n random variables; μ is the vector of their mean values; C is their covariance matrix. The minimisation of Eq. (1) is performed subjected to the constraint G(x) = 0 where G(x) = 0 represents the limit state surface. This surface separates the n-dimensional domain of random variables into two regions: a failure region represented by G(x) ≤ 0 and a safe region given by G(x) > 0. In case of analytically-unknown system response as is the case in the present paper, several approaches based on the RSM were proposed in the literature with the aim of calculating the reliability index and the corresponding design point. The approach by Tandjiria et al. (2000) was shown to be efficient (Youssef Abdel Massih and Soubra 2008; Mollon et al. 2009) and will be used in this paper. The basic idea of this method is to approximate the system response Y(x) by an explicit function of the random variables, and to improve the approximation via iterations. The expression of the system response used in this paper is given by:

$$ {\text{Y}}\left( {\text{x}} \right) = {\text{a}}_{0} + \sum\limits_{{{\text{i}} = 1}}^{\text{n}} {{\text{a}}_{\text{i}} .{\text{x}}_{\text{i}} } + \sum\limits_{{{\text{i}} = 1}}^{\text{n}} {{\text{b}}_{\text{i}} .{\text{x}}_{\text{i}}^{2} } $$

(2)

where x_i are the random variables (μ _i and σ _i being their mean and standard deviation values); n is the number of random variables; and (a _i , b _i ) are coefficients to be determined. A brief explanation of the algorithm used in this paper is given as follows:

• 1. Evaluate the system response Y(x) at the mean value point μ and at the 2n points each at μ ± kσ where k is arbitrarily chosen equal to 1 in this paper;

• 2. The above 2n + 1 values of Y(x) are used to solve Eq. (2) and find the coefficients (a _i , b _i ). Then, the performance function G(x) can be constructed to give a tentative response surface function;

• 3. Solve Eq. (1) to obtain a tentative design point and a tentative β _HL subjected to the constraint that the tentative performance function of step 2 be equal to zero;

• 4. Repeat steps 1 to 3 until convergence of β _HL . Each time step 1 is repeated, the 2n + 1 sampled points are centered at the new tentative design point of step 3.

Concerning the numerical implementation of the RSM algorithm described above, the determination of β_HL requires (1) the resolution of Eq. (2) for the 2n + 1 sampled points, and (2) the minimization of β_HL given by Eq. (1). These two operations constitute a single iteration and were done using the optimization toolbox available in Matlab. Several iterations were performed until convergence of β_HL. Convergence is considered to be reached when the absolute difference between two successive values of the reliability index becomes smaller than 10⁻².

From the first order reliability method (FORM) and the Hasofer–Lind reliability index β _HL , one can approximate the failure probability by $P_{f} \approx \varPhi \left( { - \beta_{HL} } \right)$ where $\varPhi \left( . \right)$ is the cumulative distribution function of a standard normal variable.

3 Reliability Analysis of Circular Footings

As mentioned before, this paper deals with the reliability analysis of a circular foundation subjected to an inclined load. Two modes of failure (soil punching and footing sliding) were considered at ULS. Also, two modes of failure (exceedance of tolerable vertical and horizontal displacements of the foundation) were considered at SLS. The uncertain parameters were modelled as random variables. These are the soil shear strength parameters (c, φ) at ULS and the soil elastic properties (E, ν) at SLS.

After a description of the deterministic models and the performance functions used in the probabilistic analysis, the probabilistic numerical results are presented and discussed.

3.1 Deterministic Model

In this paper, the system response considered at ULS is the safety factor F defined using the strength reduction method. As will be shown later in this paper, the use of this safety factor has a great advantage in the reliability analysis at ULS since it simultaneously considers the effect of the two failure modes (i.e. the footing sliding and the soil punching). Concerning the SLS, two system responses are considered. These are the vertical and horizontal footing displacements. Recent literature on the computation of the foundation settlement can be found in Abate et al. (2008) among others.

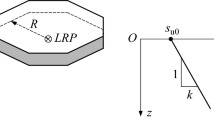
The deterministic models used in this paper to calculate the system responses are based on FLAC^3D software. A circular footing of a prescribed radius (R = 1 m) that rests on a (c, φ) soil domain of radius equal to 5R and depth equal to 5R was considered in the analysis. Because of symmetry, only one half of the entire soil domain was studied (Fig. 1). The mesh is composed of 6,040 zones. It was obtained after several verification runs. For the displacement boundary conditions, the bottom boundary was assumed to be fixed and the cylindrical boundary was constrained in motion in the horizontal X and Y directions. Concerning the (Z, X) vertical plane of symmetry, it was constrained in motion in the perpendicular direction.

Fig. 1

Soil domain and mesh used in the analysis

A conventional elastic perfectly plastic model based on Mohr–Coulomb failure criterion was used to represent the soil (not only for the ULS analyses but also for the SLS analyses) in order to take into account the possible plastification that may occur even under the service loads near the edges of the foundation. Concerning the footing, an elastic behavior was assumed in the SLS analysis; however, an elastic perfectly plastic model based on Mohr–Coulomb failure criterion was used in the ULS since the computation of the safety factor in FLAC^3D cannot be achieved if an elastic model was adopted. To overcome this shortcoming, a very large value was adopted for the cohesion parameter of the foundation. Finally, the interface between the soil and the footing was assumed to follow the same model as the soil (i.e. an elastic perfectly plastic model based on Mohr–Coulomb failure criterion). The same values of the soil shear strength parameters are adopted for the interface in order to simulate a perfectly rough interface. The values of the soil, footing, and interface properties used for the ULS and SLS analyses are given in Table 1. These values are hypothetical and are used only for illustrative purposes. It should be emphasized that the soil Young modulus is equal to 60 M Pa. This value was adopted in the SLS analysis when computing the footing displacements; however, a much greater arbitrary value of 390 M Pa was used in the ULS analysis to lead to a rapid computation of the safety factor. This arbitrary value has no influence on the obtained value of the safety factor.

Table 1 Shear strength and elastic properties of soil, footing, and interface

3.1.1 Deterministic Results

The (H, V) interaction diagram computed using the values of the soil characteristics given in Table 1 is shows in Fig. 2. Each point of this diagram is obtained by first searching a steady state of static equilibrium under the vertical load component V. Then, the corresponding H component is computed by searching a steady state of plastic flow using a prescribed horizontal velocity of 10⁻⁶ m/timestep. Notice that for the point corresponding to the vertical load case, only a displacement control method was used to compute the ultimate vertical load. The maximal point of the interaction diagram corresponds to (V = 2660 kN, H = 744.24 kN), i.e. to a load inclination α = 15.6°.

Fig. 2

Interaction diagrams (H, V) corresponding to F = 1 and other contour lines of F

The contours of the maximum shear strain corresponding to different points on interaction diagram (i.e. points A, B, O′, C, D) are shows in Fig. 3. This figure shows that for point A where V is small, the footing sliding is the most predominant while the punching mode is negligible. When increasing V, the punching mode increases and the sliding mode gradually decreases. For point D where V is very large with respect to H, the soil punching is the most predominant while the footing sliding is negligible. This means that both failure modes co-exist for all the loading configurations despite the fact that all the loading configurations correspond to failure with F = 1.

Fig. 3

Contour lines of the maximum shear strain for different load configurations on the interaction diagram

Figure 2 shows the contour lines of the safety factor for three arbitrary chosen values of F (F = 1.2; 1.3; 1.5). These contour lines are obtained as before (when constructing the interaction diagram) but using the soil shear strength parameters c_d and φ_d (instead of c and φ) where c_d = c/F and φ_d = tan⁻¹[tan (φ)/F]. It should be emphasized here that for each of these contour lines, the same behavior observed above was found to be valid herein (i.e. both failure modes exist for all the loading configurations of a given contour line of F). As a conclusion, the safety factor F can consider the simultaneous effect of the two failure modes and it provides a unique safety level of the soil-foundation system. Finally, notice that the maximal points of all the contour lines of F were found to correspond to the same load inclination as that of the interaction diagram (i.e. α = 15.6°) and thus, they are located on the same line that joins the origin and the maximal point of the interaction diagram.

3.2 Performance Functions

A footing subjected to an inclined loading may be analysed at ULS as a system consisting of two different failure modes. Typically, these modes are the footing sliding and the soil punching. To calculate the failure probability of such type of footings, two performance functions with two different system responses are required. This paper makes use of a unique system response. This is the safety factor F defined previously in the deterministic analysis using the strength reduction method. As was shown before, this response is able to take into account the two failure modes simultaneously and it provides a unique safety level of the soil-footing system. It should be mentioned that the safety factor F is defined with respect to the shear strength parameters c and tan φ. This factor is commonly used in the slope stability analysis. In the framework of this paper, it is the factor by which the available shear strength parameters c and tan φ have to be reduced to bring the soil-foundation system to failure. The performance function based on this safety factor is given as follows:

$$ {\text{G}}_{ 1} = {\text{F}} - 1 $$

(3)

For SLS, two performance functions were used. They are defined with respect to prescribed tolerable vertical and horizontal displacements of the footing centre. These performance functions are given by:

$$ {\text{G}}_{2} = {\text{v}}_{\hbox{max} } - {\text{v}} $$

(4)

$$ {\text{G}}_{3} = {\text{u}}_{\hbox{max} } - {\text{u}} $$

(5)

where v _max and u _max are the tolerable vertical and horizontal displacements of the footing and v and u are the computed footing vertical and horizontal displacements due to the (H, V) applied loads.

4 Probabilistic Numerical Results

This section aims at presenting the probabilistic results. The illustrative values used for the statistical moments (mean and coefficient of variation) of the different random variables are given in Table 2. As shows in this table, two cases of normal (i.e. Gaussian) and non-normal (i.e. non-Gaussian) variables were considered. For the case of normal distributions, all random variables are considered to follow a Gaussian distribution. However; for the case of non-normal distributions; c, E and ν are assumed to be log-normally distributed and φ is assumed to follow a beta distribution. These distributions are commonly adopted in literature (see for instance Fenton and Griffiths 2002, 2003). On the other hand, two cases of correlated and uncorrelated random variables were examined. In the case of correlated random variables, a negative correlation of ρ = −0.5 was assumed between c and φ at ULS or between E and ν at SLS (see for instance Youssef Abdel Massih and Soubra 2008).

Table 2 Statistical moments and correlation of the different random variables

4.1 Loading Configurations with Non-predominance of Sliding or Punching at ULS

The effect of V on the factor of safety and the failure probability P_f (calculated by FORM approximation), was shown in Fig. 4 for H = 447.66 kN. The random variables (c, φ) were considered as non-normal and correlated. The failure probability P_f presents a minimum (and the safety factor presents a maximum) for the same vertical load component V = 1,600 kN, i.e. when H/V = 0.28 or α = 15.6^o. This inclination is exactly the one of the maximal points of the contour lines of F.

Fig. 4

Effect of V on the safety factor F and the failure probability Pf at ULS for a prescribed H value

The fact that the failure probability exhibits a minimum may be explained as follows: For small values of V, sliding of the foundation is predominant and the failure probability due to this mode is very high. As V increases, the effect of sliding decreases and that of soil punching gradually increases until both modes of failure become non-predominant and induce a minimal simultaneous effect on the failure probability. More increase in V leads to an increasingly failure probability. This is due to a more and more predomination of the punching failure mode; the sliding failure mode becomes of smaller importance in this case. It should be mentioned that the same explanation given for P_f remains valid for the factor of safety. The maximal value of the safety factor corresponds to the case of non-predominance of neither modes of failure.

As a conclusion, both the probabilistic analysis and the deterministic analysis indicate that line OO′ of Fig. 2 can be regarded as the line for which the load configurations do not exhibit neither footing sliding predomination nor soil punching predomination. This line is therefore (from both deterministic and probabilistic frameworks) the line that separates the two zones of predominance of footing sliding and soil punching. This observation means that the line separating the zones of footing sliding and soil punching is independent of the soil statistical parameters (types of probability distributions, coefficients of variation and correlations between random variables).

Table 3 presents the design points (c*, φ*), the corresponding partial safety factors (F _c  = μ _c /c ^*, F _φ  = tan (μ _φ )/ tan φ ^*), the reliability index β_HL and the failure probability P_f obtained by FORM for the same cases considered in Fig. 4. Notice that the negative values of the reliability index β_HL for very small and very high values of V reflect the cases where c* and φ* are higher than their mean values. These configurations correspond to P_f higher than 50 %. They reflect the footing sliding for small values of V and the soil punching for high values of V. From Table 3, one may observe that for the load inclination corresponding to the minimal value of P_f, the values of c* and φ* are minimal. This is to be expected since the smaller the mobilized soil shear strength c* and φ*, the greater is the safety factor and the smaller is the failure probability. Notice finally that c* and φ* allow the practical engineer to estimate the effective safety on each resistance component.

Table 3 Design points, partial safety factors, reliability index and failure probability for the inclined loading case at ULS when H = 447.66 kN

4.2 Loading Configurations with Non-predominance of Neither Modes of Failure at SLS

Figure 5 presents the probability of failure (defined with respect to a prescribed tolerable displacement) versus the vertical load component V when H = 447.66 kN for the three following cases: (1) a prescribed tolerable vertical displacement v_max = 3.00 cm, (2) a prescribed tolerable horizontal displacement u_max = 1.50 cm, and (3) a system failure probability involving both tolerable displacements of v_max = 3.00 cm and u_max = 1.50 cm. The system failure probability was calculated according to the equations presented in Ang and Tang (1975). Non-Gaussian uncorrelated variables are considered.

Fig. 5

Probability of failure at SLS versus V when H = 447.66 kN

Figure 5 indicates that, for the curve corresponding to u_max, the probability of failure presents a minimum value. This is because, at small V values, the horizontal movement of the footing is predominant. This leads to a high failure probability. As V increases, the horizontal movement decreases because of the increase in the shearing resistance at the soil-footing interface. This leads to a gradual decrease in the failure probability. When punching begins to predominate, one obtains an increase in the failure probability due to an increase in the horizontal footing displacement. For the curve corresponding to v_max, the probability of failure increases with the increase of V. This is due to the increase in the vertical displacement. It can be noticed that the system failure probability is slightly larger or at least equal to the highest failure probability component when V is smaller than 1,600 kN, i.e. where a single mode of failure is predominant (exceedance of u_max). It becomes larger than both components when V is greater than 1,600 kN, i.e. where both failure modes contribute to the failure probability as may be easily seen from Table 4. As expected, the minimum value of the system failure probability at SLS corresponds exactly to the same value of V for which the failure probability presents a minimum at ULS, i.e. to the same load inclination (α = 15.6^o). This means that the load inclination which gives the minimum failure probability at ULS leads to the smallest possible movement of the foundation. It can be concluded that line OO′ (Fig. 2) which separates the punching and sliding zones at ULS can also be used in SLS to know if the (H, V) loading configuration leads to a predomination of horizontal or vertical displacement.

Table 4 Effect of V on (i) Probability of exceeding v_max, (ii) Probability of exceeding u_max and (iii) System failure probability when H = 447.66kN

4.3 Sensitivity Analysis

The aim of this section is first to study the effect of the statistical characteristics of the shear strength parameters (distribution type, coefficient of variation and correlation between random variables) on the value of the failure probability. This study was carried out in the case of a vertically loaded footing. It is followed by a study of the variability of the ultimate bearing capacity in the case of an inclined load.

4.3.1 Effect of the Probability Distribution Type and the Correlation Between Random Variables on the Failure Probability

The aim of this section is to investigate the effect of the probability distribution type and the correlation between the shear strength parameters on the failure probability of a vertically loaded footing. Both assumptions of normal and non-normal random variables were studied. Also, both correlated and uncorrelated random variables were considered in the analyses. Figure 6 shows that for a given value of V, the negative correlation between the soil shear strength parameters decreases the failure probability while the assumption of non-normal random variables has a negligible effect on this failure probability. Thus, focus should be made in practice on the rigorous determination of the possible correlation between the shear strength parameters.

Fig. 6

Probability of failure at ULS versus V for different assumptions on the probability distribution and the correlation

4.3.2 Effect of the Coefficients of Variation of the Shear Strength Parameters on the Failure Probability

The effect of the coefficients of variation of the shear strength parameters on the failure probability was investigated in Fig. 7. The random variables (c, φ) were considered non-normal and correlated. This study indicates (as expected) that for a given vertical load V, the increase in the coefficient of variation of a random variable increases the failure probability. Figure 7 also shows that the failure probability is more sensitive to a variation in the soil friction angle than to a variation in the soil cohesion. For instance, when V = 2835.06 kN, the failure probability increases by 95.6 % when COV_c increases 100 %. However, it increases by 347.4 % when COV_φ increase by only 50 %. This reflects the important role of the variability of the soil friction angle in the determination of the failure probability. Therefore, care should be taken on the rigorous determination of COV_φ in practice.

Fig. 7

Probability of failure at ULS versus V for different values of the coefficients of variation of the random variables

4.3.3 Effect of the Load Inclination on the Failure Probability

Figure 8 shows the effect of the load inclination α on the failure probability. Non-normal and correlated random variables were considered in the analyses. Figure 8 indicates that for a vertically loaded footing (α = 0°) where only punching failure exists, the failure probability is small. However, for the inclined loading case where both modes of failure co-exist, the failure probability significantly increases with the increase of the load inclination α (i.e. with the increase of the predominance of the sliding failure mode).

Fig. 8

Failure probability at ULS versus V for different values of the load inclination α

5 Conclusion

The aim of this paper was to determine the failure probability and the corresponding most predominant failure mode at both ULS and SLS of a circular foundation resting on a (c, φ) soil and subjected to an inclined load. The deterministic models were based on 3D numerical simulations using the Lagrangian explicit finite difference code FLAC^3D. Two modes of failure (soil punching and footing sliding) were considered at ULS. Also, two modes of failure (exceedance of tolerable vertical and horizontal displacements of the foundation) were considered at SLS. The uncertain parameters were modeled as random variables. These are the soil shear strength parameters (c, φ) at ULS and the soil elastic properties (E, ν) at SLS. The probabilistic analyses made use of the Hasofer–Lind reliability index for the computation of the footing reliability. The RSM was used to find an approximation of the system responses. The main findings can be summarized as follows:

• 1. The safety factor F obtained using the strength reduction method has the ability to simultaneously consider the combined effect of both failure modes at ULS, thus avoiding the use of two separate performance functions.

• 2. There is a load inclination for which the load configurations do not exhibit predominance of neither soil punching nor footing sliding. This inclination (which is independent of the soil variability) is that of the maximal point of the interaction diagram. Loading configurations (H, V) corresponding to this inclination are situated on the line joining the origin and the maximum point of the interaction diagram. Thus, this line subdivides the (H, V) interaction diagram into two zones where either soil punching or footing sliding is predominant.

• 3. The load inclination for which there is no predominance of neither soil punching nor footing sliding is the one for which the failure probability is minimum (and the safety factor is maximum) with respect to all other load configurations having the same value of the horizontal load component.

• 4. At SLS, a probabilistic analysis (based on a system failure probability against tolerable horizontal and vertical displacements of the footing) has shown that the system failure probability at SLS is higher than or at least equal to the highest failure probability component. It has also shown that the system failure probability presents a minimum. As expected, the load inclination leading to the minimal system failure probability at SLS corresponds exactly to the one obtained at ULS. This corresponds to the minimum movement of the footing center.

• 5. The knowledge of the load inclination corresponding to no predominance of neither modes of failure (at ULS or SLS) allows one to know the mode of failure which is predominant in the computation of the failure probability for a given load inclination.

• 6. A probabilistic sensitivity analysis has been performed at ULS. It has shown that (1) the correlation between the shear strength parameters decreases the failure probability; however, the non-normality of these variables does not significantly affect this failure probability and (2) the failure probability is more sensitive to the variation of φ than that of c. It was also found that the failure probability is significant for the inclined loading case where the sliding failure mode is predominant. This failure probability becomes small for the vertical loading case where only the punching mode is present.