1 Introduction

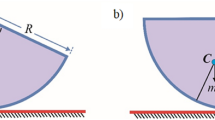
The Sitnikov problem is a special case of the restricted three-body problem, which has many applications in celestial mechanics and dynamical astronomy (Kovacs and Erdi 2007). The problem has been known for a long time and renewed the interest in the problem by Sitnikov’s paper in which the existence of oscillating motion for three-body problem was proved (Sitnikov 1960). In this particular case, two bodies with equal mass, as called primaries, orbit around their common center of mass due to their Newtonian gravitational forces, and a third body with negligible mass oscillates along a line, perpendicular to the orbital plane of the primaries, as shown in Fig. 1. The motion of the massive bodies can be either circular or elliptical, and the problem is to determine the motion of the third body along the perpendicular line under the Newtonian gravitational forces of the primaries.

Fig. 1
figure 1

Schematic of the Sitnikov problem (Kovacs and Erdi 2007)

Full size image

The problem can be presented by a nonlinear second-order ordinary differential equation that is not integrable. Then, exact solution of the problem is not accessible. Instead several numerical solutions are employed by Liu and Sun (1990), Dvorak (1993) and Kovacs and Erdi (2007) to exhibit the problem. Due to the importance of analytical solution of the problem, a lot of methods have been applied to the problem by a number of scientists to describe its analytical solution. Wodnar (1995) constructed an easy method to handle high precision analytical solution for the circular Sitnikov system. Hagel (1991) introduced a new analytic approach to the solution of the Sitnikov problem that is valid for bounded small amplitude solutions and eccentricities of the primary bodies. Regular and chaotic solutions of the Sitnikov problem around resonance orbits are provided by Jalali and Pourtakdost (1997). Faruque (2003) presented an approximate analytical solution of the problem for low primary eccentricities. Hagel and Lhotka performed a high-order perturbation approach to the problem using Floquet theory (Hagel and Lhotka 2005). This problem is considered by means of the Fourier expansion by Manshadi et al. (2007). Hagel used an original method of rewriting the couple system of second-order differential equation as a function iteration in such a way as to decouple the two equations at any iteration step and solved the decoupled equation by Poincare’ Lindstedt perturbation technique (Hagel 2009). Hagel found an exactly integrable system that could estimate well the Sitnikov problem with small amplitudes and small primaries eccentricities (Hagel 2015).

In this paper, along all existing attempts for discovering inside of the Sitnikov problem, the method of multiple scales (MMS) that is one of the classical perturbation techniques for solving nonlinear differential equation is employed to investigate the problem. At first, the Sitnikov equation is approximated with Taylor series expansion of nonlinear terms and then is reformed in such a way that nonlinear terms be negligible contrast to other terms. Therefore, the resulting equation is summation of terms with and without eccentricity parameter. The equation without eccentricity parameter is known as circular form whereas the equation with eccentricity parameter is known as elliptical form. The MMS method is applied to nonlinear differential equation of circular and elliptical forms at two steps separately. Finally, summation of results of mentioned steps is presented as an analytical result of the Sitnikov problem that is compared to results of numerical solution. Results show that MMS approximation of the Sitnikov problem is consistent with numerical method whereas analytic approximation contains amplitude and frequency of third body oscillation that can help to understand principles of physics govern to this problem. For higher accuracy and fidelity of solution, higher-order perturbation method can investigated in the future work.

2 The Sitnikov Problem

The Sitnikov problem presents one case of the elliptic restricted problem of three bodies. Two heavy primary bodies with equal mass (\(m_{1} = m_{2} = m\)) move on two elliptical orbits according Kepler’s laws. A third massless body (\(P_{3}\)) moves on an axis perpendicular to the primaries plane. In this configuration, \(P_{3}\) is only affected by a force perpendicular to the primaries plane and, therefore, the motion remains on the central axis denoted by \(Z\) in Fig. 1. Let \(Z\) be the coordinate describing the position of the third body, where \(Z = 0\) corresponds to the center of mass. Then, the normalized equation of motion of third body can be presented as follows (Liu and Sun 1990):

$$d^{2} Z/dt^{2} = - Z/(Z^{2} + r^{2} (t))^{3/2} ,$$
(1)

where

$$r(t) = a(1 - \varepsilon \cos t) + o(\varepsilon^{2} ).$$
(2)

Up to the ε order, we have

$$d^{2} Z/dt^{2} = - Z/(Z^{2} + a^{2} )^{3/2} - 3a^{2} Z\varepsilon \cos t/(Z^{2} + a^{2} )^{5/2} ,$$
(3)

where \(r(t)\) is distance of primaries to their center of mass and \(a\) is half of normalized elliptic diameter (\(a = 1/2\)). The time is normalized so that the period of the primaries is \(2\pi\). With applying Taylor series expansion on nonlinear terms of Eq. (3) in the point (t = 0, Z = 0), the Sitnikov equation can present as follows:

$$\ddot{Z} + \frac{1}{{a^{3} }}Z - \frac{3}{{2a^{5} }}Z^{3} + \frac{3}{{a^{3} }}\varepsilon Z\cos t - \frac{15}{{2a^{5} }}\varepsilon Z^{3} \cos t = 0,$$
(4)

where \(\varepsilon\) (0 ≤ \(\varepsilon\) < 0.1) is eccentricity value from physics of the Sitnikov problem that at this paper is introduced as perturbation parameter. This equation with following initial conditions is investigated by MMS method:

$$Z(0) = Z_{0} \begin{array}{*{20}c} {} & {\dot{Z}(0) = \dot{Z}_{0} } \\ \end{array} .$$
(5)

3 The Method of Multiple Scales

Multiple-scale analysis is a global perturbation scheme that is useful in systems characterized by disparate time scales, such as weak dissipation in an oscillator. These effects could be insignificant on short-time scales but become important on long-time scales (Nayfeh and Mook 1995). The underlying idea of MMS is to consider the response to be a function of multiple independent variables or scales instead of a single variable (Nayfeh and Mook 1995). With the method of multiple scales, changing the original ordinary differential equation into a system of partial differential equations permits enough generality in the form of the solution to obtain an excellent approximation (Nayfeh 1993). Suppose the anharmonic oscillator model as follows:

$$\ddot{x} + \sum\limits_{n = 1}^{{}} {\alpha_{n} } x^{n} = 0,\begin{array}{*{20}c} {} & {x(0) = x_{0} ,\dot{x}(0) = \dot{x}_{0} } \\ \end{array} ,$$
(6)

where \(\alpha_{n}\), Taylor series coefficients of nonlinear term of dynamic model, are constant. Substituting the multiple scales expansion: \(T_{0} = t,\begin{array}{*{20}l} {} \\ \end{array} T_{1} \left|\,= \right.\varepsilon t,\begin{array}{*{20}l} {} \\ \end{array} T_{2} = \varepsilon^{2} t, \ldots\), and applying the chain rule for differentiation, yields

$$\begin{aligned} \frac{d}{dt} = \sum\limits_{n = 0}^{\infty } {\frac{\partial }{{\partial T_{n} }}} \frac{{\partial T_{n} }}{\partial t} = \frac{\partial }{{\partial T_{0} }} + \varepsilon \frac{\partial }{{\partial T_{1} }} + \varepsilon^{2} \frac{\partial }{{\partial T_{2} }} + \cdots = D_{0} + \varepsilon D_{1} + \varepsilon^{2} D_{2} + \cdots \hfill \\ \hfill \\ \end{aligned}$$
(7)
$$\begin{aligned} \frac{{d^{2} }}{{dt^{2} }} = \frac{{\partial^{2} }}{{\partial T_{0}^{2} }} + \varepsilon [\frac{{\partial^{2} }}{{\partial T_{1} \partial T_{0} }} + \frac{{\partial^{2} }}{{\partial T_{0} \partial T_{1} }}] + \varepsilon^{2} [\frac{{\partial^{2} }}{{\partial^{2} T_{1} }} + \frac{{\partial^{2} }}{{\partial T_{0} \partial T_{2} }} + \frac{{\partial^{2} }}{{\partial T_{2} \partial T_{0} }}] + \cdots = \cdots \hfill \\ D_{0}^{2} + 2\varepsilon D_{1} D_{0} + \varepsilon^{2} (D_{1}^{2} + 2D_{2} D_{0} ) + \cdots \hfill \\ \end{aligned}$$
(8)

Expanding \(x(t)\) in an asymptotic series of \(\varepsilon\),

$$x(t) = x_{0} + \varepsilon x_{1} + \varepsilon^{2} x_{2} + \cdots$$
(9)

And separating into individual orders in \(\varepsilon\), yields the sequence of problem,

$$\begin{aligned} o(\varepsilon^{0} ):D_{0}^{2} x_{0} + \omega_{0}^{2} x_{0} = 0, \, \alpha_{1} = \omega_{0}^{2} \hfill \\ o(\varepsilon^{1} ):D_{0}^{2} x_{1} + \omega_{0}^{2} x_{1} = - 2D_{0} D_{1} x_{0} - \alpha_{2} x_{0}^{2} \hfill \\ o(\varepsilon^{2} ):D_{0}^{2} x_{2} + \omega_{0}^{2} x_{2} = - 2D_{0} D_{1} x_{1} - D_{1}^{2} x_{0}^{2} - 2D_{0} D_{2} x_{0} - 2\alpha_{2} x_{0} x_{1} - \alpha_{3} x_{0}^{3} \hfill \\ \, \vdots \, \vdots \, \vdots \, \vdots \, \hfill \\ \end{aligned}$$
(10)

The \(o(\varepsilon^{0} )\) equation is simple linear harmonic oscillator, and it is convenient to write the solution in the following form:

$$x_{0} = A(T_{1} ,T_{2} )e^{{i\omega_{0} T_{0} }} + \bar{A}(T_{1} ,T_{2} )e^{{ - i\omega_{0} T_{0} }} ,$$
(11)

where \(A\) is an unknown complex function and \(\bar{A}\) is the complex conjugate of \(A\). Here, \(A\) is only constant with respect to the fastest timescale \(T_{0}\) and will in general depend on all slower timescales \(T_{i} ,i = 1,2, \ldots\). The explicit time dependence of \(A\) on these slower timescales will appear at progressively higher orders in \(\varepsilon\).

By substituting \(x_{0}\) in second equation (\(o(\varepsilon^{1} )\)) and removing secular terms, \(A\) will be defined based on order of timescale and these activities can continue to required order of \(\varepsilon\). Finally, by applying initial conditions on \(x(t)\), \(A\) and \(x(t)\) will obtain.

4 The Sitnikov Equation Investigation by MMS

Any perturbation theory is applicable if the problem cannot be solved exactly, but can be formulated by adding a “small” term to the mathematical description of the exactly solvable problem. So, Eq. (4) is reformed as follows to decrease effect of nonlinear term compare with linear terms.

$$\ddot{z} + \frac{1}{{a^{3} }}z - \frac{3}{{2a^{5 - 2k} }}z^{3} + \frac{3}{{a^{3} }}\varepsilon z\cos t - \frac{15}{{2a^{5 - 2k} }}\varepsilon z^{3} \cos t = 0,$$
(12)

where \(z = a^{ - k} Z\) and \(k\) is an integer bigger than two that can be selected arbitrary.

Above equation which is explained before contains two parts: one of them is unperturbed (without \(\varepsilon\)) and other is perturbed (with \(\varepsilon\)). If \(\varepsilon = 0\), Eq. (12) will represent the circular Sitnikov problem. Authors assume that the equation of circular Sitnikov problem is basic of three bodies’ dynamic model where deviation from circular to elliptical form can present with two last terms of the Eq. (12) that is cleared with eccentricity parameter ε. Base on perturbation theory, solution of the Eq. (12) can be presented as small perturbation of circular form solution. Then, at first step solution of circular form of the Sitnikov problem is examined by MMS and then is used to find solution of elliptical form of the Sitnikov problem in next step by applying MMS to the Eq. (12) directly.

4.1 The Circular Form of the Sitnikov Problem

When \(\varepsilon = 0\), the Eq. (12) will be simplified to the following form without perturbation term.

$$\ddot{z} + \frac{1}{{a^{3} }}z - \frac{3}{{2a^{5 - 2k} }}z^{3} = 0.$$
(13)

This ordinary differential equation is nonlinear and there is not exact solution; MMS method is employed to solve this equation. For this purpose, we suppose that nonlinear term is negligible compared to other terms and can consider it with \(\eta\) parameter as small perturbation parameter whereas \(\eta\) is equal 1. This parameter is considered to apply the MMS method to the Eq. (13). We rewrite Eq. (13) as follows:

$$\ddot{z} + \frac{1}{{a^{3} }}z - \frac{3}{{2a^{5 - 2k} }}\eta z^{3} = 0.$$
(14)

We apply MMS method such as explained before step by step to find response of this equation. Suppose first-order estimation of \(z\) is enough then consider

$$z(t,\eta ) = z_{0} (T_{0} ,T_{1} , \ldots ) + \eta z_{1} (T_{0} ,T_{1} , \ldots ) + O(\eta^{2} ).$$
(15)

And apply chain rule operator on \(z\) and substitute in the Eq. (14),

$$\begin{aligned} \left( {D_{0}^{2} + 2\eta D_{0} D_{1} + \cdots } \right)\left( {z_{0} + \eta z_{1} + \eta^{2} z_{2} \ldots } \right) + \frac{1}{{a^{3} }}\left( {z_{0} + \eta z_{1} + \eta^{2} z_{2} \ldots } \right) - \cdots \hfill \\ \frac{3}{{2a^{5 - 2k} }}\eta \left( {z_{0} + \eta z_{1} + \cdots } \right)^{3} = 0. \hfill \\ \end{aligned}$$
(16)

Separate into individual orders in \(\eta\), yields the sequence of problem,

$$o(\eta^{0} ):D_{0}^{2} z_{0} + \omega_{0}^{2} z_{0} = 0$$
(17)
$$o(\eta^{1} ):D_{0}^{2} z_{1} + \omega_{0}^{2} z_{1} = - 2D_{0} D_{1} z_{0} + \frac{3}{{2a^{5 - 2k} }}z_{0}^{3} ,$$
(18)

where \(\omega_{0} = 1/a^{3/2}\) and assume result of the Eq. (17) as follows:

$$z_{0} = A(T_{1} )e^{{i\omega_{0} T_{0} }} + \bar{A}(T_{1} )e^{{ - i\omega_{0} T_{0} }} .$$
(19)

With substituting z 0 in right hand side of Eq. (18),

$$D_{0}^{2} z_{1} + \omega_{0}^{2} z_{1} = \left[ { - 2i\omega_{0} D_{1} A + \frac{{9A^{2} \bar{A}}}{{2a^{5 - 2k} }}} \right]e^{{i\omega_{0} T_{0} }} + \frac{{3A^{3} }}{{2a^{5 - 2k} }}e^{{3i\omega_{0} T_{0} }} + {\text{cc}},$$
(20)

where cc denotes the complex conjugate of the preceding terms. The secular term should be removed to have steady state solution. Therefore

$$- 2i\omega_{0} D_{1} A + \frac{{9A^{2} \bar{A}}}{{2a^{5 - 2k} }} = 0,$$
(21)

where \(A\), that is convenient to write it in the polar form \(A = \frac{1}{2}\alpha e^{i\beta } .\), α is constant and β is function of \(T_{1}\), can present as follows:

$$A = \frac{1}{2}\alpha e^{{i\left( { - \frac{{9\omega_{0} \alpha^{2} }}{{16a^{2 - 2k} }}T_{1} + \beta_{0} } \right)}} .$$
(22)

\(z_{1}\) From Eq. (20),

$$z_{1} = - \frac{{3A^{3} }}{{16a^{2 - 2k} }}e^{{3i\omega_{0} T_{0} }} + cc$$
(23)

Finally refer to Eq. (15) and some simplification considering \(\eta = 1\), solution of the circular form of the Sitnikov equation is:

$$z(t) = \alpha \cos (\omega t + \beta ) - \frac{{3\alpha^{3} }}{{64a^{2 - 2k} }}\cos 3(\omega t + \beta ),$$
(24)

where

$$\omega = \omega_{0} - \frac{{9\alpha^{2} }}{{16a^{2 - 2k} }}\omega_{0} .$$
(25)

By imposing initial condition Eq. (5) and straightforward technique, we have

$$\begin{aligned} &\alpha_{0} = - \sqrt {a^{ - 2k} Z_{0}^{2} + a^{ - 2k + 3} \dot{Z}_{0}^{2} } \times {\text{sign }}(\dot{Z}_{0} ) \hfill \\ &\beta_{0} = \cos^{ - 1} (a^{ - k} Z_{0} /\alpha_{0} ) \hfill \\ &\alpha = \alpha_{0} + \frac{{3\alpha_{0}^{3} }}{{64a^{2 - 2k} }}\left( {2\cos (2\beta_{0} ) - \cos (4\beta_{0} )} \right) \hfill \\ &\beta = \beta_{0} + \frac{{3\alpha_{0}^{2} }}{{64a^{2 - 2k} }}\left( {2\sin (2\beta_{0} ) + \sin (4\beta_{0} )} \right). \hfill \\ \end{aligned}$$
(26)

4.2 The Elliptical Form of the Sitnikov Problem

Equation (24), that is the solution of the circular form of the Sitnikov problem, can be presented as the solution of following equivalent linear ordinary differential equation:

$$\ddot{z} + \omega^{2} z - \frac{{3\alpha^{3} \omega^{2} }}{{8a^{2 - 2k} }}\cos 3(\omega t + \beta ) = 0.$$
(27)

So, comparison the Eq. (27) with the Eq. (13) yields

$$\ddot{z} + \omega_{0}^{2} z - \frac{3}{{2a^{5 - 2k} }}z^{3} \equiv \ddot{z} + \omega^{2} z - \frac{{3\alpha^{3} \omega^{2} }}{{8a^{2 - 2k} }}\cos 3(\omega t + \beta ),$$
(28)

where

$$\omega = \omega_{0} - \frac{{9\alpha^{2} }}{{16a^{2 - 2k} }}\omega_{0} .$$
(29)

With this consistent approximation, the elliptical Sitnikov Eq. (12) can present as following form:

$$\ddot{z} + \omega^{2} z + \frac{3}{{a^{3} }}\varepsilon z\cos t - \frac{15}{{2a^{5 - 2k} }}\varepsilon z^{3} \cos t = \frac{{3\alpha^{3} \omega^{2} }}{{8a^{2 - 2k} }}\cos 3(\omega t + \beta ).$$
(30)

We apply MMS method such as used before step by step to find solution of this equation. We assume that the solution can be represented by following expansion form

$$z(t,\varepsilon ) = z_{0} (T_{0} ,T_{1} , \ldots ) + \varepsilon z_{1} (T_{0} ,T_{1} , \ldots ) + \varepsilon^{2} z_{1} (T_{0} ,T_{1} , \ldots ) + o(\varepsilon^{3} ).$$
(31)

Apply chain rule operator on \(z\) and substitute in Eq. (30), then

$$\begin{aligned} \left( {D_{0}^{2} + 2\varepsilon D_{0} D_{1} + \varepsilon^{2} \left( {D_{1}^{2} + 2D_{0} D_{2} } \right)} \right)\left( {z_{0} + \varepsilon z_{1} + \varepsilon^{2} z_{2} \ldots } \right) + \cdots \hfill \\ \omega^{2} (z_{0} + \varepsilon z_{1} + \varepsilon^{2} z_{2} \ldots ) + \frac{3}{{a^{3} }}\varepsilon \left( {z_{0} + \varepsilon z_{1} + \varepsilon^{2} z_{2} \ldots } \right)\cos T_{0} - \cdots \hfill \\ \frac{15}{{2a^{5 - 2k} }}\varepsilon \left( {z_{0} + \varepsilon z_{1} + \varepsilon^{2} z_{2} } \right)^{3} \cos T_{0} = \frac{{3\alpha^{3} \omega^{2} }}{{8a^{2 - 2k} }}\cos 3(\omega T_{0} + \beta ) \hfill \\ \end{aligned}$$
(32)

Separate into individual orders in \(\varepsilon\), yields the sequence of problem,

$$o(\varepsilon^{0} ):D_{0}^{2} z_{0} + \omega^{2} z_{0} = \frac{{3\alpha^{3} \omega^{2} }}{{8a^{2 - 2k} }}\cos 3(\omega T_{0} + \beta )$$
(33)
$$o(\varepsilon^{1} ):D_{0}^{2} z_{1} + \omega^{2} z_{1} = - 2D_{0} D_{1} z_{0} - \frac{3}{{a^{3} }}z_{0} \cos T_{0} + \frac{15}{{2a^{5 - 2k} }}z_{0}^{3} \cos T_{0} ,$$
(34)

where the Eq. (33) is same as Eq. (27), the equivalent linear ordinary differential equation of circular form. According to what was mentioned on the previous section, solution of it can present as follows:

$$z_{0} = A(T_{1} ,T_{2} )e^{{i\omega T_{0} }} - \frac{{3A(T_{1} ,T_{2} )^{3} }}{{16a^{2 - 2k} }}e^{3i\beta } e^{{3i\omega T_{0} }} + {\text{cc}},$$
(35)

where \(A\) is an unknown complex function and \(\bar{A}\) is the complex conjugate of A. We use the fact that

$$\cos T_{0} = \frac{{e^{{iT_{0} }} + e^{{ - iT_{0} }} }}{2}.$$
(36)

Substituting for \(z_{0}\) from (35) into (34) gives

$$\begin{aligned} D_{0}^{2} z_{1} + \omega^{2} z_{1} = - 2i\omega D_{1} Ae^{{i\omega T_{0} }} + \frac{27}{{8a^{2 - 2k} }}i\omega A^{2} D_{1} Ae^{{i3\omega T_{0} }} + \cdots \hfill \\ \, \left( {\frac{{45A^{2} \bar{A}}}{{4a^{5 - 2k} }} - \frac{{135A^{3} \bar{A}^{2} }}{{64a^{7 - 4k} }} - \frac{3A}{{2a^{3} }}} \right)e^{{iT_{0} (\omega \pm 1)}} + \cdots \hfill \\ \frac{{129A^{3} }}{{32a^{5 - 2k} }}e^{3i\beta } e^{{iT_{0} (3\omega \pm 1)}} - \frac{{135A^{5} }}{{64a^{7 - 4k} }}e^{3i\beta } e^{{iT_{0} (5\omega \pm 1)}} + {\text{cc}}, \hfill \\ \end{aligned}$$
(37)

where \(\pm\) denotes two separate terms \(+\) and \(-\) with same coefficients. Any particular solution of (37) has a secular term containing the factor \(e^{{i\omega T_{0} }}\) unless

$$D_{1} A = 0 \to A = A_{0} + o(\varepsilon^{2} ), \, A_{0} = \alpha = {\text{constant}} .$$
(38)

Then, the solution of (37) is

$$\begin{aligned} z_{1} = (\frac{{45\alpha^{3} }}{{4a^{5 - 2k} }} - \frac{{135\alpha^{5} }}{{64a^{7 - 4k} }} - \frac{3\alpha }{{2a^{3} }})\frac{1}{{\omega^{2} - (\omega \pm 1)^{2} }}e^{{iT_{0} (\omega \pm 1)}} + \cdots \hfill \\ \, \frac{{129\alpha^{3} }}{{32a^{5 - 2k} }}\frac{1}{{\omega^{2} - (3\omega \pm 1)^{2} }}e^{3i\beta } e^{{iT_{0} (3\omega \pm 1)}} - \frac{{135\alpha^{5} }}{{64a^{7 - 4k} }}\frac{1}{{\omega^{2} - (5\omega \pm 1)^{2} }}e^{3i\beta } e^{{iT_{0} (5\omega \pm 1)}} + {\text{cc}}. \hfill \\ \end{aligned}$$
(39)

By recalling that \(T_{0} = t\), \(z_{0}\) and \(z_{1}\) can be obtained as follows

$$z_{0} = \alpha \cos (\omega t) - \frac{{3\alpha^{3} }}{{8a^{2 - 2k} }}\cos (3\omega t + 3\beta )$$
(40)
$$\begin{aligned} z_{1} = \left( {\frac{{45\alpha^{3} }}{{2a^{5 - 2k} }} - \frac{{135\alpha^{5} }}{{32a^{7 - 4k} }} - \frac{3\alpha }{{a^{3} }}} \right)\frac{1}{{\omega^{2} - (\omega \pm 1)^{2} }}\cos \left( {(\omega \pm 1)t} \right) + \cdots \hfill \\ \, \frac{{129\alpha^{3} }}{{16a^{5 - 2k} }}\frac{1}{{\omega^{2} - (3\omega \pm 1)^{2} }}\cos \left( {(3\omega \pm 1)t + 3\beta } \right) - \cdots \hfill \\ \, \frac{{135\alpha^{5} }}{{32a^{7 - 4k} }}\frac{1}{{\omega^{2} - (5\omega \pm 1)^{2} }}\cos \left( {(5\omega \pm 1)t + 3\beta } \right) \hfill \\ \end{aligned}$$
(41)

Finally, Sitnikov first-order solution can be presented as following form

$$z(t,\varepsilon ) = z_{0} (t) + \varepsilon z_{1} (t).$$
(42)

5 Results and Discussion

Figures 2 and 3 illustrate the solution of MMS compare with numerical solution for the circular form of the Sitnikov problem, \(\varepsilon = 0\). Evaluations verify that the MMS results are consistent with numerical solution and for higher accuracy, order of MMS solution can increase. With increasing initial velocity of third body, \(\dot{Z}_{0}\), the error of approximate solution will increase slowly. We should point that peaks of error graph in all figures is due to small value of \(Z_{\text{Num}}\) when crossing the line \(Z = 0\).

Fig. 2
figure 2

The Sitnikov problem evaluation by MMS at ε = 0, \(\dot{Z}_{0} = 0.1\)

Full size image
Fig. 3
figure 3

The Sitnikov problem evaluation by MMS at ε = 0, \(\dot{Z}_{0} = 0.2\)

Full size image

Figures 4 and 5 illustrate the results of MMS compare with numerical solution for the circular form of the Sitnikov problem, \(\varepsilon \ne 0\). For different value of initial conditions and \(\varepsilon\) the approximation is evaluated that MMS solution is consistent with numerical solution and for higher accuracy, order of MMS solution can increase. It is obvious that MMS covers only the Sitnikov problem with very small \(\varepsilon\) and equilibrium point should be at \(z = 0\). Percentage fit error (PFE) with respect to numerical data can be used to judge the suitability of the MMS analytical solution and accuracy of approximation:

$${\text{PFE}} = \frac{{(1/N)\sum\nolimits_{k = 1}^{N} {\left( {z_{k} - \hat{z}_{k} } \right)^{2} } }}{{(1/N)\sum\nolimits_{k = 1}^{N} {z_{k}^{2} } }} \times 100,N:{\text{number of data}},$$
(43)

where \(z\) and \(\hat{z}\) are respectively numerical and MMS value of \(Z(t)\). PFE of \(Z(t)\) approximation with MMS method with different \(\varepsilon\) and \(\dot{Z}_{0}\) is summarized in Table 1.

Fig. 4
figure 4

The Sitnikov problem evaluation by MMS at ε = 0.001, \(\dot{Z}_{0} = 0.1\)

Full size image
Fig. 5
figure 5

The Sitnikov problem evaluation by MMS at ε = 0.010, \(\dot{Z}_{0} = 0.1\)

Full size image
Table 1 The PFE (%) of Z(t) approximation with MMS
Full size table

6 Conclusion

In this paper, the Sitnikov problem with a new approach based on perturbation technique, the method of multiple scales, is investigated and it presented a semi-analytical solution that can help to understand principles of physics governed in this problem. Evaluation of results depicts that MMS solution is consistent with numerical solution for small eccentricity value. Further, in comparison to numerical solution, MMS presented semi-analytical solution with definition of amplitude and frequency of third body oscillation. Accuracy of MMS solution is dependent on order of scales that the Sitnikov equation can investigate more accurate at higher order scaling. With increasing eccentricity value, difference between \(z(t)\) from MMS and numerical method will grow up that until \(\varepsilon = 0.05\) can be acceptable but velocity of third mass oscillation will be significantly different with numerical estimation. This inconsistency and higher-order approximation solution should be investigated at future activities.