The Hamiltonian of an orbiter perturbed by a third body in an elliptic inclined orbit can be formulated as (Bertachini de Almeida Prado 2003)
$$\begin{aligned} {\mathcal {H}} = - \frac{\mu }{{2a}} - \left( {\frac{{{G m_3}}}{{{r_3}}}} \right) \sum \limits _{n = 2}^\infty {{{\left( {\frac{r}{{{r_3}}}} \right) }^n}} {P_n}\left( {\cos \varphi } \right) , \end{aligned}$$
(1)
where \({\mu }\) is the gravitational parameter of the central body; a is the semimajor axis of the orbiter; \(m_3\) is the mass of the perturbing body; G is the universal gravitational constant; r, \(r_3\) are the radial distances of the orbiter and the perturbing body from the central body; and \({\varphi }\) is the angle between the orbiter and perturbing body, determined by
$$\begin{aligned} \cos \varphi = \frac{\varvec{r}}{r}\cdot \frac{{\varvec{r}_3}}{{r_3}}, \end{aligned}$$
(2)
where radial vectors in the inertial frame can be expressed in terms of orbital elements as (Vallado 2001)
$$\begin{aligned} \varvec{r}= & {} r\left[ {\begin{array}{*{20}{c}} {{{\mathrm{c}}_\varOmega }{{\mathrm{c}}_\omega } - {{\mathrm{s}}_\varOmega }{{\mathrm{s}}_\omega }{{\mathrm{c}}_i}}&{}{ - {{\mathrm{c}}_\varOmega }{{\mathrm{s}}_\omega } - {{\mathrm{s}}_\varOmega }{{\mathrm{c}}_\omega }{{\mathrm{c}}_i}}&{}{{{\mathrm{s}}_\varOmega }{{\mathrm{s}}_i}}\\ {{{\mathrm{s}}_\varOmega }{{\mathrm{c}}_\omega } + {{\mathrm{c}}_\varOmega }{{\mathrm{s}}_\omega }{{\mathrm{c}}_i}}&{}{ - {{\mathrm{s}}_\varOmega }{{\mathrm{s}}_\omega } + {{\mathrm{c}}_\varOmega }{{\mathrm{c}}_\omega }{{\mathrm{c}}_i}}&{}{ - {{\mathrm{c}}_\varOmega }{{\mathrm{s}}_i}}\\ {{{\mathrm{s}}_\omega }{{\mathrm{s}}_i}}&{}{{{\mathrm{c}}_\omega }{{\mathrm{s}}_{i}}}&{}{{{\mathrm{c}}_i}} \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {{{{\mathrm{c}}}_f}}\\ {{{{\mathrm{s}}} _f}}\\ 0\end{array}} \right] , \end{aligned}$$
(3a)
$$\begin{aligned} {\varvec{r}_{3}}= & {} {r_3}\left[ {\begin{array}{*{20}{c}} {{{\mathrm{c}}_{{\varOmega _3}}}{{\mathrm{c}}_{{\omega _3}}} - {{\mathrm{s}}_{{\varOmega _3}}}{{\mathrm{s}}_{{\omega _3}}}{{\mathrm{c}}_{{i_3}}}}&{}{ - {{\mathrm{c}}_{{\varOmega _3}}}{{\mathrm{s}}_{{\omega _3}}} - {{\mathrm{s}}_{{\varOmega _3}}}{{\mathrm{c}}_{{\omega _3}}}{{\mathrm{c}}_{{i_3}}}}&{}{{{\mathrm{s}}_{{\varOmega _3}}}{{\mathrm{s}}_{{i_3}}}}\\ {{{\mathrm{s}}_{{\varOmega _3}}}{{\mathrm{c}}_{{\omega _3}}} + {{\mathrm{c}}_{{\varOmega _3}}}{{\mathrm{s}}_{{\omega _3}}}{{\mathrm{c}}_{{i_3}}}}&{}{ - {{\mathrm{s}}_{{\varOmega _3}}}{{\mathrm{s}}_{{\omega _3}}} + {{\mathrm{c}}_{{\varOmega _3}}}{{\mathrm{c}}_{{\omega _3}}}{{\mathrm{c}}_{{i_3}}}}&{}{ - {{\mathrm{c}}_{{\varOmega _3}}}{{\mathrm{s}}_{{i_3}}}}\\ {{{\mathrm{s}}_{{\omega _3}}}{{\mathrm{s}}_{{i_3}}}}&{}{{{{\mathrm{c}}} _{{\omega _3}}}{{{\mathrm{s}}} _{{i_3}}}}&{}{{{{\mathrm{c}}} _{{i_3}}}} \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {{{{\mathrm{c}}} _{{f_3}}}}\\ {{{{\mathrm{s}}} _{{f_3}}}}\\ 0 \end{array}} \right] , \end{aligned}$$
(3b)
where \({\text {s}}_x \buildrel \Delta \over = \sin (x)\), \(\text {c}_x \buildrel \Delta \over = \cos (x)\). Substituting Eq. (3) into Eq. (2) yields
$$\begin{aligned} \cos \varphi = \alpha \cos f + \beta \sin f, \end{aligned}$$
(4)
where
$$\begin{aligned} \begin{aligned} \alpha&= \left( {\cos \omega \cos \theta - \sin \omega \cos i\sin \theta } \right) \cos {u_3} + \left( \sin \omega \sin i\sin {i_3} + \cos \omega \cos {i_3}\sin \theta \right. \\&\quad \left. + \,\sin \omega \cos i\cos {i_3}\cos \theta \right) \sin {u_3} \\&\buildrel \Delta \over = {\alpha _1}\cos u_3 + {\alpha _2}\sin u_3 ,\\ \end{aligned} \end{aligned}$$
(5a)
$$\begin{aligned} \begin{aligned} \beta&= \left( { - \sin \omega \cos \theta - \cos \omega \cos i\sin \theta } \right) \cos {u_3} + \left( \cos \omega \sin i\sin {i_3} - \sin \omega \cos {i_3}\sin \theta \right. \\&\quad \left. +\, \cos \omega \cos i\cos {i_3}\cos \theta \right) \sin {u_3} \\&\buildrel \Delta \over = {\beta _1}\cos u_3 + {\beta _2}\sin u_3 , \end{aligned} \end{aligned}$$
(5b)
and
$$\begin{aligned} \theta= & {} \varOmega - {\varOmega _3} , \end{aligned}$$
(6a)
$$\begin{aligned} {u_3}= & {} {\omega _3} + {f_3}. \end{aligned}$$
(6b)
Considering that the radius of the perturbing body is much larger than that of the spacecraft \(\left( {{r_3} \gg r} \right) \), the Hamiltonian, after truncating the Legendre polynomials of the disturbing function up to second order, becomes
$$\begin{aligned} {\mathcal {H}} = - \frac{\mu }{{2a}} - \frac{{G {m}_3 }}{{2{r_3}}}{\left( {\frac{r}{{{r_3}}}} \right) ^2}\left( {3{{\cos }^2}\varphi - 1} \right) . \end{aligned}$$
(7)
We use the relation
$$\begin{aligned} G\left( {{m_1} + {m_3}} \right) = {n_3}^2{a_3}^3 , \end{aligned}$$
(8)
where \(m_1\) is the mass of the central body, \(n_3\) is the mean motion of the perturbing body, and \(a_3\) is the semimajor axis of the perturbing body. Substituting Eq. (4) into Eq. (7) yields
$$\begin{aligned} {\mathcal {H}} = - \frac{\mu }{{2a}} - \frac{{k{n_3}^2{a_3}^3}}{{2{r_3}}}{\left( {\frac{r}{{{r_3}}}} \right) ^2}\left( {3{\alpha ^2}{{\cos }^2}f + 3{\beta ^2}{{\sin }^2}f + 3\alpha \beta \sin 2f - 1} \right) , \end{aligned}$$
(9)
where
$$\begin{aligned} k=m_3/(m_1+m_3) . \end{aligned}$$
(10)
In order to use the canonical theory, Delaunay elements \(\{L,G,H,l,g,h\}\) are introduced,
$$\begin{aligned} L&= \sqrt{\mu a}, \quad \qquad l = M, \end{aligned}$$
(11a)
$$\begin{aligned} G&= L\sqrt{1 - {e^2}},\quad g = \omega , \end{aligned}$$
(11b)
$$\begin{aligned} H&= G\cos i,\quad h = \varOmega . \end{aligned}$$
(11c)
Moreover, the Hamiltonian is a function of the true anomaly, argument of perigee, right ascension of the ascending node and inclination of the perturbing body, as shown in Eqs. (5) and (9), other than the orbital elements of the orbiter. However, the periods of the argument of perigee, right ascension of ascending node and inclination of the perturbing body are much longer than the periods of the other elements. These slowly varying elements of the perturbing body can be assumed constant. Only the variation of the true anomaly of the perturbing body should be considered. This introduces one more degree of freedom. Additional two canonical variables \((M_3,T)\) are introduced as in Giacaglia et al. (1970), satisfying
$$\begin{aligned} \frac{{\mathrm{d}{M_3}}}{{\mathrm{d}t}}&= \frac{{\partial {\mathcal {H}}{^ \times }}}{{\partial T}} = {n_3} , \end{aligned}$$
(12a)
$$\begin{aligned} \frac{{\mathrm{d}T}}{{\mathrm{d}t}}&= -\frac{{\partial {\mathcal {H}}{^ \times }}}{{\partial {M_3}}} , \end{aligned}$$
(12b)
where \(M_3\) is the mean anomaly of the perturbing body, so the new Hamiltonian becomes
$$\begin{aligned} \begin{aligned} {{\mathcal {H}}^ \times }&= {\mathcal {H}} + {n_3}T \\&= - \frac{\mu }{{2a}} + {n_3}T - \frac{{k{n_3}^2{a_3}^3}}{{2{r_3}}}{\left( {\frac{r}{{{r_3}}}} \right) ^2}\left( {3{\alpha ^2}{{\cos }^2}f + 3{\beta ^2}{{\sin }^2}f + 3\alpha \beta \sin 2f - 1} \right) . \end{aligned} \end{aligned}$$
(13)
Comparing the new Hamiltonian with that in De Saedeleer (2006) (where the third-body perturbation, contained in the Hamiltonian, was expressed in a rotating frame) reveals that the Hamiltonians have similar forms. The term \({n_3}T\) can be approximated as the Coriolis effect term \(-\,{n_3}H\) appearing in De Saedeleer (2006), where H is the same as defined in Eq. (11c). Thus, the new canonical variable represents the angular momentum, and its magnitude is approximately H. Based on the two-body relationship, the ratios between these terms are approximated by
$$\begin{aligned} k_1&= \frac{{{n_3}T}}{{-\,\mu /(2a)}} \approx \frac{{{n_3}H}}{{\mu /(2a)}} \approx \frac{{{n_3}\sqrt{\mu a} \sqrt{1 - {e^2}} \cos i}}{{\mu /(2a)}} \approx \frac{{{n_3}}}{n}\left( {2\sqrt{1 - {e^2}} \cos i} \right) ,\end{aligned}$$
(14a)
$$\begin{aligned} k_2&= \dfrac{{\dfrac{{k{n_3}^2{a_3}^3}}{{2{r_3}}}{{\left( {\dfrac{r}{{{r_3}}}} \right) }^2}\left( {3{\alpha ^2}{{\cos }^2}f + 3{\beta ^2}{{\sin }^2}f + 3\alpha \beta \sin 2f - 1} \right) }}{{\mu /(2a)}}\nonumber \\&= \frac{{kn_3^2}}{{{n^2}}}\frac{{{{\left( {1 - {e^2}} \right) }^2}{{({e_3}\cos {f_3} + 1)}^3}}}{{{{\left( {1 - {e_3}^2} \right) }^3}{{(e\cos f + 1)}^2}}}\left( {3{\alpha ^2}{{\cos }^2}f + 3{\beta ^2}{{\sin }^2}f + 3\alpha \beta \sin 2f - 1} \right) , \end{aligned}$$
(14b)
where n is the mean motion of the orbiter. Furthermore, \(k_1\) and \(k_2\) can be approximated as \(n_3/n\) and \(k n_3^2/n^2\). For a lunar orbiter, perturbed by the third-body effect induced by Earth, the mass ratio shown in Eq. (10) is nearly 1, and \(n_3\) is smaller than n. Choosing \(n_3/n\) as the small parameter, \(n_3 T\) and the third-body perturbation term can be regarded as first order and second order, respectively. The Hamiltonian can be rearranged as
$$\begin{aligned} {\mathcal {H}}^ \times = {\mathcal {H}}_0 + {\mathcal {H}}_1 + {\mathcal {H}}_2, \end{aligned}$$
(15)
with
$$\begin{aligned} {\mathcal {H}}_{0}&= - \frac{{{\mu }}}{{2{a}}} , \end{aligned}$$
(16a)
$$\begin{aligned} {\mathcal {H}}_{1}&= {n_3}T , \end{aligned}$$
(16b)
$$\begin{aligned} {\mathcal {H}}_{2}&= - \frac{{k{n_3}^2{a_3}^3}}{{2{r_3}}}{\left( {\frac{r}{{{r_3}}}} \right) ^2}\left( {3{\alpha ^2}{{\cos }^2}f + 3{\beta ^2}{{\sin }^2}f + 3\alpha \beta \sin 2f - 1} \right) . \end{aligned}$$
(16c)
As shown in Eq. (13), the Hamiltonian contains trigonometric functions of f, \(\omega \), \(\varOmega \), and \(f_3\). According to the periods of these angles, it can be divided into short-period, medium-period, and long-period variations. The terms containing f represent short-period variations, which are usually several hours. The angle \(f_3\) has the period of the perturbing body, i.e., about one month for a lunar orbiter, which can be regarded as the medium-period variation. The periods of \(\omega \) and \(\varOmega \) are several years for a lunar orbiter perturbed by Earth (De Saedeleer 2006), constituting the long-period variation. The orbiter dynamics including secular and long-period variations will be derived via von Zeipel’s method (Kozai 1959a) in the following subsection.
2.1 Elimination of the short-period variation
According to von Zeipel’s algorithm, the Hamiltonian \({\mathcal {H}}(L,G,H,T,l,g,h,M_3)\) is transformed into \({\mathcal {H}}^*(L',G',H',T',-,g',h',M_3')\) under the generating function
$$\begin{aligned} S^*=L'l+G'g+H'h+T'M_3+S_1^*+S_2^* , \end{aligned}$$
(17)
where \(S_1^*\) and \(S_2^*\) are the first-order and second-order terms in \(n_3\), respectively. Equating like-order terms in the new Hamiltonian \({\mathcal {H^*}}\) and the original one \({\mathcal {H}}^{\times }\) yields
$$\begin{aligned} {\mathcal {H}}_0^*&= {{\mathcal {H}}_0}(L') , \end{aligned}$$
(18a)
$$\begin{aligned} {\mathcal {H}}_1^*&= {{\mathcal {H}}_1}(T') + \frac{{\partial S_1^*}}{{\partial l}}\frac{{\partial {{\mathcal {H}}_0}}}{{\partial L'}} , \end{aligned}$$
(18b)
$$\begin{aligned} {\mathcal {H}}_2^*&= {{\mathcal {H}}_2} + \frac{{\partial S_2^*}}{{\partial l}}\frac{{\partial {{\mathcal {H}}_0}}}{{\partial L'}} + \frac{1}{2}{\left( {\frac{{\partial S_1^*}}{{\partial l}}} \right) ^2}\frac{{{\partial ^2}{{\mathcal {H}}_0}}}{{\partial L{'^2}}} + \frac{{\partial S_1^*}}{{\partial M_3}}\frac{{\partial {\mathcal {H}}_1}}{{\partial T'}}, \end{aligned}$$
(18c)
$$\begin{aligned} {\mathcal {H}}_3^{{*}}&= \frac{{\partial S_3^*}}{{\partial l}}\frac{{\partial {{\mathcal {H}}_0}}}{{\partial L'}} + \frac{1}{6}{\left( {\frac{{\partial S_1^*}}{{\partial l}}} \right) ^3}\frac{{{\partial ^3}{{\mathcal {H}}_0}}}{{\partial L{'^3}}} + \frac{{\partial S_1^*}}{{\partial l}}\frac{{\partial S_2^*}}{{\partial l}}\frac{{{\partial ^2}{{\mathcal {H}}_0}}}{{\partial L{'^2}}}+\frac{{\partial S_2^*}}{{\partial {M_3}}}\frac{{\partial {{\mathcal {H}}_1}}}{{\partial T'}} \nonumber \\&\quad +\frac{1}{2}{\left( {\frac{{\partial S_1^*}}{{\partial {M_3}}}} \right) ^2}\frac{{{\partial ^2}{{\mathcal {H}}_1}}}{{\partial T{'^2}}} + \frac{{\partial S_1^*}}{{\partial l}}\frac{{\partial {{\mathcal {H}}_2}}}{{\partial L'}} + \frac{{\partial S_1^*}}{{\partial h}}\frac{{\partial {{\mathcal {H}}_2}}}{{\partial H'}} + \frac{{\partial S_1^*}}{{\partial g}}\frac{{\partial {{\mathcal {H}}_2}}}{{\partial G'}}\nonumber \\&\quad + \frac{{\partial S_1^*}}{{\partial {M_3}}}\frac{{\partial {{\mathcal {H}}_2}}}{{\partial T'}} - \frac{{\partial S_1^*}}{{\partial G'}}\frac{{\partial {\mathcal {H}}_2^*}}{{\partial g'}} - \frac{{\partial S_1^*}}{{\partial H'}}\frac{{\partial {\mathcal {H}}_2^*}}{{\partial h'}} - \frac{{\partial S_1^*}}{{\partial T'}}\frac{{\partial {\mathcal {H}}_2^*}}{{\partial {M_3}}}. \end{aligned}$$
(18d)
Solving Eqs. (18a) and (18b) yields
$$\begin{aligned} {\mathcal {H}}_0^* = - \frac{{{\mu }}}{{2a'}},\quad {\mathcal {H}}_1^* = {n_3}T',\quad {S_1^*} = 0. \end{aligned}$$
(19)
Substituting Eq. (19) into Eq. (18c),
$$\begin{aligned} {\mathcal {H}}_2^*= {{\mathcal {H}}_2} + \frac{{\partial S_2^*}}{{\partial l}}\frac{{\partial {{\mathcal {H}}_0}}}{{\partial L'}}, \end{aligned}$$
(20)
the solutions are
$$\begin{aligned} {\mathcal {H}}_2^*= & {} \frac{1}{{2\pi }}\int \limits _0^{2\pi } {{{\mathcal {H}}_2}\mathrm{d}l}\nonumber \\= & {} - \frac{{k{n_3}^2{a'^2}{a_3}^3}}{{4{r_3}^3}}\left[ {3{{\alpha '} ^2}\left( {4{e'^2} + 1} \right) - 3{{\beta '} ^2}\left( {{e'^2} - 1} \right) - 3{e'^2} - 2} \right] , \end{aligned}$$
(21)
and
$$\begin{aligned} \begin{aligned} {\mathcal {S}}_2^*&= \frac{{L{'^3}}}{{{\mu ^2}}}\int {\left( {{\mathcal {H}}_2^* - {{\mathcal {H}}_2}} \right) } {\mathrm{d}}l \\&= \frac{{L{'^3}}}{{{\mu ^2}}}{\mathcal {H}}_2^*l + \frac{{L{'^3}}}{{{\mu ^2}}}\frac{{k{n_3}^2{a_3}^3}}{{2{r_3}^3}}\left\{ {3{\alpha ^2}\int {{r^2}{{\cos }^2}f\mathrm{d}l + 3{\beta ^2}\int {{r^2}{{\sin }^2}f\mathrm{d}l } } } \right. \\&\quad \left. +\, 3\alpha \beta \int {{r^2}\sin 2f\mathrm{d}l - } \int {{r^2}\mathrm{d}l} \right\} . \end{aligned} \end{aligned}$$
(22)
Using the two-body relations,
$$\begin{aligned} r&= \frac{{a\left( {1 - {e^2}} \right) }}{{1 + e\cos f}} , \end{aligned}$$
(23a)
$$\begin{aligned} \mathrm{d}l&= \frac{{{{\left( {1 - {e^2}} \right) }^{3/2}}}}{{{{\left( {1 + e\cos f} \right) }^2}}}\mathrm{d}f. \end{aligned}$$
(23b)
Using a symbolic algebra software, the following integrals are calculated:
$$\begin{aligned}&\int {{r^2}{{\cos }^2}f\mathrm{d}l} = {a^2}{\left( {1 - {e^2}} \right) ^{\frac{7}{2}}}\int {\frac{{{{\cos }^2}f}}{{{{\left( {1 + e\cos f} \right) }^4}}}\mathrm{d}f} \nonumber \\&\quad = {a^2}\left( {4{e^2} + 1} \right) {\tan ^{ - 1}}\left[ {\sqrt{\frac{{1 - e}}{{1 + e}}} \tan \left( {\frac{f}{2}} \right) } \right] - \frac{{{a^2}\sqrt{1 - {e^2}} \sin f}}{{12{{(e\cos f + 1)}^3}}}\nonumber \\&\qquad \times \, \left[ {6\left( {2{e^4} + 9{e^2} - 1} \right) \cos f + e\left( {6{e^4} + 14{e^2} + \left( {6{e^4} + 10{e^2} - 1} \right) \cos 2f + 25} \right) } \right] , \end{aligned}$$
(24a)
$$\begin{aligned}&\int {{r^2}{{\sin }^2}f\mathrm{d}l} = {a^2}{\left( {1 - {e^2}} \right) ^{\frac{7}{2}}}\int {\frac{{{{\sin }^2}f}}{{{{\left( {1 + e\cos f} \right) }^4}}}\mathrm{d}f} \nonumber \\&\quad = - {a^2}\left( {{e^2} - 1} \right) {\tan ^{ - 1}}\left[ {\sqrt{\frac{{1 - e}}{{1 + e}}} \tan \left( {\frac{f}{2}} \right) } \right] + \frac{{{a^2}\sqrt{1 - {e^2}} \left( {{e^2} - 1} \right) \sin f}}{{12{{(e\cos f + 1)}^3}}} \nonumber \\&\qquad \times \,\left\{ {6\left( {{e^2} + 1} \right) \cos f + e\left[ {\left( {2{e^2} + 1} \right) \cos 2f - 2{e^2} + 11} \right] } \right\} , \end{aligned}$$
(24b)
$$\begin{aligned}&\int {{r^2} \mathrm{d}l} = {a^2}{\left( {1 - {e^2}} \right) ^{\frac{7}{2}}}\int {\frac{1}{{{{\left( {1 + e\cos f} \right) }^4}}}\mathrm{d}f} \nonumber \\&\quad = {a^2}\left( {3{e^2} + 2} \right) {\tan ^{ - 1}}\left[ {\sqrt{\frac{{1 - e}}{{1 + e}}} \tan \left( {\frac{f}{2}} \right) } \right] - \frac{{{a^2}e\sqrt{1 - {e^2}} \sin f}}{{12{{(e\cos f + 1)}^3}}}\nonumber \\&\qquad \times \, \left[ {8{e^4} + \left( {4{e^2} + 11} \right) {e^2}\cos 2f + 6\left( {{e^2} + 9} \right) e\cos f + {e^2} + 36} \right] . \end{aligned}$$
(24c)
Utilizing the two-body relationship between the eccentric anomaly E and true anomaly f (Vallado 2001),
$$\begin{aligned} \tan \left( {\frac{E}{2}} \right) = \sqrt{\frac{{1 - e}}{{1 + e}}} \tan \left( {\frac{f}{2}} \right) , \end{aligned}$$
(25)
yields
$$\begin{aligned} {\tan ^{ - 1}}\left[ {\sqrt{\frac{{1 - e}}{{1 + e}}} \tan \left( {\frac{f}{2}} \right) } \right] ={\frac{E}{2}}. \end{aligned}$$
(26)
Substituting Eq. (26) into Eq. (24) yields
$$\begin{aligned} \int {{r^2}{{\cos }^2}f\mathrm{d}l}&= \frac{1}{2}{a'^2}\left( {4{e'^2} + 1} \right) E - \frac{{{a'^2}\sqrt{1 - {e'^2}} \sin f}}{{12{{(e'\cos f + 1)}^3}}}\left[ {6\left( {2{e'^4} + 9{e'^2} - 1} \right) \cos f} \right. \nonumber \\&\quad \left. { +\, e'\left( {6{e'^4} + 14{e'^2} + \left( {6{e'^4} + 10{e'^2} - 1} \right) \cos 2f + 25} \right) } \right] , \end{aligned}$$
(27a)
$$\begin{aligned} \int {{r^2}{{\sin }^2}f\mathrm{d}l}&= - \frac{1}{2}{a'^2}\left( {{e'^2} - 1} \right) E + \frac{{{a'^2}\sqrt{1 - {e'^2}} \left( {{e'^2} - 1} \right) \sin f}}{{12{{(e'\cos f + 1)}^3}}} \nonumber \\&\quad \times \, \left\{ {6\left( {{e'^2} + 1} \right) \cos f} \right. \left. { + e'\left[ {\left( {2{e'^2} + 1} \right) \cos 2f - 2{e'^2} + 11} \right] } \right\} , \end{aligned}$$
(27b)
$$\begin{aligned} \int {{r^2} \mathrm{d}l}&= \frac{1}{2}{a'^2}\left( {3{e'^2} + 2} \right) E - \frac{{{a'^2}e'\sqrt{1 - {e'^2}} \sin f}}{{12{{(e'\cos f + 1)}^3}}}\left[ {8{e'^4} + {e'^2}} \right. \nonumber \\&\quad \left. { +\, \left( {4{e'^2} + 11} \right) {e'^2}\cos 2f + 6\left( {{e'^2} + 9} \right) e'\cos f + 36} \right] . \end{aligned}$$
(27c)
It is noticed that a singularity happens when integrating \(r^2\sin {2f}\) with respect to f. It can be avoided by using an eighth-order Taylor series expansion,
$$\begin{aligned} \begin{aligned} \frac{{\sin 2f}}{{{{\left( {1 + e\cos f} \right) }^4}}}&\approx \sin 2f\left\{ {1 - 4\left( {e\cos f} \right) + 10{{\left( {e\cos f} \right) }^2} - 20{{\left( {e\cos f} \right) }^3} + 35{{\left( {e\cos f} \right) }^4} } \right. \\&\quad \left. { -\, 56{{\left( {e\cos f} \right) }^5} + 84{{\left( {e\cos f} \right) }^6} - 120{{\left( {e\cos f} \right) }^7} + 165{{\left( {e\cos f} \right) }^8} } \right\} , \end{aligned} \end{aligned}$$
(28)
which results in the approximation,
$$\begin{aligned} \begin{aligned} \int {{r^2}\sin 2f} \mathrm{d}l&\approx {a'^2}{\left( {1 - {e'^2}} \right) ^{7/2}}\left\{ { - \frac{{33}}{{512}}{e'^8}\left[ {5\left( {84{{\cos }^2}f + 24\cos 4f + 9\cos 6f + 2\cos 8f} \right) } \right. } \right. \\&\quad \left. +\, \cos 10f \right] + \frac{{80}}{3}{e'^7}{\cos ^9}f - \frac{{21}}{{128}}{e'^6}\left( {56\cos 2f + 28\cos 4f + 8\cos 6f } \right. \\&\quad \left. +\, \cos 8f \right) + 16{e'^5}{\cos ^7}f - \frac{{35}}{{96}}{e'^4}\left( {30{{\cos }^2}f + 6\cos 4f + \cos 6f} \right) \\&\quad \left. +\, 8{e'^3}{\cos ^5}f { - \frac{5}{8}{e'^2}\left( {8{{\cos }^2}f + \cos 4f} \right) + \frac{8}{3}e'{{\cos }^3}f - \frac{1}{2}\cos 2f} \right\} . \end{aligned} \end{aligned}$$
(29)
Finally, substituting Eqs. (21), (27), (29) into Eq. (22) yields the short-period generating function
$$\begin{aligned} \begin{aligned} S_2^*&= - \frac{{k{n_3}^2{a'^{7/2}}\sqrt{1 - {e'^2}} {{\left( {1 + {e_3}\cos {f_3}} \right) }^3}}}{{24{\mu ^{1/2}}{{\left( {1 - {e_3}^2} \right) }^3}{{\left( {1 + e'\cos f} \right) }^3}}}\left\{ {3{{\alpha '} ^2}\left( {1 - {e'^2}} \right) \sin f \left[ {\left( {6{e'^2} - 1} \right) (e'\cos 2f } \right. } \right. \\&\quad +\, 6\cos f) \left. { + e'\left( {6{e'^2} + 19} \right) } \right] + 3{{\beta '} ^2}{\left( {{e'^2} - 1} \right) ^2}\sin f\left[ {e'(\cos 2f + 5) + 6\cos f} \right] \\&\quad -\, e'\left( {1 - {e'^2}} \right) \sin f\left[ {{e'^2} + 5e'(e'\cos 2f + 6\cos f) + 24} \right] - 36{\alpha '} {\beta '} {\left( {1 - {e'^2}} \right) ^3} \\&\quad \times \, {\left( {1 + e'\cos f} \right) ^3}\left\{ { - \frac{{33}}{{512}}{e'^8}\left[ {5\left( {84{{\cos }^2}f + 24\cos 4f + 9\cos 6f + 2\cos 8f} \right) } \right. } \right. \\&\quad \left. { +\, \cos 10f} \right] + \frac{{80}}{3}{e'^7}{\cos ^9}f - \frac{{21}}{{128}}{e'^6}\left( {56\cos 2f + 28\cos 4f + 8\cos 6f + \cos 8f} \right) \\&\quad +\, 16{e'^5}{\cos ^7}f - \frac{{35}}{{96}}{e'^4}\left( {30{{\cos }^2}f + 6\cos 4f + \cos 6f} \right) + 8{e'^3}{\cos ^5}f \\&\quad \left. {\left. { -\, \frac{5}{8}{e'^2}\left( {8{{\cos }^2}f + \cos 4f} \right) + \frac{8}{3}e'{{\cos }^3}f - \frac{1}{2}\cos 2f} \right\} } \right\} . \end{aligned} \end{aligned}$$
(30)
Then, substituting Eqs. (19), (21) and (30) into Eq. (18d) yields the third-order Hamiltonian
$$\begin{aligned} \begin{aligned} {\mathcal {H}}_3^{*}&= \frac{1}{{2\pi }}\int \limits _0^{2\pi } {\frac{{\partial S_2^*}}{{\partial h}}\frac{{\partial {{\mathcal {H}}_1}}}{{\partial H'}}\mathrm{d}l} \\&= - \frac{{k{n_3}^3{a'^{7/2}}{e'^2}{{\left( {1 - {e'^2}} \right) }^5}{{({e_3}\cos {f_3} + 1)}^4}}}{{65536{\mu ^{1/2}}{{\left( {1 - {e_3}^2} \right) }^{9/2}}}}\left( {5623695{e'^{12}} + 9482544{e'^{10}} + 10961216{e'^8}} \right. \\&\quad \left. { +\, 8736000{e'^6} + 4227840{e'^4} + 1971200{e'^2} + 479232} \right) \left\{ {{\alpha _1}'{\beta _1}'\cos ({f_3} + {\omega _3})} \right. \\&\quad \times \left[ { - 3{e_3}\sin {f_3}\cos ({f_3} + {\omega _3}) - 2({e_3}\cos {f_3} + 1)\sin ({f_3} + {\omega _3})} \right] + \left( {{\alpha _1}'{\beta _2}' + {\alpha _2}'{\beta _1}'} \right) \\&\quad \times \left( {\cos (2{f_3} + 2{\omega _3}) - \frac{1}{4}{e_3}\left[ {\cos ({f_3} + 2{\omega _3}) - 5\cos (3{f_3} + 2{\omega _3})} \right] } \right) \\&\quad \left. { +\, {\alpha _2}'{\beta _2}'\sin ({f_3} + {\omega _3})\left[ {2({e_3}\cos {f_3} + 1)\cos ({f_3} + {\omega _3}) - 3{e_3}\sin {f_3}\sin ({f_3} + {\omega _3})} \right] } \right\} . \end{aligned} \end{aligned}$$
(31)
For the second-order solution, it is not necessary to obtain the third-order generating function.
2.2 Elimination of the medium-period variation
The terms in the Hamiltonian depending on \(M_3\) induce the medium-period variation. Using the generating function
$$\begin{aligned} {S^{*{{*}}}} = L''l' + G''g' + H''h' + S_1^{**} + S_2^{**}, \end{aligned}$$
(32)
the new Hamiltonian \({\mathcal {H}}^{**}(L'',G'',H'',T''-,g'',h'',-)\) is determined by
$$\begin{aligned} {\mathcal {H}}_0^{**}&= {{\mathcal {H}}_0^{*}}(L'') , \end{aligned}$$
(33a)
$$\begin{aligned} {\mathcal {H}}_1^{**}&= {{\mathcal {H}}_1^{*}}(T'') , \end{aligned}$$
(33b)
$$\begin{aligned} {\mathcal {H}}_2^{**}&= {\mathcal {H}}_2^{*} + \frac{{\partial S_1^{**}}}{{\partial {M_3'}}}\frac{{\partial {\mathcal {H}}_1^{*}}}{{\partial T''}}, \end{aligned}$$
(33c)
$$\begin{aligned} {\mathcal {H}}_3^{{{**}}}&={\mathcal {H}}_3^{{*}} + \frac{{\partial S_2^{**}}}{{\partial {M_3'}}}\frac{{\partial {\mathcal {H}}_1^{*}}}{{\partial T''}}+\frac{1}{2}{\left( {\frac{{\partial S_1^{**}}}{{\partial {M_3'}}}} \right) ^2}\frac{{{\partial ^2}{\mathcal {H}}_1^{*}}}{{\partial T'{'^2}}} + \frac{{\partial S_1^{**}}}{{\partial h'}}\frac{{\partial {\mathcal {H}}_2^{*}}}{{\partial H''}} \nonumber \\&\quad +\, \frac{{\partial S_1^{**}}}{{\partial g'}}\frac{{\partial {\mathcal {H}}_2^{*}}}{{\partial G''}} + \frac{{\partial S_1^{**}}}{{\partial {M_3'}}}\frac{{\partial {\mathcal {H}}_2^{*}}}{{\partial T''}} - \frac{{\partial S_1^{**}}}{{\partial G''}}\frac{{\partial {\mathcal {H}}_2^{**}}}{{\partial g'}} - \frac{{\partial S_1^{**}}}{{\partial H''}}\frac{{\partial {\mathcal {H}}_2^{**}}}{{\partial h'}}. \end{aligned}$$
(33d)
According to Eqs. (33a) and (33b), we obtain
$$\begin{aligned} {\mathcal {H}}_0^{**}&= - \frac{{{\mu }}}{{2a'}}, \end{aligned}$$
(34a)
$$\begin{aligned} {\mathcal {H}}_1^{**}&= {n_3}T'' . \end{aligned}$$
(34b)
Based on Eq. (33c), the second-order term in the Hamiltonian is
$$\begin{aligned} \begin{aligned} {\mathcal {H}}_2^{**}&= \frac{1}{{2\pi }}\int \limits _0^{2\pi } {{\mathcal {H}}_2^*\mathrm{d} {{M_3'}}} \\&= - \frac{{k{n_3}^2{a''^2}}}{{128{{\left( {1 - {e_3}^2} \right) }^{3/2}}}}\left\{ {3{e''^2}\left\{ {40\sin i''\sin 2{i_3}\sin 2\omega ' \sin \theta ' + 4\sin 2i''} \right. } \right. \\&\quad \times \, \sin 2{i_3}\left( {3 - 5\cos 2\omega ' } \right) \cos \theta ' - 40\cos i''{\sin ^2}{i_3}\sin 2\omega ' \sin 2\theta ' + {\sin ^2}{i_3} \\&\quad \times \,\cos 2\theta ' \left[ {10\left( {\cos 2i'' + 3} \right) \cos 2\omega ' + 12{{\sin }^2}i''} \right] + \left( {3\cos 2{i_3} + 1} \right) \\&\quad \left. { \times \,\left( {10{{\sin }^2}i''\cos 2\omega ' + 3\cos 2i'' + 1} \right) } \right\} + 2\left[ {12{{\sin }^2}i''{{\sin }^2}{i_3}\cos 2\theta ' } \right. \\&\quad \left. {\left. { +\, 12\sin 2i''\sin 2{i_3}\cos \theta ' + \left( {3\cos 2i'' + 1} \right) \left( {3\cos 2{i_3} + 1} \right) } \right] } \right\} , \end{aligned} \end{aligned}$$
(35)
and the generating function \(S_1^{**}\) is determined by
$$\begin{aligned} S_1^{**}&= \frac{1}{{{n_3}}}\int {\left( {{\mathcal {H}}_2^{**} - {\mathcal {H}}_2^*} \right) } \mathrm{d} {{M_3'}} \nonumber \\&= \frac{{k{n_3}{a''^2}}}{{16{{\left( {1 - {e_3}^2} \right) }^{3/2}}}}\left\{ { - 2\left[ {3\left( {4{e''^2} + 1} \right) \left( {{\alpha _1''}^2 + {\alpha _2''}^2} \right) + 3\left( {1 - {e''^2}} \right) \left( {{\beta _1''}^2 + {\beta _2''}^2} \right) } \right. } \right. \nonumber \\&\quad \left. { -\, 6{e''^2} - 4} \right] \left[ {2{{\tan }^{ - 1}}\left( {\sqrt{\frac{{1 - {e_3}}}{{1 + {e_3}}}} \tan \frac{{{f_3}}}{2}} \right) - \frac{{\sqrt{1 - {e_3}^2} {e_3}\sin {f_3}}}{{({e_3}\cos {f_3} + 1)}} - {f_3}} \right. \nonumber \\&\quad \left. { -\, {e_3}\sin {f_3}} \right] + \left[ {\left( {{\alpha _1''}^2 - {\alpha _2''}^2} \right) \left( {4{e''^2} + 1} \right) - \left( {{e''^2} - 1} \right) \left( {\beta _1''}^2 - {\beta _2''}^2\right) } \right] \nonumber \\&\quad \times \, \left\{ {{e_3}\left[ {3\sin ({f_3} + 2{\omega _3}) + \sin (3{f_3} + 2{\omega _3})} \right] + 3\sin (2{f_3} + 2{\omega _3})} \right\} \nonumber \\&\quad -\, 2\left[ {{e''^2}(4{\alpha _1''}{\alpha _2''} - {\beta _1''}{\beta _2''}) + {\alpha _1''}{\alpha _2''} + {\beta _1''}{\beta _2''}} \right] \left\{ {{e_3}\left[ {3\cos ({f_3} + 2{\omega _3})} \right. } \right. \nonumber \\&\quad \left. {\left. {\left. { +\, \cos (3{f_3} + 2{\omega _3})} \right] + 3\cos (2{f_3} + 2{\omega _3})} \right\} } \right\} . \end{aligned}$$
(36)
Substituting Eqs. (34), (35) and (36) into Eq. (33d), the third-order Hamiltonian term is
$$\begin{aligned} \begin{aligned} {\mathcal {H}}_3^{**}&= \frac{1}{{2\pi }}\int \limits _0^{2\pi } {{\mathcal {H}}_3^*\mathrm{d}\left( {{M_3}'} \right) } +\frac{1}{{2\pi }}\int \limits _0^{2\pi } {\left\{ {\frac{{\partial S_1^{**}}}{{\partial h'}}\frac{{\partial {\mathcal {H}}_2^*}}{{\partial H''}} + \frac{{\partial S_1^{**}}}{{\partial g'}}\frac{{\partial {\mathcal {H}}_2^*}}{{\partial G''}} } \right. } \\&\quad \left. -\, \frac{{\partial S_1^{**}}}{{\partial G''}}\frac{{\partial {\mathcal {H}}_2^{**}}}{{\partial g'}} - \frac{{\partial S_1^{**}}}{{\partial H''}}\frac{{\partial {\mathcal {H}}_2^{**}}}{{\partial h'}} \right\} \mathrm{d}\left( {{M_3}'} \right) , \end{aligned} \end{aligned}$$
(37)
and the second-order generating function is
$$\begin{aligned} \begin{aligned} S_2^{**}&= \frac{1}{{{n_3}}}\int \left\{ {\mathcal {H}}_3^{{{**}}} - {\mathcal {H}}_3^{{*}} - \frac{{\partial S_1^{**}}}{{\partial h'}}\frac{{\partial {\mathcal {H}}_2^{*}}}{{\partial H''}} - \frac{{\partial S_1^{**}}}{{\partial g'}}\frac{{\partial {\mathcal {H}}_2^{*}}}{{\partial G''}} + \frac{{\partial S_1^{**}}}{{\partial G''}}\frac{{\partial {\mathcal {H}}_2^{**}}}{{\partial g'}} + \frac{{\partial S_1^{**}}}{{\partial H''}}\frac{{\partial {\mathcal {H}}_2^{**}}}{{\partial h'}} \right\} \mathrm{d} {{M_3'}}\\&\buildrel \Delta \over = S_{21}^{{{*}}*} + S_{22}^{{{*}}*}, \end{aligned} \end{aligned}$$
(38)
where
$$\begin{aligned} S_{21}^{{{*}}*}&= \frac{1}{{{n_3}}}\int {\left\{ {\frac{1}{{2\pi }}\int \limits _0^{2\pi } {{\mathcal {H}}_3^*\mathrm{d}\left( {{M_3}'} \right) } - {\mathcal {H}}_3^{{*}}} \right\} } \mathrm{d}\left( {{M_3}'} \right) , \end{aligned}$$
(39a)
$$\begin{aligned} S_{22}^{{{*}}*}&= \dfrac{1}{{{n_3}}}\int {\left\{ \begin{array}{l} \dfrac{1}{{2\pi }}\int \limits _0^{2\pi } {\left\{ {\dfrac{{\partial S_1^{**}}}{{\partial h'}}\dfrac{{\partial {\mathcal {H}}_2^*}}{{\partial H''}} + \dfrac{{\partial S_1^{**}}}{{\partial g'}}\dfrac{{\partial {\mathcal {H}}_2^*}}{{\partial G''}} - \dfrac{{\partial S_1^{**}}}{{\partial G''}}\dfrac{{\partial {\mathcal {H}}_2^{**}}}{{\partial g'}} - \dfrac{{\partial S_1^{**}}}{{\partial H''}}\dfrac{{\partial {\mathcal {H}}_2^{**}}}{{\partial h'}}} \right\} \mathrm{d}\left( {{M_3}'} \right) } \\ \quad -\, \dfrac{{\partial S_1^{**}}}{{\partial h'}}\dfrac{{\partial {\mathcal {H}}_2^*}}{{\partial H''}} - \dfrac{{\partial S_1^{**}}}{{\partial g'}}\dfrac{{\partial {\mathcal {H}}_2^*}}{{\partial G''}} + \dfrac{{\partial S_1^{**}}}{{\partial G''}}\dfrac{{\partial {\mathcal {H}}_2^{**}}}{{\partial g'}} + \dfrac{{\partial S_1^{**}}}{{\partial H''}}\dfrac{{\partial {\mathcal {H}}_2^{**}}}{{\partial h'}} \end{array} \right\} } \mathrm{d}\left( {{M_3}'} \right) . \end{aligned}$$
(39b)
According to Eq. (31), it is found that
$$\begin{aligned} \frac{1}{{2\pi }}\int \limits _0^{2\pi } {{\mathcal {H}}_3^*\mathrm{d}{M_3}'} =0. \end{aligned}$$
(40)
Furthermore,
$$\begin{aligned} \begin{aligned} S_{21}^{{{*}}*}&= - \frac{1}{{{n_3}}}\int {{\mathcal {H}}_3^{{*}}} \mathrm{d}{M_3} \\&= \frac{{k{n_3}^2{a''^{7/2}}{e''^2}{{\left( {1 - {e''^2}} \right) }^5}}}{{1048576{\mu ^{1/2}}}}\left( {5623695{e''^{12}} + 9482544{e''^{10}} + 10961216{e''^8}} \right. \\&\quad \left. { +\, 8736000{e''^6} + 4227840{e''^4} + 1971200{e''^2} + 479232} \right) \\&\quad \times \,\left\{ {{\alpha _1''}{\beta _1''}P + \left( {{\alpha _1''}{\beta _2''} + {\alpha _2''}{\beta _1''}} \right) Q + {\alpha _2''}{\beta _2''}F} \right\} , \end{aligned} \end{aligned}$$
(41)
where
$$\begin{aligned} P&= \frac{1}{{{{\left( {1 - {e_3}^2} \right) }^3}}}\left\{ {\cos 2{\omega _3}\left\{ {4{e_3}\left( {{e_3}^2 + 3} \right) \cos {f_3} + 4\left( {3{e_3}^2 + 2} \right) \cos 2{f_3}} \right. } \right. \nonumber \\&\quad \left. { +\, {e_3}\left[ {{e_3}^2\cos 5{f_3} + 3\left( {{e_3}^2 + 4} \right) \cos 3{f_3} + 6{e_3}\cos 4{f_3}} \right] } \right\} \nonumber \\&\quad +\, 2{e_3}\left[ {3\left( {{e_3}^2 + 4} \right) \cos {f_3} + {e_3}({e_3}\cos 3{f_3} + 6\cos 2{f_3})} \right] \nonumber \\&\quad \left. { -\, 8\sin 2{f_3}\sin 2{\omega _3}{{({e_3}\cos {f_3} + 1)}^3}} \right\} , \end{aligned}$$
(42a)
$$\begin{aligned} Q&=\frac{1}{{{{\left( {1 - {e_3}^2} \right) }^3}}}\left\{ {\sin 2{\omega _3}\left[ {{e_3}^3\cos 5{f_3} + 6{e_3}^2\cos 4{f_3} + 4\left( {{e_3}^2 + 3} \right) {e_3}\cos {f_3}} \right. } \right. \nonumber \\&\quad \left. { +\, 3\left( {{e_3}^2 + 4} \right) {e_3}\cos 3{f_3} + 4\left( {3{e_3}^2 + 2} \right) \cos 2{f_3}} \right] \nonumber \\&\quad \left. { +\, 8\sin 2{f_3}\cos 2{\omega _3}{{({e_3}\cos {f_3} + 1)}^3}} \right\} , \end{aligned}$$
(42b)
$$\begin{aligned} F&= \frac{1}{{{{\left( {1 - {e_3}^2} \right) }^3}}}\left\{ { - \cos 2{\omega _3}\left\{ {4{e_3}\left( {{e_3}^2 + 3} \right) \cos {f_3} + 4\left( {3{e_3}^2 + 2} \right) \cos 2{f_3}} \right. } \right. \nonumber \\&\quad \left. { +\, {e_3}\left[ {{e_3}^2\cos 5{f_3} + 3\left( {{e_3}^2 + 4} \right) \cos 3{f_3} + 6{e_3}\cos 4{f_3}} \right] } \right\} \nonumber \\&\quad +\, 2{e_3}\left[ {3\left( {{e_3}^2 + 4} \right) \cos {f_3} + {e_3}({e_3}\cos 3{f_3} + 6\cos 2{f_3})} \right] \nonumber \\&\quad \left. { + \,8\sin 2{f_3}\sin 2{\omega _3}{{({e_3}\cos {f_3} + 1)}^3}} \right\} . \end{aligned}$$
(42c)
Using the Hamiltonian \({\mathcal {H}}_2^{**}\) in Eq. (35) and the generating function \(S_1^{**}\) in Eq. (36), we can calculate the integral term in Eq. (39b),
$$\begin{aligned} \begin{aligned}&\frac{{\partial S_1^{**}}}{{\partial h'}}\frac{{\partial {\mathcal {H}}_2^*}}{{\partial H''}} + \frac{{\partial S_1^{**}}}{{\partial g'}}\frac{{\partial {\mathcal {H}}_2^*}}{{\partial G''}} - \frac{{\partial S_1^{**}}}{{\partial G''}}\frac{{\partial {\mathcal {H}}_2^{**}}}{{\partial g'}} - \frac{{\partial S_1^{**}}}{{\partial H''}}\frac{{\partial {\mathcal {H}}_2^{**}}}{{\partial h'}}\\&\quad = \frac{{{k^2}{n_3}^2{a''^{7/2}}}}{{1024{\mu ^{1/2}}{{\left( {1 - {e_3}^2} \right) }^3}}}\left\{ {\left\{ {6{e''^2}\left[ { - \sin 2i''(5\cos 2\omega ' - 3)\left( { - 2{{\sin }^2}{i_3}\cos 2\theta ' + 3\cos 2{i_3}} \right. } \right. } \right. } \right. \\&\qquad \left. { +\, 1} \right) - 20\sin 2\omega ' \left( {\sin i''{{\sin }^2}{i_3}\sin 2\theta ' + \cos i''\sin 2{i_3}\sin \theta ' } \right) + 4\cos 2i''\sin 2{i_3} \\&\qquad \left. { \times \, (5\cos 2\omega ' - 3)\cos \theta ' } \right] + 4\left[ {\sin 2i''\left( { - 6{{\sin }^2}{i_3}\cos 2\theta ' + 9\cos 2{i_3} + 3} \right) } \right. \\&\qquad \left. {\left. { -\, 12\cos 2i''\sin 2{i_3}\cos \theta ' } \right] } \right\} {f_{gh}}\left( {{A_1},{B_1},{C_1}} \right) + \left\{ {4{e''^2}\left[ { - \sin 2i''(\cos 2{i_3} + 3)} \right. } \right. \\&\qquad \times \, (5\cos 2\omega ' - 3)\cos 2\theta ' + 4\sin 2{i_3}\left( {\cos 2i''(5\cos 2\omega ' - 3)\cos \theta ' - 5\cos i''} \right. \\&\qquad \left. { \times \,\sin 2\omega ' \sin \theta ' } \right) + 10\sin i''(\cos 2{i_3} + 3)\sin 2\omega ' \sin 2\theta ' + 6\sin 2i''{\sin ^2}{i_3} \\&\qquad \left. { \times \, (5\cos 2\omega ' - 3)} \right] + 8\sin 2i''(\cos 2{i_3} + 3)\cos 2\theta ' - \cos 2i''\sin 2{i_3}\cos \theta ' \\&\qquad \left. { -\, 3\sin i''\cos i''{{\sin }^2}{i_3}} \right\} {f_{gh}}\left( {{A_{_2}},{B_2},{C_2}} \right) + \left\{ {32\sin \theta ' (\sin 2i''\cos {i_3}\cos \theta ' } \right. \\&\qquad -\, \cos 2i''\sin {i_3}) + 8{e''^2}\left[ {10\sin 2\omega ' (\cos i''\sin {i_3}\cos \theta ' - \sin i''\cos {i_3}\cos 2\theta ' )} \right. \\&\qquad \left. {\left. { +\, 2\cos 2i''\sin {i_3}(5\cos 2\omega ' - 3)\sin \theta ' + \sin 2i''\cos {i_3}(3 - 5\cos 2\omega ' )\sin 2\theta '} \right] } \right\} \\&\qquad \times \,{f_{gh}}\left( {{A_3},{B_3},{C_3}} \right) + 3e''\left[ { - 80\sin i''\sin 2{i_3}\sin 2\omega ' \sin \theta ' - 2{{\sin }^2}{i_3}\cos 2\theta ' } \right. \\&\qquad \times \, \left( {10(\cos 2i'' + 3)\cos 2\omega ' + 12{{\sin }^2}i''} \right) + 80\cos i''{\sin ^2}{i_3}\sin 2\omega ' \sin 2\theta ' \\&\qquad +\, 8\sin 2i''\sin 2{i_3}(5\cos 2\omega ' - 3)\cos \theta ' - 2(3\cos 2{i_3} + 1)\left( {10{{\sin }^2}i''\cos 2\omega ' } \right. \\&\qquad \left. {\left. { +\, 3\cos 2i'' + 1} \right) } \right] {f_g}\left( {{A_1},{B_1},{C_1}} \right) + 2e''\left[ {(\cos 2{i_3} + 3)\cos 2\theta ' \left( {12{{\sin }^2}i''} \right. } \right. \\&\qquad \left. {+\,10(\cos 2i'' + 3)\cos 2\omega ' } \right) + 8\sin 2{i_3}\left( {\sin 2i''(5\cos 2\omega ' - 3)\cos \theta ' - 10\sin i''} \right. \\&\qquad \left. { \times \, \sin 2\omega ' \sin \theta ' } \right) - 40\cos i''(\cos 2{i_3} + 3)\sin 2\omega ' \sin 2\theta ' + 12{\sin ^2}{i_3}\left( {3\cos 2i''} \right. \\&\qquad \left. {\left. { +\, 10{{\sin }^2}i''\cos 2\omega ' + 1} \right) } \right] {f_g}\left( {{A_{_2}},{B_2},{C_2}} \right) + 8e\left[ {\cos {i_3}\sin 2\theta ' \left( {6{{\sin }^2}i''} \right. } \right. \\&\qquad \left. {+\,5(\cos 2i'' + 3)\cos 2\omega ' } \right) + 20\sin 2\omega ' (\cos i''\cos {i_3}\cos 2\theta ' + \sin i''\sin {i_3}\cos \theta ' )\\&\qquad \left. {\left. { +\, 2\sin 2i''\sin {i_3}(5\cos 2\omega ' - 3)\sin \theta ' } \right] {f_g}\left( {{A_3},{B_3},{C_3}} \right) } \right\} , \end{aligned} \end{aligned}$$
(43)
where the functions \({f_{gh}}\left( {\chi ,\gamma ,\kappa } \right) \), \({f_{g}}\left( {\chi ,\gamma ,\kappa } \right) \) are
$$\begin{aligned} \begin{aligned} {f_{gh}}\left( {\chi ,\gamma ,\kappa } \right)&= \frac{1}{{8\sqrt{1 - {e''^2}} \sin i''}}\left\{ {24\chi \sin i''\sin {i_3}\sin \theta ' (\sin i''\sin {i_3}\cos \theta ' + \cos i''\cos {i_3})} \right. \\&\quad +\, 4\gamma \left[ {\sin 2i''\sin 2{i_3}\sin \theta ' - {{\sin }^2}i''(\cos 2{i_3} + 3)\sin 2\theta ' } \right] + 8\kappa \sin i''\\&\quad \times \,\left( {\sin i''\cos {i_3}\cos 2\theta ' - \cos i''\sin {i_3}\cos \theta ' } \right) + {e''^2}\left\{ {2\cos {i_3}\left[ {\sin {i_3}(3\chi + 2\gamma )} \right. } \right. \\&\quad \times \, \left( {5(\sin 3i'' - \sin i'')\sin 2\omega ' \cos \theta ' + \sin 2i''(5\cos 2\omega ' + 3)\sin \theta ' } \right) \\&\quad \left. { -\, 5\kappa \sin 2i''\sin i''\sin 2\omega ' \sin 2\theta ' + 2\kappa {{\sin }^2}i''(5\cos 2\omega ' + 3)\cos 2\theta ' } \right] \\&\quad -\, 5{\sin ^2}i''\cos i''\sin 2\omega ' \left[ {\cos 2{i_3}(3\chi + 2\gamma )(\cos 2\theta ' + 3) + 6(\chi - 2\gamma ){{\sin }^2}\theta } \right] \\&\quad -\, {\sin ^2}i''(5\cos 2\omega ' + 3)\sin 2\theta ' \left[ {\cos 2{i_3}(3\chi + 2\gamma ) - 3\chi + 6\gamma } \right] \\&\quad \left. {\left. { +\, 2\kappa \sin {i_3}\left[ {5(\sin 3i'' - \sin i'')\sin 2\omega ' \sin \theta ' - \sin 2i''(5\cos 2\omega ' + 3)\cos \theta ' } \right] } \right\} } \right\} , \end{aligned} \end{aligned}$$
(44a)
$$\begin{aligned} \begin{aligned} {f_g}\left( {\chi ,\gamma ,\kappa } \right)&= \frac{5}{{16}}e''\sqrt{1 - {e''^2}} \left\{ { - \sin 2\omega ' \left[ {(\cos 2i'' + 3)\cos 2\theta ' \left( {\cos 2{i_3}(3\chi + 2\gamma ) - 3\chi + 6\gamma } \right) } \right] } \right. \\&\quad +\, 4\sin 2i''\sin 2{i_3}(3\chi + 2\gamma )\cos \theta ' - 6{\sin ^2}i''\left( {\cos 2{i_3}(3\chi + 2\gamma ) + \chi - 2\gamma } \right) \\&\quad \left. { +\, 8\kappa \sin 2i''\sin {i_3}\sin \theta ' + 4\kappa (\cos 2i'' + 3)\cos {i_3}\sin 2\theta } \right] + 8\cos i''\cos 2\omega \\&\quad \times \, \left[ {2\kappa \cos {i_3}\cos 2\theta ' - \sin 2\theta ' \left( {\gamma (\cos 2{i_3} + 3) - 3\chi {{\sin }^2}{i_3}} \right) } \right] \\&\quad \left. { +\, 16\sin i''\sin {i_3}\cos 2\omega ' \left[ {\kappa \cos \theta ' - \cos {i_3}(3\chi + 2\gamma )\sin \theta '} \right] } \right\} , \end{aligned} \end{aligned}$$
(44b)
and corresponding variables \(A_i\), \(B_i\), \(C_i\) (\(i=1,2,3\)) are
$$\begin{aligned} {A_1}&= 2\left( {1 - \frac{{2{{\left( {1+{e_3}\cos {f_3}} \right) }^3}}}{{{{\left( {1 - {e_3}^2} \right) }^{3/2}}}}} \right) \left\{ {{M_3} - {e_3}\sin {f_3} - {f_3}} \right\} , \end{aligned}$$
(45a)
$$\begin{aligned} {B_1}&= - \frac{{{{\left( {1+{e_3}\cos {f_3}} \right) }^3}}}{{4{{\left( {1 - {e_3}^2} \right) }^{3/2}}}}\left\{ {{e_3}\left[ {3\sin ({f_3} + 2{\omega _3}) + \sin (3{f_3} + 2{\omega _3})} \right] + 3\sin (2{f_3} + 2{\omega _3})} \right\} , \end{aligned}$$
(45b)
$$\begin{aligned} {C_1}&= - \frac{{{{\left( {1+{e_3}\cos {f_3}} \right) }^3}}}{{{{\left( {1 - {e_3}^2} \right) }^{3/2}}}}\left\{ {{e_3}\left[ {3\cos ({f_3} + 2{\omega _3}) + \cos (3{f_3} + 2{\omega _3})} \right] + 3\cos (2{f_3} + 2{\omega _3})} \right\} , \end{aligned}$$
(45c)
$$\begin{aligned} {A_{_2}}&= - \left\{ {{e_3}\left[ {3\cos ({f_3} + 2{\omega _3}) + \cos (3{f_3} + 2{\omega _3})} \right] + 3\cos (2{f_3} + 2{\omega _3})} \right\} \nonumber \\&\quad +\, \frac{{6\cos 2{u_3}{{\left( {1+{e_3}\cos {f_3}} \right) }^3}}}{{{{\left( {1 - {e_3}^2} \right) }^{3/2}}}}\left\{ {{M_3} - {e_3}\sin {f_3} - {f_3}} \right\} , \end{aligned}$$
(45d)
$$\begin{aligned} {B_2}&= \frac{{3{{\left( {1+{e_3}\cos {f_3}} \right) }^3}\cos 2{u_3}}}{{8{{\left( {1 - {e_3}^2} \right) }^{3/2}}}}\left\{ {{e_3}\left[ {3\sin ({f_3} + 2{\omega _3}) + \sin (3{f_3} + 2{\omega _3})} \right] + 3\sin (2{f_3} + 2{\omega _3})} \right\} , \end{aligned}$$
(45e)
$$\begin{aligned} {C_2}&= \frac{{3{{\left( {1+{e_3}\cos {f_3}} \right) }^3}\cos 2{u_3}}}{{2{{\left( {1 - {e_3}^2} \right) }^{3/2}}}}\left\{ {{e_3}\left[ {3\cos ({f_3} + 2{\omega _3}) + \cos (3{f_3} + 2{\omega _3})} \right] + 3\cos (2{f_3} + 2{\omega _3})} \right\} , \end{aligned}$$
(45f)
$$\begin{aligned} {A_3}&= \frac{1}{2}\left\{ {{e_3}\left[ {3\sin ({f_3} + 2{\omega _3}) + \sin (3{f_3} + 2{\omega _3})} \right] + 3\sin (2{f_3} + 2{\omega _3})} \right\} \nonumber \\&\quad +\, \frac{{12{{\left( {1+{e_3}\cos {f_3}} \right) }^3}\sin 2{u_3}}}{{{{\left( {1 - {e_3}^2} \right) }^{3/2}}}}\left\{ {{M_3} - {e_3}\sin {f_3} - {f_3}} \right\} , \end{aligned}$$
(45g)
$$\begin{aligned} {B_3}&= \frac{{3{{\left( {1+{e_3}\cos {f_3}} \right) }^3}\sin 2{u_3}}}{{4{{\left( {1 - {e_3}^2} \right) }^{3/2}}}}\left\{ {{e_3}\left[ {3\sin ({f_3} + 2{\omega _3}) + \sin (3{f_3} + 2{\omega _3})} \right] + 3\sin (2{f_3} + 2{\omega _3})} \right\} , \end{aligned}$$
(45h)
$$\begin{aligned} {C_3}&= \frac{{3{{\left( {1+{e_3}\cos {f_3}} \right) }^3}\sin 2{u_3}}}{{{{\left( {1 - {e_3}^2} \right) }^{3/2}}}}\left\{ {{e_3}\left[ {3\cos ({f_3} + 2{\omega _3}) + \cos (3{f_3} + 2{\omega _3})} \right] + 3\cos (2{f_3} + 2{\omega _3})} \right\} . \end{aligned}$$
(45i)
It is noticed that the integration variable only appears in \(A_i\), \(B_i\), \(C_i\). In addition, the functions \({f_{gh}}\left( {\chi ,\gamma ,\kappa } \right) \), \({f_{g}}\left( {\chi ,\gamma ,\kappa } \right) \) do not have coupling terms. Thus, the integration of Eq. (43) reduces to integrating \(A_i\), \(B_i\), \(C_i\). The integration is conducted using true anomaly as the independent variable, utilizing the third-order approximation of the mean anomaly (Battin 1999),
$$\begin{aligned} \begin{aligned} {M_3}&= {f_3} + \frac{{{e_3}^2}}{{3{{\left( {\sqrt{1 - {e_3}^2} + 1} \right) }^3}}}\left[ \left( { - 6{e_3}^2 + 9\sqrt{1 - {e_3}^2} + 9} \right) \sin 2{f_3} \right. \\&\quad \left. -\, 2{e_3}\left( {3\sqrt{1 - {e_3}^2} + 1} \right) \sin 3{f_3} \right] - 2{e_3}\sin {f_3}, \end{aligned} \end{aligned}$$
(46)
and
$$\begin{aligned} \mathrm{d}{M_3} = \frac{{{{\left( {1 - {e_3}^2} \right) }^{3/2}}}}{{{{\left( {1 + {e_3}\cos {f_3}} \right) }^2}}}\mathrm{d}{f_3}. \end{aligned}$$
(47)
In addition, it is necessary to use a Taylor series expansion to avoid singularity,
$$\begin{aligned} \mathrm{d}{M_3} = {\left( {1 - {e_3}^2} \right) ^{3/2}}\left[ {1 - 2{e_3}\cos {f_3} + 3{{({e_3}\cos {f_3})}^2} - 4{{({e_3}\cos {f_3})}^3} + O\left( {{{({e_3}\cos {f_3})}^4}} \right) } \right] \mathrm{d}{f_3}. \end{aligned}$$
(48)
As a result,
$$\begin{aligned} S_{22}^{**}&= \frac{{{k^2}{n_3}^2{a''^{7/2}}}}{{1024{\mu ^{1/2}}{{\left( {1 - {e_3}^2} \right) }^3}}}\left\{ {\left\{ {6{e''^2}\left[ { - \sin 2i''(5\cos 2\omega ' - 3)\left( { - 2{{\sin }^2}{i_3}\cos 2\theta ' + 3\cos 2{i_3}} \right. } \right. } \right. } \right. \nonumber \\&\quad \left. { +\, 1} \right) - 20\sin 2\omega ' \left( {\sin i''{{\sin }^2}{i_3}\sin 2\theta ' + \cos i''\sin 2{i_3}\sin \theta ' } \right) + 4\cos 2i''\sin 2{i_3} \nonumber \\&\quad \left. { \times \, (5\cos 2\omega ' - 3)\cos \theta ' } \right] + 4\left[ {\sin 2i''\left( { - 6{{\sin }^2}{i_3}\cos 2\theta ' + 9\cos 2{i_3} + 3} \right) } \right. \nonumber \\&\quad \left. {\left. { -\, 12\cos 2i''\sin 2{i_3}\cos \theta ' } \right] } \right\} {f_{gh}}\left( {{A_1^{**}},{B_1^{**}},{C_1^{**}}} \right) + \left\{ {4{e''^2}\left[ { - \sin 2i''(\cos 2{i_3} + 3)} \right. } \right. \nonumber \\&\quad \times \,(5\cos 2\omega ' - 3)\cos 2\theta ' + 4\sin 2{i_3}\left( {\cos 2i''(5\cos 2\omega ' - 3)\cos \theta ' - 5\cos i''} \right. \nonumber \\&\quad \left. { \times \, \sin 2\omega ' \sin \theta ' } \right) + 10\sin i''(\cos 2{i_3} + 3)\sin 2\omega ' \sin 2\theta ' + 6\sin 2i''{\sin ^2}{i_3} \nonumber \\&\quad \left. { \times \, (5\cos 2\omega ' - 3)} \right] + 8\sin 2i''(\cos 2{i_3} + 3)\cos 2\theta ' - \cos 2i''\sin 2{i_3}\cos \theta ' \nonumber \\&\quad \left. { - \,3\sin i''\cos i''{{\sin }^2}{i_3}} \right\} {f_{gh}}\left( {{A_{_2^{**}}},{B_2^{**}},{C_2^{**}}} \right) + \left\{ {32\sin \theta ' (\sin 2i''\cos {i_3}\cos \theta ' } \right. \nonumber \\&\quad -\, \cos 2i''\sin {i_3}) + 8{e''^2}\left[ {10\sin 2\omega ' (\cos i''\sin {i_3}\cos \theta ' - \sin i''\cos {i_3}\cos 2\theta ' )} \right. \nonumber \\&\quad \left. {\left. { +\, 2\cos 2i''\sin {i_3}(5\cos 2\omega ' - 3)\sin \theta ' + \sin 2i''\cos {i_3}(3 - 5\cos 2\omega ' )\sin 2\theta '} \right] } \right\} \nonumber \\&\quad \times \,{f_{gh}}\left( {{A_3^{**}},{B_3^{**}},{C_3^{**}}} \right) + 3e''\left[ { - 80\sin i''\sin 2{i_3}\sin 2\omega ' \sin \theta ' - 2{{\sin }^2}{i_3}\cos 2\theta ' } \right. \nonumber \\&\quad \times \, \left( {10(\cos 2i'' + 3)\cos 2\omega ' + 12{{\sin }^2}i''} \right) + 80\cos i''{\sin ^2}{i_3}\sin 2\omega ' \sin 2\theta ' \nonumber \\&\quad +\, 8\sin 2i''\sin 2{i_3}(5\cos 2\omega ' - 3)\cos \theta ' - 2(3\cos 2{i_3} + 1)\left( {10{{\sin }^2}i''\cos 2\omega ' } \right. \nonumber \\&\quad \left. {\left. { +\, 3\cos 2i'' + 1} \right) } \right] {f_g}\left( {{A_1},{B_1},{C_1}} \right) + 2e''\left[ {(\cos 2{i_3} + 3)\cos 2\theta ' \left( {12{{\sin }^2}i''} \right. } \right. \nonumber \\&\quad \left. {+\,10(\cos 2i'' + 3)\cos 2\omega ' } \right) + 8\sin 2{i_3}\left( {\sin 2i''(5\cos 2\omega ' - 3)\cos \theta ' - 10\sin i''} \right. \nonumber \\&\quad \left. { \times \, \sin 2\omega ' \sin \theta ' } \right) - 40\cos i''(\cos 2{i_3} + 3)\sin 2\omega ' \sin 2\theta ' + 12{\sin ^2}{i_3}\left( {3\cos 2i''} \right. \nonumber \\&\quad \left. {\left. { +\, 10{{\sin }^2}i''\cos 2\omega ' + 1} \right) } \right] {f_g}\left( {{A_{_2^{**}}},{B_2^{**}},{C_2^{**}}} \right) + 8e\left[ {\cos {i_3}\sin 2\theta ' \left( {6{{\sin }^2}i''} \right. } \right. \nonumber \\&\quad \left. {+\,5(\cos 2i'' + 3)\cos 2\omega ' } \right) + 20\sin 2\omega ' (\cos i''\cos {i_3}\cos 2\theta ' + \sin i''\sin {i_3}\cos \theta ' )\nonumber \\&\quad \left. {\left. { +\, 2\sin 2i''\sin {i_3}(5\cos 2\omega ' - 3)\sin \theta ' } \right] {f_g}\left( {{A_3^{**}},{B_3^{**}},{C_3^{**}}} \right) } \right\} , \end{aligned}$$
(49)
where \(A_i^{**}\), \(B_i^{**}\), \(C_i^{**}\) (\(i=1,2,3\)) are given in “Appendix A.”
2.3 Transformation between osculating elements and mean elements
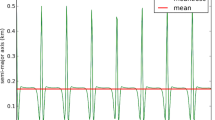
The elements after double averaging are commonly referred to as mean elements. The transformation between mean elements and osculating elements will be discussed in this section.
Under the generating functions \(S_2^{*}\), \(S_1^{**}\), and \(S_2^{**}\), the mean elements \((L'',G''\) \(,H'',l'',g'',h'')\) are converted to the osculating elements (L, G, H, l, g, h) by
$$\begin{aligned} \begin{aligned} L= & {} L'' + \frac{{\partial S_1^{**}}}{{\partial l'}} + \frac{{\partial S_2^{**}}}{{\partial l'}} + \frac{{\partial S_2^*}}{{\partial l}},\quad l= & {} l'' - \frac{{\partial S_1^{**}}}{{\partial L''}} - \frac{{\partial S_2^{**}}}{{\partial L''}} - \frac{{\partial S_2^*}}{{\partial L'}} ,\\ G= & {} G'' + \frac{{\partial S_1^{**}}}{{\partial g'}} + \frac{{\partial S_2^{**}}}{{\partial g'}} + \frac{{\partial S_2^*}}{{\partial g}},\quad g= & {} g'' - \frac{{\partial S_1^{**}}}{{\partial G''}} - \frac{{\partial S_2^{**}}}{{\partial G''}} - \frac{{\partial S_2^*}}{{\partial G'}} ,\\ H= & {} H'' + \frac{{\partial S_1^{**}}}{{\partial h'}} + \frac{{\partial S_2^{**}}}{{\partial h'}} + \frac{{\partial S_2^*}}{{\partial h}},\quad h= & {} h'' - \frac{{\partial S_1^{**}}}{{\partial H''}} - \frac{{\partial S_2^{**}}}{{\partial H''}} - \frac{{\partial S_2^*}}{{\partial H'}}. \end{aligned} \end{aligned}$$
(50)
It is observed that the short-period generating function \(S_2^*\) in Eq. (30) is a function of osculating elements and singly averaged elements, and the medium-period generating functions \(S_1^{**}\) in Eq. (36) and \(S_2^{**}\) in Eq. (38) are functions of singly averaged elements and mean elements. To obtain an explicit conversion, the expression must only contain mean elements. The elements in the second-order generating function can be changed into mean elements directly, because the errors are of high order. However, the singly averaged elements in \(S_1^{**}\) cannot be replaced directly, because the error is of the first order. As a consequence, the replacement introduces correction terms with second-order magnitude (Nie and Gurfil 2018),
$$\begin{aligned} \begin{aligned} {L_{M2O,c}}&= - \frac{{{\partial ^2}S_1^{**}}}{{\partial l'{'^2}}}\frac{{\partial S_1^{**}}}{{\partial L''}} - \frac{{{\partial ^2}S_1^{**}}}{{\partial l''\partial g''}}\frac{{\partial S_1^{**}}}{{\partial G''}} - \frac{{{\partial ^2}S_1^{**}}}{{\partial l''\partial h''}}\frac{{\partial S_1^{**}}}{{\partial H''}},\\ {G_{M2O,c}}&= - \frac{{{\partial ^2}S_1^{**}}}{{\partial g''\partial l''}}\frac{{\partial S_1^{**}}}{{\partial L''}} - \frac{{{\partial ^2}S_1^{**}}}{{{\partial ^2}g''}}\frac{{\partial S_1^{**}}}{{\partial G''}} - \frac{{{\partial ^2}S_1^{**}}}{{\partial g''\partial h''}}\frac{{\partial S_1^{**}}}{{\partial H''}},\\ {H_{M2O,c}}&= - \frac{{{\partial ^2}S_1^{**}}}{{\partial h''\partial l'}}\frac{{\partial S_1^{**}}}{{\partial L''}} - \frac{{{\partial ^2}S_1^{**}}}{{\partial h''\partial g''}}\frac{{\partial S_1^{**}}}{{\partial G''}} - \frac{{{\partial ^2}S_1^{**}}}{{{\partial ^2}h''}}\frac{{\partial S_1^{**}}}{{\partial H''}},\\ {l_{M2O,c}}&= \frac{{{\partial ^2}S_1^{**}}}{{\partial L''\partial l''}}\frac{{\partial S_1^{**}}}{{\partial L''}} + \frac{{{\partial ^2}S_1^{**}}}{{\partial L''\partial g''}}\frac{{\partial S_1^{**}}}{{\partial G''}} + \frac{{{\partial ^2}S_1^{**}}}{{\partial L''\partial h''}}\frac{{\partial S_1^{**}}}{{\partial H''}},\\ {g_{M2O,c}}&= \frac{{{\partial ^2}S_1^{**}}}{{\partial G''\partial l''}}\frac{{\partial S_1^{**}}}{{\partial L''}} + \frac{{{\partial ^2}S_1^{**}}}{{\partial G''\partial g''}}\frac{{\partial S_1^{**}}}{{\partial G''}} + \frac{{{\partial ^2}S_1^{**}}}{{\partial G''\partial h''}}\frac{{\partial S_1^{**}}}{{\partial H''}},\\ {h_{M2O,c}}&= \frac{{{\partial ^2}S_1^{**}}}{{\partial H''\partial l''}}\frac{{\partial S_1^{**}}}{{\partial L''}} + \frac{{{\partial ^2}S_1^{**}}}{{\partial H''\partial g''}}\frac{{\partial S_1^{**}}}{{\partial G''}} + \frac{{{\partial ^2}S_1^{**}}}{{\partial H''\partial h''}}\frac{{\partial S_1^{**}}}{{\partial H''}}. \end{aligned} \end{aligned}$$
(51)
Finally, the mean elements can be transformed into osculating elements by
$$\begin{aligned} \begin{aligned} L&= L'' + {L_{sp2}''} + {L_{mp1}''} + {L_{mp2}''} + {L_{M2O,c}},\quad l = l'' + {l_{sp2}''} + {l_{mp1}''} + {l_{mp2}''} + {l_{M2O,c}} ,\\ G&= G'' + {G_{sp2}''} + {G_{mp1}''} + {G_{mp2}''} + {G_{M2O,c}},\quad g =g'' + {g_{sp2}''} + {g_{mp1}''} + {g_{mp2}''} + {g_{M2O,c}} ,\\ H&= H'' + {H_{sp2}''} + {H_{mp1}''} + {H_{mp2}''} + {H_{M2O,c}},\quad h = h'' + {h_{sp2}''} + {h_{mp1}''} + {h_{mp2}''} + {h_{M2O,c}}, \end{aligned} \end{aligned}$$
(52)
where
$$\begin{aligned} \begin{aligned} {L_{sp2}''}&= \frac{{\partial S_2^*}}{{\partial l''}} ,\quad {G_{sp2}''} = \frac{{\partial S_2^*}}{{\partial g''}},\quad {H_{sp2}''} = \frac{{\partial S_2^*}}{{\partial h''}} ,\\ {l_{sp2}''}&= - \frac{{\partial S_2^*}}{{\partial L''}} ,\quad {g_{sp2}''} = - \frac{{\partial S_2^*}}{{\partial G''}},\quad \;\;{h_{sp2}''} = - \frac{{\partial S_2^*}}{{\partial H''}} ,\\ {L_{mp1}''}&= \frac{{\partial S_1^{**}}}{{\partial l''}} ,\quad {G_{mp1}''} = \frac{{\partial S_1^{**}}}{{\partial g''}} ,\quad {H_{mp1}''} = \frac{{\partial S_1^{**}}}{{\partial h''}},\\ {l_{mp1}''}&= - \frac{{\partial S_1^{**}}}{{\partial L''}} ,\quad {g_{mp1}''} = - \frac{{\partial S_1^{**}}}{{\partial G''}},\quad {h_{mp1}''} = - \frac{{\partial S_1^{**}}}{{\partial H''}} ,\\ {L_{mp2}''}&= \frac{{\partial S_2^{**}}}{{\partial l''}} ,\quad {G_{mp2}''} = \frac{{\partial S_2^{**}}}{{\partial g''}},\quad {H_{mp2}''} = \frac{{\partial S_2^{**}}}{{\partial h''}},\\ {l_{mp2}''}&= - \frac{{\partial S_2^{**}}}{{\partial L''}} ,\quad {g_{mp2}''} = - \frac{{\partial S_2^{**}}}{{\partial G''}},\quad {h_{mp2}''} = - \frac{{\partial S_2^{**}}}{{\partial H''}}. \end{aligned} \end{aligned}$$
(53)
These expressions are given in Appendix B (provided as an electronic supplement), and the values are determined by using mean elements.
According to Eq. (50), the mean elements can be calculated by
$$\begin{aligned} \begin{aligned} L''&= L - \frac{{\partial S_1^{**}}}{{\partial l'}} - \frac{{\partial S_2^{**}}}{{\partial l'}} - \frac{{\partial S_2^*}}{{\partial l}},\quad l'' = l + \frac{{\partial S_1^{**}}}{{\partial L''}} + \frac{{\partial S_2^{**}}}{{\partial L''}} + \frac{{\partial S_2^*}}{{\partial L'}},\\ G''&= G - \frac{{\partial S_1^{**}}}{{\partial g'}} - \frac{{\partial S_2^{**}}}{{\partial g'}} - \frac{{\partial S_2^*}}{{\partial g}},\quad g'' = g + \frac{{\partial S_1^{**}}}{{\partial G''}} + \frac{{\partial S_2^{**}}}{{\partial G''}} + \frac{{\partial S_2^*}}{{\partial G'}},\\ H''&= H - \frac{{\partial S_1^{**}}}{{\partial h'}} - \frac{{\partial S_2^{**}}}{{\partial h'}} - \frac{{\partial S_2^*}}{{\partial h}},\quad h'' = h + \frac{{\partial S_1^{**}}}{{\partial H''}} + \frac{{\partial S_2^{**}}}{{\partial H''}} + \frac{{\partial S_2^*}}{{\partial H'}}. \end{aligned} \end{aligned}$$
(54)
To obtain the explicit conversion from osculating elements to mean elements, all elements in the right-hand side of Eq. (54) should be osculating elements. For the second-order solution, the osculating elements can be substituted into all second-order terms, because the errors are of higher order; however, for the first-order terms, the errors are of second order. Taking \(\frac{{\partial S_1^{**}}}{{\partial l'}}\) as an example, and using Taylor’s theorem, \(\frac{{\partial S_1^{**}}}{{\partial l'}}\) can be expressed as
$$\begin{aligned} \begin{aligned} \frac{{\partial S_1^{**}}}{{\partial l'}}&= \frac{{\partial S_1^{**}\left( {L'',G'',H'',l',g',h'} \right) }}{{\partial l'}} \\&= \frac{{\partial S_1^{**}\left( {L,G,H,l,g,h} \right) }}{{\partial l}} + \frac{{{\partial ^2}S_1^{**}\left( {L,G,H,l,g,h} \right) }}{{\partial l\partial L}}\left( {L'' - L} \right) \\&\quad +\, \frac{{{\partial ^2}S_1^{**}\left( {L,G,H,l,g,h} \right) }}{{\partial l\partial G}}\left( {G'' - G} \right) + \frac{{{\partial ^2}S_1^{**}\left( {L,G,H,l,g,h} \right) }}{{\partial l\partial H}}\left( {H'' - H} \right) \\&\quad +\, \frac{{{\partial ^2}S_1^{**}\left( {L,G,H,l,g,h} \right) }}{{\partial {l^2}}}\left( {l' - l} \right) + \frac{{{\partial ^2}S_1^{**}\left( {L,G,H,l,g,h} \right) }}{{\partial l\partial g}}\left( {g' - g} \right) \\&\quad +\, \frac{{{\partial ^2}S_1^{**}\left( {L,G,H,l,g,h} \right) }}{{\partial l\partial h}}\left( {h' - h} \right) + \frac{1}{2}\frac{{{\partial ^3}S_1^{**}\left( {L,G,H,l,g,h} \right) }}{{\partial l\partial {L^2}}}{\left( {L'' - L} \right) ^2} + \cdot \cdot \cdot \;. \end{aligned} \end{aligned}$$
(55)
According to Eq. (54), Eq. (55) can be written as
$$\begin{aligned} \begin{aligned} \frac{{\partial S_1^{**}}}{{\partial l'}}&= \frac{{\partial S_1^{**}\left( {L,G,H,l,g,h} \right) }}{{\partial l}} + \frac{{{\partial ^2}S_1^{**}\left( {L,G,H,l,g,h} \right) }}{{\partial l\partial L}}\left( -{\frac{{\partial S_1^{**}}}{{\partial l'}} - \frac{{\partial S_2^{**}}}{{\partial l'}} - \frac{{\partial S_2^*}}{{\partial l}}} \right) \\&\quad + \frac{{{\partial ^2}S_1^{**}\left( {L,G,H,l,g,h} \right) }}{{\partial l\partial G}}\left( -{\frac{{\partial S_1^{**}}}{{\partial g'}} - \frac{{\partial S_2^{**}}}{{\partial g'}} - \frac{{\partial S_2^*}}{{\partial g}}} \right) \\&\quad +\frac{{{\partial ^2}S_1^{**}\left( {L,G,H,l,g,h} \right) }}{{\partial l\partial H}}\left( - {\frac{{\partial S_1^{**}}}{{\partial h'}} - \frac{{\partial S_2^{**}}}{{\partial h'}} - \frac{{\partial S_2^*}}{{\partial h}}} \right) \\&\quad + \frac{{{\partial ^2}S_1^{**}\left( {L,G,H,l,g,h} \right) }}{{\partial {l^2}}}\left( { \frac{{\partial S_2^*}}{{\partial L'}}} \right) + \frac{{{\partial ^2}S_1^{**}\left( {L,G,H,l,g,h} \right) }}{{\partial l\partial g}}\left( { \frac{{\partial S_2^*}}{{\partial G'}}} \right) \\&\quad + \frac{{{\partial ^2}S_1^{**}\left( {L,G,H,l,g,h} \right) }}{{\partial l\partial h}}\left( { \frac{{\partial S_2^*}}{{\partial H'}}} \right) \\&\quad + \frac{1}{2}\frac{{{\partial ^3}S_1^{**}\left( {L,G,H,l,g,h} \right) }}{{\partial l\partial {L^2}}}{\left( -{\frac{{\partial S_1^{**}}}{{\partial l'}} - \frac{{\partial S_2^{**}}}{{\partial l'}} - \frac{{\partial S_2^*}}{{\partial l}}} \right) ^2} + \cdot \cdot \cdot \;. \end{aligned} \end{aligned}$$
(56)
For the second-order solution, terms are truncated up to second order, and Eq. (56) becomes
$$\begin{aligned} \begin{aligned} \frac{{\partial S_1^{**}}}{{\partial l'}}&= \frac{{\partial S_1^{**}\left( {L,G,H,l,g,h} \right) }}{{\partial l}} - \frac{{{\partial ^2}S_1^{**}\left( {L,G,H,l,g,h} \right) }}{{\partial l\partial L}}\left( {\frac{{\partial S_1^{**}}}{{\partial l'}}} \right) \\&\quad -\, \frac{{{\partial ^2}S_1^{**}\left( {L,G,H,l,g,h} \right) }}{{\partial l\partial G}}\left( {\frac{{\partial S_1^{**}}}{{\partial g'}}} \right) - \frac{{{\partial ^2}S_1^{**}\left( {L,G,H,l,g,h} \right) }}{{\partial l\partial H}}\left( {\frac{{\partial S_1^{**}}}{{\partial h'}}} \right) . \end{aligned} \end{aligned}$$
(57)
Furthermore, the osculating elements can be substituted into the last three terms, because these are second-order terms, so
$$\begin{aligned} \begin{aligned} \frac{{\partial S_1^{**}}}{{\partial l'}}&= \frac{{\partial S_1^{**}\left( {L,G,H,l,g,h} \right) }}{{\partial l}} - \frac{{{\partial ^2}S_1^{**}\left( {L,G,H,l,g,h} \right) }}{{\partial l\partial L}}\frac{{\partial S_1^{**}\left( {L,G,H,l,g,h} \right) }}{{\partial l}} \\&\quad -\, \frac{{{\partial ^2}S_1^{**}\left( {L,G,H,l,g,h} \right) }}{{\partial l\partial G}}\frac{{\partial S_1^{**}\left( {L,G,H,l,g,h} \right) }}{{\partial g}}\\&\quad -\, \frac{{{\partial ^2}S_1^{**}\left( {L,G,H,l,g,h} \right) }}{{\partial l\partial H}}\frac{{\partial S_1^{**}\left( {L,G,H,l,g,h} \right) }}{{\partial h}}. \end{aligned} \end{aligned}$$
(58)
Finally, \(\frac{{\partial S_1^{**}}}{{\partial l'}}\) can be expressed as
$$\begin{aligned} \frac{{\partial S_1^{**}}}{{\partial l'}} = \frac{{\partial S_1^{**}}}{{\partial l}}+{L_{O2M,c}} \end{aligned}$$
(59)
with
$$\begin{aligned} {L_{O2M,c}} = - \frac{{{\partial ^2}S_1^{**}}}{{\partial l\partial L}}\frac{{\partial S_1^{**}}}{{\partial l}} - \frac{{{\partial ^2}S_1^{**}}}{{\partial l\partial G}}\frac{{\partial S_1^{**}}}{{\partial g}} - \frac{{{\partial ^2}S_1^{**}}}{{\partial l\partial H}}\frac{{\partial S_1^{**}}}{{\partial h}}. \end{aligned}$$
(60)
Other correction terms can be determined in a similar way. Based on Eqs. (53), (54) and (60), the transformation from osculating elements to mean elements can be described as
$$\begin{aligned} \begin{aligned} L''&= L - {L_{sp2}} - {L_{mp1}} - {L_{mp2}} - {L_{O2M,c}},\quad l''= l - {l_{sp2}} - {l_{mp1}} - {l_{mp2}} - {l_{O2M,c}},\\ G''&= G - {G_{sp2}} - {G_{mp1}} - {G_{mp2}}- {G_{O2M,c}},\quad g''=g - {g_{sp2}} - {g_{mp1}} - {g_{mp2}}- {g_{O2M,c}} ,\\ H''&= H - {H_{sp2}} - {H_{mp1}} - {H_{mp2}}- {H_{O2M,c}},\quad h''= h - {h_{sp2}} - {h_{mp1}} - {h_{mp2}}- {h_{O2M,c}}, \end{aligned} \end{aligned}$$
(61)
where the correction terms are
$$\begin{aligned} \begin{aligned} {L_{O2M,c}}&= - \frac{{\partial ^2 S_1^{**}}}{{\partial l\partial L}}\frac{{\partial S_1^{**}}}{{\partial l}} - \frac{{\partial ^2 S_1^{**}}}{{\partial l\partial G}}\frac{{\partial S_1^{**}}}{{\partial g}} - \frac{{\partial ^2 S_1^{**}}}{{\partial l\partial H}}\frac{{\partial S_1^{**}}}{{\partial h}},\\ {G_{O2M,c}}&= - \frac{{\partial ^2 S_1^{**}}}{{\partial g\partial L}}\frac{{\partial S_1^{**}}}{{\partial l}} - \frac{{\partial ^2 S_1^{**}}}{{\partial g\partial G}}\frac{{\partial S_1^{**}}}{{\partial g}} - \frac{{\partial ^2 S_1^{**}}}{{\partial g\partial H}}\frac{{\partial S_1^{**}}}{{\partial h}},\\ {H_{O2M,c}}&= - \frac{{{\partial ^2}S_1^{**}}}{{\partial h\partial L}}\frac{{\partial S_1^{**}}}{{\partial l}} - \frac{{{\partial ^2}S_1^{**}}}{{\partial h\partial G}}\frac{{\partial S_1^{**}}}{{\partial g}} - \frac{{{\partial ^2}S_1^{**}}}{{\partial h\partial H}}\frac{{\partial S_1^{**}}}{{\partial h}},\\ {l_{O2M,c}}&= \frac{{{\partial ^2}S_1^{**}}}{{\partial L\partial L}}\frac{{\partial S_1^{**}}}{{\partial l}} + \frac{{{\partial ^2}S_1^{**}}}{{\partial L\partial G}}\frac{{\partial S_1^{**}}}{{\partial g}} + \frac{{{\partial ^2}S_1^{**}}}{{\partial L\partial H}}\frac{{\partial S_1^{**}}}{{\partial h}},\\ {g_{O2M,c}}&= \frac{{{\partial ^2}S_1^{**}}}{{\partial G\partial L}}\frac{{\partial S_1^{**}}}{{\partial l}} + \frac{{{\partial ^2}S_1^{**}}}{{\partial G\partial G}}\frac{{\partial S_1^{**}}}{{\partial g}} + \frac{{{\partial ^2}S_1^{**}}}{{\partial G\partial H}}\frac{{\partial S_1^{**}}}{{\partial h}},\\ {h_{O2M,c}}&= \frac{{{\partial ^2}S_1^{**}}}{{\partial H\partial L}}\frac{{\partial S_1^{**}}}{{\partial l}} + \frac{{{\partial ^2}S_1^{**}}}{{\partial H\partial G}}\frac{{\partial S_1^{**}}}{{\partial g}} + \frac{{{\partial ^2}S_1^{**}}}{{\partial H\partial H}}\frac{{\partial S_1^{**}}}{{\partial h}}. \end{aligned} \end{aligned}$$
(62)
The explicit expressions can be found in Appendix B (provided as an electronic supplement).
2.4 Equations of motion of an orbiter perturbed by a third body
In the previous section, the short-period and medium-period variations in the Hamiltonian were nullified in succession. The singly averaged and doubly averaged Hamiltonians were developed. In this section, the singly averaged and doubly averaged dynamic equations will be derived.
The singly averaged Hamiltonian \({{\mathcal {H}}^{*}}\) is
$$\begin{aligned} {{\mathcal {H}}^{*}} = - \frac{{{\mu ^2}}}{{2L{'^2}}}+{n_3}T' - \frac{{k{n_3}^2a{'^2}{a_3}^3}}{{4{r_3}^3}}\left[ {3{{\alpha '} ^2}\left( {4e{'^2} + 1} \right) - 3{{\beta '} ^2}\left( {e{'^2} - 1} \right) - 3e{'^2} - 2} \right] , \end{aligned}$$
(63)
and the doubly averaged Hamiltonian \({{\mathcal {H}}^{**}}\) is
$$\begin{aligned} \begin{aligned} {{\mathcal {H}}^{**}}&= - \frac{{{\mu ^2}}}{{2L'{'^2}}}\; + {n_3}T{''} - \frac{{k{n_3}^2{a{''}^2}}}{{128{{\left( {1 - {e_3}^2} \right) }^{3/2}}}}\left\{ {3{e{''}^2}\left\{ { -\, 40\cos i{''}{{\sin }^2}{i_3}\sin 2\omega {''} \sin 2\theta {''}} \right. } \right. \\&\quad +\, 4\sin 2i{''}\sin 2{i_3} \left( {3 - 5\cos 2\omega {''} } \right) \cos \theta {''} + 40\sin i{''}\sin 2{i_3}\sin 2\omega {''} \sin \theta {''} \\&\quad +\, {\sin ^2}{i_3}\cos 2\theta {''} \left[ {12{{\sin }^2}i{''}} \left. { + 10\left( {\cos 2i{''} + 3} \right) \cos 2\omega {''} } \right] + \left( {3\cos 2{i_3} + 1} \right) \right. \\&\quad \left. \times \,\left( {10{{\sin }^2}i{''}\cos 2\omega {''} + 3\cos 2i{''} + 1} \right) \right\} + 2\left[ {12{{\sin }^2}i{''}{{\sin }^2}{i_3}\cos 2\theta {''} }\right. \\&\quad \left. { \left. {+\, 12\sin 2i{''}\sin 2{i_3}\cos \theta {''} + \left( {3\cos 2i{''} + 1} \right) \left( {3\cos 2{i_3} + 1} \right) } \right] } \right\} , \end{aligned} \end{aligned}$$
(64)
so the singly averaged disturbing function is
$$\begin{aligned} {{\mathcal {R}}^{*}} = \frac{{k{n_3}^2a{'^2}{a_3}^3}}{{4{r_3}^3}}\left[ {3{{\alpha '} ^2}\left( {4e{'^2} + 1} \right) - 3{{\beta '} ^2}\left( {e{'^2} - 1} \right) - 3e{'^2} - 2} \right] , \end{aligned}$$
(65)
and the doubly averaged disturbing function is
$$\begin{aligned} \begin{aligned} {{\mathcal {R}}^{**}}&= \frac{{k{n_3}^2{a''^2}}}{{128{{\left( {1 - {e_3}^2} \right) }^{3/2}}}}\left\{ {3{e''^2}\left\{ { - 40\cos i''{{\sin }^2}{i_3}\sin 2\omega '' \sin 2\theta '' + 4\sin 2i''\sin 2{i_3}}\right. } \right. \\&\quad \times \left( {3 - 5\cos 2\omega '' } \right) \cos \theta '' + 40\sin i''\sin 2{i_3}\sin 2\omega '' \sin \theta '' + {\sin ^2}{i_3}\cos 2\theta '' \\&\quad {\left. \times \, \left[ {10\left( {\cos 2i'' + 3} \right) \cos 2\omega '' } \right. { + 12{{\sin }^2}i''} \right] + \left( {3\cos 2{i_3} + 1} \right) \left( {10{{\sin }^2}i''\cos 2\omega ''} \right. }\\&\quad \left. {\left. { +\, 3\cos 2i'' + 1} \right) } \right\} + 2\left[ {12{{\sin }^2}i''{{\sin }^2}{i_3}} {\left. { \times \cos 2\theta '' + 12\sin 2i''\sin 2{i_3}\cos \theta '' + } \right. } \right. \\&\quad \times \left. { \left. { ( {3\cos 2i'' + 1})\left( {3\cos 2{i_3} + 1} \right) } \right] } \right\} . \end{aligned} \end{aligned}$$
(66)
It is noticed that the singly averaged disturbing function \({{\mathcal {R}}^{*}}\) is identical to that in Liu et al. (2012), but the doubly averaged disturbing function is not. The difference results from the fact that Liu et al. (2012) averaged \((a_3^3/r_3^3)\), \(\alpha '^2\) and \(\beta '^2\) in the singly averaged disturbing function, shown in Eq. (65), separately. If we set zero inclination and eccentricity of the perturbing body, the third-body perturbation problem becomes similar to the model analyzed by Broucke (2003), and the derived doubly averaged disturbing function in Eq. (66) is changed into
$$\begin{aligned} {{\mathcal {R}}^{**}}{|_{{e_3} = 0,{i_3} = 0}} = \frac{{k{n_3}^2{a''^2}}}{{32}}\left[ {30{e''^2}{{\sin }^2}i''\cos 2\omega '' + \left( {9{e''^2} + 6} \right) \cos 2i'' + 3{e''^2} + 2} \right] , \end{aligned}$$
(67)
which is identical to the result in Broucke (2003). However, the doubly averaged disturbing function in Liu et al. (2012) becomes
$$\begin{aligned} \bar{\bar{{\mathcal {R}}}}{|_{{e_3} = 0,{i_3} = 0}} = \frac{{k{n_3}^2{a''^2}}}{{32}}\left[ {15{e''^2}(\cos 2i'' + 3)\cos 2\omega '' + \left( {9{e''^2} + 6} \right) \cos 2i'' + 3{e''^2} + 2} \right] . \end{aligned}$$
(68)
Compared with that in Broucke (2003), the error is
$$\begin{aligned} E_{\bar{\bar{{\mathcal {R}}}}{|_{{e_3} = 0,{i_3} = 0}}}=\frac{{15k{n_3}^2{a''^2}}}{8}{e''^2}{\cos ^2}i''\cos 2\omega ''. \end{aligned}$$
(69)
Based on the relationship between classical orbital elements and the Delaunay elements in Eqs. (11), the classical orbital elements can be determined by
$$\begin{aligned} a''&= \frac{{{L''^2}}}{\mu },\quad M'' = l'' , \end{aligned}$$
(70a)
$$\begin{aligned} e''&= \sqrt{1 - \frac{{{G''^2}}}{{{L''^2}}}}, \quad \omega '' = g'', \end{aligned}$$
(70b)
$$\begin{aligned} \cos i''&= \frac{H''}{G''} ,\quad \varOmega '' = h'' . \end{aligned}$$
(70c)
Taking the time derivative of Eqs. (70) yields
$$\begin{aligned} \dot{a}''&= \frac{{2L''}}{\mu }\dot{L}'' ,\quad \dot{M}'' = \dot{l}'' , \end{aligned}$$
(71a)
$$\begin{aligned} \dot{e}''&= \frac{{{G''^2}\dot{L}'' - G''L''\dot{G}''}}{{{L''^2}{\sqrt{{L''^2} - {G''^2}}}}} , \quad \dot{\omega }'' = \dot{g}'' , \end{aligned}$$
(71b)
$$\begin{aligned} \dot{i}''&= - \frac{{G''\dot{H}'' - H''\dot{G}''}}{{{G''^2}\sin i''}},\quad \dot{\varOmega }'' = \dot{h}'' . \end{aligned}$$
(71c)
Using Hamilton’s equations
$$\begin{aligned} \begin{aligned} {\dot{L''}}&= - \frac{{\partial {\mathcal {H}^{**}}}}{{\partial l''}} ,\quad {\dot{ G''}} = - \frac{{\partial {\mathcal {H}^{**}}}}{{\partial g''}} ,\quad {\dot{ H''}} = - \frac{{\partial {\mathcal {H}^{**}}}}{{\partial h''}},\\ {\dot{ l''}}&= \frac{{\partial {\mathcal {H}^{**}}}}{{\partial L''}} ,\quad {\dot{ g''}} = \frac{{\partial {\mathcal {H}^{**}}}}{{\partial G''}} ,\quad {\dot{ h''}} = \frac{{\partial {\mathcal {H}^{**}}}}{{\partial H''}}, \end{aligned} \end{aligned}$$
(72)
and
$$\begin{aligned} \frac{{\partial {{\mathcal {H}}^{**}}}}{{\partial L''}}&= \frac{{2{a''^{1/2}}}}{{{\mu ^{1/2}}}}\frac{{\partial {{\mathcal {H}}^{**}}}}{{\partial a''}} + \frac{1}{e''}\frac{{\left( {1 - {e''^2}} \right) }}{{\sqrt{\mu a''} }}\frac{{\partial {{\mathcal {H}}^{**}}}}{{\partial e''}} , \end{aligned}$$
(73a)
$$\begin{aligned} \frac{{\partial {{\mathcal {H}}^{**}}}}{{\partial G''}}&= - \frac{{\sqrt{1 - {e''^2}} }}{{\sqrt{\mu a''} e''}}\frac{{\partial {{\mathcal {H}}^{**}}}}{{\partial e''}} + \frac{{\cot i''}}{{\sqrt{\mu a''} \sqrt{1 - {e''^2}} }}\frac{{\partial {{\mathcal {H}}^{**}}}}{{\partial i''}},\end{aligned}$$
(73b)
$$\begin{aligned} \frac{{\partial {{\mathcal {H}}^{**}}}}{{\partial H}}&= - \frac{1}{{\sqrt{\mu a''} \sqrt{1 - {e''^2}} \sin i''}}\frac{{\partial {{\mathcal {H}}^{**}}}}{{\partial i''}}, \end{aligned}$$
(73c)
equations (71) can be written in terms of classical orbital elements as
$$\begin{aligned} \left\{ \begin{array}{l} \dot{a}'' =- \dfrac{{2\sqrt{a''} }}{{\sqrt{\mu }}}\dfrac{{\partial {\mathcal {H}}^{**}}}{{\partial M''}},\\ \dot{e}'' =\dfrac{{\left( {{e''^2} - 1} \right) }}{{\sqrt{\mu }\sqrt{a''} e}}\dfrac{{\partial {\mathcal {H}}^{**}}}{{\partial M''}} +\dfrac{{\sqrt{1 - {e''^2}} }}{{\sqrt{\mu }\sqrt{a''} e''}}\dfrac{{\partial {\mathcal {H}}^{**}}}{{\partial \omega '' }},\\ \dot{i}'' =\dfrac{{{1}}}{{\sqrt{\mu }\sqrt{a''}\sqrt{1 - {e''^2}} \sin i''}}\dfrac{{\partial {\mathcal {H}}^{**}}}{{\partial \varOmega '' }} - \dfrac{{\cot i''}}{{\sqrt{\mu }\sqrt{a''} \sqrt{1 - {e''^2}} }}\dfrac{{\partial {\mathcal {H}}^{**}}}{{\partial \omega '' }},\\ \dot{\varOmega }'' =- \dfrac{{{1}}}{{\sqrt{\mu }{\sqrt{a}}'' \sqrt{1 - {e''^2}} \sin i''}}\dfrac{{\partial {\mathcal {H}}^{**}}}{{\partial i''}},\\ \dot{\omega }'' =\dfrac{{\left( {{e''^2} - 1} \right) }}{{\sqrt{\mu } \sqrt{a''} \;e''\sqrt{1 - {e''^2}} }}\dfrac{{\partial {\mathcal {H}}^{**}}}{{\partial e''}} + \dfrac{{\cot i''}}{{\sqrt{\mu }\sqrt{a''} \sqrt{1 - {e''^2}} }}\dfrac{{\partial {\mathcal {H}}^{**}}}{{\partial i''}},\\ \dot{M}'' =\dfrac{{\left( {1 - {e''^2}} \right) }}{{\sqrt{\mu }\sqrt{a''} e''}}\dfrac{{\partial {\mathcal {H}}^{**}}}{{\partial e''}} + \dfrac{{2\sqrt{a''} }}{{\sqrt{\mu }}}\dfrac{{\partial {\mathcal {H}}^{**}}}{{\partial a''}}. \end{array} \right. \end{aligned}$$
(74)
Finally, substituting the singly averaged Hamiltonian of Eqs. (63) into Eqs. (74) results in the singly averaged orbit dynamics,
$$\begin{aligned} \dot{a}'&= 0 , \end{aligned}$$
(75a)
$$\begin{aligned} \dot{e}'&= - \frac{{15k{n_3}^2{a'^{3/2}}e'\sqrt{1 - {e'^2}} {{\left( {1 + {e_3}\cos {f_3}} \right) }^3}}}{{4{\mu ^{1/2}}{{\left( {1 - e_3^2} \right) }^3}}}\left\{ {2\cos 2\omega ' (\cos {i_3}\sin \theta ' \sin {u_3}} \right. \nonumber \\&\quad +\, \cos \theta ' \cos {u_3})\left[ {\cos i'(\cos {i_3}\cos \theta ' \sin {u_3} - \sin \theta ' \cos {u_3}) + \sin i'\sin {i_3}\sin {u_3}} \right] \nonumber \\&\quad -\, \sin 2\omega ' \left[ {\cos {u_3}(\cos i'\sin \theta ' + \cos \theta ' ) - \sin {u_3}\left( {\cos i'\cos {i_3}\cos \theta ' + \sin i'\sin {i_3}} \right. } \right. \nonumber \\&\quad \left. {\left. { -\, \cos {i_3}\sin \theta ' } \right) } \right] \left[ {\sin {u_3}\left( {\cos {i_3}(\cos i'\cos \theta ' + \sin \theta ') + \sin i'\sin {i_3}} \right) } \right. \nonumber \\&\quad \left. {\left. { +\, \cos {u_3}(\cos \theta ' - \cos i'\sin \theta ' )} \right] } \right\} , \end{aligned}$$
(75b)
$$\begin{aligned} \dot{i} '&= \frac{{3k{n_3}^2{a'^{3/2}}{{\left( {1 + {e_3}\cos {f_3}} \right) }^3}}}{{2{\mu ^{1/2}}\sqrt{1 - {e'^2}} {{\left( {1 - e_3^2} \right) }^3}}}\left[ {\sin {u_3}\left( {\cos i'\sin {i_3} - \sin i'\cos {i_3}\cos \theta ' } \right) } \right. \nonumber \\&\quad \left. { +\, \sin i'\sin \theta ' \cos {u_3}} \right] \left\{ {5{e'^2}\sin \omega ' \cos \omega ' \left[ {\cos i'(\cos {i_3}\cos \theta ' \sin {u_3} - \sin \theta ' \cos {u_3})} \right. } \right. \nonumber \\&\quad \left. { +\, \sin i'\sin {i_3}\sin {u_3}} \right] + \left[ {\left( {4{e'^2} + 1} \right) {{\cos }^2}\omega ' - \left( {{e'^2} - 1} \right) {{\sin }^2}\omega ' } \right] \nonumber \\&\quad \left. { \times \, (\cos {i_3}\sin \theta ' \sin {u_3} + \cos \theta ' \cos {u_3})} \right\} , \end{aligned}$$
(75c)
$$\begin{aligned} \dot{\varOmega }'&= \frac{{3k{n_3}^2{a'^{3/2}}\sin i'{{\left( {1 + {e_3}\cos {f_3}} \right) }^3}}}{{2{\mu ^{1/2}}\sqrt{1 - {e'^2}} {{\left( {1 - e_3^2} \right) }^3}}}\left[ {\sin {u_3}(\cot i'\sin {i_3} - \cos {i_3}\cos \theta ' ) + \sin \theta ' \cos {u_3}} \right] \nonumber \\&\qquad \left\{ {\left[ {\left( {{e'^2} - 1} \right) {{\cos }^2}\omega ' - \left( {4{e'^2} + 1} \right) {{\sin }^2}\omega ' } \right] \left[ {\cot i'\sin \theta ' \cos {u_3} - \sin {u_3}(\cot i'\cos {i_3}} \right. } \right. \nonumber \\&\quad \left. {\left. { \times \,\cos \theta ' + \sin {i_3})} \right] + 5{e'^2}\csc i'\sin \omega ' \cos \omega ' \left( {\cos {i_3}\sin \theta ' \sin {u_3} + \cos \theta ' \cos {u_3}} \right) } \right\} , \end{aligned}$$
(75d)
$$\begin{aligned} \dot{\omega }'&=\frac{{kn_3^2{a'^{3/2}}{{\left( {1 + {e_3}\cos {f_3}} \right) }^3}}}{{4{\mu ^{1/2}}\sqrt{1 - {e'^2}} {{\left( {1 - e_3^2} \right) }^3}}}\left\{ {6\left( {1 - {e'^2}} \right) \left\{ { - 1 - \left[ {\sin {u_3}(\cos {i_3}\sin \omega '\sin \theta ' - \sin i'} \right. } \right. } \right. \nonumber \\&\quad \times \, \sin {i_3}\cos \omega ' ) + \cos \theta ' (\sin \omega ' \cos {u_3} - \cos i'\cos {i_3}\cos \omega ' \sin {u_3}) + \cos i' \nonumber \\&\quad {\left. { \times \, \cos \omega ' \sin \theta ' \cos {u_3}} \right] ^2} + 4\left[ {\cos \omega ' (\cos {i_3}\sin \theta ' \sin {u_3} + \cos \theta ' \cos {u_3})} \right. \nonumber \\&\quad \left. {{{\left. {+\,\sin \omega ' \left( {\cos i'(\cos {i_3}\cos \theta ' \sin {u_3} - \sin \theta ' \cos {u_3}) + \sin i'\sin {i_3}\sin {u_3}} \right) } \right] }^2}} \right\} \nonumber \\&\quad -\, 6\cot i'\left[ {\sin {u_3}\left( {\cos i'\sin {i_3} - \sin i'\cos {i_3}\cos \theta ' } \right) + \sin i'\sin \theta ' \cos {u_3}} \right] \nonumber \\&\quad \times \,\left\{ {\left[ {\left( {4{e'^2} + 1} \right) {{\sin }^2}\omega ' - \left( {{e'^2} - 1} \right) {{\cos }^2}\omega ' } \right] \left[ {\cos i'(\cos {i_3}\cos \theta ' \sin {u_3} - \sin \theta ' \cos {u_3})} \right. } \right. \nonumber \\&\quad \left. {\left. {\left. { +\, \sin i'\sin {i_3}\sin {u_3}} \right] + 5{e'^2}\sin \omega ' \cos \omega ' \left( {\cos {i_3}\sin \theta ' \sin {u_3} + \cos \theta ' \cos {u_3}} \right) } \right\} } \right\} , \end{aligned}$$
(75e)
$$\begin{aligned} \dot{M}'&= \frac{{{\mu ^{1/2}}}}{{{a'^{3/2}}}} + \frac{{kn_3^2{a'^{3/2}}{{\left( {1 + {e_3}\cos {f_3}} \right) }^3}}}{{4{\mu ^{1/2}}{{\left( {1 - e_3^2} \right) }^3}}}\left\{ {6\left( {{e'^2} - 1} \right) \left[ {\cos i'\cos \omega ' \sin \theta ' \cos {u_3}} \right. } \right. \nonumber \\&\quad +\, \sin {u_3}(\cos {i_3}\sin \omega ' \sin \theta ' - \sin i'\sin {i_3}\cos \omega ' ) + \cos \theta ' (\sin \omega ' \cos {u_3} \nonumber \\&\quad {\left. { -\, \cos i'\cos {i_3}\cos \omega ' \sin {u_3})} \right] ^2} - 12\left( {3 + 2{e'^2}} \right) \left[ {\sin \omega ' \left( {\cos i'(\cos {i_3}\cos \theta ' } \right. } \right. \nonumber \\&\quad \left. {\left. { \times \, \sin {u_3} - \sin \theta ' \cos {u_3}) + \sin i'\sin {i_3}\sin {u_3}} \right) + \cos \omega ' (\cos {i_3}\sin \theta ' \sin {u_3}} \right. \nonumber \\&\quad \left. {{{\left. { +\, \cos \theta ' \cos {u_3})} \right] }^2} + 6{e'^2} + 14} \right\} . \end{aligned}$$
(75f)
Similarly, the doubly averaged orbit dynamics are
$$\begin{aligned} \dot{a}''&= 0 , \end{aligned}$$
(76a)
$$\begin{aligned} \dot{e}''&= \frac{{15k{n_3}^2{a''^{3/2}}e''\sqrt{1 - {e''^2}} }}{{32{\mu ^{1/2}}{{\left( {1 - {e_3}^2} \right) }^{3/2}}}}\left\{ {(\cos 2i'' + 3){{\sin }^2}{i_3}\sin 2\omega '' \cos 2\theta '' + 4\cos i''{{\sin }^2}{i_3}} \right. \nonumber \\&\quad \times \, \cos 2\omega '' \sin 2\theta '' - 4\sin i''\sin 2{i_3}\cos 2\omega '' \sin \theta '' - 2\sin 2i''\sin 2{i_3}\sin 2\omega '' \cos \theta '' \nonumber \\&\quad \left. { +\, {{\sin }^2}i''(3\cos 2{i_3} + 1)\sin 2\omega '' } \right\} , \end{aligned}$$
(76b)
$$\begin{aligned} \dot{i}''&=- \frac{{15k{n_3}^2{a''^{3/2}}{e''^2}\cot i''}}{{32{\mu ^{1/2}}\sqrt{1 - {e''^2}} {{\left( {1 - {e_3}^2} \right) }^{3/2}}}}\left\{ {\sin 2\omega '' \left[ {(\cos 2i'' + 3){{\sin }^2}{i_3}\cos 2\theta '' } \right. } \right. \nonumber \\&\quad \left. { -\, 2\sin 2i''\sin 2{i_3}\cos \theta ''} \right] + 4\cos i''{\sin ^2}{i_3}\cos 2\omega '' \sin 2\theta '' \nonumber \\&\quad \left. { -\, 4\sin i''\sin 2{i_3}\cos 2\omega '' \sin \theta '' + {{\sin }^2}i''(3\cos 2{i_3} + 1)\sin 2\omega '' } \right\} , \end{aligned}$$
(76c)
$$\begin{aligned} \dot{\varOmega }''&=\frac{{3k{n_3}^2{a''^{3/2}}}}{{64{\mu ^{1/2}}\sqrt{1 - {e''^2}} {{\left( {1 - {e_3}^2} \right) }^{3/2}}}}\left\{ {\cos i''\left( {5{e''^2}\cos 2\omega '' - 3{e''^2} - 2} \right) \left[ {\cos (2{i_3} - 2\theta '' )} \right. } \right. \nonumber \\&\quad \left. { +\, \cos (2{i_3}+2\theta '') + 6\cos 2{i_3} - 2\cos 2\theta '' + 2} \right] + 4\left[ {5{e''^2}\sin 2\omega '' \left( {\cot i''\sin 2{i_3}\sin \theta '' } \right. } \right. \nonumber \\&\quad \left. {\left. {\left. { +\, {{\sin }^2}{i_3}\sin 2\theta '' } \right) - \cos 2i''\csc i''\sin 2{i_3}\cos \theta '' \left( {5{e''^2}\cos 2\omega '' - 3{e''^2} - 2} \right) } \right] } \right\} , \end{aligned}$$
(76d)
$$\begin{aligned} \dot{\omega }''&=- \frac{{3k{n_3}^2{a''^{3/2}}}}{{64{\mu ^{1/2}}\sqrt{1 - {e''^2}} {{\left( {1 - {e_3}^2} \right) }^{3/2}}}}\left\{ {2{{\sin }^2}{i_3}\cos 2\theta '' \left[ {5\left( {2{e''^2} - 3} \right) \cos 2\omega ''} \right. } \right. \nonumber \\&\quad +\, 6{e''^2} \left. { + 10\cos 2i''{{\sin }^2}\omega '' - 1} \right] - 20\left( {{e''^2} - 2} \right) \cos i''{\sin ^2}{i_3}\sin 2\omega '' \sin 2\theta '' \nonumber \\&\quad +\, 2\cot i''\sin 2{i_3} \cos \theta '' \left[ {20\cos 2i''{{\sin }^2}\omega '' - 2\left( {{e''^2} - 1} \right) (5\cos 2\omega '' - 3)} \right] \nonumber \\&\quad -\, 10\csc i''\sin 2{i_3}\sin 2\omega '' \sin \theta '' \left[ {\left( {{e''^2} - 2} \right) \cos 2i'' - 3{e''^2} + 2} \right] \nonumber \\&\quad +\, 5(3\cos 2{i_3} + 1)\cos 2\omega '' \left( {2{e''^2} + \cos 2i'' - 1} \right) { - 3\cos 2{i_3} }\nonumber \\&\quad \left. { \times \, \left( {2{e''^2} + 5\cos 2i'' + 2} \right) - 2{e''^2} - 5\cos 2i'' - 3\cos 2{i_3} - 3} \right\} , \end{aligned}$$
(76e)
$$\begin{aligned} \dot{M}''&= \frac{{{\mu ^{1/2}}}}{{{a''^{3/2}}}}- \frac{{{a''^{3/2}}k{n_3}^2}}{{64{\mu ^{1/2}}{{\left( {1 - {e_3}^2} \right) }^{3/2}}}}\left\{ {120\left( {{e''^2} + 1} \right) \sin i''\sin 2{i_3}\sin 2\omega '' \sin \theta '' } \right. \nonumber \\&\quad +\, 3{\sin ^2}{i_3}\cos 2\theta '' \left[ {10\left( {{e''^2} + 1} \right) (\cos 2i'' + 3)\cos 2\omega '' + 4\left( {3{e''^2} + 7} \right) {{\sin }^2}i''} \right] \nonumber \\&\quad -\, 120\left( {{e''^2} + 1} \right) \cos i''{\sin ^2}{i_3}\sin 2\omega '' \sin 2\theta '' + 12\sin 2i''\sin 2{i_3}\cos \theta '' \nonumber \\&\quad \times \, \left[ { - 5\left( {{e''^2} + 1} \right) \cos 2\omega '' + 3{e''^2} + 7} \right] + (3\cos 2{i_3} + 1) \nonumber \\&\quad \left. { \times \, \left[ {30\left( {{e''^2} + 1} \right) {{\sin }^2}i''\cos 2\omega '' + \left( {3{e''^2} + 7} \right) (3\cos 2i'' + 1)} \right] } \right\} . \end{aligned}$$
(76f)
When the third body is in a circular equatorial orbit (\(e_3=0\), \(i_3=0\) ), the dynamics become
$$\begin{aligned} \left\{ \begin{array}{l} \dot{a}'' =0,\\ \dot{e}'' =\dfrac{{15k{n_3}^2{a''^{3/2}}}}{{8{\mu ^{1/2}}}}e''\sqrt{1 - {e''^2}} {\sin ^2}i''\sin 2\omega '' ,\\ \dot{i}'' =- \dfrac{{15kn_3^2{a''^{3/2}}}}{{16{\mu ^{1/2}}}}\dfrac{{{e''^2}}}{{\sqrt{1 - {e''^2}} }}\sin 2i''\sin 2\omega '' ,\\ \dot{\varOmega }'' =\dfrac{{3kn_3^2{a''^{3/2}}}}{{8{\mu ^{1/2}}\sqrt{1 - {e''^2}} }}\left( {5{e''^2}\cos 2\omega '' - 3{e''^2} - 2} \right) \cos i'',\\ \dot{\omega }'' = \dfrac{{3kn_3^2{a''^{3/2}}}}{{8{\mu ^{1/2}}\sqrt{1 - {e''^2}} }}\left[ {\left( {5{{\cos }^2}i'' - 1 + {e''^2}} \right) + 5\left( {1 - {e''^2} - {{\cos }^2}i''} \right) \cos 2\omega '' } \right] ,\\ \dot{M}'' = \dfrac{{{\mu ^{1/2}}}}{{{a''^{3/2}}}} - \dfrac{{kn_3^2{a''^{3/2}}}}{{8{\mu ^{1/2}}}}\left[ {\left( {3{e''^2} + 7} \right) \left( {3{{\cos }^2}i'' - 1} \right) + 15(1 + {e''^2}){{\sin }^2}i''\cos 2\omega '' } \right] , \end{array} \right. \end{aligned}$$
(77)
which is in accordance with the results shown in Broucke (2003). Comparing Eq. (76) with Eq. (77), the third body’s eccentricity only introduces a factor \(1/(1-e_3^2)^{3/2}\) in the evolution rate of the orbital elements. However, the inclination of the third body is coupled with other orbital elements, especially the right ascension of the ascending node, which does not appear in Eq. (77). A comparison of the different dynamical models will be described in the next section.