1 Introduction, equations of motion

In the restricted two-body problem (R2BP), the equations of motion describe the dynamics of a sufficiently small satellite m under the action of gravitational force effected by one large celestial body MSun (m <  < MSun). The small mass m is supposed to move (as first approximation) inside the restricted region of space near the mass MSun [1] without influencing the position of large celestial body MSun even in anywhat negligible extent (but outside the Roche’s limit [2] which is, as first approximation, not less than 7–10 RSun where RSun is the radius of the celestial body MSun). In case of Newtonian type of gravitational forces, there is a well-known analytical solution to the aforementioned problem (which has been associated earlier with Kepler’s type of orbital motions both for the satellite and large celestial body around their common barycenter if we consider m < MSun, instead of case m <  < MSun). It is also known from classical works that if a large celestial body MSun is in a fixed position in the problem under consideration or is moving with constant velocity (i.e., its motion can be referred with respect to the inertial frame), the aforeformulated problem should have the similar Kepler-type solution. Therefore, the main aim of this research concerns the investigation of a case more complicated than classical one regarding the existence of an analytical solution in non-inertial case of R2BP where \(\{ V_{{ 1}} (t) , V_{{ 2}} (t)\}\) are the components of observable variable velocity \(\vec{V}\) of central body MSun which is supposed to be moving all the time in one and the same fixed direction (in a plane of mutual orbiting m and MSun) with variable velocity under restriction (V1/V2) = const.

The problem of two bodies represents the core of celestial mechanical studies, as well as the starting point to strengthen our understanding of the n-body problem.

It is worth noting that there are a large number of both long-established and recent fundamental works concerning analytical generalization of the R2BP equations to the case of three, four or even many bodies, which should be mentioned accordingly (see among works [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,20]). We should especially emphasize the theory of orbits, which was developed in profound work [3] by V. Szebehely for the case of the circular restricted problem of three bodies (CR3BP) (primaries are rotating around their common center of mass on circular orbits) as well as the case of the elliptic restricted problem of three bodies [4,5,6] (ER3BP, primaries are rotating around barycenter on elliptic orbits) and four bodies [7,8,9] (ER4BP, in various configurations).

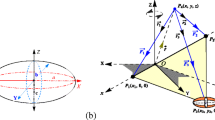
Let us consider here and below a non-rotating and non-inertial cartesian coordinate system with the origin O located at the chosen initial moment t in the center of mass of celestial body MSun which moves straight forward in one and the same fixed direction (without rotation, in a plane of mutual orbiting m and MSun) with velocity \(\vec{V}\) mentioned above under restriction to the components \((V_1/V_2) = \) const. Since transformation of velocity field \(\vec{v}\) from inertial coordinate system to the non-inertial frame of cartesian coordinate system \(\vec{r}\) = {x, y, z} is expressed as follows (see page 166 in &39 from book [10]; here below \(\vec{\Omega }\) is pseudo-vector of the constant angular rotation)

$$ \begin{aligned}\vec{v}_{\text{inertial}}& = \vec{v}_{\text{non-inertial}}+\vec{V} + \vec{\Omega } \times \vec{r},\quad \Rightarrow \hfill \\ \left( {\frac{{d \vec{v}_{\text{inertial}} }}{\text{d} t}} \right)_{\text{inertial}} &=\left( {\frac{{d \vec{v}_{\text{non-inertial}} }}{\text{d} t}} \right)_{\text{non-inertial}} + \frac{{\text{d} \vec{V} }}{\text{d} t} + 2 \vec{\Omega } \times \vec{v}_{\text{non-inertial}} + \vec{\Omega } \times (\vec{\Omega } \times \vec{r}) ,\end{aligned} $$
(1)

therefore, with the help of (1) thus far the dynamical equations of motion for small mass m with the absence of rotation \(\vec{\Omega } = \vec{0}\) can be written in a well-known form as below (see page 166 in &39 from book [10]):

$$\left\{ \begin{array}{ll}\frac{{\text{d}^{{ 2}} x}}{{\text{d} t^{ 2} }} + \frac{{\text{d} V_{{ 1}} }}{\text{d} t} = - \frac{\partial U}{{\partial x}} , \hfill \\ \frac{{\text{d}^{{ 2}} y}}{{\text{d} t^{ 2} }} + \frac{{\text{d} V_{{ 2}} }}{\text{d} t} = - \frac{\partial U}{{\partial y}} , \hfill \\ \end{array} \right.$$
(2)

where U is the potential function which should be determined as \(U = - \frac{\mu }{R} ,\quad R = \sqrt {(x + \int {V_{{ 1}} \text{d} t} )^{{ 2}} + (y + \int {V_{{ 2}} \text{d} t} )^{{ 2}} }\) (whereas \(\{ V_{{ 1}} (t), V_{{ 2}} (t)\}\) are the components of observable velocity of central body MSun motion, (V1/V2) = const) instead of a classical potential function \(U = - \frac{\mu }{R} ,\quad R = \sqrt {x^{{ 2}} + y^{{ 2}} }\) for Kepler’s formulation of R2BP (here below and above, μ = const = (m/MSun) is the gravitational mass parameter in appropriate scale). Let us remark that partial derivatives in the right parts of Eq. (2) should not be changed since expressions for \(\{ V_{{ 1}} (t), V_{{ 2}} (t)\}\) do not contain variables {x, y} but depend only on time t. Initial conditions are as follows (dot indicates (d/d t) in (3)):

$$\left\{ \begin{array} {ll}x(0) = 1 ,\, \ y(0) = 1 , \hfill \\ \dot{x}(0) = \varepsilon = \text{const}\, (\varepsilon \sim 0) ,\quad \hfill \\ \dot{y}(0) = \sqrt {1 - (\dot{x}(0))^{{ 2}} } \hfill \\ \end{array} \right\}$$
(3)

As for the generalization of the R2BP equations, let us mention that among works [12,13,14,15,16] various approaches were presented in detail.

2 Solving procedure for the system of Eq. (2) with initial data (3)

Let us transform system (2) by the change of variables \(X = x + \int {V_{{ 1}} \text{d} t} ,\quad Y = y + \int {V_{{ 2}} \text{d} t}\)

$$\left\{ \begin{array}{ll} \quad \frac{{\text{d}^{{ 2}} X}}{{\text{d} t^{ 2} }} = - \frac{{\mu X}}{{\left( {X^{{ 2}} + Y^{{ 2}} } \right)^{{ \frac{3}{2}}} }} , \hfill \\ \frac{{\text{d}^{{ 2}} Y}}{{\text{d} t^{ 2} }} = - \frac{{\mu Y}}{{\left( {X^{{ 2}} + Y^{{ 2}} } \right)^{{ \frac{3}{2}}} }} . \hfill \\ \end{array} \right.$$
(4)

Let us further transform system (4) by the change of variables X = r⋅cosφ, Y = r⋅sinφ to the polar coordinates {r = r(t), φ = φ(t)}, r = \(R = \sqrt {X^{{ 2}} + Y^{{ 2}} }\), as below

$$ \begin{aligned}&\left( {\frac{\text{d} X}{{\text{d} t}}} \right) = r^{\prime}\cos \phi - r\sin \phi \phi^{\prime},\quad \quad \left( {\frac{\text{d} Y}{{\text{d} t}}} \right) = r^{\prime}\sin \phi + r\cos \phi \phi^{\prime} , \\& \frac{{\text{d}^{{ 2}} X}}{{\text{d} t^{{ 2}} }} = r^{\prime\prime}\cos \phi - 2r^{\prime}\sin \phi \phi^{\prime} - r\cos \phi (\phi^{\prime})^{{ 2}} - r\sin \phi \phi^{\prime\prime} , \\& \left( {\frac{{\text{d}^{{ 2}} Y}}{{\text{d} t^{{ 2}} }}} \right) = r^{\prime\prime}\sin \phi + 2r^{\prime}\cos \phi \phi^{\prime} - r\sin \phi (\phi^{\prime})^{{ 2}} + r\cos \phi \phi^{\prime\prime} ,\Rightarrow\\ &\left\{ \begin{array}{ll} r^{\prime\prime}\cos \phi - 2r^{\prime}\sin \phi \phi^{\prime} - r\cos \phi (\phi^{\prime})^{{ 2}} - r\sin \phi \phi^{\prime\prime} = - \frac{{\mu \cos \phi }}{{r^{{ 2}} }} , \hfill \\ r^{\prime\prime}\sin \phi + 2r^{\prime}\cos \phi \phi^{\prime} - r\sin \phi (\phi^{\prime})^{{ 2}} + r\cos \phi \phi^{\prime\prime} = - \frac{{\mu \sin \phi }}{{r^{{ 2}} }} . \hfill \\ \end{array} \right.\end{aligned}$$
(5)

As the first step, let us multiply the first equation of the last system (5) onto cosφ, second onto sinφ, then sum the resulting equations one to the other:

$$ r^{\prime\prime} - r(\phi^{\prime})^{{ 2}} = - \frac{\mu }{{r^{{ 2}} }}\quad \Rightarrow \quad (r \cdot (\phi^{\prime}))^{{ 2}} = r \cdot r^{\prime\prime} + \frac{\mu }{r}$$
(6)

As the second step, let us multiply the first equation of the last system onto sinφ, second onto cosφ, then subtract the resulting equations one from the other:

$$\begin{aligned} &- 2r^{\prime}\phi^{\prime} - r\phi^{\prime\prime} = 0\quad \Rightarrow \quad - \frac{{2r^{\prime}}}{r} = \frac{{\phi^{\prime\prime}}}{{\phi^{\prime}}}\quad \Rightarrow \quad - \frac{2 d r}{r} = \frac{{d (\phi^{\prime})}}{{\phi^{\prime}}} \hfill \\ \quad \hfill \\ &\quad\Rightarrow \ln \left( {\frac{{r_{{ 0}}^{2} }}{{r^{{ 2}} }}} \right) = \ln \left( {\frac{{\phi^{\prime}_{{}} }}{{\phi^{\prime}_{{ 0}} }}} \right)\quad \Rightarrow \quad \phi^{\prime} = \phi^{\prime}_{{ 0}} \cdot \left( {\frac{{r_{{ 0}}^{2} }}{{r^{{ 2}} }}} \right)\end{aligned}$$
(7)

Taking into account (7), we could obtain from (6) as follows

$$ \begin{aligned} &r \cdot r^{\prime\prime} - \frac{{(\phi^{\prime}_{{ 0}} )^{{ 2}} \cdot r_{{ 0}}^{4} }}{{r^{{ 2}} }} + \frac{\mu }{r} = 0\quad \Rightarrow \quad \left\{ {\begin{array}{*{20}l} {} \\ {} \\ \end{array} \frac{d r}{{\text{d} t}} = r^{\prime} \equiv p(r) \Rightarrow r^{\prime\prime} = \frac{d p}{{d r}} \cdot p\begin{array}{*{20}c} {} \\ {} \\ \end{array} } \right\} \\ &\quad \Rightarrow \quad r \cdot \frac{d p}{{d r}} \cdot p - \frac{{(\phi^{\prime}_{{ 0}} )^{{ 2}} \cdot r_{{ 0}}^{4} }}{{r^{{ 2}} }} + \frac{\mu }{r} = 0\quad \Rightarrow \quad \frac{1}{2}\frac{{d (p^{{ 2}} )}}{d r} = \frac{{(\phi^{\prime}_{{ 0}} )^{{ 2}} \cdot r_{{ 0}}^{4} }}{{r^{{ 3}} }} - \frac{\mu }{{r^{{ 2}} }} \\ &\qquad (p^{{ 2}} - (r^{\prime}_{ 0} )^{{ 2}} ) = 2(\phi^{\prime}_{{ 0}} )^{{ 2}} \cdot r_{{ 0}}^{4} \cdot ( - \frac{1}{2}) \cdot \left( {\frac{1}{{r^{{ 2}} }} - \frac{1}{{r_{ 0}^{ 2} }}} \right) + 2\mu \left( {\frac{1}{r} - \frac{1}{{r_{ 0}^{{}} }}} \right)\quad \Rightarrow \hfill \\ \end{aligned} $$

then further after having obtained the quadrature in the left part of Eq. (8) (by appropriate approximation technique or, e.g., by series of Taylor expansions)

$$ \begin{aligned} p &= \frac{\text{d} r}{{\text{d} t}} = \sqrt {(r^{\prime}_{ 0} )^{{ 2}} + 2(\phi^{\prime}_{{ 0}} )^{{ 2}} \cdot r_{{ 0}}^{4} \cdot ( - \frac{1}{2}) \cdot \left( {\frac{1}{{r^{{ 2}} }} - \frac{1}{{r_{ 0}^{ 2} }}} \right) + 2\mu \left( {\frac{1}{r} - \frac{1}{{r_{ 0}^{{}} }}} \right)} \quad \Rightarrow \\ & \quad \int {\frac{d r}{{\sqrt {(r^{\prime}_{ 0} )^{{ 2}} - (\phi^{\prime}_{{ 0}} )^{{ 2}} \cdot r_{{ 0}}^{4} \cdot \left( {\frac{1}{{r^{{ 2}} }} - \frac{1}{{r_{ 0}^{ 2} }}} \right) + 2\mu \left( {\frac{1}{r} - \frac{1}{{r_{ 0}^{{}} }}} \right)} }}} = \pm \int {\text{d} t} \\ &\qquad \left\{ {(r^{\prime}_{ 0} )^{{ 2}} - (\phi^{\prime}_{{ 0}} )^{{ 2}} \cdot r_{{ 0}}^{4} \cdot \left( {\frac{1}{{R^{{ 2}} }} - \frac{1}{{r_{ 0}^{ 2} }}} \right) + 2\mu \left( {\frac{1}{R} - \frac{1}{{r_{ 0}^{{}} }}} \right) > 0} \right\} \end{aligned} $$
(8)

we should find then the re-inverse dependence r = r(t) (but since the power of polynomial under the sign of square root is greater than 2, the left part of (8) presents the appropriate elliptic integral). Then, afterwards, we could obtain angle φ by direct integration procedure, using (7).

3 Discussion

As we can see from the derivation above, equations of motion (1) are proven to be very hard to solve analytically. Nevertheless, we have succeeded in obtaining analytical formulae for the components of the solution (6)–(8) in the polar coordinates {r(t), φ(t)}. Let us clarify that while transforming Eq. (5) by virtue of special change of variables, we have taken into account that independent variable (time t) is not included in the left and nor right part of system (5). Therefore, we have reduced this ordinary differential equation of 2nd order (6) by an elegant change of variables \(\left\{ {\begin{array}{*{20}l} \frac{\text{d} r}{{\text{d} t}} = r^{\prime} \equiv p(r) \Rightarrow r^{\prime\prime} = \frac{\text{d} p}{{\text{d} r}} \cdot p \end{array} } \right\}\) to the 1st order differential equation. Then, having solved the equation with regard to function p(t), we should solve ODE with regard to \(p = \frac{\text{d} r}{{\text{d} t}} = \sqrt {(r^{\prime}_{ 0} )^{{ 2}} - (\phi^{\prime}_{{ 0}} )^{{ 2}} \cdot r_{{ 0}}^{4} \cdot \left( {\frac{1}{{r^{{ 2}} }} - \frac{1}{{r_{ 0}^{ 2} }}} \right) + 2\mu \left( {\frac{1}{r} - \frac{1}{{r_{ 0} }}} \right)}\) in order to obtain the final result.

To conclude, let us highlight how to transform components of solution (6)-(8) from polar back → to cartesian coordinates (including the initial conditions in general form). Quadrature (8) determines the dependence in general form t = t(r), which contains the elliptic integral in the left part of (8) {under appropriate initial conditions; the upper limit of integral equals to r, low limit equals to r0}, the right part of the quadrature (8) equals to (t–t0). We should re-inverse this expression into dependence r = r(t), which can be obtained by numerical methods only (by appropriate approximation technique or, e.g., by series of Taylor expansions).

Having obtained the dependence r = r(t) from (8), we can then obtain from formula (7) the dependence (9) for φ = φ(t):

$$\phi = \phi_{{ 0}} + \phi^{\prime}_{{ 0}} \cdot \int\limits_{{t_{{ 0}} }}^{t} {\left( {\frac{{r_{{ 0}}^{2} }}{{r^{{ 2}} (t)}}} \right) \text{d} t}$$
(9)

Let us also recall that the change of variables X = r⋅cosφ, Y = r⋅sinφ has been used for transformation of system (4). This means that the transformation of initial coordinates should be done as pointed out in (10)–(12) below:

$$\begin{aligned}& r_{{ 0}}^{{}} = \sqrt {X_{{ 0}}^{2} + Y_{{ 0}}^{2} } ,\quad \phi_{{ 0}}^{{}} = \arccos \left( {\frac{{X_{{ 0}}^{{}} }}{{\sqrt {X_{{ 0}}^{2} + Y_{{ 0}}^{2} } }}} \right) ,\\ &\left\{ { \left( {\frac{\text{d} X}{{\text{d} t}}} \right) = r^{\prime}\cos \phi - r\sin \phi \phi^{\prime},\quad \left( {\frac{\text{d} Y}{{\text{d} t}}} \right) = r^{\prime}\sin \phi + r\cos \phi \phi^{\prime} } \right\} \\& \end{aligned}$$
(10)
$$\begin{aligned}&\Rightarrow 1)\quad r^{\prime} = \left( {\frac{d X}{{\text{d} t}}} \right)\cos \phi + \left( {\frac{d Y}{{\text{d} t}}} \right)\sin \phi \quad \Rightarrow \\ &\quad r^{\prime}_{ 0} = \left( {\frac{d X}{{\text{d} t}}} \right)_{{ 0}} \cdot \left( {\frac{{X_{{ 0}}^{{}} }}{{\sqrt {X_{{ 0}}^{2} + Y_{{ 0}}^{2} } }}} \right) + \left( {\frac{d Y}{{\text{d} t}}} \right)_{{ 0}} \sin \left( {\arccos \left( {\frac{{X_{{ 0}}^{{}} }}{{\sqrt {X_{{ 0}}^{2} + Y_{{ 0}}^{2} } }}} \right)} \right) \end{aligned}$$
(11)
$$\begin{aligned}& 2)\quad \left( {\frac{d Y}{{\text{d} t}}} \right)\cos \phi - \left( {\frac{d X}{{\text{d} t}}} \right)\sin \phi = r\phi^{\prime}\quad \Rightarrow \\ &\quad \phi^{\prime}_{{ 0}} = \frac{{\left( {\frac{d Y}{{\text{d} t}}} \right)_{{ 0}} \left( {\frac{{X_{{ 0}}^{{}} }}{{\sqrt {X_{{ 0}}^{2} + Y_{{ 0}}^{2} } }}} \right) - \left( {\frac{d X}{{\text{d} t}}} \right)_{{ 0}} \sin \left( {\arccos \left( {\frac{{X_{{ 0}}^{{}} }}{{\sqrt {X_{{ 0}}^{2} + Y_{{ 0}}^{2} } }}} \right)} \right)}}{{\sqrt {X_{{ 0}}^{2} + Y_{{ 0}}^{2} } }} \end{aligned}$$
(12)

It would be also useful to discuss the possibility of considering the next generalization (in theoretical sense) of non-inertial coordinate system in (1): namely, the case of rotation with constant angular velocity of non-inertial coordinate system, in addition to obvious case of motion with variable in time velocity in one and the same fixed direction in three dimensions (when all three components of velocity are linearly dependent: \((V_1/V_2) = C_1 = const, (V_2/V_3) = C_2 = const\)). Works [18, 19] present a procedure for solving a type (1) equation for the case of rotation with constant angular velocity of non-inertial coordinate system (where \(\left( {\frac{{\text{d} \vec{r}}}{\text{d} t}} \right) = \vec{v}_{\text{non-inertial}}\))

$$ \left( {\frac{{\text{d} \vec{r}}}{\text{d} t}} \right) + \vec{\Omega } \times \vec{r} = (\vec{v}_{\text{inertial}} - \vec{V}) $$

which can be considered as being solved if we had solved the corresponding homogeneous variant of the related differential equation of the 1st order

$$ \left( {\frac{{\text{d} \vec{r}}}{\text{d} t}} \right) + \vec{\Omega } \times \vec{r} = \vec{0} $$

The latter problem was fully solved and discussed accordingly in detail in works [18, 19] (see also all related references therein in regard to this theoretical question which is beyond the topic discussed in the current research).

4 Conclusion

In this paper, we have presented a new type of the solving procedure to obtain the coordinates of the infinitesimal mass m which moves around the primary MSun (m <  < MSun) for a special kind of restricted two-body problem, where MSun moves in one and the same fixed direction (in a plane of mutual orbiting m and MSun) with variable velocity \(\vec{V} = \{ V_{{ 1}} (t) , V_{{ 2}} (t)\}\), with modified potential function \(U = - \frac{\mu }{R} ,\quad R = \sqrt {(x + \int {V_{{ 1}} \text{d} t} )^{{ 2}} + (y + \int {V_{{ 2}} \text{d} t})^{{ 2}} }\) (where \(\{ V_{{ 1}} , V_{{ 2}} \}\) are the components of observable variable velocity of central body MSun motion whereas (V1/V2) = const) instead of the classical potential function \(U = - \frac{\mu }{R} ,\quad R = \sqrt {x^{{ 2}} + y^{{ 2}} }\) for Kepler’s formulation of R2BP. Meanwhile, the system of equations of motion has been successfully explored with respect to the existence of analytical way for presentation of the solution in polar coordinates \(X = x + \int {V_{{ 1}} \text{d} t} = r \cos \phi\), \(Y = y + \int {V_{{ 2}} \text{d} t} = r \sin \phi\), r = R.

We have obtained analytical formula (8) for function t = t(r). Having obtained the re-inverse dependence r = r(t), we can then obtain the dependence φ = φ(t) via formula (7). Also, we have pointed out how to express components of solution (including initial conditions) from cartesian to polar coordinates in general form (11)–(12). Finally, we should note that such a restricted two-body problem (i.e., non-inertial R2BP in case of variable velocity \(\vec{V}\) of central body motion in a prescribed fixed direction) is found to be realistic for practical application in the real astophysical problems. Namely, when binary system (where large celestial body MSun is the leading Primary Mover) is moving with observable but variable velocity \(\vec{V} = \{ V_{{1}} (t) , V_{{2}} (t)\}\)(whereas (V1/V2) = const) toward another star system [11], such system will nevertheless keep Kepler-type motion of secondary body m <  < MSun around primary body MSun.

It is worth comparing the obtained solution with already known result via a new numerical solution calculated with help of aforepresented algorithm as follows: let us assume case \(\vec{V} = \vec{0}\) to calculate classical Kepler solution (Fig. 1), where restriction in (1)-(2) for the components of velocity is assumed to be presented as \(V_{1} = const*V_{2}\) whereas \(V_{1}, V_{2} = {0, 0}\).

Fig. 1
figure 1

Periodic results of numerical calculations for radius of orbit of planetoid R(t) in Eq. (8) for classical Kepler solution at \(\vec{V} = \vec{0}\) (from perigee at \(R_{ \min } \cong 0.1\) to apogee at \(R_{ \max } \cong 3.3\)), here restriction in (1)-(2) for the components of velocity is assumed to be presented as \(V_{1} = const* V_{2}\)where \(V_{1}, V_{2} = {0, 0}\)

Full size image

We have compared results of calculating R(t) in Eq. (8) for with those calculated with the help of (4), taking into account that \(R = \sqrt {X^{{ 2}} + Y^{{ 2}} }\)(see Figs. 2, 3 and 4): they are completely coincide for all possible variety of initial values.

Fig. 2
figure 2

Periodic results of numerical calculations for coordinate X(t) in Eq. (4) with initial conditions (3) for classical Kepler solution at \(\vec{V} = \vec{0}\), here restriction in (1)-(2) for the components of velocity is assumed to be presented as \(V_{1} = const* V_{2}\) where \(V_{1}, V_{2} = {0, 0}\)

Full size image
Fig. 3
figure 3

Periodic results of numerical calculations for coordinate Y(t) in Eq. (4) with initial conditions (3) for classical Kepler solution at \(\vec{V} = \vec{0}\), here restriction in (1)-(2) for the components of velocity is assumed to be presented as V1 = const*V2 where {V1, V2} = {0, 0}

Full size image
Fig. 4
figure 4

Periodic results of numerical calculations for dependence Y(X) in Eq. (4) with initial conditions (3) yield stable orbits with high eccentricity (for classical Kepler solution at \(\vec{V} = \vec{0}\)), here restriction in (1)-(2) for the components of velocity is assumed to be presented as V1 = const*V2 where {V1, V2} = {0, 0}

Full size image

It is worth also to remark that it would be realistic to assume that the components of velocity \(\vec{V} = \{ V_{{ 1}} (t) , V_{{ 2}} (t)\}\) are to be a functions which are linearly dependent on time t (with a small and restricted values of accelerations or deceleration for both of them); in this case, initial values for cartesian variables \(X = x + \int {V_{{ 1}} \text{d} t} ,\quad Y = y + \int {V_{{ 2}} \text{d} t}\) are equal to those presented in (3).

In this premise, let us also compare the already constructed above solution (see Figs. 1, 2, 3 and 4) with respect to the numerical solution (obtained with help of algorithm presented above, see (8)–(9)) in case \(\vec{V} = \{ V_{{ 1}} (t) , V_{{ 2}} (t)\} = 10^{{ - 2}} \cdot \{ (1 - a_{{ 1}} t), (1 - a_{{ 2}} t)\}\) where \(\{ a_{{ 1}} (t), a_{{ 2}} (t)\} = \{ 0.003 [m \cdot s^{ - 2} ], 0.003 [m \cdot s^{ - 2} ]\}\) (Figs. 5, 6, 7 and 8).

Fig. 5
figure 5

Periodic results of numerical calculations for coordinate x(t), \(x = X - \int {V_{{ 1}} \text{d} t}\) where X stems from Eq. (4) with initial conditions (3) for solution where \(\vec{V} = \{ V_{{ 1}} (t) , V_{{ 2}} (t)\} = 10^{{ - 2}} \cdot \{ (1 - a_{{ 1}} t), (1 - a_{{ 2}} t)\}\)(whereas a1 = a2)

Full size image
Fig. 6
figure 6

Periodic results of numerical calculations for coordinate y(t), \(y = Y - \int {V_{{ 2}} \text{d} t}\) where Y stems from Eq. (4) with initial conditions (3) for solution where \(\vec{V} = \{ V_{{ 1}} (t) , V_{{ 2}} (t)\} = 10^{{ - 2}} \cdot \{ (1 - a_{{ 1}} t), (1 - a_{{ 2}} t)\}\) (whereas a1 = a2)

Full size image
Fig. 7
figure 7

Periodic results of numerical calculations for plot y(x), \(x = X - \int {V_{{ 1}} \text{d} t} , y = Y - \int {V_{{ 2}} \text{d} t}\) where {X, Y} stem from Eq. (4) with initial conditions (3) for solution where \(\vec{V} = \{ V_{{ 1}} (t) , V_{{ 2}} (t)\} = 10^{{ - 2}} \cdot \{ (1 - a_{{ 1}} t), (1 - a_{{ 2}} t)\}\) (whereas a1 = a2)

Full size image
Fig. 8
figure 8

Periodic results of numerical calculations for radius of orbit of planetoid \(R_{ abs} = \sqrt {x^{{ 2}} + y^{{ 2}} }\) for solution where \(\vec{V} = \{ V_{{ 1}} (t) , V_{{ 2}} (t)\} = 10^{{ - 2}} \cdot \{ (1 - a_{{ 1}} t), (1 - a_{{ 2}} t)\}\) with \(\{ a_{{ 1}} (t), a_{{ 2}} (t)\} = \{ 0.003 [m \cdot s^{ - 2} ], 0.003 [m \cdot s^{ - 2} ]\}\).

Full size image

Let us also mention works among [21,22,23,24,25,26,27,28], where refs [21,22,23,24,25,26,26] are within the framework of the analytical approach to the study of mathematical models in applications to various nonlinear problems in electrodynamics, mechanics or dynamics of rigid body rotation.