1 Introduction

Porous media concept naturally occurs in a number of areas of applied science and engineering such as filtration, mechanics, petroleum engineering, construction engineering, hydrogeology, geophysics, biology, biophysics, material science, etc. Porous structures reduce the waveloads and wave run-up, and they are found to be very useful in the construction of floating airports, bridges, piers, docks, wave power conversion system, etc. Vertical circular cylinders are found to be more appropriate for use in the construction of coastal and offshore structures. The objective here is focused on designing marine structures that can resist various adverse atmospheric conditions. Therefore, investigation in the area of hydrodynamics has laid special emphasis on developing an optimized system in order to find a way to avoid significant hydrodynamic impacts.

For designing marine structures, it is very important to consider a number of appropriate atmospheric conditions and then propose a precise prediction of hydrodynamic impact with the structures. Therefore, of late, one focal point of research has specifically been to optimize a system/structure to avoid significant adverse hydrodynamic impacts. A concept that has gained attention is the use of porous structures which, through the pores on its surface, can contribute immensely in reducing the influence of wave-body interaction. At current time, many countries have been exploring the possibility of extracting offshore wind energy as an alternative and reliable source of non-conventional energy. For instance, South Korea has initiated one such project to check the feasibility of extracting and utilizing offshore wind energy [12]. The main goal of our present work is to find a suitable mean to reduce wave impact for which use of porous structures is seen as a possible remedy.

Calisal and Subancu [5] investigated hydrodynamic coefficients for vertical composite circular cylinders at finite water depth using matching technique through the continuity of pressure and normal velocity at the separation of surfaces. They also discussed the limiting value of the added mass for zero frequency. Yeung [33] investigated a set of data for added mass and wave damping for a floating circular cylinder in finite depth water. He calculated added mass and damping coefficients for heave, sway, and roll motions as well as the coupling coefficients for sway and roll motions. Bhatta [2] elaborated a boundary value problem for heave motion due to a vertical circular cylinder in water of finite depth. Potentials were derived by the separation of variables method and he discussed various effects of draft and radius on added mass and damping coefficient. Black et al. [3] explored the variational formulation of Schwinger [11] for water wave problems which was found to be extensively used for a discontinuous wave. They also discussed total scattering cross-section, for each of bottom and surface cylinders of circular plane. Berggren and Johansson [4] presented hydrodynamic coefficients of a circular wave energy device consisting of a buoy connected to a submerged circular plate. They used matched eigenfunction expansions method for calculating unknown coefficients. Narrow space analysis was elaborated in their investigation and a good agreement was observed with energy relations. Williams and Abul-Azm [27] considered an array of floating circular cylinders and examined the hydrodynamic interactions between the members which occurred when any member underwent prescribed forced oscillations. They calculated added mass and damping coefficient for 2–6 cylinders which led to the important result that, for certain parameter combinations, the effect of neighboring bodies on the total wave field produced values of the hydrodynamic coefficients on individual members which showed significant deviation from those for an isolated cylinder. While considering the heave oscillations of a submerged vertical cylinder, McIver and Evans [17] observed an interesting occurrence of negative added mass. They discussed the effect of free surface for the occurrence of negative added mass. They found that added mass became negative when the depth of submergence was small and free surface effects were remarkable. Williams and Li [28] investigated hydrodynamic forces and coefficients for a freely floating compound cylinder consisting of a surface-piercing cylindrical column resting on a larger, concentric cylindrical base. For certain parameter combinations, negative surge/sway added mass coefficients were observed. The numerical results for the hydrodynamic quantities were verified by the linear radiation/diffraction program UHWAVE. Linear wave interaction with a wave energy device comprising of two coaxial vertical circular cylinders of different radii was investigated by Wu et al. [31]. They established that, at low frequencies, a relatively larger radius of the submerged cylinder had a significant influence on the hydrodynamic coefficients and exciting forces/moments.

Jiang et al. [13] considered the motion of a submerged vertical cylinder in finite water depth and observed that added mass tended to increase corresponding to a reduction in water depth, whereas radiation damping was observed to be quite insensitive to any variation in depth. Yu et al. [32] described a semi-analytical method for examining wave radiation by a truncated cylinder of arbitrary cross-section. They mainly discussed added mass and damping coefficients for four types of cross-sections, namely, circular, cosine, elliptical, and quasi-elliptical. They also investigated the effect of draft of the cylinder on wave radiation. A hybrid integral equation method was developed by Yeung and Wang [34] for finding added mass, damping coefficients, and exciting forces for a spar-like structure. They explored the corresponding heave motion of the structure along with the motion of the internal free surface under incident wave excitation. Bhatta and Rahman [1] considered the scattering and radiation aspects for a floating solid cylinder in finite depth. They calculated the wave loading by decomposing the total velocity potential into four: one scattered potential and three radiated potentials. For convenience, they split the fluid domain into interior and exterior regions in order to derive the velocity potentials.

Now we discuss some significant works related to scattering and damping arising out of linear water wave interaction with porous structures. For modeling a wave-induced flow in any porous medium, the model that has found the maximum attention is probably the one devised by Sollitt and Cross [25]. In this model, two important aspects are consideration of dissipation of wave energy inside a porous medium, and evaluation of the linearized friction term f by using Lorentz Principle and an iterative procedure. Chwang [7] described a porous wave-maker theory by which the hydrodynamic pressure distribution as well as the total force on the wave-maker were investigated. Further, he established the significance of both wave effect and porous effect parameters. Darwiche et al. [8] investigated wave interaction with a semi-porous cylindrical breakwater and they derived a very important result that the wave force acting on the structure reduced due the semi-porous region of the cylinder. Adopting the familiar eigenfunction expansion method, Williams and Li [29] investigated water wave interaction with an array of surface-piercing bottom-mounted porous cylinders and they evaluated the corresponding hydrodynamic forces. Williams et al. [30] carried out an extension of the previous problem by considering water wave interaction with a floating porous cylinder. They concluded that the porosity, the size, and the location of the porous region had considerable effect on the hydrodynamic forces. Sahoo et al. [20] took up the problem of scattering of oblique incident surface waves by porous vertical barriers in finite depth. They studied the problem for four different types of barriers and made the observation that the finite angle of incidence and the porosity of the barriers had a paramount role in reducing the reflection of the incident waves.

Park et al. [18] discussed the wave exciting forces acting on an array of floating porous circular cylinders while considering the diffraction problem. To calculate the wave forces, the fluid domain was divided into three regions, namely, a single exterior region (only water), N interior regions (inner part of the porous cylinders) and another N regions consisting of the bottom faces of the porous cylinders. They investigated the wave exciting forces due to different modes of motions on an array of truncated porous circular cylinders for various numbers of the porous circular cylinders and various values of angles of the incident wave and porosity of the circular cylinders. Zhao et al. [36] discussed water wave interaction with a porous cylinder containing an inner horizontal porous plate which acted as an obstruction to render wave dissipation more effective. They carried out a series of model tests in a basin in order to compare the theoretical works and computed works. They found that an increase in porosity reduced the wave exciting forces and the efficiency of wave dissipation. Zhao et al. [37] further developed theoretical and experimental studies on the interaction of water waves with a truncated circular cylinder. The cylinder, which was partly made of porous materials, comprised of a porous sidewall and an impermeable bottom. They observed that the phenomenon of the sloshing mode that occurred at a certain wavenumber had an impact on the breakwaters. They also found that the damping coefficient consisted of two parts: in addition to the component of conventional wave radiation damping, there did exist a second component caused by porosity. Based on linear water wave theory, Zhao et al. [38] carried out theoretical as well as experimental investigations on the interaction between waves and an array of porous circular cylinders with or without an inner porous plate. Each cylinder in the array was partly made of porous materials and it specifically consisted of a porous sidewall and an impermeable bottom. In addition, an inner porous plate was fixed horizontally inside the cylinders. They mainly discussed the hydrodynamic coefficients and wave elevation, and studied the role of the draft of the cylinders, the location of the inner porous plate, and the spacing between adjacent cylinders. Park and Koo [19] discussed interaction of water waves with partially porous-surfaced circular cylinders comprising of a porous-surfaced body near the free surface and an impermeable-surfaced body with an end-capped rigid bottom below the porous region. They calculated wave exciting forces and wave run-up for different various porous-portion ratios and wave conditions.

Mandal et al. [16] discussed the hydroelastic analysis of gravity wave interaction with a system of concentric porous and flexible cylinders in which the inner cylinder was considered to be rigid, while the outer cylinder was considered as porous and flexible. They mainly investigated three cases, namely, (a) surface-piercing truncated cylinders, (b) bottom-touching truncated cylinders, and (c) completely submerged cylinders extended from the free surface to the sea-bed. They also analyzed the effects of porosity and flexibility of the outer cylinder in attenuating the hydrodynamic forces and dynamic overturning moments for different cylindrical configurations and wave characteristics. Das and Bora [9] considered a vertical porous structure placed on an elevated impermeable sea-bed and discussed wave reflection by considering two types of bottom topography in the form of a 2-step and a p-step bottoms. Higher values of the reflection coefficient were observed corresponding to lower values of porosity. Das and Bora [10] further investigated oblique linear wave damping by a vertical porous structure placed on a multi-step bottom topography in which the following cases were considered: (i) a solid vertical wall placed at a finite distance from the porous structure and (ii) an unbounded water medium after the porous structure. By using the separation of variables technique, Sarkar and Bora [22] evaluated hydrodynamic forces arising out of water wave interaction with a surface-piercing bottom-mounted compound porous cylinder. It was found that variation in values in parameters such as radius, draft, and porosity had an immense effect on both hydrodynamic loads and wave run-up. In a similar manner, by considering wave interaction with a floating compound porous cylinder in finite depth, Sarkar and Bora [23] evaluated the hydrodynamic load—the behavior of which was observed to be steady in the lower frequency. However, significant fluctuations were observed due to occurrence of resonance in the neighborhood of a specific frequency. Sarkar and Bora [24] further investigated diffraction of ocean waves by a specific type of cylinders, namely, a floating surface-piercing truncated partial-porous cylinder and then a surface-piercing bottom-mounted truncated partial-porous cylinder, by treating both cases separately. Numerical experiments were carried out in order to analyze the impact of various parameters such as porous coefficients, draft ratio, the ratio of inner and outer radii, the water depth on the quantities such as hydrodynamic force, moment, and wave run-up.

This article describes an investigation carried out on radiation of a floating surface-piercing semi-porous compound cylinder in water of finite depth. Since all motions are not very significant, we discuss only two translational motions in the x- and z-directions, i.e., surge and heave motions, respectively. We split the region into four and find the respective potentials by utilizing the given conditions. For accomplishing this, suitable matching conditions, due to continuity of pressure and velocity, along the vertical boundaries are applied to derive and solve a system of linear equations. Evaluation of those radiated potentials allows us to calculate the hydrodynamic coefficients, namely, added mass and damping coefficients, due to the motion of the structure. These coefficients play a crucial role for a structure in motion, however, small it may be. Added mass and damping coefficient for surge and heave motions are obtained for different values of radii, draft, porosity, and depth ratios. This mathematical model can be considered as an extension of a number of the earlier works, e.g., Kokkinowrachos et al. [14] and Calisal and Subancu [5], in which porosity in the structure was not taken into account. It is strongly felt that the use of porous structures to reduce wave loads is more appropriate than non-porous structures. This motivates us to consider a semi-porous compound cylinder and determine the surge and heave hydrodynamic coefficients. Subsequently, the effect of porosity and other parameters on the hydrodynamic coefficients is demonstrated through various graphs. To the best of our knowledge, work on radiation by such kind of composite cylinders has not been accomplished by anyone earlier. To sum it up, the model developed here establishes that corresponding to certain combination of the wave and structure parameters, it is possible to reduce the wave loads on the structure under consideration. It is expected that this structure and the associated model are likely to show a new direction in tackling such ocean engineering problems involving porosity of the structure. Obtained results are compared with available ones the outcome of which points to an excellent agreement which confirms the effectiveness of the present model.

2 Mathematical formulation

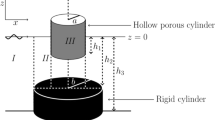
It is known that a rigid floating structure in ocean can undergo six degrees of freedom: three translational motions in the x-, y-, and z-directions known as surge, sway, and heave, respectively, and three rotational motions about x-, y-, and z-axes known as roll, pitch, and yaw, respectively. Considering the fluid to be incompressible, homogenous, and inviscid, and the motion irrotational, a train of waves of small amplitude is assumed to be incident on a vertical floating surface-piercing semi-porous compound cylinder with its porous region having a porous coefficient G. The upper surface and the lower surface of the lower cylinder are located at \({z=-h_1}\) and \({z=-h_2}\), respectively, where the z-axis is considered vertically upwards (Fig. 1). Here we plan to discuss surge and heave radiation by the cylinder for a wave of amplitude H incident on it where the finite depth of water is \({h_3}\). Let a and \({b(>a)}\), respectively, be the radii of inner and outer cylinders. Taking cylindrical coordinate system \({(r,\theta,z)}\) and due to physical considerations and convenience, we consider the following four regions: Region I \({(r\ge b, -h_3\le z\le 0)}\); Region II \((a \le r \le b, -h_1 \le z \le 0)\); Region III \((a \le r \le b, -h_2 \le z \le -h_1)\), and Region IV \((0 \le r \le b, -h_3 \le z \le -h_2)\). Further, we introduce the velocity potentials \({\varPhi _j(r, \theta, z, t)}\) as \({\varPhi_j(r, \theta, z, t)}\) = \(\text{ Re }{[\phi _j(r, \theta, z)\exp {(-\mathrm{i}\sigma t)}]}\) with \({\phi _j,\;j=1,2,3,4}\) referring to the potentials in Regions I, II, III, and IV, respectively, where \({\sigma}\) is the angular wave frequency, \({\mathrm{i}}=\sqrt{-1}\) the usual imaginary quantity, and \({\text{ Re }}\) denotes the real part of [.].

Fig. 1
figure 1

Floating surface-piercing semi-porous compound cylinder

Full size image

Each potential \({\phi _j,\;j=1,2,3,4,}\) satisfies Laplace’s equation in respective flow regions:

$${\nabla ^{2} \phi _{j} = 0,\;j = 1,2,3,4.}$$
(1)

Subsequently, the boundary conditions on the free surface \({z=0}\) and the sea-bed \({z=-h_3}\) can be written as

$$\begin{aligned} \frac{\partial \phi _j}{\partial z}-\frac{\sigma ^2}{g}\phi _j= & {} 0; \quad z=0,\quad j= 1,2, \end{aligned}$$
(2)
$$\begin{aligned} \frac{\partial \phi _1}{\partial z}= & {} 0;\quad z=-h_3,\quad r>b, \end{aligned}$$
(3)
$$\begin{aligned} \frac{\partial \phi _4}{\partial z}= & {} 0; \quad z=-h_3, \quad 0<r<b, \end{aligned}$$
(4)

where g represents the usual acceleration due to gravity. The boundary conditions on the moving solid surface \({(S_s)}\) and porous surface \({(S_p)}\) of the structure are given by Williams et al. [30] as

$$\begin{aligned} \frac{\partial \phi }{\partial n}= & {} \mathbf {v}.\mathbf {n} \quad \text{ on } \quad S_s, \end{aligned}$$
(5)
$$\begin{aligned} \frac{\partial \phi }{\partial n}= & {} \mathbf {v}.\mathbf {n}-w(r,\theta,z)\quad \text{ on } \quad S_p, \end{aligned}$$
(6)

where \({\mathbf {v}}\) is the structural velocity, \({\mathbf {n}}\) is the outward normal to the surface \({(S_s\; \text{ or } \;S_p})\). and \({w(r, \theta, z)}\) is the spatial component of the normal velocity \({W(r, \theta, z,t)}\) of the fluid passing through the semi-porous cylinder from the exterior region to the interior region with \({W(r, \theta, z,t)}\) given by

$${W(r,\theta,z,t) = {\text{Re }}[w(r,\theta ,z)\exp ( - {\text{i}}\sigma t)].}$$
(7)

The fluid flow through the porous walls obeys Darcy’s law. Therefore, the flow velocity is linearly proportional to the pressure difference across the boundary of the porous cylinder as can be seen from Taylor [26]. The hydrodynamic pressure \({P(r, \theta, z, t)}\)= \({\text{Re }}[p(r,\theta,z)\exp ( - {\text{i}}\sigma t)]\) at any point in the fluid domain can be deduced from the linearized Bernoulli’s equation as \({p={\mathrm{i}} \rho \sigma \phi},\) where \({\rho}\) is the fluid density. Therefore, the boundary condition at the porous wall \({r=b}\) can be written as [15]

$$\begin{aligned} w(r, \theta, z)=\frac{L \mathrm{i} \rho \sigma }{\varepsilon }(\phi _1-\phi _3) =\mathrm{i} k_0 G(\phi _1- \phi _3), \end{aligned}$$
(8)

where \({\varepsilon}\) is the coefficient of dynamic viscosity, \({k_0}\) is the incident wavenumber, L a coefficient having the dimension of length, and \({\phi _1}\) and \({\phi _3}\), respectively, are the velocity potentials in the fluid region \({r>b}\) and porous region \({b<r<a}\). Some more information about this porous coefficient G is detailed in Appendix.

Furthermore, the radiated velocity potential in the exterior region satisfies the Sommerfeld radiation condition in the following form:

$$\begin{aligned} \lim _{r\rightarrow \infty }\sqrt{r}\left[ \frac{\partial \varPsi _{\text{ rad },1}^{m}}{\partial r}-\mathrm{i} k_0\varPsi _{\text{ rad },1}^{m}\right] =0,\; \text{ for }\; m=1,2, \end{aligned}$$
(9)

where \({\varPsi _{\text{ rad },1}^{m}}\) is the radiated potential in the m-th mode in Region I. On the porous cylinder surface \({r=b}\), the potentials satisfy the following matching conditions:

$$\begin{aligned} \phi _1= & {} \phi _2;\quad r=b,\quad -h_1<z<0, \end{aligned}$$
(10)
$$\begin{aligned} \frac{\partial \phi _1}{\partial r}= & {} \frac{\partial \phi _2}{\partial r};\quad r=b,\quad -h_1<z<0,\end{aligned}$$
(11)
$$\begin{aligned} \frac{\partial \phi _1}{\partial r}= & {} \frac{\partial \phi _3}{\partial r};\quad r=b,\quad -h_2<z<-h_1,\end{aligned}$$
(12)
$$\begin{aligned} \phi _1= & {} \phi _4;\quad r=b,\quad -h_3<z<-h_2,\end{aligned}$$
(13)
$$\begin{aligned} \frac{\partial \phi _1}{\partial r}= & {} \frac{\partial \phi _4}{\partial r};\quad r=b,\quad -h_3<z<-h_2. \end{aligned}$$
(14)

3 Radiated potentials in the sub-domains

The total velocity potential can be decomposed into incident and radiated components as follows:

$$\begin{aligned} \phi _j=\delta _j\phi _{\text{ inc }}+\sum _{m=1}^{2} \eta _m \varPsi _{\text{ rad },j}^{m}, \end{aligned}$$
(15)

where \({\delta _1=1}\) and \({\delta _j=0}\), for \({j=2,3,4}\), \({\eta _m}\) is the structural displacement in the m-th mode and \({\varPsi _{\text{ rad },j}^{m}}\) is the radiation potential in the m-th mode in the j-th region. The radiation modes are numbered in such a way that \({m=1,2}\) correspond to surge and heave motions, respectively. The incident potential is given by

$$\begin{aligned} \phi _{\text{ inc }}= & {} -\frac{\mathrm{i} gH}{\omega }\frac{\cosh k_0(z+h_3)}{\cosh k_0h_3}\sum _{n=0}^{\infty } \tau _n J_n(k_0r)\cos n\theta, \nonumber \\ \text{ with }\nonumber \\ \tau _n= & {} {\left\{ \begin{array}{ll} 1 \quad n=0, \\ 2 \mathrm{i}^n \quad n\ge 1, \end{array}\right. } \end{aligned}$$
(16)

where \({J_n(k_0r)}\) denotes Bessel function of first kind of order n. Using eigenfunction expansion method, as in Calisal and Subancu [5], the radiated velocity potential in Region I takes the following form:

$$\begin{aligned} \varPsi _{\text{ rad }, 1}^m(r, \theta , z)= \sum _{j=0}^{\infty }A_{j}^m\cos k_j(z+h_3)T_j^{m}(k_jr)\cos \nu \theta , \end{aligned}$$
(17)

where \({\nu =1}\) for \({m=1}\) and \({\nu =0}\) for \({m=2}\), and \({A_{j}^m}\) are the undetermined coefficients. The wavenumbers \({k_j}\) \({(j=0,1,2,3,\ldots )}\) can be derived from the following dispersion relation by using the technique devised by Chamberlain and Porter [6]:

$$\begin{aligned} \sigma ^2= {\left\{ \begin{array}{ll} gk_j\tanh k_jh_3; \quad j=0,\\ -gk_j\tan k_jh_3;\quad j\ge 1. \end{array}\right. } \end{aligned}$$

The radial eigenfunctions \({T_j^{m}(k_jr)}\) have the following form:

$$\begin{aligned} T_j^{m}(k_jr)= {\left\{ \begin{array}{ll} \frac{H_{\nu }^{(1)}(k_jr)}{H_{\nu }^{(1)'}(k_jb)};\quad j=0,\\ \frac{K_{\nu }(k_jr)}{K_{\nu }'(k_jb)};\quad j \ge 1.\\ \end{array}\right. } \end{aligned}$$

Here \({H_{\nu }^{(1)}(k_jr)}\) is the Hankel function of first kind (or Bessel function of third kind) of order \({\nu}\) and \({K_\nu (k_jr)}\) the modified Bessel function of second kind of order \({\nu}\). The radiated velocity potential in Region II satisfying the structural boundary conditions is given by (Wu et al. [31])

$$\begin{aligned}&\varPsi _{\text{ rad },2}^m(r,\theta ,z)=\sum _{j=0}^{\infty }[\{(B_{j}^m S_j^{m}(\lambda _jr)+C_{j}^m R_j^{m}(\lambda _jr))\nonumber \\&\quad \cos \lambda _j(z+h_1)\}+\varPi _{2}^m]\cos \nu \theta , \end{aligned}$$
(18)

where \({B_{j}^m}\) and \({C_{j}^m}\) are the undetermined coefficients and \({\varPi _2^m}\) represents the particular solution due to the dependent mode. \({\lambda _j}\) are obtained from the following expression:

$$\begin{aligned} \sigma ^2= {\left\{ \begin{array}{ll} g\lambda _j\tanh \lambda _jh_1;\quad j=0,\\ -g\lambda _j\tan \lambda _jh_1;\quad j \ge 1. \end{array}\right. } \end{aligned}$$

The radial eigenfunctions \({S_j^{m}(\lambda _jr)}\) and \({R_j^{m}(\lambda _jr)}\) have the following forms:

$$\begin{aligned} S_j^{m}(\lambda _jr)= & {} {\left\{ \begin{array}{ll} \frac{H_{\nu }^{(1)}(\lambda _jr)}{H_{\nu }^{(1)'}(\lambda _jb)};\quad j=0, \\ \frac{I_{\nu }(\lambda _jr)}{I_{\nu }'(\lambda _jb)};\quad j \ge 1, \end{array}\right. }\nonumber \\ R_j^{m}(\lambda _jr)= & {} {\left\{ \begin{array}{ll} \frac{H_{\nu }^{(2)}(\lambda _jr)}{H_{\nu }^{(2)'}(\lambda _jb)};\quad j=0,\\ \frac{K_{\nu }(\lambda _jr)}{K_{\nu }'(\lambda _jb)};\quad j \ge 1, \end{array}\right. } \end{aligned}$$

for \({m=1,2},\) where \({H_{\nu }^{(2)}(\lambda _jr)}\) is the Hankel function of second kind of order \({\nu}\) and \({I_\nu (\lambda _jr)}\) the modified Bessel function of first kind of order \({\nu}\).

The term \({\varPi _{2}^m}\) appearing in Eq. (18) has a very important role in permitting the radiated potentials to satisfy the otherwise difficult non-homogeneous boundary conditions on the body surface. In Region II, the particular solutions \({\varPi _{2}^m}\) are given as follows:

$$\begin{aligned} \varPi _{2}^1= & {} 0, \end{aligned}$$
(19)
$$\begin{aligned} \varPi _{2}^2= & {} z+\frac{g}{\sigma ^2} . \end{aligned}$$
(20)

The suitable expression for the radiated potential in Region III satisfying structural boundary conditions is (Wu et al. [31])

$$\begin{aligned} \varPsi _{\text{ rad },3}^m(r,\theta ,z)= & {} \sum _{j=0}^{\infty }[\{(D_{j}^m V_j^{m}(\mu _jr)+E_{j}^m W_j^{m}(\mu _jr))\nonumber \\&\cos \mu _j(z+h_2)\}+\varPi _{3}^m]\cos \nu \theta , \end{aligned}$$
(21)

where \({D_{j}^m}\) and \({E_{j}^m}\) are the undetermined coefficients, and \({\mu _j}\) are obtained from the following:

$$\begin{aligned} \mu _j=\frac{\pi j}{h_2-h_1}, \quad j=0,1,2,\ldots . \end{aligned}$$

The radial eigenfunctions \({V_j^{m}(\mu _jr)}\) and \({W_j^{m}(\mu _jr)}\) have the following forms:

$$\begin{aligned} V_j^{m}(\mu _jr)= & {} {\left\{ \begin{array}{ll} \frac{r^{-\nu }}{b^{-\nu -1}};\quad j=0,\\ \frac{K_{\nu }(\mu _jr)}{K_{\nu }'(\mu _jb)};\quad j \ge 1, \end{array}\right. } \nonumber \\ W_j^{m}(\mu _jr)= & {} {\left\{ \begin{array}{ll} \frac{r^{\nu }}{b^{\nu -1}};\quad j=0,\\ \frac{I_{\nu }(\mu _jr)}{I_{\nu }'(\mu _jb)};\quad j \ge 1. \end{array}\right. } \end{aligned}$$

The particular solutions for Region III are as follows:

$$\begin{aligned} {\varPi}_{3}^1= & {} 0, \end{aligned}$$
(22)
$$\begin{aligned} {\varPi} _{3}^2= & {} z. \end{aligned}$$
(23)

The radiated velocity potential for Region IV is (Wu et al. [31])

$$\begin{aligned} \varPsi _{\text{ rad },4}^m(r, \theta , z)= \sum _{j=0}^{\infty }[F_{j}^m\cos \gamma _j(z+h_3)U_j^{m}(\gamma _jr)+\varPi _{4}^m]\cos \nu \theta, \end{aligned}$$
(24)

where \({F_{j}^m}\) are the undetermined coefficients and \({\gamma _j}\) are obtained from the following expression:

$$\begin{aligned} \gamma _j=\frac{\pi j}{h_3-h_2}, \quad j=0,1,2,\ldots . \end{aligned}$$

The radial eigenfunctions \({U_j^{m}(\gamma _jr)}\) have the following form:

$$\begin{aligned} U_j^{m}(\gamma _jr)= {\left\{ \begin{array}{ll} \frac{r^{\nu }}{b^{\nu -1}};\quad j=0,\\ \frac{I_{\nu }(\gamma _jr)}{I_{\nu }'(\gamma _jb)};\quad j \ge 1. \end{array}\right. } \end{aligned}$$

The particular solutions for Region IV are given by

$$\begin{aligned} {\varPi}_{4}^1= & {} 0, \end{aligned}$$
(25)
$$\begin{aligned} \varPi _{4}^2= & {} \bigg [(z+h_3)^2-\frac{r^2}{2}\bigg ]\frac{1}{2(h_3-h_2)}. \end{aligned}$$
(26)

4 Added mass and damping coefficient

The solution to the radiation problem for structures in motion in ocean yields the important hydrodynamic coefficients, i.e., added mass and damping coefficients. They are connected to the real and imaginary parts of the hydrodynamic reaction loads on the body arising due to prescribed body motions. The hydrodynamic force in the x- and z-directions (i.e., surge and heave) due to the motion of a cylinder in mode \({m=1,2}\) can be found out by carrying out integration of the corresponding pressure distribution over the cylinder surface. Non-dimensional surge added mass and damping coefficients can be obtained from the following (Calisal and Subancu [5]):

$$\begin{aligned} \frac{\varSigma _{11}}{\rho V}+ \mathrm{i} \frac{\varLambda _{11}}{\rho V\sigma }= & {} \sigma ^2 \int _{-h_1}^{0} \int _{0}^{2\pi } \varPsi _2^m(a, \theta, z) a\cos {\theta }\;\mathrm {d} z\mathrm {d} \theta \nonumber \\&+ \sigma ^2 \int _{-h_2}^{-h_1} \int _{0}^{2\pi } \varPsi _3^m(a, \theta, z)a \cos {\theta }\; \mathrm {d} z \mathrm {d} \theta \nonumber \\&+ \sigma ^2 \int _{-h_2}^{-h_1} \int _{0}^{2\pi } \varPsi _1^m(b, \theta, z) b\cos {\theta }\; \mathrm {d} z \mathrm {d} \theta \nonumber \\&- \sigma ^2 \int _{-h_2}^{-h_1} \int _{0}^{2\pi } \varPsi _3^m(b, \theta, z) b\cos {\theta }\; \mathrm {d} z \mathrm {d} \theta, \end{aligned}$$
(27)

where V is the volume of the cylinder.

Similarly, non-dimensional heave added mass and damping coefficients are given by (Calisal and Subancu [5]) as

$$\begin{aligned} \frac{\varSigma _{33}}{\rho V}+ \mathrm{i} \frac{\varLambda _{33}}{\rho V\sigma }= & {} \sigma ^2 \int _{0}^{b} \int _{0}^{2\pi } \varPsi _4^m(-h_2, \theta, z) r\; \mathrm {d} r\mathrm {d} \theta \nonumber \\&-\sigma ^2 \int _{a}^{b} \int _{0}^{2\pi } \varPsi _3^m(-h_2, \theta, z)r\; \mathrm {d} r \mathrm {d} \theta \nonumber \\&-\sigma ^2 \int _{a}^{b} \int _{0}^{2\pi } \varPsi _2^m(-h_1, \theta, z) r\; \mathrm {d} r\mathrm {d} \theta \nonumber \\&+ \sigma ^2 \int _{a}^{b} \int _{0}^{2\pi } \varPsi _3^m(-h_1, \theta, z)r\; \mathrm {d} r \mathrm {d} \theta . \end{aligned}$$
(28)

5 Surge motion

5.1 Calculation of unknown coefficients

By applying the boundary condition for the surge motion \((m=1)\) at \({r=a}\) for \({-h_1< z< 0}\) and the orthogonality of the eigenfunctions, we get the following relationship between the potential coefficients \({B_{\alpha }^1}\) and \({C_{\alpha }^1}\) appearing in \({\phi _2}\):

$$\begin{aligned} \Bigg ( S_{\alpha }^{1}(\lambda _ja)B_{\alpha }^1+R_{\alpha }^{1}(\lambda _ja)C_{\alpha }^1\Bigg ){\mathcal {R}}_{\alpha \alpha }= & {} {\mathcal {A}}_{\alpha },\quad \alpha \ge 0. \end{aligned}$$
(29)

Applying the matching conditions given by Eqs. (10) and (11) for the depth \({-h_1<z<0}\), along with the orthogonality of the eigenfunctions, we obtain

$$\begin{aligned}&\sum _{j=0}^{\infty }A_{j}^1T_j^{1}(k_jb){\mathcal {Q}}_{\alpha j}-\bigg (B_{\alpha }^1S_{\alpha }^1(\lambda _\alpha b)+C_{\alpha }^1R_{\alpha }^1(\lambda _\alpha b)\bigg ){\mathcal {R}}_{\alpha \alpha }\nonumber \\&\quad =\frac{ \mathrm{i} gH}{\sigma \cos k_0 h_3}\tau _1 J_{1}(k_0b){\mathcal {Q}}_{\alpha 0},\;\alpha \ge 0, \; \end{aligned}$$
(30)
$$\begin{aligned}&\sum _{j=0}^{\infty }A_{j}^1T_j^{1'}(k_jb){\mathcal {Q}}_{\alpha j}-\bigg (B_{\alpha }^1S_{\alpha }^{1'}(\lambda _\alpha b)+C_{\alpha }^1R_{\alpha }^{1'}(\lambda _\alpha b)\bigg ){\mathcal {R}}_{\alpha \alpha }\nonumber \\&\quad =\frac{\mathrm{i} gH}{\sigma \cos k_0 h_3}\tau _1 J_{1}'(k_0b){\mathcal {Q}}_{\alpha 0},\;\alpha \ge 0. \; \end{aligned}$$
(31)

Next, using Eq. (6) for the depth \({-h_2<z<-h_1}\), the matching condition (12) and the orthogonality of the eigenfunctions, we get

$$\begin{aligned}&\bigg (V_\alpha ^{1'}(\mu _\alpha b)-\mathrm{i} k_0GV_\alpha ^{1}(\mu _\alpha b)\bigg )D_\alpha ^1{\mathcal {N}}_{\alpha \alpha }\nonumber \\&\qquad +\bigg (W_\alpha ^{1'}(\mu _\alpha b)-\mathrm{i} k_0GW_\alpha ^{1}(\mu _\alpha b)\bigg )E_\alpha ^1{\mathcal {N}}{\alpha \alpha }\nonumber \\&\quad + \mathrm{i} k_0G\sum _{j=0}^{\infty }A_{j}^1T_j^{1}(k_j b){\mathcal {P}}_{\alpha j}\nonumber \\&\quad =-\frac{\mathrm{i} gH}{\sigma \cos k_0 h_3}\tau _1 J_{1}(k_0b){\mathcal {P}}_{ \alpha 0}+{\mathcal {B}}_{\alpha }\quad \alpha \ge 0, \end{aligned}$$
(32)
$$\begin{aligned}&\left( D_{\alpha }^1V_0^{1'}(\mu _\alpha b)+E_{\alpha }^1W_\alpha ^{1'}(\mu _\alpha b)\right) {\mathcal {N}}_{\alpha \alpha }-\sum _{j=0}^{\infty }A_{j}^1T_j^{1'}(k_j b){\mathcal {P}}_{\alpha j}\nonumber \\&\quad =-\frac{ \mathrm{i} gH}{\sigma \cos k_0 h_3}\tau _1 {\mathcal {P}}_{\alpha 0}J_{1}'(k_0b), \alpha \ge 0. \end{aligned}$$
(33)

Further, from the matching condition given by Eq. (14) across the boundary \({r=b}\) in the interval \({-h_3<z<-h_2}\), and using the orthogonality of the eigenfunctions, we get

$$\begin{aligned}&\sum _{j=0}^{\infty }A_{j}^1T_j^{1'}(k_j b){\mathcal {S}}_{\alpha j}-F_{\alpha }^1U_0^{1'}(\gamma _\alpha b){\mathcal {L}}_{\alpha \alpha }\nonumber \\&\quad = \frac{ \mathrm{i} gH}{\sigma \cos k_0 h_3}\tau _1 J_{1}'(k_0b) {\mathcal {S}}_{\alpha 0},\quad \alpha \ge 0,\quad \quad \end{aligned}$$
(34)

where

$$\begin{aligned} {\mathcal {Q}}_{\alpha,j}= & {} \int _{-h_1}^{0}\cos \lambda _\alpha (z+h_1)\cos k_j(z+h_3) \mathrm {d} z, \end{aligned}$$
(35)
$$\begin{aligned} {\mathcal {R}}_{\alpha,\alpha }= & {} \int _{-h_1}^{0}\cos \lambda _\alpha (z+h_1)\cos \lambda _\alpha (z+h_1)\mathrm {d} z,\end{aligned}$$
(36)
$$\begin{aligned} {\mathcal {T}}_{\alpha,\alpha }= & {} \int _{-h_2}^{-h_1}\cos \mu _\alpha (z+h_2)\cos \mu _\alpha (z+h_2) \mathrm {d} z,\end{aligned}$$
(37)
$$\begin{aligned} {\mathcal {P}}_{\alpha,j}= & {} \int _{-h_2}^{-h_1}\cos \mu _\alpha (z+h_2)\cos k_j(z+h_3)\mathrm {d} z,\end{aligned}$$
(38)
$$\begin{aligned} {\mathcal {S}}_{\alpha,j}= & {} \int _{-h_3}^{-h_2}\cos \gamma _\alpha (z+h_3)\cos k_j(z+h_3)\mathrm {d} z,\end{aligned}$$
(39)
$$\begin{aligned} {\mathcal {L}}_{\alpha,\alpha }= & {} \int _{-h_3}^{-h_2}\cos \gamma _\alpha (z+h_3)\cos \gamma _\alpha (z+h_3)\mathrm {d} z,\end{aligned}$$
(40)
$$\begin{aligned} {\mathcal {A}}_\alpha= & {} \int _{-h_1}^{0}\cos \lambda _\alpha (z+h_1)\mathrm {d} z,\end{aligned}$$
(41)
$$\begin{aligned} {\mathcal {B}}_\alpha= & {} \int _{-h_2}^{-h_1}\cos \mu _\alpha (z+h_2)\mathrm {d} z. \end{aligned}$$
(42)

In order to evaluate the hydrodynamic coefficients, it is required to find the unknown coefficients \({A^m_j}\), \({B^m_j}\), \({C^m_j}\), \({D^m_j}\), \({E^m_j}\), and \({F^m_j}\). Truncating the infinite series given by Eqs. (29)–(34) after some terms \({N=20}\), the values of the coefficients are computed. Excellent convergence is accomplished by truncating the expansion series after the first 20 terms. Similar convergence is shown in details in [22]. As a consequence, the following linear system of algebraic equations is found for determining the unknown coefficients:

$$\begin{aligned} { {\mathcal {T}}^d{\mathcal {X}}^d={\mathcal {Y}}^d,} \end{aligned}$$
(43)

where \(\mathcal X^d=[A_{1}^d,A_{2}^d,\ldots,A_{N}^d,B_{1}^d,B_{2}^d,\ldots,B_{N}^d,C_{1}^d,C_{2}^d,\ldots,C_{N}^d,D_{1}^d,D_{2}^d,\ldots,D_{N}^d,E_{1}^d,E_{2}^d,\ldots, E_{N}^d,F_{1}^d,F_{2}^d,\ldots,F_{N}^d]^t\), \({{\mathcal {T}}^d}\) are coefficient matrices and \({{\mathcal {Y}}^d}\) are the right-hand vectors.

The method adopted in Sarkar and Bora [22] is followed here too.

5.2 Validation of present model

Fig. 2
figure 2

Comparison of surge-added mass of present work with that of Williams and Li [28]

Full size image

To validate our present analytical model developed for solving the problem, we deem it suitable to compare one of the results with that of Williams and Li [28], i.e., when the cylinder is considered to be a floating compound cylinder (the curved surface of the bottom cylinder is considered impermeable). The relevant parameters in our problem are reconsidered conforming to the work of Williams and Li in order to convert to the same physical problem. Here we consider the values \({G=0}\), \({h_1/h_2=0.50}\), \({h_2/h_3=0.67}\), \({b/h_3=1}\), and \({a/b=0.60}\). Figure 2 presents an excellent agreement between both results for the dimensionless added mass for the surge motion of the cylinder. In view of this validation, our model can be considered to be efficient and hence can be utilized to study and analyze different aspects of various parameters for our subsequent experiments and also for such problems in general.

Fig. 3
figure 3

Convergence of added mass for surge motion against wavenumber corresponding to different values of N for \({a/b=1/2}\), \({h_1/h_2=1/2}\), \({h_2/h_3=1/2}\), and \({G=1}\)

Full size image
Fig. 4
figure 4

Added mass for surge motion against wavenumber corresponding to different values of a/b for \({h_1/h_2=1/2}\), \({h_2/h_3=1/2}\), and \({G=1}\)

Full size image

5.3 Numerical discussion

Here we discuss the effects of various parameters on the surge hydrodynamic coefficients acting on the cylindrical structure. The results are presented graphically and relevant observations are presented.

Figure 3 presents the convergence of added mass for surge motion with respect to N against wavenumber corresponding to different values of N for \({a/b=1/2}\), \({h_1/h_2=1/2}\), \({h_2/h_3=1/2}\), and \({G=1}\). It can easily be concluded from this figure that consideration of \({N = 20}\) provides satisfactory accuracy of evaluation of hydrodynamic coefficients, and therefore, for all subsequent figures, \(N=20\) will be considered whenever the requirement arises.

Fig. 5
figure 5

Added mass for surge motion against wavenumber corresponding to different values of G for \({h_1/h_2=1/2}\), \({h_2/h_3=1/2}\), and \({a/b=1/2}\)

Full size image
Fig. 6
figure 6

Added mass for surge motion against wavenumber corresponding to different values of \({h_2/h_3}\) for \({h_1/h_2=1/2}\), \({a/b=1/2}\), and \({G=1}\)

Full size image
Fig. 7
figure 7

Added mass for surge motion against wavenumber corresponding to different values of \({h_1/h_2}\) for \({h_2/h_3=1/2}\), \({a/b=1/2}\), and \({G=1}\)

Full size image
Fig. 8
figure 8

Damping coefficient for surge motion against wavenumber corresponding to different values of a/b for \({h_1/h_2=1/2}\), \({h_2/h_3=1/2}\), and \({G=1}\)

Full size image

In Fig. 4, the non-dimensionalized added mass \(\displaystyle \frac{\varSigma _{11}}{\rho V}\) for surge motion against wavenumber is discussed corresponding to different values of radius ratio a/b corresponding to \({h_1/h_2=1/2}\), \({h_2/h_3=1/2}\), and \({G=1}\). It is observed that added mass oscillates alternately between negative and positive values for increasing values of \({k_0h_1}\). This type of added mass is also observed in the works of McIver and Evans [17] and Wu et al. [31]. The amplitudes of the os cillation are higher in t he range \({2<k_0h_1<3}\). It is also observed that for decreasing a/b, i.e., when the radius of the inner cylinder tends to be much smaller compared to that of the outer porous cylinder, the added mass increases. It may have happened due to more energy concentration near the inner cylinder and thus resulting in an increase in added mass. Figure 5 shows the non-dimensionalized added mass \(\displaystyle \frac{\varSigma _{11}}{\rho V}\) for surge motion against wavenumber corresponding to different values of porous coefficient G for \({h_1/h_2=1/2}\), \({h_2/h_3=1/2}\) and \({a/b=1/2}\). The observation is that the added mass are not significantly affected by G. One important observation is that added mass does not vary much for different smaller values of G, say, when we take \({G=0,1, 2}\). This is due to the fact that the added mass for the semi-porous cylinder depends on the potential coefficients \({A_j^m}\), \({B_j^m}\), \({C_j^m}\), \({D_j^m}\), \({E_j^m}\), and \({F_j^m}\) which do not change appreciably. Subsequently, this is the reason added mass do not get changed for such smaller values of porosity coefficient G. However, if we consider a large range of values of G from 0 to 30, then it is observed that, for increasing values of G, the oscillating behavior of the graph becomes more pronounced. In Fig. 6, the non-dimensionalized added mass \(\displaystyle \frac{\varSigma _{11}}{\rho V}\) for surge motion against wavenumber is analyzed corresponding to different values of \({h_2/h_3}\) for \({h_1/h_2=1/2}\), \({a/b=1/2}\), and \({G=1}\). Similar pattern of graph is observed here just as in Fig. 4. The amplitude of added mass becomes higher in \({2<k_0h_1<3}\). The oscillation gets shifted towards left for decreasing values of \({h_2/h_3}\). There is a shift observed in the maxima of these curves which may be due to the phase shift of the wave when the draft of the cylindrical system changes. The non-dimensionalized added mass \(\displaystyle \frac{\varSigma _{11}}{\rho V}\) for surge motion against wavenumber corresponding to different values of \({h_1/h_2}\) for \({h_2/h_3=1/2}\), \({a/b=1/2}\), and \({G=1}\) are shown in Fig. 7. The oscillation is observed to get shifted towards right for decreasing values of \({h_1/h_2}\). Figure 8 illustrates the non-dimensionalized damping coefficient \(\displaystyle \frac{\varLambda _{11}}{\rho V\sigma }\) for surge motion against wavenumber corresponding to different values of radius ratio a/b for \(h_1/h_2=1/2\), \({h_2/h_3=1/2}\), and \({G=1}\). If a floating body is in motion in waves, then the motion in general involves six degrees of freedom. Negative damping coefficient usually appears in the so-called coupled terms. The motion in surge and yaw directions are always coupled which means that the surge motion is going to get influenced by the yaw motion. Therefore in the results, the yaw induced surge damping is negative which implies that it is not only added mass that can be negative, the occurrence of which is a quite familiar phenomenon, but damping coefficients can also take negative values under certain conditions. This type of phenomenon happens due to the coupled behavior between different motions. Similarly the motion in heave and pitch are always coupled. In that case also, the added mass and damping coefficient may be negative. Here the damping coefficient oscillates alternately between negative and positive values. This type of behavior of damping coefficient is also observed in the works of Wu et al. [31], Zheng et al. [39], and Zheng and Zhang [40]. The value of the damping coefficient becomes higher in \({2<k_0h_1<3}\) and lower in \({3.5<k_0h_1<4}\). Non-dimensionalized damping coefficient increases with decreasing radius ratio a/b, i.e., when the radius of the inner cylinder gets much smaller than that of the outer porous cylinder in \({2<k_0h_1<3}\). The occurrence of maxima and minima for added mass for the structure may be due to the constructive and destructive interference between the incident and reflected waves.

Fig. 9
figure 9

Damping coefficient for surge motion against wavenumber corresponding to different values of G for \({h_1/h_2=1/2}\), \({h_2/h_3=1/2}\), and \({a/b=1/2}\)

Full size image
Fig. 10
figure 10

Damping coefficient for surge motion against wavenumber corresponding to different values of \({h_2/h_3}\) for \({h_1/h_2=1/2}\), \({a/b=1/}2\), and \({G=1}\)

Full size image
Fig. 11
figure 11

Damping coefficient for surge motion against wavenumber corresponding to different values of \({h_1/h_2}\) for \({h_2/h_3=1/2}\), \({a/b=1/2}\), and \({G=1}\)

Full size image

Figure 9 presents the non-dimensionalized damping coefficient \(\displaystyle \frac{\varLambda _{11}}{\rho \sigma V}\) for surge motion against wavenumber corresponding to different range of values of G for \({h_1/h_2=1/2}\), \({h_2/h_3=1/2}\), and \({a/b=1/}2\). The behavior of those curves is similar even when G takes different values. However, the variation is observed to be more pronounced for higher values of G. Similar type of behavior as observed in Fig. 5 for added mass is observed here too. Next, Fig. 10 shows the non-dimensionalized damping coefficient \(\displaystyle \frac{\varLambda _{11}}{\rho \sigma V}\) for surge motion against wavenumber corresponding to different values of \({h_2/h_3}\) for \({h_1/h_2=1/2}\), \({a/b=1/2}\), and \({G=1}\). In the lower wavenumber range for decreasing values of \({h_2/h_3}\), amplitude of the damping coefficient is observed to get shifted towards left. In other words, this happens when the draft of the lower cylinder with respect to its lower surface is reduced which implies a position of the cylinder further away from the sea-bed. Figure 11 shows damping coefficient \(\displaystyle \frac{\varLambda _{11}}{\rho \sigma V}\) for surge motion against wavenumber corresponding to different values of \({h_1/h_2}\) for \({h_2/h_3=1/2}\), \({a/b=1/2}\), and \({G=1}\). The oscillation is observed to get shifted towards right for decreasing values of \({h_1/h_2}\). In other words, this happens when the draft of the lower cylinder with respect to its upper surface is reduced which makes the cylinder closer to the free surface.

6 Heave motion

6.1 Calculation of unknown coefficients

Using the boundary condition for the heave motion \({(m=2)}\) at \({r=a}\) for \({-h_1< z< 0}\) and the orthogonal property of the eigenfunctions, we get the following relationship between the potential coefficients \({B_{\alpha }^2}\) and \({C_{\alpha }^2}\) appearing in \({\phi _2}\):

$$\begin{aligned} \Bigg ( S_{\alpha }^{2}(\lambda _ja)B_{\alpha }^2+R_{\alpha }^{2}(\lambda _ja)C_{\alpha }^2\Bigg ){\mathcal {R}}_{\alpha \alpha }= & {} 0,\quad \alpha \ge 0. \end{aligned}$$
(44)

Applying the matching conditions given by Eqs. (10) and (11) for the depth \({-h_1<z<0}\), along with the orthogonality of the eigenfunctions, we obtain

$$\begin{aligned}&\sum _{j=0}^{\infty }A_{j}^2T_j^{2}(k_jb){\mathcal {Q}}_{\alpha j}-\bigg (B_{\alpha }^2S_{\alpha }^2(\lambda _\alpha b)+C_{\alpha }^2R_{\alpha }^2(\lambda _\alpha b)\bigg ){\mathcal {R}}_{\alpha \alpha }\nonumber \\&\quad =\frac{\mathrm{i} gH}{\sigma \cos k_0 h_3}\tau _1 J_{1}(k_0b){\mathcal {Q}}_{\alpha 0}-{\mathcal {C}}_{\alpha },\;\alpha \ge 0,\end{aligned}$$
(45)
$$\begin{aligned}&\sum _{j=0}^{\infty }A_{j}^2T_j^{2'}(k_jb){\mathcal {Q}}_{\alpha j}-\bigg (B_{\alpha }^2S_{\alpha }^{2'}(\lambda _\alpha b)+C_{\alpha }^2R_{\alpha }^{2'}(\lambda _\alpha b)\bigg ){\mathcal {R}}_{\alpha \alpha }\nonumber \\&\quad =\frac{ \mathrm{i} gH}{\sigma \cos k_0 h_3}\tau _1 J_{1}'(k_0b){\mathcal {Q}}_{\alpha 0},\;\alpha \ge 0. \end{aligned}$$
(46)

From Eq. (6) for the depth \({-h_2<z<-h_1}\) and the matching condition (12), along with the orthogonality of the eigenfunctions, we get

$$\begin{aligned}&\bigg (V_\alpha ^{2'}(\mu _\alpha b)-\mathrm{i} k_0GV_\alpha ^{2}(\mu _\alpha b)\bigg )D_\alpha ^2{\mathcal {N}}_{\alpha \alpha }\nonumber \\&\qquad +\bigg (W_\alpha ^{2'}(\mu _\alpha b)-\mathrm{i} k_0GW_\alpha ^{2}(\mu _\alpha b)\bigg )E_\alpha ^2{\mathcal {N}}{\alpha \alpha }\nonumber \\&\qquad + \mathrm{i} k_0G\sum _{j=0}^{\infty }A_{j}^2T_j^{2}(k_j b){\mathcal {P}}_{\alpha j}\nonumber \\&\quad =-\frac{\mathrm{i} gH}{\sigma \cos k_0 h_3}\tau _1 J_{1}(k_0b){\mathcal {P}}_{ \alpha 0}+{\mathcal {D}}_{\alpha }\quad \alpha \ge 0, \end{aligned}$$
(47)
$$\begin{aligned}&\left( D_{\alpha }^2V_0^{2'}(\mu _\alpha b)+E_{\alpha }^2W_\alpha ^{2'}(\mu _\alpha b)\right) {\mathcal {N}}_{\alpha \alpha }-\sum _{j=0}^{\infty }A_{j}^2T_j^{2'}(k_j b){\mathcal {P}}_{\alpha j}\nonumber \\&\quad =-\frac{\mathrm{i} gH}{\sigma \cos k_0 h_3}\tau _1 {\mathcal {P}}_{\alpha 0}J_{1}'(k_0b), \alpha \ge 0. \end{aligned}$$
(48)

Further, from the matching condition given by Eq. (14) at \({r=b}\) in the interval \({-h_3<z<-h_2}\), and using the orthogonality of the eigenfunctions, we get

$$\begin{aligned}&\sum _{j=0}^{\infty }A_{j}^2T_j^{2'}(k_j b){\mathcal {S}}_{\alpha j}-F_{\alpha }^2U_0^{2'}(\gamma _\alpha b){\mathcal {L}}_{\alpha \alpha }\nonumber \\&\quad = \frac{\mathrm{i} gH}{\sigma \cos k_0 h_3}\tau _1 J_{1}'(k_0b) {\mathcal {S}}_{\alpha 0}+{\mathcal {E}}_{\alpha },\; \alpha \ge 0,\; \end{aligned}$$
(49)

where \({\mathcal {Q}}_{ \alpha j}, {\mathcal {R}}_{ \alpha \alpha }, {\mathcal {T}}_{ \alpha \alpha }, {\mathcal {P}}_{ \alpha j}, {\mathcal {S}}_{ \alpha j}\), \({ {\mathcal {L}}_{ \alpha \alpha }}\) are given by Eqs. (35)–(40) and

$$\begin{aligned} {\mathcal {C}}_\alpha= & {} \int _{-h_1}^{0}\bigg (z+\frac{g}{\sigma ^2}\bigg )\cos \lambda _\alpha (z+h_1)\mathrm {d} z, \end{aligned}$$
(50)
$$\begin{aligned} {\mathcal {D}}_\alpha= & {} \mathrm{i} k_0G\int _{-h_2}^{-h_1}z\cos \mu _\alpha (z+h_2)\mathrm {d} z, \end{aligned}$$
(51)
$$\begin{aligned} {\mathcal {E}}_\alpha= & {} \frac{-b}{2(h_3-h_2)}\int _{-h_3}^{-h_2}\cos \gamma _\alpha (z+h_3)\mathrm {d} z. \end{aligned}$$
(52)

6.2 Numerical results

Fig. 12
figure 12

Added mass for heave motion against wavenumber corresponding to different values of a/b for \({h_1/h_2=0.37}\), \({h_2/h_3=0.66}\), and \({G=1}\)

Full size image

Here we discuss the effects of various parameters on the heave hydrodynamic coefficients acting on the cylindrical structure. The results are presented graphically and the observations are analyzed.

Figures 12, 13, and 14 show the added mass for heave motion against the wavenumber for different values of radius ratio a/b, porous coefficient G, and draft \({h_2/h_3}\), respectively. For all the cases, an oscillating nature is observed. Both minimum and maximum values of \(\displaystyle \frac{\varSigma _{33}}{\rho V}\) are attained at specific values of \({k_0h_1}\) for all values of a/b, G, and \({h_2/h_3}\). The value of added mass \(\displaystyle \frac{\varSigma _{33}}{\rho V}\) increases with an increase in the value of a/b, i.e., for the situation of increasing radius of the inner cylinder or decreasing radius of the outer cylinder. Also the presence of the porous region influences the impacts faced by the compound cylinder. It can be seen from Fig. 13 that with an increase in the value of the porous coefficient G, the added mass decreases. As the value of G increases, it allows more wave to pass through the structure but reduces the resistance of the structure to the wave motion. Thus, with a reduction in the value of G, the added mass acting on the cylinder increases. The added mass is also observed to be affected by the draft ratios. It is observed from Fig. 14 that the maximum value of the added mass get reduced for higher values of \({h_2/h_3}\).

Figures 15, 16, and 17 show the damping coefficient \(\displaystyle \frac{\varLambda _{33}}{\rho \sigma V}\) for heave motion against the wavenumber for different values of a/b, G, and \({h_2/h_3}\), respectively. In this case also, an oscillating behavior is observed. At low frequencies (wavenumbers), the component of the damping coefficient increases as a/b increases, i.e., when the radius of the upper cylinder gets closer to that of the lower cylinder. The heave damping coefficient is remarkably influenced by the porosity of the structure. It can be observed from Fig. 16 that an increase in damping coefficient is associated with a reduction in the values of the porous coefficient. Figure 17 presents damping coefficient \(\displaystyle \frac{\varLambda _{33}}{\rho \sigma V}\) for heave motion against wavenumber corresponding to different values of \({h_2/h_3}\) for \({h_1/h_2=0.37}\), \({a/b=0.50}\), and \({G=1}\). The oscillation is observed to get shifted towards right for increasing values of \({h_2/h_3}\). In other words, this happens when the draft of the lower cylinder with respect to its lower surface is increased which means the cylinder further away from free surface or getting closer to the sea-bed.

Fig. 13
figure 13

Added mass for heave motion against wavenumber corresponding to different values of G for \({h_1/h_2=0.37}\), \({h_2/h_3=0.66}\), and \({a/b=0.50}\)

Full size image
Fig. 14
figure 14

Added mass for heave motion against wavenumber corresponding to different values of \({h_2/h_3}\) for \({h_1/h_2=0.37}\), \({G=1}\), and \({a/b=0.50}\)

Full size image
Fig. 15
figure 15

Damping coefficient for heave motion against wavenumber corresponding to different values of a/b for \({h_1/h_2=0.37}\), \({h_2/h_3=0.66}\), and \({G=1}\)

Full size image
Fig. 16
figure 16

Damping coefficient for heave motion against wavenumber corresponding to different values of G for \({h_1/h_2=0.37}\), \({h_2/h_3=0.66}\), and \({a/b=0.50}\)

Full size image
Fig. 17
figure 17

Damping coefficient for heave motion against wave number corresponding to different values of \({h_2/h_3}\) for \({h_1/h_2=0.37}\), \({G=1}\), and \({a/b=0.50}\)

Full size image

7 Conclusion

Employing linear water wave theory, radiated potentials are derived for each sub-domain considered by taking into account the presence of a floating surface-piercing semi-porous compound cylinder in finite ocean depth. Eigenfunction expansion approach and separation of variables technique are utilized in solving this radiation problem governed by Laplace’s equation. Various matching conditions are applied to derive a system of linear equations for determining the unknown coefficients. Non-dimensionalized added mass and damping coefficients due to surge and heave motions are evaluated. Further, the effect of radius, depth, and porosity on the added mass and damping coefficient are examined. For surge motion, as the radius ratio a/b of the cylinder decreases, added mass, and damping coefficient both increase. It is observed that added mass oscillates between positive and negative values before converging corresponding to higher values of \({k_0h_1}\). Such type of peculiar behavior of added mass is also observed in the works of McIver and Evans [17] and Wu et al. [31].

It is observed that the yaw induced surge damping is negative which implies that it is not only added mass that can be negative, the occurrence of which is a quite familiar phenomenon, but damping coefficients can also take negative values under certain conditions. This type of phenomenon can be attributed to coupled behavior between different motions. The damping coefficients are found to oscillate alternately between negative and positive values. A similar phenomenon was also observed by Wu et al. [31], Zheng et al. [39], and Zheng and Zhang [40]. It is also noticed from Fig. 9 that for surge motion, the added mass is not sufficiently affected by lower values of porous coefficient G. On the other hand, consideration of a large range of values of G shows added mass exhibiting variation for higher G. But for the heave motion, added mass is influenced by the porous coefficient G (Fig. 13) − it decreases as G increases. With respect to the effect of the gap between the cylinder and depth, it is clearly observed from Fig. 14 that for fixed values of the radii and porous coefficient, the added mass for heave motion increases as \({h_2/h_3}\), i.e., the submergence of the lower face of the outer (porous) cylinder, decreases. Then, with respect to the heave motion, keeping \({h_2/h_3}\) and G fixed, the damping coefficient increases as the value of radius ratio a/b increases. For fixed values of porous coefficient and radii, it is observed that the oscillation of damping coefficient for surge motion gets shifted towards right for decreasing values of \({h_1/h_2}\). The study on wave interaction with concentric porous cylinder system is likely to be of immense help in the design of effective coastal/offshore structures such as (i) offshore fishing cage, (ii) floating production storage (FPS), (iii) tension-leg platform (TLP), and (iv) jack-up (space truss like) oil rigs as the proposed system will experience less load on the main structure. On the other hand, circular porous cylinder, and floating cage can be effectively used in the marine environment for (i) oil spill containment, (ii) temporary protection during coastal construction works, and (iii) augmentation of existing breakwaters for seasonal protection. It is expected that the results obtained in this work will provide necessary background for designing appropriate and efficient structures for reducing wave loads on such type of structures installed for various marine applications.

The obtained results are validated by comparing one result with an available result (Williams and Li [28]) and a satisfactory agreement is noticed thereby implying the effectiveness of the mathematical model and subsequent results of the present work.