1 Introduction

The present study is concerned with the diffraction of linear water waves by two vertical circular cylinders arranged in a specific manner such that this system can be considered to consist of a floating porous buoy in a vertical position above a bottom-mounted caisson. For reasonable understanding, the porous buoy can be approximated as a porous vertical cylinder whereas the caisson can be considered as a solid rigid vertical cylinder. This configuration may be considered to represent a wave energy device, also sometimes called an oscillating water column (OWC), which can be used to conveniently capture the immense and easily available power of ocean waves and convert it to electrical energy. The energy extracted by the upper porous cylinder is usually transferred to a liquid pump properly placed on the lower rigid cylinder. Since the primary objective is to capture waves as much as possible, there is a requirement of positioning the device in an appropriate manner. Due to the rapid reduction of natural resources, the idea of using renewable non-conventional energy has subsequently accorded immense importance to such devices. While designing marine structures, it is always of utmost importance to take into account the possible existing atmospheric conditions and then to propose an almost accurate prediction of the hydrodynamic impact on the structures. In this context, of late, one of the main directions of research has specifically been in optimizing a system or a structure which will be able to withstand significant adverse hydrodynamic actions. At present, the focus is on exploring the possibility of the use of suitable porous structures, which, due to the pores on its surface, can make significant contribution in reducing the impact of wave–body interaction. That is why many countries are exploring the feasibility of extracting offshore wind and wave energy to be used as an alternative to conventional energy. Additionally, this energy is inexpensive, readily available and reliable. For example, South Korea has already started working on one such project to extract and utilize offshore wind energy through windmills installed in ocean [10].

The whole world witnessed global oil crisis in 1970. From then onward, the concept of bringing renewable energy into fore has kicked off. Along side, a sizeable endeavor has been undertaken precisely on research and burgeoning activities that relate to solar, wind and ocean energy. This development has come to the aid of strengthening the study of the existing gap between renewable and non-renewable energy. In the recent past, it has been observed that WEC (wave energy converter) systems require high cost in comparison with traditional electricity produced from coal, hydro, nuclear power plants. The appealing power of the WEC can be further intensified through the consolidation of a WEC into other maritime structures such as breakwater pier or jetty, making it sustainable from economy point of view. Detailed information regarding consolidation of breakwater and wave energy device over the stand-alone wave energy device can be found in Mustapa et al. [15]. Waveloads and the competence of converting cylinders as wave energy device have received considerable attention from designers. The diffraction by a system of two cylinders, as considered here, can be related to the corresponding diffraction problem of a wave energy device. It may be mentioned here that our current work involves the wave interaction with the structure, mainly looking at the hydrodynamic force and wave run-up rather than focussing on the wave energy tapping aspect.

At the outset, it is considered pertinent to discuss some relevant important works carried out over the last few decades. These works directly or indirectly influence the WEC construction and utilization. Ursell [30], a leading researcher in water wave scattering and allied problems, studied the small oscillation of a long and floating horizontal cylinder in finite ocean depth. He evaluated the amplitude of wave at some distance from the cylinder and also the relevant added mass of the cylinder corresponding to its vertical motion. MacCamy and Fuchs [13], by employing eigenfunction expansion, calculated the force and moment acting on cylindrical piles by diffraction of water waves. By applying the eigenfunction expansion approach, Spring and Monkmeyer [28] analytically studied diffraction of linear water waves by an array of bottom-mounted impermeable circular cylinders. This result can be considered as an extension of that of MacCamy and Fuchs [13].

Sahoo [18] considered a configuration consisting of an inner rigid circular cylinder and a vertical coaxial permeable hollow cylinder and examined cylindrical surface waves in infinite ocean depth by utilizing Havelock’s expansion theorem and some properties of Bessel functions. Hassan and Bora [9] investigated the radiation problem due to surge motion of a hollow riding cylinder that was placed above a coaxial solid cylinder in finite ocean depth. They evaluated and discussed the behavior of the associated surge added mass and surge damping coefficients.

The study of water wave interaction with porous structures is considered to be more important and significant from realistic and application point of view. For formulating problems pertaining to wave-induced flow in any porous medium, the model devised by Sollitt and Cross [27] has attracted massive attention. This model reckons wave energy dissipation inside a porous medium, and Lorentz Principle and an iterative procedure were instrumental in evaluating the linearized friction term f. Chwang [2] developed a porous wave-maker theory and investigated the distribution of hydrodynamic pressure and the total force exerted on the wave-maker. They also established that the parameters associated with wave propagation and porosity had immense impact on the outcomes. Darwiche et al. [3], by using eigenfunction expansion method, investigated the interaction of water waves with a semi-porous cylindrical breakwater and they produced a very important result which established that the semi-porous portion of the cylinder was instrumental in the reduction of the wave force. Yu [34] came up with a new result for a fluid flow passing through a thin porous structure used as a breakwater in ocean. He found that ignoring the inertial effect of the porous medium was instrumental in achieving an underestimate of the performance of the structures. Williams and Li [31] considered a breakwater in the form of a semi-porous cylinder surrounding a rigid vertical circular cylinder that was mounted on a storage tank, and they investigated its interaction with water waves. The wave field exhibited a significant change and the presence of the semi-porous cylindrical breakwater led to significant reduction in hydrodynamic forces. Williams and Li [32] extended their investigation by studying interaction of water waves with an array of surface-piercing bottom-mounted porous cylinders and evaluated the associated hydrodynamic forces exerted on them.

Sankarbabu et al. [19] considered the diffraction of water waves by an array of surface-piercing bottom-mounted porous cylinders and observed various impacts that the wave and structural parameters exhibited. Das and Bora [4] discussed reflection of linear water waves by a vertical porous structure placed on an elevated impermeable sea-bed by considering a 2-step and a p-step bottom topography. They observed an increase in the values of the reflection coefficient corresponding to lower values of porosity. Das and Bora [5] further investigated an obliquely incident wave on a vertical porous structure placed on a multi-step bottom topography by considering a solid vertical wall in water placed at a finite distance from the porous structure and again by placing the wall at infinity. Koley et al. [11] investigated the oblique wave trapping by bottom-standing and surface-piercing porous structures of finite width placed at a finite distance from a vertical rigid wall. The solutions of the associated boundary value problems were obtained analytically by using the eigenfunction expansion method and also numerically by using a multidomain boundary-element method. Various aspects of structural configurations in trapping surface gravity waves were analyzed from the computed results on the reflection coefficients and the hydrodynamic forces. Singla et al. [25] investigated the scattering of obliquely incident water waves by a surface-piercing porous box in finite depth of fluid. They computed physical quantities of interest like reflection and transmission coefficients. They also discussed some special cases such as wave interaction with (i) rigid box and (ii) single/double porous barriers in the absence of submerged porous plate. They found that the height and width of the porous box played important roles not only in wave trapping inside the structure, but also in dissipating a major part of wave energy by the structure to reduce wave transmission for creating a calm region on the lee side of the structure. Again Singla et al. [26] discussed the effectiveness of a floating porous plate for mitigating the wave-induced structural response of a very large floating structure using the eigenfunction expansion method. The elastic plate was modeled using thin plate theory, and the wave past the porous plate was based on the assumptions of the generalized porous wave-maker theory. They found that the amplitude of the periodic oscillatory pattern in the wave reflection reduces with an increase in the length of the porous plate of moderate porosity. Ning et al. [16] investigated the diffraction of water waves by a truncated cylinder consisting of an upper porous side-wall and an inner column. They found that the associated wave forces and moments reduced corresponding to an increasing draft ratio. Sarkar and Bora [20] evaluated hydrodynamic forces on a surface-piercing bottom-mounted compound porous cylinder due to its interaction with water waves. It was observed that parameters such as radius, draft and porosity immensely influenced hydrodynamic loads and wave run-up. In a similar manner, Sarkar and Bora [21] evaluated the hydrodynamic force arising for the case of a floating compound porous cylinder in finite ocean depth. It was observed that the hydrodynamic load exhibited a steady behavior in the lower frequency. However, on the other hand, occurrence of fluctuations was noticed probably due to resonance prevailing near a particular frequency. Sarkar and Bora [22] further investigated diffraction of ocean waves by a specific type of cylinders, namely, a floating surface-piercing truncated partial-porous cylinder and then a surface-piercing bottom-mounted truncated partial-porous cylinder, by treating both cases separately. Numerical experiments were carried out in order to analyze the impact of parameters, such as porous coefficients, draft ratio, the ratio of inner and outer radii, the water depth on the quantities hydrodynamic force, moment and wave run-up. After that, Sarkar and Bora [23] extended their previous problem in [22] and they discussed the radiation of ocean waves by a floating surface-piercing truncated partial-porous cylinder. They considered the surge and heave motions of the cylinder to calculate the added mass and damping coefficients. Guo et al. [7] investigated oblique wave interaction with a submerged horizontal flexible porous membrane in finite water depth. They analyzed the effects of spring stiffness, porous effect parameter, submergence depth, structural length, angle of incidence and flow pattern on reflection, transmission, dissipation coefficients, membrane deflection and vertical force. Liu et al. [12] experimentally and theoretically discussed waveloads on quasi-ellipsoid-type foundations coaxially surrounded by perforated breakwaters. They also validated the experimental results with the occurrence of the “phase jump” when the waveloads on the breakwater were minimum.

In the present work, the interaction of linear surface waves with a cylindrical system consisting of two coaxial vertical cylinders is theoretically investigated. Here, we discuss two cases: (i) a system consisting of a hollow porous cylinder at the top and a rigid solid cylinder at the bottom, (ii) a solid porous cylinder at the top with a rigid solid cylinder considered at the bottom. The entire fluid region is split into a number of subregions. By employing linear water wave theory and eigenfunction expansion, the problem is solved analytically in each fluid region by an appropriate use of the conditions on and across the boundaries. The impacts of various parameters due to the wave and the structure on the exciting forces exerted on the upper and lower cylinders are illustrated graphically. We calculate the forces on the cylinders induced by diffraction, and the expectation is that these outcomes may be appropriately utilized in designing effective devices. Further, it is also anticipated to benefit the engineers in selecting optimally important parameters such as depth, porosity, the radii of cylinders and the gaps between the cylinders. This specific model, trusted not to have been considered earlier, is likely to throw new lights in tackling ocean engineering problems that involve different configurations of porous structures.

Fig. 1
figure 1

Schematic diagram of the configuration

Full size image

2 Two coaxial cylinders: an upper hollow porous cylinder and a lower rigid solid cylinder

2.1 Theoretical formulation

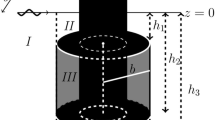
Two coaxial cylinders, a hollow upper cylinder with porous side-wall and a solid rigid lower cylinder, are considered such that the upper one floats and the lower one is placed at the ocean bottom. A cylindrical coordinate system \((r,\theta , z)\) is considered with the origin on \(z=0\) along the axis of the cylinders and the z-axis pointing vertically upward where a and b are the radii of the upper and lower cylinders, respectively, and \(h_1\) is the draft of the upper cylinder. The bottom of lower cylinder is located at depth \(z=-h_3\) with its upper surface at \(z=-h_2\) (Fig. 1). For convenience and practical point of view, the whole fluid domain is split into three regions: Region I \((r\ge b, -h_3\le z\le 0)\); Region II \((a \le r \le b, -h_2 \le z \le 0)\) and Region III \((0 \le r \le a, -h_2 \le z \le 0)\) in each of which the velocity potentials are defined by \(\varPhi _j\) for \(j=1,2,3\) as \(\varPhi _j(r, \theta , z, t)= \text{ Re }{[\phi _j(r, \theta , z)\exp {(-\mathrm{i}\omega t)}]}\), with \(\text{ Re }\) denoting the real part of the quantity in brackets, \(\omega \) the angular wave frequency and \(\mathrm{i}=\sqrt{-1}\) the usual imaginary quantity. Subsequently, the incident velocity potential due to a wave of amplitude H and angular wave frequency \(\omega \) that propagates in the positive x-direction takes the following form [8, 13, 20]:

$$\begin{aligned} \phi _{\text {inc}}= & {} -\frac{\mathrm{i} gH}{\omega }\frac{\cosh k_0(z+h_3)}{\cosh k_0h_3}\sum _{m=0}^{\infty } \beta _m J_m(k_0r)\cos m\theta ,\nonumber \\ \text{ where }\nonumber \\ \beta _m= & {} {\left\{ \begin{array}{ll} 1,\;\;\text{ for } \quad m=0 , \\ 2\mathrm{i}^m,\;\;\text{ for } \quad m\ge 1, \end{array}\right. } \end{aligned}$$
(1)

with \(J_m(.)\) as the Bessel function of first kind of order m, \(k_0\) the incident wavenumber and g the acceleration due to gravity. For such a flow, Laplace’s equation is satisfied by each potential \(\phi _j\):

$$\begin{aligned} \nabla ^2\phi _j= & {} 0; \quad j=1,2,3, \end{aligned}$$
(2)

where \(\phi _j, j=1,2,3\) represent the potentials in regions I, II and III, respectively.

To construct the boundary value problems for \(\phi _j\), the boundary conditions on the free surface, sea-bed and the surface of the lower cylinder can be written in the following form:

$$\begin{aligned} \frac{\partial \phi _j}{\partial z}-\frac{\omega ^2}{g}\phi _j= & {} 0; \quad \text{ at }\quad z=0,\quad j= 1,2,3, \end{aligned}$$
(3)
$$\begin{aligned} \frac{\partial \phi _1}{\partial z}= & {} 0;\quad \text{ at }\quad z=-h_3,\quad r>b, \end{aligned}$$
(4)
$$\begin{aligned} \frac{\partial \phi _2}{\partial z}= & {} 0;\quad \text{ at }\quad z=-h_2,\quad a<r<b, \end{aligned}$$
(5)
$$\begin{aligned} \frac{\partial \phi _1}{\partial r}= & {} 0;\quad \text{ at }\quad r=b, \quad -h_3<z<-h_2, \end{aligned}$$
(6)
$$\begin{aligned} \frac{\partial \phi _3}{\partial z}= & {} 0;\quad \text{ at }\quad z=-h_2, \quad 0<r<a. \end{aligned}$$
(7)

The important condition on the porous surface of the structure is (Williams et al. [33])

$$\begin{aligned} \frac{\partial \phi _3}{\partial r}= & {} \mathrm{i} k_0G(\phi _2- \phi _3)\quad \text{ on } \quad r=a, \quad -h_1<z<0. \end{aligned}$$
(8)

The parameter G denotes the dimensionless porous parameter as used by Chwang [2]. Further, G can be expressed in the from \(G_r +\mathrm{i} G_i\) as used by Yu [34], where \(G_r\) and \(G_i\), respectively, denote the real part and the imaginary part. The diffracted velocity potential \(\phi _1\) in the exterior region satisfies the Sommerfeld radiation condition:

$$\begin{aligned} \lim _{r\rightarrow \infty }\sqrt{r}\left[ \frac{\partial (\phi _1-\phi _{\text {inc}})}{\partial r}-\mathrm{i} k_0(\phi _1-\phi _{\text {inc}})\right] =0. \end{aligned}$$
(9)

On the boundary \(r=b\), the relevant potentials \(\phi _1\) and \(\phi _2\) must satisfy the following matching conditions due to continuity of velocity and pressure:

$$\begin{aligned} \frac{\partial \phi _1}{\partial r}= & {} \frac{\partial \phi _2}{\partial r}; \quad -h_2<z<0, \end{aligned}$$
(10)
$$\begin{aligned} \phi _1= & {} \phi _2;\quad -h_2<z<0. \end{aligned}$$
(11)

Similarly, at the boundary \(r=a\), the relevant potentials \(\phi _2\) and \(\phi _3\) must satisfy following matching conditions:

$$\begin{aligned} \frac{\partial \phi _2}{\partial r}= & {} \frac{\partial \phi _3}{\partial r};\quad -h_2<z<-h_1, \end{aligned}$$
(12)
$$\begin{aligned} \phi _2= & {} \phi _3;\quad -h_2<z<-h_1. \end{aligned}$$
(13)

Using eigenfunction expansion method, expression for each potential \(\phi _j,j=1,2,3\) can be obtained as infinite series of orthogonal functions valid in the respective fluid region. The diffracted velocity potential for Region I takes the following form [21]:

$$\begin{aligned} \phi _1(r,\theta ,z)=-\frac{\mathrm{i} gH}{\omega }\left[ \sum _{m=0}^{\infty } \tau _m J_m(k_0r)\frac{\cosh k_0(z+h_3)}{\cosh k_0h_3}\cos m\theta + \sum _{m=0}^{\infty }\cos m\theta \sum _{j=0}^{\infty }{\mathcal {A}}_{mj}{\mathcal {Z}}_j^{(1)}(k_jz) {\mathcal {T}}_m^{(1)}(k_jr)\right] , \end{aligned}$$
(14)

where the unknown coefficients \({\mathcal {A}}_{mj}\) are to be determined. The wavenumbers \(k_j\) \((j=0,1,2,3,\ldots )\) are derived from the following dispersion relations:

$$\begin{aligned} \omega ^2=\left\{ \begin{array}{ll} &{}gk_j\tanh k_jh_3; \quad j=0,\\ &{}-gk_j\tan k_jh_3;\quad j\ge 1.\end{array}\right. \end{aligned}$$
(15)

To compute the wavenumbers \(k_j\) from (15), the technique adopted by Chamberlain and Porter [1] is utilized. For the benefit of readers, the technique is discussed in Appendix 6.

The vertical eigenfunctions \({\mathcal {Z}}_j^{(1)}(k_jz)\) are defined as

$$\begin{aligned} {\mathcal {Z}}_j^{(1)}(k_jz)= {\left\{ \begin{array}{ll} \frac{\cosh k_j(z+h_3)}{\cosh k_jh_3};\quad j=0,\\ \frac{\cos k_j(z+h_3) }{\cos k_jh_3}; \quad j\geqslant 1. \end{array}\right. } \end{aligned}$$

\({\mathcal {T}}_m^{(1)}(k_jr)\), the radial eigenfunctions in (14), are as follows:

$$\begin{aligned} {\mathcal {T}}_m^{(1)}(k_jr)= {\left\{ \begin{array}{ll} \frac{H_{m}^{(1)}(k_jr)}{H_{m}^{(1)'}(k_jb)};\quad j=0,\\ \frac{K_{m}(k_jr)}{K_{m}'(k_jb)};\quad j\geqslant 1, \end{array}\right. } \end{aligned}$$

with \(H_{m}^{(1)}(k_jr)\) and \(K_m(k_jr)\), respectively, denoting Hankel function of first kind and modified Bessel function of second kind of order m. Velocity potential \(\phi _2\) in Region II satisfies the structural boundary conditions and has the following form [8]:

$$\begin{aligned} \phi _2(r,\theta ,z)=-\frac{\mathrm{i} gH}{\omega }\left[ \sum _{m=0}^{\infty }\sum _{j=0}^{\infty }\left\{ {\mathcal {B}}_{mj} {\mathcal {S}}_m^{(1)}(\lambda _jr)+{\mathcal {C}}_{mj}{\mathcal {R}}_m^{(1)}(\lambda _jr)\right\} {\mathcal {Z}}_j^{(2)}(\lambda _jz)\cos m\theta \right] , \end{aligned}$$
(16)

where the unknowns \({\mathcal {B}}_{mj}\) and \({\mathcal {C}}_{mj}\) are to be determined. The eigenvalues \(\lambda _j\) are derived from

$$\begin{aligned} \omega ^2= \left\{ \begin{array}{ll} &{}g\lambda _j\tanh \lambda _jh_2;\quad j=0,\\ &{}-g\lambda _j\tan \lambda _jh_2;\quad j \ge 1.\end{array}\right. \end{aligned}$$
(17)

The vertical eigenfunctions \({\mathcal {Z}}_j^{(2)}(\lambda _jz)\) are defined as

$$\begin{aligned} {\mathcal {Z}}_j^{(2)}(\lambda _jz)= {\left\{ \begin{array}{ll} \frac{\cosh \lambda _j(z+h_2)}{\cosh \lambda _jh_2};\quad j=0,\\ \frac{\cos \lambda _j(z+h_2) }{\cos \lambda _jh_2}; \quad j\geqslant 1. \end{array}\right. } \end{aligned}$$

The pair of radial eigenfunctions \({\mathcal {S}}_{m}^{(1)}(\lambda _jr)\) and \({\mathcal {R}}_m^{(1)}(\lambda _jr)\) appearing in (16) have the following forms:

$$\begin{aligned} {\mathcal {S}}_{m}^{(1)}(\lambda _jr)= {\left\{ \begin{array}{ll} \frac{H_{m}^{(1)}(\lambda _jr)}{H_{m}^{(1)'}(\lambda _jb)};\quad j=0,\\ \frac{I_{m}(\lambda _jr)}{I_{m}'(\lambda _jb)};\quad j \ge 1, \end{array}\right. } \quad \quad {\mathcal {R}}_m^{(1)}(\lambda _jr)= {\left\{ \begin{array}{ll} \frac{H_{m}^{(2)}(\lambda _jr)}{H_{m}^{(2)'}(\lambda _jb)};\quad j=0,\\ \frac{K_{m}(\lambda _jr)}{K_{m}'(\lambda _jb)};\quad j \ge 1, \end{array}\right. } \end{aligned}$$

where \(H_{m}^{(2)}(\lambda _jr)\) and \(I_m(\lambda _jr)\), respectively, denote Hankel function of second kind and modified Bessel function of first kind of order m.

Now the potential \(\phi _3\) in region III takes the following form:

$$\begin{aligned} \phi _3(r,\theta ,z)=-\frac{\mathrm{i} gH}{\omega }\left[ \sum _{m=0}^{\infty }\cos m\theta \sum _{j=0}^{\infty }{\mathcal {D}}_{mj}{\mathcal {Z}}_j^{(2)}(\lambda _jz) {\mathcal {U}}_m^{(1)}(\lambda _jr)\right] , \end{aligned}$$
(18)

where \({\mathcal {D}}_{mj}\) are the unknown coefficients to be determined. The radial eigenfunctions \({\mathcal {U}}_m^{(1)}(\lambda _jr)\) are as follows:

$$\begin{aligned} {\mathcal {U}}_m^{(1)}(\lambda _jr)= {\left\{ \begin{array}{ll} \frac{J_{m}(\lambda _jr)}{J_{m}'(\lambda _ja)};\quad j=0,\\ \frac{I_{m}(\lambda _jr)}{I_{m}'(\lambda _ja)};\quad j\geqslant 1. \end{array}\right. } \end{aligned}$$

2.2 Determination of unknown coefficients

Applying the matching conditions (10) and (11) for \(-h_2<z<0\) and the orthogonality of the depth eigenfunctions \({\mathcal {Z}}_\alpha ^{(2)}(\lambda _\alpha z)\), the following are obtained:

$$\begin{aligned} \sum _{j=0}^{\infty }{\mathcal {A}}_{mj}{\mathcal {T}}_j^{(1)'}(k_jb){\mathcal {Q}}_{\alpha j}-\bigg ({\mathcal {B}}_{m\alpha }{\mathcal {S}}_{m}^{(1)'}(\lambda _\alpha b)+{\mathcal {C}}_{m\alpha }{\mathcal {R}}_{m}^{(1)'}(\lambda _\alpha b)\bigg ){\mathcal {V}}_{\alpha \alpha }= & {} -\beta _m J_{m}'(k_0b){\mathcal {Q}}_{\alpha 0},\;\alpha \ge 0,\quad \end{aligned}$$
(19)
$$\begin{aligned} \sum _{j=0}^{\infty }{\mathcal {A}}_{mj}{\mathcal {T}}_j^{(1)}(k_jb){\mathcal {Q}}_{\alpha j}-\bigg ({\mathcal {B}}_{m\alpha }{\mathcal {S}}_{m}^{(1)}(\lambda _\alpha b)+{\mathcal {C}}_{m\alpha }{\mathcal {R}}_{m}^{(1)}(\lambda _\alpha b)\bigg ){\mathcal {V}}_{\alpha \alpha }= & {} -\beta _m J_{m}(k_0b){\mathcal {Q}}_{\alpha 0},\;\alpha \ge 0. \quad \end{aligned}$$
(20)

Again using the condition (12), along with the orthogonality of eigenfunctions \({\mathcal {Z}}_\alpha ^{(2)}(\lambda _\alpha z)\), we obtain

$$\begin{aligned} \sum _{j=0}^{\infty }{\mathcal {D}}_{m\alpha }{\mathcal {U}}_{ m}^{(1)'}(\lambda _\alpha a){\mathcal {L}}_{\alpha j}-\sum _{j=0}^{\infty }\bigg ({\mathcal {B}}_{m\alpha }{\mathcal {S}}_{m}^{(1)'} (\lambda _\alpha a)+{\mathcal {C}}_{m\alpha }{\mathcal {R}}_{m}^{(1)'}(\lambda _\alpha a)\bigg ){\mathcal {L}}_{\alpha j}= & {} 0,\quad \;\alpha \ge 0.\quad \end{aligned}$$
(21)

Now application of the porous wall condition (8) for the depth \(-h_1<z<0\) and the orthogonality of the eigenfunctions \({\mathcal {Z}}_\alpha ^{(2)}(\lambda _\alpha z)\) gives the following:

$$\begin{aligned}&\sum _{j=0}^{\infty }\bigg ({\mathcal {U}}_{m}^{(1)'}(\lambda _j a)+\mathrm{i} k_0G{\mathcal {U}}_{m }^{(1)}(\lambda _j a)\bigg ){\mathcal {D}}_{mj }{\mathcal {W}}_{\alpha j}+\mathrm{i} k_0G\sum _{j=0}^{\infty }\bigg ({\mathcal {B}}_{mj}{\mathcal {S}}_{j}^{(1)}(\lambda _j a)+{\mathcal {C}}_{mj}{\mathcal {R}}_{j}^{(1)}(\lambda _j a)\bigg ){\mathcal {W}}_{\alpha j}=0,\nonumber \\&\quad \alpha \ge 0, \end{aligned}$$
(22)

where

$$\begin{aligned} {\mathcal {Q}}_{\alpha ,j}= & {} \int _{-h_2}^{0}{\mathcal {Z}}_\alpha ^{(2)}(\lambda _\alpha z){\mathcal {Z}}_j^{(1)}(k_jz) \mathrm {d} z, \end{aligned}$$
(23)
$$\begin{aligned} {\mathcal {V}}_{\alpha ,\alpha }= & {} \int _{-h_2}^{0}{\mathcal {Z}}_\alpha ^{(2)}(\lambda _\alpha z){\mathcal {Z}}_\alpha ^{(2)}(\lambda _\alpha z) \mathrm {d} z, \end{aligned}$$
(24)
$$\begin{aligned} {\mathcal {L}}_{\alpha ,j}= & {} \int _{-h_2}^{-h_1}{\mathcal {Z}}_\alpha ^{(2)}(\lambda _\alpha z){\mathcal {Z}}_j^{(2)}(\lambda _j z) \mathrm {d} z, \end{aligned}$$
(25)
$$\begin{aligned} {\mathcal {W}}_{\alpha ,j}= & {} \int _{-h_1}^{0}{\mathcal {Z}}_\alpha ^{(2)}(\lambda _\alpha z){\mathcal {Z}}_j^{(2)}(\lambda _j z)\mathrm {d} z. \end{aligned}$$
(26)

For such studies, two important aspects are the exciting forces and the wave run-up. Wave exciting forces are those forces which are induced by the direct action of the incident waves on the body. In linear theory, these forces are directly proportional to the wave amplitude, which is assumed to be small. Wave run-up is defined as the maximum onshore elevation reached by a wave, relative to the wave-averaged shoreline position. In order to obtain the exciting forces and wave run-up, the unknown coefficients are required to be computed. By truncating each of the infinite series appearing in Eqs. (19)–(22) after some terms \(N=20\), the values of the coefficients \({\mathcal {A}}_{mj}\), \({\mathcal {B}}_{mj}\), \({\mathcal {C}}_{mj}\) and \({\mathcal {D}}_{mj}\) are computed. It is worthwhile mentioning that excellent convergence is attained by such truncation as already described in [20]. As a consequence, the following linear system of algebraic equations is obtained for determining the unknowns:

$$\begin{aligned} {\mathcal {H}}_l{\mathcal {X}}_l={\mathcal {E}}_l , \end{aligned}$$
(27)

with \( {\mathcal {X}}_l=[{\mathcal {A}}_{l1},{\mathcal {A}}_{l2},\ldots , {\mathcal {A}}_{lN},{\mathcal {B}}_{l1},{\mathcal {B}}_{l2},\ldots ,{\mathcal {B}}_{lN},{\mathcal {C}}_{l1},{\mathcal {C}}_{l2},\ldots , {\mathcal {C}}_{lN},{\mathcal {D}}_{l1},{\mathcal {D}}_{l2},\ldots ,{\mathcal {D}}_{lN}]^t\), \({\mathcal {H}}_l\) the coefficient matrices, \({\mathcal {E}}_l\) the right-hand vectors.

Gaussian elimination method that was adopted in [20] is employed here also for solving this system of equations.

To justify the selection of \(N=20\) for evaluating the coefficients \({\mathcal {A}}_{mj}\), \({\mathcal {B}}_{mj}\), \({\mathcal {C}}_{mj}\) and \({\mathcal {D}}_{mj}\), we present two tables (Tables 1, 2) for the coefficients \({\mathcal {A}}_{mj}\) and \({\mathcal {B}}_{mj}\) from which it becomes clear why \(N=20\) is selected. The values of the coefficients between \(N=20\) and \(N=25\) have very small variations which can be easily neglected. It is found that the values of the potential coefficients are correct up to six decimal places. A similar convergence was also observed by Mandal et al. [14] too. However, for each table, we choose only two coefficients for want of space. It may be noted that values for the rest of the coefficients also follow a similar trend.

Table 1 Coefficients \({\mathcal {A}}_{1N}\) for \(G=1\), \(a/b=0.50\), \(h_2/h_3=0.66\) and \(h_1/h_2=0.37\)
Full size table
Table 2 Coefficients \({\mathcal {B}}_{1N}\) for \(G=1\), \(a/b=0.50\), \(h_2/h_3=0.66\) and \(h_1/h_2=0.37\)
Full size table

2.3 Horizontal exciting forces and wave run-up

The exciting forces acting on the upper and the lower cylinders in the direction of wave propagation can be computed by integrating the pressure at the surface of the structure. The forces \(\tilde{{{\mathcal {F}}}}_x^{j}=\text{ Re }[{\tilde{F}}_x^{j}\exp ({-\mathrm{i}\omega t})]\) for \(j=1,2\) (\(j=1\) refers to upper cylinder and \(j=2\) to lower cylinder) are defined as follows:

$$\begin{aligned} {\tilde{F}}_x^{1}= & {} \mathrm{i} \omega \rho \int _{-h_1}^{0} \int _{0}^{2\pi } \phi _3(a,\theta ,z) \cos {\theta }\;\mathrm {d} z\mathrm {d} \theta -\mathrm{i} \omega \rho \int _{-h_1}^{0} \int _{0}^{2\pi } \phi _2(a,\theta ,z) \cos {\theta }\; \mathrm {d} z \mathrm {d} \theta ,\;\;\;\;\;\;\;\;\;\;\;\;\;\; \end{aligned}$$
(28)
$$\begin{aligned} {\tilde{F}}_x^{2}= & {} -\mathrm{i} \omega \rho \int _{-h_3}^{-h_2} \int _{0}^{2\pi } \phi _1(b,\theta ,z) \cos {\theta }\; \mathrm {d} z \mathrm {d} \theta .\;\;\;\;\;\;\;\;\;\;\;\;\;\; \end{aligned}$$
(29)

The exciting forces at the upper and lower cylinder are non-dimensionalized by dividing \({\tilde{F}}_x^{1}\) and \({\tilde{F}}_x^{2}\) by \(\rho g a h_2H\) and \(\rho g b h_2H\), respectively (Froude–Krylov force acting on cylinders of radius a and b, respectively). The Froude–Krylov force is the force introduced by the unsteady pressure field generated by undisturbed waves. The Froude–Krylov force does, together with the diffraction force, make up the total non-viscous forces acting on a floating body in regular waves. Therefore, the Froude–Krylov force is the force that the fluid would exert on the body, had the presence of the body not disturbed the flow. We now denote the non-dimensionalized exciting forces for upper and lower cylinder by \( F^1_x=\displaystyle \frac{|{{\tilde{F}}}_x^1|}{|\rho g a h_2H|}\) and \( F^2_x=\displaystyle \frac{|{{\tilde{F}}}_x^1|}{|\rho g b h_2H|}\), respectively. Similar kind of non-dimensionalization is noticed to have been followed by Ning et al. [16], Sarkar and Bora [24] and Williams and Li [31].

The wave run-up for the exterior and interior regions, as given by \(\eta _j(r,\theta ,t)=Re[\zeta _j(r,\theta )\exp ({-\mathrm{i}\omega t})]\) for \(j=1,2,3\) (j denoting regions I, II and III), is calculated by applying the following dynamic free surface condition:

$$\begin{aligned} \eta _j=-\frac{1}{g}\frac{\partial \phi _j}{\partial t},\quad z=0,\quad j=1,2,3. \end{aligned}$$
(30)

2.4 Numerical discussion

In practice, G always possesses positive real and imaginary parts but when the resistance effect against the flow dominates the inertial effect of the fluid inside the porous material, then G becomes real. Conforming to our problem, we discuss only real part of G, that means when resistance effect dominates inertial effect. Further, it is observed that even if G is imaginary or a mix of real and imaginary, there is no significant deviation at all from present results. In this context, we later produce two results by considering complex values of G.

Fig. 2
figure 2

Exciting forces \(\displaystyle F_x^1\) and \(\displaystyle F_x^2\) against wavenumber for various values of radius ratio a/b with \(h_1/h_2=0.37\), \(h_2/h_3=0.66\) and \(G=1\)

Full size image

Figure 2a and b, respectively, presents the exciting forces \(\displaystyle F_x^1\) acting on the upper cylinder and \(\displaystyle F_x^2\) on the lower cylinder plotted against wavenumber for various values of radius ratio a/b with \(G=1\), \(h_1/h_2=0.37\) and \(h_1/h_3=0.66\). From Fig. 2a, it is observed that the value of the force is initially nonzero. For certain values of \( k_0h_2,\) waveload on the upper cylinder becomes very low and it creates turning points. This may be due to the interaction of incoming and scattered waves leading to destructive interference near the upper cylinder. The clear observation is that higher forces occur for lower values of a/b. This is due to more energy getting concentrated near the upper cylinder and consequently resulting in an increase in exciting force. It establishes that the size of the cylinder needs to be adjusted for getting higher or lower force on the cylinder surface. Higher values of the force occur for lower values of a/b, i.e., when the radius of the upper cylinder tends to be much smaller compared to that of the lower cylinder. Also from Fig. 2b, it is observed that all curves maintain a similar trend (i.e., start from zero and then take increasing values as the values of the wavenumber increase). That the higher values of force correspond to the lower values of radius ratio a/b means that for a much smaller upper cylinder or a much bigger lower cylinder, an increase in exciting force occurs.

Fig. 3
figure 3

Exciting forces \(\displaystyle F_x^1\) and \(\displaystyle F_x^2\) against wavenumber corresponding to different values of \(h_1/h_2\) for \(a/b=0.50\), \(h_2/h_3=0.66\) and \(G=1\)

Full size image

The exciting forces \(\displaystyle F_x^1\) acting on the upper cylinder and \(\displaystyle F_x^2\) on the lower cylinder corresponding to different values of \(h_1/h_2\) with fixed values \(G=1\), \(h_2/h_3=0.66\) and \(a/b=0.50\) are plotted against wavenumber in Fig. 3a and b, respectively. In Fig. 3a, the same trend of graph pattern as observed in Fig. 2a is observed. The oscillation is observed to get shifted toward left for increasing values of \(h_1/h_2\). The occurrence of shift in these curves may be due to the phase shift of the wave with the change of the drafts of the porous cylindrical system. The main observation is that the higher values of the force occur within lower values of \(h_1/h_2\), i.e., when the draft of the upper cylinder with respect to its upper surface is reduced which makes the cylinder closer to the free surface. Figure 3b shows that the exciting force \(\displaystyle F_x^2\) acting on the lower cylinder takes higher values corresponding to lower values of \(h_1/h_2\). This implies that when the draft of the upper cylinder is less, then the force acting on the lower cylinder increases due to a larger fluid region between the cylinders.

Fig. 4
figure 4

Exciting force \(\displaystyle F_x^1\) plotted against wavenumber for different values of porous coefficients G with fixed values \(a/b=0.50\), \(h_2/h_3=0.66\) and \(h_1/h_2=0.37\)

Full size image

In Fig. 4a and b, the exciting force \(\displaystyle F_x^1\) acting on the upper cylinder is examined by plotting it against wavenumber corresponding to various values of porous coefficient G (real values in Fig. 4a and complex values in Fig. 4b) for the fixed values \(a/b=0.5\), \(h_2/h_3=0.66\) and \(h_1/h_2=0.37\). From Fig. 4a, it is clearly visible that G has a reasonable influence on the exciting forces and all curves exhibit similar behavior as in the earlier cases. Also, lower values of porous coefficient give rise to higher values of force. As the porous coefficient G takes increasing values, more waves pass through the structure which brings reduction of the resistance of the cylinder to the wave motion. Also from Fig. 4b, it is observed that there is no significant effect of the imaginary part of the porous parameter on exciting force on the upper hollow porous cylinder and hence consideration of real G is justified for further investigation. In other words, the inertial effect corresponding to G is not significant enough.

Figures 5 and 6 present contour plots of the wave run-up nearer the free surface corresponding to two different values of frequency. They illustrate that when the wave gets scattered by the cylinder, the elevation gets reduced. By comparison of these two figures, it is clearly noticed that corresponding to higher frequency incident waves, the pattern of the diffracted wave becomes more assertive in addition to the observation of appearance of more number of wave ripples in the annular region.

Fig. 5
figure 5

Contour plot for the wave run-up \(\displaystyle |\zeta _1(r,\theta )|/H\) at free surface for \(k_0b=3.5\), \(a/b=0.50\), \(h_1/h_2=0.37\), \(h_2/h_3=0.66\) and \(G=1\)

Full size image
Fig. 6
figure 6

Contour plot for the wave run-up \(\displaystyle |\zeta _1(r,\theta )|/H\) at free surface for \(k_0b=1.75\), \(a/b=0.50\), \(h_1/h_2=0.37\), \(h_2/h_3=0.66\) and \(G=1\)

Full size image

It is clear from the results that due to the porosity of the cylinder, dissipation of wave energy occurs which results in reduction of wave energy. The energy loss is given by the difference of the energy due to the presence of the solid wall, i.e., for \(G=0\) and that due to the presence of the porous wall divided by the energy due to the presence of the solid wall (see Richey et al. [17]), i.e.,

$$\begin{aligned} {\text{ Energy } \text{ loss }}= & {} \frac{\text{ Energy } \text{ in } \text{ the } \text{ presence } \text{ of } \text{ the } \text{ solid } \text{ wall }-\text{ Energy } \text{ in } \text{ the } \text{ presence } \text{ of } \text{ the } \text{ porous } \text{ wall }}{\text{ Energy } \text{ in } \text{ the } \text{ presence } \text{ of } \text{ the } \text{ solid } \text{ wall }} \times 100. \quad \nonumber \\ \end{aligned}$$
(31)

Based on (31), we present Table 3 which gives some idea about energy loss due to various values of the porosity of the porous wall.

Table 3 Energy loss due to the hollow porous cylinder for various values of G with \(k_0h_2=0.25\), \(a/b=0.50\), \(h_2/h_3=0.66\) and \(h_1/h_2=0.37\)
Full size table
Fig. 7
figure 7

Schematic diagram of the second problem

Full size image

3 Two coaxial cylinders: upper porous cylinder and lower rigid cylinder

3.1 Theoretical formulation

In this case, we take up two coaxial cylinders such that the upper cylinder of radius a is fully porous (it is no more hollow) with an impermeable bottom and the lower cylinder of radius b is rigid. There are four fluid regions considered: Region I \((r\ge b, -h_3\le z\le 0)\); Region II \((a \le r \le b, -h_2 \le z \le 0)\) ; Region III \((0 \le r \le a, -h_2 \le z \le -h_1)\) and Region IV \((0 \le r \le a, -h_1 \le z \le 0)\) (Fig. 7). In each of these regions, the velocity potentials are defined by \(\varPhi _j(r,\theta ,z,t)=\text{ Re( }\phi _j(r,\theta ,z)\exp (-\mathrm{i} \omega t))\) for \(j=1,2,3,4\). In this case also, each potential satisfies Laplace’s equation in the respective region as defined above. The boundary conditions on the free surface, sea-bed and the surface of the bottom cylinder are same as Eqs. (3)–(6) from the first problem along with the following additional conditions for \(\phi _3\) and \(\phi _4\):

$$\begin{aligned} \frac{\partial \phi _4}{\partial z}= & {} 0;\quad \text{ at }\quad z=-h_1,\quad 0<r<a, \end{aligned}$$
(32)
$$\begin{aligned} \frac{\partial \phi _3}{\partial z}= & {} 0;\quad \text{ at }\quad z=-h_2,\quad 0<r<a, \end{aligned}$$
(33)
$$\begin{aligned} \frac{\partial \phi _3}{\partial z}= & {} 0;\quad \text{ at }\quad z=-h_1, \quad 0<r<a. \end{aligned}$$
(34)

The condition on the porous boundary wall has the following form [29]:

$$\begin{aligned} \frac{\partial \phi _4}{\partial r}= & {} \mathrm{i} k_0G(\phi _2-\phi _4)\quad \text{ on } \quad r=a, \quad -h_1<z<0. \end{aligned}$$
(35)

The matching conditions are expressed by Eqs. (10) and (11) along with the following additional conditions:

$$\begin{aligned} \frac{\partial \phi _4}{\partial r}= & {} \frac{\partial \phi _2}{\partial r};\quad \text{ at } \quad r=a,\quad -h_1<z<0, \end{aligned}$$
(36)
$$\begin{aligned} \frac{\partial \phi _3}{\partial r}= & {} \frac{\partial \phi _2}{\partial r};\quad \text{ at } \quad r=a,\quad -h_2<z<-h_1, \end{aligned}$$
(37)
$$\begin{aligned} \phi _3= & {} \phi _2;\quad \text{ at } \quad r=a,\quad -h_2<z<-h_1. \end{aligned}$$
(38)

The potentials \(\phi _1\) and \(\phi _2\) are given by (14) and (16), respectively. Further, \(\phi _3\) has the following form:

$$\begin{aligned} \phi _3(r, \theta ,z)=-\frac{\mathrm{i} gH}{\omega }\left[ \sum _{m=0}^{\infty }\cos m\theta \sum _{j=0}^{\infty }\left[ {\mathcal {F}}_{mj}{\mathcal {N}}_m^{(1)} (\mu _jr)\right] {\mathcal {Z}}_j^{(3)}(\mu _jz)\right] , \end{aligned}$$
(39)

where \({\mathcal {F}}_{mj}\) are the coefficients to be determined. The vertical eigenfunctions \({\mathcal {Z}}_j^{(3)}(\mu _jz)\) are defined as

$$\begin{aligned} {\mathcal {Z}}_j^{(3)}(\mu _jz)= {\left\{ \begin{array}{ll} \frac{\sqrt{2}}{2};&{}\quad j=0,\\ \cos \mu _j(z+h_2); &{}\quad j\geqslant 1. \end{array}\right. } \end{aligned}$$

\(\mu _j\) can be found from

$$\begin{aligned} \mu _j=\frac{\pi j}{h_2-h_1},&\quad j=0,1,2,\ldots . \end{aligned}$$

The radial eigenfunctions \({\mathcal {N}}_m^{(1)}\) appearing in (39) are as follows:

$$\begin{aligned} {\mathcal {N}}_m^{(1)}= {\left\{ \begin{array}{ll} \frac{r^{m}}{a^{m-1}};&{}\quad j=0,\\ \frac{I_{m}(\mu _jr)}{I_{m}'(\mu _ja)};&{}\quad j\geqslant 1. \end{array}\right. } \end{aligned}$$

Now potential \(\phi _4\) in Region IV takes the form

$$\begin{aligned} \phi _4(r,\theta ,z)=-\frac{\mathrm{i} gH}{\omega }\left[ \sum _{m=0}^{\infty }\cos m\theta \sum _{j=0}^{\infty }{\mathcal {G}}_{mj}{\mathcal {Z}}_j^{(4)}(\sigma _jz) {\mathcal {O}}_m^{(1)}(\sigma _jr)\right] , \end{aligned}$$
(40)

where \({\mathcal {G}}_{mj}\) are unknown coefficients. The vertical eigenfunctions \( {\mathcal {Z}}_j^{(4)}(\sigma _jz)\) here are defined as

$$\begin{aligned} {\mathcal {Z}}_j^{(4)}(\sigma _jz)= {\left\{ \begin{array}{ll} \frac{\cosh \sigma _j(z+h_1)}{\cosh \sigma _jh_1};&{}\quad j=0,\\ \frac{\cos \sigma _j(z+h_1)}{\cos \sigma _jh_1};&{} \quad j\geqslant 1. \end{array}\right. } \end{aligned}$$

The wavenumbers \(\sigma _j\) \((j=0,1,2,3,\ldots )\) are derived from the following dispersion relations:

$$\begin{aligned} \omega ^2= {\left\{ \begin{array}{ll} g\sigma _j\tanh \sigma _jh_1; &{}\quad j=0,\\ -g\sigma _j\tan \sigma _jh_1;&{}\quad j\ge 1. \end{array}\right. } \end{aligned}$$

The radial eigenfunctions \({\mathcal {O}}_m^{(1)}(\sigma _jr)\) are as follows:

$$\begin{aligned} {\mathcal {O}}_m^{(1)}(\sigma _jr)= {\left\{ \begin{array}{ll} \frac{J_{m}(\sigma _jr)}{J_{m}'(\sigma _ja)};&{}\quad j=0,\\ \frac{I_{m}(\sigma _jr)}{I_{m}'(\sigma _ja)};&{}\quad j\geqslant 1. \end{array}\right. } \end{aligned}$$

3.2 Determination of unknown coefficients

Applying the matching conditions (10) and (11) for \(-h_2<z<0\) and also the orthogonality of the eigenfunctions, we get the first two equations (19) and (20). Then, using matching condition (36) for the depth \(-h_1<z<0\), along with the orthogonality of the eigenfunctions \( {\mathcal {Z}}_\alpha ^{(4)}(\sigma _\alpha z)\), we get

$$\begin{aligned} {\mathcal {G}}_{m\alpha }{\mathcal {O}}_{m}^{(1)'}(\sigma _\alpha a){\mathcal {X}}_{\alpha \alpha }-\sum _{j=0}^{\infty }\bigg ({\mathcal {B}}_{mj}{\mathcal {S}}_{j}^{(1)'}(\lambda _j a)+{\mathcal {C}}_{mj}{\mathcal {R}}_{j}^{(1)'}(\lambda _j a)\bigg ){\mathcal {P}}_{\alpha j}= & {} 0,\quad \;\alpha \ge 0.\quad \end{aligned}$$
(41)

Again using the condition (37) for the depth \(-h_2<z<-h_1\), along with the orthogonality of eigenfunctions \( {\mathcal {Z}}_\alpha ^{(3)}(\mu _\alpha z)\), we obtain

$$\begin{aligned} \bigg ({\mathcal {F}}_{m\alpha }{\mathcal {N}}_{m}^{(1)'}(\mu _\alpha a)\bigg ){\mathcal {K}}_{\alpha \alpha }-\sum _{j=0}^{\infty }\bigg ({\mathcal {B}}_{mj}{\mathcal {S}}_{j}^{(1)'}(\lambda _j a)+{\mathcal {C}}_{mj}{\mathcal {R}}_{j}^{(1)'}(\lambda _j a)\bigg ){\mathcal {Y}}_{\alpha j}= & {} 0,\quad \;\alpha \ge 0.\quad \quad \quad \end{aligned}$$
(42)

Similarly, with the help of matching condition (35) for the depth \(-h_1<z<0\), along with orthogonality of the eigenfunctions \( {\mathcal {Z}}_\alpha ^{(4)}(\sigma _\alpha z)\), we get

$$\begin{aligned} {\mathcal {G}}_{m\alpha }(1+\mathrm{i} k_0 G{\mathcal {O}}_{m}^{(1)}(\sigma _\alpha a)){\mathcal {X}}_{\alpha \alpha }-\mathrm{i} k_0G\sum _{j=0}^{\infty }\bigg ({\mathcal {B}}_{mj}{\mathcal {S}}_{j}^{(1)}(\lambda _j a)+{\mathcal {C}}_{mj}{\mathcal {R}}_{j}^{(1)}(\lambda _j a)\bigg ){\mathcal {P}}_{\alpha j}= & {} 0,\quad \;\alpha \ge 0,\quad \end{aligned}$$
(43)

where

$$\begin{aligned} {\mathcal {P}}_{\alpha ,j}= & {} \int _{-h_1}^{0}{\mathcal {Z}}_\alpha ^{(4)}(\sigma _\alpha z){\mathcal {Z}}_j^{(2)}(\lambda _jz) \mathrm {d} z, \end{aligned}$$
(44)
$$\begin{aligned} {\mathcal {X}}_{\alpha ,\alpha }= & {} \int _{-h_1}^{0}{\mathcal {Z}}_\alpha ^{(4)}(\sigma _\alpha z){\mathcal {Z}}_\alpha ^{(4)}(\sigma _\alpha z)\mathrm {d} z, \end{aligned}$$
(45)
$$\begin{aligned} {\mathcal {Y}}_{\alpha ,j}= & {} \int _{-h_2}^{-h_1}{\mathcal {Z}}_\alpha ^{(3)}(\mu _\alpha z){\mathcal {Z}}_j^{(2)}(\lambda _jz)\mathrm {d} z, \end{aligned}$$
(46)
$$\begin{aligned} {\mathcal {K}}_{\alpha ,\alpha }= & {} \int _{-h_2}^{-h_1}{\mathcal {Z}}_\alpha ^{(3)}(\mu _\alpha z){\mathcal {Z}}_\alpha ^{(3)}(\mu _\alpha z)\mathrm {d} z. \end{aligned}$$
(47)

To calculate the unknown coefficients, the same technique as used in the earlier problem is followed here too.

Fig. 8
figure 8

Comparison of hydrodynamic force of the present work with that of Garrett [6]

Full size image

4 Validation of the present model

To validate our present analytical model for solving the problem, we compare one result with that of Garrett [6], i.e., when the upper cylinder is considered to be a solid impermeable cylinder (i.e., \(G=0\)) and the height of the lower cylinder is taken to be zero, i.e., the lower cylinder is not present at all in this comparison case. All the parameters in our problem are reconsidered conforming to Garrett’s work so that our problem can be converted to the same physical problem. We consider a floating cylinder corresponding to \(G = 0, h_3/a =0.75, (h_1-h_3)/a =0.50\). Figure 8 depicts the hydrodynamic force acting on outer wall for both Garrett’s work and our work from which an excellent agreement is reached. In view of this, our model can be considered effective and hence can be utilized to study and analyze different aspects of various parameters for such problems.

Fig. 9
figure 9

Exciting force \(\displaystyle F_x^1\) and \(\displaystyle F_x^2\) plotted against wavenumber for various values of radius ratio a/b with \(h_1/h_2=0.37\), \(h_2/h_3=0.66\) and \(G=1\)

Full size image

4.1 Numerical discussion

In Fig. 9a and b, the exciting forces \(\displaystyle F_x^1\) acting on the upper cylinder and \(\displaystyle F_x^2\) acting on the lower cylinder are plotted, respectively, against wavenumber for various values of radius ratio a/b with fixed values \(G=1\), \(h_1/h_2=0.37\) and \(h_2/h_3=0.66\). Figure 9a shows that the exciting force acting on the upper cylinder increases corresponding to a reduction in the value of the radius ratio. Comparing Figs. 2a and 9a, it is clearly visible that the exciting force for this case (presence of solid porous cylinder at the top) is higher at \(r=a\) than that in the earlier case (presence of hollow porous cylinder at the top). Higher values of the force occur for lower values of a/b, i.e., when the radius of the upper cylinder tends to be much smaller compared to that of the lower cylinder. Figure 9b indicates that the wave force acting on the lower cylinder increases as the radius ratio a/b decreases. This implies that in order to achieve lower forces, the configuration is to be made such that the sizes of the lower and the upper cylinder must not be much different from each other with the restriction \(a<b\).

Fig. 10
figure 10

Exciting forces \(\displaystyle F_x^1\) and \(\displaystyle F_x^2\) against wavenumber corresponding to different values of \(h_1/h_2\) for \(a/b=0.50\), \(h_2/h_3=0.66\) and \(G=1\)

Full size image

Figure 10a and b, respectively, presents the exciting forces \(\displaystyle F_x^1\) acting on the upper cylinder and \(\displaystyle F_x^2\) acting on the lower cylinder plotted against wavenumber corresponding to various values of draft \(h_1/h_2\) with \(G=1\), \(h_2/h_3=0.66\) and \(a/b=0.50\). Figure 10a shows that force increases when \(h_1/h_2\) decreases. This implies that the draft of the upper cylinder has a significant effect on the exciting force. Further, the exciting force acting at the cylinder surface \(r=a\) in Fig. 10a is found to be similar to that observed in Fig. 3a. The main observation is that the higher values of the force occur within lower values of \(h_1/h_2\), i.e., when the draft of the upper cylinder with respect to its upper surface is reduced which makes the cylinder closer to the free surface. From Fig. 10b, the observation here is that the force increases corresponding to decreasing values of \(h_1/h_2\). This shows that a lower value of the draft of the upper cylinder, which results in a larger fluid region between the cylinders, is responsible for the occurrence of higher force on the lower cylinder.

Fig. 11
figure 11

Exciting force \(\displaystyle F_x^1\) acting on the upper cylinder plotted against wavenumber for different values of porous coefficient G with fixed values \(a/b=0.50\), \(h_2/h_3=0.66\) and \(h_1/h_2=0.37\)

Full size image

Figure 11 depicts the variation of exciting force \(\displaystyle F_x^1\) at \(r=a\) plotted against dimensionless wavenumber for various values of G (both real and complex) corresponding to the fixed values \(h_1/h_2=0.37\), \(h_2/h_3=0.66\) and \(a/b=0.50\). Comparing Figs. 4 and 11, it is evident that for the earlier case (presence of hollow porous cylinder at the top), the exciting force is not as pronounced as is observed in this case (presence of solid porous cylinder at the top). The peak value of the force occurs for \(G=1\) and the force on the upper cylinder, in general, reduces corresponding to increasing values of |G|. This establishes the influence of the porosity of the upper cylinder on the exciting forces.

Comparing the results of both the cases of keeping a hollow porous or a solid porous cylinder at the top, it can be seen that corresponding to the same set of values of radius ratio a/b, draft \(h_1/h_2\) and porous coefficient G, the exciting force is higher for the solid porous cylinder case than the hollow porous cylinder case.

Based on (31), as observed for the earlier case, here also we can observe reduction of wave energy due to dissipation by the porous structure under consideration. Energy loss by the solid porous cylinder is presented in Table 4 corresponding to various values of G.

Table 4 Energy loss due to the solid porous cylinder for various values of G with \(k_0h_2=0.25\), \(a/b=0.50\), \(h_2/h_3=0.66\) and \(h_1/h_2=0.37\)
Full size table

5 Conclusion

The current work caries out a theoretical study on the interaction of linear water waves with a system consisting of two coaxial vertical cylinders in the form of a riding hollow or a solid porous cylinder at the top and a bottom-mounted solid rigid cylinder. The radius of the lower cylinder is taken to be greater than the radius of the upper cylinder. By using the familiar methods of eigenfunction expansion and separation of variables, this diffraction problem governed by Laplace’s equation is solved. The main objective here is to study the exciting force and wave run-up due to the system interacting with the water waves. Subsequently, it is concluded through appropriate graphical representation that variation of values in radii, draft and porosity has significant impact on the exciting force and wave run-up. It is found that for the first case (i.e., a riding hollow porous cylinder at the top), the force acting on the upper cylinder takes increasing values corresponding to lower values of radius ratio a/b. Further, for this case, the force becomes higher also corresponding to lower values of draft \(h_1/h_2\). It is observed that higher force occurs corresponding to lower porous coefficients. It is also observed that for fixed radius, porosity and depth, the wave run-up is more visible corresponding to increasing values of wavenumber. It is further observed that the exciting force for the second case (i.e., a solid porous cylinder at the top) is higher at the surface of the upper cylinder than that in the first case (i.e., a hollow porous cylinder at the top). Since wave energy is dissipated due to the porosity of the structure, results are also presented for energy loss corresponding to various porosity values which establish that more energy reduction takes place due to consideration of higher porosity values. For the second case (i.e., a solid porous cylinder at the top), higher values of the force occur within lower values of draft ratio (\(h_1/h_2\)). Also, the force increases for lower values of radius ratio (a/b). A successful validation shows that the current model will be effective for such problems. This model can be considered as a wave energy device. Proper positioning of the device will allow the device to capture more waves. The expectation here is that the configuration and formulations suggested and results obtained in this work will provide essential information to design suitable and effective porous structures that may be installed in ocean and that these structures will efficiently serve as wave energy devices and also for other meaningful purposes.