Wave trapping by porous breakwater near a rigid wall under the influence of ocean current

Abstract

The present work investigates the water wave interaction with bottom-standing thick porous trapezoidal-shaped structures and shore-side vertical rigid wall in the presence of uniform ocean currents. This study has been done to understand the impact of different physical parameters like friction, porosity, and ocean currents along with different structural parameters (width and height) on different phenomena like wave energy reflection, wave forces, wave energy dissipation, etc. The quadratic boundary element method-based numerical technique has been used to solve the boundary value problem. The structural porosity is modeled using Sollitt and Cross’s model of water wave interaction with thick porous structures. Several results associated with the wave energy reflection and energy dissipation have been analyzed. Also, the wave force exerted by the incoming waves has been investigated to check the stability and sustainability of the right vertical rigid wall and porous structure. The Doppler-shift effect is observed in wave transformation characteristics due to the presence of ocean currents. The impact of following and opposing ocean currents can be seen in the graph of wave energy reflection, dissipation, and wave forces. The periodic patterns can be observed clearly in wave characteristics like wave energy reflection, dissipation, and wave forces when plotted against the non-dimensional separation gap between the porous breakwater and shore-side rigid seawall.

Introduction

Due to the widespread use of the breakwaters in coastal areas, the protection of solid seawall structures, safe harboring and protecting the cliffs, emerged beaches¹, and dunes from exceptional wave loads coming from the deep ocean has attracted a lot of attention recently². It has been observed that the constant incidence of wave stroke has reduced the service life of several types of seawalls, including vertical (Concrete, Steel Sheet Piling), curved (concave, convex), mount (Riprap, Gabion), and stepped seawalls structures³. Because they are primarily inflexible, seawalls reflect as much wave energy as possible towards the deep sea. Due to this, these kinds of seawalls experience high wave loads due to their reflective nature. Generally, the collapse of these seawalls results in substantial economic, shoreline, and environmental loss for coastal communities. Therefore, researchers and specialists recommended impermeable buildings with rigid structures/breakwaters to safeguard these various forms of seawalls. Since wave load is huge when impermeable breakwaters are subjected to wave impact because nearly all of the wave energy is reflected to the deep sea, resulting again damage to these impermeable and rigid structures/breakwaters⁴. To mitigate the failure of seawalls along with rigid and impermeable structures, the coastal engineers proposed a range of porous structures in different geometric arrangements. Since permeable structures absorb/trap wave energy^5,6,7 and reduce wave height in coastal zones, they have been frequently erected as breakwaters for long-term protection of shorelines and reduction of risks related to large wave loads. A trapped wave is the term used to describe the time-harmonic free fluctuation of a fluid that is restricted to a specific region⁸. Now, when developing porous structures, there is a significant emphasis on safeguarding marine installations by efficiently dissipating the highest possible amount of wave energy and establishing a tranquility zone. Therefore, by combining one or more of the three physical processes, such as wave reflection, wave energy dissipation, and the phase change of the incident and reflected waves, it is often possible to create a tranquil zone⁹. This can be done by adding a porous structure at a specific distance from an existing marine structure. Additionally, fish and other marine species may be artificially bred or nurtured in these tranquility zones.

In the last several decades, based on the linear water wave theory, many theoretical and numerical investigations have been conducted on thin and thick porous structures installed over seafloors as well as on surface-piercing structures. Sollit and Cross¹ created the first model for wave-induced flow in a porous material. For such boundary value problems involving porous structures, the potential theory has been applied^10,11. By taking into account various types of rubble-mound breakwaters, which serve as a good representation of the majority of common porous structures, the boundary element method is employed to obtain numerical solutions to such scattering problems¹². Yu and Chawng¹³ investigated the movement of waves in a two-layer fluid through a porous structure. Further, in addition, the concept of wave trapping was generalized by Wang et al.¹⁴ to create a wave-trapping mechanism employing a flexible porous structure positioned adjacent to the end wall of a channel using porous wavemaker theory of Chwang¹⁵. Yip et al.¹⁶ generalized the theory developed by Sahoo et. al.⁸ of trapping and generation of surface waves by partial porous structures to examine how absorbent and flexible structures might trap waves. In a two-layer fluid, Behera et al.¹⁷ investigated how bottom-standing and surface-piercing porous and flexible structures placed near a rigid wall can trap oblique waves. Following the small-amplitude water wave theory Koley et. al.⁹ investigated the oblique wave trapping by bottom-standing and surface-piercing porous structures situated at a specific distance from a vertical rigid wall. In this study, it has been concluded that the region enclosed by the rigid wall and porous structure can frequently absorb a significant portion of the incident waves, resulting in minimal incident wave reflection. Gao et al.¹⁸ researched a new option for the mitigation of harbor oscillations via changing the bottom profile, which is feasible as long as the navigating depth is guaranteed. Further, Gao et al.¹⁹ did a systematic analysis with a fully nonlinear Boussinesq model for the harbour resonance condition to determine the appropriate bar wavelength that may achieve the best mitigation effect, as well as the effects of the number and amplitude of sinusoidal bars. Later, Gao et al.²⁰ studied and investigated the ability of Bragg resonant reflection to successfully reduce the primary resonant mode and the harbor’s overall resonance caused by irregular wave groups. Recently, various researchers^21,22,23,24 studied the wave trapping by a permeable membrane with different bottom configurations for normal and oblique waves placed near a rigid wall. Both the least squares method and the eigenfunction expansion method have been employed to deal with the related boundary value problem. The study shows that when the absolute values of the porous-effect parameter of the membrane increase, the wave reflection decreases. Further, for certain distances between the porous barrier and rigid wall, it is discovered that an undulated bed produces more instances of optimal reflection than a flatbed. On the other hand, another study has been given by Khan et. al.²⁵ using multi-domain BEM with constant and linear approaches for wave trapping by a multi-layered trapezoidal-shaped breakwater. According to this study, when the armor layer is at least twice as big as the filter layer, the incoming wave energy is completely dissipated for short waves and significantly attenuated for long waves, achieving an efficiency of more than $80\%$. Now, an interesting phenomenon can be observed in the research available in the literature for water wave trapping. When two boxes/structures are situated at the mean free surface and water waves approach these boxes/structures, some waves are reflected into the sea, while others are transmitted in the lee side of the structure. In this situation, the fluid resonance phenomenon, commonly known as “gap resonance,” that occurs inside the small spaces (known as transient gap) between these boxes/structures has garnered more attention throughout the last few decades. This phenomenon occurs when the incoming wave frequency in a narrow gap is the same as, or very near, the fluid’s resonance frequency (see Gao et al.²⁶). According to Gao et al.²⁷ and Gong et al.²⁸, the extreme oscillation of the free sea surface within the gap may cause unusually high wave loads acting on the marine structures and excessive motions of the structure, ultimately posing a threat to operation safety at the coastline. Additionally, water-wave scattering and energy dissipation by floating buoys (porous elastic plates, thin membranes) of different configurations and shapes are also considered for navigation channels, fisheries, aquaculture, and wave protection barriers. Liang et. al.²⁹ presented a study of the wave reflection and transmission properties as well as the stress created by the waves on the mooring line by introducing the spar buoy floating breakwater. Gesraha³⁰ investigated wave scattering by a long, rectangular breakwater with two thin sideboards extending vertically downward. It has been found that the sideboards increase the additional mass and heave damping coefficients while lowering the other damping coefficients, which decreases the transmission coefficient and responses. Some research works^31,32 have sought to look at the hydrodynamic properties of floating structures, using the element-free Galerkin method and boundary element method to assess their overall performance. Shen et al.³³ discovered the effects of the sill on the additional mass, damping coefficients, wave excitation force, transmission, and reflection coefficients and thoroughly investigated these physical quantities using analytical solutions. Alongside, Loukogeorgaki and Angelides³⁴ demonstrated how an anchored floating breakwater behaves in the frequency domain when typical incidence waves are present. Sannasiraj³⁵ examined the dynamics of several floating structures using the finite element method. In this study, the main focus was to analyze the hydrodynamic behavior of multi-bodies in a multi-directional wave environment.

Now, taking into account the studies mentioned earlier, one more factor affects most marine hydrodynamics: ocean currents. In other words, wave-current interactions are the most fascinating and realistic problems in physical oceanography and ocean engineering. Phillips³⁶ found that the presence of these currents may sometimes exert a substantial influence on both the velocity and trajectory of the waves. Consequently, the presence of currents can impact the effectiveness of wave barriers³⁷. Also, some experimental studies were conducted to investigate the interaction between surface gravity waves and currents propagating over both rough and smooth seabeds (see^38,39,40) and⁴¹ used BEM and perturbation approaches with sufficiently low Froude numbers to resolve wave-current interactions. Earlier, a study by Smith⁴² concluded that the design or adjustment of inlet channels for navigation or dredging activities depends on the changes in wave heights and wavelengths that occur when ocean waves enter an inlet against an ebb tide. Additionally, the interaction of waves and currents with a submerged plate wave barrier³⁷ and submerged trapezoidal-shaped breakwaters⁴³ was also examined. It was observed that the mean velocity profile exhibited notable deviations from the predictions made by a linear superposition of wave and current velocities. In other words, the current intensity in proximity to a smooth seabed is increased, whereas conversely, it is diminished in the case of a rough seabed, owing to the existence of the current. Moreover, the experiments above have indicated a direct correlation between the incident wavelength and the wave period in the case of both following and opposing currents. It is worth noting that the wave heights remained consistent regardless of the direction of the current flow. Recently Dora et al.⁴⁴ and Swami et al.⁴⁵ studied the surface piercing porous structure placed with a vertical rigid wall and trapezoidal shaped bottom standing porous breakwaters respectively. According to these studies, due to the following currents, the force and reflection coefficient on porous structures increases. Further, due to the following current a right shift can be seen in the wave transformation characteristics. Furthermore, to minimize the negative effects of coastal threats, to optimize the performance of existing operational breakwaters, and to build efficient coastal protection mechanisms, it is imperative to understand the complicated interactions that exist among waves, currents, and breakwaters. Consequently, more studies in this field are required to enhance the management and designing of coastal structures as well as to enhance our understanding of the behavior of wave-current breakwater systems. There is very little literature that has studied wave trapping by bottom-standing porous breakwaters in the presence of ocean currents. Hence, wave trapping by bottom-standing porous breakwaters in front of a vertical rigid wall is examined in this work when current flows parallel to the wall, the uniformity of streamwise currents may be affected in the presence of large coastal structures⁴⁴. Consequently, the analysis is done by taking into account the current that is running down the wall. Ocean currents play a significant role in affecting breakwaters by influencing wave energy attenuation, altering sediment transport patterns, exerting forces on the structures, causing scouring, and impacting navigation safety around the breakwater-protected areas. Understanding these interactions are crucial for effective coastal engineering and navigation planning to ensure the stability and functionality of the breakwater structures and maintain safety for maritime activities. Further, studying ocean currents’ interaction with breakwaters enhances our understanding of coastal dynamics, improves engineering designs, evaluates environmental impacts, validates predictive models, fosters scientific innovation, and develops sustainable coastal management practices. This study fills gaps in the current literature, expands interdisciplinary understanding, and provides a foundation for further academic exploration and practical application in coastal engineering and environmental sciences.

The current study examines the entrapment of water waves in the presence of ocean currents by a thick, permeable, trapezoidal-shaped bottom-standing breakwater. The breakwater is placed over a flat, rigid, and impermeable seabed. The widely accepted Sollitt and Cross model (1972) is used to model the flow through the thick porous breakwater. The overall structure of the paper is as follows. The mathematical model is given in Section 2 along with the suitable formulation. The comprehensive solutions utilizing the BEM-based numerical technique are presented in Section 3. In Section 4, the energy balance equation is given in order to measure the specific kind of energy loss that results from the presence of a thick porous structure. In Section 5, the numerical results associated with the wave transformation characteristics (i.e., wave reflection, transmission, dissipation, and wave forces) in the presence of following and opposing currents are provided. The final section, Section 6, presents the conclusions drawn from the numerical results.

Mathematical formulation

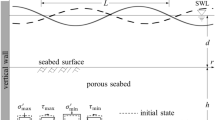
In the present research, the small-amplitude water wave theory is used to analyze wave trapping by thick porous structures that is kept at a finite distance from a vertical rigid wall. In this study, a fully submerged bottom-standing trapezoidal-shaped structure is taken into consideration. It is assumed that the porous structure is submerged in the fluid at a depth d unit from the mean free surface $z=0$. The top layer width of the breakwater is 2b, and the bottom layer width is L and the breakwater is placed in water of finite depth h. The porous structure occupies the region $-h \le z \le -h+d$ with the gap region $-h+d \le z \le 0$ (see Fig. 1). Along the y-axis, it is assumed that this structure is infinitely long. The distance $r_g$ separates the solid wall from the porous structure. According to Fig. 1, the porous breakwater’s seaside and lee side incline at angles of $\theta _1$ and $\theta _2$, respectively, with the base horizontal line. The normal incident wave impinges on the porous breakwater along the direction of $-x$ to x. Fig. 1 illustrates how the entire water domain is split into two parts, $R_1$ and $R_2$, respectively. It is presumed that the water is inviscid and incompressible by nature. Further, the water motion is considered to be irrotational and simple harmonic in time t with angular frequency $\omega$. Under the mean free surface, we assume that a uniform current with velocity $U_0$ flows in the direction of the wave propagation. Therefore, the form of the total velocity potential $\Phi _j(x,z,t)$ for $j=1, 2$ is written as (see^45,46 for details)

$$\begin{aligned} \Phi _j(x,z,t)= U_0x+\phi _j(x,z,t), \end{aligned}$$

(1)

where $\phi _j(x,z,t)= \Re \left\{ e^{-\textrm{i} \omega t} \phi _j(x,z)\right\}$ with $\Re$ being the real part of the wave potential $\phi _j(x,z,t)$. Here, the spatial components of the velocity potential $\phi _j(x,z,t)$ for $j=1,2$ satisfy the Laplace equation

$$\begin{aligned} \left( \frac{\partial ^2}{\partial x^{2}}+\frac{\partial ^{2}}{\partial z^{2}}\right) \phi _j(x,z)=0,\quad \text{ for }\;\;j=1,2. \end{aligned}$$

(2)

The boundary condition on still water surface is given by (see⁴⁶ for details)

$$\begin{aligned} \displaystyle \frac{\partial \phi _1}{\partial n}-K \phi _1=0, \quad \text{ on } \hspace{0.2cm} \Gamma _{6}, \end{aligned}$$

(3)

where $K=\omega ^2_r/g$ with $\omega _r=\omega -U_0 k$ being termed as “Doppler shifted frequency” (see⁴⁷ for more details), which is the wave frequency relative to the ambient current. $\partial /\partial n$ represents the normal derivative. Moreover, the condition for the rigid uniform bottom and seawall is provided as

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{\partial \phi _{1}}{\partial n}=0, &{}\quad \text{ on } \Gamma _{2} \cup \Gamma _{4} \cup \Gamma _{5},\\ \displaystyle \frac{\partial \phi _{2}}{\partial n}=0, &{}\quad \text{ on } \Gamma _{7}. \end{array}\right. } \end{aligned}$$

(4)

The fluid pressure and mass flux are continuous at $\Gamma _{3}$. So, boundary condition between open water region $R_1$ and porous region $R_2$ is given by (see⁴⁸)

$$\begin{aligned} \displaystyle \frac{\partial \phi _1}{\partial n} = -\varepsilon \frac{\partial \phi _2}{\partial n}, \quad \phi _1=(m+\textrm{i}f)\phi _2, \quad \text{ on }\;\;\Gamma _{3}, \end{aligned}$$

(5)

where $\varepsilon$, m, and f are porosity, inertial, and friction coefficients, respectively of the porous region $R_2$ (see¹ for more details). The value m can be calculated using the formula $\displaystyle m=1+\left( \frac{1-\varepsilon }{\varepsilon }\right) C_m$, where $C_m$ is the added mass coefficient for porous medium grains. The expression for the friction coefficient is given by

$$\begin{aligned} \displaystyle f= \frac{1}{\omega }\frac{\displaystyle \int _{R_2} d \Omega \int _{t}^{t+T} \Bigg \{\frac{\varepsilon ^2\nu |\vec q|^2}{K_p}+\frac{\varepsilon ^3 C_f}{\sqrt{K_p}}|\vec q|^3 \Bigg \}dt}{ \displaystyle \int _{R_2}d \Omega \int _{t}^{t+T} \varepsilon |\vec q|^2 dt}, \end{aligned}$$

(6)

where $\vec q$ is the seepage velocity vector at any point in the porous region $R_2$. Furthermore, $\nu$ is the kinematic viscosity, $K_p$ is the intrinsic permeability, and $C_f$ is the dimensionless turbulence resistance coefficient for porous material in region $R_2$. Often, the intrinsic permeability $K_p$ and turbulence resistance coefficient $C_f$ are computed using the empirical formulae given in⁴⁹. Assuming an imaginary boundary $\Gamma _{1}$ is fixed three times away from the breakwater such that on the imaginary boundary, the local wave modes’ effect will disappear. Therefore, the far-field boundary condition is given by

$$\begin{aligned} \phi _1(x,z)= e^{\textrm{i}k_0x}{\mathscr {F}}_0(k_0,z) +R_0e^{-\textrm{i}k_0x}{\mathscr {F}}_0(k_0,z), \quad \text{ as } \;\; x\rightarrow -\infty , \end{aligned}$$

(7)

where $R_0$ is unknown coefficients associated with the reflection coefficient. Eq. (7) can be re-written in the following form as

$$\begin{aligned} \displaystyle \frac{\partial {\left( \phi _1 - \phi ^{inc}\right) }}{\partial n} = \textrm{i} k_0(\phi _1-\phi ^{inc}), \quad \text{ on } \;\; \Gamma _{1}, \end{aligned}$$

(8)

with $\phi ^{inc}(x,z)$ being incident wave potential. The form of $\phi ^{inc}(x,z)$ is given as (see⁴⁸ for details)

$$\begin{aligned} \phi ^{inc}(x,z)= e^{\textrm{i} k_0 x} {\mathscr {F}}_0(k_0,z), \quad \text{ with } \quad {\mathscr {F}}_0(k_0,z)= \left( \frac{-\textrm{i} g A}{\omega _r}\right) \left( \frac{\cosh \left( k_0(h+z)\right) }{\cosh (k_0h)} \right) . \end{aligned}$$

(9)

Here, $k_{0}$ is positive real root of the dispersion relation $\displaystyle \omega ^2_r=g k\tanh (kh)$. It is noteworthy that the eigenfunction ${\mathscr {F}}_0$ satisfies the following property

$$\begin{aligned} \displaystyle \int _{-h}^{0}{\mathscr {F}}_0(k_0,z){\mathscr {F}}_0^*(k_0,z) dz= \left( \frac{g^2A^2}{\omega ^2_r}\right) \left( \frac{2k_0h+\sinh (2k_0h)}{4k_0\cosh ^2(k_0h)} \right) , \end{aligned}$$

(10)

where ${\mathscr {F}}_0^*(k_0,z)$ represents the complex conjugate of ${\mathscr {F}}_0(k_0,z)$.

Figure 1

Vertical cross-section of the porous breakwater with a rigid wall.

BEM based numerical solution technique

This section covers the application of the BEM-based solution technique to the boundary value problem, which was covered in Section 2. Here, the solution procedure covers the wave trapping in the presence of current using a thick, porous, trapezoidal-shaped submerged breakwater. The above-discussed boundary value problem is first transformed into a system of second-kind Fredholm integral equations in this solution process. Subsequently, the system of integral equations is discretized using the BEM-based solution methodology, which transforms the integral equations into a system of linear algebraic equations. Free-space Green’s function is typically utilized in the BEM solution technique. The following differential equation is satisfied by the free space Green’s function G for the present problem as

$$\begin{aligned} \nabla ^{2} G(x,z;x_0,z_0)= \delta (x-x_0)(z-z_0), \end{aligned}$$

(11)

where $(x_0,z_0)$ is source point and (x, z) is field point. The Green’s function $G(x,z;x_0,z_0)$ is given by

$$\begin{aligned} G(x, z;x_0,z_0)=-\frac{1}{2\pi } \ln (r), \quad \text{ where }\;\; r=\sqrt{(x-x_0)^{2}+(z-z_0)^{2}}, \end{aligned}$$

(12)

where r is the distance between the source point and the field point. The normal derivative of the Green’s function $G(x,z;x_0,z_0)$ is given by

$$\begin{aligned} \frac{\partial G}{ \partial n}= -\frac{1}{2 \pi r} \left( \frac{\partial r}{\partial n} \right) = -\frac{1}{2 \pi r}\left( n_x \frac{\partial r}{\partial x} + n_z \frac{\partial r}{\partial z}\right) , \end{aligned}$$

(13)

where the components of the unit normal vector along the x and z axes, respectively, are denoted by $n_x$ and $n_z$. In order to derive the integral equation, the Green’s second identity is utilized on the velocity potential $\phi (x,z)$ and the Green’s function $G(x,z;x_0,z_0)$. Consequently, the resultant integral equation takes the following form (see⁵⁰ for more details)

$$\begin{aligned} \frac{1}{2}\phi (x_0,z_0) =\int _{\Gamma }\left[ \phi (x,z)\frac{\partial G}{\partial n}\left( x,z;x_0,z_0\right) - G\left( x,z;x_0,z_0\right) \frac{\partial \phi }{\partial n}(x,z)\right] d\Gamma (x,z), \quad \text{ for } \quad (x_0,z_0) \in \Gamma . \end{aligned}$$

(14)

By substituting the boundary conditions (3)–(8) into Eq. (14), we emerge the next pair of integral equations for regions $R_1$ and $R_2$ as

$$\begin{aligned}{} & {} \displaystyle -\frac{1}{2}\phi _1 + \int _{\Gamma _{1}} \left( \frac{\partial G}{\partial n}-\textrm{i} k_0 G \right) \phi _1 d \Gamma + \int _{\Gamma _{2} \cup \Gamma _{4} \cup \Gamma _{5}} \frac{\partial G}{\partial n} \phi _1 d \Gamma + \int _{\Gamma _{3}} \left( (m + \textrm{i} f)\phi _2 \frac{\partial G}{\partial n}+ \varepsilon G \frac{\partial \phi _2}{\partial n} \right) d \Gamma \nonumber \\{} & {} \quad + \int _{\Gamma _{6}} \left( \frac{\partial G}{\partial n}-KG \right) \phi _1 d \Gamma = \int _{\Gamma _1} \left( \frac{\partial \phi ^{inc}}{\partial n}-\textrm{i} k_0 \phi ^{inc} \right) G d\Gamma , \end{aligned}$$

(15)

$$\begin{aligned}{} & {} \quad -\frac{1}{2}\phi _2 + \int _{\Gamma _{7}} \phi _2 \frac{\partial G}{\partial n} d \Gamma + \int _{\Gamma _{3}} \left( \phi _2 \frac{\partial G}{\partial n} - G \frac{\partial \phi _2}{\partial n} \right) d \Gamma = 0. \end{aligned}$$

(16)

In order to solve the integral Eqs. (15) and (16), a discretization technique is employed to divide the entire boundaries of the regions $R_1 \cup R_2$ into a finite number of elements. For the quadratic boundary element method, the unknowns $\phi _j$ and $\partial \phi _j / \partial n$ are expressed in terms of interpolation functions as (see⁵⁰ for details)

$$\begin{aligned} \phi _j (\xi )= \begin{bmatrix} u^1&u^2&u^3 \end{bmatrix} \begin{bmatrix} \phi ^1_j\\ \phi ^2_j\\ \phi ^3_j \end{bmatrix}, \qquad \displaystyle \frac{\partial \phi _j}{\partial n} (\xi )= \begin{bmatrix} u^1&u^2&u^3 \end{bmatrix} \begin{bmatrix} \displaystyle \frac{\partial \phi ^1_j}{\partial n}\\ \displaystyle \frac{\partial \phi ^2_j}{\partial n}\\ \displaystyle \frac{\partial \phi ^3_j}{\partial n} \end{bmatrix}, \end{aligned}$$

(17)

with the interpolation functions being given as the following

$$\begin{aligned} \displaystyle u^1=\frac{1}{2} \xi (\xi -1), \quad \displaystyle u^2=(1-\xi )(1+\xi ), \quad \displaystyle u^3=\frac{1}{2} \xi (1+\xi ). \end{aligned}$$

(18)

Therefore, we can write the terms of the integration as the following

$$\begin{aligned}{} & {} \int _{\Gamma } \phi _j (x,z)\;\frac{\partial G}{\partial n}\left( x,z;x_0,z_0\right) d\Gamma = \begin{bmatrix} h^{ij}_1&h^{ij}_2&h^{ij}_3 \end{bmatrix} \begin{bmatrix} \phi ^1_j\\ \phi ^2_j\\ \phi ^3_j \end{bmatrix}, \end{aligned}$$

(19)

$$\begin{aligned}{} & {} \displaystyle \int _{\Gamma } \frac{\partial \phi _j}{\partial n} (x,z) \;G\left( x,z;x_0,z_0\right) d\Gamma = \begin{bmatrix} g^{ij}_1&g^{ij}_2&g^{ij}_3 \end{bmatrix} \begin{bmatrix} \displaystyle \frac{\partial \phi ^1_j}{\partial n}\\ \displaystyle \frac{\partial \phi ^2_j}{\partial n}\\ \displaystyle \frac{\partial \phi ^3_j}{\partial n}\end{bmatrix}, \end{aligned}$$

(20)

where

$$\begin{aligned} \displaystyle h^{ij}_k=\int _{\Gamma _j} u^k \displaystyle \frac{\partial G}{\partial n} \;d\Gamma , \qquad \displaystyle g^{ij}_k=\int _{\Gamma _j} u^k G \;d\Gamma \end{aligned}$$

(21)

It is important to acknowledge that the values of $h_k^{ij}$ and $g_k^{ij}$ for $k=1,2,3$ are computed utilizing the Gauss-Legendre quadrature formulas, specifically for the scenario when $i \ne j$. The scenario when $i=j$ is considered, the quantities $h_k^{ij}$ and $g_k^{ij}$ are computed analytically (see⁵⁰). Using the expressions (19) and (20), the system of integral equations (15) and (16) are converted into a system of linear algebraic equations which are solved to determine the unknowns $\phi _j$ and $\partial \phi _j / \partial n$ over each boundary element.

Energy balance relation

The energy balance relation for the case when the incident waves interact with the porous breakwater placed over a rigid impermeable seabed and situated at a finite distance away from a rigid wall is inferred in this section. Since it is commonly known that as water waves pass through the porous breakwaters, a portion of the incoming wave energy is dissipated. Quantifying this specific kind of porosity-related energy loss is desirable^51,52,53,54. In order to gain a better understanding of the behavior of wave reflection, transmission, dissipation, etc., an energy balance relation will be built using Green’s second identity. The computed results in a variety of scenarios will also be validated using it. The following relation is obtained by applying Green’s second identity to $\phi$ and $\partial \phi / \partial n$ on each of the two regions depicted in Fig. 1.

$$\begin{aligned} \displaystyle \int _{\Gamma _j}\left( \phi _j \frac{\partial \phi ^*_j}{\partial n} - \phi ^*_j \frac{\partial \phi _j}{\partial n}\right) d \Gamma _j =0. \end{aligned}$$

(22)

In the above expression, $\Gamma _j$ represents the total boundaries of the regions $R_j$ for $j=1,2$. Now, in region $R_1$, there are no contributions from the boundaries $\Gamma _j$ for $j=2, 4, 5, 6$. So, the only contributions come from the boundaries $\Gamma _j$ for $j=1,3$. These contributions are stated as follows

$$\begin{aligned}{} & {} \Gamma _1: \int _{\Gamma _1}\left( \phi _1 \frac{\partial \phi ^*_1}{\partial n} - \phi ^*_1 \frac{\partial \phi _1}{\partial n}\right) d \Gamma _1 =2\textrm{i} k_0 \left( -1+|R_0|^2\right) {\widetilde{A}}, \quad \;\; \text{ where } \quad {\widetilde{A}}=-\left( \frac{A^2g^2}{\omega ^2_r}\right) \frac{\sinh (2k_0h)+2k_0h}{4k_0\cosh ^2(k_0h)}, \end{aligned}$$

(23)

$$\begin{aligned}{} & {} \Gamma _j: \int _{\Gamma _j}\left[ \phi _j \frac{\partial \phi ^*_j}{\partial n} - \phi ^*_j \frac{\partial \phi _j}{\partial n}\right] d \Gamma _j =0, \hspace{2cm} \text {for j=2, 4, 5, 6}. \end{aligned}$$

(24)

Again, in region $R_2$, the boundary $\Gamma _7$ has no contribution. Based on the boundary condition Eq. (5), only $\Gamma _3$ has the following contribution

$$\begin{aligned} \displaystyle \Gamma _3: \int _{\Gamma _3}\left( \phi _1 \frac{\partial \phi ^*_1}{\partial n} - \phi ^*_1 \frac{\partial \phi _1}{\partial n}\right) d \Gamma _3 +\int _{\Gamma _3}\left( \phi _2 \frac{\partial \phi ^*_2}{\partial n} - \phi ^*_2 \frac{\partial \phi _2}{\partial n}\right) d \Gamma _3=-2 \textrm{i} \Im \left( \int _{\Gamma _3} \left[ \varepsilon \left( m+\textrm{i}f\right) -1\right] \phi _2 \frac{\partial \phi ^*_2}{\partial n} d\Gamma _3 \right) , \end{aligned}$$

(25)

where $\Im$ indicates the imaginary part of the given term. Using Eqs. (23)–(25) into Eq. (22), we get the final energy identity as

$$\begin{aligned} \displaystyle K_r^2 + K_d=1, \quad \text{ where } \quad K_r=|R_0|, \end{aligned}$$

(26)

and the term $K_d$ takes the following form

$$\begin{aligned} K_d=-\frac{1}{k_0 {\widetilde{A}}}\Im \left[ \int _{\Gamma _3} \left[ \varepsilon (m+\textrm{i}f)-1\right] \phi _2 \frac{\partial \phi ^*_2}{\partial n} d\Gamma _3 \right] . \end{aligned}$$

(27)

Here, $K_d$ indicates the energy dissipated in the presence of current due to the interaction between the incident wave and the thick porous trapezoidal-shaped breakwater. In the equations mentioned above, $\phi _j^*$ is the complex conjugate of $\phi _j$.

Results and discussions

This section analyses numerical data for wave energy dissipation and reflection induced by a thick, porous, trapezoidal-shaped bottom-standing breakwater and wave forces on the breakwater’s sea-side wall and the right vertical rigid wall caused by incoming waves. In particular, a thorough discussion is held regarding the impact of different uniform current speed, friction, and porosity parameters on the wave forces and wave scattering coefficients resulting from incoming waves that are reflected and dissipated. The physical parameters used in this investigation are as follows: $h=10$m (water depth), $g=9.81$m/$\hbox {s}^2$ (gravitational acceleration), $b/h=1.0$ (dimensionless half top width of the breakwater), $T=8$s (wave period), $d/h=0.25$ (dimensionless submergence depth of the breakwater) or $H=(h-d)/h=0.75$ (dimensionless height of breakwater), $\theta _1=\theta _2=\pi /4$ (left and rigid sloping angle of trapezoidal shape breakwater), $m=1$ (inertial coefficient), $f=1$ (friction coefficient), $\varepsilon =0.4$ (breakwater’s porosity), $\displaystyle F_0=U_0/\sqrt{gh}=0.3$ (Froude number/dimensionless ocean current speed), and dimensionless wavenumber ${\tilde{k}}=k_0h$ unless otherwise mentioned. The dimensionless horizontal wave force $F_x$ and vertical wave force $F_z$ acting on the sea-side surface of $\Gamma _{3}$ of the porous breakwater are determined using the following formulae

$$\begin{aligned} F_x= \Re \Biggl \{ \frac{\textrm{i}\omega _r}{gh^2} \int \phi n_x d\Gamma \Biggl \}, \hspace{1cm} F_z= \Re \Biggl \{ \frac{\textrm{i}\omega _r}{gh^2} \int \phi n_z d\Gamma \Biggl \}, \end{aligned}$$

(28)

also, the dimensionless horizontal force $F_x^r$ acting on the right vertical rigid wall (boundary $\Gamma _{5}$) is given by

$$\begin{aligned} F_x^r= \Re \Biggl \{ \frac{\textrm{i}\omega _r}{gh^2} \int \phi n_x d\Gamma \Biggl \}. \end{aligned}$$

(29)

It should be noted that only the hydrodynamic pressure is considered in the expressions of Eqs. (28) and (29).

Numerical convergence study

The convergence of solutions for the given physical model using the boundary element method is examined in this subsection under various values of Froude number and structural porosity $\varepsilon$. The panel size $p_s$ used to discretize the physical boundaries determines how well the boundary element method-based numerical computations converge. An inverse relationship exists between the panel size $p_s$ and the wavenumber associated with the incident wave. The dependence of the panel size $p_s$ on the wavenumber $k_0$ is displayed in the following form: (see⁵⁵ for more details)

$$\begin{aligned} p_s=\frac{1}{\kappa k_0}, \end{aligned}$$

(30)

where $\kappa$ (proportionality constant) needs to be obtained from the convergence study. To attain numerical convergence, the discretization process modulates $\kappa$ to determine the panel size. The convergence of BEM-based solutions for wave scattering by bottom-standing trapezoidal porous breakwater with vertical rigid wall in the presence of ocean currents $F_0$, porosity $\varepsilon$, and non-dimensional separation gap $r_g/\lambda$ is shown in Tables 1, 2 and 3 respectively. The numerical values of $K_r$ are seen to converge up to three decimal places for $\kappa \ge 35$ in Tables 1, 2 and 3. Therefore, unless otherwise stated, the value of $\kappa = 35$ is kept constant in the remaining numerical computations.

Table 1 Convergence of numerical solutions for different values of the Froude number $F_0=U_0/\sqrt{gh}$.

Table 2 Convergence of numerical solutions for different values of the porosity parameter $\varepsilon$.

Table 3 Convergence of numerical solutions for different values of non-dimensional separation gap $r_g/\lambda$.

Table 4 Energy balance relation (26) for the given physical problem for different values of the Froude number $F_0=U_0/\sqrt{gh}$.

Validation

The specific terms connected to the energy identity (as stated in Eq. (26)) are calculated for a range of values of ${\tilde{k}}$ in the presence of following and opposing current to confirm the accuracy of the BEM-based numerical solutions. The results are displayed in Table 4. It is seen that the obtained numerical results satisfy the energy identity obtained from Eq. (26). For the problem of water wave scattering by a submerged porous breakwater, the present numerical findings are compared with the numerical findings of Akarni et al.⁵⁶ in the presence of current in Fig. 2a. The other parameters are extracted from Akarni et al.⁵⁶ as $h=2.5m$, $\varepsilon =0.0$, $b/h=1.75$, $d/h=0.5$, $m=f=1.0$, $A=0.020$, and $U_0=F_0\sqrt{gh}=+0.2m/s$. The present numerical results are seen to agree well with the solutions of Akarni et al.⁵⁶. Figure 2a shows the accuracy and precision of the present BEM-based numerical solutions. Further, in the absence of ocean current, a comparison between the present BEM-based numerical findings in Fig. 2b,c with the results of Driscoll et al.⁵⁷, Losada⁵⁸, and Mei and Black⁵⁹ for a single impermeable rectangular-shaped submerged breakwater example is demonstrated. For this, the parameters of interest from Driscoll et al.⁵⁷ and Losada⁵⁸ for rectangular-shaped submerged breakwater are taken as $h=0.5$m, $\varepsilon =0.0$, $b=0.39$m, $d=0.12$m, $A=0.0125$m, and $U_0=F_0\sqrt{gh}=+0.0$m/s, and from Mei and Black⁵⁹, the parameters are taken as $h=10$m, $\varepsilon =0.0$, $d/h=0.5$, $A=0.01$, and $U_0=F_0\sqrt{gh}=+0.0$m/s. The existing result is in close match with the findings of Driscoll et al.⁵⁷, Losada⁵⁸ and Mei and Black⁵⁹, as shown in Fig. 2b,c.

Figure 2

Variation of (a) $K_r$, vs ${\tilde{k}}$ under the influence of ocean current ($U_0=F_0\sqrt{gh}=+0.2$m/s), (b) $K_r$ and $K_t$ vs ${\tilde{k}}$ without the influence of ocean current ($U_0=0.0$m/s) (c) $K_r$, vs $k_0d$ without the influence of ocean current ($U_0=0.0$m/s).

Numerical findings

In Fig. 3a,b, the reflection coefficient $K_r$ and dissipation coefficient $K_d$ are plotted with respect to non-dimensional wavenumber ${\tilde{k}}$ for numerous values of Froude number $F_0$. Fig. 3a shows that $K_r$ follows an oscillatory decreasing pattern with the variation in ${\tilde{k}}$. Furthermore, the oscillating pattern becomes less prominent as $F_0$ increases. Overall, Fig. 3a shows how the opposing current lowers and the following current increases the reflection and amplitude of oscillations associated with the wave reflection curve⁵⁶. These similar observations can be found in⁴⁶. Further, the energy dissipation $K_d$ exhibits a pattern that is opposite to that of the reflection coefficient $K_r$, as seen in Fig. 3b. The oscillatory pattern of $K_r$ in Fig. 3a is similar as provided in^25,44. Moreover, the wave frequency transformation $\omega _r=\omega -U_0k_0$ causes a right shift in the curves related to $K_r$ and $K_d$ as the Froude number $F_0$ increases⁴⁴. This frequency shift is termed as “Doppler shift” (see⁶⁰ for details). The reflection and dissipation curves for $F_0=-0.1$ are discontinued for ${\tilde{k}}>3.0$ as the waves get completely blocked due to the opposing current.

Figure 3

Variation of (a) reflection coefficient $K_r$, and (b) dissipation coefficient $K_d$ vs ${\tilde{k}}$ for different values of $F_0$.

Figure 4

Variation of (a) reflection coefficient $K_r$, and (b) dissipation coefficient $K_d$ vs ${\tilde{k}}$ for different values of $\varepsilon$.

In Fig. 4a,b, reflection coefficient $K_r$ and dissipation coefficient $K_d$ are plotted with respect to dimensionless wavenumber ${\tilde{k}}$ for numerous values of porosity parameter $\varepsilon$. Figure 4a,b show that for non-porous structure ($\varepsilon =0$), there is a complete reflection occurring and no dissipation is taking place. But as soon as the value of $\varepsilon$ increases, reflection gets lower, and dissipation gets higher. As porosity increases, the water flow through porous breakwater also increases, resulting in an increment in wave dissipation and abatement of wave reflection energy^52,61. In other words, the higher the value of $\varepsilon$, the higher the dissipation and the lower the reflection.

Figure 5

Variation of (a) reflection coefficient $K_r$, (b) dissipation coefficient $K_d$ vs ${\tilde{k}}$ for different values of f.

In Fig. 5a,b, $K_r$ and $K_d$ are plotted as a function of ${\tilde{k}}$ for numerous values of friction coefficient f. Figure 5a,b show that the reflection $K_r$ decreases in an oscillatory pattern with the increment in ${\tilde{k}}$. For smaller values of f ($f \le 1.0$), $K_r$ becomes lower and $K_d$ becomes higher with an increase in the friction coefficient f⁹. However, for higher friction coefficient f, i.e., for $f \ge 1.0$, no significant differences in $K_r$ and $K_d$ are observed. Furthermore, $K_d$ has the opposite pattern of that of $K_r$. Similar kinds of patterns of $K_r$ were reported in⁹.

Figure 6

Variation of (a) horizontal force $F_x$, (b) vertical force $F_z$, and (c) horizontal force $F^r_x$ acting on the rigid wall vs ${\tilde{k}}$ for different values of $F_0$.

Figure 6a–c show the variation of $F_x$, $F_z$ and $F^r_x$ against $\tilde{k}$ for various values of $F_0$. It is found that when ${\tilde{k}}$ varies, both the horizontal forces $F_x$, $F^r_x$, and the vertical force $F_z$ fluctuate in the oscillatory pattern. As $F_0$ grows, the oscillating pattern for $F_x$ and $F_z$ becomes less noticeable. Along this, $F_x$ decreases significantly in the long wavelength profile, and then it increases slightly in the short wavelength profile. The number of oscillations in the $F^r_x$ curve is less, and associated oscillation amplitudes are more as compared to $F_x$ and $F_z$. The phase changes occur in $F_x$, $F_z$, and $F^r_x$ curves because of the change in the Froude number $F_0$.

Figure 7

Variation of (a) horizontal force $F_x$, (b) vertical force $F_z$, and (c) horizontal force $F^r_x$ acting on the rigid wall vs ${\tilde{k}}$ for different values of f.

Figure 7a–c show the variation of $F_x$, $F_z$ and $F^r_x$ against $\tilde{k}$ for different values of f. It is found that when ${\tilde{k}}$ gets higher values, both the horizontal forces $F_x$ and $F_x^r$, and vertical force $F_z$ follow a decreasing oscillatory pattern. Also, the highest optimum value of $F_x$ and $F_z$ gets less as the value of the friction coefficient increases from 0.1 to 2.0. Moreover, the force $F_x^r$ gets minimum in the long wavelength region for the least value of f.

Figure 8

Variation of (a) horizontal force $F_x$, (b) vertical force $F_z$, and (c) horizontal force $F^r_x$ on rigid wall vs ${\tilde{k}}$ for different values of $\varepsilon$.

Figure 8a–c show the variation of $F_x$, $F_z$ and $F^r_x$ against $\tilde{k}$ for various values of $\varepsilon$. It is found that when ${\tilde{k}}$ gets higher values, both the horizontal force $F_x$ and vertical force $F_z$ follow a decreasing oscillatory pattern as Fig. 8a,b. On the other hand, the force on the right rigid wall $F^r_x$ follows an abrupt oscillatory pattern. For the lowest value of $\varepsilon$, it reaches a minimum in the long wavelength region and a maximum in the intermediate wavelength region at an approximate value of ${\tilde{k}}=1.35$. All wavelengths of the wave force on the breakwater’s seaside surface exhibit an oscillatory diminishing pattern as porosity increases. This is because, with the high porosity of the structure, a greater dissipation of wave energy occurs. A similar pattern can be observed in Behera and Khan⁶² for various values of $\varepsilon$ and f.

Figure 9

Variation of (a) reflection coefficient $K_r$, and (b) dissipation coefficient $K_d$ vs $r_g/\lambda$ for different values of $F_0$.

Figure 9a,b show the variation of $K_r$ and $K_d$ against non-dimensional separation gap $r_g/\lambda$ ($\lambda$ is the incident wavelength) for numerous values of $F_0$. Both $K_r$ and $K_d$ follow the oscillatory pattern. It can be observed that as the Froude number $F_0$ increases from $-0.1$ to 0.5, the number of oscillations in $K_r$ decreases. At higher current speed, higher reflection $K_r$, and lower dissipation $K_d$ occur. In short, it can also be observed that $K_r$ is amplified by the following current and diminished by the opposing current. The dissipation coefficient $K_d$ follows just the opposite pattern of the reflection coefficient $K_r$. It was reported by¹⁴ that for a thin porous barrier, the maximum wave reflection occurs for $r_g/\lambda =n/2,n=0,1,2,\cdots$. Further, minimum wave reflection occurs for $r_g/\lambda =\left( 2n+1\right) /4,n=0,1,2,\cdots$⁸. In the present case, because of the presence of thick porous breakwater and ocean currents, the aforementioned relations for maximum and minimum don’t hold.

Figure 10

Variation of (a) reflection coefficient $K_r$, and (b) dissipation coefficient $K_d$ vs $r_g/\lambda$ for different values of $\varepsilon$.

Figure 10a,b show the variation of $K_r$ and $K_d$ against non-dimensional separation gap $r_g/\lambda$ for various values of porosity $\varepsilon$. Here $K_r$ and $K_d$ follow a periodic pattern except for the porosity value $\varepsilon =0$. It can be observed that for $\varepsilon =0$, there is a complete reflection of incoming waves occurs without any loss of wave energy due to no porosity. Further, as $\varepsilon$ increases from 0 to 0.4, a higher amount of wave energy dissipation takes place, and the reflection coefficient $K_r$ decreases significantly. A similar trend can be observed in Panduranga and Koley⁶³.

Figure 11

Variation of (a) reflection coefficient $K_r$, and (b) dissipation coefficient $K_d$ vs $r_g/\lambda$ for different values of f.

Figure 11a,b show the variation of $K_r$ and $K_d$ versus non-dimensional separation gap $r_g/\lambda$ for different values of f. Here $K_r$ and $K_d$ follow a periodic pattern. The reflection coefficient $K_r$ decreases with an increase in the value of friction coefficient f within the range $0\le f \le 1.0$ (see⁹). The dissipation coefficient $K_d$ follows a reverse trend. It is evident that for a wide range of values of f, some local optima in $K_r$ and $K_d$ are observed along with a rise in the value of $r_g/\lambda$. The occurrences of local optima can be attributed to various factors, including phase shifts in incoming waves and reflected waves in the presence of porous structures positioned a finite distance from the rigid wall.

Figure 12

Variation of (a) horizontal force $F_x$, (b) vertical force $F_z$, and horizontal force $F_x^r$ on rigid wall vs $r_g/\lambda$ for different values of $F_0$.

Figure 12a–c show the variation of $F_x$, $F_z$ and $F^r_x$ versus $r_g/\lambda$ for various value of Froude number $F_0$. It is found that when $r_g/\lambda$ varies, the patterns of the horizontal forces $F_x$, $F^r_x$, and the vertical force $F_z$ are repeated with consecutive maxima and minima. The horizontal and vertical wave forces are $180^{\circ }$ out of phase. Figure 12c shows that the amplitude of oscillation in wave forces gets higher for higher $F_0$.

Figure 13

Variation of (a) horizontal force $F_x$, and (b) vertical force $F_z$, and (c) horizontal force $F_x^r$ acting on the rigid wall vs $r_g/\lambda$ for different values of f.

Figure 13a–c show the variation of $F_x$, $F_z$ and $F^r_x$ versus $r_g/\lambda$ for various value of friction coefficient f. It is found that when $r_g/\lambda$ varies, both the horizontal forces $F_x$, $F^r_x$, and the vertical force $F_z$ show alternative maxima and minima values as the friction coefficient f increases. The amplitude of the oscillation of the horizontal force $F_x$ and vertical force $F_z$ acting on the seaside face of the breakwater reduces as the values of f get higher from 0.1 to 2.0. From Fig. 13c, it is clear that when the friction coefficient f increases, the amplitude of the wave force $F^r_x$ acting on the solid wall decreases. This happens because of higher wave energy dissipation with an increasing friction coefficient f (see⁹).

Figure 14

Variation of (a) horizontal force $F_x$, (b) vertical force $F_z$, and (c) horizontal force $F_x^r$ acting on the rigid wall vs $r_g/\lambda$ for different values of $\varepsilon$.

Figure 14a–c show the variation of $F_x$, $F_z$, and $F^r_x$ against non-dimensional separation gap $r_g/\lambda$ for various value of porosity $\varepsilon$. It is found that when $r_g/\lambda$ varies, both the horizontal forces $F_x$, $F^r_x$, and the vertical force $F_z$ show minima and maxima periodically as the porosity $\varepsilon$ increases. As porosity $\varepsilon$ increases, there is a noticeable shift of the optima to the right in $F_x$, $F_z$, and $F^r_x$. The breakwater’s seaside face experiences oscillations of the horizontal force $F_x$ and vertical force $F_z$, with a reduction in amplitude as $\varepsilon$ values increase from 0.0 to 0.4. The oscillation amplitude of the wave force $F^r_x$ acting on the rigid wall is decreasing as the porosity $\varepsilon$ grows. A comparison between Figs. 12a–c and 14a–c shows similar pattern for all the forces.

Figure 15

Variation of (a) reflection coefficient $K_r$, and (b) dissipation coefficient $K_d$ vs ${\tilde{k}}$ for different values of b/h.

In Fig. 15a–b, the reflection coefficient $K_r$ and dissipation coefficient $K_d$ are plotted with respect to non-dimensional wavenumber ${\tilde{k}}$ for numerous values of dimensionless width of the breakwater b/h. Figure 15a shows that $K_r$ follows an oscillatory decreasing pattern in long, intermediate, and short wavelength regimes. The oscillating pattern becomes more prominent and the wavelength of this oscillatory pattern decreases as b/h grows. On the other hand, in Fig. 15b, the energy dissipation coefficient $K_d$ follows an opposite pattern as that of $K_r$. In other words, as the structural width goes lower to higher values, the energy dissipation $k_d$ increases significantly. For higher values of b/h, $100\%$ of wave energy dissipation occurs for some particular values of wavenumber ${\tilde{k}}$. This may happen because as structural size increases, more surface area of the porous breakwater interacts with incident waves. These results into higher wave energy dissipation and lower wave energy reflection⁶⁴.

Figure 16

Variation of (a) reflection coefficient $K_r$, and (b) dissipation coefficient $K_d$ vs ${\tilde{k}}$ for different values of H/h.

In Fig. 16a,b, the dissipation coefficient $K_d$ and reflection coefficient $K_r$ are displayed against the non-dimensional wavenumber ${\tilde{k}}$ over a range of dimensionless structural height values of the breakwater H/h. As can be seen in Fig. 16a, $K_r$ exhibits an oscillating decreasing pattern in the long, intermediate, and short wavelength regimes. This oscillating pattern’s wavelength rises as H/h moves from lower to higher values. Conversely, the energy dissipation coefficient $K_d$ in Fig. 16b exhibits a pattern that is opposite to that of $K_r$. Additionally, with higher values of H/h, the oscillatory patterns of $K_r$ and $K_d$ shift to the left. The energy dissipation $K_d$ increases dramatically when the structural width goes from lower to greater values. In the short wavelength profile, nearly $100\%$ of wave energy dissipates at for some particular values of H/h. This might happen because when a porous breakwater gets wider and bigger, its surface area increases and it interacts with incident waves more. This results in higher wave energy dissipation and less reflection⁶².

Figure 17

Variation of (a) horizontal force $F_x$, (b) vertical force $F_z$, and (c) horizontal force $F^r_x$ on rigid wall vs ${\tilde{k}}$ for different values of b/h.

Figure 17a–c show the variation of $F_x$, $F_z$ and $F^r_x$ against ${\tilde{k}}$ for various values of b/h. It is found that when ${\tilde{k}}$ varies, both the horizontal forces $F_x$, $F^r_x$, and the vertical force $F_z$ fluctuate in an oscillating manner. There is a left shift in all the figures as b/h increases. Here, $F_x$ has a maximum around ${\tilde{k}}=1.0$ for the least value of b/h. Also, $F_x$ is higher for higher values of b/h in the short wavelength regime. It is noticeable that $F_z$ has an opposite pattern to that of $F_x$. Further, the wavelength and amplitude of oscillation of $F^r_x$ decrease as b/h increases, and the minima occurs around ${\tilde{k}} \approx 1.0$.

Figure 18

Variation of (a) horizontal force $F_x$, (b) vertical force $F_z$, and (c) horizontal force $F^r_x$ on rigid wall vs ${\tilde{k}}$ for different values of H/h.

Figure 18a–c show the variation of $F_x$, $F_z$ and $F^r_x$ against ${\tilde{k}}$ for various values of H/h. It is found that when ${\tilde{k}}$ varies, both the horizontal forces $F_x$, $F^r_x$, and the vertical force $F_z$ fluctuate in an oscillating manner. There is a left shift in all the figures as H/h increases. Here, $F_x$ decreases as ${\tilde{k}}$ increases. Also, $F_x$ decreases when the wavenumber grows. It is noticeable that $F_z$ has an opposite pattern to that of $F_x$. Further, the wavelength and amplitude of oscillation of $F^r_x$ decrease as H/h increases, and the minima occur around ${\tilde{k}} \approx 0.9$.

Figure 19

Variation of (a) reflection coefficient $K_r$, and (b) dissipation coefficient $K_d$ vs $r_g/\lambda$ for different values of b/h.

Figure 19a,b show the variation of $K_r$ and $K_d$ versus non-dimensional separation gap $r_g/\lambda$ for different values of b/h. Figure 19 shows that $K_r$ and $K_d$ follow a wavy pattern with variation in $r_g/\lambda$. Reflection coefficient $K_r$ decreases and dissipation coefficient $K_d$ increases with an increase in dimensionless structural width b/h. This happens because of the increase of surface area of the porous structure results into dissipation of more wave energy, and also a part of wave energy is trapped in the gap region between the porous structure and the vertical right rigid wall. On the other hand, for all the values of structural width, minima and maxima of $K_r$ occur for some particular values of $r_g/\lambda$. Moreover, the minima and maxima can occur for many reasons, including phase shifts in incoming and reflected waves in the presence of porous structures located a finite distance from the rigid wall.

Figure 20

Variation of (a) horizontal force $F_x$, (b) vertical force $F_z$, and (c) horizontal force $F^r_x$ on rigid wall vs $r_g/\lambda$ for different values of b/h.

Figure 20a–c show the variation of $F_x$, $F_z$ and $F^r_x$ against $r_g/\lambda$ for various values of b/h. It is found that when $r_g/\lambda$ varies, both the horizontal forces $F_x$, $F^r_x$, and the vertical force $F_z$ follow a periodic pattern. The amplitude of this periodic pattern decreases as b/h increases. Also, $F_x$ is higher for higher b/h. $F_z$ follows a reverse pattern that of $F_x$. For $F_x$ and $F_z$, extreme values occur for some particular values of $r_g/\lambda$. Further, $F^r_x$ also oscillates with increasing $r_g/\lambda$. The amplitude of this oscillation decreases as b/h increases. Moreover, $F^r_x$ has global extreme values for the least b/h.

Figure 21

Variation of (a) reflection coefficient $K_r$, and (b) dissipation coefficient $K_d$ vs $r_g/\lambda$ for different values of H/h.

In Figure 21a,b, the variation of $K_r$ and $K_d$ vs the non-dimensional separation gap $r_g/\lambda$ for various values of H/h is displayed. $K_r$ and $K_d$ exhibit a wavy pattern with variation in $r_g/\lambda$, as seen in Fig. 21. As the dimensionless structural height H/h increases, the reflection coefficient $K_r$ falls, and the dissipation coefficient $K_d$ increases. This occurs as a result of the porous structure’s increased surface area dissipating more wave energy and some of the wave energy being trapped in the space between it and the vertical stiff wall to the right. Conversely, minima and maximum of $K_r$ and $K_d$ exist for all values of the structural height, but only for specific values of $r_g/\lambda$. Furthermore, a variety of factors, such as phase shifts in incoming and reflected waves in the presence of porous structures at a finite distance from the rigid wall, might cause the minima and maxima to occur.

Figure 22

Variation of (a) horizontal force $F_x$, (b) vertical force $F_z$, and (c) horizontal force $F^r_x$ on rigid wall vs $r_g/\lambda$ for different values of H/h.

In Fig. 22a–c, the variation of $F_x$, $F_z$, and $F^r_x$ against $r_g/\lambda$ for different values of H/h is displayed. It is discovered that the vertical force $F_z$ and the horizontal forces $F_x$, $F^r_x$ follow a periodic pattern when $r_g/\lambda$ varies from lower to higher values. As H/h rises, the periodic pattern’s amplitude falls. Additionally, at higher H/h, $F_x$ is higher. The pattern of $F_z$ is the opposite of that of $F_x$. Extreme values for some specific values of $r_g/\lambda$ occur for $F_x$ and $F_z$. Moreover, when $r_g/\lambda$ increases, $F^r_x$ oscillates as well. This oscillation’s amplitude diminishes as H/h rises. Additionally, for the lowest H/h, $F^r_x$ possesses global extreme values.

Figure 23

Free surface elevation $\eta /h$ for various values of (a) $F_0$ and (b) f.

Figure 23a show that when $F_0$ values increase, the incident wave amplitude decreases while the wavelength increases. This is caused by the ’Doppler effect’ in the presence of ocean currents. A strong following current forces water waves to pass through the porous structure, causing wave breaking and energy dissipation. Further, Fig. 23b reveals that as the friction coefficient increases, the wave amplitude also decreases slightly. This may happen because as f increases, higher energy dissipation takes place which helps the incident wave amplitude to get lower.

Conclusions

The trapping of water waves by a thick, porous, bottom-standing breakwater with a trapezoidal shape under the influence of ocean currents is demonstrated in this manuscript. An approach based on the boundary element method is used to solve the associated boundary value problem. Scattering parameters such as the reflection and dissipation coefficients, wave forces acting on the seaside wall of the breakwater, and rigid seawall as functions of different kinds of physical and structural parameters like porosity, friction coefficient, non-dimensional gap between structure and rigid wall, dimensionless structural width and height, and uniform current speed are demonstrated in this study. For validation purposes, the energy balance relation is derived and checked with the present BEM-based numerical solutions. Also, experimental, analytical, and numerical findings available in the literature are used to validate the present physical model. The present model shows a good agreement with the studies available in the literature. The following are significant findings from the present investigation. The results show the reflection coefficient, dissipation coefficient, horizontal and vertical wave forces acting on the seaside wall of the breakwater and the horizontal wave force acting on the rigid seawall changes in an oscillatory manner when incident wavelength becomes shorter irrespective of variation in other parameters like porosity or friction coefficient, etc. This oscillatory pattern falls off with the increase in Froude number $F_0$. The dissipation coefficient $K_d$ follows a pattern opposite to that of the reflection coefficient $K_r$. The structural porosity also plays a vital role in wave energy dissipation. The reflection coefficient $K_r$ decreases as the friction coefficient f increases. On the other hand, the oscillating amplitude of the wave forces decreases for higher values of friction coefficient f and the porosity $\varepsilon$. Now, due to the non-dimensional separation gap $r_g/\lambda$, there are periodic patterns observed along with periodic maxima and minima in the curves of $K_r$, $K_d$, $F_x$, $F_z$, and $F^r_x$. It can be observed that $K_r$ is amplified by the following current and diminished by the opposing current. A similar kind of behavior except periodic pattern can be observed for the curves of $K_r$ and $K_d$ for numerous values of porosity $\varepsilon$ and friction coefficient f as earlier these are plotted against $\tilde{k}$. Further, it becomes apparent that the vertical force $F_z$ and the horizontal forces $F_x$, $F^r_x$, exhibit optimum values when the Froude number $F_0$ grows. The wave force $F^r_x$ acting on the solid wall diminishes as the friction coefficient f increases. There is a discernible shift to the right in $F_x$, $F_z$, and $F^r_x$ when porosity $\varepsilon$ increases and the wave force $F^r_x$ acting on the rigid wall decreases because larger values of $\varepsilon$ result in greater wave energy dissipation. The structural parameters like dimensionless width b/h and height H/h are also responsible for variations in wave energy reflection, dissipation, and wave forces. Furthermore, the wave amplitude diminishes for higher values of $F_0$ and f. So, in short words, it is observable that for the maximum dissipation and minimum wave loads, the structural width can be taken twice of the water depth and structural height can be taken 1/3$^{rd}$ of the water depth. The value of the porosity of the breakwater can be taken moderate for best performance. The least value of the friction coefficient of the breakwater can be taken $f=1$. The maximum dissipation and minimum wave forces acting on the structure and vertical rigid wall occurs in short wave length regime $\tilde{k} \ge 2.0$. So this model can give best performance in the short wavelength regime. This work shows that, in the presence of current, the present physical model, which is based on the BEM-based numerical technique, can accurately predict wave reflection, wave energy dissipation, and wave forces acting on the porous breakwater and vertical rigid seawall. After summarizing all the findings from present investigations, it can be seen that the present model has practical engineering implications across several key areas. Engineers can design more effective coastal protection structures and optimize marine renewable energy devices by harnessing concentrated wave energy, enhancing port infrastructure, improving navigation safety, and supporting climate resilience against rising sea levels and extreme weather. Environmental considerations are critical, aiming to effectively dissipate wave energy while minimizing ecological impact. Additionally, wave trapping finds diverse applications, from aquaculture and tourism to offshore wind farms, oil platforms, desalination plants, erosion control, and wave-driven pumps, highlighting its versatility in coastal and marine engineering solutions.

Moreover, studying wave interaction with breakwaters in the presence of ocean currents presents several significant challenges. Some are as follows.

• Understanding the complex interaction of waves and currents in fluid dynamics is crucial for impacting wave height, energy dissipation, and the overall effectiveness of breakwaters, requiring advanced mathematical models and computational simulations.

• Ocean currents can modify wave propagation patterns, causing wave heights to fluctuate unpredictably near breakwaters. This variability poses challenges for designing breakwaters that consistently mitigate wave energy and protect coastal structures.

• Scale effects also come into play, as laboratory experiments may not fully replicate the behavior of full-scale breakwaters in the ocean. Bridging this gap requires validation through field studies and observations.

Furthermore, the future scopes of studying ocean current and wave interaction with breakwaters is promising and multifaceted. Some are pointed in the following

• Advancements in computational modeling using some modern software (OpenFoam, Ansys-aqua, AI-Machine-learning tools) and data analytics will enhance predictive capabilities, allowing for more precise design and optimization of breakwaters tailored to specific coastal conditions.

• Integration of renewable energy technologies, such as wave energy converters integrated into breakwater structures, could provide sustainable power solutions.

• There is also a growing trend towards multi-functional breakwaters that integrate habitat enhancement, aquaculture, and recreational amenities, promoting sustainable coastal development.

• Advancements in sensor technologies will enhance real-time monitoring capabilities, improving our understanding of complex ocean dynamics and optimizing breakwater designs.

Overall, the present quantitative and qualitative data show how to build a porous breakwater with ocean waves and currents to create a calm zone to protect existing marine structures. These findings can be applied to the creation of all-encompassing coastal protection strategies that take into account the environmental and topographical conditions around the shorelines.