Introduction

Measles is a highly communicable infectious disease caused by paramyxovirus, which transmits through air and human to human direct contact. It is reported by the World Health Organization (WHO) [44], that 140,000 measles related death cases and 73% drop in measles cases occurred between the years 2000 and 2019 globally. The first clinical manifestation associated to measles disease is high fever accompanied with nasal discharge, red and watery eyes, cough, small white spots, rash on the face and body etc., which occurs within 10–12 days. It is also reported that measles induced encephalitis occurs as a result of the infection of brain during the rash face of the disease. Also, this acute form of measles leads to a disease called Sub-acute Sclerosing Pan-Encephalitis (SSPE), which is a degenerative neurological condition that destroys the brain nerve cells which causes mental illness and death. Encephalitis is diagnosed using the magnetic resonance imaging and analysis of cerebrospinal fluid, while it is treated using corticosteroids and intravenous fluids [13, 14, 26]. It is also interesting to note that, relapse of measles occurs with all the clinical signs of the disease after the attack is apparently over, but measles is still present in the system [15, 18]. Vaccination has been an effective intervention strategy to mitigate the spread of measles using the Measles–Mumps–Rubella (MMR) vaccine. This vaccine fight against three diseases namely, measles, mumps, and rubella. The Center for Disease Control (CDC) approves of children getting two doses of MMR vaccine, beginning the first dose to infants between the ages of 12–15 months, and the second dose between the ages of 4–6 years [12]. Developing countries of the world are currently challenged by this menace, with the highest burden on Nigeria [2]. The Nigerian Center for Disease and Control (NCDC) reported that 6112 and 7112 cases of measles occur between the year 2019 and 2020, which has prompted the federal government of Nigeria to declare mass awareness and vaccination against the disease [10, 27, 28, 31,32,33].

Mathematical models described by the nonlinear autonomous ordinary differential equations have been adopted many times to describe the dynamics of the spread of infectious diseases using several quantitative and qualitative techniques [21, 24, 25, 41, 43]. Several models have been derived to depict measles disease. Aldila and Asrianti [5] did a short review of measles disease dynamics by comparing models of measles disease earlier formulated by different authors and create another open problem in the future. Momoh et al. [30] and Bakare, Adekunle and Kadiri [11] formulated a model to describe the impact of latency, stability analysis and numerical implementation of a deterministic measles model. Peter et al. [37], investigated the existence and uniqueness of the model of measles with vaccination as control to reduce the class of exposed and infected individuals, while Fred et al. [16], and Okyere-Siabouh and Adetunde [36], formulated a simple Susceptible–Exposed–Infected–Recovered (SEIR) model to describe measles infection in Cape coast metropolis of Ghana and Kisii county in Kenya respectively. Their results showed that the basic threshold is less than unity and 93.75% of humans exceed the herd level immunity, which drives out the disease in the region. Other works describing the population dynamics of measles disease transmission using numerical techniques to obtain the approximate solutions of the model [1, 6,7,8] and [19, 20, 23, 34, 35], proved useful to this study.

Fractional or non-classical calculus is an important area of mathematics that have been successfully applied to the field of physics, biology, social science, finance, engineering, epidemiology etc [3, 4, 9, 17, 22, 29, 38, 45]. The advantage of fractional calculus of different differential and integral operators is that, firstly, there is freedom of choice to adopt fractional operators of any arbitrary orders, whereas it is not applicable to standard order derivative. Also, it possess the memory and hereditary characteristics that incorporate all past information, thereby giving rise to proper prediction of the model. This study consider the novel fractional derivative called the ABC operator, with the aid of Mittag-Leffler functions. The ABC operator came into existence due to the fact that Caputo and Fabrizio proposed a fractional order derivative based on exponential function to solve problems of singular kernel. They also reveal that their derivative was effective for some groups of physical problems. Furthermore, some issues were shown against this derivative because the kernel was non-singular and non-local which implies that the integral associate is not a fractional operator. In order to solve the issue of non-sigular and non-local kernel, Atangana and Baleanu derived two fractional derivatives in the sense of Caputo and Riemann–Liouville. In their results, the derivatives now possess fractional integral as anti-derivative of their operators. Therefore, since the nonlinear dynamics and crossover effect of several physical and biological phenomena cannot be explained appropriately with the classical order derivative because of its singular kernel, a generalized Mittag-Leffler function as non local and non singular kernel is explored by Atangana and Baleanu [42]. However, fractional derivatives have been applied to measles disease dynamics. Qureshi [39], derived a new five compartmental mathematical model of measles disease with conformable derivative of order \(\alpha \) in the sense of Caputo–Lioville operator of order \(\beta \). The basic reproduction number \(R_{o}\) is computed to be 2.2674e02 and the impact of several biological parameters on the system is investigated with numerical simulations, using the Adams–Moulton numerical method where the measles infection is discovered to vanish at \(\alpha \ge 1\) under the fractional conformable derivative which greatly reduce the burden of infection if either infectious contact rate is reduced and timely vaccination is applied. In addition, Qureshi and Memon [40] applied the Atangana–Baleanu operator to a fractional mathematical model of measles under the real of measles incidence in Pakistan from May–December 2018. They obtain the fitted values for the transmission coefficient \(\beta \) and fractional order parameter \(\alpha \) using the nonlinear least square curve fitting method. Also, they used the fixed point approach to analyze the existence and uniqueness of the model, while their numerical simulations for the classical and fractional measles model show a better fit for the real data about the infected individuals with the solution obtained via fractional order ABC operator. Different values of the model parameters are taken to observe their impacts on the fractional model system thereby suggesting the reduction in the contact rate of measles infected individuals with the susceptible population.

Motivated by the aforementioned literature on the formulation of model describing measles disease dynamics, which are mostly on the qualitative analysis, impact of single and double dose of vaccination, fitting data on measles incidence of some nations to the model and the application of fractional derivatives with some fractional operators some measles model, In the context of the earlier studies, this work consider what is different from the other authors. In this work, a new six compartmental deterministic model describing the transmission of measles in two distinct groups of measles infected and measles induced encephalitis infected humans with relapse combined with effect of double dose of vaccination and treatment is considered. Furthermore, the classical order derived model is changed to integer order and studied under the ABC sense. In addition, the proposed ABC model is fitted to the measles prevalence in Nigeria relative to the year 2020, to predict the level of intervention strategies in Nigeria towards curtailing the disease. To the best of the author’s knowledge, this work has not been considered. The remaining part of the article is structured into sections. Second section deals with the mathematical model derivation, while third section involves the existence, uniqueness and the positivity analysis of the proposed fractional order measles model. Fourth section deals with local and global asymptotic stability analysis of the measles free and endemic equilibrium as well as the computation of \(R_{ms}\). Finally, fifth section deals with the numerical implementation of the proposed Atangana–Baleanu–Caputo measles model, graphical illustrations, conclusion and future direction of the work.

The Mathematical Model

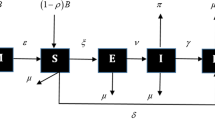
In this section, the idea to this work is extended from the work of [39, 40]. In order to derive the mathematical model, the total human host population is divided into population of susceptible humans \(S_m\), vaccinated humans \(V_e\), measles infected humans \(I_m\), measles induced encephalitis infected humans \(I_e\), treated humans \(T_m\) and recovered humans \(R_m\), such that the total human host population \(N_m(t)=S_m(t)+V_e(t)+,I_m(t)+I_e(t)+T_m(t)+R_m(t)\). In the model set up, fraction of susceptible humans are vaccinated or having maternal immunity at the rate \(\rho \), and susceptible humans are recruited at the rate \(\theta _h\). Susceptible humans received first and second dose of vaccination at the rates \(\phi _1\) and \(\phi _2\), while the rate at which the vaccine wanes is denoted \(\alpha \). The direct transmission rates between susceptible and measles and measles induced encephalitis infected humans are denoted \(\beta _a\) and \(\beta _b\) respectively, while the progression rate to treatment class is \(\sigma _1\). The treatment rate of measles induced encephalitis humans and natural recovery of humans are respectively denoted by \(\sigma _2\) and \(\eta _1\) while the recovery, relapse, natural death and death related to measles induced encephalitis infection rates are denoted by \(\eta _2, \gamma , \mu \) and \(d_1\) respectively. Therefore the classical order system of first order ordinary differential equations governing the model system is given by

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{S_m}=(1-\rho )\theta _h+(1-\phi _2)\alpha V_e-(\phi _1+\mu )S_m-\beta _a I_m S_m - \beta _b I_e S_m,\\ \dot{V_e}=\rho \theta _h-(\mu +(1-\phi _2)\alpha )V_e+\phi _1 S_m,\\ \dot{I_m}=\beta _a I_m S_m - (\mu +\sigma _1 + \eta _1)I_m+\gamma R_m,\\ \dot{I_e}=\beta _b I_e S_m - (\mu +\sigma _2+d_1)I_e,\\ \dot{T_m}=\sigma _1 I_m+\sigma _2 I_e-(\mu +\eta _2)T_m,\\ \dot{R_m}=\eta _1 I_m+\eta _2 T_m-(\gamma +\mu )R_m. \end{array}\right. } \end{aligned}$$
(1)

Since epidemiological processes are better described using derivatives of fractional order compared to classical order case. Then, changing the first order time derivatives in the classical model system Eq. (1) into the fractional derivative of order \(\tau \) in the sense of ABC operator yields

$$\begin{aligned} {\left\{ \begin{array}{ll} ^{ABC}{D^\tau _{0, \tau }}(\dot{S_m})=(1-\rho )\theta _h+(1-\phi _2)\alpha V_e-(\phi _1+\mu )S_m-\beta _a I_m S_m - \beta _b I_e S_m,\\ ^{ABC}{D^\tau _{0, \tau }}(\dot{V_e})=\rho \theta _h-(\mu +(1-\phi _2)\alpha )V_e+\phi _1 S_m,\\ ^{ABC}{D^\tau _{0, \tau }}(\dot{I_m})=\beta _a I_m S_m - (\mu +\sigma _1 + \eta _1)I_m+\gamma R_m,\\ ^{ABC}{D^\tau _{0, \tau }}(\dot{I_e})=\beta _b I_e S_m - (\mu +\sigma _2+d_1)I_e,\\ ^{ABC}{D^\tau _{0, \tau }}(\dot{T_m})=\sigma _1 I_m+\sigma _2 I_e-(\mu +\eta _2)T_m,\\ ^{ABC}{D^\tau _{0, \tau }}(\dot{R_m})=\eta _1 I_m+\eta _2 T_m-(\gamma +\mu )R_m, \end{array}\right. } \end{aligned}$$
(2)

subject to the initial conditions \(S_m\ge 0, V_e\ge 0, I_m\ge 0, I_e\ge 0, T_m\ge 0, R_m\ge 0\). The ABC fractional order operator is used in (2) due of its crossover effect, which surpasses index and power laws and enhance the proper prediction of the measles disease transmission model.

Fig. 1
figure 1

Transmission diagram of measles disease interactions in Eq. (2)

Full size image

Parameter Estimation and Data Fitting

This subsection discusses about the estimated and fitted parameters used for the proposed ABC system (2) on the basis of the available real statistical incidence data of measles epidemic of 36 states of Nigeria relative to the year 2020, obtained from the NCDC website [26], as displayed in Table 1. Some of the parameters involved in the fitting are estimated. For instance, the demographic parameter \(\theta _h\) for the Nigeria nation is estimated to be 37.269 per 1000 people in a year [28], where \(\frac{\theta _h}{\mu }=3.2192\) year\(^{-1}\) is the limiting human total population in the absence of measles disease. Also, the demographic death rate \(\mu \) is taken to be 11.577, so that \(\frac{1}{\mu }=0.0863\) year\(^{-1}\). In other to fit the data, the model system Eq. (2) may be expressed in the following form, where the function

$$\begin{aligned} y'= f(t, y, \varsigma ), \ \ y(t_0) = y_0. \end{aligned}$$
(3)

where t denotes the time, y denotes the vector of model solution, and \(\varsigma \) is the vector of unknown parameters respectively. The residual of the system is given by

$$\begin{aligned} residual_i(\varsigma ) = f(t_i, y(i) , \varsigma ) - y_{real}(i), \end{aligned}$$
(4)

and the error is

$$\begin{aligned} error (\varsigma ) = \sum _{i=1} (y(i)y_{real}(i))^2. \end{aligned}$$
(5)

The real data is represented by \(y_{real}(i)\) and \(y(i) = y (t_i, \theta )\) is the model solution to Eq. (3) for a given \(\varsigma \). The objective function is minimized such that min \({ error} (\varsigma )\) subject to Eq. (3) is used to obtain the optimal parameters.

Table 1 The meanings of estimated and fitted parameter values
Full size table

Parameter Estimation Algorithm

The parameter estimation algorithm used in obtaining the fitted values, via the global optimization search package in computational software maple is given below.

  • Adopt initial parameter and state variable values.

  • Solve the proposed fractional ABC model together with first step.

  • Investigate the error.

  • Minimize to obtain new set of parameter values with model outcome to get a good agreement with real data.

  • Check the convergence criteria. If it does not converge, go back to second step.

  • Iteration continues until the convergence criteria for the parameters is achieved.

Table 2 Data on measles prevalence in Nigeria relative to year 2020 [24]
Full size table
Fig. 2
figure 2

Simulation of the observed measles incidence relative to the year 2020 fitted to the proposed ABC model (2) and the residuals

Full size image

Figure 2a shows the comparison of the aforementioned real data with the curve of infected population obtained under the ABC measles epidemic model system Eq. (2), with the best fitted values as shown in Table 1. This further show the failure of vaccination and treatment effort. It is observed that as time increases, the disease transmission increases, while Fig. 2b shows the residuals of the fit with small scattering.

Existence and Uniqueness of the Proposed ABC Model System

Preliminaries

Definition 1

[9] Suppose that a function \(g(t)\in \mathfrak {I}^1(0, T), T>0\) and \(\tau \in (0, 1)\), then the ABC of fractional derivative of order \(\tau \) is defined as

$$\begin{aligned} ^{ABC} D_{o,t}^{\tau }[g(t)]=\frac{ABC(\tau )}{1-\tau }\int ^t_0 g^{'}(s)\zeta _{\tau }\Big [\frac{-\tau }{1-\tau }(t-s)^\tau \Big ]ds, \end{aligned}$$
(6)

where \(ABC(\tau )\) satisfying \(ABC(0)=ABC(1)=1\) denotes the normalization function and \(\zeta _{\tau }(.)\) is the one parameter Mittag-Leffler function.

Definition 2

[9] Suppose that \(\tau \in (0, 1)\) and g(t) is a function of t, then the ABC of fractional integral of order \(\tau \) is defined as

$$\begin{aligned} ^{ABC} D_{o,t}^{\tau }[g(t)]=\frac{1-\tau }{ABC(\tau )}g(t)+\frac{\tau }{ABC(\tau )\Gamma (\tau )}\int ^t_0 (t-s)^{\tau -1}g(s)ds. \end{aligned}$$
(7)

Theorem 1

[39, 40] Suppose that F(X) is a banach space of the real values continuous functions defined on the interval \(X=[0, T]\) with sup norm and \(G=F(X)\times F(X)\times F(X)\times F(X)\times F(X)\times F(X)\) with the norm \(||S_m, V_e, I_m, I_e, T_m, R_m|| = ||S_m||+||V_e||+||I_m||+||I_e||+||T_m||+||R_m||\) where \(||S_m||=sup\left\{ |S_m(t):t\in X,\right\} , ||V_e||=sup\left\{ |V_e(t):t\in X\right\} , ||I_m||=sup\left\{ |I_m(t):t\in X \right\} , ||I_e||=sup\left\{ |I_e(t):t\in X \right\} , ||T_m||=sup\left\{ |T_m(t):t\in X \right\} \), and \(||R_m||=sup\left\{ |R_m(t):t\in X\right\} \)

Proof

Applying the fractional ABC operator on both sides of Eq. (2) yields

$$\begin{aligned} {\left\{ \begin{array}{ll} S_m(t)-S(0)= ^{ABC}{D^\tau _{0, \tau }}(\dot{S_m})=\left\{ (1-\rho )\theta _h+(1-\phi _2)\alpha V_e\right. \\ \left. -(\phi _1+\mu )S_m-\beta _a I_m S_m - \beta _b I_e S_m\right\} ,\\ V_e(t)-V_e(0)=^{ABC}{D^\tau _{0, \tau }}(\dot{V_e})=\rho \theta _h-(\mu +(1-\phi _2^\tau )\alpha )V_e+\phi _1 S_m,\\ I_m(t)-I_m(0)=^{ABC}{D^\tau _{0, \tau }}(\dot{I_m})=\beta _a I_m S_m - (\mu +\sigma _1 + \eta _1)I_m+\gamma R_m,\\ I_e(t)-I_e(0)=^{ABC}{D^\tau _{0, \tau }}(\dot{I_e})=\beta _b I_e S_m - (\mu +\sigma _2+d_1)I_e,\\ T_m(t)-T_m(0)=^{ABC}{D^\tau _{0, \tau }}(\dot{T_m})=\sigma _1 I_m+\sigma _2 I_e-(\mu +\eta _2)I_m,\\ R_m(t)-R_m(0)=^{ABC}{D^\tau _{0, \tau }}(\dot{R_m})=\eta _1 I_m+\eta _2 T_m-(\gamma +\mu )R_m. \end{array}\right. } \end{aligned}$$
(8)

Applying Definition 2 on model system Eq. (2), one obtains

$$\begin{aligned} {\left\{ \begin{array}{ll} S_m(t)-S_m(0)=\frac{1-\tau }{ABC(\tau )}P_1(S_m(t), t)+\frac{\tau }{ABC(\tau )\Gamma (\tau )}\int ^t_0(t-q)^{\tau - 1}P_1(S_m(q), q)dq,\\ V_e(t)-V_e(0)=\frac{1-\tau }{ABC(\tau )}P_2(V_e(t), t)+\frac{\tau }{ABC(\tau )\Gamma (\tau )}\int ^t_0(t-q)^{\tau - 1}P_2(V_e(q), q)dq,\\ I_m(t)-I_m(0)=\frac{1-\tau }{ABC(\tau )}P_3(I_m(t), t)+\frac{\tau }{ABC(\tau )\Gamma (\tau )}\int ^t_0(t-q)^{\tau - 1}P_3(I_m(q), q)dq,\\ I_e(t)-I_e(0)=\frac{1-\tau }{ABC(\tau )}P_4(I_e(t), t)+\frac{\tau }{ABC(\tau )\Gamma (\tau )}\int ^t_0(t-q)^{\tau - 1}P_4(I_e(q), q)dq,\\ T_m(t)-T_m(0)=\frac{1-\tau }{ABC(\tau )}P_5(T_m(t), t)+\frac{\tau }{ABC(\tau )\Gamma (\tau )}\int ^t_0(t-q)^{\tau - 1}P_5(T_m(q), q)dq,\\ R_m(t)-R_m(0)=\frac{1-\tau }{ABC(\tau )}P_6(R_m(t), t)+\frac{\tau }{ABC(\tau )\Gamma (\tau )}\int ^t_0(t-q)^{\tau - 1}P_6(R_m(q), q)dq,\\ \end{array}\right. } \end{aligned}$$
(9)

where

$$\begin{aligned} {\left\{ \begin{array}{ll} P_1(S_m(t), t)=(1-\rho )\theta _h+(1-\phi _2)\alpha V_e-(\phi _1+\mu )S_m-\beta _a I_m S_m - \beta _b I_e S_m,\\ P_2(V_e(t), t)=\rho \theta _h-(\mu +(1-\phi _2)\alpha )V_e+\phi _1 S_m,\\ P_3(I_m(t), t)=\beta _a I_m S_m - (\mu +\sigma _1 + \eta _1)I_m+\gamma R_m,\\ P_4(I_e(t), t)=\beta _b I_e S_m - (\mu +\sigma _2+d_1)I_e,\\ P_5(T_m(t), t)=\sigma _1 I_m+\sigma _2 I_e-(\mu +\eta _2)I_m,\\ P_6(R_m(t), t)=\eta _1 I_m+\eta _2 T_m-(\gamma +\mu )R_m. \end{array}\right. } \end{aligned}$$
(10)

Given that \(S_m(t), V_e(t), I_m(t), I_e(t), T_m(t)\) and \(R_m(t)\) have an upper bound, then

$$\begin{aligned} P_1(S_m(t), t), P_2(V_e(t), t),P_3(I_m(t), t),P_4(I_e(t), t),P_5(T_m(t), t) \end{aligned}$$

and \(P_6(R_m(t), t)\) are said to satisfy the Lipschitz condition. Let \(S_m(t)\) be two functions, so that

$$\begin{aligned} ||P_1(S_m(t), t)-P_1(S_{m1}(t), t)||=||-(\phi _1+\mu )S_m(t)+(\phi _1+\mu ) S_{m1}(t)||. \end{aligned}$$
(11)

Considering \(w_1=||\phi +\mu ||\), we obtain

$$\begin{aligned} ||P_1(S_m(t), t)-P_1(S_{m1}(t), t)||\le w_1=||S_m(t)-S_{m1}(t)||. \end{aligned}$$
(12)

In the same manner, one obtains

$$\begin{aligned} {\left\{ \begin{array}{ll} ||P_2(V_e(t), t)-P_2(V_{e1}(t), t)||\le w_2=||V_e(t)-V_{e1}(t)||,\\ ||P_3(I_m(t), t)-P_3(I_{m1}(t), t)||\le w_3=||I_m(t)-I_{m1}(t)||,\\ ||P_4(I_e(t), t)-P_4(I_{e1}(t), t)||\le w_4=||I_e(t)-I_{e1}(t)||,\\ ||P_5(T_m(t), t)-P_5(T_{m1}(t), t)||\le w_5=||T_m(t)-T_{m1}(t)||,\\ ||P_6(R_m(t), t)-P_6(R_{m1}(t), t)||\le w_6=||R_m(t)-R_{m1}(t)||. \end{array}\right. } \end{aligned}$$
(13)

Hence, the Lipschitz condition is satisfied for all the functions \(S_m(t), V_e(t), I_m(t), I_e(t), T_m(t)\) and \(R_m(t)\), where \(w_1,w_2, w_3,w_4,w_5,\) and \(w_6\) are the corresponding Lipschitz constants. Furthermore, Eq. (9) can be written recursively as

$$\begin{aligned} {\left\{ \begin{array}{ll} S_m(t)=\frac{1-\tau }{ABC(\tau )}P_1(S_{m_{n-1}}(t), t)+\frac{\tau }{ABC(\tau )\Gamma (\tau )}\int ^t_0(t-q)^{\tau - 1}P_1(S_{m_{n-1}}(q), q)dq+S_m(0),\\ V_e(t)=\frac{1-\tau }{ABC(\tau )}P_2(V_{e_{n-1}}(t), t)+\frac{\tau }{ABC(\tau )\Gamma (\tau )}\int ^t_0(t-q)^{\tau - 1}P_2(V_{e_{n-1}}(q), q)dq+V_e(0),\\ I_m(t)=\frac{1-\tau }{ABC(\tau )}P_3(I_{m_{n-1}}(t), t)+\frac{\tau }{ABC(\tau )\Gamma (\tau )}\int ^t_0(t-q)^{\tau - 1}P_3(I_{m_{n-1}}(q), q)dq+I_m(0),\\ I_e(t)=\frac{1-\tau }{ABC(\tau )}P_4(I_{e_{n-1}}(t), t)+\frac{\tau }{ABC(\tau )\Gamma (\tau )}\int ^t_0(t-q)^{\tau - 1}P_4(I_{e_{n-1}}(q), q)dq+I_e(0),\\ T_m(t)=\frac{1-\tau }{ABC(\tau )}P_5(T_{m_{n-1}}(t), t)+\frac{\tau }{ABC(\tau )\Gamma (\tau )}\int ^t_0(t-q)^{\tau - 1}P_5(T_{m_{n-1}}(q), q)dq+T_m(0),\\ R_m(t)=\frac{1-\tau }{ABC(\tau )}P_6(R_{m_{n-1}}(t), t)+\frac{\tau }{ABC(\tau )\Gamma (\tau )}\int ^t_0(t-q)^{\tau - 1}P_6(R_{m_{n-1}}(q), q)dq+R_m(0).\nonumber \end{array}\right. }\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\\ \end{aligned}$$
(14)

Taking the difference of the successive terms together with the initial conditions in Eq. (2), the following system of equations are derived, given by

$$\begin{aligned} {\left\{ \begin{array}{ll} \lambda _{S_{m, \ n}}(t)=S_m(t)-S_{m_{n-1}}(t)=\frac{1-\tau }{ABC(\tau )}(P_1(S_{m_{n-1}}(t), t)-P_1(S_{m_{n-2}}(t)))+\frac{\tau }{ABC(\tau )\Gamma (\tau )}\\ \int ^t_0(t-q)^{\tau - 1}P_1(S_{m_{n-1}}(q), q)-P_1(S_{m_{n-2}}(q), q)dq,\\ \lambda _{V_{e, \ n}}(t)=V_e(t)-V_{e_{n-1}}(t) =\frac{1-\tau }{ABC(\tau )}(P_2(V_{e_{n-1}}(t), t)-P_2(V_{e_{n-2}}(t), t))+\frac{\tau }{ABC(\tau )\Gamma (\tau )}\\ \int ^t_0(t-q)^{\tau - 1}P_2(V_{e_{n-1}}(q), q)-P_2(V_{e_{n-1}}(q), q)dq,\\ \lambda _{I_{m, \ n}}(t)=I_m(t)-I_{m_{n-1}}(t)=\frac{1-\tau }{ABC(\tau )}(P_3(I_{m_{n-1}}(t), t)-P_3(I_{m_{n-2}}(t), t))+\frac{\tau }{ABC(\tau )\Gamma (\tau )}\\ \int ^t_0(t-q)^{\tau - 1}(P_3(I_{m_{n-1}}(q), q)-P_3(I_{m_{n-2}}(q), q))dq,\\ \lambda _{I_{e, \ n}}(t)=I_e(t)-I_{e_{n-1}}(t)=\frac{1-\tau }{ABC(\tau )}(P_4(I_{e_{n-1}}(t), t)-P_4(I_{e_{n-2}}(t), t))+\frac{\tau }{ABC(\tau )\Gamma (\tau )}\\ \int ^t_0(t-q)^{\tau - 1}(P_4(I_{e_{n-1}}(q), q)-P_4(I_{e_{n-2}}(q), q))dq,\\ \lambda _{T_{m, \ n}}(t)=T_m(t)-T_{m_{n-1}}(t)=\frac{1-\tau }{ABC(\tau )}(P_5(T_{m_{n-1}}(t), t)-P_5(T_{m_{n-2}}(t), t))+\frac{\tau }{ABC(\tau )\Gamma (\tau )}\\ \int ^t_0(t-q)^{\tau - 1}(P_5(T_{m_{n-1}}(q), q)-P_5(T_{m_{n-2}}(q), q))dq,\\ \lambda _{R_{m, \ n}}(t)=R_m(t)-R_{m_{n-1}}(t)=\frac{1-\tau }{ABC(\tau )}(P_6(R_{m_{n-1}}(t), t)-P_6(R_{m_{n-2}}(t), t))\frac{\tau }{ABC(\tau )\Gamma (\tau )}\\ \int ^t_0(t-q)^{\tau - 1}(P_6(R_{m_{n-1}}(q), q)-P_6(R_{m_{n-2}}(q), q))dq.\nonumber \end{array}\right. }\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\\ \end{aligned}$$
(15)

Also, it should be noted that \(S_{m, \ n}(t)=\sum ^n_{j=0}\lambda _{S_{m, j}}(t), V_{e, \ n}(t)=\sum ^n_{j=0}\lambda _{V_{e, j}}(t), I_{m, \ n}(t)=\sum ^n_{j=0}\lambda _{I_{m, j}}(t), I_{e, \ n}(t)=\sum ^n_{j=0}\lambda _{I_{e, j}}(t), T_{m, \ n}(t)=\sum ^n_{j=0}\lambda _{T_{m, j}}(t)\) and \(R_{m, \ n}(t)=\sum ^n_{j=0}\lambda _{R_{m, j}}(t)\), Using Eqs.(12) and (13) and taking into account that

$$\begin{aligned} {\left\{ \begin{array}{ll} \lambda _{S_{m,\ n-1}}(t)=S_{m_{n-1}}(t)-S_{m_{n-2}}(t),\\ \lambda _{V_{e,\ n-1}}(t)=V_{e_{n-1}}(t)-V_{e_{n-2}}(t),\\ \lambda _{I_{m,\ n-1}}(t)=I_{m_{n-1}}(t)-I_{m_{n-2}}(t),\\ \lambda _{I_{e,\ n-1}}(t)=I_{e_{n-1}}(t)-I_{e_{n-2}}(t),\\ \lambda _{T_{m,\ n-1}}(t)=T_{m_{n-1}}(t)-T_{m_{n-2}}(t),\\ \lambda _{R_{m,\ n-1}}(t)=R_{m_{n-1}}(t)-R_{m_{n-2}}(t), \end{array}\right. } \end{aligned}$$
(16)

Then, the following are derived.

$$\begin{aligned} {\left\{ \begin{array}{ll} ||\lambda _{S_{m, n}}(t)||\le \frac{1-\tau }{ABC(\tau )}w_1||\lambda _{S_{m, n-1}}(t)||+\frac{\tau }{ABC(\tau )\Gamma (\tau )}w_1\int _0^t(t-q)^{\tau -1}||\lambda _{S_{m, n-1}}(q)||dq,\\ ||\lambda _{V_{e, n}}(t)||\le \frac{1-\tau }{ABC(\tau )}w_2||\lambda _{V_{e, n-1}}(t)||+\frac{\tau }{ABC(\tau )\Gamma (\tau )}w_2\int _0^t(t-q)^{\tau -1}||\lambda _{V_{e, n-1}}(q)||dq,\\ ||\lambda _{I_{m, n}}(t)||\le \frac{1-\tau }{ABC(\tau )}w_3||\lambda _{I_{m, n-1}}(t)||+\frac{\tau }{ABC(\tau )\Gamma (\tau )}w_3\int _0^t(t-q)^{\tau -1}||\lambda _{I_{m, n-1}}(q)||dq,\\ ||\lambda _{I_{e, n}}(t)||\le \frac{1-\tau }{ABC(\tau )}w_4||\lambda _{I_{e, n-1}}(t)||+\frac{\tau }{ABC(\tau )\Gamma (\tau )}w_4\int _0^t(t-q)^{\tau -1}||\lambda _{I_{e, n-1}}(q)||dq,\\ ||\lambda _{T_{m, n}}(t)||\le \frac{1-\tau }{ABC(\tau )}w_5||\lambda _{T_{m, n-1}}(t)||+\frac{\tau }{ABC(\tau )\Gamma (\tau )}w_5\int _0^t(t-q)^{\tau -1}||\lambda _{T_{m, n-1}}(q)||dq,\\ ||\lambda _{R_{m, n}}(t)||\le \frac{1-\tau }{ABC(\tau )}w_6||\lambda _{R_{m, n-1}}(t)||+\frac{\tau }{ABC(\tau )\Gamma (\tau )}w_6\int _0^t(t-q)^{\tau -1}||\lambda _{R_{m, n-1}}(q)||dq. \end{array}\right. } \end{aligned}$$
(17)

\(\square \)

Theorem 2

[39, 40] The proposed fractional order measles ABC operator model Eq. (2) possess a unique solution for some \(t_o\in [0, T]\) if the following condition holds true.

$$\begin{aligned} \frac{1-\tau }{ABC(\tau )}w_j+\frac{1-\tau }{ABC(\tau )\Gamma (\tau )}w_j^\tau \ t_o<1,\quad j=1,\ldots ,6 . \end{aligned}$$
(18)

Proof

It is clear that \(S_m(t), V_e(t), I_m(t), I_e(t), T_m(t)\) and \(R_m(t)\) are bounded functions and they also satisfy the Lipschitz condition. Also the expressions \(P_1, P_2, P_3, P_4, P_5\) and \(P_6\) satisfy the Lipschitz condition as shown in Eqs. (12) and (13). Hence, employing the recursive principle with the application of Eq. (17), the following system are derived.

$$\begin{aligned} {\left\{ \begin{array}{ll} ||\lambda _{S_{m, n}}||\le ||S_m(0)||\Big (\frac{1-\tau }{ABC(\tau )}w_1+\frac{\tau t_o}{ABC(\tau )\Gamma (\tau )}w_1\Big )^n,\\ ||\lambda _{V_{e, n}}||\le ||V_e(0)||\Big (\frac{1-\tau }{ABC(\tau )}w_2+\frac{\tau t_o}{ABC(\tau )\Gamma (\tau )}w_2\Big )^n,\\ ||\lambda _{I_{m, n}}||\le ||I_m(0)||\Big (\frac{1-\tau }{ABC(\tau )}w_3+\frac{\tau t_o}{ABC(\tau )\Gamma (\tau )}w_3\Big )^n,\\ ||\lambda _{I_{e, n}}||\le ||I_e(0)||\Big (\frac{1-\tau }{ABC(\tau )}w_4+\frac{\tau t_o}{ABC(\tau )\Gamma (\tau )}w_4\Big )^n,\\ ||\lambda _{T_{m, n}}||\le ||T_m(0)||\Big (\frac{1-\tau }{ABC(\tau )}w_5+\frac{\tau t_o}{ABC(\tau )\Gamma (\tau )}w_5\Big )^n,\\ ||\lambda _{R_{m, n}}||\le ||R_m(0)||\Big (\frac{1-\tau }{ABC(\tau )}w_6\frac{\tau t_o}{ABC(\tau )\Gamma (\tau )}w_6\Big )^n. \end{array}\right. } \end{aligned}$$
(19)

Therefore, the sequences obtained above exist and satisfy \(||\lambda _{S_{m,n}}(\tau )||\rightarrow 0, ||\lambda _{V_{e,n}}(\tau )||\rightarrow 0, ||\lambda _{I_{m,n}}(\tau )||\rightarrow 0, ||\lambda _{I_{e,n}}(\tau )||\rightarrow 0, ||\lambda _{T_{m,n}}(\tau )||\rightarrow 0\) and \(||\lambda _{R_{m,n}}(\tau )||\rightarrow 0\) and \(n\rightarrow \infty \). Moreover, from Eq. (19) and making use of the triangular inequality for any r yields

$$\begin{aligned} {\left\{ \begin{array}{ll} ||S_{m_{n+r}}(t)-S_{m_n}(t)||\le \sum _{j=n+1}^{n+r} L_1^j=\frac{L_1^{n+1}-L_1^{n+r+1}}{1-L_1},\\ ||V_{e_{n+r}}(t)-V_{e_n}(t)||\le \sum _{j=n+1}^{n+r} L_2^j=\frac{L_2^{n+1}-L_2^{n+r+1}}{1-L_2}, \\ ||I_{m_{n+r}}(t)-I_{m_n}(t)||\le \sum _{j=n+1}^{n+r} L_3^j=\frac{L_3^{n+1}-L_3^{n+r+1}}{1-L_3},\\ ||I_{e_{n+r}}(t)-I_{e_n}(t)||\le \sum _{j=n+1}^{n+r} L_4^j=\frac{L_4^{n+1}-L_4^{n+r+1}}{1-L_4},\\ ||T_{m_{n+r}}(t)-T_{m_n}(t)||\le \sum _{j=n+1}^{n+r} L_5^j=\frac{L_5^{n+1}-L_5^{n+r+1}}{1-L_5},\\ ||R_{m_{n+r}}(t)-R_{m_n}(t)||\le \sum _{j=n+1}^{n+r} L_6^j=\frac{L_6^{n+1}-L_6^{n+r+1}}{1-L_6},\\ \end{array}\right. } \end{aligned}$$
(20)

where \(L_1,L_2,L_3,L_4,L_5\) and \(L_6\) are the terms mentioned within Eq. (19). Therefore \(S_{m_n}, V_{e_n}, I_{m_n}, I_{e_n}, T_{m_n}\) and \(R_{m_n}\) compose the Cauchy sequences in F(x), which is uniformly convergent. The limit of these sequences is the unique solution of Eq. (2) demonstrated when the limit theory in Eq. (14) as \(n\rightarrow \infty \) is applied. Therefore, the existence of the unique solution for the fractional order ABC model system Eq. (2) is proved. \(\square \)

Positivity and Boundedness of the Proposed ABC Model Solutions

Theorem 3

[21, 24, 41] The solutions \((S_m(t), V_e(t), I_m(t), I_e(t), T_m(t), R_m(t))\) of the fractional order ABC model Eq. (2) are nonnegative for all \(t\ge 0\) with nonnegative initial conditions in \(R^{+6}\).

Proof

It is clear that the existence and uniqueness of the ABC model system Eq. (2) is in \((0, \infty )\). Since the human population exist, then

$$\begin{aligned} {\left\{ \begin{array}{ll} ^{ABC}{D^\tau _{0, \tau }}({S_m(t)})|_{k({S_m})}=(1-\rho )\theta _h+(1-\phi _2)\alpha V_e\ge 0,\\ ^{ABC}{D^\tau _{0, \tau }}({V_e(t)})|_{k({V_e})}=\rho \theta _h+\phi _1 S_m\ge 0,\\ ^{ABC}{D^\tau _{0, \tau }}({I_m(t)})|_{k({I_m})}=\beta _a S_m+\gamma R_m\ge 0,\\ ^{ABC}{D^\tau _{0, \tau }}({I_e(t)})|_{k({I_e})}=\beta _b S_m \ge 0,\\ ^{ABC}{D^\tau _{0, \tau }}({T_m(t)})|_{k({T_m})}=\sigma _1 I_m+\sigma _2 I_e\ge 0,\\ ^{ABC}{D^\tau _{0, \tau }}({R_m(t)})|_{k({R_m})}=\eta _1 I_m+\eta _2 T_m\ge 0, \end{array}\right. } \end{aligned}$$
(21)

where \(k(\tau )=\left\{ \tau (t)=0, \ S_m, V_e, I_m, I_e, T_m, R_m \in F(R^{+6})\right\} \) and \(\tau \in \left\{ S_m, V_e, I_m, I_e, T_m, R_m\right\} \). From the theorem above, any solution of the ABC model system Eq. (2) is such that \((S_m(t), V_e(t), I_m(t), I_e(t), T_m(t), R_m(t))\in R^{+6}, \forall t\ge 0\). \(\square \)

Theorem 4

[21, 24, 41] The domain \(\wedge =\left\{ (S_m, V_e, I_m, I_e, T_m, R_m \in (R^{+6}):N_m\le \frac{\theta _h}{\mu }\right\} \) is a positively invariant set for the proposed ABC fractional model Eq. (2), where \(N_m(t)=S_m(t)+V_e(t)+I_m(t)+I_e(t)+T_m(t)+R_m(t)\).

Proof

The summation of the total number of human population in Eq. (2) yields

$$\begin{aligned} ^{ABC}{D^\tau _{0, \tau }}N_m(t)=\theta _h-\mu N_m\le \theta _h-\mu N_m(t). \end{aligned}$$
(22)

Solving the above inequality, one obtains

$$\begin{aligned} \lim _{t\rightarrow \infty }{} { sup} N_m(t)\le \frac{\theta _h}{\mu }. \end{aligned}$$
(23)

Therefore, from Eq. (23), the epidemiologically relevant domain in the sense of measles disease transmission is given by

$$\begin{aligned} \wedge =\left\{ (S_m, V_e, I_m, I_e, T_m, R_m) \in (R^{+6}):N_m\le \frac{\theta _h}{\mu }\right\} . \end{aligned}$$
(24)

Hence the ABC fractional measles disease model Eq. (2) is restricted to the solution set \(\wedge \). \(\square \)

Asymptotic Stability Analysis and Basic Reproduction Number \((R_{ms})\)

In order to examine the stability of the ABC model (2), the two basic equilibria, namely, the measles-free and measles-endemic eqilibria. Let \(^{ABC}{D^\tau _{0, \tau }} S_m = 0, ^{ABC}{D^\tau _{0, \tau }} V_e = 0, ^{ABC}{D^\tau _{0, \tau }} I_m = 0, ^{ABC}{D^\tau _{0, \tau }} I_e = 0, ^{ABC}{D^\tau _{0, \tau }} T_m = 0, ^{ABC}{D^\tau _{0, \tau }} R_m = 0\) , the measles-free equilibrium is given by

$$\begin{aligned} {\left\{ \begin{array}{ll} E_m=(S_m^o, V_e^o, I_m^o, I_e^o, T_m^o, R_m^o)=\\ \Big (S_m^o=\frac{(1-\rho )\theta _h+((1-\phi _2)\alpha ) \rho \theta _h}{(\phi _1+\mu )(\mu +(1-\phi _2)\alpha )},\\ V_e^o=\frac{\rho \theta _h}{\mu +((1-\phi _2)\alpha )}, I_m^o=0, I_e^o=0, T_m^o=0, R_m^o=0, \Big ) \end{array}\right. } \end{aligned}$$
(25)

while the measles-endemic equilibrium is given by

$$\begin{aligned} {\left\{ \begin{array}{ll} E_m^*=(S_m^*, V_e^*, I_m^*, I_e^*, T_m^*, R_m^*)= &{}\Big (S_m^*=\frac{(1-\phi _2)\alpha V_e^*+(1-\rho )\theta }{\beta _a I_m^*+\beta _b I_e^*+\mu +\phi _1}, \ V_e^*=\frac{\rho \theta +\phi _1}{\alpha \phi _2-\mu },\\ &{} I_m^* = \frac{\gamma R_m}{\mu +\eta _1+\sigma _1-\beta _a S_m^*}, \ I_e^*=\frac{\beta I_e^*}{(\mu +\sigma _2+d_1)I_e^*},\\ &{} T_m^*=\frac{\sigma _1 I_m^*+\sigma _2 I_e^*}{\mu +\eta _2}, \ R_m^*=\frac{I_m^* \eta _1+T_m^* \eta _2}{\gamma +\mu } \Big ) \end{array}\right. } \end{aligned}$$
(26)

Basic Reproduction Number \((R_{ms})\)

Here, the next generation matrix method [17, 20] is employed to obtain the basic reproduction number \(R_{ms}\) of the proposed ABC model system Eq. (2), where the two matrices F and V are given by

$$\begin{aligned} F= & {} \begin{pmatrix} 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad \beta _a S^o_{m}&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad \beta _b S^o_{m}&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \end{pmatrix}\nonumber \\ V= & {} \begin{pmatrix} (\phi _1+\mu )&{}\quad (1-\phi _2)\alpha &{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ \phi _1&{}\quad (\mu +(1-\phi _2)\alpha )&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad (\mu +\sigma _1+\eta _1)&{}\quad 0&{}\quad 0&{}\quad \gamma \\ 0&{}\quad 0&{}\quad 0&{}\quad (\mu +\sigma _2+d_1)&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad (\mu +\eta _2)&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad (\gamma +\mu )\\ \nonumber \end{pmatrix}\\ \end{aligned}$$
(27)

where

$$\begin{aligned} R_{ms}(F\cdot V^{-1})=\frac{\beta _a\beta _b((1-\rho )\theta _h+((1-\phi _2)\alpha )\cdot \rho \theta _h}{(\mu +\sigma _1+\eta _1)(\mu +\sigma _2+d_1)(\phi _1+\mu )(\mu +(1-\phi _2)\alpha )}, \end{aligned}$$
(28)

is the vaccination controlled basic reproduction number \((R_{ms})\) governing the measles epidemic spread in the human host population. If \(R_{ms}<1\), then measles die out in the system, while the persistence leading to high epidemic burden of measles occur when \(R_{ms}>1\).

Local and Global Asymptotic Stability of the Measles-Free Equilibrium

Theorem 5

[21, 24, 41] The measles-free equilibrium point \(E_m\) should satisfy \(Re(q_i)<0, i=1,\ldots ,6\) for being locally asymptotically stable, where q denote the eigenvalues of the Jacobian matrix computed at such equilibria.

Proof

Linearizing the ABC fractional model Eq. (2) around the measles-free equilibrium \(E_m\) (25), the following Jacobian matrix is derived, given by

$$\begin{aligned} J(E_m)= \begin{pmatrix} -(\phi _1+\mu )&{}(1-\phi _2)\alpha &{}0&{}0&{}0&{}0\\ \phi _1&{}-(\mu +(1-\phi _2)\alpha )&{}0&{}0&{}0&{}0\\ 0&{}0&{}\beta _a S^o_{m} - (\mu +\sigma _1+\eta _1)&{}0&{}0&{}\gamma \\ 0&{}0&{}0&{}\beta _b S^o_{m} - (\mu +\sigma _2+d_1)&{}0&{}\gamma \\ 0&{}0&{}\sigma _1&{}\sigma _2&{}-(\mu +\eta _2)&{}0\\ 0&{}0&{}\eta _1&{}\eta _2&{}0&{}-(\gamma +\mu )\\ \nonumber \end{pmatrix}\!\!\!\!\!\!\!\!\\ \end{aligned}$$
(29)

It is clear from Eq. (29), that the negative eigenvalues of the \(6\times 6\) Jacobian matrix are \(q_1=-(\phi _1+\mu )<0, q_2=-(\mu +(1-\phi _2)\alpha )<0, q_5=-(\mu +\eta _1)<0, q_6=-(\gamma +\mu )<0\), except the quantities \(\beta _a S_m-(\mu +\sigma _1+\eta _1)\) and \(\beta _b S_m- (\mu +\sigma _2+d_1)\) which are positive, which reduces Eq. (29) to a two dimensional matrix given by

$$\begin{aligned} J(E_m)= \begin{pmatrix} \beta _a S^o_{m}-(\mu +\sigma _1+\eta _1)&{}\quad 0\\ 0&{}\quad \beta _b S^o_{m}(\mu +\sigma _2+d_1) \end{pmatrix}, \end{aligned}$$
(30)

such that after the simplification of Eq. (30), one obtains

$$\begin{aligned} \beta _a\beta _b S_m^o-(\mu +\sigma _1+\eta _1)(\mu +\sigma _2+d_1)>\frac{(\mu +\sigma _1+\eta _1)(\mu +\sigma -2+d_1)}{(\mu +\sigma _1+\eta _1)(\mu +\sigma _2+d_1)}. \end{aligned}$$
(31)

Since \(S^o_{m}\) has been defined earlier in (25), then

$$\begin{aligned}&\frac{\beta _a\beta _b((1-\rho )\theta +((1-\phi _2)\alpha )\cdot \rho \theta }{(\mu +\sigma _1+\eta _1)(\mu +\sigma _2+d_1)(\phi _1+\mu )(\mu +(1-\phi _2)\alpha )} >\frac{(\mu +\sigma _1+\eta _1)(\mu +\sigma -2+d_1)}{(\mu +\sigma _1+\eta _1)(\mu +\sigma _2+d_1)}. \end{aligned}$$
(32)

It is clear from Eq. (32), that \(R_{ms}<1\) if \(-R_{ms}>-1\). Hence, the measles-free equilibrium of model system Eq. (2) is locally asymptotically stable. \(\square \)

Theorem 6

[21, 24, 41] The measles-free equilibrium Eq. (25) of ABC model system Eq. (2) is globally asymptotically stable if \(R_{ms}< 1.\)

Proof

Using the comparison technique, the equation for the infected classes in (2) is considered and simplified as follows

$$\begin{aligned} \begin{pmatrix} \dot{I_m}\\ \dot{I_e} \end{pmatrix}\!=\!\Big (\frac{S_m}{N_m}\Big )\begin{pmatrix} \dot{I_m}\\ \dot{I_e} \end{pmatrix}-V\begin{pmatrix} {I_m}\\ {I_e} \end{pmatrix} \!=\!(F-V) \begin{pmatrix} {I_m}\\ {I_e} \end{pmatrix}-\Big (1-\frac{S}{N}\Big )F\begin{pmatrix} {I_m}\\ {I_e} \end{pmatrix}\le (F-V)\begin{pmatrix} {I_m}\\ {I_e}\nonumber \end{pmatrix},\!\!\!\!\!\!\!\!\\ \end{aligned}$$
(33)

where F and V are earlier defined. Therefore, the linearized differential inequality system is stable whenever \(R_{ms}<1\) . By standard comparison theorem, we obtain

$$\begin{aligned} (I_m, I_e)\rightarrow (0, 0), \ \ t\rightarrow \infty . \end{aligned}$$
(34)

Substituting \(I_m=I_e=0\) in the ABC model system Eq. (2) becomes

$$\begin{aligned} (S_m, V_e, T_m, R_m)=\Big (\frac{(1-\rho )\theta +((1-\phi _2)\alpha ) \rho \theta }{(\phi _1+\mu )(\mu +(1-\phi _2)\alpha )}, \frac{\rho \theta }{\mu +((1-\phi _2)\alpha )}, 0, 0, 0, 0, \Big ), \end{aligned}$$
(35)

which converges to the measles free equilibrium Eq. (25) as \(t\rightarrow \infty \). Hence, the measles-free equilibrium \(E_m\) of Eq. (25) is globally asymptotically stable whenever \(R_{ms}<1\). \(\square \)

Numerical Implementation and Discussions of Simulations

Numerical Implementation

Here, the proposed fractional ABC model system Eq. (2) under the ABC fractional operator of order \(\tau \) is numerically solved. The approximate solutions are obtained using the algorithm in the novel method developed by [35]. The advantage of this method is to enhance the limitation of other well known existing methods of Adams–Bashforth, Eulers etc., since they cannot solve non-local, non-singular kernel fractional derivatives in terms of efficiency and convergence. The nonlinear fractional differential equation with respect to the ABC fractional derivative of order \(\tau \) yields

$$\begin{aligned} ^{ABC} D_t^\tau \varpi (t)=\Psi (t, \varpi (t)), \ \varpi (0)=\varpi _o, \ 0\le t\le \zeta , \end{aligned}$$
(36)

together with the following initial conditions \(\varpi ^{(\nu )}=\varpi _o^{\nu }, \ \ \nu =0,1,2,\ldots ,[\tau ]-1.\) Using the fundamental principles of fractional calculus, Eq. (36) is transformed into a fractional integral equation as

$$\begin{aligned} \varpi (t)-\varpi (0)=\frac{1-\tau }{ABC(\tau )}\Psi (t, \varpi (t))+\frac{\tau }{\Gamma (\tau )ABC(\tau )}\int ^t_0 (t-t)^{\tau -1}\Psi (\tau , \tau (t))dt. \end{aligned}$$
(37)

At the point \(t_{n+1}, n=0,1,2\ldots \) we have from Eq. (37), that

$$\begin{aligned} {\left\{ \begin{array}{ll} \varpi (t_{n+1})-\varpi (0)=\frac{1-\tau }{ABC(\tau )}\Psi (t_n, \varpi (t_n))+\frac{\tau }{\Gamma (\tau )ABC(\tau )}\int ^{t_{n+1}}_0 (t_{n+1}-t)^{\tau -1}\Psi (\zeta , \tau (\zeta ))d\zeta \\ =\frac{1-\tau }{ABC(\tau )}\Psi (t_n, \varpi (t_n))+\frac{\tau }{\Gamma (\tau )ABC(\tau )}\sum _{k=0}^n\int ^{t_{k+1}}_{t_k} (t_{n+1}-t)^{\tau -1}\Psi (\zeta , \tau (\zeta ))d\zeta .\nonumber \end{array}\right. }\!\!\!\!\!\!\\ \end{aligned}$$
(38)

The function \(\Psi (\zeta , \tau (\zeta ))\), within the interval \([t_k, t_{k+1}]\), employing the two- step Lagrange polynomial interpolation approximately yields

$$\begin{aligned} {\left\{ \begin{array}{ll} G_k(\zeta )=\frac{\zeta -t_{k-1}}{t_k-t_{k-1}}\Psi (t_k,\tau (t_k))- \frac{\zeta -t_{k}}{t_k-t_{k-1}}\Psi (t_{k-1},\tau (t_{k-1}))\\ =\frac{\Psi (t_k, \zeta (t_k))}{h}(\zeta -t_{k-1})-\frac{\Psi (t_{k-1}, \zeta (t_{k-1}))}{h}(\zeta -t_{k})\\ \cong \frac{\Psi (t_k, \zeta (t_k))}{h}(\zeta -t_{k-1})-\frac{\Psi (t_{k-1}, \zeta (t_{k-1}))}{h}(\zeta -t_{k}). \end{array}\right. } \end{aligned}$$
(39)

Using the approximation in Eq. (39), where h is the step length, we obtain from Eq. (38),

$$\begin{aligned} {\left\{ \begin{array}{ll} \tau _{n+1}=\tau (0)+\frac{(1-\tau )}{ABC(\tau )}\psi (t_n, \tau (t_n))+\frac{\tau }{ABC(\tau )\times \Gamma (\tau )}\times \sum _{k=0}^n\Big (\frac{\Psi (t_k, \tau _{k-1}}{h}\int ^{t_{k+1}}_{t_k}\\ (\zeta -t_k-1)(t_{n+1}-t)^{\zeta _1}d\zeta -\frac{\Psi (t_{k_1}, \zeta _{k-1})}{h}\int ^{t_{k+1}}_{t_k}(\zeta -t_k)(t_{n+1}-t)^{\tau -1}d\zeta \Big ) \end{array}\right. } \end{aligned}$$
(40)

Without generality loss, we consider

$$\begin{aligned} P_{\tau , k, 1}= \int ^{t_{k+1}}_{t_k}(\zeta -t_{k-1})(t_{n+1}-\zeta )^{\zeta -1}d\zeta , \end{aligned}$$
(41)

and

$$\begin{aligned} P_{\tau , k, 2}= \int ^{t_{k+1}}_{t_k}(\zeta -t_k)(t_{n+1}-\zeta )^{\zeta -1}d\zeta , \end{aligned}$$
(42)

so that

$$\begin{aligned} P_{\tau , k,1}=h^{\tau +1}\frac{(n+1-k)^\tau (n-k+2+\tau )-(n-k)^\tau (n-k+2+2\tau )}{\tau (\tau +1)} \end{aligned}$$
(43)

and

$$\begin{aligned} P_{\tau ,k,2}=h^{\tau +1}\frac{(n+1-k)^{\tau +1}-(n-k)^\tau (n-k+1+\tau )}{\tau (\tau +1)}. \end{aligned}$$
(44)

Thus integrating Eqs. (42), (43) and (44), and replacing them in Eq. (40), yields

$$\begin{aligned} {\left\{ \begin{array}{ll} \varpi _{n+1}=\varpi (0)+\frac{(1-\tau )}{ABC(\tau )}\Psi (t_n, \varpi (t_n))+\frac{\tau }{ABC(\tau )}\sum ^n_{k=0}\times \Big (\frac{h^\tau \Psi (t_k, \tau _k)}{\Gamma (\tau +2)}\\ ((n+1-k)^\tau (n-k+2+\tau )-(n-k)^\tau (n-k+2+2\tau ))\Big )-\frac{\tau }{ABC(\tau )}\sum ^n_{k=0}\\ \Big (\frac{h^\tau \Psi (t_{k-1}, \tau _{k-1})}{\Gamma (\tau +2)}((n+1-k)^\tau (n-k+2+\tau )-(n-k)^\tau (n-k+1+\tau ))\Big ). \end{array}\right. } \end{aligned}$$
(45)

Equation (45) represent the numerical scheme for the ABC fractional derivative. Therefore employing this scheme to the proposed ABC model system Eq. (2) yields the following;

$$\begin{aligned}&{\left\{ \begin{array}{ll} S_{m_{n+1}}=S_m(0)+\frac{(1-\tau )}{ABC(\tau )}\Psi (t_n, {S_m}(t_n))+\frac{\tau }{ABC(\tau )}\sum ^n_{k=0}\times \Big (\frac{h^\tau \Psi (t_k, S_{m_k})}{\Gamma (\tau +2)}\\ ((n+1-k)^\tau (n-k+2+\tau )-(n-k)^\tau (n-k+2+2\tau ))\Big )-\frac{\tau }{ABC(\tau )}\\ \sum ^n_{k=0}\Big (\frac{h^\tau \Psi (t_{k-1}, {S_m}_{k-1})}{\Gamma (\tau +2)}((n+1-k)^\tau (n-k+2+\tau )-(n-k)^\tau (n-k+1+\tau ))\Big ), \end{array}\right. } \end{aligned}$$
(46)
$$\begin{aligned}&{\left\{ \begin{array}{ll} V_{e_{n+1}}=V_e(0)+\frac{(1-\tau )}{ABC(\tau )}\Psi (t_n, {V_e}(t_n))+\frac{\tau }{ABC(\tau )}\sum ^n_{k=0}\times \Big (\frac{h^\tau \Psi (t_k, V_{e_k})}{\Gamma (\tau +2)}\\ ((n+1-k)^\tau (n-k+2+\tau )-(n-k)^\tau (n-k+2+2\tau ))\Big )-\frac{\tau }{ABC(\tau )}\\ \sum ^n_{k=0}\Big (\frac{h^\tau \Psi (t_{k-1}, {V_e}_{k-1})}{\Gamma (\tau +2)}((n+1-k)^\tau (n-k+2+\tau )-(n-k)^\tau (n-k+1+\tau ))\Big ), \end{array}\right. } \end{aligned}$$
(47)
$$\begin{aligned}&{\left\{ \begin{array}{ll} I_{m_{n+1}}=I_m(0)+\frac{(1-\tau )}{ABC(\tau )}\Psi (t_n, {I_m}(t_n))+\frac{\tau }{ABC(\tau )}\sum ^n_{k=0}\times \Big (\frac{h^\tau \Psi (t_k, I_{m_k})}{\Gamma (\tau +2)}\\ ((n+1-k)^\tau (n-k+2+\tau )-(n-k)^\tau (n-k+2+2\tau ))\Big )-\frac{\tau }{ABC(\tau )}\sum ^n_{k=0}\\ \Big (\frac{h^\tau \Psi (t_{k-1}, {I_m}_{k-1})}{\Gamma (\tau +2)}((n+1-k)^\tau (n-k+2+\tau )-(n-k)^\tau (n-k+1+\tau ))\Big ), \end{array}\right. } \end{aligned}$$
(48)
$$\begin{aligned}&{\left\{ \begin{array}{ll} I_{n_{n+1}}=I_n(0)+\frac{(1-\tau )}{ABC(\tau )}\Psi (t_n, {I_n}(t_n))+\frac{\tau }{ABC(\tau )}\sum ^n_{k=0}\times \Big (\frac{h^\tau \Psi (t_k, I_{n_k})}{\Gamma (\tau +2)}\\ ((n+1-k)^\tau (n-k+2+\tau )-(n-k)^\tau (n-k+2+2\tau ))\Big )-\frac{\tau }{ABC(\tau )}\sum ^n_{k=0}\\ \Big (\frac{h^\tau \Psi (t_{k-1}, {I_n}_{k-1})}{\Gamma (\tau +2)}((n+1-k)^\tau (n-k+2+\tau )-(n-k)^\tau (n-k+1+\tau ))\Big ), \end{array}\right. } \end{aligned}$$
(49)
$$\begin{aligned}&{\left\{ \begin{array}{ll} T_{m_{n+1}}=T_m(0)+\frac{(1-\tau )}{ABC(\tau )}\Psi (t_n, {T_m}(t_n))+\frac{\tau }{ABC(\tau )}\sum ^n_{k=0}\times \Big (\frac{h^\tau \Psi (t_k, T_{m_k})}{\Gamma (\tau +2)}\\ ((n+1-k)^\tau (n-k+2+\tau )-(n-k)^\tau (n-k+2+2\tau ))\Big )-\frac{\tau }{ABC(\tau )}\sum ^n_{k=0}\\ \Big (\frac{h^\tau \Psi (t_{k-1}, {T_m}_{k-1})}{\Gamma (\tau +2)}((n+1-k)^\tau (n-k+2+\tau )-(n-k)^\tau (n-k+1+\tau ))\Big ), \end{array}\right. } \end{aligned}$$
(50)
$$\begin{aligned}&{\left\{ \begin{array}{ll} R_{m_{n+1}}=R_m(0)+\frac{(1-\tau )}{ABC(\tau )}\Psi (t_n, {R_m}(t_n))+\frac{\tau }{ABC(\tau )}\sum ^n_{k=0}\times \Big (\frac{h^\tau \Psi (t_k, R_{m_k})}{\Gamma (\tau +2)}\\ ((n+1-k)^\tau (n-k+2+\tau )-(n-k)^\tau (n-k+2+2\tau ))\Big )-\frac{\tau }{ABC(\tau )}\sum ^n_{k=0}\\ \Big (\frac{h^\tau \Psi (t_{k-1}, {R_m}_{k-1})}{\Gamma (\tau +2)}((n+1-k)^\tau (n-k+2+\tau )-(n-k)^\tau (n-k+1+\tau ))\Big ). \end{array}\right. } \end{aligned}$$
(51)

Discussions of Simulations

Here, the numerical simulations for the proposed measles infection ABC model system Eq. (2) is presented. A novel iterative technique, proposed in recent study of [35], is used to obtain the approximate solutions of the proposed fractional type ABC measles model Eq. (2) using the fitted and estimated values in Table 1.

Fig. 3
figure 3

Simulations of the effect of the measles transmission and relapse parameters of the proposed ABC measles model Eq. (2)

Full size image
Fig. 4
figure 4

Simulations of the effect of vaccination parameters of the proposed ABC measles model Eq. (2)

Full size image

Figure 3a–c displays the simulations of the fitted values of the effect of transmission \(\beta _a\), \(\beta _b\) and relapse \(\gamma \) rates in measles infected and measles induced encephalitis individuals. In Fig. 3a, b, a slight increase occurs which in turn decreases to the endemic state as time increases. This is due to the fact that infection rate is higher in the host population compared to the level of vaccination interventions implemented, which must be scaled up in order to bring down the infection near zero. Also, Fig. 3c shows that as time increases some certain individuals after temporary improvement against measles infection experience relapse of the disease in their body system. Furthermore, Fig. 4a–c displays the simulations of the fitted values of the effect of vaccination in the human host community. Figure 4a, c reveals that after the first and second dose of vaccination of individuals denoted \(\phi _1\) and \(\phi _2\), there is a decrease in likelihood of acquiring infection and that the vaccine wanes quickly as depicted in Fig. 3b, while Table 3 shows the peak values and times for the graphical behaviors. This shows that the level of vaccination is low compared to the endemic burden of the disease since the simulations fail to converge to the measles-free equilibrium. From the physical (epidemiological) point of view, Figs. 3 and 4 shows the long term (12 months) behavior of the disease transmission and vaccination efforts applied. The curve of measles infection transmission rates fails to flatten out in 12 months, which means that vaccination efforts of first and second dose coverage is low, and the vaccine wanes quickly, which sustains measles endemicity in Nigeria.

Table 3 Peak values and times
Full size table

Conclusion

An epidemiological model of measles disease transmission in distinct classes of measles infected and measles induced encephalitis infected humans with the effect of vaccination, treatment and relapse under the fractional ABC sense is rigorously examined. The model is validated by fitting measles prevalence data of all Nigerian states relative to the year 2020. Using the nonlinear least square algorithm via the direct search optimization package in computational software maple, the fitted and estimated parameter values and the basic reproduction \(R_{ms}\) number are obtained. The Computation of the \(R_{ms}(R_{ms}\approx 1.34)\) reveal that an individual is being infected on the average in the naive susceptible population in Nigeria despite vaccination and treatment coverage, there is still a significant population of un-immunized individuals, which results in the disease being in an endemic state in the nation Nigeria. To this effect, the Nigerian government should scale up sufficient attention to vaccination logistics, so that it can reach rural areas, regular supervision, intermittent sensitization through media and special attention to children and families with low socio-economic status to prevent immunization gaps, which may lead to high prevalence of measles in the future. Analytically, the existence and uniqueness of the model is established, while the model is found to be locally and globally asymptotically stable when \(R_{ms<1}\). A novel numerical technique that combines fractional calculus with two step Lagranges polynomial is employed to solve and obtain the approximate solutions of the proposed ABC model system equations. The fractional order \(\tau \) is varied using the fitted parameters and the results reveal that despite the intervention measures like vaccination and treatment, the simulation curves converges to the endemic state, which implies that measles is still an endemic burden on the Nigerian nation. Also, the numerical scheme proved to be efficient and convergent with less computational cost. This work is open to further research by considering the impact of seasonality of measles transmission using spatial models, impact of fractional optimal controls of media and educational awareness and socio-economic status of humans in the host community as well as considering the impact of other fractional operators like the Caputo–Fabrizio, Grunwald–Letnikov, just to mention a few.