Introduction

Measles, which is caused by the measles virus, is a highly transmissible disease with endemic areas found in the tropical regions, although outbreaks also occur in temperate zones (Moss 2017). It is recorded as one of the most dreadful diseases in human history, leading to millions of deaths over the years. The measles virus, belonging to the “Morbillivirus genus” in the Paramyxoviridae family, shares close resemblance with the now-eradicated rinderpest virus affecting cattle. It is believed to have evolved from an ancestral virus as a zoonotic infection in communities where humans and cattle lived in close proximity, establishing itself in human populations approximately 5000–10,000 years ago during the expansion of Middle-Eastern river valley civilizations.

Measles is a global phenomenon, with transmission patterns varying between temperate and tropical climates. In temperate countries, transmission intensifies in late winter and early spring, while in tropical regions, it tends to increase after the rainy season. Before the advent of measles vaccination, epidemics occurred every 2 or 3 years, their duration influenced by factors such as population size, crowding, and immunity levels. In regions where measles is endemic, the majority of children contract the virus by the age of 10. In the past, when measles was endemic in the United States, over 90% of individuals were infected by age 15 (Guerrant et al. 2006). Despite higher vaccination coverage levels in certain countries, susceptible populations can accumulate over time, leading to explosive outbreaks occurring every 5–7 years.

Measles has an incubation period of approximately 10 days from exposure to the onset of fever, with an additional 4 days for the appearance of the characteristic rash. The virus is most contagious 1–3 days before the onset of fever and cough. The secondary attack rate among susceptible household contacts is reported to exceed 80%, and outbreaks have been documented in populations where only 3–7% of individuals were susceptible. Communicability diminishes significantly following the appearance of the rash. Several types of vaccines have also been recommended for use against measles vaccines (Demicheli et al. 2013).

Fractional calculus has gained prominence as a valuable tool for modeling biological processes, mainly due to its capacity to account for “memory effect”, a very important aspects in understanding such processes. The initial formulation of fractional differential operators featuring power-law kernels was introduced by Caputo (1967). However, these formulations rely on singular kernels, imposing limitations on their applicability in simulating biological and physical processes. To overcome these constraints, Caputo and Fabrizio (2015), as well as Atangana and Baleanu (2016), updated the definitions of fractional-operators. In the literature, various methods have been proposed to solve fractional order models (Akindeinde et al. 2022).

Mathematical models have also been formulated to understand the dynamics of measles. For instance, Mossong and Muller (2003) utilized a mathematical model to evaluate the epidemiological implications of vaccinated individuals transmitting the measles virus. The model anticipated that, following a prolonged absence of circulating virus, 80% of all the seroconverted vaccinated persons would exhibit titers below the protective threshold. Garba et al. (2017) designed and scrutinized a mathematical model for measles transmission within a population. Their study assessed the collective impact of vaccination and measles treatment in the population. The authors in Aldila and Asrianti (2019) conducted an analysis of a measles model incorporating a two-step vaccination process and quarantine. The model categorized individuals into compartments based on their vaccination status, distinguishing those with one dose and those with two doses. The study aimed to investigate the effectiveness of quarantine in controlling measles spread compared to vaccination strategies. In their work, the study outlined in Fakhruddin et al. (2020) constructed both deterministic and stochastic models for measles transmission, considering vaccination and a hospitalized compartment. The research aimed to identify the most influential parameters for proposing effective control strategies. It suggested that providing treatment access is more beneficial than vaccination during an outbreak. Memon et al. (2020) emphasized the critical importance of achieving a high vaccine coverage rate for effective disease control. Additionally, the study in Xue et al. (2020) analyzed a dynamic model that incorporated periodic transmission and asymptomatic infection with waning immunity. The objective was to identify parameters influencing the seasonal fluctuation of measles and propose optimal control measures to minimize the number of infected individuals and associated costs. Alemneh and Belay (2023) developed a deterministic model of measles transmission dynamics by considering the impact of indirect contact rate. Further studies on the mathematical modeling of measles transmission are available in Peter et al. (2023d, 2018), along with additional references cited in those works. To the best of our knowledge, this is the first study to consider the impact of treatment failure on the transmission dynamics of measles. Despite the considerable research on modeling measles epidemics, there is a need for a comprehensive mathematical model investigating the impact of treatment failure and vaccination using a fractional-order model. Therefore, this paper aims to formulate a novel non-integer mathematical model for measles, analyze the existence and uniqueness of the solution, and identify parameters influencing disease dynamics. The non-standard finite difference (NSFD) scheme will be utilized to analyze the solution, a method previously employed by various authors in modeling fractional-order systems, including Shah et al. (2021), ud Din et al. (2020), Sinan et al. (2023), Xu et al. (2022), Tong et al. (2021), Maamar et al. (2024) and Peter et al. (2023a). NSFD has proven to be a reliable tool for finding numerical solutions to fractional-order models, offering advantages such as positivity, stability, and adherence to conservation laws, making it preferable over other methods like perturbation/decomposition schemes (Shah et al. 2021; Maamar et al. 2024). The hope is that this study will pave the way for further research in epidemiological modeling.

The rest of this paper is structured as follows: Method which includes model formulation and analysis are described in “Method”. “Numerical scheme” consists of the numerical scheme. Results and discussion are given in “Results”. Finally, in “Conclusion”, we have provided conclusions of this article. Table 1 shows a detailed description of the parameters, while the model’s compartmental flow diagram is shown in Fig. 1. The existence, uniqueness and stability results are also added in the Appendix section

Method

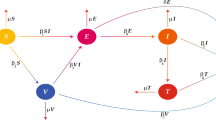
We formulate a new mathematical model of measles infection transmission with six compartments (Fig. 1). These are, susceptible humans S(t), vaccinated humans V(t), exposed humans E(t), infected humans I(t), hospitalised humans H(t) and recovered humans R(t). The susceptible population is increased by immigration or newborns at a constant rate \(\upphi \), also, the susceptible individual acquired temporary immunity at a rate \(\tau \) and loose immunity at a rate \(\rho \), the parameter \(\alpha \) represent the force of infection between the susceptible and infected individuals in the population, the progression rate from exposed to infected class is at a rate \(\beta \), \(\sigma \) represent fraction of individuals that are hospitalised as a result of complicated measles infection while the rest of \((1- \sigma ) \kappa \) recovered naturally. \(\kappa \) represent the movement rate out of infected class. Proportion of individual in the hospitalised class moved back to infected class as a result of treatment failure at a rate \(\theta \varepsilon \) while the rest of \((1-\varepsilon ) \theta \), recovered class as a result of treatment at a rate. There is a natural death at a rate \(\mu \) in all the classes and the disease induced death rate in infected and hospitalised class at the rate \(\delta \). The descriptions above can be illustrated in a system of differential equations in 1, while the model’s compartmental flow diagram is shown in Fig. 1. The model variables and parameter description are given in Tables 1 and 2.

Fig. 1
figure 1

Schematic diagram of the model

Full size image
Table 1 Description of the model variables
Full size table
Table 2 Model parameter values and description
Full size table
$$\begin{aligned} \begin{aligned} {}^{C}D^{\xi }_{t} S(t)&=\upphi +\tau V-\alpha SI-(\mu +\rho )S,\\ {}^{C}D^{\xi }_{t} V(t)&=\rho S -(\tau +\mu )V,\\ {}^{C}D^{\xi }_{t} E(t)&=\alpha S I-(\mu +\beta )E,\\ {}^{C}D^{\xi }_{t} I(t)&= \theta \varepsilon H +\beta E-(\sigma +\mu +\delta _1)I,\\ {}^{C}D^{\xi }_{t} H(t)&=\sigma \kappa I-(\theta +\mu +\delta _2)H,\\ {}^{C}D^{\xi }_{t} R(t)&=(1-\kappa ) \sigma I+(1-\varepsilon )\theta H-\mu R.\\ \end{aligned} \end{aligned}$$
(1)

where, \(^CD^{\xi }_{t}\) defines the Caputo derivative of order \(\xi \). The system (1) can be represented in the compact form given as:

$$\begin{aligned} {\left\{ \begin{array}{ll} {}_{0}^{C}D_{t}^{\xi }{K}(t) &{} =\mathcal {K}(t,{K}(t)), \\ {K}(0) &{} =K_{0}, \end{array}\right. } \end{aligned}$$
(2)

where, \(K(t)=\begin{pmatrix} S(t)&V(t)&E(t)&I(t)&H(t)&H(t)&R(t) \end{pmatrix}^{T}\in \mathbb {R}^{6}\), for each \(t\in \mathcal {J}=[0,b]\). That is, \(K: J \rightarrow \mathbb {R}^{6}\) is a function. Also, \(\mathcal {K}:\mathcal {J} \times \mathbb {R}^{6}\rightarrow \mathbb {R}^{6}\) defines a function.

$$\begin{aligned} \begin{aligned} \mathcal {K}_{1}(t,K(t))&=\upphi +\tau V-\alpha SI-(\mu +\rho )S, \\ \mathcal {K}_{2}(t,K(t))&=\rho S -(\tau +\mu )V, \\ \mathcal {K}_{3}(t,K(t))&=\alpha S I-(\mu +\beta )E, \\ \mathcal {K}_{4}(t,K(t))&=\theta \varepsilon H +\beta E-(\sigma +\mu +\delta _1)I, \\ \mathcal {K}_{5}(t,K(t))&=\sigma \kappa I-(\theta +\mu +\delta _2)H, \\ \mathcal {K}_{6}(t,K(t))&= (1-\kappa ) \sigma I+(1-\varepsilon )\theta H-\mu R. \\ \end{aligned} \end{aligned}$$
(3)

Equation (3) can be written in form of the Volterra integral equation given by

$$\begin{aligned} K(t)=K(0)+\frac{ 1 }{\Gamma (\xi )}\int _{0}^{t}(t-\varphi )^{\xi -1} \mathcal {K}(\varphi ,K(\varphi ))d\varphi \end{aligned}$$
(4)

The model analysis

In this section the local asymptotic stability and boundedness of system (1) is analysed by giving a proof.

Boundedness of the total population

Theorem 0.1

The closed set

$$\begin{aligned} \mathcal {D} =\bigg .\bigg \{(S(t), V(t), E(t), I(t), H(t), R(t)) \in \mathfrak {R}_{+}^{6}: S(t) + V(t) + E(t) + I(t) + H(t) + R(t) \le \frac{\upphi }{\mu }\bigg .\bigg \}, \end{aligned}$$

is positively invariant in relation to the system (1).

Proof

Adding all the equations of system (1) gives

$$\begin{aligned} ^{C}_{0} D^\xi _t N = \upphi - \mu N(t) - (\delta _{1} I + \delta _{2} H), \end{aligned}$$
(5)

where, \(N(t) = S(t) + V(t) + E(t) + I(t) + H(t) + R(t)\). From (5), we have

$$\begin{aligned} ^{C}_{0} D^\xi _t N < \upphi - \mu N, \end{aligned}$$
(6)

Applying Laplace transform on (6), we obtain that

$$\begin{aligned} s^\xi \mathcal {L}\{N(t)\}-s^{\xi -1}N(0)\le \frac{\upphi }{s}-\mu \mathcal {L}\{N(t)\}, \end{aligned}$$

which further implies that

$$\begin{aligned} \mathcal {L}\{N(t)\}\le \frac{\upphi }{s(s^\xi +\mu )}+N(0)\frac{s^{\xi -1}}{s^\xi +\mu }. \end{aligned}$$
(7)

By partial fraction, the above expression reduces to

$$\begin{aligned} \mathcal {L}\{N(t)\}\le \frac{\upphi }{\mu }\left( \frac{1}{s} \right) -\left( \frac{\upphi }{\mu }-N(0) \right) \frac{s^{\xi -1}}{s^\xi +\mu }. \end{aligned}$$
(8)

The inverse Laplace transform gives

$$\begin{aligned} N(t) \le \frac{\upphi }{\upmu }-\left( \frac{\upphi }{\upmu }-N(0) \right) E_\xi \left( -\mu t^\xi \right) . \end{aligned}$$
(9)

Since the Mittag–Leffler function has asymptotic behaviour, we have \(N(t)\le \frac{\upphi }{\mu }\) as \(t\rightarrow \infty \). Therefore, system (3) has solutions in \(\mathcal {D}\) and hence is positively invariant. \(\square \)

The Basic reproduction number of the model

The fundamental concept of the basic reproduction number involves estimating the anticipated number of secondary infections generated by a single infectious individual throughout their entire period of infectivity in a population that is entirely susceptible to the measles virus. This crucial metric serves as a determinant for evaluating the potential for disease invasion. Specifically, if the calculated value surpasses one, it indicates the likelihood of an outbreak, whereas a value below one suggests that the disease is likely to fade out. To compute the basic reproduction number, we proceed as follows: The disease free equilibrium (DFE) of the model (1) is:

$$\begin{aligned} \begin{aligned} \psi _{0}&=\left( S^{*}, V^{*}, E^{*}, I^{*}, H^{*}, R^{*} \right) \\&=\left( \frac{\upphi (\tau + \mu )}{\mu (\tau + \mu + \rho )}, \frac{ \rho \upphi }{\mu (\tau + \mu + \rho )},0,0,0,0\right) . \end{aligned} \end{aligned}$$

Following the approach from [2023b], the transfer matrices (denoting the appearance of new infections and transitions in and out of the disease compartments) for the model are, respectively given by

$$\begin{aligned}{} & {} F= \begin{pmatrix} 0&{} \frac{\alpha \upphi (\tau + \mu )}{\mu (\tau + \mu + \rho )} &{} 0 \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ \end{pmatrix} \end{aligned}$$
(10)
$$\begin{aligned}{} & {} V= \begin{pmatrix} \mu + \beta &{} 0 &{} 0 \\ -\beta &{} \sigma + \mu + \delta _{1} &{} -\theta \varepsilon \\ 0 &{} -\sigma \kappa &{} \theta + \mu + \delta _{2} \\ \end{pmatrix} \end{aligned}$$
(11)

The basic reproduction number of the model (1) is the spectral radius of \(FV^{-1}\) and is given by

$$\begin{aligned} {\mathcal {R}}_{0} = \frac{\alpha \beta \upphi (\tau + \mu ) (\theta + \mu + \delta _{2})}{\mu (\mu + \beta ) [(\sigma + \mu + \delta _{1})(\mu + \delta _{2}) + \theta (\delta _1 + \mu ) + \theta \sigma (1-\varepsilon \kappa )](\tau + \mu + \rho )} \end{aligned}$$

Local asymptotic stability of the disease free equilibrium (DFE) of the model

Theorem 0.2

The system’s DFE, \(\mathcal {Z}_{0}\), is locally asymptotically stable (LAS) if \(\mathcal {R}_{0}<1\), and unstable if \(\mathcal {R}_{0}>1\).

Proof

The stability of system (1) in the neighborhood of the DFE is analyzed by Jacobian of system (1) evaluated at DFE, \(\mathcal {Z}_{0}\), which is given by:

$$\begin{aligned} \begin{pmatrix} - (\mu + \rho ) &{} \tau &{} 0 &{} - \frac{\alpha \upphi (\tau + \mu )}{\mu (\tau + \mu + \rho )} &{} 0 &{} 0 \\ \rho &{} -(\tau + \mu ) &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} - (\mu + \beta ) &{} \frac{\alpha \upphi (\tau + \mu )}{\mu (\tau + \mu + \rho )} &{} 0 &{} 0 \\ 0 &{} 0 &{} \beta &{} -(\sigma + \mu + \delta _{1}) &{} \theta \varepsilon &{} 0\\ 0 &{} 0 &{} 0 &{} \sigma \kappa &{} - (\theta + \mu + \delta _{2}) &{} 0 \\ 0 &{} 0 &{} 0 &{} (1-\kappa )\sigma &{} (1-\varepsilon ) \theta &{} -\mu \\ \end{pmatrix} \end{aligned}$$

The eigenvalues are given by:

$$\begin{aligned} \lambda _1 = - (\mu + \rho ), \quad \lambda _2 = -(\tau + \mu ), \quad \lambda _3 = - \mu , \end{aligned}$$

and the solution of the characteristic polynomial:

$$\begin{aligned} \begin{aligned}&\lambda ^3 + [(\mu + \beta ) + (\sigma + \mu + \delta _{1}) + (\theta + \mu + \delta _{2})] \lambda ^2 \\&\quad + \bigg [(\mu + \beta ) (\sigma + \mu + \delta _{1}) + (\mu + \beta ) (\theta + \mu + \delta _{2}) \\&\quad + (\sigma + \mu + \delta _{1}) (\theta + \mu + \delta _{2}) - \frac{\alpha \beta \upphi (\tau + \mu )}{\mu (\tau + \mu + \rho )} - \varepsilon \theta \kappa \sigma \bigg ] \lambda \\&\quad + \mu (\mu + \beta ) [(\sigma + \mu + \delta _{1})(\mu + \delta _{2}) + \theta (\delta _1 + \mu ) \\&\quad + \theta \sigma (1-\varepsilon \kappa )](\tau + \mu + \rho ) (1 - \mathcal {R}_{0}) = 0 \end{aligned} \end{aligned}$$
(12)

From the Routh–Hurwitz criterion, the equation above has roots with negative real parts if and only if \(\mathcal {R}_{0}<1\). Hence, the DFE is locally asymptotically stable if \(\mathcal {R}_{0} <1\). \(\square \)

Numerical scheme

Non- Standard Finite Difference Scheme for Caputo fractional derivative

In order solve numerically system (1) we have to choose the fractional operator as follows:

The Caputo derivative of function f(t) of order \(\xi \in (0,1)\) is defined as

$$\begin{aligned} {}^{C} D^{{\xi }}_{t}\left[ f(t)\right] =\frac{1}{\Gamma (1-\xi )}~\int ^{t}_{0} \frac{f^{'}(\theta )}{(t-\theta )^{\xi }}\,\,d\theta . \end{aligned}$$
(13)

The discretization of domain [0,  T] is given as

$$\begin{aligned} t_j=j~h,\qquad j=0,1,2,3, \dots \end{aligned}$$
(14)

where \(h=\frac{T}{N}\), N represent number of sub intervals and T is final time. Now at \(t=t_{j+1}\), Caputo derivative becomes

$$\begin{aligned} {}^{C}D^{{\xi }}_{t}\left[ f(t)\right] |_{t=t_{j+1}}=\frac{1}{\Gamma (1-\xi )}~\int ^{t_{j+1}}_{0} \frac{f^{'}(\theta )}{(t_{j+1}-\theta )^{\xi }}\,\,d\theta , \end{aligned}$$
(15)

or

$$\begin{aligned} {}^{C}D^{{\xi }}_{t}\left[ f(t)\right] |_{t=t_{j+1}}=\frac{1}{\Gamma (1-\xi )}~\sum _{k=0}^j~\int ^{t_{k+1}}_{t_{k}} f^{'}(\theta )~(t_{j+1}-\theta )^{-\xi }\,\,d\theta , \end{aligned}$$
(16)

Now we approximate \(f^{'}(\theta )=\frac{df(\theta )}{d\theta }\) on \([t_k,~t_{k+1}]\) as

$$\begin{aligned} \frac{df(\theta )}{d\theta }=\frac{f^{k+1}-f^{k}}{\Psi (h)}, \end{aligned}$$
(17)

where \(f^{k}=f(t_k)\) and \(\Psi (h)=\frac{e^{\mu h-1}}{\mu }=h+O(h^2)\), where \(\mu \) is the natural death rate.

Now (16) becomes

$$\begin{aligned} {}^{C}D^{{\xi }}_{t}\left[ f(t)\right] |_{t=t_{j+1}}\approx \frac{1}{\Gamma (1-\xi )}~\sum _{k=0}^j~\int ^{t_{k+1}}_{t_{k}} \frac{f^{k+1}-f^{k}}{\Psi (h)}~(t_{j+1}-\theta )^{-\xi }\,\,d\theta , \end{aligned}$$
(18)

or

$$\begin{aligned} {}^{C}D^{{\xi }}_{t}\left[ f(t)\right] |_{t=t_{j+1}}=\frac{1}{\Gamma (2-\xi )}~\sum _{k=0}^j~ \frac{f^{k+1}-f^{k}}{\Psi (h)}~A_{\xi ,j}^k, \end{aligned}$$
(19)

where

$$\begin{aligned} A_{\xi ,j}^k= & {} (1-\xi )\int ^{t_{k+1}}_{t_{k}}~(t_{j+1}-\theta )^{-\xi }\,\,d\theta \nonumber \\= & {} h^{1-\xi }[(j-k+1)^{1-\xi }-(j-k)^{1-\xi }]. \end{aligned}$$
(20)

The denominator function

The denominator function, which is an important element of the NSFDs is now derived for the fractional system (1): Adding all the equations of the model (1) gives,

$$\begin{aligned} {}^{C}_{0}D_{t}^{\xi } N(t) \le \upphi - \mu N, \end{aligned}$$

with

$$\begin{aligned} \begin{aligned} N(t)\le N(0)E_{\xi }(-\mu h^{\xi })+\upphi h^{\xi }E_{\xi , \xi +1}(-\mu h^{\xi }) \end{aligned} \end{aligned}$$
(21)

where \(E_{\xi , \xi +1}\) is the Mittag-Leffler function and \(h=(t_{k+1}-t_k)\)

Let \(t_{0}=0<t_1<t_2<\cdot \cdot \cdot <t_N=T\), such that \(t_k=\frac{kN}{K}\) and \(N\in \mathbb {Z}^+\)

For \(t>0\) and \(0<\xi <1\), the Caputo fractional derivative is expressed as

$$\begin{aligned} D^{\xi }_tf(t)\vert _{t=t_{k+1}}=\frac{1}{\Gamma (1-\xi )}\sum _{j=0}^k\int _{t_j}^{t_{j+1}}\frac{df(s)}{ds}(t_{k+1}-s)^{-\xi }ds \end{aligned}$$
(22)

Upon discretizing \(\frac{df(s)}{ds}\) on \([t_{j}, t_{j+1}]\) we have that

$$\begin{aligned} \frac{df(s)}{ds}=\frac{f^{j+1}-f^j}{\Psi (h)} \end{aligned}$$

where h is the mesh size and \(f^j=f(t_{j})\).

But,

$$\begin{aligned} D^{\xi }_tf(t)\vert _{t=t_{k+1}}\approx \frac{1}{\Gamma (2-\xi )}\sum _{j=0}^{k} \triangle _{\xi , k}^j\frac{f^{j+1}-f^j}{\Psi (h)} \end{aligned}$$

with,

$$\begin{aligned} \triangle _{\xi , k}^j=\left( (t_{k+1}-t_{j})^{1-\xi }-(t_{k+1}-t_{j+1})^{1-\xi } \right) \end{aligned}$$

If \(j=k\) then,

$$\begin{aligned} \triangle _{\xi , k}^k=\left( (t_{k+1}-t_k)^{1-\xi }-(t_{k+1}-t_{k+1})^{1-\xi } \right) =(t_{k+1}-t_k)^{1-\xi }=h^{1-\xi } \end{aligned}$$
(23)

When \(t=t_{k+1}\) then we obtain

$$\begin{aligned} \begin{aligned}&\frac{1}{\Gamma (2-\xi )}\sum _{j=0}^k\triangle ^j_{\xi , k}\frac{f^{j+1}-f^j}{\Psi (h)}\\&\quad =F(f^{k+1}), ~k=1, 2, \ldots , K-1 \end{aligned} \end{aligned}$$
(24)

Applying the NSFD scheme (24) as proposed in Maamar et al. (2024) to the inequality (21) we have that

$$\begin{aligned} \frac{1}{\Gamma (2-\xi )}\sum _{j=0}^k\triangle ^j_{\xi , k}\frac{(N^{j+1}-N^j)}{\Psi (h)}\le \upphi -\mu N^{k+1} \end{aligned}$$
(25)

at \(j=k\), we have that

$$\begin{aligned}{} & {} \frac{h^{1-\xi }}{\Gamma (2-\xi )}\frac{(N^{k+1}-N^k)}{\Psi (h)}+\sum _{j=0}^{k-1}\triangle _{\xi , k}^j(N^{j+1}-N^j)\nonumber \\{} & {} \quad \le \Gamma (2-\xi )\Psi (h)(\upphi -\mu N^{k+1}) \end{aligned}$$
(26)

Now,

$$\begin{aligned}{} & {} N^{k+1}\left( h^{1-\xi }+\mu \Gamma (2-\xi )\Psi (h)\right) \le h^{1-\xi }N^k+\Gamma (2-\xi )\Psi (h)\upphi \nonumber \\{} & {} \quad -\sum _{j=0}^{k-1}\triangle _{\xi , k}^j(N^{j+1}-N^j) \end{aligned}$$
(27)

Thus,

$$\begin{aligned} N^{k+1}\le \frac{h^{1-\xi }N^k+\upphi \Gamma (2-\xi )\Psi (h)-\sum _{j=0}^{k-1}\triangle _{\xi , k}^j(N^{j+1}-N^j)}{h^{1-\xi }+\mu \Gamma (2-\xi )\Psi (h)} \end{aligned}$$
(28)

When \(k=0\), we have that

$$\begin{aligned} \begin{aligned} N^1\le \left( \frac{h^{1-\xi }N^0}{h^{1-\xi }+\mu \Gamma (2-\xi )\Psi (h)}+\frac{\upphi \Gamma (2-\xi )\Psi (h)}{h^{1-\xi }+\mu \Gamma (2-\xi )\Psi (h)}\right) \end{aligned} \end{aligned}$$
(29)

To determine the denominator function, \(\Psi (h)\), we compare Eqs. (21) and (29) using the terms containing the initial population at time \(t=0\).

Hence,

$$\begin{aligned} \Psi (h)=\frac{h^{1-\xi }\left( 1-E_{\xi }(-\mu h^{\xi })\right) }{\mu \Gamma (2-\xi )E_{\xi }(-\mu hh^{\xi })} \end{aligned}$$

Applying the NSFD to the fractional system (1), we have

$$\begin{aligned} \begin{aligned}&\dfrac{1}{\Gamma (2-\xi )}~\sum _{k=0}^j~ \dfrac{S^{k+1}-S^{k}}{\Psi (h)}~A_{\xi ,j}^k \\&\quad = \upphi + \tau V^{j} - \alpha S^{j+1} I^{j} - (\mu + \rho )S^{j+1}\\&\dfrac{1}{\Gamma (2-\xi )}~\sum _{k=0}^j~ \dfrac{V^{k+1}-V^{k}}{\Psi (h)}~A_{\xi ,j}^k \\&\quad = \rho S^{j+1} - (\tau + \mu )V^{j+1}\\&\dfrac{1}{\Gamma (2-\xi )}~\sum _{k=0}^j~ \dfrac{E^{k+1}-E^{k}}{\Psi (h)}~A_{\xi ,j}^k\\&\quad = \alpha S^{j+1} I^{j} - (\mu + \beta )E^{j+1}\\&\dfrac{1}{\Gamma (2-\xi )}~\sum _{k=0}^j~ \dfrac{I^{k+1}-I^{k}}{\Psi (h)}~A_{\xi ,j}^k \\&\quad = \theta \varepsilon H^{j} + \beta E^{j+1} - (\sigma + \mu + \delta _{1})I^{j+1}\\&\dfrac{1}{\Gamma (2-\xi )}~\sum _{k=0}^j~ \dfrac{H^{k+1}-H^{k}}{\Psi (h)}~A_{\xi ,j}^k\\&\quad = \sigma \kappa I^{j+1} - (\theta + \mu + \delta _{2})H^{j+1}\\&\dfrac{1}{\Gamma (2-\xi )}~\sum _{k=0}^j~ \dfrac{R^{k+1}-R^{k}}{\Psi (h)}~A_{\xi ,j}^k \\&\quad = (1- \kappa ) \sigma I^{j+1} + (1 - \varepsilon ) \theta H^{j+1} - \mu R^{j+1}\\ \end{aligned} \end{aligned}$$
(30)

so that,

$$\begin{aligned} \begin{aligned} S^{j+1}&= \dfrac{h^{1-\xi }S^j + \Psi (h) \Gamma (2-\xi ) (\upphi + \tau V^{j}) - \sum _{k=0}^{j-1}(S^{k+1}-S^{k})~A_{\xi ,j}^k}{h^{1-\xi } + \Psi (h) \Gamma (2-\xi ) \left[ \alpha I^{j} + (\mu + \rho ) \right] },\\ \\ V^{j+1}&= \dfrac{h^{1-\xi }V^j + \Psi (h) \Gamma (2-\xi ) (\rho S^{j+1}) - \sum _{k=0}^{j-1}(V^{k+1}-V^{k})~A_{\xi ,j}^k}{h^{1-\xi } + \Psi (h) \Gamma (2-\xi )(\tau + \mu )},\\ \\ E^{j+1}&= \dfrac{h^{1-\xi }E^j + \Psi (h) \Gamma (2-\xi ) \alpha S^{j+1} I^{j} - \sum _{k=0}^{j-1}(E^{k+1}-E^{k})~A_{\xi ,j}^k}{h^{1-\xi } + \Psi (h) \Gamma (2-\xi ) (\mu + \beta ) },\\ \\ I^{j+1}&= \dfrac{h^{1-\xi }I^j + \Psi (h) \Gamma (2-\xi ) (\theta \varepsilon H^{j} + \beta E^{j+1}) - \sum _{k=0}^{j-1}(I^{k+1}-I^{k})~A_{\xi ,j}^k}{h^{1-\xi } + \Psi (h) \Gamma (2-\xi ) (\sigma + \mu + \delta _{1})},\\ \\ H^{j+1}&= \dfrac{h^{1-\xi }H^j + \Psi (h) \Gamma (2-\xi ) (\sigma \kappa I^{j+1}) - \sum _{k=0}^{j-1}(H^{k+1}-H^{k})~A_{\xi ,j}^k}{h^{1-\xi } + \Psi (h) \Gamma (2-\xi ) (\theta + \mu + \delta _{2})},\\ \\ \\ R^{j+1}&= \dfrac{h^{1-\xi }R^j + \Psi (h) \Gamma (2-\xi ) \left[ (1-\kappa ) \sigma I^{j+1} + (1-\varepsilon ) \theta H^{j+1} \right] - \sum _{k=0}^{j-1}(R^{k+1}-R^{k})~A_{\xi ,j}^k}{h^{1-\xi } + \Psi (h) \Gamma (2-\xi ) \mu }.\\ \end{aligned} \end{aligned}$$
(31)

Results

Sensitivity analysis of \(\mathcal {R}_0\)

Due to the likelihood of uncertainty in the estimation of parameters, a detailed and comprehensive global sensitivity analysis is conducted in this section, employing the methodology introduced in Blower and Dowlatabadi (1994). The analysis incorporates the Latin hypercube sampling (LHS) to sample the model’s parameters. In carrying out sensitivity, the partial rank correlation coefficient (PRCC) is computed between the parameter values in the response function and the function values derived from the sensitivity analysis. Each LHS run involves 1000 simulations of the model (1). The PRCC values, ranging from \(-1\) to 1, denote the strength and direction of the relationship. Positive (negative) value indicates a positive (negative) relationship, while the magnitude reflects the measure of sensitivity. A magnitude close to zero implies very minimal impact, whereas a magnitude close to one indicates a very significant impact. The response functions under consideration will be the associated basic reproduction numbers.

Sensitivity analysis of the measles reproduction number with respect to all the parameters is presented in Fig. 2a. It can be seen that, the measles transmission rate: \(\alpha \) (which is positively correlated) and transition rate out of the infected class: \(\sigma \) (negatively correlated) are the most influential parameters. Other parameters which are positively correlated include: progression rate from exposed to infected class: \(\beta \), vaccination wane rate: \(\tau \), movement rate from hospitalized class: \(\theta \) and treatment failure rate: \(\varepsilon \) while other negatively correlated parameters are: vaccination rate: \(\rho \), the measles induced death rates for infected and hospitalized individuals: \(\delta _1\) and \(\delta _2\), the fraction of individuals that are hospitalized: \(\kappa \). Thus, increase in the positively correlated parameters would negatively impact the dynamics of measles epidemic within the population, while increment in the negatively correlated parameters would positively impact the dynamics of measles. Particularly if little or no efforts are put in place to check surge in the measles transmission rate, then measles is sure to become endemic in the population while increase in the transition out of infected class due to hospitalization, treatment and natural recovery would positively bring down the burden of measles within the population. It is also interesting to point out that, increase in treatment failure rate adversely affect the dynamics of measles epidemic. Contour and surface plots of the measles reproduction number with respect to the rho, tau, beta and \(\epsilon \) are presented in Figs. 3 and 4. These additional simulations also buttress the impacts highlighted in the sensitivity analysis plots.

Fig. 2
figure 2

Sensitivity analysis of the: a measles reproduction number, b peak size of exposed population, c peak size of infected population, d peak size of hospitalized population

Full size image
Fig. 3
figure 3

Sensitivity analysis of \(R_{0}\) using contour and surface plots

Full size image
Fig. 4
figure 4

Sensitivity analysis of \(R_{0}\) using contour and surface plots

Full size image

Time evolutions

Simulations to validate the theoretical analyses carried out in the previous sections are now performed. To assess the long time dynamics of the disease under a measles-free scenario, simulations are carried out in Fig. 5 via the Non-standard finite discretization scheme and the ODE45 solver when the order of the fractional derivative is near one. Firstly, it is observed that the NSFD scheme behaves very closely with the ODE45 solver for values of the fractional order very near to one, thereby validating the accuracy of the scheme under a well defined denominator function given in terms of the Mittag–Leffler function. Secondly, it is observed that, under this scenario, the trajectories of the system all converge to the measles-free steady state when the reproduction number \(\mathcal {R}_{0}<1\). Also, numerical experiments to validate the theoretical analysis under an endemic steady state are performed in Fig. 6. It can also be observed that, all solution trajectories converge to the measles-endemic steady state when the associated reproduction number, \(\mathcal {R}_{0}\) is greater than one.

Fig. 5
figure 5

Comparison of NSFD and ODE45 when \(\xi =0.99\) and when \(R_{0} <1\)

Full size image
Fig. 6
figure 6

Comparison of NSFD and ODE45 when \(\xi =0.99\) and when \(R_{0} >1\)

Full size image

Effect of vaccination and treatment parameters

Numerical assessments of the epidemiological impact of measles vaccination are presented in Fig. 7. It can be observed in these figures that, as the measles vaccination rate is stepped from \(\rho = 0.10\) to \(\rho = 0.130\), while fixing the order of the derivative at \(\xi = 0.90\), there is a significant reduction in the exposed, infected and hospitalized individuals as can be seen in Fig. 7a–c. Thus, to curtail the spread of measles within the population, efforts should be stepped to provide safe and effective mass measles vaccination for all susceptible individuals.

Numerical assessments of the epidemiological impact of treatment failure are presented in Fig. 8. It can be observed in these figures that, as the treatment failure rate increases from \(\xi = 0.02\) to \(\xi = 0.8\), while fixing the order of the derivative at \(\xi = 0.90\), there is a significant increase in the exposed, infected and hospitalized individuals as can be seen in Fig. 8a–c. These trends in the behaviour of the infected classes also confirms the sensitivity analyses results presented earlier.

Fig. 7
figure 7

Impact of vaccination on the infected classes when \(\xi =0.90\) and when \(R_{0}>1\)

Full size image
Fig. 8
figure 8

Impact of treatment failure on the infected classes when \(\xi =0.90\) and when \(R_{0}>1\)

Full size image

Effect of fractional order

Simulations to assess the impact of memory effect on the dynamics of all the epidemiological components of the model are presented in Fig. 9. It can be seen that the singular kernel inherent in the definition of the Caputo fractional operator, which is lacking in the integer derivative, has influence on the various classes of the model. The variations in the compartments as the order is varied from \(\xi = 0.90\) to \(\xi = 0.98\) are also greatly observed for the infected classes.

Fig. 9
figure 9

Impact of varying fractional order \(\xi \) on the different model classes when \(R_{0}>1\)

Full size image

Conclusion

In this work, we have developed and analyze a fractional-order model for measles epidemic incorporating vaccination and treatment failure. The model is analyzed qualitatively and quantitatively to gain robust understanding into control measures required to curb this menace. Stability analysis around the neighbourhood of measles-free steady state is carried out to determine properties of the important threshold called reproduction number, which is necessary to quantitatively analyze the formulated model. Sensitivity analyses of this threshold and the state solutions using the Latin hypercube sampling (LHS) and contour/surface plots reveal the dominance of effective contact rate, progression and transition rates in influencing the general dynamics of measles epidemic. Furthermore, the fractional non-standard discretization scheme using a well defined denominator function is used to numerically solve the designed model. Scenario analyses to assess the impact of vaccination and treatment failure show that an effective and safe vaccination programme could significantly reduce the spread of measles while uncontrolled treatment failure could adversely increase the burden of measles within a population.

The major highlights of the numerical analysis are presented below:

  1. (i)

    The solution profiles of all epidemiological compartments when the reproduction numbers are both below one and greater than one are graphically presented using the fractional Non-standard finite discretization scheme.

  2. (ii.)

    It was observed that, for the scenarios when the measles associated reproduction number \(\mathcal {R}_{0}\) is less than one and when it is greater than one, the solution trajectories converge to the infection-free and measles-endemic steady states, respectively.

  3. (iii.)

    Sensitivity analyses using the Latin Hypercube Sampling (LHS), and also using contour plots and surface plots are performed on the model’s reproduction number. The impact of influential parameters are graphically presented. Worthy of mention, is the influential impact of measles transmission rate and treatment failure rate (positively correlated) and measles vaccination rates (negatively correlated).

  4. (iii)

    Different scenario analyses to investigate the impact of measles vaccination measures on the infected individuals are presented. It was observed that enhanced measles vaccination programme under the administration of safe and highly effective vaccine could curtail the spread of measles within the population.

This study also has some limitations which can necessitate further research in this direction. The study did not consider within-host dynamics of measles transmission. It also did not consider the co-infection of measles with other viral or bacterial diseases. These can be taken upon for study in the near future. Also, a robust stochastic or agent-based version of the current model could also be investigated for a future study. Novel and efficient fractional numerical scheme could also be developed to study the current model. On the biological side, with more reliable data and information, the current model could be fit to real data in the near future.