1 Introduction

In daily life, deterioration of items becomes a critical problem. Generally, deterioration is decay or damage of such items that cannot be used for its original purpose. Items, such as canned fruits, foods, vegetables, etc., deteriorate due to expiration of date. Ghare and Schrader [1] were the first authors to introduce deterioration in inventory model. They established the basic inventory model with constant rate of deterioration. Covert and Philip [2] extended Ghare and Schrader’s [1] model for the deterioration by assuming a two-parameter Weibull distribution. If the inventory is more and deterioration exists, there is a possibility to deteriorate more items. Based on this idea, Balkhi and Benkherouf [3] presented an inventory model for deteriorating items with stock-dependent and time-varying demand rate for a finite planning horizon. Chung and Wee [4] explained a scheduling and replenishment plan for an integrated deteriorating inventory model with stock-dependent selling rate. Generally, the preservation of product is used to reduce the deterioration rate of product, but it is directly related to an investment amount on it. Hsu et al. [5] developed an inventory policy on an investment by the retailers under the preservation technology to reduce the rate of product’s deterioration.

In the classical EOQ model, it is often assumed that shortages are either completely backlogged or completely lost. In reality, because of well behavior and reputation the supplier, some customers are willing to wait until replenishment, especially if the waiting time is short, while others are more impatient and go elsewhere. It indicates the supplier has lost the opportunity to earn more profit, disappointed customers, and probably put some doubts in customer’s mind about the nature of the storage capacity of the supplier. An EOQ model for deteriorating items with and without backorders was explained by Widyadana et al. [6]. To describe the nature of the inventory system, Giri et al. [7] explained an inventory model with time dependent deterioration rate, shortage, and ramp-type demand rate. The demand rate may not always ramp-type. In this direction, Manna and Chaudhuri [8] discussed an EOQ model for deteriorating items for both time-dependent demand and deterioration. Sana [9] derived an inventory model by assuming time-varying deterioration and partial backlogging. Sett et al. [10] developed a two-warehouse inventory model with increasing demand and time varying deterioration. Based on finite replenishment policy, Sarkar [11] explained an inventory model with time-dependent demand and deterioration rate. He considered the maximum lifetime of a product. Deterioration of products may not always deterministic type, it may follow probabilistic nature some times. Most recently, Sarkar [12] developed a production-inventory model for three different types of continuously distributed deterioration functions. Sarkar and Sarkar [13] explained a control inventory problem with probabilistic deterioration. They solved the inventory model with the help of Euler–Lagrange method.

Without using the calculations for optimality from differential calculus, how inventory model with shortages can be solved, Cárdenas-Barrón [14] explained it by using basic algebraic procedure. Cárdenas-Barrón [15, 16] discussed two different inventory models on optimal manufacturing batch size with rework process at single-stage production system. Cárdenas-Barrón [17] extended this concept for the optimal batch sizing in a multi-stage production system with rework process. Sometimes managers prefers to use planned backorders to reduce the total system cost. In this direction, Cárdenas-Barrón [18] presented an inventory model with rework process at a single-stage manufacturing system with planned backorders. Recently, Cárdenas-Barrón [19–21], Sarkar [22], Cárdenas-Barrón et al. [23], and Wee and Wang [24] discussed their excellent models in this direction.

In real life situation, display stock-level plays an important role in marketing sectors. To carry on higher sales, retailers have to store large amount of items such that the customer can choose the best one from a wide range of items. After a long survey, it is observed that the demand rate is proportional with the stock level i.e., the demand rate is high if the stored amount is high and the demand rate is low if the stored amount is very small. In this direction, Balakrishnan et al. [25] extended an inventory-dependent demand model from the existing literature to a suitable classification of products with early replenishment. They explained that the optimal cycle time is governed by the conventional trade-off between ordering and holding costs, whereas the reorder point connects to a promotions-oriented cost-benefit perspective. They proved that the optimal policy yields significantly higher profits than cost-based inventory policies, highlighting the importance of profit-driven inventory management. It is usually detected in the supermarket that more display of the consumer goods in large quantities attracts more customers and generates higher demand. Furthermore, when the shortages occur, some customers are willing to wait for backorder and others would turn to buy from other sellers. In some inventory systems, such as fashionable commodities, the length of the waiting time for the next replenishment would determine whether the backorder will be accepted or not. Therefore, the backorder rate is variable and dependent on the waiting time for the next replenishment. Wu et al. [26] represented an optimal replenishment policy for non-instantaneous deteriorating items with stock-dependent demand and partial backlorder. Hou [27] proposed an inventory model for deteriorating items, stock-dependent consumption rate, and shortages over a finite planning horizon. How long a product can be stored in the storage space, based on it, it can be stated that the holding cost is not always constant. Alfares [28] addressed an inventory model with stock-level dependent demand rate and variable holding cost. Sarkar et al. [29] discussed an inventory model for stock-dependent demand with the production of imperfect products. Sarkar et al. [30] developed an imperfect production model with reliability and safety stock. Sarkar et al. [31] discussed a production-inventory model for time-varying demand with inflation and time value of money. Sarkar and Sarkar [32] considered an inventory model with time varying demand and deterioration. Sarkar et al. [33] developed an inventory model for imperfect production with inflation and time value of money. Sarkar and Sarkar [34] and Sarkar et al. [35] proposed two deteriorating inventory model with partial backlogging. Sarkar et al. [36] developed a continuous review inventory model with backorder price discount under controllable lead time. Sarkar and Moon [37] discussed an inventory model with variable backorder rate, quality improvement, and setup cost reduction. They proved the global optimum solution analytically.

Contribution of that model compared with other models is given in Table 1.

Table 1 Comparison between the contributions of different authors
Full size table

In this proposed model, an effort has been made to develop an inventory model for the fixed lifetime product with time varying deterioration rate. It is common that the customer may buy a single item from a large amount of stocks, i.e., the demand rate may go up or down if the on-hand inventory level increases or decreases. For this reason, the retailers have to store a large amount of items to their stored places. To deal with such kind of situations, the model considers stock-dependent demand. In many inventory models, researchers have considered constant deterioration. But in real life situation, many items deteriorate due to their fixed lifetime. In this regard, the model assumes time varying deterioration rate. If the demand is more and the production is less shortages will arise. No one would like to face shortages, still based on customers demand, it may arise. For that purpose, the model considers variable backorder rate to control the situation during the stock-out period. Therefore, this model is described with the combination of stock-dependent demand, variable deterioration, and time varying backorder rate. Rest of the paper is designed as follows: in Sect. 2, notation and assumptions are given. In Sect. 3, the mathematical model is derived. Numerical experiments and sensitivity analysis are presented to illustrate the model in Sect. 4. In Sect. 5, some special cases and their comparisons are discussed. Finally, conclusions are made in Sect. 6.

2 Notation and assumptions

To develop this model, the following notation and assumptions are used.

2.1 Notation

\(\theta (t)\) :

time-dependent deterioration rate

L :

maximum lifetime of product (time unit)

D(I(t)):

inventory dependent demand (units)

A :

ordering cost ($/per order)

\(t_{1}\) :

time when the inventory level reaches at zero level (time unit)

\(c_{1}\) :

holding cost ($/unit/unit time)

\(c_{2}\) :

deterioration cost ($/unit)

\(c_{3}\) :

shortage cost ($/unit)

\(c_{4}\) :

backordering cost ($/unit)

\(\delta >0\) :

constant parameter

T :

length of order cycle (time unit)

Q :

order quantity (units/cycle)

\(Z(t_{1},T)\) :

total relevant cost ($/unit time)

The following assumptions are considered to discuss the model.

2.2 Assumptions

  1. 1.

    The model deals with a single type of item.

  2. 2.

    Product, having fixed lifetime, may be deteriorated with increasing value of time. The deterioration rate of these type of products should depend on fixed lifetime of products as well as variable increasing time. An interesting relation between the variable increasing-time and the fixed lifetime of products is when increasing-time can reach to the maximum lifetime of the products, the products cannot be used any more, i.e., the deterioration rate is \(100\,\%\). Thus, the deterioration rate is assumed as \(\theta (t)=\frac{1}{1+L-t}\), where \(L>t\) and L is the maximum lifetime of products at which the total on-hand inventory deteriorates. When t increases, \(\theta (t)\) increases and Lim\(_{t\rightarrow L}\theta (t)\rightarrow 1\).

  3. 3.

    The demand rate D(I(t)) is a function of instantaneous inventory level I(t) and also deterministic; D(I(t)) is taken as following form

    $$D(I(t))= \left\{ \begin{array}{ll} a+bI(t)&{} {\rm if}\quad i(t)> 0,\\ a&{} {\rm if}\quad i(t)\le 0. \end{array}\right\}$$
  4. 4.

    Backorder is permitted. The model considers that a fraction of demand is backorderd and backorder rate is a decreasing function of the waiting time. Let us assume the fraction as \(B(t) =\frac{1}{1+\delta t}\), where t is the waiting time up to the next replenishment.

  5. 5.

    Within the time interval \([0, t_{d}]\), the product has no deterioration. Deterioration occurs within the time interval \([t_{d}, t_{1}]\) at a variable deterioration rate \(\theta (t)\).

  6. 6.

    \(I_{1}(t)\) denotes the inventory level at any time \(t\in [0,t_{d}]\) without the deterioration of product. \(I_{2}(t)\) stands for the inventory level at any time \(t\in [t_{d}, t_{1}]\) with the product’s deterioration. \(I_{3}(t)\) signifies the inventory level at any time \(t\in [t_{1},T]\) with the product’s shortage.

  7. 7.

    The replenishment rate is infinite and lead time is considered as negligible.

3 The mathematical model

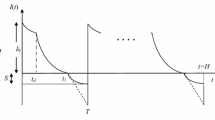
Section 3 presents the derivation of mathematical model to obtain retailer’s optimal policy for fixed lifetime products with time-dependent backorder rate. According to notation and assumptions described above, the behavior of the inventory system has been depicted in Fig. 1. The problem definition has been defined in Sect. 3.1. In Sect. 3.2., the model formulation has been developed based on the problem formulation.

Fig. 1
figure 1

Graphical representation of inventory level versus time within the planning horizon [0,T]

Full size image

3.1 Problem definition

Nowadays, deterioration of products is a common phenomenon in all fields. Those products, which have fixed lifetime, are very much insightful regarding deterioration. Many products such as fruits, vegetables, volatile liquids, and others not only deteriorate continuously due to evaporation, obsolescence, spoilage, but also they have their expiration dates (i.e., a deteriorating item has its maximum lifetime). Thus, maximum lifetime of products is considered in this model. It is well known that, anyone can prefer to buy any products by choosing within a lot of items, thus the model assumed stock-dependent demand pattern. Finally, the aim is to minimize the cost by assuming the fixed lifetime of products, stock-dependent demand, and deterioration of products as well as the retailer’s optimal strategy.

3.2 Model formulation

Suppose the inventory cycle starts with maximum inventory level \(I_{max}\) at \(t=0\). The inventory level decreases during the time interval \(\left[ 0, t_{d}\right]\) due to inventory dependent demand. Finally, inventory level falls at zero level during the time interval \(\left[ t_{d}, t_{1}\right]\) for both inventory dependent demand and deterioration. The total process repeats itself after a scheduling time T. The total inventory system is shown in Fig. 1.

From Fig. 1, it is shown that during the time interval \(\left[ 0, t_{d}\right]\), the inventory level decreases owing to inventory dependent demand rate. Hence, the governing differential equation is to signify the inventory system at any time t as

$$\begin{aligned} \frac{dI_{1}\left( t\right) }{dt}&= {} -\left[ a+bI_{1}\left( t\right) \right] ,\quad 0\le t \le t_{d}, \end{aligned}$$
(1)

with \(I_{1}\left( 0\right) =I_{max}.\)

Solving (1), inventory level \(I_{1}\left( t\right)\) is obtained as

$$\begin{aligned} I_{1}(t)=\left( I_{max}+\frac{a}{b}\right) e^{-bt}-\frac{a}{b},\quad 0\le t \le t_{d} \end{aligned}$$
(2)

Due to inventory-dependent demand as well as deterioration, the inventory level decreases during the interval \(\left[ t_{d}, t_{1}\right]\). Thus, the differential equation is to signify the inventory system at any time t

$$\begin{aligned}&\frac{dI_{2}\left( t\right) }{dt}+\theta \left( t\right) I_{2}\left( t\right) =-\left[ a+bI_{2}\left( t\right) \right] \nonumber \\&\quad i.e., \frac{dI_{2}\left( t\right) }{dt}+\frac{I_{2}\left( t\right) }{1+L-t}=-\left[ a+bI_{2}\left( t\right) \right] ,\quad t_{d}\le t \le t_{1}\nonumber \\&\quad {\rm with}\, I_{2}\left( t_{1}\right) =0 \end{aligned}$$
(3)

Solving (3), the inventory level \(I_{2}\left( t\right)\) is obtained as

$$\begin{aligned} I_{2}\left( t\right) =a\lambda e^{-bt}\left[ \eta _{1}\ln \left( \frac{\lambda }{\xi }\right) +b(t-t_{1})\right] \end{aligned}$$
(4)

[Expanding the exponential term and taking upto first order approximation for integration]

See Appendix A for \(\lambda ,\eta _{1},\) and \(\xi\).

Considering continuity of \(I\left( t\right)\) at \(t=t_{d},\) it follows from (2) and (4) that

$$\begin{aligned} I_{1}\left( t_{d}\right)&=I_{2}\left( t_{d}\right) \nonumber \\&\Rightarrow \left(I_{max}+\frac{a}{b}\right)e^{-bt_{d}}-\frac{a}{b}=a\lambda e^{-bt_{d}}[\eta _{1}\ln \phi +b(t-t_{1})] \end{aligned}$$

Now the maximum inventory level for each cycle is

$$\begin{aligned} I_{max}=\frac{a}{b}\left( e^{bt_{d}}-1\right) +a\varphi \left[ b(t_{d}-t_{1})+\eta _{1}\ln \phi \right] \end{aligned}$$
(5)

Substituting (5) in (2), one has

$$\begin{aligned} I_{1}\left( t\right) =\frac{a}{b}[e^{b(t_{d}-t)}-1]+a\varphi e^{-bt}[b(t_{d}-t_{1})+\eta _{1}\ln \phi ] \end{aligned}$$
(6)

During the time interval \(\left[ t_{1}, T\right],\) the demand at time t is partially backlogged at a fraction \(\frac{1}{1+\delta \left( T-t\right) }.\) Hence, the differential equation is to symbolize the inventory system at any time t as

$$\begin{aligned} \frac{dI_{3}\left( t\right) }{dt}&= {} -aB\left( T-t\right) \nonumber \\&= {} -\frac{a}{1+\delta \left( T-t\right) },\quad t_{1}\le t \le T\nonumber \\&\quad {\rm with}\quad I_{3}\left( t_{1}\right) =0 \end{aligned}$$
(7)

Solving (7), the inventory level \(I_{3}\left( t\right)\) is as follows:

$$\begin{aligned} I_{3}\left( t\right) =\frac{-a}{\delta }\{\ln [1+\delta (T-t_{1})]-\ln [1+\delta \left( T-t\right) ]\},\quad t_{1}\le t \le T \end{aligned}$$
(8)

Putting \(t=T\) in (8), the maximum amount of demand backlogged per cycle can be obtained as

$$\begin{aligned} S=-I_{3}\left( T\right) =\frac{a}{\delta }\{\ln [1+\delta \left( T-t_{1}\right) ]\} \end{aligned}$$
(9)

Thus the ordered quantity Q can be obtained from (5) and (9) as

$$\begin{aligned} Q\,= \,& {} I_{max}+S\nonumber \\&= {} \frac{a}{b}[e^{b(t_{d}-t)}-1]+a\varphi [b(t_{d}-t_{1})+\eta _{1}\ln \phi ] +\frac{a}{\delta }\{\ln [1+\delta \left( T-t_{1}\right) ]\} \end{aligned}$$
(10)

The system consists of the following relevant costs.

  1. (a)

    Ordering cost is \(=A\).

  2. (b)

    Holding cost \(\left( HC\right)\) is \(=c_{1}\left[ \int _{0}^{t_{d}}I_{1}\left( t\right) dt+\int _{t_{d}}^{t_{1}}I_{2}\left( t\right) dt\right]\)

    $$\begin{aligned}=\, & {} ac_{1}\left[ \left( \varphi \left\{ b(t_{d}-t_{1})+\eta _{1}\ln \phi \right\} +\frac{e^{bt_{d}}}{b}\right) \left( \frac{1-e^{-bt_{d}}}{b}\right) -\frac{t_{d}}{b}+\frac{\mu \eta _{1}}{36}\right. \nonumber \\&\left. +\frac{1}{b^2}[\eta _{8}(\eta _{6}+b\eta _{7})+b^2\eta _{9}] -\frac{(\eta _{5}\eta _{6}+b\eta _{7})}{b^2}[bt_{1}+\eta _{1}\ln \xi ]\right] \end{aligned}$$
    (11)
  3. (c)

    Deterioration cost \(\left( DC\right)\) is \(=c_{2}\left[ I_{2}\left( t_{d}\right) -\int _{t_{d}}^{t_{1}}D\left( I\left( t\right) \right) dt\right]\)

    $$\begin{aligned}&= {} ac_{2}\left[ \varphi e^{-bt_{d}}\{\eta _{1}\ln \phi +b(t_{d}-t_{1})\}-(t_{1}-t_{d})-\frac{b\eta _{1}\mu }{36}\right. \nonumber \\&\left. -\frac{1}{b}[\eta _{8}(\eta _{6}+b\eta _{7})+b^2\eta _{9}]+\frac{(\eta _{5}\eta _{6}+b\eta _{7})}{b}[bt_{1}+\eta _{1}\ln \xi ]\right] \end{aligned}$$
    (12)
  4. (d)

    Shortage cost \(\left( SC\right)\) is \(= c_{3}\left\{ \int _{t_{1}}^{T}\left[ -I_{3}\left( t\right) \right] dt\right\}\)

    $$\begin{aligned} =\frac{c_{3}a}{\delta }\left[ \left( T-t_{1}\right) -\frac{\ln \left\{ 1+\delta \left( T-t_{1}\right) \right\} }{\delta }\right] \end{aligned}$$
    (13)
  5. (e)

    Opportunity cost \(\left( OC\right)\) is \(= c_{4}\int _{t_{1}}^{T}a\left[ 1-B\left( T-t\right) \right] dt\)

    $$\begin{aligned} =c_{4}a\left[ \left( T-t_{1}\right) -\frac{\ln \left\{ 1+\delta \left( T-t_{1}\right) \right\} }{\delta }\right] \end{aligned}$$
    (14)

    Hence, the total inventory cost per cycle is given by

    $$\begin{aligned} Z= \,& {} \frac{1}{T}\left[ A+HC+DC+SC+OC\right] \nonumber \\= \,& {} \frac{1}{T}\left[ A+c_{1}\left\{ \int _{0}^{t_{d}}I_{1}\left( t\right) dt+\int _{t_{d}}^{t_{1}}I_{2}\left( t\right) dt\right\} +c_{2}\left\{ I_{2}\left( t_{d}\right) -\int _{t_{d}}^{t_{1}}D\left( I\left( t\right) \right) dt\right\} \right. \nonumber \\&\left. +\,c_{3} \left\{ \int _{t_{1}}^{T}\left[ -I_{3}\left( t\right) \right] dt\right\} +c_{4}\left\{ \int _{t_{1}}^{T}a\left[ 1-B\left( T-t\right) \right] dt\right\} \right] \nonumber \\=\, & {} \frac{a}{T}\left[ \frac{A}{a}+c_{1}\left\{ \left( \varphi \left[ b(t_{d}-t_{1})+\eta _{1}\ln \phi \right] +\frac{e^{bt_{d}}}{b}\right) \left( \frac{1-e^{-bt_{d}}}{b}\right) -\frac{t_{d}}{b}\right\} \right. \nonumber \\&+\,(c_{1}-bc_{2})\left\{ \frac{\mu \eta _{1}}{36}+\frac{1}{b^2}[\eta _{8}(\eta _{6}+b\eta _{7})+b^2\eta _{9}] -\frac{(\eta _{5}\eta _{6}+b\eta _{7})}{b^2}\left[ bt_{1}+\eta _{1}\ln \xi \right] \right\} \nonumber \\&+\,c_{2}[\varphi e^{-bt_{d}}\left\{ \eta _{1}\ln \phi +b(t_{d}-t_{1})\right\} -(t_{1}-t_{d})]\nonumber \\&\left. +\,\left( \frac{c_{3}}{\delta }+c_{4}\right) \left( \left( T-t_{1}\right) -\frac{\ln \left\{ 1+\delta \left( T-t_{1}\right) \right\} }{\delta }\right) \right] \end{aligned}$$
    (15)

3.3 Solution procedure

The objective in this paper is to minimize the total cost. For minimization of the cost function, the necessary condition is that the first order derivatives of the cost function with respect to the decision variables are zero and the sufficient condition is that the principal minors are positive. It can be proved numerically that the cost function is minimum, but it is possible to obtain the analytical derivation by classical optimization technique, that is why, numerical procedure is not used in this model. To test this study, numerical experiments are used.

Hence the necessary and sufficient conditions are

$$\begin{aligned} \frac{\partial Z}{\partial t_{1}}= 0, \,\,\frac{\partial Z}{\partial T}= 0 \end{aligned}$$

and

$$\begin{aligned} \frac{\partial ^2 Z}{\partial t_{1}^2}> 0,\,\, \frac{\partial ^2 Z}{\partial t_{1}^2}\frac{\partial ^2 Z}{\partial T^2}-\left( \frac{\partial Z}{\partial t_{1}\partial T}\right) ^2>0 \end{aligned}$$

Now from the necessary conditions

$$\begin{aligned} \frac{\partial Z}{\partial t_{1}}&= {} \frac{a}{T}\left[ \left( \frac{c_{3}}{\delta }+c_{4}\right) \left( \frac{\delta \left( t_{1}-T\right) }{1+\delta \left( T-t_{1}\right) }\right) -c_{2}+\left\{ \frac{c_{1}}{b}(1-e^{-bt_{d}})+c_{2}e^{-bt_{d}}\right\} \left( \frac{bt_{1}+1}{\xi }\right) \varphi \right. \nonumber \\&\left. +(c_{1}-bc_{2}) \left\{ \frac{1}{b}(\eta _{5}\eta _{6}+b\eta _{7})\left( \frac{\eta _{1}}{\xi b}-1\right) +\eta _{1}\xi \eta _{12}\ln \xi \right\} \right] =0 \end{aligned}$$
(16)

and

$$\begin{aligned} \frac{\partial Z}{\partial T}&= \frac{a}{T^2}\left [\left( \frac{c_{3}+\delta c_{4}}{\delta }\right) \left\{ \frac{\left( T-t_{1}\right) \left( \delta t_{1}-1\right) }{1+\delta \left( T-t_{1}\right) }+\frac{1}{\delta }\ln \left[ 1+\delta \left( T-t_{1}\right) \right] \right\} -\frac{A}{a}-c_{1}\left \{\left (\vphantom{\left.+\eta _{1}\ln \phi ]+\frac{e^{bt_{d}}}{b}\right )}\varphi [b(t_{d}-t_{1})\right.\right.\right.\nonumber \\&\quad\left.\left.+\eta _{1}\ln \phi ]+\frac{e^{bt_{d}}}{b}\right ) \left( \frac{1-e^{-bt_{d}}}{b}\right) -\frac{t_{d}}{b}\right \}-(c_{1}-bc_{2})\Bigg \{\frac{\mu \eta _{1}}{36} +\frac{1}{b^2}\left[ \eta _{8}(\eta _{6}+b\eta _{7})+b^2\eta _{9}\right] \nonumber \\&\quad\left.-\frac{(\eta _{6}\eta _{5}+b\eta _{7})}{b^2}\left[ bt_{1}+\eta _{1}\ln \xi \right] \Bigg \}-c_{2}\left\{ \varphi e^{-bt_{d}}\left[ \eta _{1}\ln \phi +b(t_{d}-t_{1})\right] -(t_{1}-t_{d})\right\} \right]=0 \end{aligned}$$
(17)

From (16) and (17), the value of T can be written as

$$\begin{aligned} T=t_{1}+\frac{M}{\delta (P-M)} \end{aligned}$$
(18)

and

$$\begin{aligned}&P\left[ \frac{\left( T-t_{1}\right) \left( \delta t_{1}-1\right) }{1+\delta \left( T-t_{1}\right) }+\frac{1}{\delta }\ln \left[ 1+\delta \left( T-t_{1}\right) \right] \right] -\frac{A}{a}-c_{1}\left\{ \left( \varphi \left( b(t_{d}-t_{1})+\eta _{1}\ln \phi \right) +\frac{e^{bt_{d}}}{b}\right) \right. \nonumber \\&\times \left. \left( \frac{1-e^{-bt_{d}}}{b}\right) -\frac{t_{d}}{b}\right\} -(c_{1}-bc_{2})\left\{ \frac{\mu \eta _{1}}{36} +\frac{1}{b^2}[\eta _{8}(\eta _{6}+b\eta _{7})+b^2\eta _{9}] -\frac{(\eta _{6}\eta _{5}+b\eta _{7})}{b^2}\right. \nonumber \\& \times \left.\left[ bt_{1}+\eta _{1}\ln \xi \right] \right\} -c_{2}\left\{ \varphi e^{-bt_{d}}\left[\eta _{1}\ln \phi +b(t_{d}-t_{1})\right] -(t_{1}-t_{d})\right\} =0 \end{aligned}$$
(19)

Using (18) into (19), the following equation is derived

$$\begin{aligned}&\frac{\delta t_{1}-1}{\delta }M-\frac{P}{\delta } \ln \left[ 1-\frac{M}{P}\right] -\frac{A}{a}-c_{1}\left\{\left( \varphi[b(t_{d}-t_{1})+\eta _{1}\ln \phi ]+\frac{e^{bt_{d}}}{b}\right) \left( \frac{1-e^{-bt_{d}}}{b}\right) \right. \nonumber \\&\left. -\frac{t_{d}}{b}\right\} -(c_{1}-bc_{2})\left\{ \frac{\mu \eta _{1}}{36} +\frac{1}{b^2}[\eta _{8}(\eta _{6}+b\eta _{7})+b^2\eta _{9}] -\frac{(\eta _{6}\eta _{5}+b\eta _{7})}{b^2}\left[ bt_{1}+\eta _{1}\ln \xi \right] \right\} \nonumber \\&-c_{2}\left\{ \varphi e^{-bt_{d}}[\eta _{1}\ln \phi +b(t_{d}-t_{1})]-(t_{1}-t_{d})\right\} =0 \end{aligned}$$
(20)

Lemma 1

(a):

If \(\frac{\delta t_{d}-1}{\delta }N-\frac{P}{\delta } \ln \left[ 1-\frac{N}{P}\right] -\frac{A}{a}-\frac{c_{1}}{b^2}(e^{bt_{d}}-bt_{d}-1)\le 0,\) then the solution of \((t_{1},T),\) which satisfies (18) and (19), not only exists but also unique.

(b):

If \(\frac{\delta t_{d}-1}{\delta }N-\frac{P}{\delta } \ln \left[ 1-\frac{N}{P}\right] -\frac{A}{a}-\frac{c_{1}}{b^2}(e^{bt_{d}}-bt_{d}-1)>0,\) then the solution of (\(t_{1},T\)), which satisfies (18) and (19), does not exist.

Proof

(a) From assumptions and notation, one has \(T>t_{1}\). Hence (18) implies

$$\begin{aligned} \frac{M}{\delta (P-M)}>0. \end{aligned}$$

Because the numerator part, \(M>0\) thus the denominator part, \(\delta (P-M)>0\). From this inequality, one can find the value of \(t_{1}\) as \(t_{1}^{b}\) (say).

From (20), F(x) is defined as

$$\begin{aligned} F(x)= \,& {} \frac{\delta x-1}{\delta }M_{1}-\frac{P}{\delta } \ln \left[ 1-\frac{M_{1}}{P}\right] -\frac{A}{a}-c_{1}\left\{ \left( \varphi \left( b(t_{d}-x)+\eta _{1}\ln \phi _{1}\right) +\frac{e^{bt_{d}}}{b}\right) \left( \frac{1-e^{-bt_{d}}}{b}\right) \right. \nonumber \\&\left. -\frac{t_{d}}{b}\right\} -(c_{1}-bc_{2})\left\{ \frac{\mu _{1}\eta _{1}}{36} +\frac{1}{b^2}[\eta _{8}(\xi _{2}+b\xi _{3})+b^2\xi _{4}] -\frac{(\xi _{2}\eta _{5}+b\xi _{3})}{b^2}[bx+\eta _{1}\ln \xi _{1}]\right\} \nonumber \\&-c_{2}\left\{ \varphi e^{-bt_{d}}\left( \eta _{1}\ln \phi _{1}+b(t_{d}-x)\right) -(x-t_{d})\right\} =0 \end{aligned}$$
(21)

Differentiating \(F\left( x\right)\) with respect to \(x\in (t_{d},t_{1}^b)\) yields

$$\begin{aligned} \frac{dF\left( x\right) }{dx}=\, & {} c_{2}e^{-bt_{d}}\varphi \left( b-\frac{\eta _{1}}{\xi _{1}}\right) -\frac{1}{b}(1-e^{-bt_{d}})\left( \frac{\eta _{1}}{\xi _{1}}-b\right) c_{1}\varphi +\xi _{13}-(c_{1}-bc_{2}) \nonumber \\&\times \left\{ \frac{1}{b}(b\xi _{5}+\eta _{8}(\xi _{6}-e^{-bx}))-\frac{1}{b^2}\{(b\xi _{6} -b\eta _{5}e^{-bx})(bx+\eta _{1}\ln \xi _{1})\}\right. \nonumber \\&\left. +\frac{\eta _{1}\xi _{11}}{36}-\frac{1}{b^2}\left( b-\frac{\eta _{1}}{\xi _{1}}\right) (\xi _{2}\eta _{5}+b\xi _{3})-\xi _{14}\right\} -\frac{1}{\delta }(1-\delta x)\xi _{12}+\frac{\xi _{12}}{\delta \xi _{15}}>0 \end{aligned}$$

Hence \(F\left( x\right)\) is strictly increasing function with respect to \(x\in [t_{d},t_{1}^b).\) By using assumption one has

$$\begin{aligned} F\left( t_{d}\right) =\frac{\delta t_{d}-1}{\delta }N-\frac{P}{\delta } \ln \left[ 1-\frac{N}{P}\right] -\frac{A}{a}-\frac{c_{1}}{b^2}\left( e^{bt_{d}}-bt_{d}-1\right) \le 0 \end{aligned}$$

and it can be shown that \(\lim _{x\rightarrow t_{1}^b-}F\left( x\right) =+\infty.\) Using the Intermediate Value Theorem, there exist an unique \(t_{1}^*\in [t_{d},t_{1}^b)\) such that \(F(t_{1}^*)=0,\) i.e., \(t_{1}^*\) is a unique solution of (20). Using the value of \(t_{1}^*,\) the value of T can be obtained from (18) as

$$\begin{aligned} T^*=t_{1}^*+\frac{M(t_{1}^*)}{\delta (P-M(t_{1}^*))} \end{aligned}$$

(b) If \(\frac{\delta t_{d}-1}{\delta }N-\frac{P}{\delta } \ln \left[ 1-\frac{N}{P}\right] -\frac{A}{a}-\frac{c_{1}}{b^2}(e^{bt_{d}}-bt_{d}-1)>0,\) then from (21), one has \(F\left( t_{d}\right) >0.\) \(F\left( x\right)\) is a strictly increasing function of \(x\in [t_{d},t_{1}^b)\) that implies \(F\left( x\right) >0, \forall x\in [t_{d},t_{1}^b).\) Thus, \(F\left( t_{1}\right) \ne 0 \, \forall t_{1}\in [t_{d},t_{1}^b).\) This completes the proof. \(\square\)

Lemma 2

(a):

The total relevant cost per unit time \(Z\left( t_{1},T\right)\) is convex and has global minimum solution at the optimal point \((t_{1}^*, T^*),\) which satisfies (18), (19) and \(\frac{\delta t_{d}-1}{\delta }N-\frac{P}{\delta } \ln \left[ 1-\frac{N}{P}\right] -\frac{A}{a}-\frac{c_{1}}{b^2}(e^{bt_{d}}-bt_{d}-1)\le 0.\)

(b):

The total relevant cost per unit time \(Z(t_{1},T)\) has a minimum value at the optimal point \((t_{1}^*,T^*),\) where \(t_{1}^*=t_{d}\) and \(T^*=t_{d}+\frac{N}{\delta (P-N)},\) if \(\frac{\delta t_{d}-1}{\delta }N-\frac{P}{\delta } \ln \left[ 1-\frac{N}{P}\right] -\frac{A}{a}-\frac{c_{1}}{b^2}(e^{bt_{d}}-bt_{d}-1)>0.\)

Proof

(a) For global minimum solution of the relevant cost function \(Z\left( t_{1},T\right) ,\) the conditions are the all principal minors are positive definite at the optimum point \((t_{1}^*,T^*),\) i.e.,

$$\begin{aligned} \frac{\partial ^2Z(t_{1}^*,T^*)}{\partial {t_{1}^*}^2}>0 \end{aligned}$$
(22)

and

$$\begin{aligned} \frac{\partial ^2Z(t_{1}^*,T^*)}{\partial {t_{1}^*}^2}\frac{\partial ^2Z(t_{1}^*,T^*)}{\partial {T^*}^2}-\left( \frac{\partial Z(t_{1}^*,T^*)}{\partial t_{1}^*\partial T^*}\right) ^2>0 \end{aligned}$$
(23)

The values of \([\frac{\partial ^2Z(t_{1}^*,T^*)}{\partial {t_{1}^*}^2}, \frac{\partial ^2Z(t_{1}^*,T^*)}{\partial {T^*}^2},\) and \(\frac{\partial Z(t_{1}^*,T^*)}{\partial t_{1}^*\partial T^*}]\) are given in Appendix B.

The principal minors are strictly greater than zero. This can be proved easily by the algebraic property \(XY-Z^2>0\) when both \(X>Z\) and \(Y>Z\). From condition \(\frac{\delta t_{d}-1}{\delta }N-\frac{P}{\delta } \ln \left[ 1-\frac{N}{P}\right] -\frac{A}{a}-\frac{c_{1}}{b^2}(e^{bt_{d}}-bt_{d}-1)\le 0,\) (22), and (23), it can be easily shown that \((t_{1}^*,\,T^*)\) is the global minimum solution of \(Z\left( t_{1},T\right)\). The algebraic rule \(XY-Z^2>0\) is satisfied when both \(X>Z\) and \(Y>Z\) [See Sarkar and Moon [37]].

(b) If \(\frac{\delta t_{d}-1}{\delta }N-\frac{P}{\delta } \ln \left[ 1-\frac{N}{P}\right] -\frac{A}{a}-\frac{c_{1}}{b^2}(e^{bt_{d}}-bt_{d}-1)>0,\) then \(F\left( x\right) >0\) \(\forall x\in [t_{d},t_{1}^b).\) Hence,

$$\begin{aligned} \frac{\partial Z(t_{1},T)}{\partial T}&= {} \frac{\alpha }{T^2}\left[ \frac{\delta t_{1}-1}{\delta }M-\frac{P}{\delta } \ln \left( 1-\frac{M}{P}\right) -\frac{A}{a}-c_{1}\left\{ \left( \varphi \left( b(t_{d}-t_{1})+\eta _{1}\ln \phi \right) +\frac{e^{bt_{d}}}{b}\right) \right. \right. \nonumber \\&\left. \times \left( \frac{1-e^{-bt_{d}}}{b}\right) -\frac{t_{d}}{b}\right\} -(c_{1}-bc_{2})\left\{ \frac{\mu \eta _{1}}{36} +\frac{1}{b^2}[\eta _{8}(\eta _{6}+b\eta _{7})+b^2\eta _{9}] -\frac{(\eta _{6}\eta _{5}+b\eta _{7})}{b^2}\right. \nonumber \\&\left. \left. \times \left[ bt_{1}+\eta _{1}\ln \xi \right] \right\} -c_{2}\left\{ \varphi e^{-bt_{d}}\left( \eta _{1}\ln \phi +b(t_{d}-t_{1})\right) -(t_{1}-t_{d})\right\} \right] \\&= {} \frac{\alpha }{T^2}F(t_{1})>0,\quad \forall t_{1}\in [t_{d},t_{1}^b) \end{aligned}$$

which implies \(Z\left( t_{1},T\right)\) is strictly increasing function of T. Therefore, \(Z\left( t_{1},T\right)\) has a minimum value when T is minimum and from (18) the minimum value of T is

$$\begin{aligned} t_{d}+\frac{N}{\delta (P-N)}\quad {\rm as}\quad t_{1}=t_{d}. \end{aligned}$$

Therefore, \(Z\left( t_{1},T\right)\) has a minimum value at \((t_{1}^*,T^*),\) where \(t_{1}^*=t_{d}\) and

$$\begin{aligned} T^*=t_{d}+\frac{N}{\delta (P-N)} \end{aligned}$$

This completes the proof. \(\square\)

4 Numerical experiments

In order to illustrate the above solution procedure, some numerical examples and sensitivity analysis are given. The uniqueness of our model is also established numerically in Example 1 and 2. If L,  the maximum lifetime of product, is not available, then the future of this model is described in Example 3 and 4. In Example 5 and 6, the comparison of numerical results of this model with Wu et al.’s [26] model are discussed.

4.1 Numerical examples

This model considers some numerical examples to check the uniqueness of our solution and some input parametric values are used to obtain the optimum results. Some conditions are verified with the analytical results. It is satisfied with the condition of the lemma also.

4.1.1 Example 1

To illustrate the model, the following parametric values are considered in appropriate units: \(A=\$200\)/order, \(a=300\), \(b=0.01\), \(c_{1}=\$0.2\)/unit/week, \(c_{2}=\$0.3\)/unit, \(c_{3}=\$0.4\)/unit, \(c_{4}=\$0.9\)/unit, \(\delta =0.04\), \(t_{d}=0.4\) week, and \(L=6\) weeks.

The condition of Lemma 1(a) is checked as follows:

$$\begin{aligned}&\frac{\delta t_{d}-1}{\delta }N-\frac{P}{\delta } \ln \left[ 1-\frac{N}{P}\right] -\frac{A}{a}-\frac{c_{1}}{b^2}\left( e^{bt_{d}}-bt_{d}-1\right) = -0.64<0. \end{aligned}$$

Thus from Lemma 1(a), the optimal length of inventory interval \(t_{1}^*\) and the optimal length of order cycle \(T^*\) are given by \(t_{1}^*=1.67\) weeks and \(T^*=2.77\) weeks. Therefore, the minimum total cost per unit time is \(Z^*=\$137.45/\)week. The graphical representation of the minimum total cost function with respect to \(t_{1}\) and T is given in Fig. 2.

Fig. 2
figure 2

Variation of total cost versus time at zero inventory level and cycle length (Example 1)

Full size image

4.1.2 Example 2

To illustrate the model, the following parametric values are considered in appropriate units: \(A=\$100\)/order, \(a=1000\), \(b=0.01\), \(c_{1}=\$0.2\)/unit/week, \(c_{2}=\$0.3\)/unit, \(c_{3}=\$0.4\)/unit, \(c_{4}=\$0.9\)/unit, \(\delta =0.04\), \(t_{d}=0.9\) week, and \(L=6\) weeks.

The condition of Lemma 2(b) is checked as follows:

$$\begin{aligned}&\frac{\delta t_{d}-1}{\delta }N-\frac{P}{\delta } \ln \left[ 1-\frac{N}{P}\right] -\frac{A}{a}-\frac{c_{1}}{b^2}\left( e^{bt_{d}}-bt_{d}-1\right) =0.02>0. \end{aligned}$$

Thus from Lemma 2(b), the optimal length of inventory interval is \(t_{1}^*=t_{d}=0.9\) week and the optimal length of inventory cycle is \(T^*=1.29\) weeks. Hence, the minimum total cost per unit time is \(Z^*=\$165.94/\)week. The graphical representation of the minimum total cost function with respect to T is given in Fig. 3.

Fig. 3
figure 3

Variation of total cost versus changing cycle length (Example 2)

Full size image

If L,  the maximum lifetime of products, is not a available to us, then the illustration of this model can be shown by this numerical examples.

4.1.3 Example 3

In this example, all parameters are same as in Example 1 except \(L=0.\) The condition of Lemma 1(a) is checked as follows:

$$\begin{aligned}&\frac{\delta t_{d}-1}{\delta }N-\frac{P}{\delta } \ln \left[ 1-\frac{N}{P}\right] -\frac{A}{a}-\frac{c_{1}}{b^2}\left( e^{bt_{d}}-bt_{d}-1\right) = -0.64<0. \end{aligned}$$

Thus from Lemma 1(a), the optimal length of inventory interval \(t_{1}^*\) and the optimal length of order cycle \(T^*\) are given by \(t_{1}^*=0.70\) weeks and \(T^*=2.05\) weeks. Therefore, the minimum total cost per unit time is \(Z^*=\$167.69\)/week which is more than the optimum value of this model. The graphical representation of the minimum total cost function with respect to \(t_{1}\) and T is given in Fig. 4.

Fig. 4
figure 4

Variation of total cost versus time at zero inventory level and cycle length (Example 3)

Full size image

4.1.4 Example 4

For this example the same parametric value as in Example 2 except \(L=0\) are considered. The condition of Lemma 2(b) is checked as follows:

$$\begin{aligned} \frac{\delta t_{d}-1}{\delta }N-\frac{P}{\delta } \ln \left[ 1-\frac{N}{P}\right] -\frac{A}{a}-\frac{c_{1}}{b^2}\left( e^{bt_{d}}-bt_{d}-1\right) =0.02>0. \end{aligned}$$

Thus from Lemma 2(b), the optimal length of inventory interval is \(t_{1}^*=t_{d}=0.9\) week and the optimal length of inventory cycle is \(T^*=1.29\) weeks. Hence, the minimum total cost per unit time is \(Z^*=\$165.94/\)week.

The graphical representation of the minimum total cost function with respect to T is given in Fig. 5.

Fig. 5
figure 5

Variation of total cost versus changing cycle length (Example 4)

Full size image

Note: The important managerial insight can be concluded for \(L=0\) as the total cost is more than the cost with some finite value of L,  i.e., if the industry has the information about the value of L, then the total cost can be minimized.

4.1.5 Example 5

From the numerical data of Wu et al. [26], the following parametric values are considered in appropriate units: \(A=\$250\)/order, \(a=600\), \(b=0.1\), \(c_{1}=\$0.5\)/unit/week, \(c_{2}=\$1.5\)/unit, \(c_{3}=\$2.5\)/unit, \(c_{4}=\$2\)/unit, \(\delta =2\), \(t_{d}=0.0833\) week, \(L=15\) weeks.

(In Wu et al.’s [26] model \(a=\alpha\) and \(b=\beta\))

Using these values, the optimal solution of this model is \(\{t_{1}^*=1.46\,{\rm week}, T^*=1.57\, {\rm week}, Z^*(t_{1},T)=\$357.231/ {\rm week}\}\) and the optimal solution of Wu et al.’s [26] model is \(\{t_{1}^*=1.0334\,{\rm weeks}, T^*=1.1687\,{\rm weeks}, TVC^*(t_{1},T)=\$415.224/{\rm week}\}\) Therefore, this model has saved \((\$415.224-\$357.231)=\$57.993\) than Wu et al.’s [26] model.

4.1.6 Example 6

For this example, the model assumes the same parametric values as in Wu et al.’s [26] model: \(A=\$50\)/order, \(a=1000\), \(b=0.1\), \(c_{1}=\$0.5\)/unit/week, \(c_{2}=\$1.5\)/unit, \(c_{3}=\$2.5\)/unit, \(c_{4}=\$2\)/unit, \(\delta =2\), \(t_{d}=0.5\) week, \(L=10\) weeks.

(In Wu et al.’s [26] model \(a=\alpha\)).

Using these parametric values, the optimal solution of this model is

$$\left\{ t_{1}^*=t_{d}=0.5\, {\rm week}, T^*=0.54\, {\rm week}, Z^*\left( t_{1},T\right) =\$219.365/{\rm week} \right\}$$

and the optimal solution of Wu et al.’s [26] model is

$$\{t_{1}^*=t_{d}=0.5\, {\rm week}, T^*=0.9523\, {\rm week}, TVC^*(t_{1},T)=\$563.414/{\rm week}\}$$

Therefore, this model has saved \((\$563.414-\$219.365)=\$344.049\) than Wu et al.’s [26] model.

4.2 Sensitivity analysis

This section studies the effects of changes in parameters such as \(A, a, b,c_{1}, c_{2}, c_{3}, \delta ,\) and L on the total cost. The sensitivity analysis is performed by changing each of the parameters by \(-50, -25, +25\), and \(+50\,\%\), taking one parameter at a time while keeping the remaining parameters unchanged. The results are presented in Table 2 (see Fig. 6).

Table 2 Sensitivity analysis for the key parameters
Full size table
Fig. 6
figure 6

Effect of changes of parameters in (\(-\)50 to +50 %) on total cost

Full size image

From Table 2, the discussion of sensitivity analysis of the key parameters are as follows:

  • If ordering cost A increases, then material handelling cost, shipping cost, placing order’s cost increase; as a result the total relevant cost \(Z^*\) increases. From Table 2, it is observed that this parameter is highly sensitive cost parameter compare to the other cost parameters in the system.

  • The value of the demand parameter a increases indicates the value of the demand increases. The total relevant cost \(Z^*\) increases with the increase of demand parameter a. From the above table, it is shown that \(Z^*\) is highly sensitive to changes in a. But for the positive change and negative change in total cost for this parameter does not follow symmetrical change.

  • Increasing value of the demand parameter b decreases the total relevant cost \(Z^*\). From the above table, it may conclude that \(Z^*\) is less sensitive to changes in b.

  • If the values of the cost parameter \(c_{1}\), \(c_{2}\), and \(c_{3}\) increase, then the total relevant cost \(Z^*\) increases. \(Z^*\) is highly sensitive to changes in \(c_{1}\) and \(c_{3}\) and \(Z^*\) is less sensitive to the change in \(c_{2}\).

  • An increasing value of the parameter \(\delta\) increases the total relevant cost \(Z^*\) of the system.

  • If the value of maximum lifetime L increases, the total relevant cost \(Z^*\) decreases.

5 Some special cases and their comparisons

In this section, four special cases and their numerical comparisons are discussed. This section gives some different physical phenomenons. If backorder is present, how the model will work and if it is not present, then how the model will work. During the absence of some realistic phenomenons, what will be the cost functions those are explained.

5.1 Case 1: model with complete backlogging

If \(\delta =0\) (i.e., \(B\left( t\right) =1\,\forall t\ge 0\)), then the corresponding inventory model becomes a complete backlogging inventory model. Hence, the total relevant cost \(Z_{1}\left( t_{1},T\right)\) for this special case is given by

$$\begin{aligned} Z_{1}\left( t_{1},T\right)&= {} \frac{a}{T}\left[ \frac{A}{a}+c_{1}\left\{ \left( \varphi \left( b(t_{d}-t_{1})+\eta _{1}\ln \phi \right) +\frac{e^{bt_{d}}}{b}\right) \left( \frac{1-e^{-bt_{d}}}{b}\right) -\frac{t_{d}}{b}\right\} \right. \nonumber \\&+(c_{1}-bc_{2})\left\{ \frac{\mu \eta _{1}}{36}+\frac{1}{b^2}[\eta _{8}(\eta _{6}+b\eta _{7})+b^2\eta _{9}] -\frac{(\eta _{6}\eta _{5}+b\eta _{7})}{b^2}\left[ bt_{1}+\eta _{1}\ln \xi \right] \right\} \nonumber \\&+\left.c_{2}\left\{ \varphi e^{-bt_{d}}\left( \eta _{1}\ln \phi +b(t_{d}-t_{1})\right) -(t_{1}-t_{d})\right\} +\frac{c_{3}}{2}\left( T-t_{1}\right) ^2\right] \end{aligned}$$

5.2 Case 2: model without shortage

If \(\delta \rightarrow \infty\), then from (18), it can be obtained \(T\approx t_{1}\). Therefore, in this case, the model becomes without shortage model and the corresponding relevant cost \(Z_{2}\left( T\right)\) is given by

$$\begin{aligned} Z_{2}\left( T\right)&= {} \frac{a}{T}\left[ \frac{A}{a}+c_{1}\left\{ \left( \varphi \left[ b(t_{d}-t_{1})+\eta _{1}\ln \phi \right] +\frac{e^{bt_{d}}}{b}\right) \left( \frac{1-e^{-bt_{d}}}{b}\right) -\frac{t_{d}}{b}\right\} \right. \nonumber \\&+(c_{1}-bc_{2})\left\{ \frac{\mu \eta _{1}}{36}+\frac{1}{b^2}\left[ \eta _{8}(\eta _{6}+b\eta _{7})+b^2\eta _{9}\right] -\frac{(\eta _{6}\eta _{5}+b\eta _{7})}{b^2}\left[ bt_{1}+\eta _{1}\ln \xi \right] \right\} \nonumber \\&+\left. \left.c_{2}\left\{ \varphi e^{-bt_{d}}\left[ \eta _{1}\ln \phi +b(t_{d}-t_{1})\right] -(t_{1}-t_{d})\right\} \right] \right| _{t_{1}=T} \end{aligned}$$

5.3 Case 3: model with instantaneous deterioration and complete backlogging

If \(t_{d}=0\) and \(\delta =0\), then the corresponding inventory model is a model with instantaneous deterioration and complete backlogging, and the total relevant cost is given by

$$\begin{aligned} Z_{3}(t_{1},T)&= {} \frac{a}{T}\Bigg [\frac{A}{a}+(c_{1}-bc_{2})\Bigg \{\frac{1}{b^2}\left( (e^{-bt_{d}}-1)\eta _{8}+b\eta _{8}t_{1}e^{-bt_{1}} +b^2t_{1}^2e^{-bt_{1}}\right) -\frac{\mu _{3}t_{1}}{b}\nonumber \\&+\eta _{1}\Big (\frac{\mu _{2}}{36} -\frac{\mu _{3}}{b^2}\ln \xi \Big )\Bigg \}+c_{2}\left\{ (1+L)\left( \eta _{1}\ln \left( \frac{1+L}{\xi }\right) -bt_{1}\right) -t_{1}\right\} \nonumber \\&+\frac{c_{3}}{2}(T-t_{1}^2) \Bigg ] \end{aligned}$$

5.4 Case 4: model with instantaneous deterioration and without shortages

If \(t_{d}=0\) and \(\delta \rightarrow \infty\), then the corresponding inventory model is a model with instantaneous deterioration and without shortages, and the total relevant cost is given by

$$\begin{aligned} Z_{4}(T)&= {} \frac{a}{T}\left[ \frac{A}{a}+(c_{1}-bc_{2})\left\{ \frac{1}{b^2}\left( (e^{-bt_{d}}-1)\eta _{8}+b\eta _{8}t_{1}e^{-bt_{1}} +b^2t_{1}^2e^{-bt_{1}}\right) -\frac{\mu _{3}t_{1}}{b}\right. \right. \nonumber \\&\left. +\eta _{1}\left( \frac{\mu _{2}}{36} -\frac{\mu _{3}}{b^2}\ln \xi \right) \right\} +c_{2}\left\{ (1+L)\left( \eta _{1}\ln \left( \frac{1+L}{\xi }\right) -bt_{1}\right) -t_{1}\right\} \nonumber \\&\left. \left. +\frac{c_{3}}{2}(T-t_{1}^2) \right] \right| _{t_{1}=T} \end{aligned}$$

5.5 Numerical comparison between above three models

The model takes the following parametric value in appropriate units: \(A=\$200\)/order, \(a=300\), \(b=0.01\), \(c_{1}=\$0.2\)/unit/week, \(c_{2}=\$0.3\)/unit, \(c_{3}=\$0.4\)/unit, \(c_{4}=\$0.9\)/unit, \(\delta =0.04\), \(t_{d}=0.4\) week, and \(L=6\) weeks.

The total cost for Case 1, Case 2, Case 3, and Case 4 are \(Z_{1}^*\left( t_{1},T\right) =\$135.872\)/week, \(Z_{2}^*\left( t_{1},T\right) =\$177.487\)/week, \(Z_{3}^*\left( t_{1},T\right) =\$139.354\)/week, \(Z_{4}^*\left( T\right) =\$183.82\)/week, respectively.

A simple clarification of the above results is as follows: Case 4 is the least flexible among all models as it contains instantaneous deterioration and without shortage. Hence, it agrees to the most expensive state of affairs. Beside this, Case 1 is the most flexible model and it corresponds to the least expensive circumstance.

6 Conclusions

In this competitive marketing environment, to keep higher sales, retailers stored huge amount of inventories to attract more customers. In this direction, the proposed study developed an inventory model for a single type of item with inventory-dependent demand. In the inventory literature, most of the deterioration is considered as constant or exponential along with the infinite replenishment rate. Some of the items may deteriorate in course of time. In this regard, the model considered an inventory model for time-varying deterioration rate with time-varying partial backlogging for products with fixed lifetime. This model minimized the associated cost function at the optimal values of the decision variables. This paper contains two effective lemmas, which gave the optimal solutions that satisfied the existence and uniqueness property of the solutions. This model obtained more savings than the exiting model (Wu et al. [26]). Finally, some numerical examples, graphical representations, special cases, and their comparisons, difference with another models, and sensitivity analysis are explained. This model used the concept of fixed lifetime of product as in time-varying deterioration rate. If the fixed lifetime of the product is not available, this model gave some numerical results for it. Therefore, products which have fixed lifetime and the deterioration rate is time-dependent, the managers of the different industries can follow this strategies to make more savings. There are several extensions of this work that could constitute future research related in this field. This model can be extended in several ways, like multi-item inventory models, inflations, reliability of the items, etc. One another extension can be considered by assuming the demand as a function of price and advertising. Another interesting research may be conducted by considering stochastic lead time along with crashing cost to reduce the lead time. This study can be extended further by considering the preservation technology cost for the deteriorating products.