1 Introduction

In the past decades, compared with asymptotic stabilization, the systems with finite-time convergence demonstrate some nice features, such as faster convergence, high accuracies and better robustness to uncertainties, and these benefits render that the method of finite-time stabilization becomes one of the most appealing tools in practical applications, lots of works have been obtained for a large variety of systems (e.g., see [1,2,3,4,5,6,7,8,9,10,11]). The fundamental research of the finite-time stability is proposed in [1]. Subsequently, a lot of finite-time control problems of linear/nonlinear systems have been solved. For the time-varying systems and impulsive dynamical systems, some sufficient conditions of the finite-time stability are established in [6, 7]. The finite-time control problems for time-varying linear systems are studied in [8, 9] using linear matrix inequalities (LMIs) method. For the disturbed system with mismatching condition, the problem of finite-time output regulation control is investigated based on a composite control design method in [10]. For a class of nonlinear time-varying interconnected systems, the decentralized control problem is studied in [12]. The finite-time stability problem of a class of homogeneous stochastic nonlinear systems modeled by stochastic differential equations is studied in [11] and it is shown that the finite-time stability of stochastic system can be ensured under some appropriate conditions.

In recent years, some significant results of finite-time control problems for different types of uncertain systems have been reported (e.g., see [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27]). The authors in [14] study the problem of finite-time stabilization for nonlinear systems by Hölder continuous state feedback. For nonlinear systems with parametric and dynamic uncertainties, the non-smooth finite-time stabilization problem is investigated in [16]. For the SISO nonlinear systems, assume that the system of non-linear functions is unknown, and the adaptive practical finite-time control problem is addressed in [26] using backstepping design method. For the nonstrict feedback nonlinear systems, a finite-time tracking control scheme based on neural network is established in [27].

As a typical class of hybrid systems, lots of interesting control problems have been addressed for switched systems (e.g., see [28,29,30,31,32,33,34]), particularly in the finite-time stability research of the switched systems (e.g., see [35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50]). The stability analysis for uncertain nonlinear switched systems is reported in [35]. The authors in [41] study the problem of finite-time stabilization for a class of switched stochastic nonlinear systems in p-normal form, and it shows that the resulting closed-loop system is finite-time stable in probability. The problem of global adaptive finite-time stabilization for a class of switched nonlinear parameterized systems is studied in [42]. Furthermore, for uncertain nonlinear systems with unknown system functions, two effective control strategies are established using fuzzy logic systems [43, 44] or NNs [27] to approximate unknown nonlinear functions. Whereafter, some research results have been obtained via approximation-based adaptive fuzzy or NN control methods for the uncertain nonlinear switched systems, for instance, see [45,46,47, 51,52,53] for adaptive fuzzy control and [48,49,50, 54] for adaptive NN control.

Note that for the above-reported works on uncertain switched systems, the desired finite-time controller is developed by employing the traditional adaptive backstepping method which leads to the repeated differentiation of the virtual control variables in the design process, and the “explosion of complexity” problem occurs. To solve this issue, this paper studies the finite-time adaptive fuzzy tracking problem for a class of strict-feedback uncertain switched systems based on DSC technique. The main work of this paper is listed as following.

  1. (i)

    To our knowledge, this paper is the first work to address the finite-time adaptive DSC for uncertain switched systems to solve the “explosion of complexity” problem which widely exists in the reported results (e.g., see [45,46,47,48,49,50, 54]), and the adaptive fuzzy controller is developed with a simple structure.

  2. (ii)

    The fuzzy logic systems are employed to approximate the unknown common dominant functions of the considered systems, and the desired controller is designed using the adaptive DSC method with a nonlinear filter based on the common Lyapunov functions. It proves that under the proposed controller, all the signals of the closed-loop system remain semiglobally bounded, and within a finite time interval, the system tracking error can converge to an arbitrarily small region.

The following is the organization of this paper. The problem statement and some preliminaries are introduced in Sect. 2. Next, adaptive dynamic surface controller design and stability analysis are presented in Sect. 3. Then, a simulation example is given in Sect. 4. A conclusion is drawn in Sect. 5.

2 Problem Statement and Some Preliminaries

Consider the uncertain strict-feedback nonlinear switched system as following

$$\left\{ \begin{array}{lll} {\dot{x}}_{i}=x_{i+1}+f_{i},_{\varrho (t)}\bar{({x}_i}), ~i=1,\ldots ,n-1\\ {\dot{x}}_{n}=u+f_{n},_{\varrho (t)}\bar{({x}_n}),\\ y=x_{1}, \end{array} \right.$$
(1)

where \({\bar{x}}_{i}=[x_{1},\ldots ,x_{i}]^\text {T} \in {R}^i,i=1,\ldots ,n\) are the states of the system, \(u\in {R}\) is the control input, and \(y\in {R}\) is the system output. \(f_{i}(\cdot ):{R}^i\rightarrow {R}\) are unknown continuously differentiable functions and \(\varrho (t): [0,\infty )\rightarrow N=\{1,2,\ldots ,p\}\) is the switching signal.

The control objective for system (1) is to design a finite-time adaptive fuzzy controller such that the system output follows the appointed reference signal \(y_r(t)\), and the boundedness of the other closed-loop signals is guaranteed.

Remark 1

The adaptive control problems have been widely reported for uncertain switched systems (e.g., see [45,46,47,48,49,50, 54, 55]). In this paper, the finite-time adaptive DSC problem is first addressed for uncertain switched systems and the proposed control scheme is developed to solve the “explosion of complexity” problem.

Definition 1

[56] The equilibrium position \(\varsigma =0\) of the nonlinear system \({\dot{\varsigma }}=f(\varsigma ,u)\) is semi-globally practical finite-time stable (SGPFS) if for all \(\varsigma (t_0)=\varsigma _0\), there exist a scalar \(\varepsilon >0\) and a settling time \(T(\varepsilon ,\varsigma _0)<\infty\) such that

$$\begin{aligned} \Vert \varsigma (t)\Vert \le \varepsilon ,&\forall t>t_0+T. \end{aligned}$$
(2)

Assumption 1

The reference signal \(y_{r}(t)\) and its derivatives \(\dot{y_{r}}(t)\) and \(\ddot{y_{r}}(t)\) are bounded.

Lemma 1

[48] Let \(c_1\), \(c_2\)and \(c_3\)be positive constants. Then for any real variables \(\chi\)and \(\zeta\), one has

$$\begin{aligned} |\chi |^{c_1}|\zeta |^{c_2}\le \frac{c_1}{c_1+c_2}c_3|\chi |^{c_1+c_2}+\frac{c_2}{c_1+c_2}c_3^{-\frac{c_1}{c_2}}|\zeta |^{c_1+c_2}. \end{aligned}$$
(3)

Lemma 2

[54] For \(z_i\in R, i=1,2,\ldots ,n\)and \(0<l<1\), one has

$$\begin{aligned} \left( \sum _{i=1}^{n}|z_i|\right) ^l\le \sum _{i=1}^{n}|z_i|^l\le n^{1-l}\left( \sum _{i=1}^{n}|z_i|\right) ^l. \end{aligned}$$
(4)

Lemma 3

[27] Consider a nonlinear system \({\dot{\varsigma }}=f(\varsigma ,u)\). Suppose that there exist a smooth positive definite function \(V(\varsigma )\)and scalars \(a_0>0\), \(0<\lambda <1\)and \(b_0>0\)such that

$$\begin{aligned} {\dot{V}}(\varsigma )\le -a_0V^\lambda (\varsigma )+b_0,&t\ge 0, \end{aligned}$$
(5)

then the nonlinear system \({\dot{\varsigma }}=f(\varsigma ,u)\)is semi-globally practical finite-time stable (SGPFS).

Lemma 4

[57, 58] For any \(\varepsilon >0\)and \(z\in {R}\), the following inequality can be obtained

$$\begin{aligned} 0\le |z|-\frac{z^2}{\sqrt{z^2+\varepsilon ^2}}<\varepsilon . \end{aligned}$$
(6)

Lemma 5

[45,46,47] For any continuous function D(x) on a compact set \(\Omega\)and an expected precision \(\varepsilon >0\), there exists an FLS \(\theta ^{*\text {T}}S(x)\)such that

$$\begin{aligned} \sup _{x\in \Omega }|D(x)-\theta ^{*\text {T}}S(x)|\le \varepsilon . \end{aligned}$$
(7)

By Lemma 5, for a given \(\varepsilon ^*>0\) and any continuous function D(x) on the set \(\Omega\), there exists an FLS \(\theta ^{*\text {T}}S(x)\), such that

$$\begin{aligned} D(x)=\theta ^{*\text {T}}S(x)+\varepsilon (x), \end{aligned}$$
(8)

where \(\varepsilon (x)\) represents the approximation error satisfying \(|\varepsilon (x)|\le \varepsilon ^*\), and \(0<S^\text {T}(x)S(x)\le 1\).

3 Adaptive Controller Design and Stability Analysis

3.1 Adaptive Controller Design

The finite-time adaptive fuzzy DSC scheme is established based on the backstepping technique, and it contains n steps as follows. The error variables are defined as \(\tilde{*}=*-\hat{*}\), where \(\hat{*}\) is the estimate of \(*\).

  • Step 1: The first surface error is defined as \(z_{1}=x_{1}-y_{r}\), and the time derivative of \(z_{1}\) is presented as

    $$\begin{aligned} {\dot{z}}_{1}={\dot{x}}_{1}-{\dot{y}}_{r}=x_{2}+f_{1},_{\varrho (t)}\bar{({x}_1})-{\dot{y}}_{r}. \end{aligned}$$
    (9)

    Then the Lyapunov function is designed as

    $$\begin{aligned} {V}_{1}=\frac{1}{2}{z}_{1}^{2}+\frac{1}{2\gamma _{1}}\tilde{{\theta }}_{1}^{2}, \end{aligned}$$
    (10)

    where \({\tilde{\theta }}_{1}\) is the error of estimate \(\theta _{1}\), and \(\gamma _{1}>0\) is a design parameter.


    In view of Eqs. (12)–(13), the following equation can be obtained

    $$\begin{aligned} \dot{{V}}_{1}=\, &{z}_{1}(x_{2}+f_{1},_{\varrho (t)}\bar{({x}_1})-{\dot{y}}_{r}) -\frac{1}{\gamma _{1}}{\tilde{\theta }}_{1}\dot{\hat{\theta }}_{1}\nonumber \\ =\, &{z}_{1}(x_{2}+f_{1},_{\varrho (t)}\bar{({x}_1})-{\dot{y}}_{r}+\alpha _{1}-\alpha _{1}) -\frac{1}{\gamma _{1}}{\tilde{\theta }}_{1}\dot{\hat{\theta }}_{1}. \end{aligned}$$
    (11)

    On the basis of \(f_{i},_{\varrho (t)}\), we can obtain the following inequality

    $$\begin{aligned} |f_{i},_{\varrho (t)}|\le \sqrt{\sum _{j=1}^{p}f_{i,j}^2}. \end{aligned}$$
    (12)

    Then let \(D_i({\bar{x}}_i)=\sqrt{\sum _{j=1}^{p}f_{i,j}^2}\), and according to Lemma 5, the following equation can be obtained

    $$\begin{aligned} D_i({\bar{x}}_i)=\theta _i^{*T}S({\bar{x}}_i)+\varepsilon _i({\bar{x}}_i). \end{aligned}$$
    (13)

    Using the Young’s inequality and based on Eq. (20), one has

    $$\begin{aligned} {z}_{1}f_{1},_{\varrho (t)}\le&|z_{1}||f_{1},_{\varrho (t)}|\nonumber \\ \le&|z_{1}||D_{1}|\nonumber \\ \le&\frac{1}{2}+\frac{1}{2}z_1^2\theta _1S_1^T({\bar{x}}_1)S_1({\bar{x}}_1)+\frac{1}{2}z_1^2+\frac{1}{2}\varepsilon _1^2, \end{aligned}$$
    (14)

    where \(\theta _1=\theta _1^{*\text {T}}\theta _1^*\).


    In view of (9)–(14), the following inequality can be obtained

    $$\begin{aligned} {\dot{V}}_1\le&\frac{1}{2}+\frac{1}{2}z_1^2\theta _1S_1^\text {T}({\bar{x}}_1)S_1({\bar{x}}_1)+\frac{1}{2}z_1^2+\frac{1}{2}\varepsilon _1^2\nonumber \\&+z_1(x_2+\alpha _1-\alpha _1-{\dot{y}}_r)-\frac{1}{\gamma _{1}}{\tilde{\theta }}_{1}\dot{\hat{\theta }}_{1}. \end{aligned}$$
    (15)

    Design the first virtual control law \(\alpha _{1}\) as

    $$\begin{aligned} \alpha _{1}=-\left( \frac{1}{2}+k_{1}\right) z_{1}+{\dot{y}}_{r}-\frac{1}{2}z_1\hat{\theta }_1S_1^\text {T}({\bar{x}}_1)S_1({\bar{x}}_1), \end{aligned}$$
    (16)

    and design the update law of \(\hat{\theta }_1\) as

    $$\begin{aligned} \dot{\hat{\theta }}_{1}=\frac{1}{2}z_1^2S_1^\text {T}({\bar{x}}_1)S_1({\bar{x}}_1) -\eta _1\hat{\theta }_1, \end{aligned}$$
    (17)

    where \(k_{1}>0\) and \(\eta _1>0\) are design parameters.


    In view of (15)–(17), one has

    $$\begin{aligned} \dot{V_{1}}\le -k_1z_1^2+z_1(x_2-\alpha _1)+\frac{1}{2}+\frac{\eta _1}{\gamma _1}\tilde{\theta _1}\hat{\theta _1}+\frac{1}{2}\varepsilon _1^2. \end{aligned}$$
    (18)

    In the backstepping design, the second error signal is designed as \(x_{2}-\alpha _{1}\) to avoid the “explosion of complexity” problem, and a filtered virtual controller \(s_{1}\) can be obtained using the following novel nonlinear filter

    $$\begin{aligned}&\tau _{1}\dot{s_{1}}=-e_{1}-\frac{\tau _{1}{\hat{M}}_{1}^{2}e_{1}}{\sqrt{{\hat{M}}_{1}^{2}e_{1}^{2}+\sigma ^{2}}}-\tau _{1}z_{1},\nonumber \\&s_{1}(0)=\alpha _{1}(0), \end{aligned}$$
    (19)

    where the first boundary layer error is presented as \(e_{1}=s_{1}-\alpha _{1}\). \({\hat{M}}_{1}\) is used to estimate \(M_{1}\) and the clarification will be provided later. \(\sigma\) is any positive constant. \(\tau _{1}\) is a filter constant and can be designed.

  • Step i \((i=2,\ldots ,n-1)\): The ith surface error is defined as \(z_{i}=x_{i}-s_{i-1}\), then the following equation can be obtained

    $$\begin{aligned} \dot{z_{i}}=x_{i+1}+f_{i},_{\varrho (t)}+\frac{{\hat{M}}_{i-1}^{2}e_{i-1}}{\sqrt{{\hat{M}}_{i-1}^{2}e_{i-1}^{2}+\sigma ^{2}}} +z_{i-1}+\frac{e_{i-1}}{\tau _{i-1}}. \end{aligned}$$
    (20)

    The Lyapunov function candidate \(V_{i}\) can be designed as

    $$\begin{aligned} V_{i}=V_{i-1}+\frac{1}{2}z_{i}^{2}+\frac{1}{2\gamma _{i}}{\tilde{\theta }}_{i}^{2}. \end{aligned}$$
    (21)

    Using the Young’s inequality and based on Lemma 5, the following inequality is obtained

    $$\begin{aligned} {z}_{i}f_{i},_{\varrho (t)}\le&|z_{i}||f_{i},_{\varrho (t)}|\nonumber \\ \le&|z_{i}||D_{i}|\nonumber \\ \le&\frac{1}{2}+\frac{1}{2}z_i^2\theta _iS_i^\text {T}({\bar{x}}_i)S_i({\bar{x}}_i)+\frac{1}{2}z_i^2+\frac{1}{2}\varepsilon _i^2, \end{aligned}$$
    (22)

    where \(\theta _i=\theta _i^{*T}\theta _i^*\).

    Then we can design the virtual control law \(\alpha _{i}\) and the update law \(\hat{\theta }_i\) as following

    $$\begin{aligned} \alpha _{i}= & {} -\left( \frac{1}{2}+k_i\right) z_i-2z_{i-1}-\frac{1}{2}z_i\hat{\theta }_iS_i^\text {T}({\bar{x}}_i)S_i({\bar{x}}_i)\nonumber \\&-\frac{{\hat{M}}_{i-1}^2e_{i-1}}{\sqrt{{\hat{M}}_{i-1}^2e_{i-1}^2+\sigma ^2}}-\frac{e_{i-1}}{\tau _{i-1}}, \end{aligned}$$
    (23)
    $$\begin{aligned} \dot{\hat{\theta }}_{i}= & {} \frac{1}{2}z_i^2S_i^\text {T}({\bar{x}}_i)S_i({\bar{x}}_i)-\eta _i\hat{\theta }_i, \end{aligned}$$
    (24)

    where \(k_{i}\) and \(\eta _{i}\) are positive design parameters, \(\hat{\theta }_{i}\) is the estimate of \(\theta _{i}\).


    In view of (20)–(24), consider the time derivative of \(V_{i}\) as

    $$\begin{aligned} \dot{V_{i}}=&\dot{V_{i-1}}+z_{i}\dot{z_{i}}-\frac{1}{\gamma _{i}}{\tilde{\theta }}_{i}\dot{\hat{\theta }}_{i}\nonumber \\ \le&-\sum _{j=1}^{i}k_{j}z_{j}^{2}+\sum _{j=1}^{i-1}z_{j}e_{j}+(x_{i+1}-\alpha _{i})z_{i}+\frac{i}{2} +\sum _{j=1}^{i}\frac{1}{2}\varepsilon _j^2\nonumber \\&+\sum _{j=1}^{i}\frac{\eta _j}{\gamma _j}{\tilde{\theta }}_j\hat{\theta }_j. \end{aligned}$$
    (25)

    The filtered virtual controller \(s_{i}\) can be obtained using the following nonlinear filter

    $$\begin{aligned}&\tau _{i}\dot{s_{i}}=-e_{i}-\frac{\tau _{i}{\hat{M}}_{i}^{2}e_{i}}{\sqrt{{\hat{M}}_{i}^{2}e_{i}^{2}+\sigma ^{2}}}-\tau _{i}z_{i},\nonumber \\&s_{i}(0)=\alpha _{i}(0), \end{aligned}$$
    (26)

    and define

    $$\begin{aligned} e_{i}=s_{i}-\alpha _{i}, \end{aligned}$$
    (27)

    where the ith boundary layer error is \(e_{i}\). \(\hat{M_{i}}\) is the estimate of \(M_{i}\) and the clarification will be presented later. \(\tau _{i}\) is a filter constant.

  • Step n: Consider the nth surface error as \(z_{n}=x_{n}-s_{n-1}\), and the following equation holds

    $$\begin{aligned} {\dot{z}}_{n}=u+f_{n},_{\varrho (t)}+ \frac{{\hat{M}}_{n-1}^{2}e_{n-1}}{\sqrt{{\hat{M}}_{n-1}^{2}e_{n-1}^{2}+\sigma ^{2}}}+ z_{n-1}+\frac{e_{n-1}}{\tau _{n-1}}. \end{aligned}$$
    (28)

    The Lyapunov function candidate \(V_{n}\) is designed as

    $$\begin{aligned} V_{n}=V_{n-1}+\frac{1}{2}z_{n}^{2}+\frac{1}{2\gamma _{n}}{\tilde{\theta }}_{n}^{2}, \end{aligned}$$
    (29)

    and consider the time derivative of \(V_{n}\) as

    $$\begin{aligned} {\dot{V}}_{n}= & {} {\dot{V}}_{n-1}+z_{n}(u+f_{n},_{\varrho (t)}+ \frac{{\hat{M}}_{n-1}^{2}e_{n-1}}{\sqrt{{\hat{M}}_{n-1}^{2}e_{n-1}^{2}+\sigma ^{2}}}\nonumber \\&+z_{n-1}+\frac{e_{n-1}}{\tau _{n-1}})-\frac{1}{\gamma _n}{\tilde{\theta }}_n\hat{\theta }_n. \end{aligned}$$
    (30)

    By applying Young’s inequality and on account of Lemma 5, the following inequality is obtained

    $$\begin{aligned} {z}_{n}f_{n},_{\varrho (t)}\le&|z_{n}||f_{n},_{\varrho (t)}|\nonumber \\ \le&|z_{n}||D_{n}|\nonumber \\ \le&\frac{1}{2}+\frac{1}{2}z_n^2\theta _nS_n^\text {T}({\bar{x}}_n)S_n({\bar{x}}_n)+\frac{1}{2}z_n^2+\frac{1}{2}\varepsilon _n^2, \end{aligned}$$
    (31)

    where \(\theta _n=\theta _n^{*\text {T}}\theta _n^*\).

    Design the actual control law u as

    $$\begin{aligned} u=&-\left( \frac{1}{2}+k_n\right) z_n-2z_{n-1}-\frac{1}{2}z_n\hat{\theta }_nS_n^\text {T}({\bar{x}}_n)S_n({\bar{x}}_n)\nonumber \\&-\frac{{\hat{M}}_{n-1}^2e_{n-1}}{\sqrt{{\hat{M}}_{n-1}^2e_{n-1}^2+\sigma ^2}}-\frac{e_{n-1}}{\tau _{n-1}}, \end{aligned}$$
    (32)

    and the update law for \(\hat{\theta }_{i}\) is chosen as

    $$\begin{aligned} \dot{\hat{\theta }}_{n}=\frac{1}{2}z_n^2S_n^\text {T}({\bar{x}}_n)S_n({\bar{x}}_n)-\eta _n\hat{\theta }_n, \end{aligned}$$
    (33)

    where \(k_{n}\), \(\eta _{n}\) are positive design parameters, \(\hat{\theta }_{n}\) is the estimate of \(\theta _{n}\).


    In view of (28)–(33), we can obtain the following inequality

    $$\begin{aligned} \dot{V_{n}}\le {-\sum _{j=1}^{n}k_{j}z_{j}^{2}+\sum _{j=1}^{n-1}z_{j}e_{j}+\frac{n}{2}+\sum _{j=1}^{n}\frac{1}{2}\varepsilon _j^2 +\sum _{j=1}^{n}\frac{\eta _j}{\gamma _j}{\tilde{\theta }}_j\hat{\theta }_j}. \end{aligned}$$
    (34)

Remark 2

From the above subsection, it can be seen that the DSC method with a nonlinear filter [58] is introduced to overcome the “explosion of complexity” problem, and by introducing a novel estimated parameter, the nonlinear filter is developed. Then, the desired fuzzy controller is designed with a simple structure and the practical finite-time stability of the closed-loop systems is guaranteed. This is the main advantage of the proposed control method.

3.2 Stability Analysis

Based on the inequality (34), the main result of this paper is presented using the following theorem.

Differentiating the boundary layer errors \(e_{i}=s_{i}-\alpha _{i}\) yields

$$\begin{aligned} {\dot{e}}_{i}=&\frac{-e_{i}}{\tau _{i}}-\frac{{\hat{M}}_{i}^{2}e_{i}}{\sqrt{{\hat{M}}_{i}^{2}e_{i}^{2}+\sigma ^{2}}}-z_{i} +B_{i}(z_{1},\ldots ,z_{i},e_{1},\ldots ,e_{i},\hat{\theta }_{1},\ldots ,\hat{\theta }_{i},\nonumber \\&{\hat{M}}_{1},\ldots ,{\hat{M}}_{i},y_{r},\dot{y_{r}},{\ddot{y}}_{r}),~i=1,\ldots ,n-1, \end{aligned}$$
(35)

where

$$\begin{aligned} B_{1}(\cdot )=&-{\dot{\alpha }}_{1}\nonumber \\ =&-\frac{\partial \alpha _{1}}{\partial x_{1}}{\dot{x}}_{1} -\frac{\partial \alpha _{1}}{\partial \hat{\theta }_{1}}\dot{\hat{\theta }}_{1} -\frac{\partial \alpha _{1}}{\partial y_{r}}{\dot{y}}_{r} -\frac{\partial \alpha _{1}}{\partial \dot{y_{r}}}{\ddot{y}}_{r}, \end{aligned}$$
(36)
$$\begin{aligned} B_{i}(\cdot )=&-\dot{\alpha _{i}}\nonumber \\ =&-\sum _{j=1}^{i}\frac{\partial \alpha _{i}}{\partial x_{j}}{\dot{x}}_{j} -\frac{\partial \alpha _{i}}{\partial \hat{\theta }_{j}}\dot{\hat{\theta }}_{j} -\frac{\partial \alpha _{i}}{\partial e_{i-1}}{\dot{e}}_{i-1}\nonumber \\&-\frac{\partial \alpha _{i}}{\partial {\hat{M}}_{i-1}}\dot{{\hat{M}}}_{i-1} -\frac{\partial \alpha _{i}}{\partial y_{r}}{\dot{y}}_{r} -\frac{\partial \alpha _{i}}{\partial \dot{y_{r}}}{\ddot{y}}_{r} \end{aligned}$$
(37)

and the functions of \(B_{i},~i=1,\ldots ,n-1\) are continuous.

The Lyapunov function candidate is considered as following

$$\begin{aligned} V=V_{n}+\sum _{i=1}^{n-1}\frac{1}{2}e_{i}^{2}+\sum _{i=1}^{n-1}\frac{1}{2\beta _{i}}{\tilde{M}}_{i}^{2}, \end{aligned}$$
(38)

where \(\beta _{i}\), \(i=1,\ldots ,n-1\) are positive design parameters.

Theorem 1

Consider the switched nonlinear strict-feedback system (1) including the nonlinear filters (19) and (26), the virtual control laws (16) and (23), the actual control law (32), and the update laws (17), (24), and (33). Under Assumption 1, there exit design parameters \(k_{i}\), \(\gamma _{i}\), \(\beta _{i}\), \(\eta _{i}\), \(i=1,\ldots ,n\), \(\tau _{j}\), and \(\rho _{j}\), \(j=1,\ldots ,n-1\) such that the following statements hold:

  1. (i)

    all the closed-loop signals are semi-globally bounded.

  2. (ii)

    the output \(y_(t)\)can track the given signal \(y_r(t)\)in finite time.

Proof

The compact sets are defined as

$$\begin{aligned} \Omega _{1}= & {} \{[y_{r},{\dot{y}}_{r},{\ddot{y}}_{r}]^\text {T}{:}y_{r}^2+{\dot{y}}_{r}^2+{\ddot{y}}_{r}^2\le B_{0}\}, \end{aligned}$$
(39)
$$\begin{aligned} \Omega _{2}= & {} \{V(t)\le q\}, \end{aligned}$$
(40)

where \(B_{0}\) and q are known positive constants. It is noted that set \(\Omega _{0}\times \Omega _{1}\) is also a compact in \(R^{4n+1}\). As a consequence, the positive constants \(M_{i}\) can be obtained with \(|B_{i}(\cdot )|\le M_{i}\) on \(\Omega _{1}\times \Omega _{2}\). It can be grasped quite clearly that the definitive values of \(M_{i}\) are unknown. Next, we will analyze the finite-time stability of the resulting closed-loop system.

The time derivative of V yields

$$\begin{aligned} {\dot{V}}=&{\dot{V}}_{n}+\sum _{i=1}^{n-1}e_{i}{\dot{e}}_{i}-\sum _{i=1}^{n-1}\frac{1}{\eta _{i}}{\tilde{M}}_{i}\dot{{\hat{M}}}_{i}\nonumber \\ \le&-\sum _{i=1}^{n}k_{i}z_{i}^{2}-\sum _{i=1}^{n-1}\frac{e_{i}^2}{\tau _{i}} -\sum _{i=1}^{n-1}\frac{{\hat{M}}_{i}^{2}e^2_{i}}{\sqrt{{\hat{M}}_{i}^{2}e_{i}^{2} +\sigma ^{2}}}\nonumber \\&+\sum _{i=1}^{n-1}M_{i}|e_{i}| -\sum _{i=1}^{n-1}\frac{1}{\beta _{i}}{\tilde{M}}_{i}\dot{{\hat{M}}}_{i}+\frac{n}{2} +\sum _{i=1}^{n}\frac{1}{2}\varepsilon _i^2+\sum _{i=1}^{n}\frac{\eta _i}{\gamma _i}{\tilde{\theta }}_i\hat{\theta }_i. \end{aligned}$$
(41)

Form Lemma 4, it follows that

$$\begin{aligned} M_{i}|e_{i}|=&{\hat{M}}_{i}|e_{i}|+{\tilde{M}}_{i}|e_{i}|\nonumber \\ \le&\frac{{\hat{M}}_{i}^{2}e_{i}^{2}}{\sqrt{{\hat{M}}_{i}^{2}e_{i}^{2}+\sigma ^{2}}} +\sigma +{\tilde{M}}_{i}|e_{i}|, \end{aligned}$$
(42)

then the following inequality can be obtained

$$\begin{aligned} {\dot{V}}\le & {} -\sum _{i=1}^{n}k_{i}z_{i}^{2}-\sum _{i=1}^{n-1}\frac{e_{i}^2}{\tau _{i}} -\sum _{i=1}^{n-1}\frac{1}{\beta _{i}}{\tilde{M}}_{i}(\dot{{\hat{M}}}_{i}-\beta _{i}|e_{i}|)\nonumber \\&+(n-1)\sigma +\frac{n}{2} +\sum _{i=1}^{n}\frac{1}{2}\varepsilon _i^2+\sum _{i=1}^{n}\frac{\eta _i}{\gamma _i}{\tilde{\theta }}_i\hat{\theta }_i. \end{aligned}$$
(43)

The update law for \({\hat{M}}_{i}\) is considered as following

$$\begin{aligned} \dot{{\hat{M}}}_{i}=\beta _{i}|e_{i}|-\rho _i{\hat{M}}_i,i=1,\ldots ,n-1. \end{aligned}$$
(44)

In view of (41)–(44), we can obtain the following inequality

$$\begin{aligned} {\dot{V}}\le & {} -\sum _{i=1}^{n}k_{i}z_{i}^{2}-\sum _{i=1}^{n-1}\frac{e_{i}^2}{\tau _{i}}+(n-1)\sigma +\sum _{i=1}^{n}\frac{\eta _i}{\gamma _i}{\tilde{\theta }}_i\hat{\theta }_i\nonumber \\&+\sum _{i=1}^{n-1}\frac{\rho _i}{\beta _i}{\tilde{M}}_i{\hat{M}}_i+\frac{n}{2}+\sum _{i=1}^{n}\frac{1}{2}\varepsilon _i^2. \end{aligned}$$
(45)

By the definition of \({\tilde{\theta }}_i\) and \({\tilde{M}}_i\), the following inequalities can be obtained

$$\begin{aligned} {\tilde{\theta }}_i\hat{\theta }_i={\tilde{\theta }}_i(\theta _i-{\tilde{\theta }}_i)\le \frac{1}{2}\theta _i^2-\frac{1}{2}{\tilde{\theta }}_i^2, \end{aligned}$$
(46)
$$\begin{aligned} {\tilde{M}}_i{\hat{M}}_i={\tilde{M}}_i(M_i-{\tilde{M}}_i)\le \frac{1}{2}M_i^2-\frac{1}{2}{\tilde{M}}_i^2. \end{aligned}$$
(47)

In view of inequalities (35)–(47), one has

$$\begin{aligned} {\dot{V}}\le & {} -\sum _{i=1}^{n} k_{i}z_{i}^{2}-\sum _{i=1}^{n-1}\frac{e_{i}^2}{\tau _{i}}-\sum _{i=1}^{n}\frac{\eta _i}{2\gamma _i}{\tilde{\theta }}_i^2 -\sum _{i=1}^{n-1}\frac{\rho _i}{2\beta _i}{\tilde{M}}_i^2\nonumber \\&+(n-1)\sigma +\sum _{i=1}^{n}\frac{\eta _i}{\gamma _i}\theta _i^2+\sum _{i=1}^{n-1}\frac{\rho _i}{2\beta _i}M_i^2+\frac{n}{2}+\sum _{i=1}^{n}\frac{1}{2}\varepsilon _i^2. \end{aligned}$$
(48)

By applying Lemma 1 and taking \(x=\sum _{i=1}^{n}(\frac{1}{2}z_i^2)\), \(y=1\), \(c_1=\lambda\), \(c_2=1-\lambda\) and \(c_3=\lambda ^{-1}\) into account, the following inequality can be obtained

$$\begin{aligned} \sum _{i=1}^{n}\left( \frac{1}{2}z_i^2\right) ^{\lambda }\le \sum _{i=1}^{n}\frac{1}{2}z_i^2+(1-\lambda )\lambda ^{\frac{\lambda }{1-\lambda }}. \end{aligned}$$
(49)

Then, the following inequality can be obtained using Lemma 2

$$\begin{aligned} -\sum _{i=1}^{n}\left( \frac{1}{2}z_i^2\right) ^{\lambda }\le -\left( \sum _{i=1}^{n}\frac{1}{2}z_i^2\right) ^{\lambda }. \end{aligned}$$
(50)

In view of (49)–(50), one has

$$\begin{aligned} -\sum _{i=1}^{n}\frac{1}{2}z_i^2\le -\left(\sum _{i=1}^{n}\frac{1}{2}z_i^2\right)^{\lambda }+(1-\lambda )\lambda ^{\frac{\lambda }{1-\lambda }}. \end{aligned}$$
(51)

Similarly, we can also obtain the following inequalities

$$\begin{aligned}&-\sum _{i=1}^{n}\frac{1}{2\gamma _i}\theta _i^2\le -\left( \sum _{i=1}^{n}\frac{1}{2\gamma _i}\theta _i^2\right) ^{\lambda }+(1-\lambda )\lambda ^{\frac{\lambda }{1-\lambda }}, \end{aligned}$$
(52)
$$\begin{aligned}&-\sum _{i=1}^{n-1}\frac{1}{2}e_i^2\le -\left( \sum _{i=1}^{n}\frac{1}{2}e_i^2\right) ^{\lambda }+(1-\lambda )\lambda ^{\frac{\lambda }{1-\lambda }}, \end{aligned}$$
(53)
$$\begin{aligned}&-\sum _{i=1}^{n-1}\frac{1}{2\beta _i}{\tilde{M}}_i^2\le -\left( \sum _{i=1}^{n}\frac{1}{2\beta _i}{\tilde{M}}_i^2\right) ^{\lambda }+(1-\lambda )\lambda ^{\frac{\lambda }{1-\lambda }}. \end{aligned}$$
(54)

In view of inequalities (48)–(54), one has

$$\begin{aligned} {\dot{V}}\le&-a_0\left(\sum _{i=1}^{n}\frac{1}{2}z_{i}^{2}\right)^{\lambda }-a_0\left( \sum _{i=1}^{n}\frac{1}{2\gamma _i}{\tilde{\theta }}_i^2\right) ^{\lambda }\nonumber \\&-a_0\left(\sum _{i=1}^{n-1}\frac{1}{2}e_{i}^2\right)^{\lambda }-a_0\left( \sum _{i=1}^{n-1}\frac{1}{2\beta _i}{\tilde{M}}_i^2\right) ^{\lambda }+b_0, \end{aligned}$$
(55)

i.e.,

$$\begin{aligned} {\dot{V}}\le&-a_0V^{\lambda }+b_0, \end{aligned}$$
(56)

where

$$\begin{aligned} a_0= & {} \min \{2k_1 \ldots 2k_n,\frac{2}{\tau _1},\ldots ,\frac{2}{\tau _{n-1}},\nonumber \\&\eta _1,\ldots ,\eta _n,\rho _1,\ldots ,\rho _{n-1}\}, \end{aligned}$$
(57)
$$\begin{aligned} b_0\,= \, & {} (n-1)\sigma +\frac{n}{2}+\sum _{i=1}^{n}\frac{1}{2}\varepsilon _i^2+\sum _{i=1}^{n}\frac{\eta _i}{\gamma _i}\left( \frac{1}{2}\theta _i^2\right) \nonumber \\&+\sum _{i=1}^{n-1}\frac{\rho _i}{\beta _i}\left( \frac{1}{2}M_i^2\right) +4(1-\lambda )\lambda ^{\frac{\lambda }{1-\lambda }}. \end{aligned}$$
(58)

Let \(\text {T}^*=\frac{1}{(1-\lambda )\xi a_0}[V^{1-\lambda }(0)-(\frac{b_0}{(1-\xi )a_0})^{\frac{1-\lambda }{\lambda }}]\), where V(0) means the initial value of V(t). On the basis of Lemma 3, for \(\forall t\ge \text {T}^*\), \(V^\lambda \le \frac{b_0}{(1-\xi )a_0}\), that is, all the signals of the closed-loop system are SGPFS. Furthermore, based on the definition of V(t), for \(\forall t\ge \text {T}^*\), we have

$$\begin{aligned} |y-y_r|\le 2\left( \frac{b_0}{(1-\xi )a_0}\right) ^{\frac{1}{2\lambda }}, \end{aligned}$$
(59)

which implies that after the finite time \(T^*\), the tracking error will be in a small neighborhood of the origin. This completes the proof. \(\square\)

4 Simulation Example

To show the availability of the presented control scheme, the switched RCL circuit system is presented in this paper, and it is shown in Fig. 1. According to [57], we describe the switched RCL circuit system as

$$\left\{ \begin{array}{lll} {\dot{x}}_{1}=x_{2}+f_{1},_{\varrho (t)}\bar{({x}_1})\\ {\dot{x}}_{2}=u+f_{2},_{\varrho (t)}\bar{({x}_2})\\ y=x_{1}, \end{array} \right.$$
(60)

where \(\varrho (t):R\rightarrow \{1,2\}\), \(f_1,_1=f_1,_2=(1/L)x_2-x_2\), \(f_2,_1=-(1/C_1)x_1-(R/L)x_2\), \(f_2,_2=-(1/C_2)x_1-(R/L)x_2\), \(x_1=q_c\) means the charge in capacitor, \(x_2=\phi _L\) stands for the flux in the inductance for this circuit, \(C_i\) denotes the ith capacitor, L is the inductance, R shows the resistance, u represents the voltage, which also means the system input. The related parameters are selected as \(R=1\), \(L=0.5\), \(C_1=60\) and \(C_2=100\). The control objective is that within a finite time interval, the system tracking error can converge to an arbitrarily small region, and the reference signal \(y_r\) is chosen as \(y_r=0.25\sin (2t)\).

Fig. 1
figure 1

Switched RCL circuit

Full size image

Nine fuzzy sets are defined over [− 2, 2] for all state variables by choosing the partitioning points as − 2, − 1.5, − 1, − 0.5, 0, 0.5, 1, 1.5, 2 and the fuzzy membership functions are presented as follows

$$\begin{aligned}&\mu _{F_i^1}(x_i)=\exp (-0.5(x_i+2)^2),\quad \mu _{F_i^2}(x_i)=\exp (-0.5(x_i+1.5)^2),\\&\mu _{F_i^3}(x_i)=\exp (-0.5(x_i+1)^2),\quad \mu _{F_i^4}(x_i)=\exp (-0.5(x_i+0.5)^2),\\&\mu _{F_i^5}(x_i)=\exp (-0.5(x_i+0)^2),\quad \mu _{F_i^6}(x_i)=\exp (-0.5(x_i-2)^2),\\&\mu _{F_i^7}(x_i)=\exp (-0.5(x_i-1.5)^2),\quad \mu _{F_i^8}(x_i)=\exp (-0.5(x_i-1)^2),\\&\mu _{F_i^9}(x_i)=\exp (-0.5(x_i-0.5)^2). \end{aligned}$$

According to (8), \(S_i\) can be constructed for \(i=1,2.\) Following Theorem 1, we can have adaptive fuzzy controller (32) with \(n=2\), the virtual control \(\alpha _1\) (16), and adaptive laws \(\dot{\hat{\theta }}_i,i=1,2\) to control system (60).

The design parameters are selected as \(k_1=30\), \(k_2=0.3\), \(\eta _1=3\), \(\eta _2=5\), \(\beta _1=0.5\), \(\rho _1=0.3\), \(\tau _1=0.2\) and \(\sigma =0.3\). The initial conditions of this switched system are presented as \(x_1(0)=0.01\), \(x_2(0)=0.1\), \(\hat{\theta }_1(0)=0.02\), \(\hat{\theta }_2(0)=0.1\) and \({\hat{M}}_1(0)=0.01\).

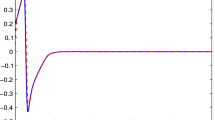
According to the above analysis, the simulation results are displayed in Figs. 2, 3, 4, 5, 6, 7. Figure 2 gives the switched signal. Figure 3 shows the output tracking performance. Figure 4 shows the tracking error. From Figs. 3, 4, we can find that the control objective of this paper has been achieved. The control signal u is presented in Fig. 5. Figure 6 expresses the curves of adaptive laws of \(\hat{\theta }_1\) and \(\hat{\theta }_2\). Figure 7 shows the adaptation of parameter \({\hat{M}}_1\). It is obvious that the boundedness of all the signals in this closed-loop system can be achieved.

Fig. 2
figure 2

Switched signal

Full size image
Fig. 3
figure 3

The reference trajectory \(y_r\) and the output signal y

Full size image
Fig. 4
figure 4

Tracking error \(z_1\)

Full size image
Fig. 5
figure 5

The control signal u

Full size image
Fig. 6
figure 6

Adaptive laws for \(\hat{\theta }_{1}\), \(\hat{\theta }_{2}\)

Full size image
Fig. 7
figure 7

Adaptive parameter \({\hat{M}}_{1}\)

Full size image

5 Conclusions

This paper studies the finite-time adaptive fuzzy tracking problem for a class of strict-feedback uncertain switched systems. The unknown system functions are approximated online using FLS. In addition, the common Lyapunov functions are presented to deal with the switched signals of this system. According to a nonlinear filter, a DSC method is presented to overcome the problem from “explosion of complexity”. The boundedness of all the signals in the closed-loop system can be guaranteed under the designed controller and adaptive laws. Furthermore, it shows that the output signal can track the reference signal to a small compact in finite time.