1 Introduction

During the past decades, backstepping technique proposed in [1] has been actively employed to address the control problem for nonlinear systems, and abundant results have been achieved [2,3,4,5,6,7,8]. To mention a few, combining backstepping technique with adaptive fuzzy approach, the authors in [2] investigate tracking control problem for uncertain single-input and single-output nonlinear systems. As for the multiple-input and multiple-output (MIMO) nonlinear systems, the authors in [3,4,5] study the tracking control problem with various conditions, such as unknown dead-zone inputs, state-constrained and time-varying delays. Combine with different nonlinear feature aforementioned, corresponding adaptive fuzzy controllers are designed to guarantee all signals in the considered systems are bounded and tracking errors are driven to a small neighborhood of the origin. Note that stochastic terms are ignored in the above considered nonlinear systems and could result into lack of practicability. To handle with the stability problem of stochastic nonlinear systems, the authors in [6] first studied the output feedback stabilization problem via the quartic Lyapunov function for stochastic continuous-time nonlinear systems. Afterwards, many meaningful results on the stochastic nonlinear systems have been obtained in [7,8,9,10,11,12]. An adaptive fuzzy output feedback control strategy is developed in [7] for uncertain stochastic nonlinear systems, where the adaptive control method is employed to solve the problem of uncertain parameters. Then, the authors in [8, 9] extend the results of [7] to stochastic strict feedback nonlinear systems with unmeasured states and stochastic nonlinear switched systems with arbitrary switchings and unmodeled dynamics, respectively. In [10], an adaptive fuzzy controller is designed via backstepping technique to address the tracking control problem of stochastic nonlinear pure feedback systems with input saturation, where the mean value theorem and piecewise smooth functions are employed to deal with the problem of nonaffine appearance in the systems and input saturation, respectively. An adaptive fuzzy control scheme based on command filtering is developed for the permanent magnet synchronous motor stochastic system in [11], where fuzzy logic systems (FLSs) are introduced to approximate unknown stochastic nonlinear functions and command filtering technique is employed to solve the problem of “explosion of complexity”.

However, there exists a drawback due to the repetitive differentiations of nonlinear functions in the aforementioned controller design process using backstepping technique, which is called “explosion of complexity” and increases computational complexity. In order to reduce the computational burden, the authors in [13] propose dynamic surface control (DSC) method for nonlinear systems, which uses the algebraic operation instead of the repeated differentiation. In this method, a new parameter is obtained by letting the virtual controller \(\alpha _{i}\) as input signal pass through a first-order filter. Then the obtained new parameter is used to replace the virtual controller \(\alpha _{i}\) during the controller design process. From then on, the DSC method is widely employed to vehicle systems in [14, 15], marine surface vessels system [16], and so on. Combining the DSC method with adaptive neural network (NN) technique or adaptive fuzzy approach, the adaptive intelligent controllers are designed for uncertain strict feedback nonlinear system in [17, 18] and interconnected pure feedback nonlinear system in [19]. Afterwards, the results of [17] are extend to the uncertain strict feedback nonlinear system with unknown control direction and disturbances in [20] and stochastic MIMO pure feedback nonlinear systems with full state constraints in [21], respectively. Similar with the DSC method, an adaptive control scheme based on the command filtering technique, which is another way to handle with the computational complexity, is proposed in [22] for surface vehicles with unknown model parameters.

On another hand, the reacher on convergence performance draws a lot of attention due to the potential applications in many industrial field. To obtain fast transient and high accuracy, the authors in [23] propose finite time control strategy via the DSC method for nonaffine nonlinear systems with dead-zone. An adaptive NN finite time controller is designed in [24] via DSC method for permanent magnet synchronous motor stochastic nonlinear systems with iron losses. However, the settling time of finite time control in the works aforementioned are related to initial states of the considered systems, thus it could result in lack of practicability when the initial states can be changed in the feasible region. For this reason, fixed time stability control strategy is developed in [25], in which the settling time is irrelevant to initial states. Subsequently, fixed time control scheme is employed for different classes switched nonlinear systems in [26,27,28]. The fixed time tracking control problem for uncertain pure feedback nonlinear systems in [29] is studied, where adaptive NN and mean value theorem are used to approximate unknown functions and handle with the problem of nonaffine appearance, respectively. In [30], a fixed time high-order sliding mode control strategy via the DSC method is proposed for chaotic oscillation in three-bus power system. The event-triggered (ET) fixed time tracking control problem for stochastic non-triangular structure nonlinear systems in [31] is addressed by utilizing the DSC method and ET control technique.

Although fruitful results on fixed time control strategy via the DSC method have been obtained from the above literature review, few efforts are paid attention to stochastic pure feedback nonlinear systems. In this paper, an adaptive fuzzy fixed time tracking control strategy based on the DSC method is proposed for stochastic pure feedback nonlinear systems to guarantee all signals in the considered systems are semiglobally uniform ultimately bounded (SGUUB) and the tracking errors are driven to a small neighborhood of the origin in a fixed time. The main contributions of this paper are listed as follows:

  1. (1)

    Compared with the studied systems in the [26,27,28], the considered systems in this paper are more general in the actual control systems due to the existence of nonaffine mapping and stochastic item. In order to deal with the problem of nonaffine appearance, the mean value theorem is introduced in stochastic nonlinear systems to invert the nonaffine structure into strict feedback form, which makes the backstepping technique suitable during the controller designed.

  2. (2)

    During the controller design process, the DSC method is used to solve the computational complexity problem caused by backstepping technique and Hession item introduced by infinitesimal generator. The virtual controller which consist of stochastic state variables is pass through a first-order filter as input signal. Then, algebraic operation is utilized in the control strategy instead of the repeated differentiation. In addition, we also introduce the adaptive fuzzy method to approximate the unknown nonlinear functions.

The rest of this paper is arranged as follows. The problem formulation and preliminaries are introduced in Sect. 2. Section 3 gives the process of fixed time adaptive fuzzy controller design via the DSC method. The proof of Theorem 1, which summarizes the main results of this paper, is given in Sect. 4. Section 5 presents a simulation to show the validity of the proposed control strategy. Section 6 concludes this paper.

2 Problem Formulations and Preliminaries

In this paper, consider the following stochastic pure feedback nonlinear systems with external disturbances:

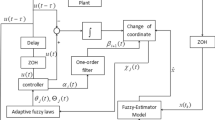
$$ { \left\{ \begin{array}{l} {\text {d}}x_{1}=(f_{1}(x_{1},x_{2})+ \hbar _{1}(t)){\text {d}}t+\varUpsilon ^{\text {T}}_{1}({x}_{1}){\text {d}}\omega \\ \qquad \qquad \vdots \\ {\text {d}}x_{i}=(f_{i}({{\bar{x}}}_{i},x_{i+1})+ \hbar _{i}(x)){\text {d}}t+\varUpsilon ^{\text {T}}_{i}({{{\bar{x}}}}_{i}){\text {d}}\omega \\ \qquad \qquad \vdots \\ {\text {d}}x_{n}=(f_{n}({{\bar{x}}}_{n},u)+ \hbar _{n}(t)){\text {d}}t+\varUpsilon ^{\text {T}}_{n}({{{\bar{x}}}}_{n}){\text {d}}\omega \\ y={{x}_{1}}, \end{array} \right. } ,$$
(1)

where \({{{\bar{x}}}_{i}}={{[{{x}_{1}},{{x}_{2}},\ldots ,{{x}_{i}}]}^{\text {T}}}\), \(i=1,2,\ldots ,n\), u and y represent the considered systems states, input and output, respectively. \(\hbar _{i}(t)\), \(i=1,2,\ldots ,n\) denote the external disturbances of the considered systems. \({\omega }\) represents an independent r-dimensional standard Wiener motion, which is defined on the complete probability space (S, F, P). \({f_{i}(\cdot )}\) and \({\varUpsilon ^{\text {T}}_{i}(\cdot )}\), \({i=1,2,\ldots ,n}\), denote the unknown smooth functions. To show the detailed control process and signals, we have added the block diagram as Fig. 1 in the following:

Fig. 1
figure 1

The block diagram of the control procedure and signals

Full size image

In this paper, the control objective is that the tracking errors converge on a small neighborhood of the origin within a fixed time and all signals in the considered systems are SGUUB by designing an adaptive fuzzy fixed time controller. Before proceeding further, some important Definitions, Lemmas and Assumptions are given as follows:

Definition 1

([8]) Consider a stochastic nonlinear system as follows:

$$ {\text {d}}\chi =f(\chi ,u){\text {d}}t+\varUpsilon (\chi ){\text {d}}\omega , ,$$
(2)

where \({\chi }\) and u represent the system state and input, respectively. \({\omega }\) denotes a r-dimensional standard Wiener motion. Then, for any given \({V(\chi )}\), the infinitesimal generator \({\ell V(\chi )}\) is defined as follow:

$$ {\ell V(\chi )}={\frac{\partial {V(\chi )}}{\partial {\chi }}}{f(\chi )}+{\frac{1}{2}}{\varUpsilon ^{\text {T}}(\chi )}{\frac{\partial ^{2} {V(\chi )}}{\partial {\chi ^{2}}}}{\varUpsilon (\chi )}. $$
(3)

Definition 2

([23]) For all time \(t>t_{1}\), the solution of the system (2), which satisfies \(\chi (t)=0\), is called to be semiglobal finite time stable and \(T_{1}(\chi _{0})\) represents settling time of the system (2) where \(\chi _{0}\) denotes the initial condition. Thus, we can obtain that the settling time \(T_{1}(\chi _{0})\) is related to the initial condition \(\chi _{0}\). If the settling time \(T_{1}(\chi _{0})\) is bounded and satisfies \(T_{1}(\chi _{0})<T_{1}\), then the system (2) is called to be semiglobal fixed time stable and the settling time \(T_{1}\) has no connection with the initial condition.

Theorem 1

([26]) For the system (2), assuming \({V(\chi )}\) is a smooth positive function and \({\chi _{1}>0},\) \({\chi _{2}>0},\) \({\gamma >0},\) \({p>1},\) \({q\in (0,1)}\) and \(\iota \in (0,1)\) such that

$$ {{\ell V(\chi )}\le {{-\chi _{1} V^{p}(\chi )}-{\chi _{2} V^{q}(\chi )}+{\gamma }},\quad {\forall {x}\in R}}. $$
(4)

Then the system (2) is called to be SGUUB and the settling time \({T_{1}}\) can be derived as

$$ {T_{1}}\le {\frac{1}{\iota \chi _{1}(p-1)}}+{\frac{1}{\iota \chi _{2}(1-q)}}. $$
(5)

Theorem 2

(Young’s Inequality [23]) For \({x,y\in R,a,b},\) \({c>0},\) we can have:

$$ {{|x|^{a}|y|^{b}}\le {\frac{a}{a+b}}{c}{|x|^{a+b}}+{\frac{b}{a+b}}{c}^{-\frac{a}{b}}{|y|^{a+b}}}. $$
(6)

Theorem 3

([24]) For \({p>1,0<q<1,x>0},\) then we have

$$ \begin{aligned} {n^{1-p}{\left( \sum _{i=1}^{n}{{x_{i}}}\right) ^{p}}}\le {\sum _{i=1}^{n}{{x_{i}}}^{p}}&\le {\left( \sum _{i=1}^{n}{{x_{i}}}\right) ^{p}},\end{aligned}$$
(7)
$$ \begin{aligned} {\left( \sum _{i=1}^{n}{{x_{i}}}\right) ^{q}}\le {\sum _{i=1}^{n}{{x_{i}}}^{q}}&\le {n^{1-q}{\left( \sum _{i=1}^{n}{{x_{i}}}\right) ^{q}}}. \end{aligned}$$
(8)

Theorem 4

([24]) For \({\alpha ,\beta \in R},\) \(\alpha \le \beta ,\) and \(p>1,\) we have

$$ \alpha (\beta -\alpha )^{p}\le {\frac{p}{p+1}}{\left( {\beta }^{p+1}-{\alpha }^{p+1}\right) }. $$
(9)

Theorem 5

([25]) For \({x,y>0},\) \({0<q<1},\) and \({p>1},\) we have

$$\begin{aligned} {\left( {\sum _{i=1}^{n}{x_{i}}}+{\sum _{i=1}^{n}{y_{i}}}\right) }^{q}&\le {\left( {\sum _{i=1}^{n}{x_{i}}}\right) ^{q}}+{\left( {\sum _{i=1}^{n}{y_{i}}}\right) ^{q}},\end{aligned}$$
(10)
$$\begin{aligned} {\left( {\sum _{i=1}^{n}{x_{i}}}+{\sum _{i=1}^{n}{y_{i}}}\right) }^{p}&\le {2^{p-1}}{\left( {\left( {\sum _{i=1}^{n}{x_{i}}}\right) ^{p}}+{\left( {\sum _{i=1}^{n}{y_{i}}}\right) ^{p}}\right) }. \end{aligned}$$
(11)

Theorem 6

([12]) There exists a continuous function H(X),  which is defined on a compact set \( \varOmega ,\) and a positive constant \(\eta ^{*}\). The continuous function H(X) can be approximated by utilizing the FLS \({W^{\text {T}}\zeta \left( X\right) }\)

$$ {H\left( X\right) ={W^{\text {T}}\zeta \left( X\right) }+{\eta },\quad \vert \eta \vert \le \eta ^{*}}, ,$$
(12)

where \({W^{\text {T}}=[w_{1},w_{2},\ldots ,w_{n}]^{\text {T}}}\) and \(\eta \) represent the optimal weight vector and the approximation error, respectively. n denotes the number of the FLS nodes and \(\zeta \left( X\right) =[a_{1}\left( X\right) ,a_{2}\left( X\right) ,\ldots ,a_{n}\left( X\right) ]\) is the fuzzy basis function. The \(a_{i}\left( X\right) \), \(i=1,2,\ldots ,n,\) represent corresponding membership and can be expressed as follows

$$\begin{aligned} {{a_{i}}{\left( X\right) }}&=\exp {\left( \frac{{\left( X-\epsilon _{k}\right) ^{\text {T}}}{\left( X-\epsilon _{k}\right) }}{{\lambda _{k}}^{\text {T}}{\lambda _{k}}}\right) }, \end{aligned},$$
(13)

where \(\epsilon _{k}=[\epsilon _{k1},\epsilon _{k2},\ldots ,\epsilon _{kn}]^{\text {T}}\) and \(\lambda _{k}=[\lambda _{k1},\lambda _{k2},\ldots ,\lambda _{kn}],\) \(i=1,2,\ldots ,n,\) represent the center vector and the width of \(a_{k}\left( X\right) ,\) respectively.

Assumption 1

([15]) \({{y_{0}},{y_{1}},\ldots ,{y_{i}}}\) denote positive constants. The reference signal \({y_{\text {d}}}\) is bounded, which satisfies \({\vert {y_{\text {d}}}\vert \le {y_{0}}}\), and its ith-order derivatives \({y^{\left( i\right) }_{\text {d}}}\), \({i=1,2,\ldots ,n}\), are bounded, which satisfy \({\vert {y^{\left( i\right) }_{\text {d}}}\vert \le {y_{i}}}\).

By employing the mean value theorem in [26] to solve the problem of nonaffine appearance in the considered systems (1), the unknown smooth functions \({f_{i}{\left( {{\bar{x}}_{i},x_{i+1}}\right) }}\) can be rewritten as

$$\begin{aligned} {f_{i}{\left( {{\bar{x}}_{i},x_{i+1}}\right) }}&=f_{i}{\left( {\bar{x}}_{i},\imath _{i}\right) }+\frac{{\partial f_{i}{\left( {{\bar{x}}_{i},x_{\rho _{i}}}\right) }}}{{\partial x_{\rho _{i}}}}{\left( {x_{i+1}-\imath _{i}}\right) }, \end{aligned}$$
(14)
$$\begin{aligned} {f_{n}{\left( {{\bar{x}}_{n},u}\right) }}&=f_{n}{\left( {\bar{x}}_{n},\imath _{n}\right) }+\frac{{\partial f_{n}{\left( {{\bar{x}}_{n},x_{\rho _{n}}}\right) }}}{{\partial x_{\rho _{n}}}}{\left( {u-\imath _{n}}\right) }, \end{aligned},$$
(15)

where \({x_{\rho _{i}}}={\rho _{i}}{x_{i+1}}+{\left( 1-{\rho _{i}}\right) }{\imath _{i}}\) and \({0<{\rho _{i}}<1}\), \({i=1,2,\ldots ,n}\), and \({\imath _{i}}\) is a known quantity at the given time \({t_{0}}\).

Substituting (14) and (15) into the system (1),we have

$$ { \left\{ \begin{array}{l} {\text {d}}x_{1}={\left( f_{1}{\left( x_{1},\imath _{1}\right) }+{c_{1}}{\left( {x_{2}-\imath _{1}}\right) }+\hbar _{1}(t)\right) }{\text {d}}t \\ +\varUpsilon ^{\text {T}}_{1}({x}_{1}){\text {d}}\omega \\ \qquad \qquad \vdots \\ {\text {d}}x_{i}={\left( f_{i}{\left( {{\bar{x}}}_{i},\imath _{i}\right) }+{c_{i}}{\left( {x_{i+1}-\imath _{i}}\right) }+\hbar _{i}(t)\right) }{\text {d}}t \\ +\varUpsilon ^{\text {T}}_{i}({{{\bar{x}}}}_{i}){\text {d}}\omega \\ \qquad \qquad \vdots \\ {\text {d}}x_{n}={\left( f_{n}{\left( {{\bar{x}}}_{n},\imath _{n}\right) }+{c_{n}}{\left( {u-{\imath _{n}}}\right) }+\hbar _{n}(t)\right) }{\text {d}}t \\ +\varUpsilon ^{\text {T}}_{n}({{{\bar{x}}}}_{n}){\text {d}}\omega \\ y={{x}_{1}}, \end{array} \right. } ,$$
(16)

where \(c_{i}={\partial f_{i}{\left( {{\bar{x}}_{i},x_{\rho _{i}}}\right) }}/{\partial x_{\rho _{i}}}\), \({i=1,2,\ldots ,n}\).

Assumption 2

([26]) The functions \({c_{i}}\) are bounded, which satisfy \({0<b\le {c_{i}}<d<\infty }\), \({i=1,2,\ldots ,n}\), where b, d are known constants.

Assumption 3

([26]) The system external disturbances \({\hbar _{i}(t)}\), \({i=1,2,\ldots ,n}\) are bounded, which satisfy \({\vert \hbar _{i}(t)\vert \le {\bar{\hbar }}_{i}}\) and \({{\bar{\hbar }}_{i}}\) are unknown positive constants.

3 Fixed Time Adaptive DSC Controller Design

In this section, a fixed time adaptive DSC controller is designed for the system (16) to achieve the control objective by utilizing backstepping and DSC technique. Firstly, the coordinate transformation is introduced as follows

$$\begin{aligned} &{z_{1}}={x_{1}-{y_{\text {d}}}},\end{aligned}$$
(17)
$$\begin{aligned}&{z_{i}}={x_{i}-{\alpha _{i-1}},\quad i=2,3,\ldots ,n}, \end{aligned},$$
(18)

where \(y_{\text {d}}\) and \({\alpha _{i-1}}\) represent the desired signal and the virtual controllers, respectively.

Let the virtual controllers \({\alpha _{i-1}}\) as the input signals pass through a first-order filter to obtain new parameters \(\beta _{i}\), which represent the first-order filter output signals, then we have

$$ \mu _{i}{{\dot{\beta }}_{i}}+\beta _{i}=\alpha _{i-1},\quad i=2, 3, \ldots ,n, ,$$
(19)

where \(\beta _{i}(0)=\alpha _{i-1}(0)\) and \(\mu _{i}\) represent time constants of the first-order filter.

The obtained new parameters \(\beta _{i}\) is used to replace the virtual controllers \({\alpha _{i-1}}\) in the fixed time adaptive controller design process, then the repeated differentiation is replaced by the algebraic operation and (18) can be rewritten as follows

$$\begin{aligned} {z_{i}}&={x_{i}-{\beta _{i}},\quad i=2,3,\ldots ,n}. \end{aligned}$$
(20)

Define \(e_{i}\) as the error variables of the first-order filter and we can obtain

$$ e_{i}=\beta _{i}-\alpha _{i-1},\quad i=2,3,\ldots ,n. $$
(21)

Step 1: According to (16), (17), (20) and (21), we can have

$$ {{\text {d}}z_{1}}={\left( f_{1}(x_{1},\imath _{1})+{c_{1}}\Big ({{z_{2}+e_{2}+\alpha _{1}}-\imath _{1}}\right) }+\hbar _{1}(t)-{{\dot{y}}_{\text {d}}}\Big ){\text {d}}t+\varUpsilon ^{\text {T}}_{1}({x}_{1}){\text {d}}\omega . $$
(22)

Then, we design the Lyapunov functional candidates as follows

$$\begin{aligned} V_{1,1}&={\frac{1}{4}}{z_{1}^{4}}+{\frac{b}{2\upsilon _{1}}}{\tilde{\theta }}^{2}_{1},\end{aligned}$$
(23)
$$\begin{aligned} V_{1,2}&={\frac{1}{2}}{e^{2}_{2}},\end{aligned}$$
(24)
$$\begin{aligned} V_{1}&=V_{1,1}+V_{1,2}, \end{aligned},$$
(25)

where the Lyapunov functional candidate \(V_{1,1}\) and the Lyapunov functional candidate \(V_{1,2}\) are employed to solve the problem of tracking error \(z_{1}\) and the first-order filter error \(e_{1}\) are driven to a small neighborhood of the origin, respectively. \({\upsilon _{1}}\) is positive designed parameter, and \(\tilde{\theta }_{1}\) represents the estimation error of \({\theta _{1}}\) defined later and \({\tilde{\theta }_{1}={\theta _{1}}-{\hat{\theta }}_{1}}\), where \({\hat{\theta }}_{1}\) is the estimation of \({\theta _{1}}\).

Then, by applying the infinitesimal operator \({\ell }\), (22) and (23), we can obtain

$$\begin{aligned} {\ell V_{1,1}}=&{z^{3}_{1}}{\Big (f_{1}(x_{1},\imath _{1})+{c_{1}}{\alpha _{1}}+{c_{1}}{e_{2}}+{c_{1}}{z_{2}}-{c_{1}}{\imath _{1}}+\hbar _{1}(t)}-{{\dot{y}}_{\text {d}}}\Big ) \\&\quad +{\frac{3}{2}}z^{2}_{1}{\varUpsilon ^{2}_{1}({x}_{1})} -{\frac{b}{\upsilon _{1}}}{\tilde{\theta }}_{1}{\dot{\hat{\theta }}}_{1}. \end{aligned}$$
(26)

Using (2), we have

$$ {\frac{3}{2}}z^{2}_{1}{\varUpsilon ^{2}_{1}({x}_{1})}\le {\frac{9}{8}}z^{4}_{1}{\varUpsilon ^{4}_{1}({x}_{1})}+{\frac{1}{2}}. $$
(27)

Substitute (27) into (26), we can have

$$\begin{aligned} {\ell V_{1,1}}\le&{z^{3}_{1}}\Big (-k_{1,2}z^{4q-3}_{1}+{H_{1}(X_{1})} \\&+{c_{1}}{\alpha _{1}}+{c_{1}}{e_{2}}+{c_{1}}{z_{2}}-{{\dot{y}}_{\text {d}}}+\hbar _{1}(t)\Big ) \\&+{\frac{1}{2}}-(1+d)z^{6}_{1}-{\frac{b}{\upsilon _{1}}}{\tilde{\theta }}_{1}{\dot{\hat{\theta }}}_{1}, \end{aligned},$$
(28)

where \({H_{1}(X_{1})}=k_{1,2}z^{4q-3}_{1}+f_{1}(x_{1},\imath _{1})+{\frac{9}{8}}z_{1}{\varUpsilon ^{4}_{1}({x}_{1})}-{c_{1}}{\imath _{1}}+(1+d)z^{3}_{1}\).

According to the (6), the unknown function \({H_{1}(X_{1})}\) can be approximated using FLS, then we can obtain

$$ {H_{1}(X_{1})}=W^{\text {T}}_{1}{\zeta _{1}}{\left( X_{1}\right) }+{\eta _{1}},\quad {\vert \eta _{1}\vert \le \eta ^{*}_{1}}, $$
(29)

where \({X_{1}=[x_{1},y_{\text {d}},{\dot{y}}_{\text {d}}]^{\text {T}}}\).

Using (2), we obtain

$$\begin{aligned} {z^{3}_{1}}{H_{1}(X_{1})}=&{z^{3}_{1}}{\left( W^{\text {T}}_{1}{\zeta _{1}}{\left( X_{1}\right) }+{\eta _{1}}\right) } \\ \le&{\frac{{z^{6}_{1}}{b}}{2{a^{2}_{1}}}}{\theta _{1}}{\zeta ^{\text {T}}_{1}}{\left( X_{1}\right) }{\zeta _{1}}{\left( X_{1}\right) }+{\frac{a^{2}_{1}}{2b}}+{\frac{1}{2}z^{6}_{1}}+{\frac{{\eta ^{*}_{1}}^{2}}{2}}, \end{aligned}$$
(30)

where \({\Vert {W_{1}}\Vert }^{2}={\theta _{1}}\) and \(a_{1}\) is positive designed parameter.

Then, the fixed time virtual controller \(\alpha _{1}\) and the adaptive law \({\dot{\hat{\theta }}}_{1}\) are designed as follows:

$$\begin{aligned}&{\alpha _{1}}={-k_{1,1}}z^{4p-3}_{1}-{\frac{{z^{3}_{1}}}{2{a^{2}_{1}}}}{\hat{\theta }}_{1}{\zeta ^{\text {T}}_{1}(X_{1})}{\zeta _{1}(X_{1})}+{\frac{{{\dot{y}}_{\text {d}}}}{c_{1}}},\end{aligned}$$
(31)
$$\begin{aligned}&{\dot{\hat{\theta }}}_{1}={\frac{{\upsilon _{1}}z^{6}_{1}}{2{a^{2}_{1}}}}{\zeta ^{\text {T}}_{1}(X_{1})}{\zeta _{1}(X_{1})}-\lambda _{1}{\hat{\theta }}_{1}-\tau _{1}{\hat{\theta }^{2p-1}}_{1} , \end{aligned}$$
(32)

where \(k_{1,1},{\lambda _{1}}\) and \({\tau _{1}}\) are positive designed parameters.

Using (2), we can have

$$ {c_{1}}{z^{3}_{1}}{z_{2}}\le {\frac{d}{2}}{z^{6}_{1}}+{\frac{d}{2}}{z^{2}_{2}},$$
(33)
$$ {c_{1}}{z^{3}_{1}}{e_{2}}\le {\frac{d}{2}}{z^{6}_{1}}+{\frac{d}{2}}{e^{2}_{2}},$$
(34)
$$ {\hbar _{1}(t)}{z^{3}_{1}}\le {\frac{{\bar{\hbar }}^{2}_{1}}{2}}+{\frac{z^{6}_{1}}{2}}. $$
(35)

By substituting (30)–(35) into (28), we have

$$\begin{aligned} {\ell V_{1,1}}&\le {-k_{1,1}}{b}{z^{4p}_{1}}-{k_{1,2}}{z^{4q}_{1}}+{\frac{d}{2}}{z^{2}_{2}}+{\frac{d}{2}}{e^{2}_{2}}+{A_{1}} \\&\quad +{\frac{b\lambda _{1}{\tilde{\theta }}_{1}{\hat{\theta }}_{1}}{\upsilon _{1}}}+{\frac{b\tau _{1}{\tilde{\theta }}_{1}{\hat{\theta }}^{2p-1}_{1}}{\upsilon _{1}}}, \end{aligned},$$
(36)

where \({A_{1}}={\frac{{\bar{\hbar }}^{2}_{1}}{2}}+{\frac{a^{2}_{1}}{2b}}+{\frac{{\eta ^{*}_{1}}^{2}}{2}}+{\frac{1}{2}}\). Combining (19) with (21), we can obtain

$$ {\dot{e}}_{2}=-{\frac{{e_{2}}}{\mu _{2}}}-{{\ell {\alpha }}_{1}}{\text {d}}t. $$
(37)

According to (16), (31) and the infinitesimal operator \(\ell \), we can obtain

$$ {\ell {\alpha _{1}}}={\phi _{2}\left( {{\bar{y}}^{(2)}_{\text {d}}},{\bar{z}}_{2},{e_{2}},{\hat{\theta }}_{1}\right) }, ,$$
(38)

where \({\phi _{2}({{\bar{y}}^{(2)}_{\text {d}}},{\bar{z}}_{2},{e_{2}},{\hat{\theta }}_{1})}={\frac{\partial {\alpha _{1}}}{\partial {x_{1}}}}{(f_{1}{\left( {\bar{x}}_{1},\imath _{1}\right) }+{c_{1}}{\left( {x}_{2}-\imath _{1}\right) }}+\hbar _{1}(t))+{\sum _{j=0}^{1}{\frac{{\partial {\alpha _{1}}}}{\partial {{y_{\text {d}}}^{(j)}}}}}\) \({{{y_{\text {d}}}^{(j+1)}}}+{\frac{1}{2}}{\frac{{\partial ^{2}{\alpha _{1}}}}{{\partial {x_{1}}}\partial {x_{1}}}}{\varUpsilon ^{\text {T}}_{1}(x_{1})}{\varUpsilon _{1}(x_{1})}+{\frac{\partial {\alpha _{1}}}{\partial {\hat{\theta }}_{1}}}{\dot{\hat{\theta }}}_{1}\) is a continuous function and satisfies \(\vert {\phi _{2}({{\bar{y}}^{(2)}_{\text {d}}},{\bar{z}}_{2},{e_{2}},{\hat{\theta }}_{1})}\vert \le \varphi _{2}\), where \(\varphi _{2}\) is a positive constants, \({{\bar{y}}^{(2)}_{\text {d}}}=[{y_{\text {d}}},{\dot{y}}_{\text {d}},{\ddot{y}}_{\text {d}}]\) and \({\bar{z}}_{2}=[z_{1},z_{2}]\)

By applying (2), (24), (37) and (38), we can obtain

$$ {\dot{V}}_{1,2}\le -{\frac{e^{2}_{2}}{\mu _{2}}}+e^{2}_{2}+{\frac{1}{4}}{\varphi ^{2}_{2}}. $$
(39)

By substituting (36) and (39) into (25), we can obtain

$$\begin{aligned} {\ell V_{1}}&\le {-k_{1,1}}{b}{z^{4p}_{1}}-{k_{1,2}}{z^{4q}_{1}}+{\frac{d}{2}}{z^{2}_{2}}-{\kappa _{2}}{e^{2}_{2}}+{A_{1}} \\&\quad +{B_{2}}+{\frac{b\lambda _{1}{\tilde{\theta }}_{1}{\hat{\theta }}_{1}}{\upsilon _{1}}} \\&\quad +{\frac{b\tau _{1}{\tilde{\theta }}_{1}{\hat{\theta }}^{2p-1}_{1}}{\upsilon _{1}}}, \end{aligned},$$
(40)

where \({\kappa _{2}=\left( {\frac{1}{\mu _{2}}}-{\frac{d}{2}}-1\right) }\) and \(B_{2}={\frac{1}{4}}{\varphi ^{2}_{2}}\).

Step \(i, (i=2,3,\ldots ,n-1)\):

According to (16), (20) and (21), we can have

$$\begin{aligned}{{\text {d}}z_{i}}&={\left( f_{i}(x_{i},\imath _{i})+{c_{i}}\Big ({{z_{i+1}+e_{i+1}+\alpha _{i}}-\imath _{i}}\right) } +\hbar _{i}(t)-{{\dot{\beta }}_{i}}\Big ){\text {d}}t \\&\quad +\varUpsilon ^{\text {T}}_{i}({{{\bar{x}}}}_{i}){\text {d}}\omega . \end{aligned}$$
(41)

Then, we design the Lyapunov functional candidates as follows

$$\begin{aligned} V_{i,1}&={\frac{1}{4}}{z_{i}^{4}}+{\frac{b}{2\upsilon _{i}}}{\tilde{\theta }}^{2}_{i}, \end{aligned}$$
(42)
$$\begin{aligned} V_{i,2}&={\frac{1}{2}}{e^{2}_{i+1}}, \end{aligned}$$
(43)
$$\begin{aligned} V_{i}&=V_{i-1}+V_{i,1}+V_{i,2}, \end{aligned},$$
(44)

where the Lyapunov functional candidates \(V_{i,1}\) and the Lyapunov functional candidates \(V_{i,2}\) are employed to solve the problem of ith-order derivatives \(z_{i}\) of tracking error \(z_{1}\) and the first-order filter errors \(e_{i}\) are driven to a small neighborhood of the origin, respectively. \({\upsilon _{i}}\) is positive designed parameter, and \(\tilde{\theta }_{i}\) represents the estimation error of \({\theta _{i}}\) defined later and \({\tilde{\theta }_{i}={\theta _{i}}-{\hat{\theta }}_{i}}\), where \({\hat{\theta }}_{i}\) is the estimation of \({\theta _{i}}\).

Then, by applying the infinitesimal operator \({\ell }\), (41) and (42), we can obtain

$$\begin{aligned} {\ell V_{i,1}}=&{z^{3}_{i}}{\Big (f_{i}(x_{i},\imath _{i})+{c_{i}}{\alpha _{i}}+{c_{i}}{e_{i+1}}+{c_{i}}{z_{i+1}}-{c_{i}}{\imath _{i}}}+\hbar _{i}(t)-{{\dot{\beta }}_{i}}\Big ) \\&\quad +{\frac{3}{2}}z^{2}_{i}{\varUpsilon ^{2}_{i}({{{\bar{x}}}}_{i})} -{\frac{b}{\upsilon _{i}}}{\tilde{\theta }}_{i}{\dot{\hat{\theta }}}_{i}. \end{aligned}$$
(45)

Using (2), we have

$$ {\frac{3}{2}}z^{2}_{i}{\varUpsilon ^{2}_{i}({{{\bar{x}}}}_{i})}\le {\frac{9}{8}}z^{4}_{i}{\varUpsilon ^{4}_{i}({{{\bar{x}}}}_{i})}+{\frac{1}{2}}. $$
(46)

Substitute (46) into (45), we can have

$$\begin{aligned} {\ell V_{i,1}}&\le {z^{3}_{i}}{\Big (-k_{i,2}z^{4q-3}_{i}+{H_{i}(X_{i})}+{c_{i}}{\alpha _{i}}+{c_{i}}{e_{i+1}}+{c_{i}}{z_{i+1}}} \\&\quad -{{\dot{\beta }}_{i}}+\hbar _{i}(t)\Big ) \\&\quad +{\frac{1}{2}}-(1+d)z^{6}_{i}-{\frac{d}{2}z^{2}_{i}}-{\frac{b}{\upsilon _{i}}}{\tilde{\theta }}_{i}{\dot{\hat{\theta }}}_{i} , \end{aligned},$$
(47)

where \({H_{i}(X_{i})}=k_{i,2}z^{4q-3}_{i}+f_{i}(x_{i},\imath _{i})+{\frac{9}{8}}z_{i}{\varUpsilon ^{4}_{i}({{\bar{x}}}_{i})}-{c_{i}}{\imath _{i}}+(1+d)z^{3}_{i}+{\frac{d}{2z_{i}}}\).

According to the (6), the unknown function \({H_{i}(X_{i})}\) can be approximated using FLS, then we can obtain

$$ {H_{i}(X_{i})}=W^{\text {T}}_{i}{\zeta _{i}}{\left( X_{i}\right) }+{\eta _{i}},\quad {\vert \eta _{i}\vert \le \eta ^{*}_{i}}, ,$$
(48)

where \({X_{i}=[{{\bar{x}}}_{i},{\bar{\hat{\theta }}}_{i-1},{\bar{y}}^{(i)}_{\text {d}}]^{\text {T}}}\) with \({\bar{\hat{\theta }}}_{i-1}=[{\hat{\theta }}_{1}, \ldots , {\hat{\theta }}_{i-1}]\) and \({\bar{y}}^{(i)}_{\text {d}}=[y_{\text {d}},\ldots ,y^{(i)}_{\text {d}}]\).

Using (2), we can obtain

$$\begin{aligned} {z^{3}_{i}}{H_{i}(X_{i})}=&{z^{3}_{i}}{\left( W^{\text {T}}_{i}{\zeta _{i}}{\left( X_{i}\right) }+{\eta _{i}}\right) } \\ \le&{\frac{{z^{6}_{i}}{b}}{2{a^{2}_{i}}}}{\theta _{i}}{\zeta ^{\text {T}}_{i}}{\left( X_{i}\right) }{\zeta _{i}}{\left( X_{i}\right) }+{\frac{a^{2}_{i}}{2b}}+{\frac{1}{2}z^{6}_{i}}+{\frac{{\eta ^{*}_{i}}^{2}}{2}}, \end{aligned},$$
(49)

where \({\Vert {W_{i}}\Vert }^{2}={\theta _{i}}\) and \(a_{i}\) is positive designed parameter.

Then, the fixed time virtual controller \(\alpha _{i}\) and the adaptive law \({\dot{\hat{\theta }}}_{i}\) are designed as follows:

$$\begin{aligned}&{\alpha _{i}}={-k_{i,1}}z^{4p-3}_{i}-{\frac{{z^{3}_{i}}}{2{a^{2}_{i}}}}{\hat{\theta }}_{i}{\zeta ^{\text {T}}_{i}(X_{i})}{\zeta _{i}(X_{i})}+{\frac{{{\dot{\beta }}_{i}}}{c_{i}}},\end{aligned}$$
(50)
$$\begin{aligned}&{\dot{\hat{\theta }}}_{i}={\frac{{\upsilon _{i}}z^{6}_{i}}{2{a^{2}_{i}}}}{\zeta ^{\text {T}}_{i}(X_{i})}{\zeta _{i}(X_{i})}-\lambda _{i}{\hat{\theta }}_{i}-\tau _{i}{\hat{\theta }^{2p-1}}_{i} , \end{aligned},$$
(51)

where \(k_{i,1},{\lambda _{i}}\) and \({\tau _{i}}\) are positive designed parameters.

Using (2), we can have

$$\begin{aligned} {c_{i}}{z^{3}_{i}}{z_{i+1}}&\le {\frac{d}{2}}{z^{6}_{i}}+{\frac{d}{2}}{z^{2}_{i+1}},\end{aligned}$$
(52)
$$\begin{aligned} {c_{i}}{z^{3}_{i}}{e_{i+1}}&\le {\frac{d}{2}}{z^{6}_{i}}+{\frac{d}{2}}{e^{2}_{i+1}},\end{aligned}$$
(53)
$$\begin{aligned} {\hbar _{i}(t)}{z^{3}_{i}}&\le {\frac{{\bar{\hbar }}^{2}_{i}}{2}}+{\frac{z^{6}_{i}}{2}}. \end{aligned}$$
(54)

By substituting (49)–(54) into (47), we have

$$\begin{aligned} {\ell V_{i,1}}&\le {-k_{i,1}}{b}{z^{4p}_{i}}-{k_{i,2}}{z^{4q}_{i}}+{\frac{d}{2}}{z^{2}_{i+1}}+{\frac{d}{2}}{e^{2}_{i+1}}+{A_{i}} \\&\quad +{\frac{b\lambda _{i}{\tilde{\theta }}_{i}{\hat{\theta }}_{i}}{\upsilon _{i}}} +{\frac{b\tau _{i}{\tilde{\theta }}_{i}{\hat{\theta }}^{2p-1}_{i}}{\upsilon _{i}}} \\&\quad -{\frac{d}{2}z^{2}_{i}}, \end{aligned},$$
(55)

where \({A_{i}}={\frac{{\bar{\hbar }}^{2}_{i}}{2}}+{\frac{a^{2}_{i}}{2b}}+{\frac{{\eta ^{*}_{i}}^{2}}{2}}+{\frac{1}{2}}\).

Combining (19) with (21), we can obtain

$$ {\dot{e}}_{i+1}=-{\frac{{e_{i+1}}}{\mu _{i+1}}}-{\dot{\alpha }}_{i}. $$
(56)

According to (16), (50) and the infinitesimal operator \(\ell \), we can obtain

$$ {\ell {\alpha _{i}}}={\phi _{i+1}\left( {\bar{z}}_{i},{{\bar{y}}^{(i+1)}_{\text {d}}},{\bar{e}}_{i+1},{\bar{\hat{\theta }}}_{i}\right) }, $$
(57)

where

$$\begin{aligned}{} & {} {\phi _{i+1}\left( {\bar{z}}_{i},{{\bar{y}}^{(i+1)}_{\text {d}}},{\bar{e}}_{i+1},{\bar{\hat{\theta }}}_{i}\right) }\\{} & {} \quad =\sum _{j=1}^{i}{\frac{\partial {\alpha _{i}}}{\partial {x_{j}}}}{(f_{j}{\left( {\bar{x}}_{j},\imath _{j}\right) }+{c_{j}}}{{({x}_{j+1}-\imath _{j})}}\\{} & {} \qquad +\hbar _{j}(t))+\sum _{j=1}^{i}{\frac{\partial {\alpha _{i}}}{\partial {\hat{\theta }}_{j}}}{\dot{\hat{\theta }}}_{j}\\{} & {} \qquad +{\frac{1}{2}}\sum _{j,k=1}^{i}{\frac{{\partial ^{2}{\alpha _{i}}}}{{\partial {x_{j}}}\partial {x_{k}}}}{\varUpsilon ^{\text {T}}_{j}({{\bar{x}}}_{j})}{\varUpsilon _{k}({{\bar{x}}}_{k})}+{\sum _{j=0}^{i}{\frac{{\partial {\alpha _{i-1}}}}{\partial {{y_{\text {d}}}^{(j)}}}}{{y_{\text {d}}}^{(j+1)}}} \end{aligned}$$

is a continuous function and satisfies \(\vert {\phi _{i+1}({\bar{z}}_{i},{{\bar{y}}^{(i+1)}_{\text {d}}},{\bar{e}}_{i+1},{\bar{\hat{\theta }}}_{i})}\vert \le \varphi _{i+1}\), where \(\varphi _{i+1}\) is a positive constants, and \({\bar{z}}_{i}=[z_{1},z_{2},\ldots ,z_{i}]\), \({\bar{y}}^{(i+1)}_{\text {d}}=[{y_{\text {d}}},{\dot{y}}_{\text {d}},\ldots ,{{y}^{(i+1)}_{\text {d}}}]\), \({\bar{e}}_{i+1}=[e_{2},e_3,\ldots ,e_{i+1}]\). By applying (2), (42), (56) and (57), we can obtain

$$ {\dot{V}}_{i,2}\le -{\frac{e^{2}_{i+1}}{\mu _{i+1}}}+e^{2}_{i+1}+{\frac{1}{4}}{\varphi ^{2}_{i+1}}. $$
(58)

By substituting (55) and (58) into (44), we can obtain

$$\begin{aligned} {\ell V_{i}}&\le -\sum _{j=1}^{i}{k_{j,1}}{b}{z^{4p}_{j}}-\sum _{j=1}^{i}{k_{j,2}}{z^{4q}_{j}} \\&\quad +\sum _{j=1}^{i}{\frac{b\lambda _{j}{\tilde{\theta }}_{j}{\hat{\theta }}_{j}}{\upsilon _{j}}}+\sum _{j=1}^{i}{\frac{b\tau _{j}{\tilde{\theta }}_{j}{\hat{\theta }}^{2p-1}_{j}}{\upsilon _{j}}} \\&\quad +\sum _{j=1}^{i}{A_{j}} +\sum _{j=2}^{i+1}{B_{j}}+{\frac{d}{2}}{z^{2}_{i+1}}-\sum _{j=2}^{i+1}{\kappa _{j}}{e^{2}_{j}}, \end{aligned},$$
(59)

where \({\kappa _{j}=\left( {\frac{1}{\mu _{j}}}-{\frac{d}{2}}-1\right) }\) and \(B_{j}={\frac{1}{4}}{\varphi ^{2}_{j}}\).

Step n:

According to (16) and (20), we can have

$$ {{\text {d}}z_{n}}={\left( f_{n}(x_{n},\imath _{n})+{c_{n}}{\left( {u-\imath _{n}}\right) } +\hbar _{n}(t)-{{\dot{\beta }}_{n}}\right) }{\text {d}}t+\varUpsilon ^{\text {T}}_{n}({{{\bar{x}}}}_{n}){\text {d}}\omega . $$
(60)

In this step, the virtual controller is replaced by the actual controller u. Thus, the first-order filter will be ignored and there no exist the dynamic surface error. Then, we design the Lyapunov functional candidates as follows

$$\begin{aligned} V_{n,1}&={\frac{1}{4}}{z_{n}^{4}}+{\frac{b}{2\upsilon _{n}}}{\tilde{\theta }}^{2}_{n},\end{aligned}$$
(61)
$$\begin{aligned} V_{n}&=V_{n-1}+V_{n,1}, \end{aligned},$$
(62)

where \({\upsilon _{n}}\) is positive designed parameter. \(\tilde{\theta }_{n}\) represents the estimation error of \({\theta _{n}}\) defined later and \({\tilde{\theta }_{n}={\theta _{n}}-{\hat{\theta }}_{n}}\), where \({\hat{\theta }}_{n}\) is the estimation of \({\theta _{n}}\).

Then, by applying the infinitesimal operator \({\ell }\), (60) and (61), we can obtain

$$\begin{aligned} {\ell V_{n,1}}&={z^{3}_{n}}{\Big (f_{n}(x_{n},\imath _{n})+{c_{n}}{u}-{c_{i}}{\imath _{n}}+\hbar _{n}(t)}-{{\dot{\beta }}_{n}}\Big ) \\&\quad +{\frac{3}{2}}z^{2}_{n}{\varUpsilon ^{2}_{n}({{{\bar{x}}}}_{n})}-{\frac{b}{\upsilon _{n}}}{\tilde{\theta }}_{n}{\dot{\hat{\theta }}}_{n}. \end{aligned}$$
(63)

Using (2), we have

$$ {\frac{3}{2}}z^{2}_{n}{\varUpsilon ^{2}_{n}({{{\bar{x}}}}_{n})}\le {\frac{9}{8}}z^{4}_{n}{\varUpsilon ^{4}_{n}({{{\bar{x}}}}_{n})}+{\frac{1}{2}}. $$
(64)

Substitute (64) into (63), we can have

$$\begin{aligned} {\ell V_{n,1}}\le&{z^{3}_{n}}{\Big (-k_{n,2}z^{4q-3}_{n}+{H_{n}(X_{n})}+{c_{n}}{u}}-{{\dot{\beta }}_{n}}+\hbar _{n}(t)\Big )-(1+d)z^{6}_{n} \\&\quad -{\frac{d}{2}z^{2}_{n}}-{\frac{b}{\upsilon _{n}}}{\tilde{\theta }}_{n}{\dot{\hat{\theta }}}_{n}+{\frac{1}{2}}, \end{aligned},$$
(65)

where \({H_{n}(X_{n})}=k_{n,2}z^{4q-3}_{n}+f_{n}(x_{n},\imath _{n})+{\frac{9}{8}}z_{n}{\varUpsilon ^{4}_{n}({{\bar{x}}}_{n})}-{c_{n}}{\imath _{n}}+(1+d)z^{3}_{n}+{\frac{d}{2z_{n}}}\).

According to the (6), the unknown function \({H_{n}(X_{n})}\) can be approximated using FLS, then we can obtain

$$ {H_{n}(X_{n})}=W^{\text {T}}_{n}{\zeta _{n}}{\left( X_{n}\right) }+{\eta _{n}},\quad {\vert \eta _{n}\vert \le \eta ^{*}_{n}}, ,$$
(66)

where \({X_{n}=[{{\bar{x}}}_{n},{\bar{\hat{\theta }}}_{n-1},{\bar{y}}^{(n)}_{\text {d}}]^{\text {T}}}\) with \({\bar{\hat{\theta }}}_{n-1}=[{\hat{\theta }}_{1}, \ldots , {\hat{\theta }}_{n-1}]\) and \({\bar{y}}^{(n)}_{\text {d}}=[y_{\text {d}},\ldots ,y^{(n)}_{\text {d}}]\). Using (2), we obtain

$$\begin{aligned} {z^{3}_{n}}{H_{n}(X_{n})}=&{z^{3}_{n}}{\left( W^{\text {T}}_{n}{\zeta _{n}}{\left( X_{n}\right) }+{\eta _{n}}\right) } \\ \le&{\frac{{z^{6}_{n}}{b}}{2{a^{2}_{n}}}}{\theta _{n}}{\zeta ^{\text {T}}_{n}}{\left( X_{n}\right) }{\zeta _{n}}{\left( X_{n}\right) }+{\frac{a^{2}_{n}}{2b}}+{\frac{1}{2}z^{6}_{n}}+{\frac{{\eta ^{*}_{n}}^{2}}{2}}, \end{aligned},$$
(67)

where \({\Vert {W_{n}}\Vert }^{2}={\theta _{n}}\) and \(a_{n}\) is positive designed parameter.

Then, the fixed time actual controller u and the adaptive law \({\dot{\hat{\theta }}}_{n}\) are designed as follows:

$$\begin{aligned}&{u}={-k_{n,1}}z^{4p-3}_{n}-{\frac{{z^{3}_{n}}}{2{a^{2}_{n}}}}{\hat{\theta }}_{n}{\zeta ^{\text {T}}_{n}(X_{n})}{\zeta _{n}(X_{n})}+{\frac{{{\dot{\beta }}_{n}}}{c_{n}}},\end{aligned}$$
(68)
$$\begin{aligned}&{\dot{\hat{\theta }}}_{n}={\frac{{\upsilon _{n}}z^{6}_{n}}{2{a^{2}_{n}}}}{\zeta ^{\text {T}}_{n}(X_{n})}{\zeta _{n}(X_{n})}-\lambda _{n}{\hat{\theta }}_{n}-\tau _{n}{\hat{\theta }^{2p-1}}_{n} , \end{aligned},$$
(69)

where \(k_{n,1},{\lambda _{n}}\) and \({\tau _{n}}\) are positive designed parameters.

Using (2), we can have

$$\begin{aligned} {\hbar _{n}(t)}{z^{3}_{n}}&\le {\frac{{\bar{\hbar }}^{2}_{n}}{2}}+{\frac{z^{6}_{n}}{2}}. \end{aligned}$$
(70)

By substituting (67)–(70) into (65), we have

$$\begin{aligned} {\ell V_{n,1}}\le&{-k_{n,1}}{b}{z^{4p}_{n}}-{k_{n,2}}{z^{4q}_{n}}+{A_{n}}-{\frac{d}{2}z^{2}_{n}}+{\frac{b\lambda _{n}{\tilde{\theta }}_{n}{\hat{\theta }}_{n}}{\upsilon _{n}}}+{\frac{b\tau _{n}{\tilde{\theta }}_{n}{\hat{\theta }}^{2p-1}_{n}}{\upsilon _{n}}}, \end{aligned},$$
(71)

where \({A_{n}}={\frac{{\bar{\hbar }}^{2}_{n}}{2}}+{\frac{a^{2}_{n}}{2b}}+{\frac{{\eta ^{*}_{n}}^{2}}{2}}+{\frac{1}{2}}\). By substituting (71) into (62), we can obtain

$$\begin{aligned} {\ell V_{n}}&\le -\sum _{j=1}^{n}{k_{j,1}}{b}{z^{4p}_{j}}-\sum _{j=1}^{n}{k_{j,2}}{z^{4q}_{j}}+\sum _{j=1}^{n}{\frac{b\lambda _{j}{\tilde{\theta }}_{j}{\hat{\theta }}_{j}}{\upsilon _{j}}} \\&\quad +\sum _{j=1}^{n}{\frac{b\tau _{j}{\tilde{\theta }}_{j}{\hat{\theta }}^{2p-1}_{j}}{\upsilon _{j}}}+\sum _{j=1}^{n}{A_{j}}+\sum _{j=2}^{n}{B_{j}}-\sum _{j=2}^{n}{\kappa _{j}}{e^{2}_{j}}, \end{aligned},$$
(72)

where \({\kappa _{j}=\left( {\frac{1}{\mu _{j}}}-{\frac{d}{2}}-1\right) }\) and \(B_{j}={\frac{1}{4}}{\varphi ^{2}_{j}}\).

4 Stability Analysis

The following theorem is presented to show the main results of the proposed control strategy.

Theorem 7

For the stochastic pure feedback nonlinear systems with external disturbances (16), under (1)–(3), the virtual controller (31), (50), the actual controller (68), and the adaptive law (32), (51) and (69) can ensure that all states in the considered systems are SGUUB and the tracking errors are driven into a small neighborhood of the origin in a fixed time.

Proof

Using (3), (72) can be rewritten as follow

$$\begin{aligned} {\ell V_{n}}\le&-s\sum _{j=1}^{n}\left( {\frac{1}{4}}z^{4}_{1}\right) ^{p}-v\sum _{j=1}^{n}\left( {\frac{1}{4}}z^{4}_{1}\right) ^{q}-\sum _{j=2}^{n}{\frac{1}{2}}{\kappa _{j}}{e^{2}_{j}} \\&\quad -\sum _{j=2}^{n}{\frac{1}{2}}{\kappa _{j}}{e^{2}_{j}}-\left( \sum _{j=2}^{n}{\frac{1}{2}}{\kappa _{j}}{e^{2}_{j}}\right) ^{p} \\&\quad -\left( \sum _{j=2}^{n}{\frac{1}{2}}{\kappa _{j}}{e^{2}_{j}}\right) ^{q}+\left( \sum _{j=2}^{n}{\frac{1}{2}}{\kappa _{j}}{e^{2}_{j}}\right) ^{p}+\left( \sum _{j=2}^{n}{\frac{1}{2}}{\kappa _{j}}{e^{2}_{j}}\right) ^{q} \\&\quad +\sum _{j=1}^{n}{\frac{b\lambda _{j}{\tilde{\theta }}_{j}{\hat{\theta }}_{j}}{\upsilon _{j}}} \\&\quad +\sum _{j=1}^{n}{\frac{b\tau _{j}{\tilde{\theta }}_{j}{\hat{\theta }}^{2p-1}_{j}}{\upsilon _{j}}}+\rho , \end{aligned},$$
(73)

where \(s=\min \{bk_{j,1}n^{1-p}4^{p}: 1\le j\le n\}\), \(v=\min \{k_{j,2}4^{q}: 1\le j\le n\}\) and \(\rho =\sum _{j=1}^{n}{A_{j}}+\sum _{j=2}^{n}{B_{j}}\).

By utilizing (2), we can obtain

$$ \left( \sum _{j=2}^{n}{\frac{1}{2}}{\kappa _{j}}{e^{2}_{j}}\right) ^{q}\le \sum _{j=2}^{n}{\frac{1}{2}}{\kappa _{j}}{e^{2}_{j}}+(1-q)q^{\frac{q}{1-q}}. $$
(74)

Assume that \(e_{j}\le \sigma _{j}\), where \(\sigma _{j}\) are unknown constants. Then, we can get

$$ { \left\{ \begin{array}{l} \left( \sum _{j=2}^{n}{\frac{1}{2}}{\kappa _{j}}{e^{2}_{j}}\right) ^{p}-\sum _{j=2}^{n}{\frac{1}{2}}{\kappa _{j}}{e^{2}_{j}}<0\quad \text {if } \sigma _{j}<\sqrt{\frac{2}{\kappa _{j}}},\\ \left( \sum _{j=2}^{n}{\frac{1}{2}}{\kappa _{j}}{e^{2}_{j}}\right) ^{p}-\sum _{j=2}^{n}{\frac{1}{2}}{\kappa _{j}}{e^{2}_{j}}\le \phi \quad \text {if } \sigma _{j}\ge \sqrt{\frac{2}{\kappa _{j}}}, \end{array} \right. } ,$$
(75)

where \(\phi =\left( \sum _{j=2}^{n}{\frac{1}{2}}{\kappa _{j}}{{\sigma }^{2}_{j}}\right) ^{p}-\sum _{j=2}^{n}{\frac{1}{2}}{\kappa _{j}}{{\sigma }^{2}_{j}}\).

substituting (74) and (75) into (73) gives

$$\begin{aligned} {\ell V_{n}}\le&-s\sum _{j=1}^{n}\left( {\frac{1}{4}}z^{4}_{1}\right) ^{p}-v\sum _{j=1}^{n}\left( {\frac{1}{4}}z^{4}_{1}\right) ^{q}-\left( \sum _{j=2}^{n}{\frac{1}{2}}{\kappa _{j}}{e^{2}_{j}}\right) ^{p} \\&\quad -\left( \sum _{j=2}^{n}{\frac{1}{2}}{\kappa _{j}}{e^{2}_{j}}\right) ^{q} \\&\quad +\sum _{j=1}^{n}{\frac{b\lambda _{j}{\tilde{\theta }}_{j}{\hat{\theta }}_{j}}{\upsilon _{j}}}+\sum _{j=1}^{n}{\frac{b\tau _{j}{\tilde{\theta }}_{j}{\hat{\theta }}^{2p-1}_{j}}{\upsilon _{j}}}+\varPhi , \end{aligned},$$
(76)

where

$$ \varPhi = \left\{ \begin{array}{rl} \rho +(1-q)q^{\frac{q}{1-q}} &{} \text {if } \sigma _{j}<\sqrt{\frac{2}{\kappa _{j}}},\\ \rho +\phi +(1-q)q^{\frac{q}{1-q}} &{} \text {if } \sigma _{j}\ge \sqrt{\frac{2}{\kappa _{j}}}. \end{array} \right. $$

Using (2) and (4), we can get

$$\begin{aligned} {\tilde{\theta }_{j}}{{\hat{\theta }}_{j}}&\le {\frac{\theta ^{2}_{j}}{2}}-{\frac{\tilde{\theta }^{2}_{j}}{2}},\end{aligned}$$
(77)
$$\begin{aligned} {\tilde{\theta }_{j}}{{\hat{\theta }}^{2p-1}_{j}}&\le {\frac{2p-1}{2p}}\Big (\theta ^{2p}_{j}-\tilde{\theta }^{2p}_{j}\Big ). \end{aligned}$$
(78)

By substituting (77)–(78) into (76), we can obtain

$$\begin{aligned} {\ell V_{n}}\le&-s\sum _{j=1}^{n}\left( {\frac{1}{4}}z^{4}_{1}\right) ^{p}-v\sum _{j=1}^{n}\left( {\frac{1}{4}}z^{4}_{1}\right) ^{q}-\left( \sum _{j=2}^{n}{\frac{1}{2}}{\kappa _{j}}{e^{2}_{j}}\right) ^{p} \\&\quad -\left( \sum _{j=2}^{n}{\frac{1}{2}}{\kappa _{j}}{e^{2}_{j}}\right) ^{q} \\&\quad -\sum _{j=1}^{n}{\frac{b\lambda _{j}{\tilde{\theta }}^{2}_{j}}{2\upsilon _{j}}}-\sum _{j=1}^{n}{\frac{(2p-1)b\tau _{j}{\tilde{\theta }}^{2p}_{j}}{2p\upsilon _{j}}}+\varrho , \end{aligned},$$
(79)

where \(\varrho =\varPhi +\sum _{j=1}^{n}{\frac{b\lambda _{j}{\theta }^{2}_{j}}{2\upsilon _{j}}}+\sum _{j=1}^{n}{\frac{(2p-1)b\tau _{j}{{\theta }}^{2p}_{j}}{2p\upsilon _{j}}}\).

By utilizing (3), (58) can be rewritten as follows

$$\begin{aligned} {\ell V_{n}}\le&-h\left( \sum _{j=1}^{n}{\frac{1}{4}}z^{4}_{1}\right) ^{p}-o\left( \sum _{j=1}^{n}{\frac{1}{4}}z^{4}_{1}\right) ^{q}-h\left( \sum _{j=2}^{n}{\frac{1}{2}}{\kappa _{j}}{e^{2}_{j}}\right) ^{p} \\&\quad -o\left( \sum _{j=2}^{n}{\frac{1}{2}}{\kappa _{j}}{e^{2}_{j}}\right) ^{q} \\&\quad -h\left( \sum _{j=1}^{n}{\frac{b{\tilde{\theta }}^{2}_{j}}{2\upsilon _{j}}}\right) ^{p}-o\left( \sum _{j=1}^{n}{\frac{b{\tilde{\theta }}^{2}_{j}}{2\upsilon _{j}}}\right) ^{q}+o\left( \sum _{j=1}^{n}{\frac{b{\tilde{\theta }}^{2}_{j}}{2\upsilon _{j}}}\right) ^{q} \\&\quad -o\sum _{j=1}^{n}{\frac{b{\tilde{\theta }}^{2}_{j}}{2\upsilon _{j}}}+\varrho , \end{aligned},$$
(80)

where \(h=\min \left\{ \frac{n^{1-p}}{s}, {\frac{p(2\upsilon _{j})^{p-1}}{\tau _{j}(2p-1)b^{p-1}}}: 1\le j\le n\right\} \) and \(o=\min \{v, \lambda _{j}: 1\le j\le n\}\).

By utilizing (2), we can obtain

$$ \left( \sum \limits _{j=1}^{n}{\frac{{b\tilde{\theta }}^{2}_{j}}{2\upsilon _{j}}}\right) ^{q}\le \sum \limits _{j=1}^{n}{\frac{{b\tilde{\theta }}^{2}_{j}}{2\upsilon _{j}}}+(1-q)q^{\frac{q}{1-q}}. $$
(81)

Using (6) and (81), we can obtain

$$\begin{aligned} {\ell V_{n}}\le&-\chi _{1}\left( \sum _{j=1}^{n}{\frac{1}{4}}z^{4}_{1}+\sum _{j=2}^{n}{\frac{1}{2}}{\kappa _{j}}{e^{2}_{j}}+\sum _{j=1}^{n}{\frac{b{\tilde{\theta }}^{2}_{j}}{2\upsilon _{j}}}\right) ^{p} \\&\quad -\chi _{2}\left( \sum _{j=1}^{n}{\frac{1}{4}}z^{4}_{1}+\sum _{j=2}^{n}{\frac{1}{2}}{\kappa _{j}}{e^{2}_{j}}+\sum _{j=1}^{n}{\frac{b{\tilde{\theta }}^{2}_{j}}{2\upsilon _{j}}}\right) ^{q}+\gamma \\ \le&{-\chi _{1} V^{p}(x)}-{\chi _{2} V^{q}(x)}+{\gamma }, \end{aligned},$$
(82)

where \(\chi _{1}={\frac{h}{2^{p-1}}}\), \(\chi _{2}=o\) and \(\gamma =\varrho +\chi _{2}(1-q)q^{\frac{q}{1-q}}\).

Combining Eq. (82) with (1), we can obtain all states in the considered systems are SGUUB and the tracking errors are driven to a small neighborhood of the origin in a fixed time \(T_{1}\), where \(T_{1}\) satisfies

$$ {T_{1}}\le {\frac{1}{\iota \chi _{1}(p-1)}}+{\frac{1}{\iota \chi _{2}(1-q)}}. $$
(83)

\(\square \)

5 Simulation Studies

In this section, a numerical example is introduced to verify the effectiveness of the proposed control strategy.

According to the system (16), a second-order stochastic nonlinear system with external disturbances is considered as follows:

$$ {\left\{ \begin{array}{l} {\text {d}}x_{1}=\left( {{x}_{2}}+\hbar _{1}(t)\right) {\text {d}}t+0.01x_{1}{\text {d}}\omega ,\\ {\text {d}}x_{2}=\left( 0.3{x_{1}}{x_{2}}+u+\hbar _{2}(t)\right) {\text {d}}t+0.02x_{1}x_{2}{\text {d}}\omega ,\\ y={{x}_{1}} , \end{array} \right. } ,$$
(84)

where \(x_{1}\) and \(x_{2}\) are state variables. u and y represent system input and output. \({\hbar _{1}(t)=0.01\sin (t)}\) and \({\hbar _{2}(t)=0.02\sin (t)}\) represent system disturbances. The reference signal \(y_{\text {d}}\) is described as \(y_{\text {d}}=0.5(\cos (0.5t)+\sin (0.5t))\).

The virtual controller \(\alpha _{1}\), actual controller u and the adaptive law \(\dot{\hat{\theta }}_{1}\), \(\dot{\hat{\theta }}_{2}\) are designed as follows:

$$\begin{aligned}&\alpha _{1}=-k_{1,1}z^{4p-3}_{1}-k_{1,2}z^{4q-3}_{1}-{\frac{z^{3}_{1}}{2}}+{\frac{{\dot{y}}_{\text {d}}}{c_{1}}}-{\frac{\varDelta _{1}(t)}{c_{1}}},\end{aligned}$$
(85)
$$\begin{aligned}&u={-k_{2,1}}z^{4p-3}_{2}-{\frac{{z^{3}_{2}}}{2{a^{2}_{2}}}}{\hat{\theta }}_{2}{\zeta ^{\text {T}}_{2}(X_{2})}{\zeta _{2}(X_{2})}+{\frac{{{\dot{\beta }}_{2}}}{c_{2}}},\end{aligned}$$
(86)
$$\begin{aligned}&{{\dot{\hat{\theta }}}_{1}}=0,\end{aligned}$$
(87)
$$\begin{aligned}&{{\dot{\hat{\theta }}}_{2}}={\frac{{\upsilon _{2}}z^{6}_{2}}{2{a^{2}_{2}}}}{\zeta ^{\text {T}}_{2}(X_{2})}{\zeta _{2}(X_{2})}-\lambda _{2}{\hat{\theta }}_{2}-\tau _{2}{\hat{\theta }^{2p-1}}_{2},\end{aligned}$$
(88)
$$\begin{aligned}&\mu _{2}{\dot{\beta }_{2}}+\beta _{2}=\alpha _{1}, \quad \beta _{2}(0)=\alpha _{1}(0), \end{aligned},$$
(89)

where \(z_{1}=x_{1}-y_{\text {d}}\), \(z_{2}=x_{2}-\beta _{2}\). The initial values of the system (82) are given as \(x_{1}(0)=1\), \(x_{2}(0)=-0.1\) and \({{\dot{\hat{\theta }}}_{1}}(0)={{\dot{\hat{\theta }}}_{2}}(0)=0\). All the design parameters are selected as \(k_{1,1}=k_{2,1}=100\), \(k_{1,2}=0.2\), \(p=1.1\), \(q=0.8\), \(c_{1}=1\), \(c_{2}\)=2, \(\upsilon _{2}=0.1\), \(\lambda _{2}=0.1\), \(\tau _{2}=1\) and \(\mu _{2}=0.005\).

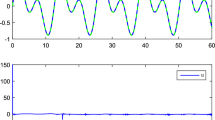
The results of the simulation are illustrated in Figs. 2, 3, 4 and 5 using the above design parameters. Figure 2 shows the trajectories of the considered systems output y and the reference signal \(y_{\text {d}}\) and we can obtain a good tracking performance. The trajectory of tracking error \(z_{1}\) is represented in Fig. 3, where the tracking error \(z_{1}\) is driven to a small neighborhood of the origin in a fixed time. Figure 4 is employed to show the trajectories of the considered systems state variables \(x_{1}\) and \(x_{2}\) and we can obtain that the state variables in the considered systems are bounded. The trajectory of the considered systems input u is shown in Fig. 5 and we can obtain the considered systems input u is bounded. Therefore, we can obtain that all the states in the considered systems are bounded and the tracking error is driven to a small neighborhood of the origin in a fixed time.

Fig. 2
figure 2

The trajectories of the considered system output y and the reference signal \(y_{\text {d}}\)

Full size image
Fig. 3
figure 3

The trajectory of tracking error \(z_{1}\)

Full size image
Fig. 4
figure 4

The trajectories of the considered system state variables \(x_{1}\) and \(x_{2}\)

Full size image
Fig. 5
figure 5

The trajectory of the considered system input u

Full size image

6 Conclusion

In this paper, a novel fixed time adaptive fuzzy dynamic surface tracking control problem is studied for stochastic pure feedback nonlinear systems with disturbances. Combined with mean value theorem, which can deal with the problem of nonaffine structure, adaptive fuzzy technique are utilized to transform the pure feedback structure into a strict feedback structure with approximated unknown nonlinear functions. The DSC method is employed to handle with the problem of “explosion of complexity” in the controller design process. A novel fixed time adaptive fuzzy control strategy is developed for the considered stochastic nonlinear systems to ensure all the signals of the considered systems are SGUUB and the tracking errors are driven to a small neighborhood of the origin in a fixed time. The strategy mentioned can also be used in many applications such as industrial control and aircraft control. Future research will focus on the stochastic pure feedback nonlinear systems with various conditions, such as full state constraints or unknown control directions by utilizing the proposed control scheme.