Fuzzy Hungarian MODI Algorithm to Solve Fully Fuzzy Transportation Problems

Abstract

In this paper, a new method is proposed to solve fully fuzzy transportation problems using the approach of the Hungarian and MODI algorithm. The objective of the proposed algorithm, namely, fuzzy Hungarian MODI algorithm, is to obtain the solution of fully fuzzy transportation problems involving triangular and trapezoidal fuzzy numbers. The introduced method together with Yager’s ranking technique gives the optimal solution of the problem. It also satisfies the conditions of optimality, feasibility, and positive allocation of cells using the elementwise subtraction of fuzzy numbers. A comparative study of the proposed method with existing procedure reveals that the solution of the proposed method satisfies the necessary conditions of a Transportation Problem (TP) to be an optimal solution in which the other methods do not guarantee. The proposed method is the extension of the Hungarian MODI method with fuzzy values. It is easy to understand and implement, as it follows the standard steps of the regular transportation problems. The method can be extended to other kinds of fuzzy transportation problems, such as unbalanced fuzzy TP, fuzzy degeneracy problem, fuzzy TP with prohibited routes, and many more.

1 Introduction

Transportation problem (TP) is a special case of Linear-Programming Problem. Transportation problems have wide applications in logistics and supply chain management for reducing the cost. It deals with the transportation of a commodity from various sources of supply to various sinks of demand in such a way that the total distribution cost is minimized. The transportation problem was introduced by Hitchcock [1]. Dantzig and Thapa [2] used the simplex method to solve the transportation problem. Charnes and Cooper [3] proposed the stepping-stone method as an alternative to the simplex method. In the transportation problem, the decision parameters, such as availability, requirement, and the transportation cost per unit, must be fixed to get a solution. Due to some uncontrollable situations, the determination of supply, demand, and unit transportation cost may be imprecise. The uncertainty in determining the data can be modelled using fuzzy notions which was introduced by Zadeh [4, 5] in the year 1965. If the requirement, availability, and the cost per unit are represented by fuzzy numbers in a TP, then the TP is called a fully fuzzy TP or TP with fuzzy environment. There are many approaches to solve a fuzzy TP, and the fuzzy linear-programming technique is one among them. Chanas et al. [6, 7] developed a method for solving the fuzzy TP using the parametric programming technique and also suggested a method by converting the given problem into a bi-criterial TP with a crisp objective function. The parametric programming method not only identifies the solution, but also gives all other alternatives. Liu and Chiang Kao [8] approached the fuzzy TP using the extension principle. Verma et al. [9] applied the fuzzy-programming technique with hyperbolic and exponential membership function. Liang et al. [10, 11] used the possibilistic linear-programming technique for fuzzy transportation planning decisions and fuzzy linear programming to solve interactive multiobjective transportation planning decision problems. Nagoorgani et al. [12] used a parametric approach to obtain a fuzzy solution for a two-stage cost-minimizing fuzzy transportation problem. Pandian et al. [13] solved the fuzzy TP with trapezoidal fuzzy numbers using the ranking technique by incorporating the fuzzy zero point method. Kumar et al. [14] introduced the general fuzzy least cost method, fuzzy north-west corner rule, and fuzzy VAM to solve fuzzy TP with generalized triangular fuzzy numbers as well as trapezoidal fuzzy numbers. In the existing methods, either the solution turns out to be a crisp value or it does not guarantee the fuzzy solution to be positive. When the solution becomes crisp, one cannot identify the corresponding fuzzy solution. If the solution has negative components, it may not become the solution of the real-world fuzzy TP. So far, the fuzzy TP, unbalanced fuzzy TP, and degeneracy fuzzy TP problems are not approached with a single algorithmic technique. The existing techniques are helpful to find the solution of a particular kind of problems. The method proposed in this paper is unique and applicable to any fully fuzzy TP. The proposed method not only gives the optimal solution, but also satisfies the feasibility condition and retains the positive allocation of cells.

The choice of a ranking technique is important for ordering the fuzzy numbers. Yuan [15], Wang et al. [16], and Chien et al. [17] proposed the properties of ranking for fuzzy numbers. In this paper, Yager’s ranking technique [18] is used to order the fuzzy numbers. It does not require the explicit form of membership function, as it uses the extreme values of $\alpha$-cut of fuzzy number. It satisfies the ranking properties of compensation, linearity, and additive. Moreover, it also provides results which are consistent with human intuition. This helps us interms of decision making. Recently, Karaman et al. [19] did a thorough literature review on fuzzy multiattribute decision and fuzzy multiobjective decision making. In the proposed method, the fuzzy Hungarian method with elementwise addition and subtraction [20–22] is used to get the assignments. Fuzzy initial basic feasible solution is obtained through the cost allocation of assigned cells. Finally, the fuzzy MODI method is applied to optimize the fuzzy transportation cost. Tabular illustrations are given for the examples.

In this paper, Sect. 2 deals with fuzzy preliminaries followed by Sect. 3 in which the proposed algorithm is given in detail. In Sect. 4, the implementation of the algorithm through examples is explained, and the comparison between the existing fuzzy zero point method [13] and the proposed method is given. In addition, the comparison between the method introduced by Amarpreet and Amit kumar [14] has been done for a case study. Section 5 describes the conclusion.

2 Preliminaries

Definition 2.1

A fuzzy set [23] can be mathematically constructed by assigning to each possible individual in the universe of discourse a value representing its grade of membership.

Definition 2.2

A fuzzy number [23] $\tilde{A}$ is a fuzzy set, whose membership function $\mu _{\bar{A}}(x)$ satisfies the following condition:

• (1) $\mu _{\tilde{A}}(x)$ is piecewise continuous.

• (2) $\mu _{\tilde{A}}(x)$ is convex.

• (3) $\mu _{\tilde{A}}(x)$ is normal, i.e., $\mu _{\tilde{A}}(x_{0})=0$.

Definition 2.3

A fuzzy number $\tilde{A}= (a,b,c)$ with membership function of the form

$$\begin{aligned} \mu _{\tilde{A}}(x) = \left\{ \begin{array}{ll} \frac{x-a}{b-a} & \quad a \le x\le b\\ 1 & \quad x=b \\ \frac{c-x}{c-b} & \quad b\le x\le c \\ 0 &\quad {\text {otherwise}}\\ \end{array}\right. \end{aligned}$$

are called a triangular fuzzy number [23], and a fuzzy number $\tilde{A}= (a,b,c,d)$ with membership function of the form

$$\begin{aligned} \mu _{\tilde{A}}(x) = \left\{ \begin{array}{ll} \frac{x-a}{b-a} & \quad a \le x \le b \\ 1 & \quad b \le x \le c \\ \frac{d-x}{d-c} & \quad c \le x\le d \\ 0& \quad {\text {otherwise}} \\ \end{array} \right. \end{aligned}$$

is called a trapezoidal fuzzy number [23]. The Triangular and Trapezoidal fuzzy numbers are depicted in Fig 1(a) and Fig 1(b).

Fig. 1

a Triangular fuzzy number. b Trapezoidal fuzzy number

Definition 2.4

The fuzzy operations [23] of fuzzy numbers are defined as

Fuzzy Addition:

$$\begin{aligned} ( a_{1},b_{1},c_{1},d_{1}) +( a_{2},b_{2},c_{2},d_{2})= & (a_{1}+ a_{2},b_{1}+b_{2},c_{1}+c_{2},d_{1}+d_{2}) \\ ( a_{1},b_{1},c_{1}) +( a_{2},b_{2},c_{2})= & (a_{1}+ a_{2},b_{1}+b_{2},c_{1}+c_{2}). \end{aligned}$$

Fuzzy Subtraction:

$$\begin{aligned} ( a_{1},b_{1},c_{1},d_{1})-( a_{2},b_{2},c_{2},d_{2})= & (a_{1}- d_{2},b_{1}-c_{2},c_{1}-b_{2},d_{1}-a_{2}) \\ ( a_{1},b_{1},c_{1}) -( a_{2},b_{2},c_{2})= & (a_{1}- c_{2},b_{1}-b_{2},c_{1}-a_{2}). \end{aligned}$$

Definition 2.5

The elementwise operations [20–22] of fuzzy numbers are defined as follows:

Elementwise Addition:

$( a_{1},b_{1},c_{1},d_{1}) +( a_{2},b_{2},c_{2},d_{2})= (a_{1}+ a_{2},b_{1}+b_{2},c_{1}+c_{2},d_{1}+d_{2})$

$( a_{1},b_{1},c_{1}) +( a_{2},b_{2},c_{2})= (a_{1}+ a_{2},b_{1}+b_{2},c_{1}+c_{2})$.

Elementwise Subtraction:

$( a_{1},b_{1},c_{1},d_{1}) -( a_{2},b_{2},c_{2},d_{2})= (a_{1}- a_{2},b_{1}-b_{2},c_{1}-c_{2},d_{1}-d_{2})$

$( a_{1},b_{1},c_{1}) -( a_{2},b_{2},c_{2}) = (a_{1}- a_{2},b_{1}-b_{2},c_{1}-c_{2})$.

Elementwise Multiplication:

$( a_{1},b_{1},c_{1},d_{1}) *( a_{2},b_{2},c_{2},d_{2})= (a_{1}* a_{2},b_{1}*b_{2},c_{1}*c_{2}, d_{1}*d_{2})$

$( a_{1},b_{1},c_{1}) *( a_{2},b_{2},c_{2})= (a_{1}* a_{2},b_{1}*b_{2},c_{1}*c_{2})$.

Definition 2.6

The Yager’s ranking [18] of a fuzzy number $\tilde{A}$ is given by

$$Y(\tilde{A}) = \int ^{1}_{0}(0.5)\left( A^{\alpha }_{U}+A^{\alpha }_{L}\right) {\text {d}} \alpha$$

where $A^{\alpha }_{L}$ = Lower $\alpha$-level cut and $A^{\alpha }_{U}$ = Upper $\alpha$-level cut. If $Y (\tilde{A}) \le Y (\tilde{B})$, then $\tilde{A} \le \tilde{B}$.

• Two fuzzy numbers $\tilde{A}$ and $\tilde{B}$ are said to be equal if they are elementwise equal.

• Two fuzzy numbers $\tilde{A}$ and $\tilde{B}$ are said to be equivalent if their crisp values $(Y(\tilde{A})=Y(\tilde{B}))$ are equal.

• A fuzzy number $\tilde{A}$ are said to be negative if all the terms in it are negative or its crisp value $(Y(\tilde{A}))$ is negative.

• A fuzzy number $\tilde{A}$ are said to be a zero fuzzy number if all the terms in it are zero or its crisp value $(Y(\tilde{A}))$ is zero.

Theorem 2.7

The fuzzy subtraction and the elementwise subtraction of fuzzy numbers are equivalent.

Proof

Let $\tilde{A}=(a_{1},a_{2},a_{3},a_{4})$ and $\tilde{B}=(b_{1},b_{2},b_{3},b_{4})$.

Using fuzzy subtraction, $\tilde{A} - \tilde{B} = (a_{1}- b_{4}, a_{2}- b_{3}, a_{3}- b_{2}, a_{4}- b_{1})$.

The membership function for this fuzzy trapezoidal number is

$$\begin{aligned} \mu _{\tilde{A}-\tilde{B}}(x) = \left\{ \begin{array}{ll} \frac{x-(a_{1}-b_{4})}{(a_{2}-b_{3})-(a_{1}-b_{4})} &\quad (a_{1}-b_{4}) \le x \le (a_{2}-b_{3}) \\ 1&\quad (a_{2}-b_{3}) \le x \le (a_{3}-b_{2}) \\ \frac{(a_{4}-b_{1})-x}{(a_{4}-b_{1})-(a_{3}-b_{2})} &\quad (a_{3}-b_{2}) \le x\le (a_{4}-b_{1}) \\0& \quad {\text {otherwise}} \\ \end{array} \right. \end{aligned}$$

To calculate the upper and lower $\alpha$-cuts, consider $\frac{x-(a_{1}-b_{4})}{(a_{2}-b_{3})-(a_{1}-b_{4})} =\alpha$ $\Rightarrow x= \alpha [(a_{2}-b_{3})-(a_{1}-b_{4})] +(a_{1}-b_{4})$ and $\frac{(a_{4}-b_{1})-x}{[(a_{4}-b_{1})-(a_{3}-b_{2})]} = \alpha \Rightarrow x= (a_{4}-b_{1})-\alpha [(a_{4}-b_{1})-(a_{3}-b_{2})]$

Using Yager’s ranking, $\int ^{1}_{0}(\frac{1}{2})(a^{\alpha }_{U}+a^{\alpha }_{L})d \alpha = (\frac{a_{1}+a_{2}+a_{3}+a_{4}-[b_{1}+b_{2}+b_{3}+b_{4}]}{4})$

where $a^{\alpha }_{L} = \alpha [(a_{2}-b_{3})-(a_{1}-b_{4})] +(a_{1}-b_{4})$ and $a^{\alpha }_{U} = [(a_{4}-b_{1})-\alpha [(a_{4}-b_{1}) -(a_{3}-b_{2})]]$.

On the other hand, the elementwise subtraction of $\tilde{A}$ and $\tilde{B}$ gives $\tilde{A} - \tilde{B}= (a_{1}- b_{1}, a_{2}- b_{2}, a_{3}- b_{3}, a_{4}- b_{4})$.

The membership function for this fuzzy trapezoidal number is

$$\begin{aligned} \mu _{\tilde{A}-\tilde{B}}(x) = \left\{ \begin{array}{ll} \frac{x-(a_{1}-b_{1})}{(a_{2}-b_{2})-(a_{1}-b_{1})} & \quad (a_{1}-b_{1}) \le x \le (a_{2}-b_{2}) \\ 1& \quad (a_{2}-b_{2}) \le x \le (a_{3}-b_{3}) \\ \frac{(a_{4}-b_{4})-x}{(a_{4}-b_{4})-(a_{3}-b_{3})} & \quad (a_{3}-b_{3}) \le x\le (a_{4}-b_{4}) \\ 0& \quad {\text {otherwise}} \\ \end{array} \right. \end{aligned}$$

Consider $\frac{x-(a_{1}-b_{1})}{(a_{2}-b_{2})-(a_{1}-b_{1})} =\alpha \,\Rightarrow x= \alpha [(a_{2}-b_{2})-(a_{1}-b_{1})] +(a_{1}-b_{1})$ and $\frac{(a_{4}-b_{4})-x}{[(a_{4}-b_{4})-(a_{3}-b_{3})]} = \alpha \Rightarrow x= (a_{4}-b_{4})-\alpha [(a_{4}-b_{4})-(a_{3}-b_{3})]$

Using Yager’s ranking, $\int ^{1}_{0}(\frac{1}{2})(a^{\alpha }_{U}+a^{\alpha }_{L})d \alpha =\Rightarrow (\frac{a_{1}+a_{2}+a_{3}+a_{4}-[b_{1}+b_{2}+b_{3}+b_{4}]}{4})$, where $a^{\alpha }_{L} = \alpha [(a_{2}-b_{2})-(a_{1}-b_{1})] +(a_{1}-b_{1})$ and $a^{\alpha }_{U} = [(a_{4}-b_{4})-\alpha [(a_{4}-b_{4}) -(a_{3}-b_{3})]]$. Hence, the fuzzy subtraction of trapezoidal (triangular) fuzzy numbers is equivalent to the elementwise subtraction of fuzzy trapezoidal (triangular) numbers. $\square$

Definition 2.8

A fully fuzzy transportation problem [6, 7] is defined as

$$\min \tilde{Z} \approx \sum ^{m}_{i=1}\sum ^{n}_{j=1}\tilde{c_{ij}} \tilde{x_{ij}}$$

subject to

$$\begin{aligned}&\sum ^{n}_{j=1}\tilde{x_{ij}} \approx \tilde{s_{i}} \qquad {\text {for}},\, i=1,2,3\ldots m, \\&\sum ^{m}_{i=1}\tilde{x_{ij}} \approx \tilde{d_{j}} \qquad {\text {for}}\,\,j=1,2,3\ldots n. \end{aligned}$$

for all $\tilde{x_{ij}} \succ \tilde{0}$, where $i=1,2,3\ldots m$ and $j=1,2,3\ldots n$.

Here, $\tilde{x_{ij}}$ is the number of units to be transported from $i{\text {th}}$ source to $j{\text {th}}$ destination, $\tilde{c_{ij}}$ is the cost of one unit to transport from $i{\text{th}}$ source to $j{\text {th}}$ destination, $\tilde{s_{i}}$ is the number of units available in the $i{\text {th}}$ source, and $\tilde{d_{j}}$ is the number of units required in the $j{\text {th}}$ destination.

The above problem can be depicted as a cost matrix given in Table 1.

Table 1 General fully fuzzy transportation problem

Definition 2.9

The fuzzy feasible solution of the fully fuzzy transportation problem is defined as a set of non-negative values $\tilde{x_{ij}}$, $i=1,2,3 \ldots m, j=1,2,3 \ldots n$, such that $\sum ^{m}_{i=1} \tilde{s_{i}} \approx \sum ^{n}_{j=1} \tilde{d_{j}}$ for $i=1,2,3\ldots m, j=1,2, \ldots n$ (i.e., total fuzzy supply is equal to total fuzzy demand).

The following theorems are proposed to get the necessary and sufficient condition for the existence of the fuzzy feasible solution of a fully fuzzy transportation problem.

Theorem 2.10

The fuzzy feasible solution of a fully fuzzy transportation problem exists if and only if $\sum ^{m}_{i=1} \tilde{s_{i}} \approx \sum ^{n}_{j=1} \tilde{d_{j}}$ for $i=1,2,3\ldots m, j=1,2, \ldots n$.

Proof

Let there be a fuzzy feasible solution to the fully fuzzy transportation problem exists. Then

$$\sum ^{m}_{i=1} \sum ^{n}_{j=1} \tilde{x_{ij}} \approx \sum ^{m}_{i=1} \tilde{s_{i}}$$

(1)

and

$$\sum ^{n}_{j=1}\sum ^{m}_{i=1}\tilde{x_{ij}} \approx \sum ^{n}_{j=1}\tilde{d_{j}} .$$

(2)

From (1) and (2), $\sum ^{m}_{i=1}\tilde{s_{i}} \approx \sum ^{n}_{j=1}\tilde{d_{j}}$.

Conversely, suppose $\sum ^{m}_{i=1}\tilde{s_{i}} \approx \sum ^{n}_{j=1}\tilde{d_{j}} \approx \tilde{k}$ (say).

Let $\tilde{\lambda _{i}} \ne \tilde{0}$ be a fuzzy number, such that $\tilde{x_{ij}} \approx \tilde{\lambda _{i}} \tilde{d_{j}} \forall i,j$.

Then, $\tilde{\lambda _{i}}$ is given by

$$\begin{aligned} \sum ^{n}_{j=1}\tilde{x_{ij}} \approx \sum ^{n}_{j=1}\tilde{\lambda _{i}}\tilde{d_{j}} \approx \tilde{\lambda _{i}} * \sum ^{m}_{i=1}\tilde{s_{i}} \approx \tilde{k}\tilde{\lambda _{i}}, \tilde{\lambda _{i}} \approx \frac{1}{\tilde{k}} * \sum ^{n}_{j=1}\tilde{x_{ij}} \approx \tilde{s_{i}}/\tilde{k}. \end{aligned}$$

Thus, $\tilde{x_{ij}}\approx \tilde{\lambda _{i}}\tilde{d_{j}} \approx \frac{\tilde{s_{i}}\tilde{d_{j}}}{\tilde{k}}, \forall i,j$.

Hence, a fuzzy feasible solution exists. $\square$

Theorem 2.11

The number of fuzzy basic variables in a fully fuzzy transportation problem is at the most $m+n-1$, where $m=$ number of rows and $n=$ number of columns.

Proof

To prove that the number of fuzzy basic variables is at the most $m+n-1$, it is enough to show that there are $m+n-1$ linearly independent equations in mn variables.

To prove this, first add m rows and then subtract from the sum of first $(n-1)$ column equations. This gives

$$\begin{aligned} \sum ^{n-1}_{j=1}\sum ^{m}_{i=1}\tilde{x_{ij}} - \sum ^{n}_{j=1}\sum ^{m}_{i=1}\tilde{x_{ij}} \approx \sum ^{n-1}_{j=1}\tilde{d_{j}}- \sum ^{m}_{i=1}\tilde{s_{i}}. \end{aligned}$$

Alternatively

$$\begin{aligned} \left( \sum ^{n}_{j=1}\sum ^{m}_{i=1}\tilde{x_{ij}}- \sum ^{m}_{i=1}\tilde{x_{in}}\right) - \sum ^{n}_{j=1}\sum ^{m}_{i=1}\tilde{x_{ij}} \approx \left( \sum ^{n}_{j=1}\tilde{d_{j}}-\tilde{d_{n}}\right) - \sum ^{m}_{i=1}\tilde{s_{i}} \end{aligned}$$

i.e., $\sum ^{m}_{i=1}\tilde{x_{in}} \approx \tilde{d_{n}}$. Thus, out of $m+n$ equations, one (any) is redundant and the remaining $m+n-1$ equations form a linearly independent set. $\square$

From Theorem 2.11, a fuzzy basic feasible solution will consist of at the most $m+n-1$ fuzzy positive variables and others being zero. In the case of degeneracy, some of the fuzzy basic variables will also be zero, i.e., the number of positive variables is less than $m+n-1$. By fundamental theorem of linear programming, one of the fuzzy basic feasible solutions will be the optimal solution.

Finally, the fuzzy optimality test is defined as follows: If we have a fuzzy feasible solution consisting of m+n-1 independent allocations and if fuzzy numbers $\tilde{u_{i}}$ and $\tilde{v_{j}}$ satisfy $\tilde{c_{ij}} \approx \tilde{u_{i}} + \tilde{v_{j}}$ for each occupied cell (i, j), then the evaluation $\tilde{D_{ij}}$ corresponding to each empty cell (i, j) is given by $\tilde{D_{ij}} \approx \tilde{c_{ij}}-\left( \tilde{u_{i}} +\tilde{v_{j}}\right)$:

• (i) If the cost difference $\tilde{D_{ij}} \succ 0$, then the fuzzy feasible solution is optimal.

• (ii) If $\tilde{D_{ij}} \prec 0$ for one or more empty cells, then allocate maximum possible cost to the cell with the largest negative value of $\tilde{D_{ij}}$. Continue the process successfully until the optimal solution is obtained, where $\tilde{D_{ij}} \succ 0$ for each empty cell.

3 Algorithms for Fully Fuzzy Transportation Problem

3.1 Fuzzy Zero Point Method [13]

• Step 1 Construct the fuzzy transportation table for the given fuzzy transportation problem and, then, convert it into a balanced one if it is not. Subtract each row entries of the fuzzy transportation table from the row minimum. Do the same for columns also.

• Step 2 Check if each column fuzzy demand is less than to the sum of the fuzzy supplies, whose reduced costs in that column are fuzzy zero. In addition, check if each row fuzzy supply is less than to the sum of the column fuzzy demands, whose reduced costs in that row are fuzzy zero. If so, go to Step 5 or go to Step 3. The resultant table is called allotment table.

• Step 3 Cover all the fuzzy zeros [excluding some entries of rows or/ and columns which do not satisfy the previous step condition] of the allotment table by the minimum number of horizontal lines and vertical lines.

• Step 4 Determine the smallest fuzzy element in the matrix not covered by lines. Subtract the smallest fuzzy element from all uncovered elements and add the same element at the intersection of the horizontal and vertical lines. The resultant matrix will be called the revised reduced fuzzy transportation, and then, go to Step 2.

• Step 5 Select a cell in the reduced fuzzy transportation table, whose reduced cost is the maximum cost. Say $(\alpha ,\beta )$. If there are more than one, then select anyone.

• Step 6 Choose a fuzzy zero cell in the corresponding row or column of the reduced fuzzy transportation table and allot the maximum possible to that cell. If not choose the next maximum.

• Step 7 Delete the fully used fuzzy supply points, and the fully received fuzzy demand points modify it to include the not used fuzzy supply and fuzzy demand points.

• Step 8 Repeat Steps 5 to 7 until all fuzzy supply points are used and all fuzzy demand points are received.

This method ensures the feasibility of the solution but does not guarantee the positive allocation of cells. In addition, there is no evidence of applying the fuzzy zero point method to degeneracy fuzzy transportation problems.

3.2 Generalized Fuzzy North-West Corner, Least Cost, and Vogel’s Approximation Methods and Fuzzy MODI Method [14]

The algorithm of generalized fuzzy north-west corner, least cost, and Vogel’s approximation methods and fuzzy MODI method is an extension/fuzzy version of the methods applied for the solution of the transportation problem with crisp values. The solution through these methods need not be positive, and hence, it may not reflect the solution of the real-life problems.

In this paper, the fuzzy version of the Hungarian MODI algorithm is proposed, and it guarantees the positive allocation of cells and satisfies the optimality and feasibility conditions. The algorithm is given as follows.

3.3 Fuzzy Hungarian MODI method

Consider the matrix representation of the fully fuzzy transportation problem considered in Table 1. If the matrix is not a square matrix, make it a square matrix by adding fuzzy zero element rows or fuzzy zero element columns and call it as an effectiveness matrix with the number of rows and columns as n.

• Step 1 Using Yagers ranking for comparing two fuzzy numbers, subtract the minimum among the cells of each row of the effectiveness matrix from all the fuzzy elements of the respective rows.

• Step 2 Repeat Step 1 for each column of the resulting matrix and call the updated matrix as the first modified matrix.

• Step 3 Follow the procedure of the Hungarian method to cover the fuzzy zero elements using a minimum number of horizontal and vertical lines. Let the sum of number of horizontal and vertical lines be N. If N = n, then an optimal assignment can be obtained and proceed to Step 6, otherwise proceed to Step 4.

• Step 4 Determine the smallest fuzzy element in the matrix not covered by N lines using Yager’s ranking. Subtract the smallest fuzzy element from all uncovered elements and add the same element at the intersection of the horizontal and vertical lines. The resultant matrix will be called the second modified matrix.

• Step 5 Repeat Steps 3 and 4 until the number of lines is equal to the order of the matrix.

• Step 6 Examine the rows one by one in the modified matrix until exactly single fuzzy zero elements are found rowwise (columnwise). Mark this fuzzy zero element using an open bracket on the top of the corresponding cell to assign the cost and crossover all other fuzzy zero elements lying in the corresponding column (row). The crossed cells cannot be considered for future assignment.

• Step 7 Repeat Step 6 successively until one of the following situation arises:

  • (a) If no unmarked fuzzy zero element is left, then proceed to Step 8.

  • (b) If there exists more than one unmarked fuzzy zero element in any column or row of the modified matrix, then mark one of the unmarked fuzzy zero element arbitrarily and cross the remaining fuzzy zero elements in its row or column. Repeat the process until no unmarked fuzzy zero element is left in the matrix.

• Step 8 Starting from the first assignment cell, allocate the least possible amount to all assignment cells as follows. Suppose the first assignment cell is (i, j), then allocate $\tilde{x_{ij}} \approx min ( \tilde{s_i}, \tilde{d_j} )$ in the cell (i, j) and update the corresponding row or column:

  • (i) If $\tilde{s_i} \prec \tilde{d_j}$, then cross out the $i{\text {th}}$ row and update the corresponding $\tilde{d_{j}}$ by $\tilde{d_{j}}-\tilde{s_{i}}$.

  • (ii) If $\tilde{s_i} \succ \tilde{d_j}$, then cross out the $j{\text {th}}$ column and update the corresponding $\tilde{s_{i}}$ by $\tilde{s_{i}}-\tilde{d_{j}}$.

  • (iii) If $\tilde{s_i}\approx \tilde{d_j}$, then cross out the corresponding row as well as the corresponding column.

• Step 9 If the fuzzy cost is not zero in supply and demand and all the assigned cells are allocated, then choose the smallest fuzzy element in non assigned cells and repeat Step 8 until the fuzzy cost becomes zero in supply and demand. The obtained one is the fuzzy feasible solution (FFS).

• Step 10 Apply fuzzy modified distribution method to optimize the FFS:

  • Find the FFS of FFTP using the fuzzy Hungarian method.

  • For each $i{\text {th}}$ row and $j{\text {th}}$ column, introduce $\tilde{u_{i}}$ and $\tilde{v_{j}}$, respectively. Write $\tilde{u_{i}}$ at the end of each $i{\text {th}}$ row and $\tilde{v_{j}}$ at the end of each $j{\text {th}}$ column. Assume any one of $\tilde{u_{i}}$ or $\tilde{v_{j}}$ to be zero fuzzy number.

  • For all the allocated cells, using the relation $\tilde{c_{ij}} \approx \tilde{u_{i}} + \tilde{v_{j}}$, find the values of $\tilde{u_{i}}$ and $\tilde{v_{j}}$.

  • For the non allocated cells, find $\tilde{D_{ij}} \approx \tilde{c_{ij}}-\left( \tilde{u_{i}} +\tilde{v_{j}}\right)$ and put them in the corner of the corresponding cell. Then, there exist two cases:

    • If all $\tilde{D_{ij}}\succ \tilde{0}$, then the FFS obtained is fuzzy optimal solution.

    • If there exists at least one $\tilde{D_{ij}}$, such that $\tilde{D_{ij}}\prec \tilde{0}$, then the obtained FFS is not fuzzy optimal solution and go to the next step.

  • In the fully fuzzy transportation problem, choose the most negative $\tilde{D_{ij}}$. Make the cell which is most negative as allocated cell by assigning the fuzzy quantity $\tilde{\theta }$ and construct a loop as follows: rule for making the loop: reaching the nearest allocated cell from the newly allocated cell by moving either horizontally or vertically with the constrain that the turning of the loop is allowed only in the allocated cell.

  • Adding and subtracting $\tilde{\theta }$ in the corners of the loop, where the value of $\tilde{\theta }$ is taken as minimum of the fuzzy entries from which $\tilde{\theta }$ is subtracted.

  • Replacing the value of $\tilde{\theta }$, the next improvised fuzzy feasible solution is obtained.

  • Repeat these steps again and again, until all $\tilde{D_{ij}}\succ \tilde{0}$ appear. The obtained fuzzy solution is the fuzzy optimal solution.

4 Numerical Examples

Example I

Consider the fully fuzzy transportation problem with triangular numbers given in Table 2

Table 2 Example I: fuzzy transportation problem

Solution:

As the total supply (4, 15, 27) is equal to the total demand (4, 15, 27), this problem will be called a balanced fuzzy TP.

Note that the matrix representation of the problem is not a square one and, hence, introduces a fuzzy zero cost row to make it as a square matrix. The converted matrix is given in Table 3.

Table 3 Initial step

In Table 4, the fuzzy costs and fuzzy units of fuzzy transportation table are given with their crisp values.

Table 4 Fuzzy transportation problem with crisp values

Choose the smallest fuzzy number in each and every row and subtract it with the other elements in the corresponding row. Repeat the same for the columns also. The resultant matrix is given in Table 5.

Table 5 Steps 1 and 2

Table 6 Steps 3, 4, and 5

Cover the fuzzy zeros by the minimum number of lines and is given in Table 6 with a dark-black mark to represent the corresponding covering of lines. Here, in this example, the order of the matrix is four, where as the number of lines covering the fuzzy zeros is equal to three.

Choose the minimum fuzzy number, i.e., (1, 1, 1), from the uncovered fuzzy numbers. Subtract (1, 1, 1) from all the other uncovered fuzzy numbers and add the same to the fuzzy numbers, which are in the intersection of the covering lines. The resultant matrix is given in Table 7.

Table 7 Steps 3, 4, and 5

Table 8 Steps 3, 4, and 5

Again, cover the fuzzy zeros using the minimum number of lines and it is given in Table 8. Note that the number of covering lines is equal to the order of the matrix.

Using Steps 6 and 7, the assignment can be made accordingly. The assignment table is given in Table 9.

Table 9 Steps 6 and 7

Table 10 Example I

Table 11 Example I

Table 12 Example I

Table 13 Example I

Table 14 Example I

From Table 9, we can identify the first assignment cell as (1, 4). Using Step 8, allocate the least possible amount, i.e., the supply (0, 3, 6) to the cell (1, 4). The corresponding representation is given in Table 10. Now, strike out the first row, then update the demand (2, 1, 2) by subtracting the least supply. By repeatedly doing this process using Steps 8 and 9, the updated tabular values are given from Tables 11, 12, 13, and 14. From Table 14, the value $(-1,2,4)$ can be assigned to the second row first column.

The consolidated tabular values are given in Table 15, and the corresponding fuzzy feasible solution can be obtained as

$$\begin{aligned}\hbox {T.C}& \approx (-1,1,4) * (0,3,6) + (2,5,8) * (1,4,7 ) + (0,5,10) * (0,3,5) \\&\quad+\,(4,9,16 ) * (-1,2,4) + (1,4,7) * (2,1,2) + (2,7,13) * (2,2,3) \approx (4,74,247). \end{aligned}$$

From Table 15, the number of allocations is equal to 6 which is equal to $m+n-1=4+3-1=6$. Using fuzzy MODI method, the optimal solution is obtained after three iterations. The fuzzy optimal solution and the corresponding fuzzy transportation cost (T.C) are given as follows:

$$\begin{aligned}\hbox {Fuzzy T.C} &\approx (-2,3,8) * (0,3,6) + (2,5,8) * (0,3,5) + (0,5,10) * (0,3,5) \\ &\quad+\,(0,5,10 ) * (1,1,2) + (1,4,7) * (2,4,8) + (2,7,13) * (1,1,1) \approx (4,67,227). \end{aligned}$$

Table 15 Fuzzy feasible solution of Example I

Example II

Consider the fully fuzzy transportation problem with trapezoidal fuzzy numbers [13] given in Table 16.

Solution :

Table 16 Example II: problem illustration

This problem is an unbalanced fuzzy transportation problem, since the total fuzzy supply $(6,17,21,32)\ne$ the total fuzzy demand (8, 17, 21, 30). To make this as a balanced one, we introduce an additional column with fuzzy costs as fuzzy zeros and the fuzzy demand as $(-.2,0,0,.2)$. By applying the proposed algorithm, the corresponding fuzzy feasible solution can be obtained as (37, 112, 159, 284) and is given in Table 17.

Note that the number of allocations is one less than the sum of rows and columns of the given problem. The fuzzy transportation cost is given by

$$\begin{aligned} {\text {T.C}}= & (1,2,3,4) * (1,6,7,12) + (-1,0,1,2) * (0,1,2,3 ) \\&+ (3,5,6,8 ) * (4,1,1,-2) + (12,15,16,19) * (1,3,4,6) \\&+ (5,8,9,12)*(1,4,4,7)+(7,9,10,12)*(1,2,3,4) \\&+ (0,0,0,0)*(-2,0,0,2)\approx (37,112,159,284). \end{aligned}$$

After applying the fuzzy modified distribution method, the corresponding cost is given as

$$\begin{aligned} {\text {T.C}}= & (1,3,4,6) * (1,5,6,10) + (9,11,12,14 ) * (0,1,1,2 ) \\&+ (5,6,7,8) * (0,1,2,3) + (3,5,6,8 ) * (5,7,8,10) \\&+ (12,15,16,19) * (1,1,1,1) + (7,9,10,12) * (1,2,3,4) \\&+ (0,0,0,0)*(-2,0,0,2) \approx (35,100,144,259). \end{aligned}$$

The membership function for the obtained result is

• According to the decision maker, the minimum transportation cost will lie between 35 and 259 units.

• The overall level of satisfaction of the decision maker about the statement that the minimum transportation cost will lie between 100 and 144 units is 100 

• The overall level of the satisfaction of the decision maker for the remaining values of minimum transportation cost can be obtained as follows: let $x_{0}$ represents the minimum transportation cost, then the overall level of satisfaction of the decision maker for $x_{0}$ is $\mu _{\tilde{A}}(x_{0})\times 100$

  where

  $$\begin{aligned} \mu _{\tilde{A}}(x) = \left\{ \begin{array}{ll} \frac{x-35}{65} & 35 \le x \le 100 \\ 1 & 100 \le x \le 144 \\ \frac{259-x}{115} & 144 \le x\le 259 \\ 0 & {\text {otherwise}} \\ \end{array} \right. \end{aligned}$$

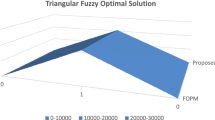
Note: Using the fuzzy zero point method, the optimum solution of the above problem is given as $(-274,58,188,575)$. The negativity involved in the solution has no role in the real-time applications. In addition, there is no evidence of applying the fuzzy zero point method to degeneracy fuzzy transportation problem. The proposed algorithm yields the optimal solution as (35, 100, 144, 259) that satisfies the positive allocation of cells and also satisfies the optimality condition.

Table 17 Fuzzy feasible solution of Example II

Example III

The case study considered in Amarpreet and Amit [14] has been considered to implement the proposed algorithm and is given as follows.

Dali Company is the leading producer of soft drinks and low- temperature foods in Taiwan. Currently, Dali plans to develop the South-East Asian market and broadens the visibility of Dali products in the Chinese market. Notably, following the entry of Taiwan to the World Trade Organization, Dali plans to seek strategic alliance with prominent international companies, and introduced international bread to lighten the embedded future impact. In the domestic soft drinks market, Dali produces tea beverages to meet demand from four distribution centers in Taichung, Chiayi, Kaohsiung, and Taipei with production being based on three plants in Changhua, Touliu, and Hsinchu. According to the preliminary environmental information, the following summarizes the potential supply available from these three plants, the forecast demand from the four distribution centers and the unit transportation costs for each route used by Dali for the upcoming season. The environmental coefficients and related parameters generally are imprecise numbers with triangular possibility distributions over the planning horizon due to incomplete or unobtainable information. For example, the available supply of the Changhua plant is (7.2,8,8.8) thousand dozen bottles, the forecast demand of the Taichung distribution center is (6.2,7,7.8) thousand dozen bottles, and the transportation cost per dozen bottles from Changhua to Taichung is (8,10,10.8) [cost is in dollars]. Due to transportation costs being a major expense, the management of Dali is initiating a study to reduce these costs as much as possible. The fully fuzzy transportation problem with trapezoidal fuzzy numbers of the Dali Company is given in Table 18. Here, the supply and demand are in tonnes.

Table 18 Example III problem illustration

Solution:

This is an unbalanced problem as the last cell in Table 18 indicates that there is some difference between supply and demand. To make it as a balanced transportation problem, add an additional row as zero entries of triangular fuzzy numbers and make the problem as a balanced one.

The number of allocations is seven which is equal to $m+n-1=4+4-1=7$.

Applying the proposed algorithm, the fuzzy feasible solution is given by

$$\begin{aligned}{\text {T.C}} &\approx (8,10,10.8) * (6.2,7,7.8) + (6,8,8.8 ) * (7.8,9,10.2) \\&\quad + (7.8,10,10.8) * (6.5,8,9.5) + (0,0,0 ) * (-0.3,0,0.3) \\&\quad + (20.4,22,24) * (1,1,1)+ (18.2,20,22) * (4.2,5,5.8) \\&\quad + (9.6,12,13 )* (3.7,4,4.3)\approx (279.46,392, 484.1). \end{aligned}$$

After applying the fuzzy modified distribution method

$$\begin{aligned}{\text {T.C}} &\approx (8,10,10.8) * (6.2,7,7.8) + (6,8,8.8 ) * (7.8,9, 10.2) \\&\quad + (7.8,10,10.8) * (1.3,2,2.7) + (9.6,12,13 ) * (8.9,10,11.1) \\&\quad + (10,12,13 ) * (4.2,5,5.8) + (8,10,10.6) * (1,1,1) \\&\quad + (0,0,0 ) * (-0.3,0,0.3) \approx (241.98,352,433.66) \\&\quad \approx (241980,352000,433660)\,{\text {dollars}}. \end{aligned}$$

The membership function for the obtained result is

• According to the decision maker, the minimum transportation cost will lie between 241,980 and 433,660 dollars.

• The overall level of the satisfaction of the decision maker about the statement that the minimum transportation cost will be 352,000 dollars is 100 

• The overall level of the satisfaction of the decision maker for the remaining values of minimum transportation cost can be obtained as follows: Let $x_{0}$ represents the minimum transportation cost, then the overall level of satisfaction of the decision maker for $x_{0}$ is $\mu _{\tilde{A}}(x_{0})\times 100$, where

  $$\begin{aligned} \mu _{\tilde{A}}(x) = \left\{ \begin{array}{ll} \frac{x-241980}{110020} & 241980 \le x\le 352000\\ 1 & x=352000 \\ \frac{433660-x}{81660} & 352000\le x\le 433660 \\ 0 & {\text {otherwise}}\\ \end{array}\right. \end{aligned}$$

Remark 4.1

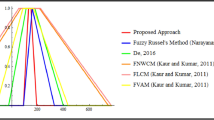
In [10], this problem was solved using possibilistic linear-programming technique and the solution of the case study is given as (352000, 315800, and 367000), which is not a triangular fuzzy number, since a triangular fuzzy number (a, b, c) should satisfy the relation $(a \le b \le c)$. The fuzzy transportation cost using the fuzzy Hungarian MODI method is (241980, 352000, 433660), which is a fuzzy number. In the literature [3] for solving transportation problems, tabular methods are preferred as compared to linear-programming techniques, and so it can be suggested to use the proposed method instead of possibilistic linear-programming method for solving the fully fuzzy transportation problems.

Remark 4.2

In [14], this problem was converted to a generalized fuzzy numbers and solved by finding the fuzzy basic feasible solution using the fuzzified version of north-west corner rule, least cost method, Vogel’s approximation method, and optimum solution using the fuzzified version of the modified distribution method. The solution is given as (279600, 352000, 382000; 1) dollars. The calculated cost using the fuzzy Hungarian MODI method is (241980, 352000, 433660) dollars and it satisfies the optimality and feasibility conditions. The number of iterations in fuzzy modified distribution method is reduced in the fuzzy Hungarian MODI method because of the use of elementwise subtraction. Therefore, the convergence of the solution is faster in this fuzzy Hungarian MODI method compared to the method described in [14].

Note: The comparative study between the existing and the proposed methods is given in Table 19.

Table 19 Comparison table

5 Conclusions

In this paper, an efficient method called the fuzzy Hungarian MODI algorithm is proposed and implemented to solve fully fuzzy transportation problem with triangular fuzzy numbers. The method is also extended for solving the fully fuzzy transportation problem with trapezoidal fuzzy numbers. The fuzzy Hungarian MODI method has the advantage of obtaining the fuzzy optimal solution which satisfies the feasibility, optimality conditions, and the positive values in all the allocated cells. A comparative study of this method with the methods based on [13, 14] reveals that the method based on the elementwise subtraction gives the optimal solution with positive allocations. The proposed method satisfies all necessary conditions to be an optimal solution. An advantage of the proposed method is that it is systematic and easy to understand. It can also be used to solve unbalanced transportation problems and transportation problem with degeneracy. It serves as an important tool for the decision makers to handle various types of logistic problems involving fuzzy parameters.