Heuristic algorithm for an optimal solution of fully fuzzy transportation problem

Abstract

Several problems involving uncertainties can be modeled with fuzzy numbers according to the type of these uncertainties. It is natural to express the solution to such a problem with fuzzy numbers. In this study, we consider the fully fuzzy transportation problem. All input parameters of the problem are expressed with fuzzy numbers given in the parametric form. We propose a new heuristic algorithm to approximate the fuzzy optimal solution. The fuzzy problem is solved by transforming it into two independent parametric problems with the proposed method. We first divide the interval [0, 1] into a sufficiently large number of equal intervals, then write a linear programming problem for each partition point and solve these problems by transforming them into transportation problems. The proposed algorithm is supported by examples.

1 Introduction

The classical transportation problem is a one-stage supply chain planning problem. This problem was first formulated by Hitchcock [1]. For this reason, it is also called the Hitchcock problem in the literature. The supply chain can be multi-stage or contain some uncertainties. Also, unlike the Hitchcock model, carriers can require a fixed charge in addition to the per-unit fee. Due to these variations, we encounter research on many types of transportation problems in the literature [2,3,4,5,6].

Naturally, real-life problems can contain uncertain parameters [7]. As it is known, problems involving uncertainty can be modeled with the help of interval analysis, fuzzy sets, or stochastic analysis, depending on the type of uncertainty. If the values of the variables containing uncertainty are in a certain range with a certain membership degree, it is useful to apply the theory of fuzzy sets to this problem. Modeling the transportation problem, which is an optimization problem, with the help of fuzzy sets has some difficulties. These difficulties are mainly because the concepts of order that have been defined so far between fuzzy numbers are not mathematically sufficient. For example, they do not satisfy the axioms of ordering or partial ordering. We can categorize the published studies examining the fuzzy transportation problem into two groups. In the first group, special fuzzy numbers (triangular fuzzy numbers, trapezoidal fuzzy numbers, and generalized trapezoidal fuzzy numbers) were used in the definition of the problem, and the classical transport problem was solved for the real numbers determining these fuzzy numbers. On the other hand, in studies in the second group, an order is defined between fuzzy numbers and the fuzzy problem is converted to the classical one using a ranking function.

One of the first studies in the first group is [8]. In this study, an algorithm is proposed to solve fuzzy-restricted transportation problems and the relationship between the algebraic structure of the optimal solution of the classical problem and its fuzzy equivalent is investigated. However, Chanas et al. [9] show that the propositions in that study are not correct and they suggest solving a fuzzy problem by parametric programming methods. Chanas and Kuchta [10] define the optimal solution by considering the fuzzy transport problem over $\alpha$-cuts of fuzzy numbers and propose a method to find this solution. Tada and Ishii [11] formulate the integer fuzzy transportation problem and propose a method by converting the problem to a programming problem over the membership function. Liu and Kao [12] apply the extension principle to a fuzzy transportation problem.

One of the most comprehensive and remarkable studies in the first group was done by Ebrahimnejad [13]. In this study, an efficient algorithm for the solution of the fuzzy transportation problem is proposed and explained in examples. However, since the proposed algorithm is applied to the endpoints and core of fuzzy numbers, it can only be valid when all the limitations and prices are given by fuzzy numbers with linear membership functions (triangular, trapezoidal, etc.)

Studies in the second group [14,15,16,17,18,19] define a rank function on fuzzy numbers and the problem is transformed into a classical transport problem by using ranking. However, it is debatable how accurately the rank functions reflect reality. For example, Kaur and Kumar [18] examined the fuzzy transport problem with trapezoidal numbers, and to compare trapezoidal numbers, they averaged the real numbers that determine this number. In another study [15] the rank function is defined as $(a+4b+c)/6$ for the triangular fuzzy number given by (a, b, c). Although the algorithms proposed in these studies have theoretical importance, they have difficulty reflecting reality. There are two reasons for that; firstly, a fuzzy number or uncertainty cannot be expressed with just a real number, this approach contradicts the logic of fuzziness. Secondly, rank functions defined in that way do not satisfy ordering or partial ordering axioms.

In recent years, apart from the studies in these two groups, researchers have proposed to solve the fuzzy transport problem approximately with metaheuristic optimization algorithms. Singh and Singh [20] applied the particle swarm optimization algorithm to solve the problem. In the present study, we propose a new algorithm to find an approximate optimal solution to the fuzzy transportation problem. Our approach to the fuzzy problem is similar to the approach followed in [13].

The contributions of this study can be listed as:

• In our fuzzy model, fuzzy numbers are given in parametric form; these numbers are almost the most general form of fuzzy numbers and cover all special cases.

• The transportation problem is solved by dividing the fuzzy number’s parameter into a finite but sufficient large number of pieces and then an approximate solution is constructed by consolidating the solutions found.

• All of the linear programming problems are transformed into the classical transportation problem, therefore, the result is obtained without using the simplex algorithm.

• The fuzzy solutions, obtained in all algorithms that do not use a ranking function, are in the form of the same type of fuzzy numbers as the input data of the problem. For example, if the input data are trapezoidal numbers, the solutions obtained are also trapezoidal numbers. The reason behind this is, that such algorithms solve the classical transportation problem for real components defining input fuzzy numbers and combining the results linearly. Since the Fully Fuzzy Transportation problem includes the multiplication of fuzzy numbers, it loses its linearity feature. This prevents the solution from being the same type as the input data in the general case. On the other hand, with our proposed method, the fuzzy solution obtained may not be the same kind of fuzzy number as the input data even though it does not use a ranking function. For example, although the input data is triangular fuzzy numbers, the result of the algorithm has not to be triangular fuzzy numbers or even any special fuzzy numbers when our method is applied.

The rest of the study is organized as follows. Necessary preliminary information about fuzzy numbers and classical transport problems is explained in Sect. 2. In Sect. 3, we define the fully fuzzy transportation problem and transform it into two independent parametric transportation problems. In Sect. 4, we present the proposed numerical algorithm, and in Sect. 5, we solve examples. Finally, we make concluding remarks in Sect. 6.

2 Preliminary information

2.1 Preliminary information on fuzzy sets theory

Let us define the concept of parametric fuzzy numbers following the study [21].

Definition 1

A fuzzy number $\tilde{{f}}=\left( {\underline{f},\overline{f} } \right)$ is an ordered pair of functions $\underline{f}(\cdot )$ and $\overline{f} (\cdot )$ holding three conditions below:

• 1. $\underline{f}:[0,\,1]\rightarrow R$ is a bounded, non-decreasing, left continuous function,

• 2. $\overline{f}:[0,\,1]\rightarrow R$ is a bounded, non-increasing, left continuous function,

• 3. For all $r\in [0,\,1]$ the inequality $\underline{f}(r)\le \overline{f} (r)$ holds.

If the ranges of functions $\underline{f}(\cdot )$ and $\overline{f} (\cdot )$ mentioned in Definition 1 are $R^{+}$, then number $\tilde{{f}}=\left( {\underline{f},\overline{f} } \right)$ is called as positive fuzzy number.

Definition 2

Let real numbers a, b, c satisfying the condition $a<c<b$ be given. If $\underline{f}(r)=a+(c-a)r$ and $\overline{f} (r)=b+(c-b)r$ the fuzzy number $\tilde{{f}}=\left( {\underline{f},\overline{f} } \right)$ is called triangular number and denoted shortly as $\tilde{{f}}=(a,c,b)$.

Membership functions of triangular numbers are defined by the formula below:

$$\begin{aligned} \mu (x)=\left\{ {{\begin{array}{ll} \frac{x-a}{c-a},&{}\quad if\; a\le x\le c \\ \frac{b-x}{b-c},&{}\quad if\; c\le x\le b \\ \end{array} }} \right. \end{aligned}$$

Definition 3

Let real numbers a, b, c, d holding the condition $a<c<d<b$ be given. If $\underline{f}(r)=a+(c-a)r$ and $\overline{f} (r)=b+(d-b)r$ the fuzzy number $\tilde{{f}}=\left( {\underline{f},\overline{f} } \right)$ is called trapezoidal number and denoted shortly as $\tilde{{f}}=(a,c,d,b)$.

The membership function of trapezoidal numbers is defined by the formula below:

$$\begin{aligned} \mu (x)=\left\{ {{\begin{array}{ll} \frac{x-a}{c-a},&{}\quad if\;a\le x\le c \\ 1,&{}\quad if\;c\le x\le d \\ \frac{b-x}{b-d},&{}\quad if\;d\le x\le b \\ \end{array} }} \right. \end{aligned}$$

We should note that for a real number of a if we choose $\underline{f}(r)\equiv a$ and $\overline{f} (r)\equiv a$, then this number can be denoted as a fuzzy number $\tilde{{f}}=\left( {\underline{f},\overline{f} } \right)$ in parametric form.

For fuzzy numbers $\tilde{{f}}_{1} =(\underline{f}_{1},\overline{f}_{1} )$ and $\tilde{{f}}_{2} =(\underline{f}_{2},\overline{f}_{2} )$ defined in parametric form, sorting, and arithmetic operations are defined below:

• 1. $\tilde{{f}}_{1} =\tilde{{f}}_{2} \Leftrightarrow \underline{f}_{1} (r)=\underline{f}_{2} (r)$ and $\;\overline{f}_{1} (r)=\overline{f}_{2} (r);$ for all $r\in [0,\;1]$

• 2. $\tilde{{f}}_{1}<\tilde{{f}}_{2} \Leftrightarrow \underline{f}_{1} (r)<\underline{f}_{2} (r)$ and $\;\overline{f}_{1} (r)<\overline{f}_{2} (r);$ for all $r\in [0,\;1]$

• 3. $\tilde{{f}}_{1}>\tilde{{f}}_{2} \Leftrightarrow \underline{f}_{1} (r)>\underline{f}_{2} (r)$ and $\;\overline{f}_{1} (r)>\overline{f}_{2} (r);$ for all $r\in [0,\;1]$

• 4. $\tilde{{f}}_{1} +\tilde{{f}}_{2} =(\underline{f}_{1} (r)+\underline{f}_{2} (r),\;\overline{f}_{1} (r)+\overline{f}_{2} (r))$

  Since we examine only positive fuzzy numbers in this study, let us define multiplication operation for only positive fuzzy numbers as:

• 5. $\tilde{{f}}_{1} \tilde{{f}}_{2} =(\underline{f}_{1} (r)\underline{f}_{2} (r),\;\overline{f}_{1} (r)\overline{f}_{2} (r))$, if $\tilde{{f}}_{1}>0,\;\tilde{{f}}_{2} >0$

2.2 Preliminary information on classical transportation problem

Let us assume that there are m suppliers and n distributors. The unit cost of transporting a product from the $i^{th}$ supplier to the $j^{th}$ distributor is $c_{ij}$. Moreover, capacity of $i^{th}$ supplier is $s_{i}$ and capacity of $j^{th}$ distributor is $d_{j}$. Let’s assume that the total capacity of the suppliers is equal to the total capacity of the distributors. In other words, the following equality called the balance condition, is satisfied:

$$\begin{aligned} \sum \limits _{i=1}^m {s_{i} } =\sum \limits _{j=1}^n {d_{j} } \end{aligned}$$

Then, the classical transportation problem is defined as follows [1]:

$$\begin{aligned} \sum \limits _{i=1}^m {\sum \limits _{j=1}^n {c_{ij} x_{ij} \rightarrow \min } } \end{aligned}$$

(1)

$$\begin{aligned} \sum \limits _{j=1}^n {x_{ij} =s_{i} } \end{aligned}$$

(2)

$$\begin{aligned} \sum \limits _{i=1}^m {x_{ij} =d_{j} } \end{aligned}$$

(3)

$$\begin{aligned} x_{ij} \ge 0 \end{aligned}$$

(4)

for all $i=1,\;2,\ldots ,m$ and for all $j=1,\;2,\ldots ,n$

A matrix $X=(x_{ij} )$ holding conditions (2–4) is called a feasible solution. Feasible solution minimizing the objective function (1) is called an optimal solution. The following Hitchcock theorem is well-known:

Theorem 1

([1]) For an optimal solution $X=(x_{ij} )$, number of positive cells is at most $m+n-1$.

There are efficient algorithms such as the North–West corner method, the least cost cell method, Vogel method for finding an initial feasible solution [22]. Today, researchers still propose algorithms for finding better initial feasible solutions.

We use the North–West corner method in the proposed algorithm to find the initial solutions. This algorithm can produce an initial feasible solution in processing time O(n) when $m=n$. The main idea behind this method can be described below: we first compare numbers $s_{1}$ and $d_{1}$. If $s_1 < d_1$, then by assigning $x_{11} =s_{1},x_{12} =0,\;x_{13} =0,\ldots ,\;x_{1n} =0$, we make $d_{1} =d_{1} -s_{1}$ and $s_{1} =0$. If $s_{1} >d_{1}$, then by assigning $x_{11} =d_{1},\;x_{21} =0,\;x_{31} =0,\ldots ,\;x_{m1} =0$, we make $s_{1} =s_{1} -d_{1}$ and $d_{1} =0$. If $s_{1} =d_{1}$, then by assigning $x_{11} =s_{1} =d_{1}$ and assigning 0 to all other elements of the first row and first column of feasible solution matrix, we have $s_{1} =d_{1} =0$. After this step, at least one row or column of a feasible solution matrix will be determined and the number of rows or columns will decrease by 1. Then we can repeat the same steps for the remaining matrix. For example, if the condition holds in the first step, then it means that the first row of the solution matrix is determined. In this case, since the cell (2, 1) will be the North–West cell, we have to compare $s_{2}$ and $d_{1}$ in the next step. If the condition $s_{1} >d_{1}$ holds in the first step, then it means that the first column of the solution matrix is determined and now the North–West cell is (1, 2); that is, we have to compare $s_{1}$ and $d_{2}$. If the equality holds in the first step, then the North–West cell will be (2,2) and numbers $s_{2}$ and $d_{2}$ will be compared. We will continue these steps until the solution matrix is completely determined.

After the initial suitable solution with $m+n-1$ number of cells is found, the MODI (or with its other name $u-v$ ) method can be applied to find the optimal solution [22]. Main idea behind the MODI algorithm is: Numbers $u_{i}$ corresponding each $i^{th}$ row and numbers $v_{j}$ corresponding each $j^{th}$ row is found based on nonempty cells of the initial solution considering the formula $u_{i} +v_{j} =c_{ij}$. The first number is assigned as 0 (Value of $u_{i}$ or $v_{j}$ corresponding to the first row or column is usually taken as 0). Then, the penalty points are calculated based on $P_{ij} =u_{i} +v_{j} -c_{ij}$ considering the empty cells of the initial solution. If for all i and j, condition $P_{ij} \le 0$ holds, then the optimal solution is found. Otherwise, starting from the cell having the largest penalty number, a closed path (loop) is created. There should be only 2 cells in each row or column and all cells should be full except the first one. Also, 2 consecutive cells on the path must either be in the same row or the same column. Then the empty cell is marked with ‘$+$’ and the next is marked with ‘-’ and all cells on the path are marked consecutively ‘$+$’ and ‘-’. The cell marked with ‘$+$’ with the smallest number is found, this number is subtracted from cells with the ‘$+$’ sign and is added to the cells with ‘-’, and a new feasible solution is obtained. Then, the above steps are repeated until the optimal solution is found.

Table 1 Initial table for the MODI algorithm

As an example, a transportation problem and an initial solution to this problem are given in Table 1. In the table, the capacities of the suppliers are given in the last column and the capacities of the distributors are given in the bottom row. The numbers written after the / sign in the table show the transportation prices and the numbers written before that sign show the values of the initial solution. For example, the meaning of 70/2 written in the cell at the intersection of $S_1$ and $D_1$ is: 70 units of product are planned to be transported from $S_1$ to $D_1$ and the cost per unit of this transportation is 2. If the number is not written before the / sign, it is not planned to transport a product in this direction. Let’s explain one step of the MODI algorithm in this example. First, let’s calculate the u and v values with the formula $u_i+v_j=c_{ij}$ according to the filled cells (cells showing that a product is planned to be transported). Let’s take $u_1=0$. Accordingly, $v_1=2$ and $v_4=6$. Since $v_4=6$ then $u_3=4$, and from here $v_2=0, u_2=5, v_3=-3$ are found. Now, let’s calculate the penalty points with $P_{ij}=u_i+v_j-c_{ij}$ formula for empty cells. $P_{12}=-2, P_{13}=-9, P_{21}=3, P_{24}=9, P_{31}=1, P_{33}=-2$ are found. If these values were all less than or equal to 0, the optimal solution would be found. Let’s take the one with the largest P value among the cells with the positive value. In this example, this cell is (2, 4). Let’s find a path starting from this cell and returning to this cell, passing through filled cells, provided that there is only one cell in each row and each column: $(2,4)\rightarrow (2,2)\rightarrow (3,2)\rightarrow (3,4)\rightarrow ( 2,4)$. Then, put a “$+$” sign in the starting cell and alternately put “−” and “$+$” signs in the cells on the path. Accordingly, cell (2, 4) will be marked with “$+$”, cell (2, 2) with “−”, cell (3, 2) with “$+$” and cell (2, 4) with “−”. Then, add the minimum number (20 from cell (2, 2) in this example) in the cells marked with “−” to the cells marked with “$+$”, and subtract from the cells marked with “-”. After these operations, our transport area will have changed as shown in Table 2.

Table 2 After applying one step of the MODI algorithm

According to the first transportation plan, the cost between the considered 4 cells was $5\times 20+4\times 100+10\times 50=1000$. In the plan obtained after applying the MODI algorithm, this cost became $4\times 120+10\times 30+1\times 20=800$, that is, it decreased.

3 Fully fuzzy transportation problem

Let us assume that there are m suppliers and n distributors. Fuzzy transportation problem can be defined as:

$$\begin{aligned} F=\sum \limits _{i=1}^m {\sum \limits _{j=1}^n {\tilde{{c}}_{ij} \tilde{{x}}_{ij} \rightarrow \min } } \end{aligned}$$

(5)

$$\begin{aligned} \sum \limits _{j=1}^n {\tilde{{x}}_{ij} } =\tilde{{s}}_{i} \end{aligned}$$

(6)

$$\begin{aligned} \sum \limits _{i=1}^m {\tilde{{x}}_{ij} } =\tilde{{d}}_{j} \end{aligned}$$

(7)

$$\begin{aligned} \tilde{{x}}_{ij} \ge 0 \end{aligned}$$

(8)

for all $i\in \left\{ {\;1,\;2,\ldots ,n} \right\}$ and $j\in \left\{ {\;1,\;2,\ldots ,m} \right\}$.

Here $\tilde{{c}}_{ij} =(\underline{c}_{ij} (r),\overline{c}_{ij} (r)),\;\tilde{{s}}_{i} =(\underline{s}_{i} (r),\overline{s}_{i} (r)),\;\tilde{{d}}_{j} =(\underline{d}_{j} (r),\overline{\;d}_{j} (r))$ are given fuzzy numbers in parametric form. In this study, we assume that the balance condition

$$\begin{aligned} \sum \limits _{i=1}^m {\tilde{{s}}_{i} } = \sum \limits _{j=1}^n {\tilde{{d}}_{j} } \end{aligned}$$

(9)

for the fully fuzzy transportation problem is satisfied. The condition (9) means that we have

$$\begin{aligned} \sum \limits _{i=1}^m {\underline{s}_{i} (r)} =\sum \limits _{j=1}^n { \underline{d}_{j} (r)} \end{aligned}$$

(10)

and

$$\begin{aligned} \sum \limits _{i=1}^m {\overline{s}_{i} (r)} =\sum \limits _{j=1}^n { \overline{d}_{j} (r)} \end{aligned}$$

(11)

Let us write the solution $\tilde{{x}}_{ij}$ of the problem (5–8) in the parametric form as $\tilde{{x}}_{ij} =(\underline{x}_{ij} (r),\;\overline{x}_{ij} (r))$. Therefore, the problem (5–8) turns into the following parametric problem:

$$\begin{aligned} \sum \limits _{i=1}^m {\sum \limits _{j=1}^n {\left[ {\underline{c}_{ij} (r)\underline{x}_{ij} (r),\;\overline{c}_{ij} (r)\overline{x}_{ij} (r)} \right] \rightarrow \min } } \end{aligned}$$

(12)

$$\begin{aligned} \sum \limits _{j=1}^n {\underline{x}_{ij} (r)} =\underline{s}_{i} (r) \end{aligned}$$

(13)

$$\begin{aligned} \sum \limits _{i=1}^m {\underline{x}_{ij} (r)} =\underline{d}_{j} (r) \end{aligned}$$

(14)

$$\begin{aligned} \underline{x}_{ij} (r)\ge 0 \end{aligned}$$

(15)

$$\begin{aligned} \sum \limits _{j=1}^n {\overline{x}_{ij} (r)} =\overline{s}_{i} (r) \end{aligned}$$

(16)

$$\begin{aligned} \sum \limits _{i=1}^m {\overline{x}_{ij} (r)} =\overline{d}_{j} (r) \end{aligned}$$

(17)

$$\begin{aligned} \overline{x}_{ij} (r)\ge \underline{x}_{ij} (r) \end{aligned}$$

(18)

for all $i\in \left\{ {\;1,\;2,\ldots ,m} \right\}$ and $j\in \left\{ {\;1,\;2,\ldots n} \right\}$

According to the ordering property of fuzzy numbers, the problem of seeking the minimum value of the objective function (12) is equivalent to the problem of seeking the minimum value of both the two objective functions given below:

$$\begin{aligned} \sum \limits _{i=1}^m {\sum \limits _{j=1}^n {\underline{c}_{ij} (r)\underline{x}_{ij} (r)} } \rightarrow \min \end{aligned}$$

(19)

$$\begin{aligned} \sum \limits _{i=1}^m {\sum \limits _{j=1}^n {\overline{c}_{ij} (r)\overline{x} _{ij} (r)} } \rightarrow \min \end{aligned}$$

(20)

Since the constraints in the problem (12–18) are separable, this problem can be divided into 2 problems:

It can be noted that the objective function (19) depends only on $\underline{x}_{ij}$ and (20) depends only on $\overline{x}_{ij}$. Besides, constraints (13–15) for $\underline{x}_{ij}$ are independent from the constraints (16–17) for $\overline{x}_{ij}$. Then, the problem (12–18) can be divided into two separate problems:

1. Problem A: Minimization of the objective function (19) under conditions (13–15),

and (after solving Problem A)

2. Problem B: Minimization of the objective function (20) under conditions (16–18).

Once the mentioned problems are solved, i.e. $\underline{x}_{ij}$ and $\overline{x}_{ij}$ (the left and right ends of the fuzzy solution) are determined, we will construct the solution $(\underline{x}_{ij}(r), \overline{x}_{ij}(r))$, and thus express the fuzziness of the solution. It is worth emphasizing that $\underline{x}_{ij}(1)=\overline{x}_{ij}(1)$ represents the core (crisp part) of the fuzzy solution, and $(\underline{x}_{ij}(r)-\underline{x}_{ij}(1), \overline{x}_{ij}(r)-\overline{x}_{ij}(1))$ represents its fuzziness.

4 The proposed numerical algorithm

In this section, we describe the proposed numerical algorithm. While developing our algorithm, we were inspired by the work of Ebrahimnejad for special fuzzy numbers ([13]) and by the method proposed by Gasilov et al. [23] and by Gasilov [24] for fuzzy and interval differential equations, respectively.

Let us divide the interval $\left[ {0,\;1} \right]$ into k number equal subintervals with the help of the points $r_{0} =0<r_{1}<r_{2}<\cdots <r_{k} =1$. The main idea of the method is solving Problems A and B iteratively for numbers $r_{i}$. Note that these problems are classical linear programming problems. We propose to transform these problems into classical transportation problems and solve them with the help of the algorithms described in the preliminary information.

Now, let us explain our solution method. First, we solve Problem A for the $r=r_{0}$. The obtained optimal solution we denote as $\underline{X}_{0}^{*} =(\underline{x}_{ij}^{*} (r_{0} ))$. Let $\underline{z}_{0}^{*}$ be the optimal value of the objective function (19).

Then iteratively for each $t\in \{1,\ldots ,k\}$, we put $r=r_{t}$ in the objective function (19) and change the constraints as below:

$$\begin{aligned} \sum \limits _{j=1}^n {\underline{x}_{ij} (r_{t} )} =\underline{s}_{i} (r_{t}) \end{aligned}$$

(21)

$$\begin{aligned} \sum \limits _{i=1}^m {\underline{x}_{ij} (r_{t} )} =\underline{d}_{j} (r_{t}) \end{aligned}$$

(22)

$$\begin{aligned} \underline{x}_{ij} (r_{t} )\ge \underline{x}_{ij}^{*} (r_{t-1} ) \end{aligned}$$

(23)

for all $i\in \left\{ {\;1,\;2,\ldots ,m} \right\}$ and $j\in \left\{ {\;1,\;2,\ldots ,n} \right\}$.

We note that the balance condition

$$\begin{aligned} \sum \limits _{i=1}^m {\underline{s}_{i} (r_{t})} =\sum \limits _{j=1}^n { \underline{d}_{j} (r_{t})} \end{aligned}$$

(24)

is satisfied due to (10).

Let $\underline{X}_{t}^{*} =(\underline{x}_{ij}^{*} (r_{t} ))$ be the optimal solution of (19) under conditions (21–23) and $\underline{z}_{t}^{*}$ be the corresponding optimal value of the objective function (19) for $t=1,\;2,..,k$.

Proposition 1

For all $t=1,\;2,\ldots ,k$, the inequality $\underline{z}_{t-1}^{*} \le \underline{z}_{t}^{*}$ holds.

Proof

According to the first condition in the definition of fuzzy numbers, we have the inequality $\underline{c}_{ij} (r_{t-1} )\le \underline{c}_{ij} (r_{t} )$. Moreover, from the constraint (23), the inequality $\underline{x}_{ij}^{*} (r_{t-1} )\le \underline{x}_{ij}^{*} (r_{t} )$ holds. Therefore, we obtain the desired inequality

$$\begin{aligned} \underline{z}_{t-1}^{*} =\sum \limits _{i=1}^m {\sum \limits _{j=1}^n {\underline{c}_{ij} (r_{t-1} )\underline{x}_{ij}^{*} (r_{t-1} )} } \le \sum \limits _{i=1}^m {\sum \limits _{j=1}^n {\underline{c}_{ij} (r_{t} )\underline{x}_{ij}^{*} (r_{t} )} } =\underline{z}_{t}^{*}\;\; \end{aligned}$$

$\square$

We note that the minimization of (19) under conditions (21–23) is not classical transportation problem. We can transform this problem into a classical transportation problem by the substitution of the variables. For this, we do the following substitution:

$$\begin{aligned} \underline{x}_{ij} (r_{t} )=\underline{y}_{ij} (r_{t} )+\underline{x}_{ij}^{*} (r_{t-1} ) \end{aligned}$$

Therefore, we obtain

$$\begin{aligned} \underline{z}_{t} =\sum \limits _{i=1}^m {\sum \limits _{j=1}^n {\underline{c}_{ij} (r_{t} )\underline{x}_{ij} (r_{t} )} } =\sum \limits _{i=1}^m {\sum \limits _{j=1}^n {\underline{c}_{ij} (r_{t} )\underline{y}_{ij} (r_{t} )} } +\sum \limits _{i=1}^m {\sum \limits _{j=1}^n {\underline{c}_{ij} (r_{t} )\underline{x}_{ij}^{*} (r_{t-1} )} } \end{aligned}$$

Since the second term is a constant in the expression of $\underline{z}_{t}$, the problem of the seeking minimum of this function becomes equivalent to the minimization of the first term:

$$\begin{aligned} \sum \limits _{i=1}^m {\sum \limits _{j=1}^n {\underline{c}_{ij} (r_{t} )\underline{y}_{ij} (r_{t} )} } \rightarrow \min \end{aligned}$$

(25)

As a result of our substitution, constraint (21) becomes as follows:

$$\begin{aligned} \sum \limits _{j=1}^n {\underline{(y}_{ij} (r_{t} )} +\underline{x}_{ij}^{*} (r_{t-1} ))=\sum \limits _{j=1}^n {\underline{y}_{ij} (r_{t} )} +\sum \limits _{j=1}^n {\underline{x}_{ij}^{*} } (r_{t-1} ))=\underline{s}(r_{t} ) \end{aligned}$$

Since $\sum \limits _{j=1}^n {\underline{x}_{ij}^{*} (r_{t-1} )=\underline{s}(r_{t-1} )}$, so we can rewrite the constraint (21) in the form below:

$$\begin{aligned} \sum \limits _{j=1}^n {\underline{y}_{ij} (r_{t} )} =\underline{s}(r_{t} )-\underline{s}(r_{t-1} ) \end{aligned}$$

(26)

Note that according to the first condition in the definition of fuzzy numbers, the numbers on the right-hand side of the constraint (26) are non-negative. Similarly, the constraints (22–23) can be written as follows after the substitution:

$$\begin{aligned} \sum \limits _{i=1}^m {\underline{y}_{ij} (r_{t} )} =\underline{d}_{j} (r_{t} )-\underline{d}_{j} (r_{t-1} ) \end{aligned}$$

(27)

$$\begin{aligned} \underline{y}_{ij} (r_{t} )\ge 0 \end{aligned}$$

(28)

for all $i\in \left\{ {\;1,\;2,\ldots ,m} \right\}$ and $j\in \left\{ {\;1,\;2,\ldots ,n} \right\}$.

Note that according to the first condition in the definition of fuzzy numbers, the numbers on the right-hand side of the constraint (27) are non-negative. The problem (25–28) is a classical transportation problem. We can summarize the discussion above with the following steps.

Step 1 To find an initial feasible solution to Problem A for $r=r_{0}$, apply the North–West corner algorithm. Then find an optimal solution $\underline{X}_{0}^{*} =(\underline{x}_{ij}^{*} (r_{0} ))$ and the optimal value $\underline{z}_{0}^{*}$ of the objective function for this problem by applying MODI algorithm.

Step 2 Assign $t=1$.

Step 3 Apply North–West corner algorithm to the problem (25–28) for $r=r_{t}$ to find initial feasible solution. Then find an optimal solution $\underline{Y}_{t}^{*} =(\underline{y}_{ij}^{*} (r_{t} ))$ of the problem by applying the MODI algorithm.

Step 4 Get an optimal solution of the (19) under conditions (21–23) by the formula $\underline{X}_{t}^{*} =\underline{Y}_{t}^{*} +\underline{X}_{t-1}^{*}$

Step 5 Calculate the optimal value of the function (19) by the formula $\underline{z}_{t}^{*} =\sum \limits _{i=1}^m {\sum \limits _{j=1}^n {\underline{c}_{ij} (r_{t} )\underline{x}_{ij}^{*} (r_{t} )} }$

Step 6 $t=t+1$

Step 7 If $t\le k$ then go to Step 3, otherwise stop.

After applying these steps, we can find the values of the first components of the fuzzy optimal solution $\tilde{{x}}_{ij}^{*} =(\underline{x}_{ij}^{*} (r),\overline{x}_{ij}^{*} (r))$ and fuzzy optimal value $\tilde{{z}}^{*}=(\underline{z}^{*}(r),\overline{z} ^{*}(r))$ of the problem (5–8) for the $r=r_{0} =0,\;r=r_{1},\ldots ,r=r_{k} =1$. We can express the functions $\underline{x}_{ij}^{*} (\cdot )$ and $\underline{z}^{*}(\cdot )$ approximately by using these values. Similarly, by solving Problem B we can find the functions $\overline{x}_{ij}^{*} (\cdot )$ and $\overline{z}^{*}(\cdot )$ approximately. However, in this case, we begin from $r=r_{k} =1$ and perform calculations from right to left. The reason is that the parametric function representing the right-hand side is non-increasing due to 2nd condition in the definition of the fuzzy number. In other words, we first solve Problem B for $r=r_{k} =1$. Now let’s explain how to use condition (18) when we solve problem B. We use this condition only once when solving problem B for $r=r_{k} =1$ as follows:

$$\begin{aligned} \overline{x}_{ij} (1)\ge \underline{x}_{ij}^{*} (1) \end{aligned}$$

(29)

As a result, for $r=r_{k} =1$ we find an optimal solution $\overline{X}_{k}^{*} =(\overline{x}_{ij}^{*} (r_k ))$ and optimal value $\overline{z}_{k}^{*}$ of the objective function. Then we solve, the following problems for $t=k-1,\;k-2,\ldots ,0$ iteratively:

$$\begin{aligned} \sum \limits _{i=1}^m {\sum \limits _{j=1}^n {\overline{c}_{ij} (r_{t} )\overline{x}_{ij} (r_{t} )} } \rightarrow \min \end{aligned}$$

(30)

$$\begin{aligned} \sum \limits _{j=1}^n {\overline{x}_{ij} (r_{t} )} =\overline{s}_{i} (r_{t} ) \end{aligned}$$

(31)

$$\begin{aligned} \sum \limits _{i=1}^m {\overline{x}_{ij} (r_{t} )} =\overline{d}_{j} (r_{t} ) \end{aligned}$$

(32)

$$\begin{aligned} \overline{x}_{ij} (r_{t} )\ge \overline{x}_{ij}^{*} (r_{t+1} ) \end{aligned}$$

(33)

for all $i\in \left\{ {\;1,\;2,\ldots ,m} \right\}$ and $j\in \left\{ {\;1,\;2,\ldots ,n} \right\}$

Here, we denote optimal solution of the problem (30–33) for $t=k-1,\;k-2,\ldots ,0$ by $\overline{X}_{t}^{*} =(\overline{x}_{ij}^{*} (r_{t} ))$ and optimal value of the objective function by $\overline{z} _{t}^{*}$.

Proposition 2

For $t=k-1,\;k-2,\ldots ,0$, the inequality $\overline{z} _{t}^{*} \ge \overline{z}_{t+1}^{*}$ holds.

Proof of Proposition 2 is similar to the proof of Proposition 1.

Since Problem B is not a classical transportation problem to solve the problem for $r=r_{k} =1$ we use a substitution $\overline{x}_{ij} (1 )=\overline{y}_{ij} (1 )+\underline{x}_{ij}^{*} (1)$. After this substitution, the problem becomes the following classical transportation problem:

$$\begin{aligned} \sum \limits _{i=1}^m {\sum \limits _{j=1}^n {\overline{c}_{ij} (1 )\overline{y}_{ij} (1 )} } \rightarrow \min \end{aligned}$$

(34)

$$\begin{aligned} \sum \limits _{j=1}^n {\overline{y}_{ij} (1 )} =\overline{s} (1 )-\underline{s} (1 ) \end{aligned}$$

(35)

$$\begin{aligned} \sum \limits _{i=1}^m {\overline{y}_{ij} (1 )} =\overline{d}_{j} (1 )-\underline{d}_{j} (1 ) \end{aligned}$$

(36)

$$\begin{aligned} \overline{y}_{ij} (1 )\ge 0 \end{aligned}$$

(37)

for all $i\in \left\{ {\;1,\;2,\ldots ,m} \right\}$ and $j\in \left\{ {\;1,\;2,\ldots ,n} \right\}$

Similarly, since the problem (30–33) is not a classical transportation problem, we use a substitution, $\overline{x}_{ij} (r_{t} )=\overline{y}_{ij} (r_{t} )+\overline{x}_{ij}^{*} (r_{t+1} )$. After this substitution, we have to solve the following classical transportation problem:

$$\begin{aligned} \sum \limits _{i=1}^m {\sum \limits _{j=1}^n {\overline{c}_{ij} (r_{t} )\overline{y}_{ij} (r_{t} )} } \rightarrow \min \end{aligned}$$

(38)

$$\begin{aligned} \sum \limits _{j=1}^n {\overline{y}_{ij} (r_{t} )} =\overline{s} (r_{t} )-\overline{s} (r_{t+1} ) \end{aligned}$$

(39)

$$\begin{aligned} \sum \limits _{i=1}^m {\overline{y}_{ij} (r_{t} )} =\overline{d}_{j} (r_{t} )-\overline{d}_{j} (r_{t+1} ) \end{aligned}$$

(40)

$$\begin{aligned} \overline{y}_{ij} (r_{t} )\ge 0 \end{aligned}$$

(41)

for all $i\in \left\{ {\;1,\;2,\ldots ,m} \right\}$ and $j\in \left\{ {\;1,\;2,\ldots ,n} \right\}$

According to the second condition in the definition of the fuzzy number, the numbers on the right-hand side of the constraints (35), (36),(39) and (40) are non-negative. To find the expressions of the functions $\overline{x}_{ij}^{*}(\cdot )$ and $\overline{z}^{*}(\cdot )$ approximately, we apply the steps below:

Step 1 To find an initial feasible solution apply the North–West corner algorithm to the problem (34–37). Then find an optimal solution $\overline{Y}_{k}^{*}=\overline{Y}^{*}(1) =(\overline{y}_{ij}^{*} (1 ))$ for this problem by applying the MODI algorithm.

Step 2 Find an optimal solution $\overline{X} _{k}^{*} =\overline{X}^{*}(1)=(\overline{x}_{ij}^{*}(1)$) and optimal value $z_{k}^{*}=z^{*}(1)$ of the objective function in Problem B for $r=r_{k} =1$ by the formulas:

$$\begin{aligned} \overline{X} _{k}^{*} =\overline{Y}_{k}^{*} +\underline{X}_{k}^{*} \\ \overline{z}_{k}^{*} =\sum \limits _{i=1}^m {\sum \limits _{j=1}^n {\overline{c}_{ij} (1 )\overline{x}_{ij}^{*} (1 )} } \end{aligned}$$

Step 3 Assign $t=k-1$

Step 4 Apply North–West corner algorithm to the problem (38–41) for $r=r_{t}$ to find initial feasible solution. Then find an optimal solution $\overline{Y} _{t}^{*} =(\overline{y}_{ij}^{*} (r_{t} ))$ of the problem by applying MODI algorithm.

Step 5 Get an optimal solution of the problem (30–33) by the formula $\overline{X} _{t}^{*} =\overline{Y}_{t}^{*} +X_{t+1}^{*}$.

Step 6 Calculate the optimal value of the function (30) by the formula $\overline{z}_{t}^{*} =\sum \limits _{i=1}^m {\sum \limits _{j=1}^n {\overline{c}_{ij} (r_{t} )\overline{x}_{ij}^{*} (r_{t} )} }$

Step 7 $t=t-1$

Step 8 If $t\ge 0$, then go to Step 4, otherwise stop.

After applying these steps, we can find the values of the second components of the fuzzy optimal solution $\tilde{{x}}_{ij}^{*} =(\underline{x}_{ij}^{*} (r),\overline{x}_{ij}^{*} (r))$ and fuzzy optimal value $\tilde{{z}}^{*}=(\underline{z}^{*}(r),\overline{z} ^{*}(r))$ of the problem (5–8) for the $r=r_{0} =0,\;r=r_{1},\ldots ,r=r_{k} =1$. By using these values we can express the functions $\overline{x}_{ij}^{*}(\cdot )$ and $\overline{z}^{*}(\cdot )$ approximately. Therefore, we find fuzzy optimal solution $\tilde{{x}}_{ij}^{*} =(\underline{x}_{ij}^{*} (r),\overline{x}_{ij}^{*} (r))$ and the optimal value $\tilde{{z}}^{*}=(\underline{z}^{*}(r),\overline{z}^{*}(r))$ of the fuzzy objective function approximately.

5 Sample problems and results

In this section, we apply our algorithm to some examples. Example 3 is taken from the work of Ebrahimnejad [13]. He solves this example for the trapezoidal fuzzy numbers in his work. We compare the proposed algorithm with Ebrahimnejad’s algorithm in Examples 3 and 4.

Example 1

Suppose that there are 2 suppliers and 2 distributors. Let the following fuzzy numbers give the capacities of suppliers and distributors:

$$\begin{aligned} \;\tilde{{s}}_{1} =(\underline{s}_{1} (r),\overline{s}_{1} (r))=(-2r^{2}+11r+20,\;-10r+39) \\ \tilde{{s}}_{2} =(\underline{s}_{2} (r),\overline{s}_{2} (r))=(30r+50,\;-2r^{2}-19r+101) \\ \tilde{{d}}_{1} =(\underline{d}_{1} (r),\overline{d}_{1} (r))=(20r+15,\;-2r^{2}\;-13r+50) \\ \tilde{{d}}_{2} =(\underline{d}_{2} (r),\overline{d}_{2} (r))=(-2r^{2}+21r+55,-16r+90) \end{aligned}$$

Moreover, costs for transporting unit product from a supplier with number $i\in \{1,\;2\}$ to the distributor $j\in \{1,\;2\}$ are given by fuzzy numbers:

$$\begin{aligned} \;\;\;\tilde{{c}}_{11} =(2r+2,-2r+6);\, \tilde{{c}}_{12} =(-2r^{2}+5r+1,-6r+10) \\ \tilde{{c}}_{21} =(2r+3,-2r+7);\, \tilde{{c}}_{22} =(2r+4,-4r^{2}-2r+12) \end{aligned}$$

Since $\tilde{{s}}_{1} +\tilde{{s}}_{2} =\tilde{{d}}_{1} +\tilde{{d}}_{2}$, the balance condition is satisfied. We divide the interval $\left[ {0,\;1} \right]$ into k numbers equal subintervals by the points $r_{0} =0<r_{1}<r_{2}<\cdots <r_{k} =1$. To explain the proposed algorithm clearly, we choose $k=2$. We first solve the problem for the left ends of fuzzy numbers. The input of the problem for the first step of our algorithm is shown in Table 3.

Table 3 Example1: Input data of left-end problem for $r_{0} =0$

After applying the North–West corner algorithm, we find an initial feasible solution as $\underline{x}_{11} =15,\;\underline{x}_{12} =5,\;\underline{x}_{21} =0,\;\underline{x}_{22} =50$. The input of the MODI algorithm is given in the Table 4.

Table 4 Example 1: Input data of MODI algorithm for the left-end problem for $r_{0} =0$

According to MODI algorithm we calculate the values u and v by formula $u_{i} +v_{j} =\underline{c}_{ij}$ by checking nonempty cells. For this we first put $u_{1} =0$. From $u_{1} +v_{1} =\underline{c}_{11}$ we get $v_{1} =2$, from $u_{1} +v_{2} =\underline{c}_{12}$ we obtain $v_{2} =1$ and from $u_{2} +v_{2} =\underline{c}_{22}$ we get $u_{2} =3$. Then we calculate penalties by the formula $P_{ij} =u_{i} +v_{j} -\underline{c}_{ij}$ for empty cells. In this example, we have only one empty cell. For this cell $P_{21} =u_{2} +v_{1} -\underline{c}_{21} =3+2-3=2>0$. We mark the cells (2,1) and (1,2) by “+”, and the cells (1,1) and (2,2) by “-”. The minimum value in the negative cells is 15, so we subtract 15 from the values of these cells and we add 15 to the positive cells. After this operation, we find the solution $\underline{X}_{0}$ as below:

$$\begin{aligned} \underline{X}_{0} =\left[ {{\begin{array}{*{20}c} 0 &{} {20} \\ {15} &{} {35} \\ \end{array} }} \right] \end{aligned}$$

For this solution from the MODI algorithm, we calculate the values $u_{1} =0,\;v_{2} =1,\;u_{2} =3,\;v_{1} =0,\;P_{11} =-2$. Since $P_{11} < 0$, we find an optimal solution. For this solution optimal value is $\underline{z}_{0}^{*} =1\times 20+3\times 15+4\times 35=205$.

The solutions of the other cases ($t=1 \;(r_1= 0.5)$ and $t=2 \;(r_2=1)$) for the left-end problem are given in Table 5.

Table 5 Example 1: Solutions of the left-end problem for $t=1 \;(r_1= 0.5)$ and $t=2 \;(r_2=1)$

Now we solve the problem (30–33) to find the right end of the fuzzy optimal solution. Let’s first solve the problem for $t=2$ $(r_2=1)$. So we need to solve the problem (34–37). Input data for this problem are given in Table 6.

Table 6 Example 1: Input data of the right-end problem for $r_{2} =1$

The only solution to this problem is

$$\begin{aligned} \overline{Y}_{2}^{*} =\left[ {{\begin{array}{*{20}c} 0 &{} {0} \\ {0} &{} {0} \\ \end{array} }} \right] \end{aligned}$$

Hence we find an optimal solution

$$\begin{aligned} \overline{X}_{2}^{*} =\left[ {{\begin{array}{*{20}c} 0 &{} {29} \\ {35} &{} {45} \\ \end{array} }} \right] \end{aligned}$$

For this solution, the optimal value is $\overline{z}_{2}^{*} =561$. The solutions to the other cases ($t=1 \;(r_1=0.5)$ and $t=0 \;(r_0=0)$ are shown in the Table 7.

Table 7 Example 1: Solutions of the right-end problem for $t=1 \;(r_1= 0.5)$ and $t=0 \;(r_0=0)$

Thus, we found the left-end and right-end of the fuzzy optimal solution and fuzzy optimal value at 3 different points. These values are shown in Table 8.

Table 8 Example 1: Fuzzy optimal solution and fuzzy optimal value for $r=0 \;\; r= 0.5$ and $r=1)$

Now we can combine the points found for the left end of a fuzzy number with an increasing function and those found for the right end with a decreasing function. The simplest way to do this is to connect consecutive points with line segments because there is no condition for the left and right end functions to be smooth in the definition of parametric fuzzy numbers. In this study, computer-assisted solutions of the examples were made using MATLAB, and the graphics of the solutions were drawn using the standard MATLAB functions. Another way is to use one of the monotone polynomial fitting methods [25]. Since in this example we have 3 points for each component of the fuzzy optimal solution, let’s write the second-degree polynomial passing through these points and check whether the resulting polynomial is monotonic in the range [0,1]. For example, since $\underline{x}_{11}^{*}(0)=0$, $\underline{x}_{11}^{*}(0.5)=0$ and $\underline{x}_{11}^{*}(1)=0$, it is clear that the polynomial sought is $\underline{x}^{*}(r)=0$ for every r. Since $\underline{x}_{12}^{*}(0)=20$, $\underline{x}_{12}^{*}(0.5)=25$ and $\underline{x}_{12}^{*}(1)=29$, so $\underline{x}_{12}^{*}(r)={-2r^{2}+11r+20}$. We can easily see that this function is increasing in the range [0,1]. Similarly, we can build other functions and consequently assume that the approximate optimal solution is as follows:

$$\begin{aligned} \underline{X}^{*}(r)=\left[ {{\begin{array}{lc} 0 &{} {-2r^{2}+11r+20} \\ {20r+15} &{} {10r+35} \\ \end{array} }} \right] \end{aligned}$$

Accordingly, the left end of the objective function is as follows:

$$\begin{aligned} \underline{z}^{*}= (-2r^{2}+11r+20)(-2r^{2}+5r+1)+(20r+15)(2r+3)+(10r+35)(2r+4) \end{aligned}$$

Therefore, $\underline{z}^{*}=4r^{4}-32r^{3}+73r^{2}+311r+205$

$$\begin{aligned} \overline{X}^{*}(r) =\left[ {{\begin{array}{lc} \;\;\;0 &{} {-10r+39} \\ {-2r^{2}-13r+50} &{} {-6r+51} \\ \end{array} }} \right] \end{aligned}$$

For this solution, the expression of the objective function at the right end will be as follows:

$$\begin{aligned} \overline{z}^{*}=(-6r+10)(-10r+39)+(-2r+7)(-2r^{2}-13r+50)+(-4r^{2}-2r+12)(-6r+51), \end{aligned}$$

i.e.

$$\begin{aligned} \overline{z}^{*}=28r^{3}-120r^{2}-699r+1352\end{aligned}$$

The fuzzy optimal solution of Example 1 obtained on the computer with the proposed algorithm by taking $k=1000$ is shown in Fig. 1, and the fuzzy optimal value is shown in Fig. 2. In these figures values of r are shown on the horizontal axis and the values of the appropriate functions on the vertical axis.

Fig. 1

Example 1: Fuzzy optimal solution ($k=1000$)

Fig. 2

Example 1: The fuzzy number representing the optimal value of the objective function ($k=1000$)

Remark 1

Actually, we cannot claim that the fuzzy solution $\tilde{{X}}=(\underline{X}(r),\overline{X}(r) )$ we obtained is the exact solution of the problem. Also, the functions $\underline{x}_{ij}(r)$ and $\overline{x}_{ij}(r)$ may not be always expressed with a polynomial function same degree with input functions as in Example 1. We show this situation in Example 2 below.

Example 2

Suppose 2 suppliers and 2 distributors are given. Let the capacities of suppliers and distributors be given by the following fuzzy numbers.

$$\begin{aligned} \;\;\;\;\tilde{{s}}_{1} =(\underline{s}_{1} (r),\overline{s}_{1} (r))=(-2r^{2}+11r+20,\;-20r+49) \\ \tilde{{s}}_{2} =(\underline{s}_{2} (r),\overline{s}_{2} (r))=(30r+50,\;-2r^{2}-9r+91) \\ \;\;\;\tilde{{d}}_{1} =(\underline{d}_{1} (r),\overline{d}_{1} (r))=(20r+15,\;-2r^{2}\;-13r+50) \\ \;\;\;\tilde{{d}}_{2} =(\underline{d}_{2} (r),\overline{d}_{2} (r))=(-2r^{2}+21r+55,-16r+90) \end{aligned}$$

Moreover, transportation costs for transporting unit product from supplier with number $i\in \{1,\;2\}$ to the distributor $j\in \{1,\;2\}$ are given by fuzzy numbers:

$$\begin{aligned} \\ \;\;\;\;\;\;\;\;\;\;\;\tilde{{c}}_{11} =(2r+2,-2r+6);\; \tilde{{c}}_{12} =(-2r^{2}+5r+1,-6r+10) \\ \tilde{{c}}_{21} =(2r+3,-2r+7);\; \tilde{{c}}_{22} =(2r+4,-4r^{2}+10) \end{aligned}$$

Since $\tilde{{s}}_{1} +\tilde{{s}}_{2} =\tilde{{d}}_{1} +\tilde{{d}}_{2}$, the balance condition is satisfied.

We apply the proposed algorithm to this example for $k=2$. We note that the left ends of the fuzzy numbers in Example 2 are the same as the left ends of the numbers in Example 1. Therefore, the left end of the fuzzy optimal solution of the problem will be the same as the solution in Example 1. By applying the proposed algorithm to the right ends for $t=2\;(r_{2} =1),\;t=1\;(r_{1} =0.5),\;t=0\;(r_{0} =0)$ we obtain the following optimal solutions, respectively:

$$\begin{aligned} \overline{X}_{2}^{*} =\left[ {{\begin{array}{*{20}c} 0 &{} {29} \\ {35} &{} {45} \\ \end{array} }} \right] ;\, \overline{X}_{1}^{*} =\left[ {{\begin{array}{*{20}c} 2 &{} {37} \\ {41} &{} {45} \\ \end{array} }} \right] ;\, \overline{X}_{0}^{*} =\left[ {{\begin{array}{*{20}c} 9 &{} {40} \\ {41} &{} {50} \\ \end{array} }} \right] \end{aligned}$$

Since $\overline{d}_{1}$ is a second-order polynomial function, we can expect that either $\overline{x}_{11}$ or $\overline{x}_{21}$ is a second-order polynomial function non-increasing over [0,1]. However, we find that $\overline{x}_{21} (0)=\overline{x}_{21} (0.5)=41$, so according to Roll theorem $\overline{x}_{21}$ cannot be non-decreasing over [0,1] and second-order polynomial function. In this case, $\overline{x}_{11}$ has to be a second-order polynomial function. Let $\overline{x}_{11} (r)=a(r-b)(r-1)$. Since $\overline{x}_{11} (0)=9$ we have $a.b=9$. From $\overline{x}_{11} (0.5)=2$ we get $2=a(0.5-b)(-0.5)$. Hence $-4=0.5a-ab$, and $a=10,\;b=0.9$. As a result, we find the function $\overline{x}_{11} (r)=10r^{2}-19r+9$, but this function is decreasing over $\left( {0,\;\frac{19}{20}} \right)$ and is increasing over $\left( {\frac{19}{20},\;1} \right)$. We know about optimal solutions for the right ends if the optimal solution is

$$\begin{aligned} \overline{X}^{*}(r)=\left[ {{\begin{array}{*{20}c} {\overline{x}_{11}^{*} (r)} &{} {\overline{x}_{12}^{*} (r)} \\ {\overline{x}_{21}^{*} (r)} &{} {\overline{x}_{22}^{*} (r)} \\ \end{array} }} \right] \end{aligned}$$

then $\overline{X}^{*} (1)=\left[ {{\begin{array}{*{20}c} 0 &{} {29} \\ {35} &{} {45} \\ \end{array} }} \right]$, $\overline{X}^{*} (0.5)=\left[ {{\begin{array}{*{20}c} 2 &{} {37} \\ {41} &{} {45} \\ \end{array} }} \right] , \overline{X}^{*} (0)=\left[ {{\begin{array}{*{20}c} 9 &{} {40} \\ {41} &{} {50} \\ \end{array} }} \right]$.

The graphical representation of the fuzzy optimal solution for Example 2 is given in Fig. 3.

Fig. 3

Example 2: Fuzzy optimal solution ($k=2$)

The fuzzy number expressing the value of the objective function for this optimal solution is given in Fig. 4.

Fig. 4

Example 2: Fuzzy optimal value ($k=2$)

Example 3

Suppose 3 suppliers and 4 distributors are given. Let the capacities of suppliers and distributors be given by the following fuzzy numbers.

$$\begin{aligned}\\\;\;\;\tilde{{s}}_{1} =(\underline{s}_{1}(r), \overline{s}_{1}(r))= (55r+3500, -420r+4000)\\\;\;\;\;\tilde{{s}}_{2} =(\underline{s}_{2}(r), \overline{s}_{2}(r))=(-50r+3125, -10r+3200)\\\;\;\;\;\;\tilde{{s}}_{3} =(\underline{s}_{3}(r), \overline{s}_{3}(r))=(520r+2475,-125r+3400) \\\\\;\;\;\;\tilde{{d}}_{1} =(\underline{d}_{1}(r), \overline{d}_{1}(r))=(450r+2050, -350r+3050)\\\;\;\tilde{{d}}_{2} =(\underline{d}_{2}(r), \overline{d}_{2}(r))=(50r+3000, -100r+3200)\\\tilde{{d}}_{3} =(\underline{d}_{3}(r), \overline{d}_{3}(r))=(50r+2100, -60r+2250)\\\tilde{{d}}_{4} =(\underline{d}_{4}(r), \overline{d}_{4}(r))=(75r+1950, -45r+2100)\end{aligned}$$

Transportation charges are as follows:

$$\begin{aligned} \tilde{{c}_{11}}=(19+r,\;22-r);\;\;\;\tilde{{c}_{12}}=(59+3r,\;65-2r)\; \\ \;\;\;\;\;\;\tilde{{c}_{13}}=(90+5r,\;99-2r);\tilde{{c}_{14}}=(150+10r,\;170-5r) \\ \;\;\tilde{{c}_{21}}= (97+2r,\;105-2r);\tilde{{c}_{22}}=(15+2r,\;21-2r) \\ \;\;\;\;\;\;\;\;\;\;\;\tilde{{c}_{23}}=(110+2r,\;119-4r);\tilde{{c}_{24}}=(190+20r,\;240-20r) \\ \;\;\;\;\;\;\;\;\tilde{{c}_{31}}= (260+2r,\;270-6r);\tilde{{c}_{32}}=(240+7r,\;255-6r) \\ \;\;\;\;\;\;\;\;\;\tilde{{c}_{33}}=(272+2r,\;290-11r); \tilde{{c}_{34}}=(320+6r,\;340-8r)\\ \end{aligned}$$

This problem is formulated with trapezoidal numbers in [13], and the following optimal solution is found:

$$\begin{aligned}\\\;\;\;\;\;\;\;\tilde{{x}}_{11}^{*}=(2050,2105,2130,2410)\;\;\tilde{{x}}_{12}^{*}=(0,0,0,0)\;\;\\\;\;\;\;\;\;\;\tilde{{x}}_{13}^{*}=(1450,1450,1450,1450)\;\;\tilde{{x}}_{14}^{*}=(0,0,0,0)\;\;\\\;\;\;\;\;\;\;\tilde{{x}}_{21}^{*}=(0,0,0,0)\;\;\tilde{{x}}_{22}^{*}=(3000,3050,3065,3075)\;\;\\\tilde{{x}}_{23}^{*}=(125,125,125,125)\;\;\tilde{{x}}_{24}^{*}=(0,0,0,0)\;\;\\\;\;\tilde{{x}}_{31}^{*}=(0,395,570,570)\;\;\tilde{{x}}_{32}^{*}=(0,0,35,115)\;\;\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\tilde{{x}}_{33}^{*}=(525,575,615,615)\;\;\tilde{{x}}_{34}^{*}=(1950,2025,2055,2100)\;\;\end{aligned}$$

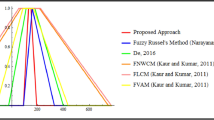
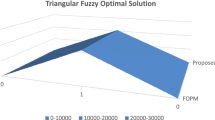
For this solution, the optimal value is determined as (999, 500, 1, 166, 890, 1, 359, 725). We note that in [13] there is a statement that $\tilde{{x}}_{ij}$’s are non-negative triangular fuzzy numbers, but we think this is a typo since the solution found is expressed in trapezoidal fuzzy numbers, not in triangular numbers. We solve this example for $k=1,2,4,1000$ by our proposed algorithm. For $k=1$ our solution coincides with the solution found in [13]. The graphics of this solution are shown in Figs. 5, 6 and 7. When Example 3 was solved for $k=2$, a change was seen in the components $X_{12},\;X_{13},\;X_{32},\;X_{33}$, but the other components remained unchanged. The graphics of the changing components are shown in Figs. 8 and 9. The difference between the solution of the $k=4$ case and the solution of the $k=2$ case was also in the same components $X_{12},\;X_{13},\;X_{32},\;X_{33}$. The graphics of these components are shown in Figs. 10 and 11. In the case of $k=1000$, all components of the fuzzy optimal solution are shown in Figs. 12, 13 and 14

Fig. 5

Example 3: Fuzzy optimal solution $\tilde{{x}}_{1j}$ ($k=1$)

Fig. 6

Example 3: Fuzzy optimal solution $\tilde{{x}}_{2j}$ ($k=1$)

Fig. 7

Example 3: Fuzzy optimal solution $\tilde{{x}}_{3j}$ ($k=1$)

Fig. 8

Example 3: Fuzzy optimal solution $\tilde{{x}}_{1j}$ ($k=2$)

Fig. 9

Example 3: Fuzzy optimal solution $\tilde{{x}}_{3j}$ ($k=2$)

Fig. 10

Example 3: Fuzzy optimal solution $\tilde{{x}}_{1j}$ ($k=4$)

Fig. 11

Example 3: Fuzzy optimal solution $\tilde{{x}}_{3j}$ ($k=4$)

Fig. 12

Example 3: Fuzzy optimal solution $\tilde{{x}}_{1j}$ ($k=1000$)

Fig. 13

Example 3: Fuzzy optimal solution $\tilde{{x}}_{2j}$ ($k=1000$)

Fig. 14

Example 3: Fuzzy optimal solution $\tilde{{x}}_{3j}$ ($k=1000$)

With the proposed algorithm, the value of the objective function of this problem is shown in Fig. 15.

Fig. 15

Example 3: Fuzzy optimal value ($k=1000$)

Example 4

Suppose 2 suppliers and 2 distributors are given. Let the capacities of suppliers and distributors be given by the following fuzzy numbers.

$$\begin{aligned}\\ \tilde{{s}}_{1} =(\underline{s}_{1} (r),\overline{s}_{1} (r))=(9r+20,\;-20r+49) \\ \tilde{{s}}_{2} =(\underline{s}_{2} (r),\overline{s}_{2} (r))=(30r+50,\;-11r+91) \\ \tilde{{d}}_{1} =(\underline{d}_{1} (r),\overline{d}_{1} (r))=(20r+15,\;-15r+50) \\ \tilde{{d}}_{2} =(\underline{d}_{2} (r),\overline{d}_{2} (r))=(19r+55,-16r+90) \end{aligned}$$

Moreover, transportation charges for a unit product from a supplier with number $i\in \{1,\;2\}$ to the distributor $j\in \{1,\;2\}$ are given by fuzzy numbers:

$$\begin{aligned}\\ \tilde{{c}}_{11} =(2r+2,-2r+6) \\ \;\;\tilde{{c}}_{12} =(3r+1,-6r+10) \\ \tilde{{c}}_{21} =(2r+3,-2r+7) \\ \;\;\tilde{{c}}_{22} =(2r+4,-4r+10) \end{aligned}$$

Since $\tilde{{s}}_{1} +\tilde{{s}}_{2} =\tilde{{d}}_{1} +\tilde{{d}}_{2}$, the balance condition is satisfied.

If we solve Example 4 with the method suggested by Ebrahimnejad [13], we get the fuzzy optimal solution shown in Fig. 16 and the fuzzy optimal value shown in Fig. 17. (In our proposed algorithm, this means getting $k=1$.) We see that since all fuzzy numbers given in Example 1 are triangular numbers then the obtained fuzzy optimal solution and the fuzzy optimal value are triangular numbers.

Fig. 16

Example 4: Fuzzy optimal solution ($k=1$)

Fig. 17

Example 4: Fuzzy optimal value ($k=1$)

However, since both charges and variables are fuzzy numbers in a fully fuzzy transportation problem, the problem loses its linearity. Therefore, it is difficult to expect the fuzzy optimal solution and the fuzzy value to be the same as the type of fuzzy inputs given in the problem. We can see this in Figs. 18 and 19 when we apply our proposed algorithm to this example by choosing $k=4$.

Fig. 18

Example 4: Fuzzy optimal solution ($k=4$)

Fig. 19

Example 4: Fuzzy optimal value ($k=4$)

6 Conclusion

In this study, we consider the fully fuzzy transportation problem. In the problem, transportation charges, and supplier and distributor capacities are expressed with fuzzy numbers given in the parametric form. We first transform the fuzzy problem into 2 independent problems with a method similar to the method proposed for interval differential equations in study [26]. Then we formulate these linear programming problems as in [13], but we have two important differences from [13]. Firstly, our proposed method is not only valid for the endpoints and core of the fuzzy number but also works for the general case. Secondly, we solve linear programming problems more easily by transforming them into transportation problems. We solve examples showing that our proposed algorithm applies to all fuzzy numbers given in the parametric form.