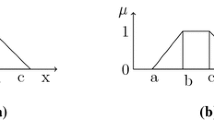An efficient computational approach for basic feasible solution of fuzzy transportation problems

Abstract

In this paper, an improved algorithm has been proposed for solving fully fuzzy transportation problems. The proposed algorithm deals with finding a starting basic feasible solution to the transportation problem with parameters in fuzzy form. The proposed algorithm is an amalgamation of two existing approaches that can be applied to a balanced fuzzy transportation problem where uncertainties are represented by trapezoidal fuzzy numbers. Instead of transforming these uncertainties into crisp values, the proposed algorithm directly handles the fuzzy nature of the problem. To illustrate its effectiveness, the article presents several numerical examples in which parameter uncertainties are characterized using trapezoidal fuzzy numbers. A comparative analysis is performed between the algorithm’s outcomes and the existing results. The existing results are compared with the obtained results. A case study has also been discussed to enhance the significance of the algorithm.

1 Introduction

The transportation problem is a type of structured linear programming problem which is widely worked upon. Transportation problem has diverse range of applications like in finding location with lowest cost for new office/warehouse, scheduling problems, managing flow of water from reservoirs, minimize shipping costs, production and capacity planning, inventory control and many more. In the current competitive environment, organizations are keen on providing best services in lowest possible costs. Since the exchange of goods and services makes up a significant portion of the economy, researching transportation issues and figuring up practical solutions to them becomes more crucial.

The transportation problem encompasses three primary parameters: transportation costs, demand quantities, and supply quantities at different destinations or supply points. The classical transportation problems are based on the assumption that all these values are precisely known. While modelling a problem, it is thus expected that the values of these parameters are known in exact numbers. However, achieving this level of precision is often unfeasible due to the influence of various external factors, introducing uncertainties into these parameters. These uncertainties can be incorporated into the problem by fuzzy number representation of the parameters. The transportation problem in which representation of parameters is by fuzzy numbers is called a fuzzy transportation problem (FTP). Fuzzy transportation problems are particularly well-suited for addressing real-world scenarios, thereby yielding more robust and practical solutions. Many researchers collected and analysed real time data by conducting interviews, group discussions or by forming a questionnaire (Littlewood and Kiyumbu 2018; Elif 2022; Clifton and Handy 2003; Chandrasekaran, et al. 2023; Salleh, et al. 2021).

In (1941), Hitchcock first presented a model for transportation problem. Koopmans (1947) in his paper discussed about how to use transportation system optimally. Stepping stone method was proposed as a substitute to simplex method in 1954 (Charnes and Cooper 1954). Dantzig (1963) worked with primal simplex transportation method. An algorithm for minmax transportation problem was introduced in 1986 (Ahuja 1986). Another method for finding starting solution was proposed (Kirca and Statir 1990) for transportation problem. Least cost method (LCM), North-West corner method (NWCM) and Vogel’s approximation method (VAM) are three widely used methods used to solve transportation problems by finding starting basic feasible solution.

In literature, several different algorithms have been put up to solve fuzzy transportation problem. Pandian and Natarajan (2010b) solved fuzzy transportation problem with mixed constraints. Many researchers (Pandian and Natarajan 2010a; Kaur and Kumar 2012; Shanmugasundari and Ganesan 2013) have worked on fuzzy versions of Vogel’s approximation method, zero-point method, modified distribution method, north west corner rule. Gani et al. (2011) suggested a fuzzy simplex type algorithm to solve FTP. Sam'an et al. (2018) suggested new algorithm named modified fuzzy transportation algorithm for solving the problems. Muthuperumal et al. (2020) discussed an algorithm to solve unbalanced transportation problem.

Different representations like dodecagonal fuzzy numbers (Mathew and Kalayathankal 2019) and heptagonal fuzzy numbers (Malini 2019) have also been used for solving transportation problems to incorporate maximum uncertainty. Basirzadeh (2011) used arbitrary fuzzy numbers and solved the transportation problem using parametric form. Many authors (Malini 2019; Kaur and Kumar, 2011a, 2012; Ebrahimnejad 2014; Thamaraiselvi and Santhi 2015; Ghadle and Pathade 2017) have used generalized representations of fuzzy numbers to find the solution of generalized fuzzy transportation problem. Kumar and Kaur (2011b) introduced new representation named JMD representation of trapezoidal fuzzy numbers. L-R representations of fuzzy numbers have also been used in representing fuzzy transportation problem (Kaur and Kumar, 2011c; Ebrahimnejad 2016). Vinoliah and Ganesan (2017) suggested solution by using parametric representation of trapezoidal fuzzy numbers in fuzzy transportation problems. George et al. (2020) also used modified Vogel’s approximation method in parametric form.

In this paper, a novel method is used to identify the initial basic workable solution of fully fuzzy transportation problem. This approach can be applied to solve fully fuzzy transportation problem when the uncertainties are represented by trapezoidal fuzzy numbers. This algorithm does not require conversion of fuzzy problem into crisp form. The paper is further organised as follows:

Section 2 discusses some basic definitions and arithmetic operations. Section 3 introduces fuzzy transportation problem and the algorithm used to find basic feasible solution. Solution of some numerical problems and Case study using proposed algorithm has been discussed in Sects. 4 and 5 respectively. Results and Conclusion have been discussed in Sect. 6 and 7 respectively.

2 Basic preliminaries

This section discusses some basic definitions related to fuzzy sets (Savitha and Mary 2017).

Fuzzy Set The set of pairs $\widetilde{A}= \{(x, {\mu }_{A} (x)): x\in X\}$ is known as fuzzy set $\widetilde{A}$ in a universe of discourse X, where ${\mu }_{A} (x):$ X $\to [\mathrm{0,1}]$ is referred to as the membership value of x ∈ X in the fuzzy set $\widetilde{A}$.

Fuzzy number A fuzzy subset $\widetilde{A}$ of the real line; with piecewise continuous membership function ${\mu }_{\widetilde{A }}: R \to [\mathrm{0,1}]$ such that ${\mu }_{\widetilde{A}}$ is normal and fuzzy convex, is called a fuzzy number.

Trapezoidal fuzzy number: With the membership function ${\mu }_{\widetilde{A}}$ as described below; a Trapezoidal fuzzy number is defined as $({b}_{1},{b}_{2},{b}_{3},{b}_{4})$, denoted by $\widetilde{A}$.

$$\mu_{{\widetilde{A }}} \left( x \right) = \left\{ {\begin{array}{*{20}l} 0 & {{\text{for}} \,x \le b_{1} } \\ {\frac{{x - b_{1} }}{{b_{2} - b_{1} }}} & {{\text{for }}\,b_{1} \le x < b_{2} } \\ 1 & {{\text{for}}\, b_{2} \le x < b_{3} } \\ {\frac{{b_{4} - x}}{{b_{4} - b_{3} }}} & {{\text{for}}\, b_{3} \le x < b_{4} } \\ 0 & {{\text{for}}\, x \ge b_{4} } \\ \end{array} } \right.$$

2.1 Ranking method (Mohideen and Kumar, 2012)

The comparison of two trapezoidal fuzzy numbers $\widetilde{{A}_{1}}= ({a}_{11} , {a}_{12} , {a}_{13} , {a}_{14} )$ and $\widetilde{{A}_{2}}= ({a}_{21} , {a}_{22} , {a}_{23} , {a}_{24} )$ can be done as:

• $\widetilde{{A}_{1}}\succ \widetilde{{A}_{2}}, if\,R\left(\widetilde{{A}_{1}}\right)>R\left(\widetilde{{A}_{2}}\right)$

• $\widetilde{{A}_{1}}\prec \widetilde{{A}_{2}}, if\,R\left(\widetilde{{A}_{1}}\right)<R\left({A}_{2}\right)$

• $\widetilde{{A}_{1}}\approx \widetilde{{A}_{2}}, if\,R\left(\widetilde{{A}_{1}}\right)=R\left(\widetilde{{A}_{2}}\right)$

where $R\left(\widetilde{{A}_{1}}\right)=\frac{{a}_{11}+{a}_{12}+{a}_{13}+{a}_{14}}{4}$ is called the rank of $\widetilde{{A}_{1}}$.

2.2 Arithmetic operations on trapezoidal fuzzy numbers

Arithmetic operations on two trapezoidal fuzzy numbers, $\widetilde{{A}_{1}}= ({a}_{11} , {a}_{12} , {a}_{13} , {a}_{14} )$ and $\widetilde{{A}_{2}}= ({a}_{21} , {a}_{22} , {a}_{23} , {a}_{24}),$ can be defined as:

• 1. Addition (Kumar 2016):

  $$\widetilde{{A}_{1}}+\widetilde{{A}_{2}} = ({a}_{11}+{a}_{21},{a}_{12}+{a}_{22},{a}_{13}+{a}_{23},{a}_{14}+{a}_{24})$$

• 2. Subtraction (Kumar 2016):

  $$\widetilde{{A}_{1}}-\widetilde{{A}_{2}} =({a}_{11}-{a}_{24},{ a}_{12}-{a}_{23},{ a}_{13}-{a}_{22},{a}_{14}-{a}_{21})$$

• 3. Multiplication (Kumar 2016; Kumar and Hussain 2015; Kumar 2020a, b):

  $$\widetilde{{A}_{1}} \times \widetilde{{A}_{2}}=\left[{a}_{11}R\left(\widetilde{{A}_{2}}\right), {a}_{12}R\left(\widetilde{{A}_{2}}\right), {a}_{13}R\left(\widetilde{{A}_{2}}\right), {a}_{14}R\left(\widetilde{{A}_{2}}\right)\right] , if\,R\left(\widetilde{{A}_{2}}\right)\ge 0$$
  $$\widetilde{{A}_{1}} \times \widetilde{{A}_{2}}=[{a}_{14}R\left(\widetilde{{A}_{2}}\right),{a}_{13}R\left(\widetilde{{A}_{2}}\right), {a}_{12}R\left(\widetilde{{A}_{2}}\right), {a}_{11}R\left(\widetilde{{A}_{2}}\right)] , if\,R\left(\widetilde{{A}_{2}}\right)<0$$

  where $R\left(\widetilde{{A}_{2}}\right)$ denotes the rank of $\widetilde{{A}_{2}}.$

Here, it can be observed that $\widetilde{{A}_{1}} \times \widetilde{{A}_{2}}=\widetilde{{A}_{2}} \times \widetilde{{A}_{1}}$ as follows:

Let $= \left({a}_{11} , {a}_{12} , {a}_{13} , {a}_{14}\right)$ and $\widetilde{{A}_{2}}= \left({a}_{21} , {a}_{22} , {a}_{23} , {a}_{24}\right)$

$$\widetilde{{A}_{1}} \times \widetilde{{A}_{2}}=\left[{a}_{11}R\left(\widetilde{{A}_{2}}\right), {a}_{12}R\left(\widetilde{{A}_{2}}\right), {a}_{13}R\left(\widetilde{{A}_{2}}\right), {a}_{14}R\left(\widetilde{{A}_{2}}\right)\right] , if\,R\left(\widetilde{{A}_{2}}\right)\ge 0$$

$$\widetilde{{A}_{1}} \times \widetilde{{A}_{2}}=[{a}_{14}R\left(\widetilde{{A}_{2}}\right),{a}_{13}R\left(\widetilde{{A}_{2}}\right), {a}_{12}R\left(\widetilde{{A}_{2}}\right), {a}_{11}R\left(\widetilde{{A}_{2}}\right)] , if\,R\left(\widetilde{{A}_{2}}\right)<0$$

$$\begin{aligned} {\text{In}}\,{\text{ either}}\,{\text{ case}},\,R\left( {\widetilde{{A_{1} }} \times \widetilde{{A_{2} }}} \right) & = \frac{{a_{11} R\left( {\widetilde{{A_{2} }}} \right) + a_{12} R\left( {\widetilde{{A_{2} }}} \right) + a_{13} R\left( {\widetilde{{A_{2} }}} \right) + a_{14} R\left( {\widetilde{{A_{2} }}} \right)}}{4} \\ & = \frac{{(a_{11} + a_{12} + a_{13} + a_{14} )R\left( {\widetilde{{A_{2} }}} \right)}}{4} = R\left( {\widetilde{{A_{1} }}} \right)R\left( {\widetilde{{A_{2} }}} \right) \\ \end{aligned}$$

Similarly,

$$\widetilde{{A}_{2}} \times \widetilde{{A}_{1}}=\left[{a}_{21}R\left(\widetilde{{A}_{1}}\right), {a}_{22}R\left(\widetilde{{A}_{1}}\right), {a}_{23}R\left(\widetilde{{A}_{1}}\right), {a}_{24}R\left(\widetilde{{A}_{1}}\right)\right] , if\,R\left(\widetilde{{A}_{1}}\right)\ge 0$$

$$\widetilde{{A}_{2}} \times \widetilde{{A}_{1}}=[{a}_{24}R\left(\widetilde{{A}_{1}}\right),{a}_{23}R\left(\widetilde{{A}_{1}}\right), {a}_{22}R\left(\widetilde{{A}_{1}}\right), {a}_{21}R\left(\widetilde{{A}_{1}}\right)] , if\,R\left(\widetilde{{A}_{1}}\right)<0$$

$$\begin{aligned} {\text{In}}\,{\text{ either}}\,{\text{ case}},\,R\left( {\widetilde{{A_{2} }} \times \widetilde{{A_{1} }}} \right) & = \frac{{a_{21} R\left( {\widetilde{{A_{1} }}} \right) + a_{22} R\left( {\widetilde{{A_{1} }}} \right) + a_{23} R\left( {\widetilde{{A_{1} }}} \right) + a_{24} R\left( {\widetilde{{A_{1} }}} \right)}}{4} \\ & = \frac{{(a_{21} + a_{22} + a_{23} + a_{24} )R\left( {\widetilde{{A_{1} }}} \right)}}{4} = R\left( {\widetilde{{A_{1} }}} \right)R\left( {\widetilde{{A_{2} }}} \right) \\ \end{aligned}$$

Since, $R\left(\widetilde{{A}_{1}} \times \widetilde{{A}_{2}}\right)= R\left(\widetilde{{A}_{2}} \times \widetilde{{A}_{1}}\right),$ we have $\widetilde{{A}_{1}} \times \widetilde{{A}_{2}}\approx \widetilde{{A}_{2}} \times \widetilde{{A}_{1}}$.

3 Fuzzy transportation problem

Aim of transportation problem is to transfer the commodities from one place to another such that the total cost involved is minimised. In crisp transportation problem, the minimised cost is found based on the given fixed values, which may not satisfy every practical situation. To deal with the uncertainty present in practical situations, fuzzy transportation problem has been used to get more accurate and realistic answers. All the quantities and costs are expressed by fuzzy numbers in this problem.

3.1 Mathematical representation of balanced fuzzy transportation problem

Consider a transportation problem that is fully fuzzy and has m sources and n destinations. Cost, demand, and supply quantities are expressed by trapezoidal fuzzy numbers. Let ${\widetilde{c}}_{ij}$ represents the unit product transportation cost to destination $j$ from source $i$. Let ${\widetilde{a}}_{i}$ be the amount of commodity present at source $i$ and ${\widetilde{b}}_{j}$ represent how much of commodity is required at location $j$. If ${\widetilde{x}}_{ij}$ is the amount moved to destination $j$ from source $i$. In order to solve the fuzzy transportation problem, problem is expressed as:

$$\begin{gathered} {\text{Minimize}} \,\tilde{Z} = \sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {\tilde{c}_{ij} \otimes \tilde{x}_{ij} } } \hfill \\ {\text{subject}}\,{\text{ to}} \,\sum\limits_{j = 1}^{n} {\tilde{x}_{ij} \approx \tilde{a}_{i} } ,\quad for\,i = 1,2, \ldots ,m \hfill \\ \sum\limits_{i = 1}^{m} {\tilde{x}_{ij} \approx \tilde{b}_{j} } ,\quad for\,j = 1,2, \ldots ,n \hfill \\ \quad \quad \quad \sum\limits_{i = 1}^{m} {\tilde{a}_{i} } = \sum\limits_{j = 1}^{n} {\tilde{b}_{j} } \hfill \\ \tilde{a}_{i} ,\tilde{b}_{j} \underline { \succ } 0, for\,i = 1,2, \ldots m \,{\text{and}} \,j = 1,2, \ldots ,n \hfill \\ \tilde{c}_{ij} \underline { \succ } \tilde{0}, for\,i = 1,2, \ldots m \,{\text{and}} \, j = 1,2, \ldots ,n \hfill \\ \end{gathered}$$

The tabular representation of fuzzy transportation table for this problem is shown in Table 1.

Table 1 General form of fully fuzzy transportation problem

3.2 Proposed algorithm for finding starting basic feasible solution

This algorithm focuses on finding starting basic feasible fuzzy cost, which can be optimized to find the minimum fuzzy cost for the given problem. The aim of the proposed algorithm is to reduce uncertainty in the starting basic feasible solution of the fully fuzzy transportation problem. Proposed algorithm is amalgamation of two existing approaches (Narayanamoorthy et al. 2013; Vinoliah and Ganesan 2017). The steps involved in the proposed method are as stated below.

Step 1 Create the balanced fuzzy transportation table for the provided fully fuzzy transportation problem, where the cost, quantity of supply, and quantity of demand are all represented by trapezoidal fuzzy numbers.

Step 2 For each row $i$, subtract each entry of a row, ${\widetilde{a}}_{ij},$ from largest entry of that row and place the resultant entries above the cost of each associated cell.

Step 3 For each column $j$, implement step 2 and place the resultant entries below the cost of each associated cell.

Step 4 Construct the reduced transportation table by replacing the value in each cell by sum of the top and bottom entries of that cell, respectively.

Step 5 For every row, let ${u}_{i}={\text{max}}cost in {i}^{th} row$ and let ${v}_{i}={\text{max}}cost in {i}^{th} column$.

Step 6 For each cell, calculate ${d}_{ij}={\widetilde{a}}_{ij}-{u}_{i}-{v}_{j}$.

Step 7 Pick the cell with most negative ${d}_{ij}$ and give that cell the highest feasible value.

Step 8 Delete fully exhausted rows or columns and repeat steps 5 to 7 till all demand and supply are met.

In the next section, some numerical examples have been solved using this algorithm. Obtained results are compared with result obtained through existing approaches.

4 Numerical examples

This section discusses two solved examples of fully fuzzy transportation problem.

Example 1

(Narayanamoorthy et al. 2013)

Solve the following balanced fuzzy transportation problem where demand, supply, and all cost coefficients are represented by trapezoidal fuzzy numbers as given in Table 2.

Table 2 Fully fuzzy transportation problem

Solution

Since the given problem is already a balanced transportation problem, then step 1 can be omitted. After performing steps 2 and 3 of the proposed approach on the given table, following table (Table 3) is obtained.

Table 3 Solution obtained after performing step 2 and 3

In each cell of Table 3, top entry represents the value obtained by step 2, middle entry represents the cell cost and bottom entry represents the value obtained by step 3.

Therefore, the reduced fuzzy transportation table becomes.

Table 4 is obtained by adding top and bottom elements of Table 3 for each cell. The fuzzy transportation table after applying the steps 5, 6, 7 and 8 of the proposed method becomes:

Table 4 Results obtained after step 4

The final allocations have been shown in Table 5. The top entry in each cell, represents cell cost and bottom entry represents the quantity allocated. The starting basic feasible cost can be calculated as

$$\begin{aligned} & = \left( {1,2,3,4} \right)\left( { - 3,3,5,11} \right) + \left( {5,7,8,11} \right)\left( {1,2,3,4} \right) + \left( {0,1,2,4} \right)\left( {0,1,2,3} \right) + \left( {3,5,6,8} \right)\left( { - 9,0,4,13} \right) + \\ & \quad \left( {5,8,9,12} \right)\left( { - 1,5,6,10} \right) + \left( {12,15,16,19} \right)\left( {1,3,4,6} \right) \\ & = \left( {89.5,129.5,148,192} \right) \\ \end{aligned}$$

Table 5 Final allocations in transportation table

The starting basic feasible cost obtained by proposed algorithm is (89.5,129.5,148,192). The uncertainty is represented in the form of trapezoidal fuzzy number. The associated membership function is given by:

$$\mu \left(x\right)=\left\{\begin{array}{c}0 for\,x\le 89.5\\ \frac{x-89.5}{40} for\,89.5\le x<129.5\\ 1 for\,129.5\le x<148\\ \frac{192-x}{44} for\,148\le x<192\\ 0 for\,x\ge 192.\end{array}\right.$$

Example 2 (Mathur, Srivastava and Paul, 2016):

Solve the following balanced fuzzy transportation problem given in Table 6, where demand, supply, and all cost coefficients are represented by trapezoidal fuzzy numbers.

Table 6 Fully fuzzy transportation problem

Solution

After performing steps 2 and 3 of the proposed approach, Table 7 is obtained.

Table 7 Entries obtained after step 2 and 3

In each cell of Table 7, top entry represents the value obtained by step 2, middle entry represents the cell cost and bottom entry represents the value obtained by step 3.

The reduced fuzzy transportation table after applying step 4 becomes:

The fuzzy transportation table after applying the steps 5, 6, 7 and 8 of the proposed method on the Table 8, it becomes:

Table 8 Result obtained after performing step 4 on Table 6

The final allocations have been shown in Table 9. The top entry in each cell, represents cell cost and bottom entry represents the quantity allocated. The starting basic feasible cost can be calculated as

Table 9 Final allocations in transportation table

$$=\left(\mathrm{1,2},\mathrm{5,9}\right)\left(\mathrm{1,5},\mathrm{7,9}\right)+ \left(\mathrm{3,5},\mathrm{8,12}\right)\left(-\mathrm{4,1},\mathrm{4,8}\right)+ \left(\mathrm{7,9},\mathrm{13,28}\right)\left(\mathrm{2,4},\mathrm{6,8}\right)+ \left(\mathrm{11,12,20,27}\right)\left(\mathrm{3,5},\mathrm{8,12}\right)+(\mathrm{0,5},\mathrm{10,15})(-8,-\mathrm{3,3},8)$$

$$=(\mathrm{124.5,151.25,250.5,405.5})$$

The associated membership function is given by

$$\mu \left(x\right)=\left\{\begin{array}{c}0 \,for\,x\le 124.5\\ \frac{x-124.5}{26.75}\, for\,124.5\le x<151.25\\ 1\, for\, 151.25\le x<250.5\\ \frac{405.5-x}{155}\, for\, 250.5\le x<405.5\\ 0\, for\, x\ge 405.5\end{array}\right.$$

5 Case study (Ngastiti, Surarso and Sutimin, 2018):

Consider the following case study of transportation problem for transportation of goods to Denmark, Purwodadi and Kendal from West Semarang, Temanggung and East Semarang. The tabular form (Table 10) of the problem is as below:

Table 10 Fully fuzzy transportation problem

Solution:

Since the given transportation table is unbalanced, first step is to balance the problem by adding an extra row with cost coefficients as zero (as shown in Table 11).

Table 11 Balanced transportation table

After performing steps 2 and 3 on balanced transportation table, Table 12 is obtained.

Table 12 Table obtained after step 2 and 3

After applying step 4 on the above table, the following table (Table 13) is obtained.

Table 13 Table obtained after step 4

After applying the further steps of algorithm to the problem, the obtained allocated final table is (Table 14):

Table 14 Final solution table

The starting basic feasible solution obtained is $(\mathrm{458750,576250,678750,880000})$.

6 Results and discussion

Example 1

As shown in Table 15, the fuzzy starting cost obtained by this algorithm is $(\mathrm{89.5,129.5,148,192})$ which has rank 139.75 whereas solution from fuzzy Russel’s method (Narayanamoorthy et al. 2013) is (158.25,90.5,158.25,328.5) which has rank 183.875. Existing method (De, 2016) gives solution as $(-\mathrm{24,111,178,398})$ which has rank 165.75. Clearly, this algorithm is providing with better results. For instance, the support is (89.5, 192) by the proposed algorithm, and is (90.5,328.5) and (− 24,398) by Russel’s (Narayanamoorthy et al. 2013) and existing method (De, 2016) respectively. For $\alpha =0.5$, $\alpha$-cut by proposed algorithm is $(\mathrm{109.5,170})$ and by Russel’s method (Narayanamoorthy et al. 2013) it is $\left(\mathrm{124.37,243.375}\right)$ and by existing method (De, 2016) it is $(\mathrm{43.5,288})$. Hence from $\alpha -$ cuts also, proposed algorithm gives solution with reduced uncertainty as compared to the already existing methods (Narayanamoorthy et al. 2013; De 2016).

Table 15 Comparison of results for Example 1

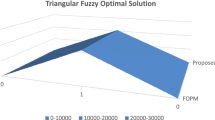
The Monalisha’s approximation method (Vimala and Prabha 2016) solves the problem after converting into crisp form, which eliminates the uncertainty involved in the problem. In comparison, the proposed algorithm solves the problem retaining its fuzzy form and the final starting basic feasible solution obtained is also fuzzy. The obtained solutions are compared in graphical representation in Fig. 1.

Figure1

Graphical representation of results of Example 1

The solution obtained by fuzzy north west corner method, fuzzy least cost method and fuzzy Vogel’s approximation method (Kaur and Kumar 2011a) are (− 405,70,214,746), (− 441,54,222,769) and (− 118,86,166,435) respectively. Rank of these solutions is 156.25, 151 and 142.25 respectively. It can be clearly observed that proposed algorithm is providing better solution as compared to these methods.

As represented in Fig. 1, the proposed approach is providing a starting basic feasible solution as a trapezoidal fuzzy number. The obtained solution has less uncertainty as compared to other solutions obtained by previous approaches (Kaur and Kumar 2011a; Narayanamoorthy et al. 2013; De, 2016). Also, the solution obtained by the proposed approach is in the form of trapezoidal fuzzy number whereas existing approach (Vimala and Prabha 2016) solves the problem in crisp form. It can be visualised that the proposed approach gives better solution.

Example 2

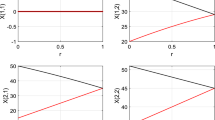
It can be clearly seen from Table 16 and Fig. 2 that the proposed method provides better solution for example 2 in terms of uncertainty. The solution obtained by given approach is.

Table 16 Comparison of results for Example 2

Fig. 2

Graphical representation of results of Example 2

$\left(\mathrm{124.5,151.25,250.5,405.5}\right)$. In comparison fuzzy least cost method (Kaur and Kumar 2011a) gives solution as $(-\mathrm{346.25,7},296.2\mathrm{5,668})$, whereas solution obtained from fuzzy Vogel’s approximation method and fuzzy north west corner rule (Kaur and Kumar, 2011a) is $(-\mathrm{199.25,54.75,248.5,521})$. The solutions obtained from Fuzzy Russel’s method (Narayanamoorthy et al. 2013) is $(-\mathrm{180.25,48.5,254.75,502})$. Fuzzy Russel’s method (De, 2016) gives $(-\mathrm{371,14,279,952})$ as the solution. Comparison clearly states that proposed algorithm is reducing the uncertainty in the starting basic feasible solution of fully fuzzy transportation problem. The suggested algorithm is also providing solution in terms of trapezoidal fuzzy number unlike Monalisha’s Approximation Method (Vimala and Prabha 2016) which gives solution in crisp form.

6.1 Results obtained for case study

Table 17 gives the results obtained on solving case study by various algorithms. The starting basic feasible solution obtained by proposed algorithm is $(\mathrm{458750,576250,678750,880000})$ which is much better solution in terms of uncertainty as compared to the solutions obtained by other algorithms.

Table 17 Comparison of results for Case Study

Fuzzy Russel’s Method (Narayanamoorthy et al. 2013) gives starting basic feasible solution as $(-2273750,-\mathrm{327500,1452500,3546250})$, and algorithm by De (De, 2016) gives $(-3075000,-\mathrm{365000,1535000,4780000})$ as the solution. Solution obtained by fuzzy north west corner method, fuzzy least cost method and fuzzy Vogel’s approximation method (Kaur and Kumar 2011a) are $(-1945000,-\mathrm{140000,1360000,3750000})$, $(-6495000,-\mathrm{1225000,2445000,8340000})$ and $(-2965000,-\mathrm{360000,1540000,4710000})$ respectively. Monalisha’s Approximation Method (Vimala and Prabha 2016) gives solution in crisp form as $565416.68$.

Figure 3 clearly shows that the proposed algorithm is providing better results for starting basic feasible solution of the problem in fuzzy form in terms of uncertainty.

Fig. 3

Graphical representation of results of case study

6.2 Statistical analysis

It can be observed from Examples 1 and 2 that the proposed approach provides the significant improvement in terms of uncertainty and minimizing the objective function. For in-depth evidence, some more random problems as Problem 1 (P1) [example 4.1 in (Pandian and Natrajan, 2010a)] and Problem 2 (P2) [example in Table 4 (Deshmukh, et al. 2018)] have been chosen from the literature. The fully fuzzy transportation problems P1 and P2 have been solved from proposed approach as well as existing approaches. Obtained results have been shared in Table 18. Graphical comparison can also be seen in Figs. 4 and 5. In order to justify the proposed approach, some statistical parameters like mean, variance, area of uncertainty and rank have been evaluated for case study (discussed in Sect. 5) as well as for Problem P1 and Problem P2 (Table 19).

Table 18 Solution of Problem 1 and Problem 2 by different methods

Fig. 4

Graphical representation of results for P1

Fig. 5

Graphical representation of results for P2

Table 19 Various statistical parameters for case study, problems P1 and P2

It has been observed that for case study, rank obtained by Fuzzy Russel’s method (Narayanmoorty et al. 2013) provides better result than the proposed approach. In terms of area under uncertainty as well as variance, proposed approach gives better result. In problem P1, proposed approach gives better results than other existing techniques but comparable results with Fuzzy Russel’s method (Narayanmoorty et al. 2013).

For problem 2 [P2], it can be seen that results obtained by proposed approach are better in terms of all parameters like mean, uncertainty, variance and rank by existing approaches. For instance, there is a significant decrease in mean, variance, rank and uncertainty area by proposed approach from existing approaches. Lesser the values of these parameters will help decision analyst to make better as well as less conflicting decision.

7 Conclusion

In order to find a starting basic solution, a new algorithm for handling fully fuzzy transportation has been presented. An alternate approach to find the starting basic feasible solution, without converting it into a crisp transportation problem has been discussed in the article. It has been seen that the proposed algorithm provides better results in terms of less computation and reduces uncertainty in compare to existing approaches. The results and other statistical parameters obtained for numerical examples and cases study have been compared with the results of existing approaches. It can be observed that the proposed approach provides solution in term of a trapezoidal fuzzy number.