1 Introduction

In practical applications, nonlinearities in plants frequently lead to the difficulties of the analysis and synthesis for control systems. Recently, the so-called Takagi–Sugeno (T–S) model has gained increasing attention because it is regarded as a powerful solution for control of complex dynamic systems [1]. If a nonlinear system is represented by the T–S fuzzy model, it will bring twofold benefits: (1) the T–S fuzzy model is capable of approximating the nonlinear system at any preciseness; (2) based on the fuzzy model, powerful linear control methods are available to solve its control problems. Over the past few decades, there have appeared a number of theoretical results on the analysis and synthesis for T–S fuzzy systems in the open literature [2–6].

On the other hand, the control of large-scale systems has attracted extensive attention due to its wide applications, such as power systems, transportation systems, industrial processes, and communication networks [7]. However, large-scale systems raise the increasing difficulty of stability analysis and control design because of the excessive information processing, strong interconnections, and different locations among subsystems. Recently, decentralization control has been proposed to large-scale systems. Its idea is firstly to partition control problems of a large-scale system into independent or almost independent subproblems. Then, using a set of independent controllers rather than a single controller, the control of the overall system can be implemented [8, 9]. More recently, T–S fuzzy model-based method has been developed for large-scale nonlinear systems, such as stability analysis [10], adaptive decentralized fuzzy controller design [11–14], filtering design [15–17], and observer-based controller design [18, 19]. In addition, remarkable efforts have been devoted to the \({\mathscr{H}}_{\infty }\) optimal control theory which deals with the problem of more robust stability [20, 21], and in the feedback loops communication networks are often used instead of point-to-point connections due to their great advantages, such as low cost, reduced weight and power requirements, and simple installation and maintenance. Nevertheless, few works have been made on the decentralized \({\mathscr{H}}_{\infty }\) sampled-data control for large-scale networked T–S fuzzy systems.

Based on the above considerations, this paper will examine the decentralized \({\mathscr{H}}_{\infty }\) sampled-data control problem for a class of continuous-time large-scale networked nonlinear systems. Each nonlinear subsystem in the considered system is represented by a Takagi–Sugeno (T–S) model and is closed by a communication channel with transformed time delay. Firstly, by utilizing an input delay approach, the sampled-data control system is formulated into the time-varying system, and we propose a two-term approximation method to reformulate the delayed system into an interconnected structure with input and output. Then, we introduce a Lyapunov–Krasovskii functional (LKF) that all Lyapunov matrices are not required to be positive definite. Combined with the scaled small gain (SSG) theorem, sufficient conditions for solving the decentralized \({\mathscr{H}}_{\infty }\) sampled-data control problem will be derived in the form of linear matrix inequalities (LMIs). The effectiveness of the proposed methods is demonstrated by two numerical examples.

The main contributions of this paper are twofold: (i) the problem of decentralized \({\mathscr{H}}_{\infty }\) sampled-data control for large-scale networked T–S fuzzy systems is studied for the first time; (ii) it is noted that control systems with sampled-data measurement can be formulated into control systems with time-varying delay [22]. Compared with the direct Lyapunov–Krasovskii functional method proposed in [15], we perform a model transformation with two-term approximation and introduce an LKF that all Lyapunov matrices are not required to be positive definite, and combined with the scaled small gain (SSG) theorem, less conservative results to the decentralized \({\mathscr{H}}_{\infty }\) sampled-data controller design of the large-scale networked T–S fuzzy system are derived in terms of linear matrix inequalities (LMIs).

This rest of this paper is organized as follows. Sect. 2 formulates the problem under consideration. The main results for the decentralized \({\mathscr{H}}_{\infty }\) fuzzy sampled-data controller design are given in Sect. 3. Two simulation examples are presented to demonstrate the effectiveness of the proposed methods in Sect. 4, which is followed by conclusions in Sect. 5.

Notations. Matrix \(P>0\,({\ge}0)\) denotes P being positive definite (positive semidefinite). Sym{A} denotes \(A+A^{T}.\) \({\mathbf {I}}_{n}\) and 0\(_{m\times n}\) are used to denote the \(n\times n\) identity matrix and \(m\times n\) zero matrix, respectively. \({\mathfrak {R}}^{n}\) denotes the n-dimensional Euclidean space. \({\mathfrak {R}}^{n\times m}\) denotes the set of \(n\times m\) matrices. The subscripts n and \(m\times n\) are omitted when the size is not relevant or can be determined from the context. For a matrix \(A\in {\mathfrak {R}}^{n\times n},\) \(A^{-1}\) and \(A^{T}\) are the inverse and transpose of the matrix A,  respectively. diag{\(\cdot \cdot \cdot\)} denotes a block-diagonal matrix. \(L_{2}[0,\infty )\) refers to the space of square-summable infinite vector sequences over \([0,\infty )\). The notation \(\star\) is used to indicate the terms that can be induced by symmetry.

2 Problem Formulation and Preliminaries

We consider a continuous-time large-scale system containing N nonlinear subsystems with interconnection, where each subsystem is closed by a communication channel. Assume that the i-th nonlinear subsystem is represented by the following T–S fuzzy model:

Plant Rule \({\mathscr{R}}_{i}^{l}\): IF \(\zeta _{i1}(t)\) is \({\mathscr{F}}_{i1}^{l}\) and \(\zeta _{i2}(t)\) is \({\mathscr{F}}_{i2}^{l}\) and \(\cdots\) and \(\zeta _{ig}(t)\) is \({\mathscr{F}}_{ig}^{l}\), THEN

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}_{i}(t)=A_{il}x_{i}\left( t\right) +B_{il}u_{i}(t)+\sum \limits _{\begin{array}{c} k=1\\ k\ne i \end{array}}^{N}\bar{A}_{ikl}x_{k}(t)+B_{wil}w_{i}\left( t\right) \\ y_{i}(t)=C_{il}x_{i}(t)+D_{il}u_{i}(t)+D_{wil}w_{i}\left( t\right) ,l\in {\mathscr{L}}_{i}:=\left\{ 1,2,\ldots ,r_{i}\right\} \end{array} \right. \end{aligned}$$
(1)

where \(i\in {\mathcal{N}}:=\{1,2,\ldots ,N\};\) \({\mathscr{R}}_{i}^{l}\) denotes the l-th fuzzy inference rule for the i-th subsystem; \(r_{i}\) is the number of inference rules; \({\mathscr{F}}_{i\phi }^{l}\) \(\left( \phi =1,2,\ldots ,g\right)\) are fuzzy sets; \(x_{i}(t)\in {\mathfrak {R}}^{n_{xi}}\) denotes the system state; \(u_{i}(t)\in {\mathfrak {R}}^{n_{ui}}\) is the control input; \(y_{i}(t)\in {\mathfrak {R}}^{n_{yi}}\) is the regulated output; \(w_{i}(t)\in {\mathfrak {R}}^{n_{wi}}\) is the disturbance input, which is assumed to belong to \(L_{2}[0,\infty );\) \(\zeta _{i}(t):=[\zeta _{i1}(t),\zeta _{i2}(t),\ldots ,\zeta _{ig}(t)]\) are some measurable variables of the i-th subsystem; \((A_{il},B_{il},B_{wil},C_{il} ,\) \(D_{il},D_{wil})\) denotes the l-th local model for the i-th subsystem; and \(\bar{A}_{ikl}\) denotes the interconnection matrix between the i-th and k-th subsystems.

Define \(\mu _{il}\left[ \zeta _{i}(t)\right]\) as the normalized membership function of the inferred fuzzy set \({\mathscr{F}}_{i}^{l}:\) \(=\prod _{\phi =1}^{g}\) \({\mathscr{F}}_{i\phi }^{l}\) and

$$\begin{aligned} \mu _{il}\left[ \zeta _{i}(t)\right] :=\frac{{\small \prod }_{\phi =1}^{g} \mu _{il\phi }\left[ \zeta _{i\phi }(t)\right] }{{\small \sum }_{\varsigma =1}^{r_{i}}{\small \prod }_{\phi =1}^{g}\mu _{i\varsigma \phi }\left[ \zeta _{i\phi }(t)\right] }\ \ge 0, \quad \sum \limits _{l=1}^{r_{i}}\mu _{il}\left[ \zeta _{i}(t)\right] =1, \end{aligned}$$
(2)

where \(\mu _{il\phi }\left[ \zeta _{i\phi }(t)\right]\) is the grade of membership of \(\zeta _{i\phi }(t)\) in \({\mathscr{F}}_{i\phi }^{l}.\) In the following, we will denote \(\mu _{il}:=\mu _{il}\left[ \zeta _{i}(t)\right]\) for brevity.

By fuzzy blending, the global T–S fuzzy dynamic model can be obtained as follows:

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}_{i}(t)=A_{i}(\mu _{i})x_{i}\left( t\right) +B_{i}(\mu _{i} )u_{i}(t)+\sum \limits _{\begin{array}{c} k=1\\ k\ne i \end{array}}^{N}\bar{A}_{ik}(\mu _{i} )x_{k}(t)+B_{wi}(\mu _{i})w_{i}\left( t\right) \\ y_{i}(t)=C_{i}(\mu _{i})x_{i}(t)+D_{i}(\mu _{i})u_{i}(t)+D_{wi}(\mu _{i} )w_{i}\left( t\right) ,\quad i\in {\mathcal{N}} \end{array} \right. \end{aligned}$$
(3)

where

$$\begin{aligned} \left\{ \begin{array}{llll} A_{i}(\mu _{i}):=\sum \limits _{l=1}^{r_{i}}\mu _{il}A_{il}, &{} B_{i}(\mu _{i}):=\sum \limits _{l=1}^{r_{i}}\mu _{il}B_{il}, &{} \bar{A}_{ik}(\mu _{i} ):=\sum \limits _{l=1}^{r_{i}}\mu _{il}\bar{A}_{ikl}, &{} B_{wi}(\mu _{i} ):=\sum \limits _{l=1}^{r_{i}}\mu _{il}B_{wil},\\ C_{i}(\mu _{i}):=\sum \limits _{l=1}^{r_{i}}\mu _{il}C_{il}, &{} D_{i}(\mu _{i}):=\sum \limits _{l=1}^{r_{i}}\mu _{il}D_{il}, &{} D_{wi}(\mu _{i} ):=\sum \limits _{l=1}^{r_{i}}\mu _{il}D_{wil}. &{} \end{array} \right. \end{aligned}$$
(4)

In this paper, our objective is to design a decentralized fuzzy controller with sampled measurement such that the closed-loop large-scale fuzzy control system is asymptotically stable with an \({\mathscr{H}}_{\infty }\) performance. Before moving on, the following assumptions are firstly required.

Assumption 1

The sampler in each subsystem is clock driven, and the sampling period is a constant and satisfies

$$t_{k+1}^{i}-t_{k}^{i}=h_{i},\quad k\in {\mathbb{N}}.$$
(5)

Assumption 2

Each subsystem is closed by a communication channel, and the sampled signals at the instant \(t_{k}^{i}\) are transmitted over a communication network that induces a time-varying delay satisfying

$$\underline{\tau }_{i}\le \tau _{k}^{i}\le \bar{\tau }_{i},\quad k\in {\mathbb{N}},$$
(6)

where \(\underline{\tau }_{i}\) and \(\bar{\tau }_{i}\) are the lower and upper bounds of \(\tau _{k}^{i},k\in {\mathbb{N}},\) respectively.

Based on the above descriptions, we introduce the following decentralized fuzzy controller with sampled measurement:

Controller Rule \({\mathscr{R}}_{i}^{s}\): IF \(\zeta _{i1}(t)\) is \({\mathscr{F}}_{i1}^{l}\) and \(\zeta _{i2}(t)\) is \({\mathscr{F}}_{i2}^{l}\) and \(\cdots\) and \(\zeta _{ig}(t)\) is \({\mathscr{F}}_{ig}^{l}\), THEN

$$u_{i}\left( t\right) =K_{il}x_{i}(t_{k}^{i}-\tau _{k}^{i}),\quad t\in [t_{k}^{i},t_{k+1}^{i}),$$
(7)

where \(K_{il}\in {\mathfrak {R}}^{n_{ui}\times n_{yi}},l\in {\mathscr{L}}_{i},i\in {\mathcal{N}}\) are controller gains to be determined.

Similarly, the overall state-feedback fuzzy controller with sampled measurement is inferred as follows:

$$u_{i}\left( t\right) =K_{i}(\mu _{i})x_{i}(t_{k}^{i}-\tau _{k}^{i} ),\quad t\in [t_{k}^{i},t_{k+1}^{i}),$$
(8)

where \(K_{i}(\mu _{i}):=\sum \limits _{l=1}^{r_{i}}\mu _{il}A_{il}\).

Remark 1

It is noted that in the context of networked control systems (NCSs), the time derivative of the network-induced delay \(\tau _{k}^{i}\) is usually difficult to be known a priori due to the network-induced uncertainties. In this case, we assume that the time derivative of \(\tau _{k}^{i}\) is unknown.

Combining the system in (3) with the decentralized sampled-data fuzzy controller in (8), we have the following closed-loop fuzzy control system:

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}_{i}(t)=A_{i}(\mu _{i})x_{i}\left( t\right) +B_{i}(\mu _{i})K_{i} (\mu _{i})x_{i}(t_{k}^{i}-\tau _{k}^{i})+\sum \limits _{\begin{array}{c} k=1\\ k\ne i \end{array}}^{N}\bar{A}_{ik}(\mu _{i})x_{k}(t)+B_{wi}(\mu _{i})w_{i}\left( t\right) \\ y_{i}(t)=C_{i}(\mu _{i})x_{i}(t)+D_{i}(\mu _{i})K_{i}(\mu _{i})x_{i}(t_{k} ^{i}-\tau _{k}^{i})+D_{wi}(\mu _{i})w_{i}\left( t\right) ,t\in [t_{k}^{i},t_{k+1}^{i}),i\in {\mathcal{N}} \end{array} \right.. \end{aligned}$$
(9)

Given the large-scale T–S fuzzy system in (3), and a disturbance attenuation \(\gamma >0\), the purpose of this paper is to design a decentralized sampled-data state-feedback fuzzy controller in the form of (8) to satisfy the following two requirements simultaneously:

  1. (1)

    the closed-loop sampled-data fuzzy control system given by (9) with \(w_{i}\left( t\right) =0\) is asymptotically stable,

  2. (2)

    define \({\tilde{y}}(t)=\left[ y_{1}^{T}(t) \cdots y_{i}^{T}(t) \cdots y_{N}^{T}(t) \right] ^{T},\,{\tilde{w}}(t)=\left[ w_{1}^{T}(t) \cdots w_{i}^{T}(t) \cdots w_{N}^{T}(t) \right] ^{T},\) then the induced \(L_{2}\) norm of the operator from \({\tilde{w}}\) to the regulated output \({\tilde{y}}\) is less than \(\gamma\) under zero initial conditions

    $$\int _{0}^{\infty }{\tilde{y}}^{T}(t){\tilde{y}}(t)dt<\gamma ^{2}\int _{0}^{\infty }{\tilde{w}}^{T}(t){\tilde{w}}(t)dt$$
    (10)

    for any nonzero \({\tilde{w}}\in L_{2}[0,\infty )\).

In order to obtain better \({\mathscr{H}}_{\infty }\) performance, we will propose an input delay and a two-term approximation approach, to transform the closed-loop sampled-data control system (9) into an interconnected structure with input and output, such that the decentralized \({\mathscr{H}}_{\infty }\) sampled-data control problem is reformulated in the context of IO stability. It is noted that the IO approach proposed in this paper benefits from the scaled small gain (SSG) theorem. Interested readers can refer to [23] for more details. Here, we directly state the following lemmas:

Lemma 1

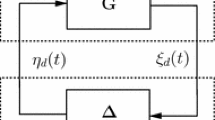
[24] Consider an interconnected system \({\mathcal{R}}_{1} :\xi _{d}(t)={\mathbf {G}}\eta _{d}(t),{\mathcal{R}}_{2}:\eta _{d}(t)={\mathbf {\Delta }}\xi _{d}(t),\) where the forward subsystem \({\mathcal{R}}_{1}\) is known with operator \({\mathbf {G}},\) and the feedback one \({\mathcal{R}}_{2}\) is unknown and time varying with operator \({\mathbf {\Delta \in }}\) \({\mathcal{M}}:=\left\{ {\mathbf {\Delta }}:\left\| {\mathbf {\Delta }}\right\| _{\infty }\le 1\right\} .\) Assume that \({\mathcal{R}}_{1}\) is internally stable, then the interconnected system is robustly stable for all \({\mathbf {\Delta \in }}\) \({\mathcal{M}}\) if \(\left\| T_{\xi }{\mathbf {G}}T_{\eta }^{-1}\right\| _{\infty }<1\) holds for some matrices \(\left\{ T_{\xi },T_{\eta }\right\} \in {\mathcal{T}}\) with \({\mathcal{T}}:=\left\{ \left\{ T_{\eta },T_{\xi }\right\} \in {\mathfrak {R}}^{n_{\eta }\times n_{\eta }}\times {\mathfrak {R}}^{n_{\xi }\times n_{\xi }}:T_{\eta },T_{\xi }{\text { nonsingular}};\left\| T_{\eta }{\mathbf {\Delta }}T_{\xi }^{-1}\right\| _{\infty }\le 1\right\} .\)

Lemma 2

[24] For any constant positive symmetric matrix \(M\in {\mathfrak {R}}^{n\times n},M^{T}=M>0,\) scalars \(d_{2}>d_{1}\ge 0,\) the following inequality holds:

$$\begin{aligned} \left( \int _{d_{1}}^{d_{2}}x\left( t\right) dt\right) ^{T}M\left( \int _{d_{1}}^{d_{2}}x\left( t\right) dt\right) \le \left( d_{2} -d_{1}\right) \int _{d_{1}}^{d_{2}}x^{T}\left( t\right) Mx\left( t\right) dt. \end{aligned}$$

Lemma 3

[25] For any constant positive semidefinite symmetric matrix \(W\in {\mathfrak {R}}^{n\times n},W^{T}=W>0,\) two positive integers \(n_{2}\) and \(n_{1}\) satisfying \(n_{2}\ge n_{1}\ge 1,\) the following inequality holds:

$$\begin{aligned} \left( \sum \limits _{k=n_{1}}^{n_{2}}x\left( k\right) \right) ^{T}W\left( \sum \limits _{k=n_{1}}^{n_{2}}x\left( k\right) \right) \le \left( n_{2}-n_{1}+1\right) \sum \limits _{k=n_{1}}^{n_{2}}x^{T}\left( k\right) Wx\left( k\right) . \end{aligned}$$

3 Main Results

In this section, we will firstly address a model transformation. Then, we introduce a Lyapunov–Krasovskii functional (LKF) and SSG theorem to the new model. Performance analysis and controller design to the decentralized \({\mathscr{H}}_{\infty }\) sampled-data control for the large-scale T–S fuzzy system in (3) will be respectively derived.

3.1 Model Reformulation

Following from the input delay approach in [22], the sampled-data control can be rewritten as a delayed control:

$$u\left( t\right) =K_{i}(\mu _{i})x_{i}(t-\eta _{i}\left( t\right) ),\quad t\in [t_{k}^{i},t_{k+1}^{i}),$$
(11)

where \(\eta _{i}\left( t\right) =t-t_{k}^{i}+\tau _{k}^{i}\).

Based on Assumption 1 and 2, we have

$$\underline{\tau _{i}}\le \eta _{i}\left( t\right) \le \bar{\eta }_{i},\bar{\eta }_{i}=\bar{\tau }_{i}+h_{i},\quad t\in [t_{k}^{i},t_{k+1}^{i} ),k\in {\mathbb{N}}.$$
(12)

It follows from (3) and (11) that the closed-loop sampled-data fuzzy control system in (9) can be rewritten as

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}_{i}(t)=A_{i}(\mu _{i})x_{i}\left( t\right) +B_{i}(\mu _{i})K_{i} (\mu _{i})x_{i}(t-\eta _{i}\left( t\right) )+\sum \limits _{\begin{array}{c} k=1\\ k\ne i \end{array}}^{N}\bar{A}_{ik}(\mu _{i})x_{k}(t)+B_{wi}(\mu _{i})w_{i}\left( t\right) \\ y_{i}(t)=C_{i}(\mu _{i})x_{i}(t)+D_{i}(\mu _{i})K_{i}(\mu _{i})x_{i}(t-\eta _{i}\left( t\right) )+D_{wi}(\mu _{i})w_{i}\left( t\right) ,t\in [t_{k}^{i},t_{k+1}^{i}),i\in {\mathcal{N}} \end{array} \right. \end{aligned}$$
(13)

To apply Lemma 1 to the decentralized \({\mathscr{H}}_{\infty }\) sampled-data fuzzy state-feedback controller design, the closed-loop fuzzy control system in (13) will be firstly transformed into an interconnected structure, i.e., the delay “uncertainty” will be pulled out and put into a feedback subsystem. Then, based on an LKF combined with the SSG theorem, the IO approach can be developed to solve the decentralized \({\mathscr{H}}_{\infty }\) sampled-data control problem. Here, we follow the idea in [26] to approximate the time-varying delay term \(x_{i} (t-\eta _{i}\left( t\right) )\) in (13) by \(x_{i}(t-\underline{\tau _{i}})\) and \(x_{i}(t-\bar{\eta }_{i}),\) and the approximation error is given by

$$\begin{aligned} \frac{\bar{\tau }_{i}-\underline{\tau _{i}}+h_{i}}{2}\varpi _{di}\left( t\right)&=x_{i}(t-\eta _{i}\left( t\right) )-\frac{1}{2}\Bigg[ x_{i}\left( t-\underline{\tau _{i}}\right) +x_{i}\left( t-\bar{\eta } _{i}\right) \Bigg] \nonumber \\&=\frac{1}{2}\int _{-\bar{\eta }_{i}}^{-\eta _{i}\left( t\right) }\dot{x} _{i}\left( t+\alpha \right) d\alpha -\frac{1}{2}\int _{-\eta _{i}\left( t\right) }^{-\bar{\tau }_{i}}\dot{x}_{i}\left( t+\alpha \right) d\alpha \nonumber \\&=\frac{1}{2}\int _{-\bar{\eta }_{i}}^{-\bar{\tau }_{i}}\rho _{i}\left( \alpha \right) \xi _{di}\left( t+\alpha \right) d\alpha , \end{aligned}$$
(14)

where \(\xi _{di}\left( t\right) =\dot{x}_{i}\left( t\right)\) and

$$\begin{aligned} \rho _{i}\left( \alpha \right) =\left\{ \begin{array}{cl} 1, &{} {\text {if }}\; \alpha \le -\eta _{i}\left( t\right) ,\\ -1, &{} {\text {if }}\;\alpha >-\eta _{i}\left( t\right) . \end{array} \right. \end{aligned}$$
(15)

Substitute (14) into the closed-loop fuzzy control system (13), and put the delay “uncertainty”\(\varpi _{di}\left( t\right)\) into a feedback subsystem. The closed-loop fuzzy control system in (13) can be rewritten as

$$\begin{aligned} {\mathcal{R}}_{i1}&:\left\{ \begin{array}{l} \dot{x}_{i}\left( t\right) =\bar{{\mathscr{A}}}_{i}(\mu _{i}){\bar{\mathcal{\xi }}}_{i}\left( t\right) +\frac{\bar{\tau }_{i}-\underline{\tau _{i}}+h_{i}}{2}B_{i}(\mu _{i})K_{i}(\mu _{i})\varpi _{di}\left( t\right) +\sum \limits _{\begin{array}{c} k=1\\ k\ne i \end{array}}^{N}\bar{A}_{ik}(\mu _{i})x_{k}(t)+B_{wi} (\mu _{i})w_{i}\left( t\right) \\ y_{i}(t)=\bar{{\mathscr{C}}}_{i}(\mu _{i}){\bar{\mathcal{\xi }}}_{i}\left( t\right) +\frac{\bar{\tau }_{i}-\underline{\tau _{i}}+h_{i}}{2}B_{i}(\mu _{i})K_{i}(\mu _{i})\varpi _{di}\left( t\right) +D_{wi}(\mu _{i})w_{i}\left( t\right) \\ \xi _{di}\left( t\right) =\dot{x}_{i}\left( t\right) \end{array} \right. \nonumber \\ {\mathcal{R}}_{i2}&:\varpi _{di}\left( t\right) ={\mathbf {\Delta }}_{i} \xi _{di}\left( t\right), \end{aligned}$$
(16)

where \(t\in [t_{k}^{i},t_{k+1}^{i}),k\in {\mathbb{N}},i\in {\mathcal{N}}\) and \({\mathbf {\Delta }}_{i}\) denotes an operator with uncertainties, and

$$\begin{aligned} \left\{ \begin{array}{l} \bar{\mathscr{A}}_{i}(\mu _{i})=\left[ \begin{array}{ccc} A_{i}(\mu _{i}){\text { }} &{} \frac{1}{2}B_{i}(\mu _{i})K_{i}(\mu _{i}) &{} \frac{1}{2}B_{i}(\mu _{i})K_{i}(\mu _{i}) \end{array} \right] ,\\ \bar{\mathscr{C}}_{i}(\mu _{i})=\left[ \begin{array}{ccc} C_{i}(\mu _{i}){\text { }} &{} \frac{1}{2}D_{i}(\mu _{i})K_{i}(\mu _{i}) &{} \frac{1}{2}D_{i}(\mu _{i})K_{i}(\mu _{i}) \end{array} \right] ,\\ {\bar{\mathcal{\xi }}}_{i}\left( t\right) =\left[ \begin{array}{ccc} x_{i}^{T}\left( t\right) {\text { }} &{} x_{i}^{T}\left( t-\underline{\tau _{i} }\right) &{} x_{i}^{T}\left( t-\bar{\eta }_{i}\right) \end{array} \right] ^{T}. \end{array} \right. \end{aligned}$$
(17)

Based on the interconnected system with two subsystems \({\mathcal{R}}_{i1}\) and \({\mathcal{R}}_{i2}\) in (16), we have the following lemma:

Lemma 4

Consider the interconnected system with two subsystems \({\mathcal{R}}_{i1}\) and \({\mathcal{R}}_{i2}\) in (16), the operator \({\mathbf {\Delta }}_{i}\) \({\mathbf {:}}\) \(\xi _{di}\left( t\right) \longmapsto \varpi _{di}\left( t\right)\) satisfies the SSG condition \(\left\| X_{i}{\mathbf {\Delta }}_{i}X_{i}^{-1}\right\| _{\infty }\le 1,\) where \(X_{i}\) are nonsingular matrices.

Proof Based on relation (14), and using Jensen’s inequality (Lemma 2) and considering zero initial conditions, we have

$$\begin{aligned}&\int _{0}^{t}\varpi _{di}^{T}\left( \alpha \right) X_{i}^{T}X_{i} \varpi _{di}\left( \alpha \right) d\alpha \nonumber \\&=\frac{1}{\left( \bar{\tau }_{i}-\underline{\tau _{i}}+h_{i}\right) ^{2} }\int _{0}^{t}\left[ \int _{-\bar{\eta }_{i}}^{-\underline{\tau _{i}}}\rho _{i}\left( \beta \right) \xi _{di}\left( \alpha +\beta \right) d\beta \right] ^{T} \times X_{i}^{T}X_{i}\left[ \int _{-\bar{\eta }_{i}}^{-\underline{\tau _{i}}} \rho _{i}\left( \beta \right) \xi _{di}\left( \alpha +\beta \right) d\beta \right] d\alpha \nonumber \\&\le \frac{1}{\left( \bar{\tau }_{i}-\underline{\tau _{i}}+h_{i}\right) ^{2}}\int _{0}^{t}\left[ \left( \bar{\tau }_{i}-\underline{\tau _{i}} +h_{i}\right) \int _{-\bar{\eta }_{i}}^{-\underline{\tau _{i}}}\rho _{i} ^{2}\left( \beta \right) \xi _{di}^{T}\left( \alpha +\beta \right) X_{i} ^{T}X_{i}\xi _{di}\left( \alpha +\beta \right) d\beta \right] d\alpha \nonumber \\&=\frac{1}{\bar{\tau }_{i}-\underline{\tau _{i}}+h_{i}}\int _{-\bar{\eta }_{i} }^{-\underline{\tau _{i}}}\left[ \int _{0}^{t}\xi _{di}^{T}\left( \alpha +\beta \right) X_{i}^{T}X_{i}\xi _{di}\left( \alpha +\beta \right) d\alpha \right] d\beta \nonumber \\&=\frac{1}{\bar{\tau }_{i}-\underline{\tau _{i}}+h_{i}}\int _{-\bar{\eta }_{i} }^{-\underline{\tau _{i}}}\left[ \int _{\beta }^{t+\beta }\xi _{di}^{T}\left( \alpha \right) X_{i}^{T}X_{i}\xi _{di}\left( \alpha \right) d\alpha \right] d\beta \nonumber \\&\le \frac{1}{\bar{\tau }_{i}-\underline{\tau _{i}}+h_{i}}\int _{-\bar{\eta }_{i}}^{-\underline{\tau _{i}}}\left[ \int _{0}^{t}\xi _{di}^{T}\left( \alpha \right) X_{i}^{T}X_{i}\xi _{di}\left( \alpha \right) d\alpha \right] d\beta \nonumber \\&=\int _{0}^{t}\xi _{di}^{T}\left( \alpha \right) X_{i}^{T}X_{i}\xi _{di}\left( \alpha \right) d\alpha . \end{aligned}$$
(18)

It is easy to see that the inequality in (18) implies \(\left\| X_{i}{\mathbf {\Delta }}_{i}X_{i}^{-1}\right\| _{\infty }\le 1,\) thus the proof is completed.

Remark 2

It can be seen from Lemma 4 that the feedback subsystem \({\mathcal{R}}_{i2}\) satisfies the property \(\left\| X_{i}{\mathbf {\Delta }}_{i}X_{i} ^{-1}\right\| _{\infty }\le 1.\) Define X \({\mathbb{=}}\) \(\underset{N}{{diag} \underbrace{\left\{ X_{1}\cdots X_{i}\cdots X_{N}\right\} }},\) \({\mathbf {\Delta }}\) \({\mathbb{=}}\) \(\underset{N}{{diag} \underbrace{\left\{ {\mathbf {\Delta }}_{1} \cdots {\mathbf {\Delta }}_{i}\cdots {\mathbf {\Delta }}_{N}\right\} }}\) , and it is easy to see that \(\left\| X{\mathbf {\Delta }}X^{-1}\right\| _{\infty }\le 1\) holds. Using Lemma 1, the interconnected system (16) is IO stable if the property \(\left\| X{\mathbf {G}}X^{-1}\right\| _{\infty }<1\) holds. Due to the fact that the closed-loop fuzzy control system in (9) and the interconnected system in (16) are equivalent, the system in (9) is also stable when the above conditions hold.

Remark 3

It is noted that in the simulation examples we will verify that the obtained results based on the IO approach are less conservative than those that are based on direct Lyapunov method.

3.2 Decentralized \({\mathscr{H}}_{\infty }\) Sampled-Data State-Feedback Controller Performance Analysis

In the following, based on a Lyapunov–Krasovskii functional combined with the SSG theorem, we will firstly present a decentralized \({\mathscr{H}}_{\infty }\) sampled-data state-feedback controller performance analysis result for the closed-loop fuzzy control system (9).

Lemma 5

Given the large-scale T–S fuzzy system in (3) and decentralized sampled-data fuzzy controller in (8), then the closed-loop fuzzy control system (9) is asymptotically stable with an \({\mathscr{H}}_{\infty }\) disturbance attenuation level \(\gamma ,\) if there exist positive definite symmetric matrices

\(\left\{ P_{i1},P_{i2},Q_{i1},Q_{i2},Z_{i1},Z_{i2},\bar{X} _{i}\right\} \in {\mathfrak {R}}^{n_{xi}\times n_{xi}},\) matrix multipliers \({\mathcal{G}} _{i}\in {\mathfrak {R}}^{\left( 5n_{xi}+n_{wi}\right) \times n_{xi}},\) and scalars \(0<\varepsilon _{i}(\mu _{i})\le \varepsilon _{0},\) such that for all \(i\in {\mathcal{N}}\) the following matrix inequalities hold:

$$\left[ \begin{array}{cc} \frac{P_{i1}}{\underline{\tau _{i}}}+Z_{i1} &{}\quad -Z_{i1}\\ \star &{}\quad Q_{i1}+Z_{i1} \end{array} \right] >0,$$
(19)
$$\left[ \begin{array}{cc} \frac{P_{i2}}{\bar{\eta }_{i}}+Z_{i2} &{}\quad -Z_{i2}\\ \star &{}\quad Q_{i2}+Z_{i2} \end{array} \right] >0,$$
(20)

and

$$\begin{aligned} \left[ \begin{array}{ccc} -{\mathbf{I}} &{}\quad {\mathbb{C}}_{i}(\mu _{i}) &{}\quad 0\\ \star &{}\quad \Theta _{i}+{\text {Sym}} \left\{ {\mathcal{G}}_{i}{\mathbb{A}}_{i} (\mu _{i})\right\} &{}\quad {\mathcal{G}}_{i}\\ \star &{}\quad \star &{}\quad -\varepsilon _{i}(\mu _{i}){\mathbf {I}} \end{array} \right] <0, \end{aligned}$$
(21)

where

$$\begin{aligned} \left\{ \begin{array}{l} \Theta _{i}=\left[ \begin{array}{cccccc} \Theta _{i(1)} &{}\quad P_{i1}+P_{i2} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ \star &{}\quad \Theta _{i(2)} &{}\quad Z_{i1} &{}\quad Z_{i2} &{}\quad 0 &{}\quad 0\\ \star &{}\quad \star &{}\quad \Theta _{i(3)} &{}\quad 0 &{}\quad 0 &{}\quad 0\\ \star &{}\quad \star &{}\quad \star &{}\quad -Q_{i2}-Z_{i2} &{}\quad 0 &{}\quad 0\\ \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad -\bar{X}_{i} &{}\quad 0\\ \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad -\gamma ^{2}{\mathbf {I}} \end{array} \right] ,\\ \Theta _{i(1)}=\underline{\tau _{i}^{2}}Z_{i1}+\bar{\eta }_{i}^{2}Z_{i2}+\bar{X}_{i},\Theta _{i(3)}=-Q_{i1}-Z_{i1},\\ \Theta _{i(2)}=Q_{i1}+Q_{i2}-Z_{i1}-Z_{i2}+\varepsilon _{0}\left( N-1\right) \sum \limits _{\begin{array}{c} k=1\\ k\ne i \end{array}}^{N}\bar{A}_{ki}^{T}\bar{A}_{ki},\\ {\mathbb{A}}_{i}(\mu _{i})=\left[ \begin{array}{cccccc} -{\mathbf {I}} &{} A_{i}(\mu _{i}){\text { }} &{} \frac{1}{2}B_{i}(\mu _{i})K_{i}(\mu _{i}) &{} \frac{1}{2}B_{i}(\mu _{i})K_{i}(\mu _{i}) &{} \frac{\left( \bar{\tau } _{i}-\underline{\tau _{i}}+h_{i}\right) }{2}B_{i}(\mu _{i})K_{i}(\mu _{i}) &{} B_{wi}(\mu _{i}) \end{array} \right] ,\\ {\mathbb{C}}_{i}(\mu _{i})=\left[ \begin{array}{cccccc} 0 &{} C_{i}(\mu _{i}){\text { }} &{} \frac{1}{2}D_{i}(\mu _{i})K_{i}(\mu _{i}) &{} \frac{1}{2}D_{i}(\mu _{i})K_{i}(\mu _{i}) &{} \frac{\left( \bar{\tau } _{i}-\underline{\tau _{i}}+h_{i}\right) }{2}D_{i}(\mu _{i})K_{i}(\mu _{i}) &{} D_{wi}(\mu _{i}) \end{array} \right] . \end{array} \right. \end{aligned}$$
(22)

Proof Choose the following Lyapunov–Krasovskii functional (LKF):

$$V(t)=\sum \limits _{i=1}^{N}V_{i}(t)=\sum \limits _{i=1}^{N}\left[ V_{i1} (t)+V_{i2}(t)\right]$$
(23)

with

$$\begin{aligned} \left\{ \begin{array}{l} V_{1i}(t)=x_{i}^{T}\left( t\right) P_{i1}x_{i}\left( t\right) +\int _{t-\underline{\tau }_{i}}^{t}x_{i}^{T}\left( \alpha \right) Q_{i1} x_{i}\left( \alpha \right) d\alpha +\,\underline{\tau }_{i}\int _{-\underline{\tau }_{i}}^{0}\int _{t+\beta }^{t}\dot{x}_{i}^{T}\left( \alpha \right) Z_{i1}\dot{x}_{i}\left( \alpha \right) d\alpha d\beta ,\\ V_{2i}(t)=x_{i}^{T}\left( t\right) P_{i2}x_{i}\left( t\right) +\int _{t-\bar{\eta }_{i}}^{t}x_{i}^{T}\left( \alpha \right) Q_{i2}x_{i}\left( \alpha \right) d\alpha +\,\bar{\eta }_{i}\int _{-\bar{\eta }_{i}}^{0}\int _{t+\beta }^{t}\dot{x}_{i}^{T}\left( \alpha \right) Z_{i2}\dot{x}_{i}\left( \alpha \right) d\alpha d\beta , \end{array} \right. \end{aligned}$$
(24)

where \(\left\{ P_{i1},P_{i2},Q_{i1},Q_{i2},Z_{i1},Z_{i2}\right\} \in {\mathfrak {R}}^{n_{xi}\times n_{xi}},i\in {\mathcal{N}}\) are symmetric matrices, and matrices \(P_{i1},P_{i2},Z_{i1},\) and \(Z_{i2}\) are positive definite.

Firstly, using Jensen’s inequality (Lemma 2), it yields

$$\begin{aligned} \underline{\tau _{i}}\int _{-\underline{\tau _{i}}}^{0}&\int _{t+\beta } ^{t}\dot{x}_{i}^{T}\left( \alpha \right) Z_{i1}\dot{x}_{i}\left( \alpha \right) d\alpha d\beta \nonumber \\&\ge \underline{\tau _{i}}\int _{-\underline{\tau _{i}}}^{0}\frac{-1}{\beta }\left[ \int _{t+\beta }^{t}\dot{x}_{i}^{T}\left( \alpha \right) d\alpha \right] Z_{i1}\left[ \int _{t+\beta }^{t}\dot{x}_{i}\left( \alpha \right) d\alpha \right] d\beta \nonumber \\&=\underline{\tau _{i}}\int _{-\underline{\tau _{i}}}^{0}\frac{-1}{\beta }\left[ x_{i}\left( t\right) -x_{i}\left( t+\beta \right) \right] ^{T}Z_{i1}\left[ x_{i}\left( t\right) -x_{i}\left( t+\beta \right) \right] d\beta \nonumber \\&=\underline{\tau _{i}}\int _{0}^{\underline{\tau _{i}}}\frac{1}{s}\left[ x_{i}\left( t\right) -x_{i}\left( t-s\right) \right] ^{T}Z_{i1}\left[ x_{i}\left( t\right) -x_{i}\left( t-s\right) \right] ds\nonumber \\&\ge \int _{0}^{\underline{\tau _{i}}}\left[ x_{i}\left( t\right) -x_{i}\left( t-s\right) \right] ^{T}Z_{i1}\left[ x_{i}\left( t\right) -x_{i}\left( t-s\right) \right] ds\nonumber \\&=\int _{t-\underline{\tau _{i}}}^{t}\left[ x_{i}\left( t\right) -x_{i}\left( \alpha \right) \right] ^{T}Z_{i1}\left[ x_{i}\left( t\right) -x_{i}\left( \alpha \right) \right] d\alpha . \end{aligned}$$
(25)

It follows from (24) and (25) that

$$\begin{aligned} V_{i1}(t)\ge \int _{t-\underline{\tau _{i}}}^{t}\left[ \begin{array}{c} x_{i}\left( t\right) \\ x_{i}\left( \alpha \right) \end{array} \right] ^{T}\left[ \left[ \begin{array}{cc} \frac{P_{i1}}{\underline{\tau _{i}}}+Z_{i1} &{}\quad -Z_{i1}\\ \star &{}\quad Q_{i1}+Z_{i1} \end{array} \right] \right] \left[ \begin{array}{c} x_{i}\left( t\right) \\ x_{i}\left( \alpha \right) \end{array} \right] d\alpha . \end{aligned}$$
(26)

Similarly, we also have

$$\begin{aligned} \bar{\eta }_{i}\int _{-\bar{\eta }_{i}}^{0}&\int _{t+\beta }^{t}\dot{x}_{i} ^{T}\left( \alpha \right) Z_{i2}\dot{x}_{i}\left( \alpha \right) d\alpha d\beta \nonumber \\&\ge \int _{t-\bar{\eta }_{i}}^{t}\left[ x_{i}\left( t\right) -x_{i}\left( \alpha \right) \right] ^{T}Z_{i2}\left[ x_{i}\left( t\right) -x_{i}\left( \alpha \right) \right] d\alpha , \end{aligned}$$
(27)

which implies that

$$\begin{aligned} V_{i2}(t)\ge \int _{t-\bar{\eta }_{i}}^{t}\left[ \begin{array}{c} x_{i}\left( t\right) \\ x_{i}\left( \alpha \right) \end{array} \right] ^{T}\left[ \begin{array}{cc} \frac{P_{i2}}{\bar{\eta }_{i}}+Z_{i2} &{}\quad -Z_{i2}\\ \star &{}\quad Q_{i2}+Z_{i2} \end{array} \right] \left[ \begin{array}{c} x_{i}\left( t\right) \\ x_{i}\left( \alpha \right) \end{array} \right] d\alpha . \end{aligned}$$
(28)

Thus, if the inequalities (19) and (20) hold, there always exist scalars \(\delta _{i}>0\) such that the property \(V(t)>\sum \limits _{i=1}^{N}\delta _{i}\left\| x_{i}\left( t\right) \right\|\) holds.

Next, by taking the derivative of \(V_{i}(t)\) along the trajectory of the forward system \({\mathcal{R}}_{i1}\) in (16), it yields

$$\begin{aligned} \dot{V}_{i}(t)&=\dot{V}_{i1}(t)+\dot{V}_{i2}(t)\nonumber \\&\quad \le 2x_{i}^{T}\left( t\right) \left( P_{1i}+P_{2i}\right) \dot{x} _{i}\left( t\right) +x_{i}^{T}\left( t\right) Q_{i1}x_{i}\left( t\right) -x_{i}^{T}\left( t-\underline{\tau _{i}}\right) Q_{i1}x_{i}\left( t-\underline{\tau _{i}}\right) \nonumber \\&\quad +x_{i}^{T}\left( t\right) Q_{i2}x_{i}\left( t\right) -x_{i}^{T}\left( t-\bar{\eta }_{i}\right) Q_{i2}x_{i}\left( t-\bar{\eta } _{i}\right) \nonumber \\&\quad +\underline{\tau _{i}^{2}}\dot{x}_{i}^{T}\left( t\right) Z_{i1}\dot{x}_{i}\left( t\right) -\underline{\tau _{i}}\int _{t-\underline{\tau _{i}}}^{t}\dot{x}_{i}^{T}\left( \alpha \right) Z_{i1}\dot{x}_{i}\left( \alpha \right) d\alpha \nonumber \\&\quad +\bar{\eta }_{i}^{2}\dot{x}_{i}^{T}\left( t\right) Z_{i2} \dot{x}_{i}\left( t\right) -\bar{\eta }_{i}\int _{t-\bar{\eta }_{i}}^{t}\dot{x}_{i}^{T}\left( \alpha \right) Z_{i2}\dot{x}_{i}\left( \alpha \right) d\alpha . \end{aligned}$$
(29)

Now, using Jensen’s inequality (Lemma 2), we have

$$\begin{aligned} -\underline{\tau _{i}}\int _{t-\underline{\tau _{i}}}^{t}\dot{x}_{i}^{T}\left( \alpha \right) Z_{i1}\dot{x}_{i}\left( \alpha \right) d\alpha&\le -\left[ \int _{t-\underline{\tau _{i}}}^{t}\dot{x}_{i}\left( \alpha \right) d\alpha \right] ^{T}Z_{i1}\left[ \int _{t-\underline{\tau _{i}}}^{t}\dot{x} _{i}\left( \alpha \right) d\alpha \right] \nonumber \\&=-\left( x_{i}\left( t\right) -x_{i}\left( t-\underline{\tau _{i} }\right) \right) ^{T}Z_{i1}\left( x_{i}\left( t\right) -x_{i}\left( t-\underline{\tau _{i}}\right) \right) . \end{aligned}$$
(30)

Similarly, we also have

$$\begin{aligned} -\bar{\eta }_{i}\int _{t-\bar{\eta }_{i}}^{t}\dot{x}_{i}^{T}\left( a\right) Z_{i2}\dot{x}_{i}\left( \alpha \right) d\alpha&\le -\left[ \int _{t-\bar{\eta }_{i}}^{t}\dot{x}_{i}\left( \alpha \right) d\alpha \right] ^{T}Z_{i2}\left[ \int _{t-\bar{\eta }_{i}}^{t}\dot{x}_{i}\left( \alpha \right) d\alpha \right] \nonumber \\&=-\left( x_{i}\left( t\right) -x_{i}\left( t-\bar{\eta }_{i}\right) \right) ^{T}Z_{i2}\left( x_{i}\left( t\right) -x_{i}\left( t-\bar{\eta }_{i}\right) \right) . \end{aligned}$$
(31)

Define \({\mathbb{\chi }}_{i}\left( t\right) =\left[ \begin{array}{cccccc} \dot{x}_{i}^{T}\left( t\right)&x_{i}^{T}\left( t\right)&x_{i} ^{T}\left( t-\underline{\tau _{i}}\right)&x_{i}^{T}\left( t-\bar{\eta } _{i}\right)&\varpi _{di}^{T}\left( t\right)&w_{i}^{T}\left( t\right) \end{array} \right] ^{T}\) and matrix multipliers \({\mathcal{G}}_{i}\) \(\in {\mathfrak {R}}^{\left( 5n_{xi}+n_{wi}\right) \times n_{xi}}\), then it follows from the forward system \({\mathcal{R}}_{i1}\) in (16) that

$$\begin{aligned} 0&=\,2\sum \limits _{i=1}^{N}{\mathbb{\chi }}_{i}^{T}\left( t\right) {\mathcal{G}}_{i}\left[ -\dot{x}_{i}\left( t\right) +\bar{{\mathscr{A}}} _{i}(\mu _{i}){\bar{\mathcal{\xi }}}_{i}\left( t\right) +\frac{\bar{\tau } _{i}-\underline{\tau _{i}}+h_{i}}{2}B_{i}(\mu _{i})K_{i}(\mu _{i})\varpi _{di}\left( t\right) +B_{wi}(\mu _{i})w_{i}\left( t\right) \right] \nonumber \\&\quad +\,2\sum \limits _{i=1}^{N}{\mathbb{\chi }}_{i}^{T}\left( t\right) {\mathcal{G}}_{i}\sum \limits _{\begin{array}{c} k=1\\ k\ne i \end{array}}^{N}\bar{A}_{ik}(\mu _{i})x_{k}(t). \end{aligned}$$
(32)

Note that

$$2\bar{x}^{T}\bar{y}\le \kappa ^{-1}\bar{x}^{T}\bar{x}+\kappa \bar{y}^{T}\bar{y},$$
(33)

where \(\bar{x},\bar{y}\in {\mathfrak {R}}^{n}\) and scalar \(\kappa >0.\)

In addition, define \(\bar{A}_{ik}\ge \bar{A}_{ik}(\mu _{i})\), and using discrete Jensen’s inequality (Lemma 3), we also have

$$\begin{aligned}&\sum \limits _{i=1}^{N}\left\{ \left[ \sum \limits _{\begin{array}{c} k=1\\ k\ne i \end{array}}^{N}\bar{A}_{ik}(\mu _{i})x_{k}(t)\right] ^{T}\left[ \sum \limits _{\begin{array}{c} k=1\\ k\ne i \end{array}}^{N}\bar{A}_{ik}(\mu _{i})x_{k}(t)\right] \right\} \nonumber \\&\le \sum \limits _{i=1}^{N}\left\{ \left[ \sum \limits _{\begin{array}{c} k=1\\ k\ne i \end{array}}^{N}\bar{A}_{ki}x_{i}(t)\right] ^{T}\left[ \sum \limits _{\begin{array}{c} k=1\\ k\ne i \end{array}}^{N}\bar{A}_{ki}x_{i}(t)\right] \right\} \nonumber \\&=\sum \limits _{i=1}^{N}\left\{ \left[ \sum \limits _{\begin{array}{c} k=1\\ k\ne i \end{array}}^{N}\bar{A}_{ki}x_{i}(t)\right] ^{T}\left[ \sum \limits _{\begin{array}{c} k=1\\ k\ne i \end{array}}^{N}\bar{A}_{ki}x_{i}(t)\right] \right\} \nonumber \\&\le \sum \limits _{i=1}^{N}\left\{ \left( N-1\right) \sum \limits _{\begin{array}{c} k=1\\ k\ne i \end{array}}^{N}x_{i}^{T}(t)\bar{A}_{ki}^{T}\bar{A} _{ki}x_{i}(t)\right\} . \end{aligned}$$
(34)

Then, by introducing scalar parameters \(0<\varepsilon _{i}(\mu _{i} )\le \varepsilon _{0},\) where \(\varepsilon _{i}(\mu _{i}):=\sum \limits _{l=1} ^{r_{i}}\mu _{il}\varepsilon _{il},i\in {\mathcal{N}},\) and using relations (33) and (34), one has

$$\begin{aligned} 0&=2\sum \limits _{i=1}^{N}{\mathbb{\chi }}_{i}^{T}\left( t\right) {\mathcal{G}}_{i}\left[ -\dot{x}_{i}\left( t\right) +\bar{{\mathscr{A}}} _{i}(\mu ){\bar{\mathcal{\xi }}}_{i}\left( t\right) +\frac{\bar{\tau } _{i}-\underline{\tau _{i}}+h_{i}}{2}B_{i}(\mu _{i})K_{i}(\mu _{i})\varpi _{di}\left( t\right) +B_{wi}(\mu _{i})w_{i}\left( t\right) \right] \nonumber \\&\quad +2\sum \limits _{i=1}^{N}{\mathbb{\chi }}_{i}^{T}\left( t\right) {\mathcal{G}}_{i}\sum \limits _{\begin{array}{c} k=1\\ k\ne i \end{array}}^{N}\bar{A} _{ik}(\mu _{i})x_{k}(t)\nonumber \\&\quad \le 2\sum \limits _{i=1}^{N}{\mathbb{\chi }}_{i}^{T}\left( t\right) {\mathcal{G}}_{i}\left[ -\dot{x}_{i}\left( t\right) +\bar{\mathscr{A}} _{i}(\mu _{i}){\bar{\mathcal{\xi }}}_{i}\left( t\right) +\frac{\bar{\tau } _{i}-\underline{\tau _{i}}+h_{i}}{2}B_{i}(\mu _{i})K_{i}(\hat{\mu }_{i} )\varpi _{di}\left( t\right) +B_{wi}(\mu _{i})w_{i}\left( t\right) \right] \nonumber \\&\quad +\sum \limits _{i=1}^{N}\left\{ \varepsilon _{i}^{-1} (\mu _{i})\chi _{i}^{T}\left( t\right) {\mathcal{G}}_{i}{\mathcal{G}}_{i}^{T} \chi _{i}\left( t\right) +\varepsilon _{i}(\mu _{i})\left[ \sum \limits _{\begin{array}{c} k=1\\ k\ne i \end{array}}^{N}\bar{A}_{ik}(\mu _{i})x_{k}(t)\right] ^{T}\left[ \sum \limits _{\begin{array}{c} k=1\\ k\ne i \end{array}}^{N}\bar{A}_{ik}(\mu _{i})x_{k}(t)\right] \right\} \nonumber \\&\quad \le 2\sum \limits _{i=1}^{N}{\mathbb{\chi }}_{i}^{T}\left( t\right) {\mathcal{G}}_{i}\left[ -\dot{x}_{i}\left( t\right) +\bar{\mathscr{A}} _{i}(\mu _{i}){\bar{\mathcal{\xi }}}_{i}\left( t\right) +\frac{\bar{\tau } _{i}-\underline{\tau _{i}}+h_{i}}{2}B_{i}(\mu _{i})K_{i}(\mu _{i})\varpi _{di}\left( t\right) +B_{wi}(\mu _{i})w_{i}\left( t\right) \right] \nonumber \\&\quad +\sum \limits _{i=1}^{N}\left[ \varepsilon _{i}^{-1} (\mu _{i}){\mathbb{\chi }}_{i}^{T}\left( t\right) {\mathcal{G}}_{i}{\mathcal{G}} _{i}^{T}\chi _{i}\left( t\right) +\varepsilon _{0}\left( N-1\right) \sum \limits _{\begin{array}{c} k=1\\ k\ne i \end{array}}^{N}x_{i}^{T}(t)\bar{A}_{ki}^{T}\bar{A}_{ki}x_{i}(t)\right] . \end{aligned}$$
(35)

Let \(\bar{X}_{i}=X_{i}^{T}X_{i},i\in {\mathcal{N}},\) and consider the following index:

$$\begin{aligned} J(t)&=\sum \limits _{i=1}^{N}J_{i}(t)\nonumber \\&=\sum \limits _{i=1}^{N}\int _{0}^{\infty }\left\{ \xi _{di}^{T}\left( t\right) \bar{X}_{i}\xi _{di}\left( t\right) -\varpi _{di}^{T}\left( t\right) \bar{X}_{i}\varpi _{di}\left( t\right) +y_{i}^{T}(t)y_{i} (t)-\gamma ^{2}w_{i}^{T}\left( t\right) w_{i}\left( t\right) \right\} dt. \end{aligned}$$
(36)

Under zero initial conditions, it can be known that \(V_{i}(0)=0\) and \(V_{i}(\infty )\ge 0.\) Then, it follows from (14), (29)–(31), (35), and (36) that

$$\begin{aligned} J(t)&\le \sum \limits _{i=1}^{N}J_{i}(t)+V_{i}(\infty )-V_{i}(0)\nonumber \\&=\sum \limits _{i=1}^{N}\int _{0}^{\infty }\left\{ \dot{V}_{i}(t)+\xi _{di} ^{T}\left( t\right) \bar{X}_{i}\xi _{di}\left( t\right) -\varpi _{di} ^{T}\left( t\right) \bar{X}_{i}\varpi _{di}\left( t\right) +\,y_{i} ^{T}(t)y_{i}(t)-\gamma ^{2}w_{i}^{T}\left( t\right) w_{i}\left( t\right) \right\} dt\nonumber \\&\le \sum \limits _{i=1}^{N}\int _{0}^{\infty }{\mathbb{\chi }}_{i}^{T}\left( t\right) \left\{ \Theta _{i}+{\text {Sym}}\left\{ {\mathcal{G}}_{i}{\mathbb{A}} _{i}(\mu _{i})\right\} +\,\varepsilon _{i}^{-1}(\mu _{i}){\mathcal{G}} _{i}{\mathcal{G}}_{i}^{T}+{\mathbb{C}}_{i}^{T}(\mu _{i}){\mathbb{C}}_{i}(\mu _{i})\right\} \chi _{i}\left( t\right) dt, \end{aligned}$$
(37)

where \(\Theta _{i},{\mathbb{A}}_{i}(\mu _{i}),\) and \({\mathbb{C}}_{i}(\mu _{i})\) are defined in (22).

Using Schur complement to (21), it is easy to see that (21) implies \(J(t)<0\) and \(\sum \nolimits _{i=1}^{N}\dot{V}_{i}(t)<0,\) which means \(\left\| X{\mathbf {G}}X^{-1}\right\| _{\infty }<1.\) Then, using Lemma 1 and 4, it can be known that the closed-loop fuzzy control system (9) is asymptotically stable. Based on \(J(t)<0\), together with the consideration of (18), it yields \(\int _{0}^{\infty }{\tilde{y}}^{T}(t){\tilde{y}}(t)dt<\gamma ^{2}\int _{0}^{\infty }{\tilde{w}}^{T}(t){\tilde{w}}(t)dt\). The proof is thus completed.

3.3 Decentralized \({\mathscr{H}}_{\infty }\) Sampled-Data State-Feedback Controller Design

Here, we will address the decentralized \({\mathscr{H}}_{\infty }\) sampled-data state-feedback controller design for the large-scale T–S fuzzy system in (3). Based on the performance analysis result in Lemma 5, and by specifying matrix multipliers \({\mathcal{G}}_{i}\) and using some matrix transformation techniques, the nonlinear matrix inequalities are formulated into the linear ones, and the corresponding result is summarized in the following theorem.

Theorem 1

Consider the large-scale T–S fuzzy system in (3). Then, a decentralized sampled-data state-feedback fuzzy controller in the form of (8) exists, such that the closed-loop fuzzy control system (9) is asymptotically stable with an \({\mathscr{H}}_{\infty }\) disturbance attenuation level \(\gamma ,\) if there exist positive definite symmetric matrices \(\left\{ \bar{P} _{i1},\bar{P}_{i2},\bar{Q}_{i1},\bar{Q}_{i2},\bar{Z}_{i1},\bar{Z}_{i2} ,{\tilde{X}}_{i}\right\} \in {\mathfrak {R}}^{n_{xi}\times n_{xi}},\) matrices \(G_{i} \in {\mathfrak {R}}^{n_{xi}\times n_{xi}},\bar{K}_{il}\in {\mathfrak {R}}^{n_{ui}\times n_{xi}},\) and scalars \(0<\epsilon _{0}\le \epsilon _{il},l\in {\mathscr{L}}_{i},\) such that for all \(i\in {\mathcal{N}}\) the following LMIs hold:

$$\begin{aligned} \left[ \begin{array}{cc} \frac{\bar{P}_{i1}}{\underline{\tau _{i}}}+\bar{Z}_{i1} &{}\quad -\bar{Z}_{i1}\\ \star &{}\quad \bar{Q}_{i1}+\bar{Z}_{i1} \end{array} \right] >0, \end{aligned}$$
(38)
$$\begin{aligned} \left[ \begin{array}{cc} \frac{\bar{P}_{i2}}{\bar{\eta }_{i}}+\bar{Z}_{i2} &{}\quad -\bar{Z}_{i2}\\ \star &{}\quad \bar{Q}_{i2}+\bar{Z}_{i2} \end{array} \right] >0, \end{aligned}$$
(39)

and

$$\begin{aligned}&\Sigma _{ill}<0,1\le l\le r_{i}\end{aligned}$$
(40)
$$\begin{aligned}&\Sigma _{ilj}+\Sigma _{ijl}<0,1\le l<j\le r_{i} \end{aligned}$$
(41)

where

$$\begin{aligned} \left\{ \begin{array}{l} \Sigma _{ilj}=\left[ \begin{array}{cccc} -\epsilon _{0}{\left( N-1\right) ^{-1}{\mathscr{E}}} &{}\quad 0 &{}\quad {\mathbb{\bar{G} }}_{ki} &{}\quad 0\\ \star &{}\quad -{\mathbf {I}} &{}\quad {\mathbb{\bar{C}}}_{ilj} &{}\quad 0\\ \star &{}\quad \star &{}\quad {\tilde{\Theta }}_{i}+{\text {Sym}} \left\{ {\mathbb{\bar{E} }}\Pi _{ilj}\right\} &{}\quad \epsilon _{il}{\mathbb{\bar{E}}}\\ \star &{}\quad \star &{}\quad \star &{}\quad -\epsilon _{il}{\mathbf {I}} \end{array} \right] ,\\ {\mathbb{\bar{G}}}_{ki}=\left[ \begin{array}{cccccc} 0 &{}\quad {\bar{\mathcal{A}}}_{ki}G_{i} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \end{array} \right] ,{\mathbb{\bar{E}}=}\left[ \begin{array}{ccc} {\mathbf {I}} &{}\quad {\mathbf {I}} &{}\quad 0_{n_{xi}\times \left( 3n_{xi}+n_{wi}\right) } \end{array} \right] ^{T},\\ {\mathbb{\bar{C}}}_{ilj}=\left[ \begin{array}{cccccc} 0 &{} C_{il}G_{i} &{} \frac{1}{2}D_{il}\bar{K}_{ij} &{} \frac{1}{2}D_{il}\bar{K}_{ij} &{} \frac{\bar{\tau }_{i}-\underline{\tau _{i}}+h_{i}}{2}D_{il}\bar{K}_{ij} &{} D_{wil} \end{array} \right] ,\\ {\tilde{\Theta }}_{i}=\left[ \begin{array}{cccccc} {\tilde{\Theta }}_{i(1)} &{}\quad \bar{P}_{i1}+\bar{P}_{i2} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ \star &{}\quad {\tilde{\Theta }}_{i(2)} &{}\quad \bar{Z}_{i1} &{}\quad \bar{Z}_{i2} &{}\quad 0 &{}\quad 0\\ \star &{}\quad \star &{}\quad {\tilde{\Theta }}_{i(3)} &{}\quad 0 &{}\quad 0 &{}\quad 0\\ \star &{}\quad \star &{}\quad \star &{}\quad -\bar{Q}_{i2}-\bar{Z}_{i2} &{}\quad 0 &{}\quad 0\\ \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad -{\tilde{X}}_{i} &{}\quad 0\\ \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad \star &{}\quad -\gamma ^{2}{\mathbf {I}} \end{array} \right] ,\\ {\tilde{\Theta }}_{i(1)}=\underline{\tau _{i}^{2}}\bar{Z}_{i1}+\bar{\eta }_{i} ^{2}\bar{Z}_{i2}+{\tilde{X}}_{i},{\tilde{\Theta }}_{i(2)}=\bar{Q}_{i1}+\bar{Q} _{i2}-\bar{Z}_{i1}-\bar{Z}_{i2},{\tilde{\Theta }}_{i(3)}=-\bar{Q}_{i1}-\bar{Z}_{i1},\\ \Pi _{ilj}=\left[ \begin{array}{cccccc} -G_{i} &{} A_{il}G_{i} &{} \frac{1}{2}B_{il}\bar{K}_{ij} &{} \frac{1}{2}B_{il} \bar{K}_{ij} &{} \frac{\bar{\tau }_{i}-\underline{\tau _{i}}+h_{i}}{2}B_{il} \bar{K}_{ij} &{} B_{wil} \end{array} \right] . \end{array} \right. \end{aligned}$$
(42)

Furthermore, a decentralized sampled-data state-feedback fuzzy controller in the form of (8) is given by

$$\begin{aligned} K_{il}=\bar{K}_{il}G_{i}^{-1},l\in {\mathscr{L}}_{i},i\in {\mathcal{N}}. \end{aligned}$$
(43)

Proof

Define \(\epsilon _{i}(\mu _{i})=\varepsilon _{i}^{-1}(\mu _{i})\) and \(\epsilon _{0}=\varepsilon _{0}^{-1},\) the inequality \(0<\varepsilon _{i} (\mu _{i})\le \varepsilon _{0}\) implies \(0<\epsilon _{0}\le \epsilon _{i}(\mu _{i}).\) Then, by applying Schur complement, the inequality in (21) can be rewritten as

$$\begin{aligned} \left[ \begin{array}{cccc} -\epsilon _{0}\left( N-1\right) ^{-1}{\mathscr{E}} &{} 0 &{} {\bar{\mathcal{A}}} _{ki}{\mathcal{E}} &{} 0\\ \star &{} -{\mathbf {I}} &{} {\mathbb{C}}_{i}(\mu _{i}) &{} 0\\ \star &{} \star &{} \bar{\Theta }_{i}+{\text {Sym}}\left\{ {\mathcal{G}}_{i} {\mathbb{A}}_{i}(\mu _{i})\right\} &{} \epsilon _{i}(\mu _{i}){\mathcal{G}}_{i}\\ \star &{} \star &{} \star &{} -\epsilon _{i}(\mu _{i}){\mathbf {I}} \end{array} \right] <0, \end{aligned}$$
(44)

where

$$\begin{aligned} \left\{ \begin{array}{l} \bar{\Theta }_{i}=\left[ \begin{array}{cccccc} \Theta _{i(1)} &{} P_{i} &{} 0 &{} 0 &{} 0 &{} 0\\ \star &{} \bar{\Theta }_{i(2)} &{} Z_{i1} &{} Z_{i2} &{} 0 &{} 0\\ \star &{} \star &{} \Theta _{i(3)} &{} 0 &{} 0 &{} 0\\ \star &{} \star &{} \star &{} -Q_{i2}-Z_{i2} &{} 0 &{} 0\\ \star &{} \star &{} \star &{} \star &{} -\bar{X}_{i} &{} 0\\ \star &{} \star &{} \star &{} \star &{} \star &{} -\gamma ^{2}{\mathbf {I}} \end{array} \right] \\ \Theta _{i(1)}=\underline{\tau _{i}^{2}}Z_{i1}+\bar{\eta }_{i}^{2}Z_{i2}+\bar{X}_{i},\bar{\Theta }_{i(2)}=Q_{i1}+Q_{i2}-Z_{i1}-Z_{i2}\\ \Theta _{i(3)}=-Q_{i1}-Z_{i1},{\mathcal{E=}}\left[ \begin{array}{cccccc} 0 &{} {\mathbf {I}} &{} 0 &{} 0 &{} 0 &{} 0 \end{array} \right] \\ {\bar{\mathcal{A}}}_{ki}=\underset{N-1}{\underbrace{\left[ \begin{array}{ccccc} \bar{A}_{1i}^{T} &{} \cdots &{} \bar{A}_{ki,k\ne i}^{T} &{} \cdots &{} \bar{A} _{Ni}^{T} \end{array} \right] }}^{T},{\mathscr{E}}{\text { }}{\mathbb{=}}{\text { }}\underset{N-1}{{\text {diag}}\underbrace{\left\{ \begin{array}{ccc} {\mathbf {I}}_{n_{xi}}&\cdots&{\mathbf{I}}_{n_{xi}} \end{array} \right\} }}. \end{array} \right. \end{aligned}$$
(45)

In addition, the conditions in (40) and (41) imply that

$$\begin{aligned} \underline{\tau _{i}^{2}}\bar{Z}_{i1}+\bar{\eta }_{i}^{2}\bar{Z}_{i2}+{\tilde{X}}_{i}-{\text {Sym}}\left\{ G_{i}\right\} <0,\quad i\in {\mathcal{N}}. \end{aligned}$$
(46)

Due to the fact that \(\underline{\tau _{i}^{2}}\bar{Z}_{i1}+\bar{\eta }_{i} ^{2}\bar{Z}_{i2}+{\tilde{X}}_{i}>0,\) we have \(G_{i}+G_{i}^{T}>0,\) which means that the matrices \(G_{i}\) are nonsingular. Now, we specify matrix multipliers \({\mathcal{G}}_{i}\) as

$$\begin{aligned} {\mathcal{G}}_{i}=\left[ \begin{array}{ccc} G_{i}^{-1}&G_{i}^{-1}&0_{n_{xi}\times \left( 3n_{xi}+n_{wi}\right) } \end{array} \right] ^{T},\quad i\in {\mathcal{N}}. \end{aligned}$$
(47)

Substitute matrix multipliers \({\mathcal{G}}_{i}\) defined in (47) into (44) and define

$$\begin{aligned} \left\{ \begin{array}{l} \Gamma _{1}:={\text {diag}}\left\{ \begin{array}{ccccccccc} {\mathscr{E}} &{} {\mathbf {I}} &{} G_{i}^{T} &{} G_{i}^{T} &{} G_{i}^{T} &{} G_{i}^{T} &{} G_{i}^{T} &{} {\mathbf {I}} &{} {\mathbf {I}} \end{array} \right\} ,\\ \bar{P}_{i1}=G_{i}^{T}P_{i1}G_{i},\bar{P}_{i2}=G_{i}^{T}P_{i2}G_{i},\bar{Q}_{i1}=G_{i}^{T}Q_{i1}G_{i},\bar{Q}_{i2}=G_{i}^{T}Q_{i2}G_{i},\\ \bar{Z}_{i1}=G_{i}^{T}Z_{i1}G_{i},\bar{Z}_{i2}=G_{i}^{T}Z_{i2}G_{i},{\tilde{X}}_{i}=G_{i}^{T}\bar{X}_{i}G_{i}. \end{array} \right. \end{aligned}$$
(48)

Then, by performing the congruence transformation to (44) by \(\Gamma _{1}\), it yields

$$\begin{aligned} \left[ \begin{array}{cccc} -\epsilon _{0}{\left( N-1\right) ^{-1}{\mathscr{E}}} &{}\quad 0 &{}\quad {\mathbb{\bar{G} }}_{ki} &{}\quad 0\\ \star &{}\quad -{\mathbf {I}} &{}\quad {\mathbb{\bar{C}}}_{i}(\mu _{i}) &{}\quad 0\\ \star &{}\quad \star &{}\quad {\tilde{\Theta }}_{i}+{\text {Sym}}\left\{ {\mathbb{\bar{E}}}\Pi _{i}(\mu _{i})\right\} &{}\quad \epsilon _{i}(\mu _{i}){\mathbb{\bar{E}}}\\ \star &{}\quad \star &{}\quad \star &{}\quad -\epsilon _{i}(\mu _{i}){\mathbf {I}}_{n_{xi}} \end{array} \right] <0, \end{aligned}$$
(49)

where \({\tilde{\Theta }}_{i},{\mathbb{\bar{E}}},\) and \({\mathbb{\bar{G}}}_{ki}\) are defined in (42), and

$$\begin{aligned} \left\{ \begin{array}{l} {\mathbb{\bar{C}}}_{i}(\mu _{i})=\left[ \begin{array}{cccc} 0 &{} C_{i}(\mu _{i})G_{i} &{} \frac{1}{2}D_{i}(\mu _{i})K_{i}(\mu _{i})G_{i} &{} \frac{1}{2}D_{i}(\mu _{i})K_{i}(\mu _{i})G_{i} \end{array} \right. \\ \left. \begin{array}{cc} \frac{\bar{\tau }_{i}-\underline{\tau _{i}}+h_{i}}{2}D_{i}(\mu _{i})K_{i}(\mu _{i})G_{i} &{} D_{wi}(\mu _{i}) \end{array} \right] ,\\ \Pi _{i}(\mu _{i})=\left[ \begin{array}{cccc} -G_{i} &{} A_{i}(\mu _{i})G_{i} &{} \frac{1}{2}B_{i}(\mu _{i})K_{i}(\mu _{i})G_{i} &{} \frac{1}{2}B_{i}(\mu _{i})K_{i}(\mu _{i})G_{i} \end{array} \right. \\ \left. \begin{array}{cc} \frac{\bar{\tau }_{i}-\underline{\tau _{i}}+h_{i}}{2}B_{i}(\mu _{i})K_{i}(\mu _{i})G_{i} &{} B_{wi}(\mu _{i}) \end{array} \right] . \end{array} \right. \end{aligned}$$
(50)

It is noted that the matrices \(G_{i}\) can be absorbed by the controller gain variable \(K_{i}(\mu _{i})\) by introducing

$$\begin{aligned} \bar{K}_{i}(\mu _{i})=K_{i}(\mu _{i})G_{i}. \end{aligned}$$
(51)

By extracting the fuzzy basis functions in (49) and taking into consideration the relations of (48) and (51), the inequality in (49) can be rewritten as

$$\begin{aligned} \sum \limits _{l=1}^{r_{i}}\mu _{ill}^{2}\Sigma _{ill}+\sum \limits _{l=1}^{r_{i} -1}\sum \limits _{j=l+1}^{r_{i}}\mu _{il}\mu _{ij}\left[ \Sigma _{ilj} +\Sigma _{ijl}\right] <0, \end{aligned}$$
(52)

where \(\Sigma _{ilj}\) is defined in (42).

In addition, define \(\Gamma _{2}:=\)diag\(\left\{ \begin{array}{cc} G_{i}^{T}&G_{i}^{T} \end{array} \right\} ,\) and by performing the congruence transformation to (19) and (20) by \(\Gamma _{2}\), respectively, (38) and (39) can be directly obtained. The proof is thus completed. \(\square\)

4 Simulation Examples

In this section, two examples will be presented to demonstrate the effectiveness of the decentralized \({\mathscr{H}}_{\infty }\) sampled-data state-feedback controller design method proposed in this paper.

Example 1

Consider a continuous-time large-scale T–S fuzzy system in the form of (1) with two interconnected subsystems as follows:

Plant Rule \({\mathscr{R}}_{i}^{l}:\) IF \(x_{i1}(t)\) is \({\mathscr{F}}_{i1}^{l},\) THEN

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}_{i}(t)=A_{il}x_{i}\left( t\right) +B_{il}u_{i}(t)+\sum \limits _{\begin{array}{c} k=1\\ k\ne i \end{array}}^{N}\bar{A}_{ik}x_{k}(t)+B_{wil}w_{i}\left( t\right) \\ y_{i}(t)=C_{il}x_{i}(t)+D_{il}u_{i}(t)+D_{wil}w_{i}\left( t\right) ,l=\left\{ 1,2\right\} ,i=\left\{ 1,2\right\} \end{array} \right., \end{aligned}$$

where

for the first subsystem, and

for the second subsystem.

The objective is to design a decentralized sampled-data state-feedback controller in the form of (8) such that the closed-loop fuzzy control system in (9) is asymptotically stable with an \({\mathscr{H}}_{\infty }\) disturbance attenuation level \(\gamma .\) Assume that the lower and upper bounds of transformed time delay are \(0.05\le \tau _{i}\left( t\right) \le 0.50,\) and the sampled period is \(h_{i}=0.05.\) It has been found that there are no feasible solutions based on the direct Lyapunov design method combined with some bounding techniques in [15]. It is noted that the choices of these bounding techniques are the main sources of conservatism. In this paper, based on a two-term approximation method, we propose an equivalent model transformation, which formulates the decentralized \({\mathscr{H}}_{\infty }\) sampled-data control problem in the context of input–output (IO) stability. Based on a Lyapunov–Krasovskii functional (LKF) that all Lyapunov matrices are not required to be positive definite, and combined with the scaled small gain (SSG) theorem, the decentralized \({\mathscr{H}}_{\infty }\) sampled-data control problem is solved for the considered system by linear matrix inequalities (LMIs). In the proposed method, no useful terms are neglected. It is hence expected that the obtained results will be less conservative.

Now, by applying Theorem 1 with the positive matrices \(\bar{Q}_{i1},\bar{Q}_{i2},\) we indeed obtain the minimum \({\mathscr{H}}_{\infty }\) performance \(\gamma _{\min }=2.0639\). By applying Theorem 1 with (38) and (39), we obtain a more better \({\mathscr{H}}_{\infty }\) performance \(\gamma _{\min }=1.6818\), and the corresponding controller gains are

$$\begin{aligned} \left[ \begin{array}{ll} K_{11}&K_{12} \end{array} \right] =\left[ \begin{array}{llll} -1.1889&\quad -0.5319&\quad -1.0707&\quad -0.4102 \end{array} \right] \end{aligned}$$

for the first subsystem, and

$$\begin{aligned} \left[ \begin{array}{ll} K_{21}&K_{22} \end{array} \right] =\left[ \begin{array}{llll} -1.0456&\quad -0.3323&\quad -0.9565&\quad -0.2964 \end{array} \right] \end{aligned}$$

for the second subsystem.

Fig. 1
figure 1

Membership functions

Full size image

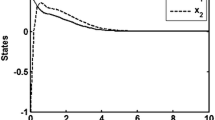
The normalized membership functions are shown in Fig. 1, where \(r_{i}=3\). Given the initial conditions \(x_{1}(0)=[1,-2]^{T},x_{2}(0)=[2,-1]^{T},\) Figs. 2 and 3 show the state responses for the subsystems 1 and 2, respectively. Then, we consider zero initial conditions and assume that the external disturbances are \(w_{1}(t)=0.4\)e\(^{-0.2t}\sin (t)\) and \(w_{2}(t)=0.6\)e\(^{-0.4t}\cos (t),\) it can be observed in Fig. 4 that the \({\mathscr{H}}_{\infty }\) performance is satisfactory, thus showing the effectiveness of the decentralized \({\mathscr{H}}_{\infty }\) sampled-data state-feedback controller design method.

Fig. 2
figure 2

State responses of subsystem 1

Full size image
Fig. 3
figure 3

State responses of subsystem 2

Full size image
Fig. 4
figure 4

Response of \({\mathscr{H}}_{\infty }\) performance

Full size image

Example 2

Consider a double-inverted pendulum system connected by a spring. The system is composed of two interconnected subsystems. The modified equations of the motion of the interconnected pendulum are given by [17]

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}_{i1}=x_{i2}\\ \dot{x}_{i2}=\frac{1}{J_{i}}u_{i}-\frac{kr^{2}}{4J_{i}}x_{i1}+\left[ \frac{m_{i}gr}{J_{i}}-\frac{kr^{2}}{4J_{i}}x_{i2}\right] \sin (x_{i1} )+\frac{1}{J_{i}}x_{i2}+\sum \limits _{\begin{array}{c} k=1\\ k\ne i \end{array}}^{2}\frac{kr^{2} }{16J_{k}}x_{k1},i=\{1,2\}, \end{array} \right. \end{aligned}$$

where \(x_{i1}\) denotes the angle of the i-th pendulum from the vertical and \(x_{i2}\) is the angular velocity of the i-th pendulum.

In this simulation, the masses of two pendulums are chosen as \(m_{1}=2\) kg and \(m_{2}=2.5\) kg;  the moments of inertia are \(J_{1}=2\) kg and \(J_{2}=2.5\) kg; the constant of the connecting torsional spring is \(k=8\) N\(\cdot\)m/rad; the length of the pendulum is \(r=1\) m; and the gravity constant is \(g=9.8\) m/s\(^{2}\). We choose two local models, i.e., by linearizing the interconnected pendulum around the origin and \(x_{i1}=\left( \pm 88^{\circ },0\right)\), the continuous-time interconnected T–S fuzzy system can be given as follows:

Plant Rule \({\mathscr{R}}_{i}^{l}\): IF \(x_{i1}(t)\) is \({\mathscr{F}}_{i}^{l}\), THEN

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}_{i}(t)=A_{il}x_{i}\left( t\right) +B_{il}u_{i}(t)+\sum \limits _{\begin{array}{c} k=1\\ k\ne i \end{array}}^{N}\bar{A}_{ik}x_{k}(t)+B_{wil}w_{i}\left( t\right) \\ y_{i}(t)=C_{il}x_{i}(t)+D_{i}(\mu _{i})u_{i}(t),l=\left\{ 1,2\right\} ,i=\left\{ 1,2\right\} \end{array} \right., \end{aligned}$$

where

for the first subsystem, and

for the second subsystem.

The normalized membership functions are shown in Fig. 1, where \(r_{i}=88^{\circ }\). In addition, we assume that the lower and upper bounds of the transformed time delay are \(0.01\le \tau _{i}\left( t\right) \le 0.23,\) and the sampled period is \(h_{i}=0.01.\) The objective is to design a decentralized sampled-data state-feedback controller in the form of (8) such that the closed-loop fuzzy control system in (9) is asymptotically stable with an \({\mathscr{H}}_{\infty }\) disturbance attenuation level \(\gamma .\) It has also been found that there are no feasible solutions based on the direct Lyapunov method proposed in [15]. Nevertheless, by applying Theorem 1 with the positive matrices \(\bar{Q}_{i1},\bar{Q}_{i2},\) we indeed obtain the minimum \({\mathscr{H}}_{\infty }\) performance \(\gamma _{\min }=4.6456\). By applying Theorem 1 with (38) and (39), we obtain a much better \({\mathscr{H}}_{\infty }\) performance \(\gamma _{\min }=3.5987\), and the corresponding controller gains are

$$\begin{aligned} \left[ \begin{array}{ll} K_{11}&\quad K_{12} \end{array} \right] =\left[ \begin{array}{llll} -2.1382&\quad -6.4694&\quad -15.5946&\quad -5.2015 \end{array} \right] \end{aligned}$$

for the first subsystem, and

$$\begin{aligned} \left[ \begin{array}{ll} K_{21}&\quad K_{22} \end{array} \right] =\left[ \begin{array}{llll} -3.4855&\quad -8.0952&\quad -20.2542&\quad -6.9602 \end{array} \right] \end{aligned}$$

for the second subsystem.

Given the initial conditions \(x_{1}(0)=[1.3,0]^{T},x_{2}(0)=[0.8,0]^{T},\) Figs. 5 and 6 show the state responses for the subsystems 1 and 2, respectively. Then, we consider zero initial conditions and assume that the external disturbances are \(w_{1}(t)=0.8\)e\(^{-0.2t}\sin (t)\) and \(w_{2}(t)=0.6\)e\(^{-0.2t}\cos (t),\) it can be observed in Fig. 7 that the \({\mathscr{H}}_{\infty }\) performance is satisfactory, thus showing the effectiveness of the decentralized \({\mathscr{H}}_{\infty }\) sampled-data state-feedback controller design method.

Fig. 5
figure 5

State responses of subsystem 1

Full size image
Fig. 6
figure 6

State responses of subsystem 2

Full size image
Fig. 7
figure 7

Response of \({\mathscr{H}}_{\infty }\) performance

Full size image

5 Conclusions

This paper investigated the decentralized \({\mathscr{H}}_{\infty }\) sampled-data control problem for a class of continuous-time large-scale networked T–S fuzzy systems. A new model transformation based on the input delay and two-term approximation approaches was proposed, such that the closed-loop sampled-data fuzzy control problem was reformulated into the IO stability framework. Based on an LKF combined with the SSG theorem, sufficient conditions for solving the decentralized \({\mathscr{H}}_{\infty }\) sampled-data control problem of the large-scale networked T–S fuzzy system were derived. It has been shown that the closed-loop fuzzy control system is asymptotically stable with an \({\mathscr{H}}_{\infty }\) performance and the controller gains were obtained by solving a set of LMIs. Two numerical examples were given to demonstrate the effectiveness of the proposed method. It is worth mentioning that in this paper the \({\mathscr{H}}_{\infty }\) sampled-data controller is decentralized. One interesting future research topic is the extension of the proposed method to the case of distributed \({\mathscr{H}}_{\infty }\) sampled-data controller.